Introducción
En esta entrada hablaremos acerca de cotas inferiores e ínfimos. Estos nuevos conceptos nos permitirán establecer intuitivamente qué quiere decir que un conjunto esté «limitado» una vez que hemos dado un orden.
Cotas inferiores
Para comenzar definiremos qué es una cota inferior. Notaremos que este concepto es muy parecido al de mínimo, sin embargo una cota inferior podría no ser elemento de $B$ un subconjunto de $A$. Veamos la definición.
Definición. Sea $(A, \leq)$ un orden parcial y sea $B\subseteq A$. Decimos que $a\in A$ es una cota inferior de $B$ si $a\leq x$ para toda $x\in B$. Si $B$ tiene por lo menos una cota inferior, diremos que $B$ está acotado inferiormente.
Ejemplo.
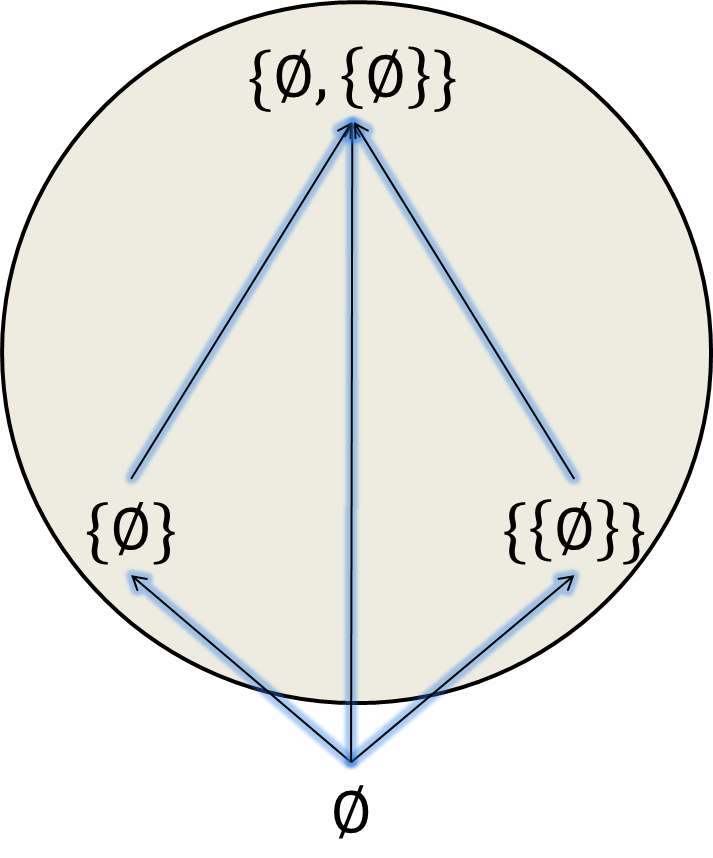
Sea $A=\set{\emptyset, \set{\emptyset}, \set{\emptyset, \set{\emptyset}}}$ y consideremos al conjunto parcialmente ordenado $(A, \subseteq)$. Sea $B= \set{\set{\emptyset}, \set{\emptyset, \set{\emptyset}}}\subseteq A$, tenemos que $\emptyset\in A$ es una cota inferior de $B$ pues $\emptyset\subseteq x$ para todo $x\in B$, como se muestra en el siguiente diagrama:
Sin embargo, podemos notar que $\emptyset\notin B$, por lo que para ser cota inferior no es necesario ser elemento de $B$, solo de $A$. Por otro lado, $\set{\emptyset}\in B$ también es una cota inferior de $B$ pues para cada $x\in B$, $\set{\emptyset}\subseteq x$. Más aún, $\set{\emptyset}$ es el elemento mínimo de $B$.
$\square$
El ejemplo anterior sugiere que la propiedad de ser mínimo implica ser cota inferior, pero no es válido el recíproco.
En este último ejemplo es posible notar que la cota inferior en un conjunto puede no ser única, y entonces podemos pensar en el conjunto que tenga a todas las cotas inferiores. Esta idea junto con el concepto de máximo motiva el concepto de ínfimo.
Ínfimos
Definición. Sea $(A, \leq)$ un orden parcial y sea $B\subseteq A$. Decimos que $a\in A$ es ínfimo de $B$ si es el elemento máximo del conjunto de todas las cotas inferiores de $B$. Lo denotaremos por $\inf(B)$.
Ejemplo.
Retomando el ejemplo anterior, si consideramos al conjunto de todas las cotas inferiores de $B$, es decir, $\set{\emptyset, \set{\emptyset}}$ tenemos que el ínfimo es $\set{\emptyset}$ pues respecto al orden de $A$, $\emptyset\subseteq \set{\emptyset}$ y por lo tanto, $\set{\emptyset}$ es el máximo de las cotas inferiores de $B$.
$\square$
Teorema. Sea $(A, \leq)$ un orden parcial y $B\subseteq A$ un conjunto no vacío. Si $B$ tiene ínfimo en el orden $\leq$, entonces es único.
Demostración.
Sea $(A,\leq)$ un orden parcial y $B\subseteq A$ no vacío. Supongamos que $B$ tiene ínfimo, es decir, que existe $a\in A$ de tal forma que $a\leq x$ para toda $x\in B$ y, si $b\in A$ es tal que $b\leq x$ para toda $x\in B$, entonces, $b\leq a$.
Supongamos que $a_1,a_2\in A$ son ínfimos de $B$. Veamos que $a_1=a_2$.
Como $a_1$ es ínfimo $B$, en particular se tiene que $a_1\leq x$ para toda $x\in B$. Luego, como $a_2$ es ínfimo de $B$ se sigue por definición que $a_1\leq a_2$. De manera análoga, como $a_2$ es ínfimo de $B$, en particular se tiene que $a_2\leq x$ para toda $x\in B$ y así, como $a_1$ es ínfimo de $B$ se sigue por definición que $a_2\leq a_1$.
Tenemos entonces que $a_1\leq a_2$ y $a_2\leq a_1$, de donde se sigue que $a_1=a_2$, lo cual demuestra la unicidad del ínfimo.
$\square$
Teorema. Sea $(A, \leq)$ un orden parcial y $B\subseteq A$ un conjunto no vacío. Si $B$ tiene un elemento mínimo $b$, entonces $b$ es el ínfimo de $B$.
Demostración.
Sea $(A, \leq)$ un orden parcial y $B\subseteq A$ un conjunto no vacío. Luego, si $b\in B$ es el elemento mínimo de $B$, entonces para cualquier $x\in B$, $b\leq x$.
Sea $C$ el conjunto de todas las cotas inferiores de $B$. Veamos que $b\in C$ y que $b=\max(C)$. Dado que $b\leq x$ para todo $x\in B$, $b$ es cota inferior de $B$ y, por tanto, $b\in C$. Luego, si $c\in C$ es cualquier elemento, entonces $c$ es cota inferior de $B$, es decir, $c\leq x$ para cualquier $x\in B$. En particular, como $b\in B$ se tiene que $c\leq b$. Esto muestra que $b=\max(C)$.
Por lo tanto, $b=\inf(B)$.
$\square$
Aún cuando ser mínimo implica ser ínfimo, no siempre va a ocurrir que el ínfimo de un conjunto sea mínimo, como ocurre en el siguiente ejemplo.
Ejemplo.
Sea $A=\set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$ y consideremos al conjunto parcialmente ordenado $(A, \subseteq)$. Sea $B= \set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}\subseteq A$. Tenemos que $\emptyset \in A$ es una cota inferior de $B$ pues $\emptyset\leq x$ para todo $x\in B$, como se muestra en el siguiente diagrama:
Sin embargo, $B$ no tiene mínimo pues no existe $x\in B$ tal que $x\leq y$ para todo $y\in B$. En efecto, si existiera tal $x$ tendría que ser simultáneamente subconjunto de $\set{\emptyset}$ y de $\set{\set{\emptyset}}$. Pero el único subconjunto que comparten estos conjuntos es $\emptyset$, que no está en $B$.
$\square$
Tarea moral
La siguiente lista de ejercicios te ayudará a reforzar el contenido de esta entrada y de la entrada anterior.
- Sean $(A, \leq)$ un orden parcial y $B\subseteq A$ un conjunto no vacío. Demuestra que si $b$ es ínfimo y $b\in B$, entonces $b$ es mínimo de $B$.
- Sean $(A, \leq)$ un orden parcial y $B,C\subseteq A$ no vacíos. Si $B$ y $C$ tienen ínfimo y $C\subseteq B$, demuestra que $inf (B)\leq inf (C)$.
- Exhibe un conjunto que esté acotado inferiormente pero que no tenga ínfimo.
- Da un ejemplo de un conjunto parcialmente ordenado $(A,\leq)$ en el cual se cumpla que el conjunto $\emptyset$ tiene ínfimo.
- Escribe las definiciones de cota inferior e ínfimo para un orden parcial estricto.
Más adelante…
La siguiente entrada estará dedicada a cotas superiores y supremos. Con esto concluiremos la sección de acotar conjuntos ordenados.
Entradas relacionadas
- Ir a Teoría de los Conjuntos I
- Entrada anterior: Teoría de los Conjuntos I: Mínimos, máximos, minimales y maximales
- Siguiente entrada: Teoría de los Conjuntos I: Cotas superiores y supremos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»