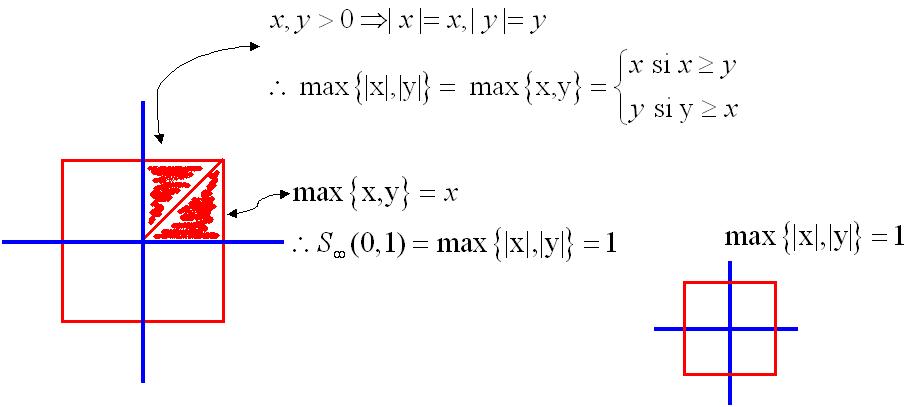Introducción.

La Topología es un área de las matemáticas que se interesa por conceptos como proximidad, continuidad, conexidad, compacidad, y muchos otros mas. Para abordarlos, es necesario establecer un cierto tipo de conjuntos (que en Topología se les conoce como los conjuntos abiertos).
$\fbox{Bola abierta}$
La bola abierta con centro en $\bar{x}_0$ y radio $r>0$, es el conjunto:
$$B(\bar{x}_0,r)=\{\bar{x}\in\mathbb{R}^n~|~\|\bar{x}-\bar{x}_0\|<r\}$$
$\fbox{Bola Cerrada}$
La bola cerrada con centro $\bar{x}_0$ y radio $r\geq
0$ es el conjunto:
$$\bar{B}(\bar{x}_0,r)=\{\bar{x}\in\mathbb{R}^n~|~\|\bar{x}-\bar{x}_0\|\leq r\}$$
$\fbox{Esfera}$
La esfera con centro $\bar{x}_0$ y radio $r\geq 0$ es el conjunto:
$$S(\bar{x}_0,r)=\{\bar{x}\in\mathbb{R}^n~|~\|\bar{x}-\bar{x}_0\|=r\}$$
Observemos que para la bola abierta $r>0$ estrictamente, mientras que la bola cerrada y la esfera pueden tener radio cero. En este último caso ambas se reducen a un punto:

\[
\bar{B}(\bar{x}_0,0)={\bar{x}_0}
\]

\[
S(\bar{x}_0,0)={\bar{x}_0}~~ \blacksquare
\]
Los conjuntos $B(\overline{x}_0,r)$, $\bar{B}(\overline{x}_0,r)$ y $S(\bar{x}_0,r)$ son subconjuntos de $\mathbb{R}^n$ y su aspecto geométrico depende de la métrica con la cual se midan las distancias.
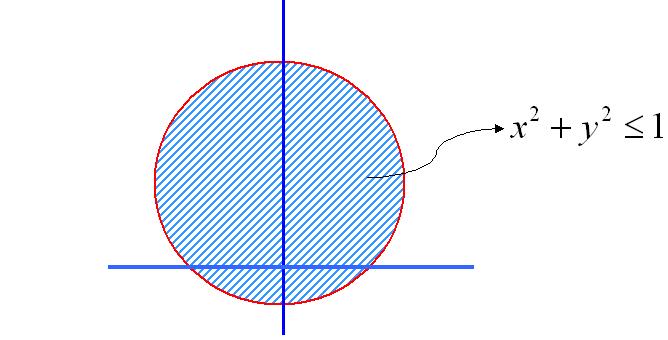
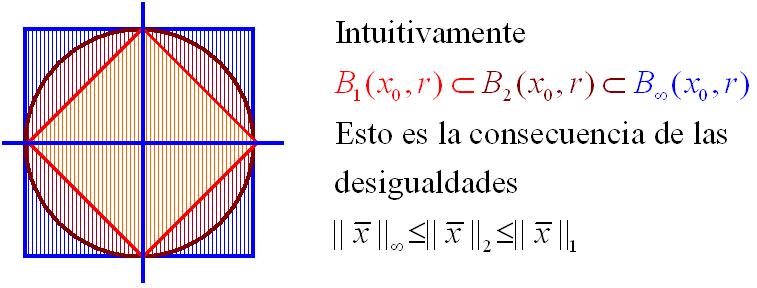
Ejemplo. \begin{align*} \overline{B}_2(0,1)&=\{\bar{x}\in\mathbb{R}^2\ |\ \|\bar{x}\|_2\leq1\} \\ &=\{\bar{x}\in\mathbb{R}^2|\sqrt{x^2+y^2}\ \leq1\} \\ &=\{(x,y)\in\mathbb{R}^2\ |\ x^2+y^2\leq1\} \end{align*}
Geométricamente

La periferia de este disco es el circulo que tiene por ecuación
$x^2+y^2=1$, que corresponde a la esfera $S_2(0,1)=\{\bar{x}\in \mathbb{R}^2\ |\
\|\bar{x}\|_2=1\}$.$~ \blacksquare$

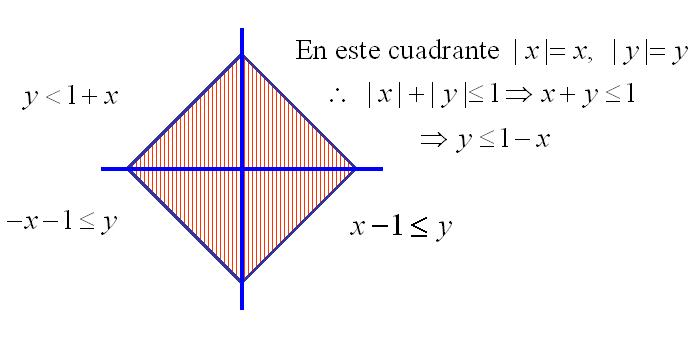
Ejemplo. Sea ahora la bola cerrada
\begin{align*} \bar{B}_2(0,1)&=\{\overline{x}\in\mathbb{R}^{2}~|~\|\bar{x}\|\leq1\} \\ &=\{(x,y)\in\mathbb{R}^2\ |\ |x|+|y|\leq1\} \end{align*}
Geométricamente

Para $S_1(0,1)=\{\bar{x}\in\mathbb{R}^2\ |\ |\bar{x}|=1\}$

Para $\overline{B}_{\infty}(0,1)=\{\bar{x}\in\mathbb{R}^2\ |\ \|\bar{x}\|_{\infty}\leq1\}$ = $\{(x,y)\in\mathbb{R}^2\ |\ \max\{|x|,|y|\}\leq1\}$

tenemos entonces que

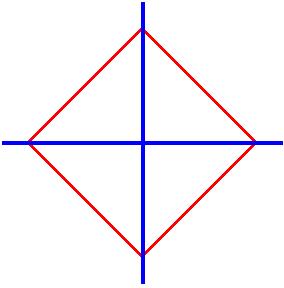
Las figuras anteriores muestran la situación geométrica, entre las bolas cerradas $\overline{B}_{1}(\overline{0},1),~\overline{B}_{2}(\overline{0},1),~\overline{B}_{\infty}(\overline{0},1)$ en forma explicita se escriben:
\[
\max\{|x_1|,\cdots,|x_n|\}\leq
\sqrt{x_1^2+\cdots+x_n^2}\ \leq
|x_1|+\cdots+|x_n|
\]
Las contenciones tanto para las bolas abiertas, como para las bolas
cerradas se siguen de las desigualdades

\[
\|\bar{x}-x_0\|_{\infty}\leq \|\bar{x}-\bar{x}_0\|_2\leq
\|\bar{x}-x_0\|_1
\]
Pues por ejemplo si $\bar{x}\in B_2(\bar{x}0,r)$ entonces $\|\bar{x}-\bar{x}_0\|_2<r$ luego $\|\bar{x}-\overline{x}_0\|_{\infty}<r$

$\therefore~~~\|\bar{x}-\bar{x}_0\|_{\infty}<r$ es decir $\overline{x}\subset
B_{\infty}(x_0,r)$ $\therefore$ $B_2(\bar{x}0,r)\subset B_{\infty}(\bar{x}_0,r)$

Si $\overline{x}\in B_1(\bar{x}_0,r)$ entonces $\|\bar{x}-\bar{x}_0\|_1<r$ luego $\|x-\bar{x}_0\|_2\leq \|\bar{x}-\bar{x}_0\|_1<r$ $\therefore$
$\|\overline{x}-\bar{x}_0\|_2<r$ $\therefore$ $\overline{x}\in B_2(x_0,r)$ $\therefore$ $B_1(\bar{x}_0,r)\subset B_2(x_0,r)$
Para las esferas no hay alguna relación similar, lo que se puede deducir de las desigualdades anteriores son las relaciones siguientes:
\[S_1(\bar{x}_0,r)\subset \overline{B}_{2}(\bar{x}_0,r)\subset\overline{B}_{\infty}(\bar{x}_0,r)\] \[S_2(\bar{x}_0,r)\subset B_{\infty}(\bar{x}0,r)\hspace{1.7cm}\] \[S_{\infty}(\bar{x}0,r)\subset \overline{B}_{\infty}(\bar{x}_0,r)\hspace{1.8cm}
\]

Conjuntos Abiertos y Conjuntos Cerrados

Un concepto importante en la topología de $\mathbb{R}^{n}$ es el de conjunto abierto. Junto con el de conjunto cerrado.
Conjunto abierto y conjunto cerrado dos conceptos duales, en un sentido que trataremos de explicar. Por ahora solamente veremos la definición de cada uno de ellos y alguna de sus propiedades más importantes.
Definición. Un conjunto $V\subset\mathbb{R}^n$ se dice que es $\textbf{abierto}$ si para cada $\bar{x}\in V$ existe una bola abierta $B(\bar{x},r)$ contenida en $V$. Es decir si para cada $\bar{x}\in V$ existe $r>0$ tal que $B(\bar{x},r)\subset V$.

Ejemplo. El espacio $\mathbb{R}^n$ es un conjunto abierto, pues dado cualquier $\bar{x}\in \mathbb{R}^n$, toda bola abierta $B(\bar{x},r)$ esta contenida en $\mathbb{R}^n$.$~~\blacksquare$

Ejemplo .Mostraremos que el $\emptyset$ es abierto.
Suponemos que el $\emptyset$ no es abierto $\therefore$ $\exists$ $x\in
\emptyset$ para el cual no es posible hallar una bola abierta $B(\bar{x},r)$ contenida en $\emptyset$. Pero esto no es posible ya que el $\emptyset$ no tiene elementos.
Entonces debemos suponer que el $\emptyset$ no es abierto ${\large\textbf{!}}$ $~~~\therefore~~~\emptyset$ es abierto.$~~\blacksquare$

Proposición. Toda bola abierta en $\mathbb{R}^n$ es un conjunto abierto.
Demostración. Sea $\bar{x}_0\in\mathbb{R}^n$ y $r>0$. Mostraremos que $B(\bar{x}_0,r)$ es un conjunto abierto. Debemos probar que para cada $\bar{x}\in B(\bar{x}_0,r)$, existe una bola abierta $B(\bar{x},r)$ contenida a su vez en la bola abierta $B(\bar{x}_0,r)$. Sea pues $\bar{x}\in B(\bar{x}_0,r)$ y consideremos $R=r-\|\bar{x}-\bar{x}_0\|$. Como $\bar{x}\in B(\bar{x}_0,r)$ se tiene entonces que $\|\bar{x}-\bar{x}_0\|<r$ $\therefore$ $R>0$. Mostraremos que la bola abierta $B(\bar{x},R)$ esta contenida en $B(\bar{x}_0,r)$.

esto prueba que $\bar{y}\in B(\bar{x}_0,r)$.$~~\blacksquare$

Ejemplo.Mostraremos que en $\mathbb{R}^2$, el semiplano superior
$$V=\{(x,y)\in\mathbb{R}^2~|~y>0\}$$
es un conjunto abierto respecto a la norma $\|\overline{x}\|_1$
Solución.

Sea $\overline{v}_{0}=(x_{0},y_{0})\in V$. Se tiene entonces que $y_{0}>0$ consideremos $r=y_{0}$ y consideremos la bola $B_{1}(\bar{v}_0,y_0)$ y sea $\bar{v}=(x,y)\in
B_1(\bar{v}_0,y_0)$ se tiene que $\|\bar{v}-\overline{v}_0\|_1<y_0$, es
decir, $|x-x_0|+|y-y_0|<y_0$. Debemos probar que $y>0$.
(1) $y$ no puede ser cero pues si $y=0$
$|x-x_0|+|y-y_0|<y_0$ $\Rightarrow$ $|x-x_0|+|y_0|<y_0$ ${\large\textbf{!}}$ (Falso)
es decir no puede ocurrir que $|x-x_0|+|y_0|$ sea menor que $y_{0}$.
(2) $y$ no puede ser negativa pues
$|x-x_0|+|y-y_0|=|x-x_0|+\underset{*}{\underbrace{|y|+y_0}}>y_0$ ${\large\textbf{!}}$ (Falso)
* $y<y_0$ $\Rightarrow$ $|y-y_0|=-y+y_0=|y|+|y_0|$ $\therefore$ $y$ tiene que ser $y>0$ $\therefore$ $B_1(\bar{v}_0,y_0)$ esta en el semiplano superior.$~~ \blacksquare$
Definición. Un conjunto $F\subset\mathbb{R}^n$ se dice que es $\textbf{cerrado}$ si su complemento $F^c=\mathbb{R}^n-F$ es un conjunto abierto.

Ejemplo. Los conjuntos $\mathbb{R}^n$ y $\emptyset$ son cerrados. En efecto $\mathbb{R}^n$ es cerrado pues su complemento $\emptyset$ es abierto. Similarmente $\emptyset$ es cerrado pues su complemento $\mathbb{R}^n$ es abierto.$~\blacksquare$

Ejemplo. Un conjunto con un solo punto ${\bar{0}}$ es cerrado ya que $\mathbb{R}^n-{\bar{0}}$ es abierto.$~~\blacksquare$

Proposición. Toda bola cerrada en $\mathbb{R}^n$ es un conjunto cerrado.
Demostración. Sea $\bar{x}_0\in \mathbb{R}^n$ y $r\geq0$. Probaremos que la bola cerrada $\bar{B}(x_0,r)$ es un conjunto cerrado, es decir, que su complemento $\mathbb{R}^n-\bar{B}(x_0,r)$ es un conjunto abierto. Sea pues $\bar{x}\in\mathbb{R}^n-\bar{B}(x_0,r)$. Mostraremos que existe una bola abierta $B(\bar{x},R)$ contenida en $\mathbb{R}^n-\bar{B}(x_0,r)$. Como $\bar{x}$ no está en la bola cerrada $\bar{B}(x_0,r)$, se tiene entonces que $\|\bar{x}-\bar{x}_0\|>r$. Definamos $R=\|\bar{x}-\bar{x}_0\|-r>0$, esto equivale a $r=\|\bar{x}-\bar{x}_0\|-R$. Veamos que $B(\bar{x},R)\subset\mathbb{R}^n-\bar{B}(x_0,r)$

luego $\|\bar{x}-\bar{x}_0\|<R+\|\bar{y}-\bar{x}_0\|$ $\therefore$ $\|\bar{x}-\bar{x}_0\|-R<\|\bar{y}-\bar{x}_0\|$, es decir, $r<\|\bar{y}-\bar{x}_0\|$. Esto significa que $\bar{y}\not\in \bar{B}(\bar{x}_0,r)$, es decir, $\bar{y}\in\mathbb{R}^n-\bar{B}(\bar{x}_0,R)$.$~~\blacksquare$

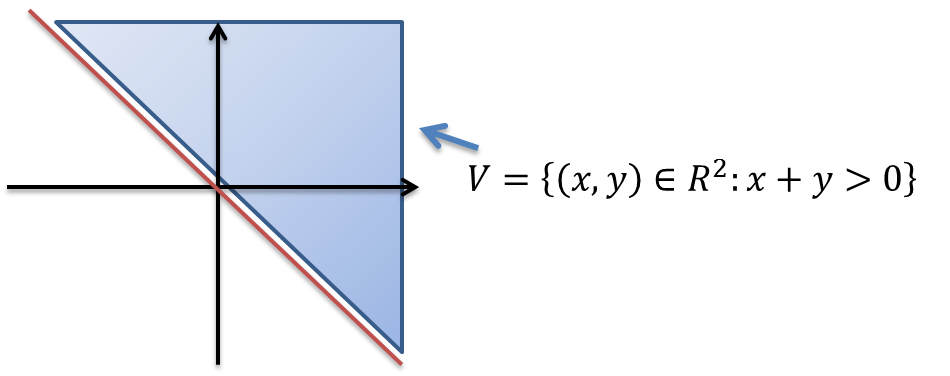
Ejemplo. Muestre que el conjunto $$V=\{(x,y)\in\mathbb{R}^{2}~|~x\leq y\}$$
es un conjunto cerrado.
Solución. Sea $V^{c}=\{(x,y)\in\mathbb{R}^{2}~|~x>y\}$. mostraremos que $V^{c}$ es un conjunto abierto

Sea $\overline{v}_{0}=(x_{0},y_{0})\in V^{c}$ entonces $x_{0}>y_{0}$. Definimos $r=x_{0}-y_{0}>0$ ahora consideramos $B(\overline{v}_{0},r)$ vamos probar que $B(\overline{v}_{0},r)\subset V^{c}$ Sea $\overline{v}_{1}=(x,y)\in B(\overline{v}_{0},r)$ con la norma $\|\overline{x}\|_{1}$ se tiene $$\|\overline{v}_{1}-\overline{v}_{0}\|_{1}<r~\Rightarrow~|x-x_{0}|+|y-y_{0}|<r~\Rightarrow~|x-x_{0}|+|y-y_{0}|<x_{0}-y_{0}$$ por lo tanto $$x-y=x-x_{0}+y_{0}-y+x_{0}-y_{0}=x_{0}-y_{0}+x-x_{0}+y_{0}-y\geq x_{0}-y_{0}-\left(|x-x_{0}|+|y-y_{0}|\right)>0$$ la última desigualdad se obtiene de la propiedad $-|x-x_{0}|\leq x-x_{0}\leq |x-x_{0}|$. De esta manera $x-y>0~\Rightarrow~x>y$ y en consecuencia $v_{1}\in V^{c}$ por lo que $V^{c}$ es un conjunto abierto y por lo tanto V es un conjunto cerrado.$~\blacksquare$
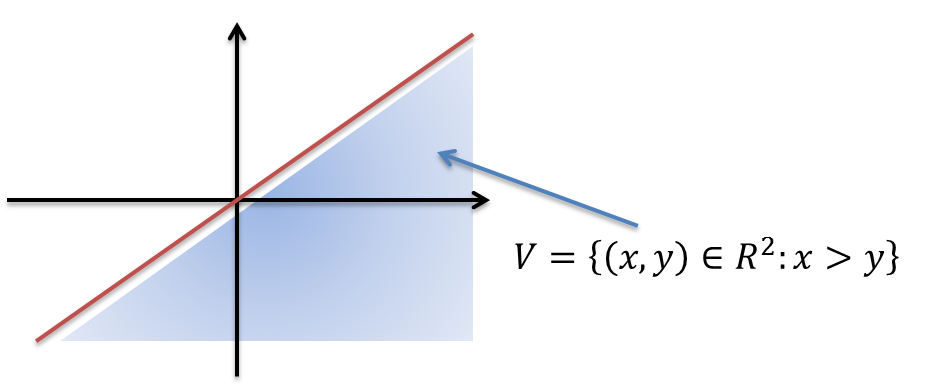
Ejemplo. Sea $V={(x,y)\in\mathbb{R}^{2}~|~x+y>0}$. Demuestre que V es un conjunto abierto

Solución. Sea $\bar{v}_{0}=(x_{0},y_{0})\in V$ entonces $x_{0}+y_{0}>0$. Definimos $r=x_{0}+y_{0}>0$ ahora consideramos $B(\bar{v},r)$ vamos probar que $B(\bar{v},r)\subset V$
Sea $\bar{v}_{1}=(x,y)\in B(\bar{v},r)$ con la norma $\|.\|_{1}$ se tiene $$\|\bar{v}-\bar{v}_{0}\|_{1}=|x-x_{0}|+|y-y_{0}|<r$$
por lo tanto
$$x+y=x-x_{0}-y_{0}+y+x_{0}+y_{0}=x_{0}+y_{0}+x-x_{0}-y_{0}+y\geq x_{0}-y_{0}-\left(|x-x_{0}|+|y-y_{0}|\right)>0$$

de esta manera $x+y>0$ y en consecuencia $\bar{v}_{1}\in V$ por lo que V es un conjunto abierto.$~~\blacksquare$

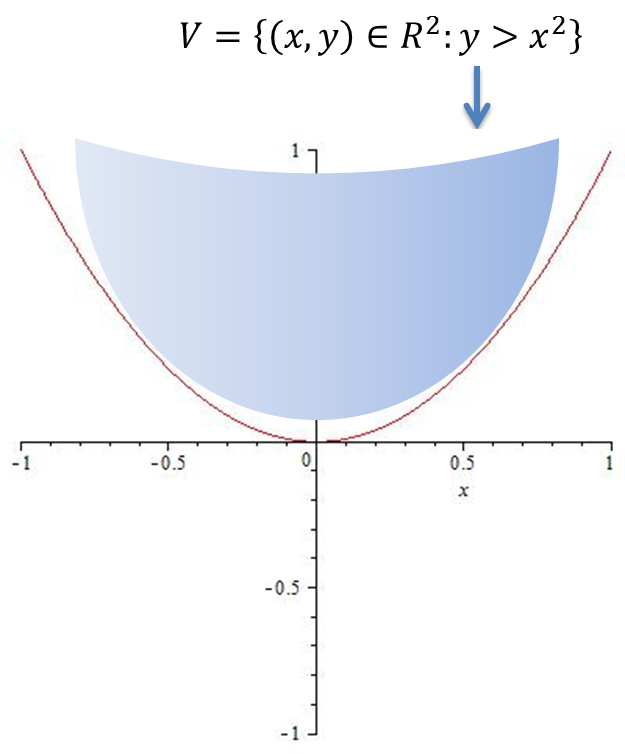
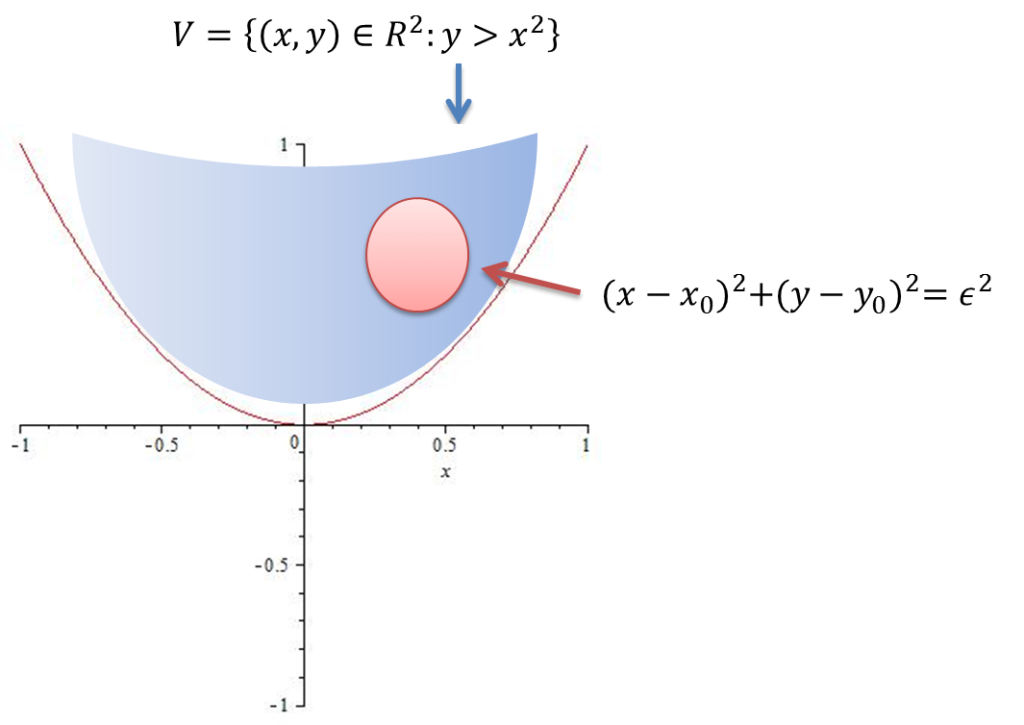
Ejemplo Sea $V=\{(x,y)\in\mathbb{R}^{2}~|~y>x^{2}\}$. Demuestre que V es un conjunto abierto

Solución. Sea $\bar{v}_{0}=(x_{0},y_{0})\in V$ entonces $y_{0}>x^{2}{0}$. Definimos $r=y_{0}+x^{2}{0}>0$ y ahora consideramos $B(\bar{v},r)=(x-x_{0})^{2}+(y-y_{0})^{2}=\epsilon^{2}$

vamos probar que $B(\bar{v},r)\subset V$.
Sea $\bar{v}_{1}=(x,y)\in B(\bar{v},r)$ cada punto en $B(\bar{v},r)$ cumple $$|x-x_{0}|<\epsilon~~~|y-y_{0}|<\epsilon$$ y usando la identidad algebraica $$x_{0}^{2}=x^{2}-2(x-x_{0})x_{0}-(x-x_{0})^{2}$$
tenemos que
$$y>y_{0}-\epsilon=x_{0}^{2}+y_{0}-x_{0}^{2}-\epsilon=x^{2}-2(x-x_{0})x_{0}-(x-x_{0})^{2}+y_{0}-x_{0}^{2}-\epsilon>x^{2}-2\epsilon x_{0}-\epsilon^{2}+y_{0}-x_{0}^{2}-\epsilon$$
Por lo tanto
$$y>x^{2}-2\epsilon x_{0}-\epsilon^{2}+y_{0}-x_{0}^{2}-\epsilon>x^{2}se~cumple~para~\epsilon=\min\left\{1,\frac{y-x_{0}^{2}}{2|x_{0}|+2}\right\}$$
de esta manera $y>x^{2}$ y en consecuencia $\bar{v}_{1}\in V$ por lo que V es un conjunto abierto.$~~\blacksquare$

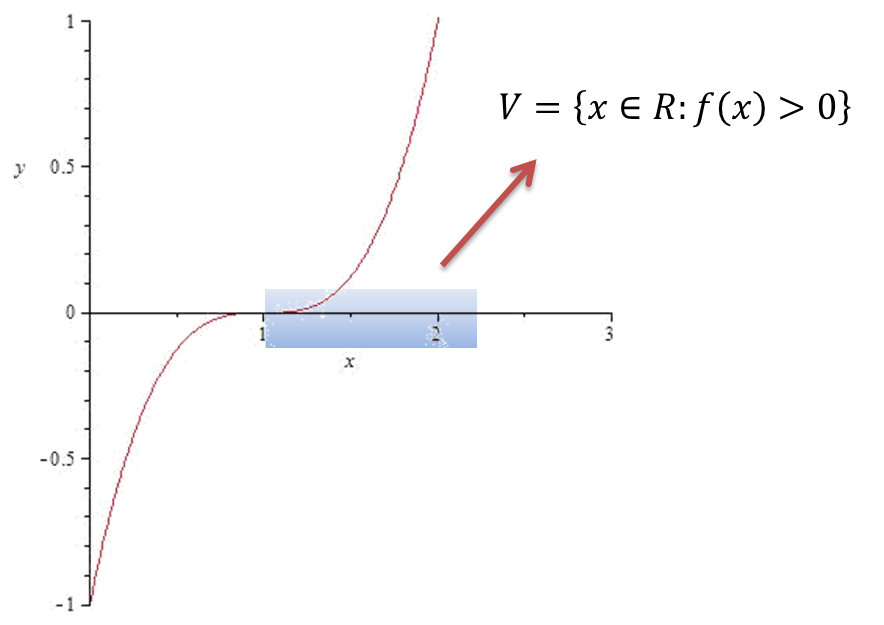
Ejemplo. Sea $V=\{x\in\mathbb{R}~|~f(x)>0\}$. Demuestre que V es un conjunto abierto

Solución. Sea $y\in V$ entonces $f(y)>0$. Definimos $\epsilon=f(y)$ y como f es continua
$$si~~0<|x-y|<\delta~\Rightarrow~|f(x)-f(y)|<\epsilon=f(y)~\Rightarrow~-f(y)<f(x)-f(y)<f(y)~\Rightarrow~0<f(x)$$
por lo tanto
$$\forall~x\in B(x,\delta)~se~tiene~f(x)>0$$de esta manera $B(y,\delta)\subset V$ por lo que V es un conjunto abierto.$~~\blacksquare$

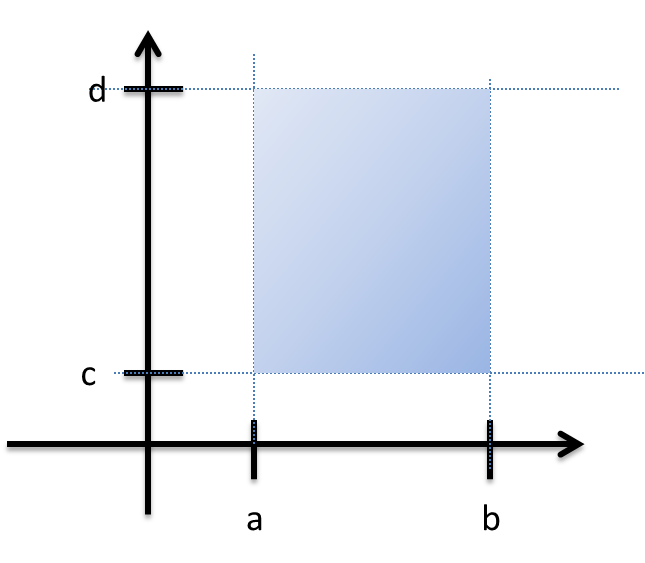
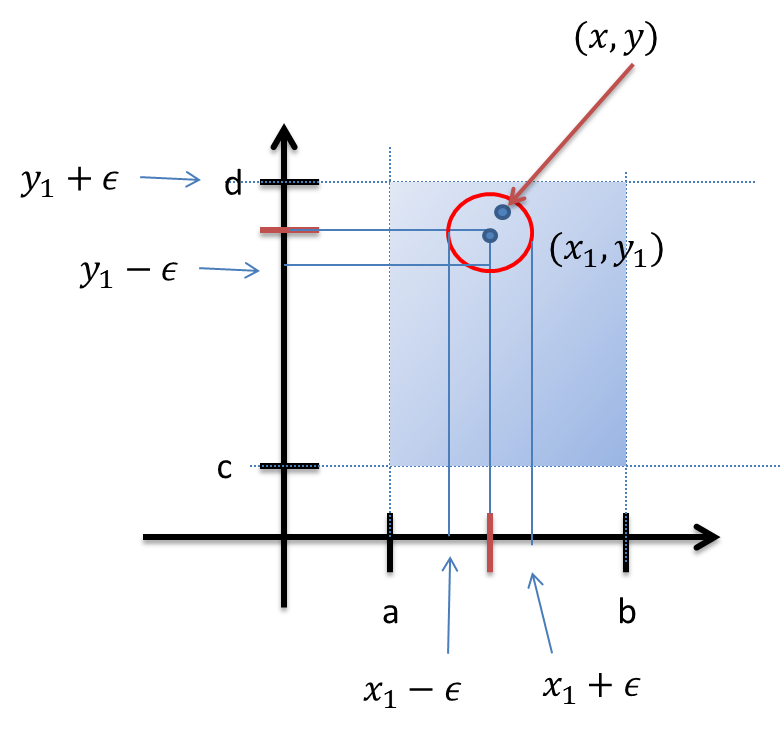
Ejemplo. Sea $V=\{(x,y)\in\mathbb{R}^{2}~|~a<x<b~,~c<y<d\}$. Demuestre que V es un conjunto abierto.

Solución. Sea $X=(x_{1},y_{1})\in V$ entonces $a<x_{1}<b$ y $c<y_{1}<d$. Definimos $\epsilon=\min\{x_{1}-a,b-x_{1},y_{1}-c,d-y_{1}\}$ por tanto si $(x,y)\in B(X,\epsilon)$

debe ocurrir
$$a<x_{1}-\epsilon<x<x_{1}+\epsilon<b~~y~~c<y_{1}-\epsilon<y<y_{1}+\epsilon<d$$
por lo tanto
$$(x,y)\in V~\therefore~B(X,\epsilon)\subset V$$y en consecuencia V es un conjunto abierto.$~~\blacksquare$

Más adelante

Una vez clasificados los puntos de $\mathbb{R}{n}$ veremos en la siguiente entrada una caracterización topológica de conjuntos de $\mathbb{R}{n}$ con sus respectivas propiedades.

Tarea Moral

1.- Prueba que si $ \overline{x} = (x_1,…,x_n) \in \mathbb{R} ^{n}$, entonces $|x_i| \leq \left\| \overline{x} \right\|$, $|x_i| \leq \left\| \overline{x} \right\| _{1}$ y $|x_i| \leq \left\| \overline{x} \right\| _{\infty}$.

2.-Demuestra que dados $a_1,…,a_n, b_1,…, b_n \in\mathbb{R}$ tales que $a_i \leq b_i$ para $i=1,..,n$, el rectángulo $[a_1,b_1] \times \cdot \cdot \cdot, [a_n,b_n]$ es un conjunto cerrado.

3.- Demuestra que $(a_1,b_1) \times \cdot \cdot \cdot, (a_n,b_n)$ es un conjunto abierto.

4.- Si $A= ([0,1] \times [0,1]) \cap (\mathbb{Q} \times \mathbb{Q})= \{ (x,y) \in \mathbb{R}^2 | x,y \in \mathbb{Q} y 0 \leq x \leq 1, 0 \leq y \leq 1 \}$

5.- Para el conjunto $A=\{(m,0) \in \mathbb{R}^2 | m \in \mathbb{Z} \}$ indica quien es:

a) int(A)

b) Fr(A)

c) ext(A)

d) ¿A es abierto o cerrado?

Introducción

El concepto de $\| \: \|$ (norma) nos da una noción de medida de un vector, la cual, generaliza la idea geométrica de distancia en la geometría euclidiana. También ayudará a tener una noción de distancia entre dos vectores en $\mathbb{R}$ o más generalmente en $\mathbb{R}^n$, es lo que nos permite hablar de limite o de convergencia.
Consideremos la noción común de distancia entre dos puntos en $\mathbb{R}^3$.
Si $\bar{x}=(x_1,x_2,x_3),~~~\bar{y}=(y_1,y_2,y_3)$
$$\|\bar{x}-\bar{y}\|=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}$$
Esta distancia la denominamos métrica euclidiana y la generalizamos
en $\mathbb{R}^n$ en la siguiente definición.
Definición. Sean $\bar{x}=(x_1,\ldots,x_n)$ y $\bar{y}=(y_1,\ldots,y_n)$ elementos cualesquiera de $\mathbb{R}^n$ definimos la distancia euclidiana entre ellos como $$d(\bar{x},\bar{y})=\|\bar{x}-\bar{y}\|=\sqrt{(x_1-y_1)^2+\ldots+(x_n-y_n)^2}$$
La función $d:\mathbb{R}^n \times \mathbb{R}^n \rightarrow\mathbb{R}$ se denomina distancia o métrica euclidiana.

Proposición. Para cualesquiera vectores $\bar{x},\,\bar{y},\,\bar{z}\,\in\,\mathbb{R}^n$ se tiene:
(a) $d(\bar{x},\bar{y})\geq 0$
(b) $d(\bar{x},\bar{y})=d(\bar{y},\bar{x})$
(c) $d(\bar{x},\bar{y})\leq d(\bar{x},\bar{z})+d(\bar{z},\bar{y})$
(d) $d(\bar{x},\bar{y})=0~~ \Rightarrow ~~ \bar{x}=\bar{y}$
Demostración.
(a) Como $d(x,y)=\|\bar{x}-\bar{y}\|\geq
0$ entonces $d(\bar{x},\bar{y})\geq 0$
tambien si $d(x,y)=0 \quad \Rightarrow \quad \|\bar{x}-\bar{y}\|=0 \quad \Rightarrow \quad \bar{x}=\bar{y}$
(b) $d(\bar{x},\bar{y})=\|\bar{x}-\bar{y}\|=\|\bar{y}-\bar{x}\|=d(\bar{y},\bar{x})$
(c) $d(\bar{x},\bar{y})=\|\bar{x}-\bar{y}\|=
\|\bar{x}-\bar{z}+\bar{z}-\bar{y}\|\leq \|\bar{x}-\bar{z}\|+\|\bar{z}-\bar{y}\| =
d(\bar{x},\bar{z})+d(\bar{z},\bar{y}).~~\blacksquare$
Proposición. La función $$d_{1}(x,y)=|x_{1}-y_{1}|+\cdots+|x_{n}-y_{n}|$$ donde $\bar{x}=(x_{1},\cdots,x_{n})$ y $\bar{y}=(y_{1},\cdots,y_{n})$ $\in \mathbb{R}^{n}$, es una métrica para el espacio euclideano $\mathbb{R}^{n}$.
Demostración. Las propiedades (a), (b) son inmediatas y para la propiedad (c) tenemos
$$|x_{i}-y_{i}|\leq|x_{i}|+|y_{i}|~~~\forall~i=1,…,n$$
sumando ambos lados de estas desigualdades para $i=1,…,n$ obtenemos
\begin{align*}d_{1}(x,z)&=\sum_{i=1}^{n}|x_{i}-z_{i}|\\&=\sum_{i=1}^{n}|x_{i}-y_{i}+y_{i}-z_{i}|\\&\leq\sum_{i=1}^{n}|x_{i}-y_{i}|+|y_{i}-z_{i}|\\&=\sum_{i=1}^{n}|x_{i}-y_{i}|+\sum_{i=1}^{n}|y_{i}-z_{i}|\\&= d_{1}(x,y)+d_{1}(y,z)\end{align*}
y en consecuencia $d_{1}$ es una métrica.$~~ \blacksquare$
Ejemplo. En $\mathbb{R}^{n}$ son métricas
\begin{align*}d_{p}(\bar{x},\bar{y})&=\left(\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac{1}{p}},~~~(p\geq 1)\\d_{\infty}(\bar{x},\bar{y})&=\max_{1\leq i\leq n}~|x_{i}-y_{i}|.~~ \blacksquare \end{align*}

Más adelante

En la siguiente entrada estudiaremos como las nociones topológicas heredadas en $\mathbb{R}^n$ nos ayudan a entender las características de proximidad y continuidad.

Tarea moral

1.- Sea $(V, \left\| \cdot \right\|)$ un espacio normado, Prueba que la función $d(v,w)= \left\| v-w \right\|$ es una métrica en $V$.

2.- Describe los conjuntos $\overline{B}= { x\in \mathbb{R}^2 : \left\| x \right\|_p \leq 1 } $ para $p=1,2, \infty $. Haz un dibujo de cada uno de ellos.

3.- Sea $V$ un espacio vectorial distinto de ${0}$. Prueba que no existe ninguna norma en $V$ que induzca la métrica discreta, es decir, no existe ninguna norma en $V$ tal que $\left\| v-w\right\| =\begin{cases}o,siv=w\\ 1 si, v\neq w\end{cases}$

4.- Prueba que si $x_1,…, x_n \in \mathbb{R}^n$ entonces $\left\| x_1 + … + x_n \right\| \leq \left\| x_1 \right\| + … + \left\| x_n \right\|$

5.- Sean $\overline{x}, \overline{y}\in \mathbb{R}^{n}$. Prueba que:

$\left\| \overline{x}+\overline{y}\right\|=\left\|x\right\|+\left\|y\right\|$ si y sólo si existe $\lambda \in \mathbb{R}$ con $\lambda > 0$, tal que $\overline{x}=\lambda \overline{y}$.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta entrada definiremos el producto de matrices que se realiza para dos matrices $A$ y $B$ tales que el número de columnas de $A$ es igual al número de filas de $B$. Veremos que la forma de multiplicar matrices es más elaborada que la suma de matrices, pero esto se debe a que el producto así definido resulta muy útil para trabajar con matrices, en particular para representar sistemas de ecuaciones de forma matricial. Veremos qué ocurre al analizar el concepto de neutro multiplicativo y de inversos multiplicativos que conocemos para el conjunto de número reales, pero ahora en el caso de las matrices, tratando de adaptar las nociones conocidas a este nuevo contexto. Finalmente definiremos la transpuesta de una matriz $A$, que se obtiene intercambiando sus filas por columnas.

En la presente nota usaremos las propiedades del producto punto de elementos en $\mathbb R^n$ para las pruebas, puedes consultarlas en el siguiente enlace: Propiedades del producto punto.

Definición

Sean $n,m$ y $r$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R),\,\, B\in \mathscr M_{n\times r}(\mathbb R)$.

El producto de $A$ con $B$ es la matriz $AB\in \mathscr M_{m\times r}(\mathbb R)$ tal que:

$(AB)_{ij}=a_{i1}b_{1j}+\cdots+a_{in}b_{nj}.$

Notación:

$ren_i A=(a_{i1},\dotsc,a_{in})$

$col_j B=(b_{1j},\dotsc,b_{nj}).$

Con esta notación $(AB)_{ij}=ren_i A\cdot col_j B,$ es decir, la entrada $ij$ de $AB$ es el producto punto del renglón $i$ de $A$ con la columna $j$ de $B$.

Ejemplos

$1.$ $A=\begin{equation*} \begin{pmatrix} 2 & -1 & 3 \\ 0 & 1 & 4 \\ \end{pmatrix} \end{equation*}$, $ B=\begin{equation*} \begin{pmatrix} 4 \\ 5 \\6 \\ \end{pmatrix} \end{equation*}$.

$AB=\begin{equation*} \begin{pmatrix} (2)(4)+(-1)(5)+3(6)\\(0)(4)+(1)(5)+(4)(6) \\ \end{pmatrix} \end{equation*}=$ $\begin{equation*} \begin{pmatrix} 21 \\ 29 \\ \end{pmatrix} \end{equation*} $

$3.$ $A=\begin{equation*} \begin{pmatrix} 1 & 4 \\ 1 & 3\\ \end{pmatrix} \end{equation*}$, $ B=\begin{equation*} \begin{pmatrix} 1 & 0 \\ 2 & 3 \\ \end{pmatrix} \end{equation*}$.

$AB=\begin{equation*}\begin{pmatrix} (1)(1)+(4)(2) & (1)(0)+(4)(3) \\ (1)(1)+(3)(2) & (1)(0)+(3)(3) \\ \end{pmatrix} =\begin{pmatrix} 9 & 12 \\ 7 & 9 \\ \end{pmatrix} \end{equation*}.$

Proposición

Sean $n,m,r$ y $s$ naturales positivos, $A, \overline{A} \in \mathscr M_{m\times n}(\mathbb R)$, $B, \overline{B} \in \mathscr M_{n\times r}(\mathbb R)$, $C \in \mathscr M_{r\times s}(\mathbb R)$ y $\lambda \in \mathbb R.$

$a)$ $A(BC)=(AB)C.$

$b)$ $(A+\overline{A})B=AB+\overline{A}B.$

$c)$ $A(B+\overline{B})=AB+A\overline{B}.$

$d)$ $\lambda (AB)=(\lambda A)B=A(\lambda B).$

Demostración

Se harán las demostraciones de $b)$ y $d)$, las dos restantes quedan de tarea moral.

Sean $n,m,r$ y $s$ naturales positivos, $A, \overline{A} \in \mathscr M_{m\times n}(\mathbb R)$, $B, \overline{B} \in \mathscr M_{n\times r}(\mathbb R)$, $C \in \mathscr M_{r\times s}(\mathbb R)$ y $\lambda \in \mathbb R.$

Demostración de $b)$

Por demostrar que $(A+\overline{A})B=AB+\overline{A}B.$

Observa que tanto $(A+\overline{A})B$ como $AB+\overline{A}B$ pertenecen a $\mathscr M_{m\times r}(\mathbb R).$

Sean $i\in \set{1,\dotsc,m}, j\in \set{1,\dotsc,r}.$

Expresión	Explicación
$((A+\overline{A})B)_{ij}=$	Partimos de un elemento arbitrario $ij$ de la matriz $(A+\overline{A})B.$
$=ren_i (A+\overline{A})\cdot col_j B$	Por definición de producto de matrices.
$=(ren_i A+ren_i \overline{A})\cdot col_j B$	Por definición de suma de matrices.
$=ren_i A\cdot col_j B+ren_i \overline{A}\cdot col_j B$	Por las propiedades del producto punto.
$=(AB)_{ij}+(\overline{A} B)_{ij}$	Por definición de producto de matrices.
$=(AB+\overline{A} B)_{ij}$	Por definición de suma de matrices.

Así, $((A+\overline{A})B)_{ij}=(AB+\overline{A}B)_{ij}$.

Concluimos que $(A+\overline{A})B$ y $AB+\overline{A}B$ son del mismo tamaño y coinciden entrada a entrada, entonces $(A+\overline{A})B=AB+\overline{A}B.$

Demostración de $b)$

Por demostrar que $\lambda (AB)=A(\lambda B).$

Tanto $\lambda (AB)$ como $A(\lambda B)$ pertenecen a $\mathscr M_{m\times r}(\mathbb R)$.

Sean $i\in \set{1,\dotsc,m}, j\in \set{1,\dotsc,r}.$

Expresión	Explicación
$(\lambda (AB))_{ij}=$	Partimos de un elemento arbitrario $ij$ de la matriz $\lambda (AB)$
$=\lambda (AB)_{ij}$	Por la definición de producto por escalar.
$=\lambda (ren_i A\cdot col_j B)$	Por la definición de producto de matrices.
$=ren_i A\cdot (\lambda col_j B)$	Por las propiedades del producto punto.
$=ren_i A\cdot col_j (\lambda B)$	Por la definición de producto por escalar.
$=(A(\lambda B))_{ij}$	Por la definición de producto de matrices.

Así, $(\lambda (AB))_{ij}=(A(\lambda B))_{ij}$.

Concluimos que $\lambda (AB)$ y $A(\lambda B)$ son del mismo tamaño y coinciden entrada a entrada, entonces $\lambda (AB)=A(\lambda B)$.

Definición

Sea $n$ un natural positivo. La matriz identidad de tamaño $n\times n$ es:

$I_n=\begin{equation*} \begin{pmatrix} 1 & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}$

es decir, la matriz $n\times n$ con unos en la diagonal y ceros fuera de la diagonal.

Proposición.

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R).$

$1.$ $A\,I_n=A.$

$2.$ $I_mA=A.$

La demostración se deja como tarea moral.

Definición

Sean $n$ un natural positivo, $A\in \mathscr M_{n\times n}(\mathbb R)$. Decimos que $A$ es una matriz invertible si existe $B\in \mathscr M_{n\times n}(\mathbb R)$ tal que:

$AB=BA=I_n.$

En este caso decimos que $B$ es una inversa de $A.$

Observación

Si $A$ es invertible su inversa es única.

Demostración

Sean $n$ un natural positivo, $A\in \mathscr M_{n\times n}(\mathbb R)$ invertible, $B,\,C\in \mathscr M_{n\times n}(\mathbb R)$ inversas de $A$. Entonces $AB=BA=I_n=AC=CA$. Así, tenemos que $AB=AC$, y multiplicando por la izquierda por $B$ a ambos lados de la igualdad tenemos que $B(AB)=B(AC)$. En virtud de la asociatividad de la multiplicación de matrices obtenemos que $(BA)B=(BA)C$, y como $BA=I_n$ se tiene que $I_nB=I_nC$. Así, $B=C$ y por lo tanto la inversa es única.

Notación: Si $A$ es invertible denotaremos por $A^{-1}$ a la matriz inversa de $A$.

Definición

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R)$. La transpuesta de $A$ es la matriz $A^t\in \mathscr M_{n\times m}(\mathbb R)$ tal que:

$(A^t)_{ij}=A_{ji}$

Ejemplos

$1.$ $A=\begin{equation*} \left(\begin{array}{rrrr} 1 & 3 & \pi &\frac{1}{4} \\ 0 & 2 & -1 & 8\\ \end{array}\right) \end{equation*}$, $ A^t =\begin{equation*} \left(\begin{array}{cr} 1 &0 \\ 3 &2 \\ \pi & -1 \\ \frac{1}{4} & 8 \\ \end{array}\right)\end{equation*}$.

$2.$ $A=\begin{equation*} \left(\begin{array}{r} 0.7 \\ -1\\ 10 \\ \end{array}\right) \end{equation*}$, $ A^t =\begin{equation*} \begin{pmatrix} 0.7 &-1 & 10 \\ \end{pmatrix} \end{equation*}$.

$3.$ $A=\begin{equation*} \left(\begin{array}{rr} 2 & -3 \\ 3 &1 \\ \end{array}\right) \end{equation*}$, $ A^t =\begin{equation*} \left(\begin{array}{rr} 2 &3 \\ -3 &1 \\ \end{array}\right) \end{equation*}.$

Proposición

Sean $n,m$ y $r$ naturales positivos, $A, B\in \mathscr M_{m\times n}(\mathbb R)$, $C\in \mathscr M_{n\times r}(\mathbb R)$ y $\lambda \in \mathbb R$.

$a)$ $(A^t)^t=A.$

$b)$ $ (A+B)^t=A^t+B^t.$

$c)$ $(\lambda A)^t=\lambda(A^t).$

$d)$ $(AC)^t=C^tA^t.$

Demostración

Se hará la demostración de $a)$, $b)$ y $d)$, el inciso $c)$ queda como tarea moral.

Sean $n,m$ y $r$ naturales positivos, $A, B\in \mathscr M_{m\times n}(\mathbb R)$, $C\in \mathscr M_{n\times r}(\mathbb R)$ y $\lambda \in \mathbb R$.

Demostración de $a)$

Observemos que $(A^t)^t,\,A\in \mathscr M_{m\times n}(\mathbb R)$.

Sean $i\in \set{1,\dotsc,m}, j\in \set{1,\dotsc,n}.$

Expresión	Explicación
$((A^t)^t)_{ij}=$	Partimos de un elemento arbitrario $ij$ de la matriz $(A^t)^t.$
$=(A^t)_{ji}$	Por la definición de transpuesta.
$=A_{ij}$	Por la definición de transpuesta.

Así, $((A^t)^t)_{ij}=A_{ij}$.

Concluimos que $(A^t)^t$ y $A$ son del mismo tamaño y coinciden entrada a entrada, entonces $(A^t)^t=A.$

Demostración de $b)$

Observemos que $(A+B)^t,\,A^t+B^t \in \mathscr M_{n\times m}(\mathbb R)$.

Sean $i\in \set{1,\dotsc,n}, j\in \set{1,\dotsc,m}.$

Expresión	Explicación
$((A+B)^t))_{ij}=$	Partimos de un elemento arbitrario $ij$ de la matriz $(A+B)^t.$
$=(A+B)_{ji}$	Por la definición de transpuesta.
$=A_{ji}+B_{ji}$	Por la definición de la suma de matrices.
$=(A^t)_{ij}+(B^t)_{ij}$	Por la definición de transpuesta.
$=(A^t+B^t)_{ij}$	Por la definición de la suma de matrices.

Así, $((A+B)^t)_{ij}=(A^t+B^t)_{ij}$.

Concluimos que $(A+B)^t$ y $A^t+B^t$ son del mismo tamaño y coinciden entrada a entrada, entonces $(A+B)^t=A^t+B^t.$

Demostración de $d).$

Notemos que $(AC)^t,\,C^tA^t \in \mathscr M_{r\times m}(\mathbb R).$

Sean $i\in \set{1,\dotsc,r}, j\in \set{1,\dotsc,m}.$

Expresión	Explicación
$((AC)^t)_{ij}=$	Partimos de un elemento arbitrario $ij$ de la matriz $(AC)^t).$
$=(AC)_{ji}$	Por la definición de transpuesta.
$=ren_j A\cdot col_i C$	Por la definición del producto de matrices.
$=col_j A^t\cdot ren_j C^t$	Por la definición de transpuesta.
$=ren_i C^t\cdot col_jA^t$	Por la conmutatividad del producto punto.
$=(C^tA^t)_{ij}$	Por la definición del producto de matrices.

Así, $((AC)^t)_{ij}=(C^tA^t)_{ij}$.

Concluimos que $(AC)^t$ y $C^tA^t$ son del mismo tamaño y coinciden entrada a entrada, entonces $(AC)^t=C^tA^t.$

$\square$

Tarea Moral

$1.$ Considera las siguientes matrices:

$A=\begin{equation*} \left(\begin{array}{rr} 3 & 0 \\ -1 & 2\\ 1 & 1 \end{array}\right) \end{equation*}$, $B=\begin{equation*} \left(\begin{array}{rr} 4 & -1 \\ 0 & 2 \end{array}\right) \end{equation*}$, $C=\begin{equation*} \left(\begin{array}{rrr} 1 & 4 & 2 \\ 3 & 1 & 5 \end{array}\right) \end{equation*}$, $D=\begin{equation*} \left(\begin{array}{rrR} 1 & 5 & 2 \\ -1 & 0 & 1\\ 3 & 2 & 4 \end{array}\right) \end{equation*}$, $E=\begin{equation*} \left(\begin{array}{rrr} 6 & 1 & 3 \\ -1 & 1 & 2\\ 4 & 1 & 3 \end{array}\right) \end{equation*}.$

Calcula, si es posible: $DA-A$, $-7E$, $A(BC)$, $(4B)C+2B.$

$2.$ Una matriz cuadrada $A$ es diagonal si todos los elementos que están fuera de la diagonal principal son cero ($A_{ij}=0$ si $i\neq j$). ¿Qué ocurre al multiplicar dos matrices diagonales?

$3.$ Sean $n$ un natural positivo, $A \in \mathscr M_{n\times n}(\mathbb R)$. Dado $t$ un natural positivo definimos $A^t$ como el producto de $A$ consigo misma $t$ veces. Demuestra o da un contraejemplo para las siguientes afirmaciones:

$i)$ $(AB)^2=A^2B^2$

$ii)$ $(A+B)^2=A^2+2AB+B^2$

$4.$ La traza de una matriz cuadrada $A$ es la suma de los elementos de su diagonal y se denota por $tr(A)$. Calcula la traza de las matrices cuadradas del ejercicio $1.$

$5.$ Sean $n$ un natural positivo, $A,B \in \mathscr M_{n\times n}(\mathbb R)$ invertibles. ¿Puedes construir una matriz inversa para $AB$ usando $A^{-1}$ y $B^{-1}$?.

$6.$ Sea $A=\begin{equation*} \left(\begin{array}{rr} a & b \\ c & d \end{array}\right) \end{equation*}\in\mathscr M_{2\times 2}(\mathbb R)$. Demuestra que si $ad-bc\neq 0$, entonces $A=\frac{1}{ad-bc}\begin{equation*} \left(\begin{array}{rr} d & -b \\- c & a \end{array}\right) \end{equation*}$ es la matriz inversa de $A$.

Más adelante

En la siguiente nota veremos las operaciones elementales por renglones para matrices, definiremos una equivalencia por renglones en las matrices y notaremos que las operaciones elementales por matrices pueden expresarse como multiplicaciones por matrices adecuadas.

Enlaces relacionados

Página principal del curso.

Enlace a la nota anterior. Nota 33. Matrices.

Enlace a la nota siguiente. Nota 35. Operaciones elementales, matrices equivalentes y matrices elementales.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta entrada estudiaremos la operaciones elementales por renglones, que son transformaciones que se pueden aplicar a las filas de una matriz con el objetivo de simplificarla, lo que ayuda por ejemplo a resolver sistemas de ecuaciones lineales. Estas operaciones incluyen intercambiar dos filas, multiplicar una fila por un número distinto de cero y sumar un múltiplo de una fila a otra fila.

Usando las operaciones elementales por renglones estableceremos una relación de equivalencia entre matrices del mismo tamaño. Las matrices equivalentes tienen propiedades algebraicas y geométricas similares. Veremos también cómo codificar la aplicación de las operaciones elementales mediante productos adecuados de matrices, para lo cual definiremos las matrices elementales. que se obtienen de una matriz identidad aplicando una sola operación elemental.

Operaciones elementales de renglones

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R),$ $\lambda \in\mathbb{R}$ con $\lambda\neq 0$, $r,s\in\{1,\dots , m\}$. Las operaciones elementales por renglones que podemos realizar en $A$ son de tres tipos:

$1.$ Intercambiar dos renglones $r$ y $s$.

$2.$ Multiplicar el renglón $r$ por el escalar $\lambda \in \mathbb R,\,\,\lambda\neq 0.$

$3.$ Sumar al renglón $r$, $\lambda$ veces el renglón $s$, con $\lambda \in \mathbb R.$

Notación

Denotaremos por $e$ a la operación elemental y por $e(A)$ a la matriz que se obtiene de $A$ al aplicar la operación $e$.

Observación

Cada operación elemental tiene una operación elemental inversa del mismo tipo.

Ejemplos

$1.$ Considera la matriz:

$A=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 4 & 5 & 6 \end{array} \right) \end{equation*}$.

Sea $e$ la operación elemental de sumar al primer renglón $3$ veces el segundo.

$e(A)= \begin{equation*} \left(\begin{array}{rrr} 13 & 17 & 21\\ 4 & 5 & 6 \end{array} \right) \end{equation*}.$

$2.$ Considera la matriz:

$B=\begin{equation*} \left(\begin{array}{rr} -1 & 0\\ 2 & 4 \\ 3 & 5 \end{array} \right) \end{equation*}$.

Sea $e$ la operación elemental que intercambia los renglones $1$ y $3.$

$e(B)=\begin{equation*} \left(\begin{array}{rr} 3 & 5\\ 2 & 4 \\ -1 & 0 \end{array} \right) \end{equation*}$.

$3.$ Considera la matriz:

$C=\begin{equation*} \left(\begin{array}{rrrr} 3 & -6 & 12 & 9\\ 1 & 3 & -2 & 4 \end{array} \right) \end{equation*}$.

Sea $e$ la operación elemental que multiplica al primer renglón por $\frac{1}{3}.$

$e(C)=\begin{equation*} \left(\begin{array}{rrrr} 1 & -2 & 4 & 3\\ 1 & 3 & -2 & 4 \end{array} \right) \end{equation*}$.

Definición

Sean $n$ y $m$ naturales positivos, $A,B\in \mathscr M_{m\times n}(\mathbb R).$ Decimos que $B$ es equivalente por renglones a $A$ si $B$ se obtiene de $A$ mediante una sucesión finita de operaciones elementales.

Notación

$A\sim B$ denota que $B$ es equivalente a $A.$

Para ser más precisos, si $B$ se obtiene de $A$ intercambiando los renglones $r$ y $s$, lo denotaremos por ${\Large{A}} \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{R_r\leftrightarrow R_s} \end{array} \Large{B},$ si $B$ se obtiene de $A$ multiplicando el renglón $r$ por el escalar $\lambda$, lo denotaremos por ${\Large{A}} \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{\lambda R_r} \end{array} \Large{B},$ y si $B$ se obtiene de $A$ sumando al renglón $r$, $\lambda$ veces el renglón $s$, lo denotaremos por ${\Large{A}} \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{R_r\rightarrow R_r+\lambda R_s} \end{array} \Large{B}$.

Definición

Sean $n$ un natural positivo, $E\in \mathscr M_{n\times n}(\mathbb R)$. Decimos que $E$ es una matriz elemental si se obtiene de la matriz identidad $I_n$ aplicando una sola operación elemental.

Ejemplos

$1.$ Las siguientes matrices son equivalentes

$\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 1 \end{array} \right) \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{R_1\leftrightarrow R_2} \end{array} \left(\begin{array}{rr} 0 & 1\\ 1 & 0 \end{array} \right) \end{equation*}$.

La matriz $\begin{equation*} \left(\begin{array}{rr} 0 & 1\\ 1 & 0 \end{array} \right) \end{equation*}$ es una matriz elemental, pues se obtiene de la identidad aplicando una sola operación elemental.

Considera la matriz $\begin{equation*} A=\left(\begin{array}{rr} a & b\\ c & d \end{array} \right) \end{equation*}$.

Si intercambiamos sus renglones obtenemos la matriz equivalente $\begin{equation*} \left(\begin{array}{rr} c & d\\ a & b \end{array} \right) \end{equation*}$.

Observa que ésta se obtiene multiplicando la matriz elemental $\begin{equation*} \left(\begin{array}{rr} 0 & 1\\ 1 & 0 \end{array} \right) \end{equation*}$ por la matriz $A$:

$\begin{equation*} \left(\begin{array}{rr} 0 & 1\\ 1 & 0 \end{array} \right) \left(\begin{array}{rr} a & b\\ c & d \end{array} \right) =\left(\begin{array}{rr} c & d\\ a & b \end{array} \right) \end{equation*}$.

$2.$ Las siguientes matrices son equivalentes

$\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 1 \end{array} \right) \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{5 R_2} \end{array} \left(\begin{array}{rr} 1 & 0\\ 0 & 5 \end{array} \right) \end{equation*}$.

La matriz $\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 5 \end{array} \right) \end{equation*}$ es una matriz elemental, pues se obtiene de la identidad aplicando una sola operación elemental.

Considera la matriz $\begin{equation*} A= \left(\begin{array}{rr} a & b\\ c & d \end{array} \right) \end{equation*}$.

Si multiplicamos el segundo renglón por $5$ obtenemos la matriz equivalente $\begin{equation*} \left(\begin{array}{rr} a & b\\ 5c & 5d \end{array} \right) \end{equation*}$.

Observa que ésta se obtiene multiplicando la matriz elemental $\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 5 \end{array} \right) \end{equation*}$ por la matriz $A$:

$\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 5 \end{array} \right) \left(\begin{array}{rr} a & b\\ c & d \end{array} \right) = \left(\begin{array}{rr} a & b\\ 5c & 5d \end{array} \right) \end{equation*}$.

$3.$ Las siguientes matrices son equivalentes

$\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ 0 & 1 \end{array} \right) \begin{array}{c} \phantom{nnn}\\ \sim\\ \small{R_2 \rightarrow R_2+(-2)R_1} \end{array} \left(\begin{array}{rr} 1 & 0\\ -2 & 1 \end{array} \right) \end{equation*}$.

La matriz $\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ -2 & 1 \end{array} \right) \end{equation*}$ es una matriz elemental, pues se obtiene de la identidad aplicando una sola operación elemental.

Considera la matriz $\begin{equation*} A= \left(\begin{array}{rr} a & b\\ c & d \end{array} \right) .\end{equation*}$

Si sumamos al segundo renglón $-2$ veces el primero obtenemos la matriz equivalente $\begin{equation*} \left(\begin{array}{rr} a & b\\ -2a+c & -2b+d \end{array} \right) \end{equation*}$.

Observa que ésta se obtiene multiplicando la matriz elemental $\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ -2 & 1 \end{array} \right) \end{equation*}$ por la matriz $A$:

$\begin{equation*} \left(\begin{array}{rr} 1 & 0\\ -2 & 1 \end{array} \right) \left(\begin{array}{rr} a & b\\ c & d \end{array} \right) =\left(\begin{array}{rr} a & b\\ -2a+c & -2b+d \end{array} \right) \end{equation*}$.

Observación 1

Sean $n$ y $m$ naturales positivos, $A \in \mathscr M_{m\times n}(\mathbb R)$ y $e$ una operación elemental, consideremos la matriz elemental $e(I_m)$ que se obtiene de $I_m$ aplicando $e$. Entonces:

$e(I_m)A=e(A)$.

La demostración se deja al lector.

Observación 2

Sean $n$ y $m$ naturales positivos, $A,B\in \mathscr M_{m\times n}(\mathbb R)$ tales que $A\sim B.$ Entonces existen $t$ un natural positivo y $E_1,\dotsc,E_t$ matrices elementales tales que:

$B=E_t\cdots E_2 E_1 A$.

Ejemplo

Matrices equivalentes	Operación elemental
$A=\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 2 & -1 & -7\\ -5 & 6 & 26 \end{array} \right) \end{equation*}\sim$	$e_1: R_2\rightarrow R_2+(-2)R_1$
$\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 0 & -7 & -17\\ -5 & 6 & 26 \end{array} \right) \end{equation*}\sim$	$e_2: R_3\rightarrow R_3+5R_1$
$\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 0 & -7 & -17\\ 0 & 21 & 51 \end{array} \right) \end{equation*}\sim$	$e_3: R_3\rightarrow R_3+3R_2$
$\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 0 & -7 & -17\\ 0 & 0 & 0 \phantom{.}\end{array} \right) \end{equation*}\sim$	$e_4: (-\frac{1}{7})R_2$
$\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 0 & 1 & \frac{17}{7}\\ 0 & 0 & 0 \phantom{.}\end{array} \right) \end{equation*}\sim$	$e_5: R_1\rightarrow R_1+(-3)R_2$
$\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & -\frac{16}{7}\\ 0 & 1 & \frac{17}{7}\\ 0 & 0 & 0 \phantom{.}\end{array} \right) \end{equation*}=B$

Por la observación 2 tenemos que:

$\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & -\frac{16}{7}\\ 0 & 1 & \frac{17}{7}\\ 0 & 0 & 0\phantom{.} \end{array} \right) \end{equation*}=$ $\begin{equation*} \left(\begin{array}{rrr} 1 & -3 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array} \right) \end{equation*}$ $\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & 0\\ 0 & -\frac{1}{7} & 0\\ 0 & 0 & 1 \end{array} \right) \end{equation*}$ $\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 3 & 1 \end{array} \right) \end{equation*}$ $\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & 0\\ 0 & 1 & 0\\ 5 & 0 & 1 \end{array} \right) \end{equation*}$ $\begin{equation*} \left(\begin{array}{rrr} 1 & 0 & 0\\ -2 & 1 & 0\\ 0 & 0 & 1 \end{array} \right) \end{equation*}$ $\begin{equation*} \left(\begin{array}{rrr} 1 & 3 & 5\\ 2 & -1 & -7\\ -5 & 6 & 26 \end{array} \right) \end{equation*}.$

De esta forma, si $E_t=e_t(I_3)$ para cada $t\in\{1,2,3,4,5\}$:

$B=E_5 E_4 E_3 E_2 E_1 A$.

Tarea Moral

$1.$ Para cada operación elemental describe cuál es su operación inversa, analiza si es una operación elemental y en su caso de qué tipo es.

$2.$ Escribe un ejemplo de una matriz elemental de tamaño $2\times 2$, una de tamaño $3\times 3$ y una de tamaño $4\times 4.$

$3.$ Sea $E$ una matriz elemental:

$i)$ ¿Es $E$ invertible?

$ii)$ En caso que lo sea ¿Cuál será su inversa?

$4.$ Sean $n$ un natural positivo, $A\in \mathscr M_{m\times n}(\mathbb R)$ y $e$ una operación elemental de matrices. Demuestra que $e(I_m)A=e(A).$

$5.$ Sea $n$ un natural positivo, $A\in \mathscr M_{n\times n}(\mathbb R)$. Si $A\sim I_n$:

$i)$ ¿Cómo queda expresada $A$ en términos de $I_n$ y de matrices elementales?

$ii)$ ¿Cómo queda expresada $I_n$ en términos de $A$ y de matrices elementales?

Más adelante

En la siguiente nota daremos la definición de una matriz escalonada reducida por renglones y veremos que cualquier matriz $A$ es equivalente a una de estas matrices escalonadas reducida por renglones.

Enlaces relacionados

Página principal del curso.

Enlace a la nota anterior. Nota 34. Multiplicación de matrices, identidad, inversas y transpuesta.

Enlace a la nota siguiente. Nota 36. Matriz escalonada reducida por renglones.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Recordemos que las matrices pueden ser pensadas como tablas de datos, así que es conveniente encontrar la forma de guardar información en ellas pero procurando que las matrices que usemos sean lo más sencillas posibles. Con esa idea en mente, en esta nota daremos la definición de lo que es una matriz escalonada reducida por renglones y veremos que toda matriz es equivalente a una matriz de este tipo.

Definición

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R).$ Decimos que $A$ es una matriz escalonada reducida por renglones si $A$ es la matriz de ceros o existe $r\in \set{1,\dotsc, m}$ tal que:

$i)$ Los primeros $r$ renglones de $A$ son los renglones no nulos, debajo de ellos sólo hay ceros.

$ii)$ Si un renglón es no nulo, su primer elemento distinto de cero es $1$ y en la columna donde se encuentra este $1$ todos los otros elementos son cero.

$iii)$ Para cada $i\in \set{1,\dotsc, r}$ sea $k_i$ la columna donde se encuentra el primer elemento no nulo del renglón $i$, entonces $k_1< k_2<\cdots <k_r$.

Ejemplo

$R=\begin{equation*} \left(\begin{array}{rrrrrrrr} \colorbox{cyan}{1} & \colorbox{cyan}{7} &\colorbox{cyan}{0} & \colorbox{cyan}{0} &\colorbox{cyan}{ $-1$}& \colorbox{cyan}{0} & \colorbox{cyan}{2} & \colorbox{cyan}{4}\\ 0 & 0 & \colorbox{cyan}{1} & \colorbox{cyan}{0} & \colorbox{cyan}{3} & \colorbox{cyan}{3} & \colorbox{cyan}{1} & \colorbox{cyan}{2} \\0 & 0 & 0 & \colorbox{cyan}{1} & \colorbox{cyan}{7} & \colorbox{cyan}{5} & \colorbox{cyan}{3} & \colorbox{cyan}{4} \\ 0 & 0 & 0 & 0 & 0& 0 & 0 & 0 \end{array} \right) \end{equation*}.$

Hemos marcado en azul el primer elemento no nulo de cada renglón y los elementos que se encuentran a su derecha, para observar como éstos dan lugar a una forma escalonada. De ahí el nombre dado a las matrices que acabamos de definir.

Veamos que $R$ cumple la definición de ser escalonada reducida por renglones:

$i)$ Los primeros $3$ renglones de $A$ son los renglones no nulos, debajo de ellos sólo hay ceros, así, en este caso $r=3$.

$ii)$ Todo renglón no nulo tiene como primer elemento distinto de cero al $1$ y en la columna donde se encuentra este $1$ todos los otros elementos son cero.

$iii)$ Para cada $i\in \set{1,2, 3}$ sea $k_i$ la columna donde se encuentra el primer elemento no nulo del renglón $i$, entonces

$k_1$ es la columna donde se encuentra el primer elemento no nulo del renglón $1$, $k_1=1$.

$k_2$ es la columna donde se encuentra el primer elemento no nulo del renglón $2$, $k_2=3$.

$k_3$ es la columna donde se encuentra el primer elemento no nulo del renglón $3$, $k_3=4$.

Así, $k_1<k_2<k_3$.

Teorema

Sean $n$ y $m$ naturales positivos. Toda matriz $A\in \mathscr M_{m\times n}(\mathbb R)$ es equivalente por renglones a una matriz escalonada reducida por renglones.

Observación

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R).$ Toda columna no nula de $A$ se puede transformar en cualquier vector canónico de $\mathbb R^m$ con operaciones elementales.

La demostración se deja al lector.

Demostración del teorema

Sean $n$ y $m$ naturales positivos, $A\in \mathscr M_{m\times n}(\mathbb R)$. Dado que por definición la matriz nula es escalonada reducida por renglones, basta probar el resultado para las matrices no nulas. La prueba sea hará por inducción sobre $n.$

Base de inducción

Para $n=1$ el resultado se cumple por la observación.

Paso inductivo

Supongamos que toda matriz $m\times n$ es equivalente a una matriz escalonada reducida por renglones.

Ésta es la hipótesis de inducción.

Demostración de que se cumple para $n+1$ usando la HI

Sea $A\in \mathscr M_{m\times (n+1)}(\mathbb R)$, consideremos la matriz $\tilde {A}$, que se obtiene de $A$ quitando la última columna. Como $\tilde{A} \in \mathscr M_{m\times n}(\mathbb R)$, por la hipotesis de inducción $\tilde{A}$ es equivalente a una matriz $\tilde {R}$ escalonada reducida por renglones.

Sea $B$ la matriz que se obtiene de $A$ aplicando las operaciones que llevan a $\tilde {A}$ en $\tilde{R}$. Veamos cómo es $B$:

Si $\tilde{R}$ es nula, en $B$ sólo la ultima columna es no nula, entonces, como consecuencia de la observación, $B$ es equivalente a una matriz escalonada reducida por renglones.

Si $\tilde {R}$ es no nula, sea $r$ el número de renglones no nulos de $\tilde{R}$. En el caso en que $b_{r+1\,n+1}=\cdots =b_{m\,n+1}=0$, $B$ es escalonada reducida por renglones. En caso contrario, por la observación, la última columna de $B$ se puede transformar mediante operaciones elementales en el $(r+1)$-ésimo vector canónico, y aplicando dichas operaciones elementales a $B$ obtenemos una matriz $R$. Además, observemos que estas últimas operaciones elementales no modifican las primeras $n$ columnas, por lo que $R$ es una matriz escalonada reducida por renglones. Así $A\sim B$ y $B\sim R$, entonces $A\sim R$, con $R$ una matriz escalonada reducida por renglones.

Ejemplo

Matrices equivalentes	Operaciones elementales
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 2 & 8 & 1 & 3\\0 & 1 & 4 & 1 & 1\\ 0 & -3 & -12 & 0 & -3\\ 0 & 2 & 8 & -1 & 2 \\ \end{array} \right) \end{equation*}\sim$	$R_1\leftrightarrow R_2$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 1 & 1\\0 & 2 & 8 & 1 & 3\\ 0 & -3 & -12 & 0 & -3\\ 0 & 2 & 8 & -1 & 2 \\ \end{array} \right) \end{equation*}\sim$	$R_2\rightarrow R_2+(-2)R_1$ $R_3\rightarrow R_3+(3)R_1$ $R_4\rightarrow R_4+(-2)R_1$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 1 & 1\\0 & 0 & 0 & -1 & 1\\ 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & -3 & 0 \\ \end{array} \right) \end{equation*}\sim$	$R_2\leftrightarrow R_3$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 1 & 1\\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & -1 & 1\\ 0 & 0 & 0 & -3 & 0 \\ \end{array} \right) \end{equation*}\sim$	$\frac{1}{3}R_2$ $\frac{1}{3}R_4$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 & 1\\ 0 & 0 & 0 & -1 & 0 \\ \end{array} \right) \end{equation*}\sim$	$R_3\rightarrow R_3+R_2$ $R_4\rightarrow R_4+R_2$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right) \end{equation*}\sim$	$R_1\rightarrow R_1-R_2$ $R_1\rightarrow R_1-R_3$
$\begin{equation*} \left(\begin{array}{rrrrr} 0 & 1 & 4 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right) \end{equation*}$	Que es una matriz escalonada reducida por renglones.

Tarea Moral

$1.$ Escalona la matriz $A=\begin{equation*} \left(\begin{array}{rrrr} 1 & 2 & 5 & 13\\ -2 & -4 & -9 & 23 \\ 5 & 10 & 24 & 62 \end{array} \right) \end{equation*}$ y expresa el resultado como producto de matrices elementales.

$2.$ Describe la forma de todas las posibles matrices $2\times 2$ escalonadas reducida por renglones. Ahora considera el mismo problema para matrices $3\times 3$.

$3.$ Sea $A\in \mathscr M_{m\times n}(\mathbb R)$. ¿Cómo puedes transformar una columna no nula de $A$ en cualquier vector canónico de $\mathbb R^m$ con operaciones elementales?

$4.$ Escalona la matriz hasta llevarla a una matriz escalonada reducida por renglones.

$A= \begin{equation*} \left(\begin{array}{rrr} 2 & 2 & -10\\ 3 & -1 & -1 \\ 4 & -1 & -1\\ -2 & 1 & 2 \end{array} \right) .\end{equation*}$

Más adelante

En la siguiente nota daremos la definición de lo que es el rango de una matriz y veremos que el rango de una matriz $A$ y el rango de una matriz $R$ escalonada reducida por renglones equivalente a $A$ es el mismo.

Enlaces relacionados

Página principal del curso.

Enlace a la nota anterior. Nota 35. Operaciones elementales, matrices equivalentes y matrices elementales.

Enlace a la nota siguiente. Nota 37. El rango de una matriz.