3.1 Definiciones
Introducción
Se tiene una correspondencia geométrica fundamental, la cual implica la transformación de cada punto del plano en una línea recta única y viceversa, mediante el uso de una circunferencia. La línea recta vinculada a un punto se denomina la polar de dicho punto, mientras que el punto mismo recibe el nombre de polo de la línea, es por ello que estudiaremos el tema de Polos y Polares.
Definición (Polos y Polares)
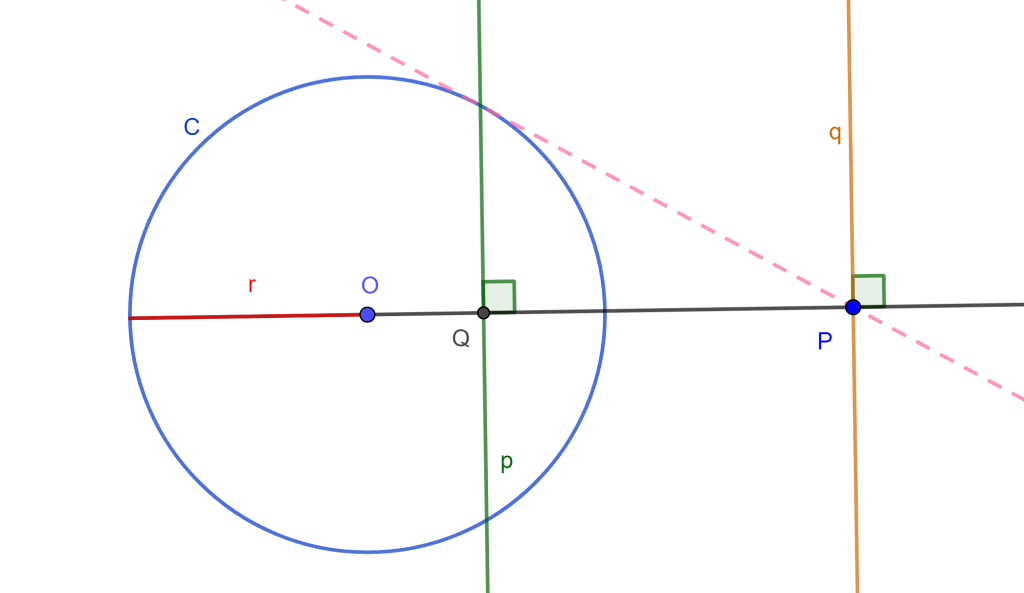
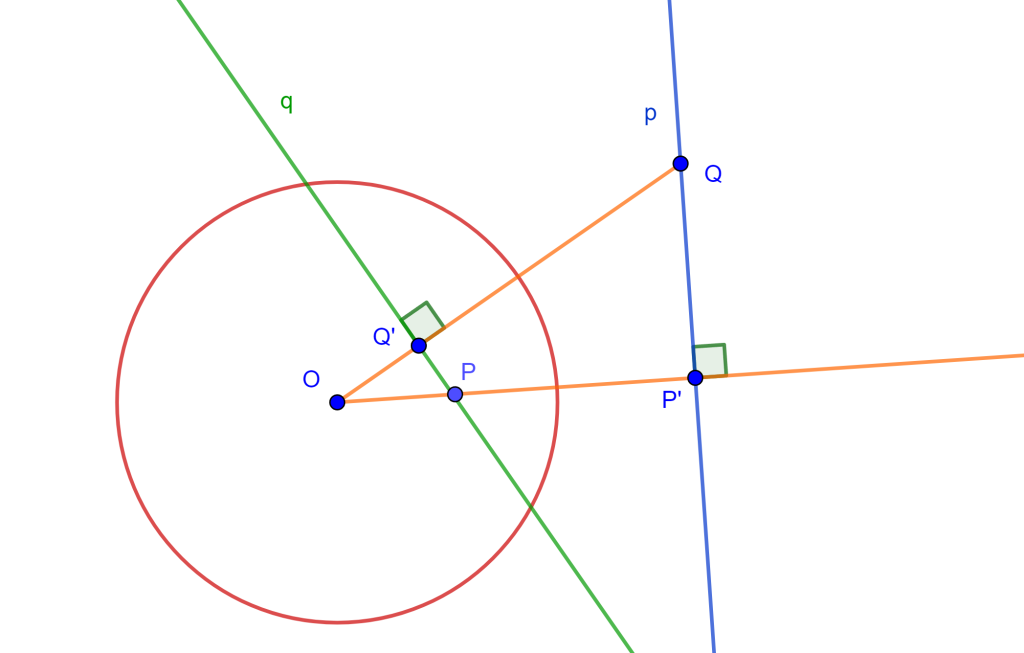
Dada una circunferencia $C(O,r)$, dos puntos inversos $P$ y $Q$ respecto a $C(O,r)$. Sea $p$ la perpendicular a $OQ$ y que pasa por $Q$, y sea $q$ la perpendicular a $OP$ y pasa por $P$.
Entonces se dirá que «$p$ es la recta polar de $P$» y «$q$ es la recta polar de $Q$» ambas respecto a $C$. De igual forma se dirá que «$Q$ es el polo de $q$» y «$P$ es el polo de $p$» ambos respecto a $C$.
Se cumplen varias propiedades:
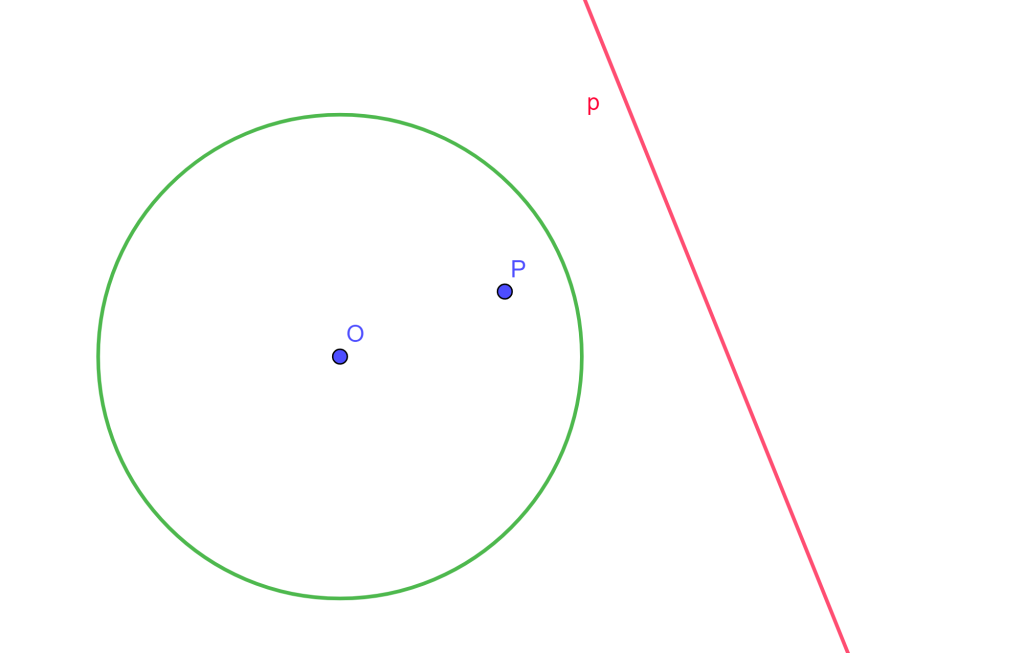
1.- Si $P$ es un punto exterior a la circunferencia, entonces $p$ es secante a la circunferencia $C$.
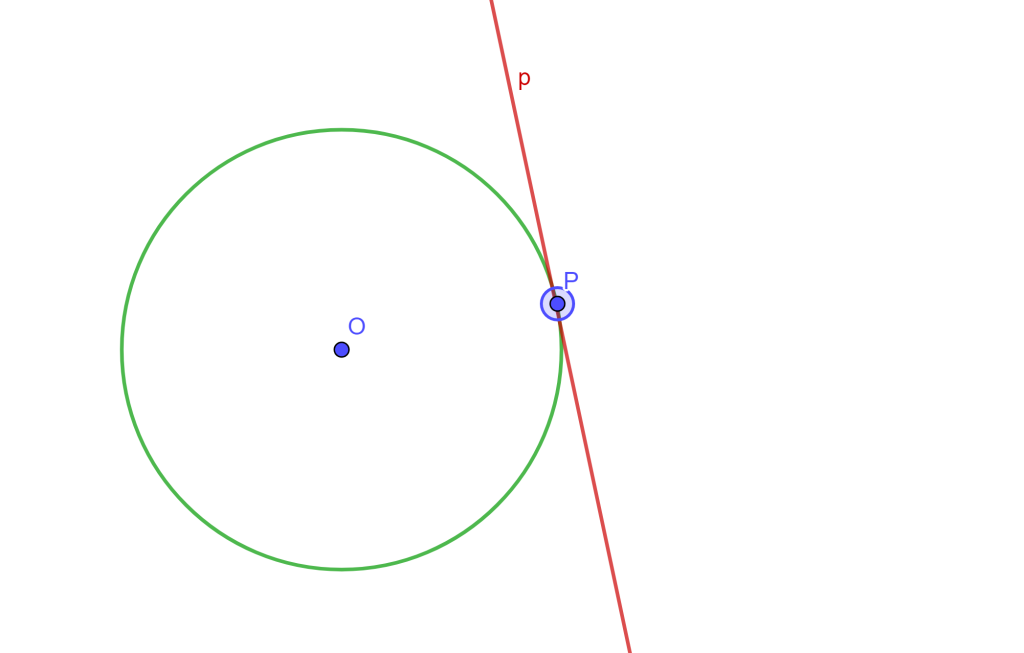
2.- Si $P$ es un punto de $C$, entonces $p$ es tangente a la circunferencia $C$.
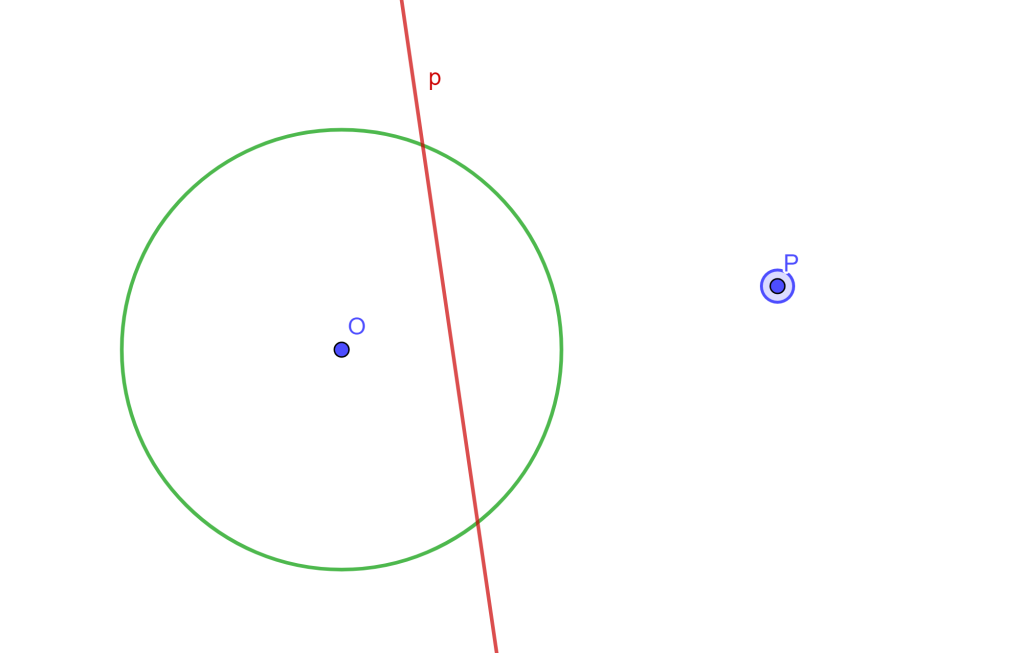
3.- Si $P$ es un punto interior a $C$, entonces $p$ es ajena a la circunferencia $C$.
4.- La polar del centro de la circunferencia es la línea al infinito, y el polo de un diámetro de circunferencia $C$ es un punto al infinito.
Teorema (Fundamental de Polos y Polares)
Si respecto a una circunferencia dada $C(O,r)$, la polar de $P$ pasa por $Q$ entonces la polar de $Q$ pasa por $P$. A las rectas $p$ y $q$, se les llama conjugadas polares y, a los puntos $P$ y $Q$ se les denomina conjugados polares.
Demostración
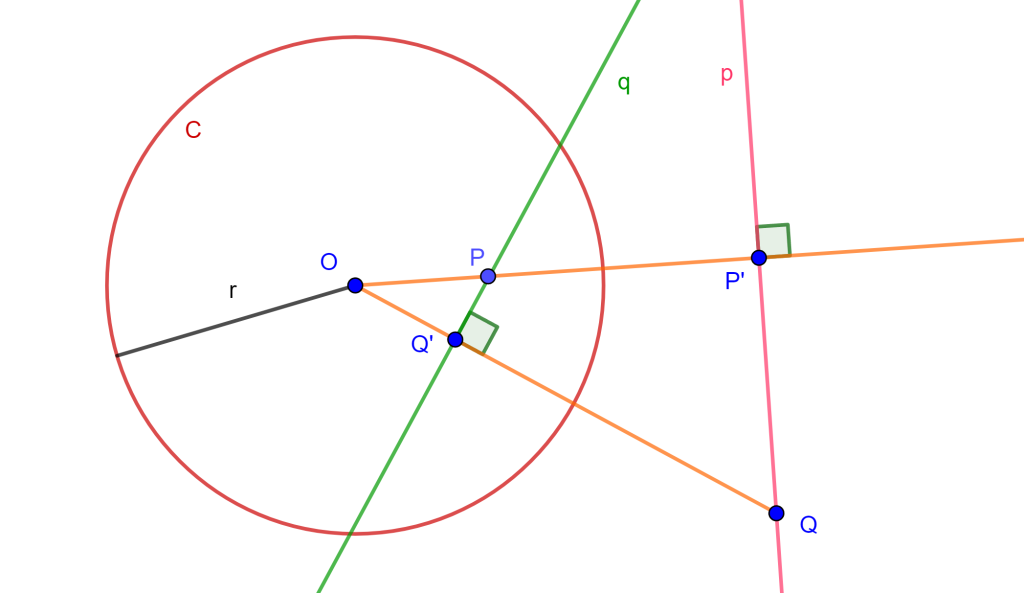
Se tiene que $p$ es la polar de $P$ y $Q$ pertenece a $p$, ahora se tiene que $Q’$ es el inverso de $Q$ entonces $OP \times OP’ = r^2 = OQ \times OQ’$, por lo cual se tiene un cuadrilátero cíclico $PP’QQ’$, entonces $Q’P$ es perpendicular a $OQ$.
Por lo tanto, $Q’P=q$ es polar de $Q$. $_\blacksquare$
Corolario (Polos y Polares)
Sean $p$ y $q$ líneas tales que, con respecto a una circunferencia $C$ dada, se dice que el polo de $p$ está en $q$, entonces el polo de $q$ está en $p$.
Demostración
Dadas $p$ y $q$ dos rectas y $P$ el polo de $p$, supongamos que $P$ está en $q$.
Sea $P’$ el inverso de $P$ y $P’$ perteneciente a $p$. Sean $OQ’$ perpendicular a $q$ y $Q$ es $OQ’$ intersección con $p$, pero $PQ’QP$ es un cuadrilatero ciclico, la circunferencia que lo contiene es ortogonal a $C$ y su inversa respecto a $C$ es ella misma, también $OP \times OP’ = OQ \times OQ’ = r^2$
Entonces $Q$ y $Q’$ son inversas, por lo tanto, $Q$ es polo de $q$. $_\blacksquare$
«Se puede decir que las polares de una hilera son las líneas de un haz y que los polos de las líneas de un haz son los puntos de una hilera.»
Definición (Puntos Conjugados)
Dados dos puntos $P$ y $Q$ con respecto a una circunferencia, tales que la polar de uno pasa por el otro, diremos que $P$ y $Q$ son puntos conjugados respecto a la circunferencia $C$.
Definición (Líneas Conjugadas)
Respecto a una circunferencia $C$, se tienen dos líneas $p$ y $q$ tales que el polo de una está en el otro, se dirá que $p$ y $q$ son rectas conjugadas respecto a la circunferencia $C$.
Se tienen las siguientes propiedades:
1.- De dos puntos conjugados distintos en una línea que interseque la circunferencia, uno está dentro y el otro fuera de la circunferencia.
Demostración
Sea $r$ la línea que contiene a $P$ y $Q$, sea $R$ el polo de $r$ por lo cual la polar de $R$ es $r$ y pasa por $P$, entonces la polar de $P$ pasa por $R$, ahora como $P$ y $Q$ son conjugados entonces la polar de $P$ pasa por $Q$, por lo cual la polar de $P$ es la línea $RQ$ !
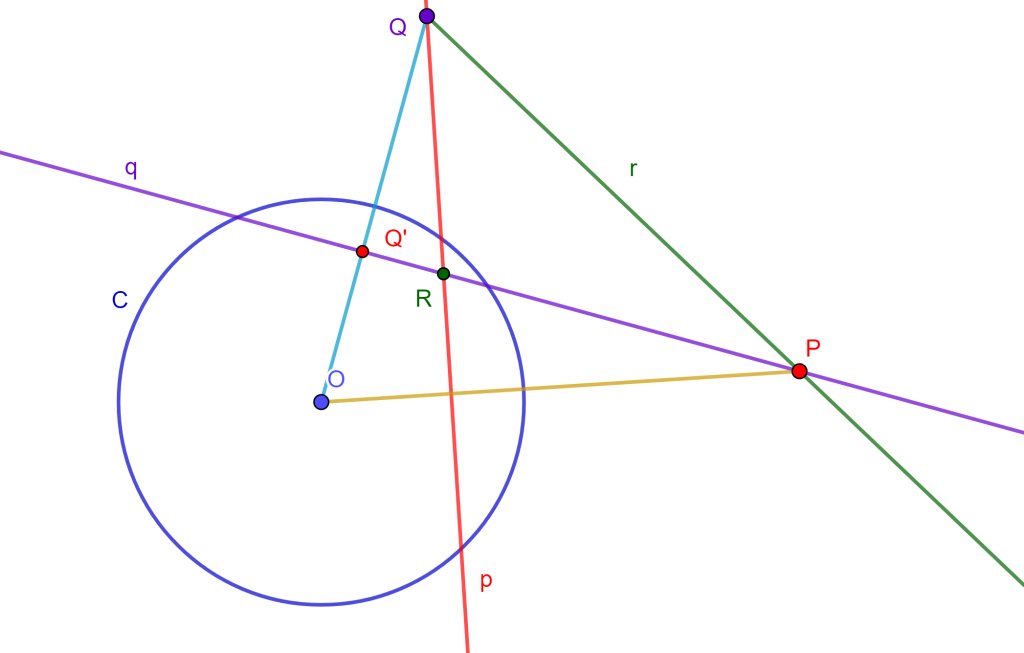
Por lo tanto, uno de los dos puntos conjugados está dentro y el otro afuera de la circunferencia. $_\blacksquare$
2.- Dadas dos líneas distintas conjugadas que se intersecan fuera de la circunferencia, una corta la circunferencia y la otra no.
3.- Cualquier punto en la circunferencia es conjugado a todos los puntos de la tangente en ese punto.
4.- Cualquier tangente a la circunferencia es conjugada a todas las líneas por su punto de contacto.
Más adelante…
La relación armónica está relacionada con respecto a lo hablado de polos y polares, por lo cual más adelante se hablara sobre teoremas relacionados con ambos temas.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Ejercicios Unidad 2 Inversión
- Siguiente entrada del curso: Relaciones Armónicas