3.2 Relaciones Armónicas
Introducción
Uno de los aspectos importantes de esta unidad es la teoría de la división armónica, la cual se relaciona con la teoría de los polos y polares, para ello veremos unos teoremas respecto a las relaciones armónicas ejemplificando esto.
Teorema
Sean dos puntos conjugados $A$ y $B$ respecto a una circunferencia $C(O,r)$, donde $A$ está dentro y $B$ está fuera, entonces $A$ y $B$ son armónicos respecto a los puntos de intersección en donde la recta que une a $A$ y $B$ se determina con la circunferencia $C$.
Demostración
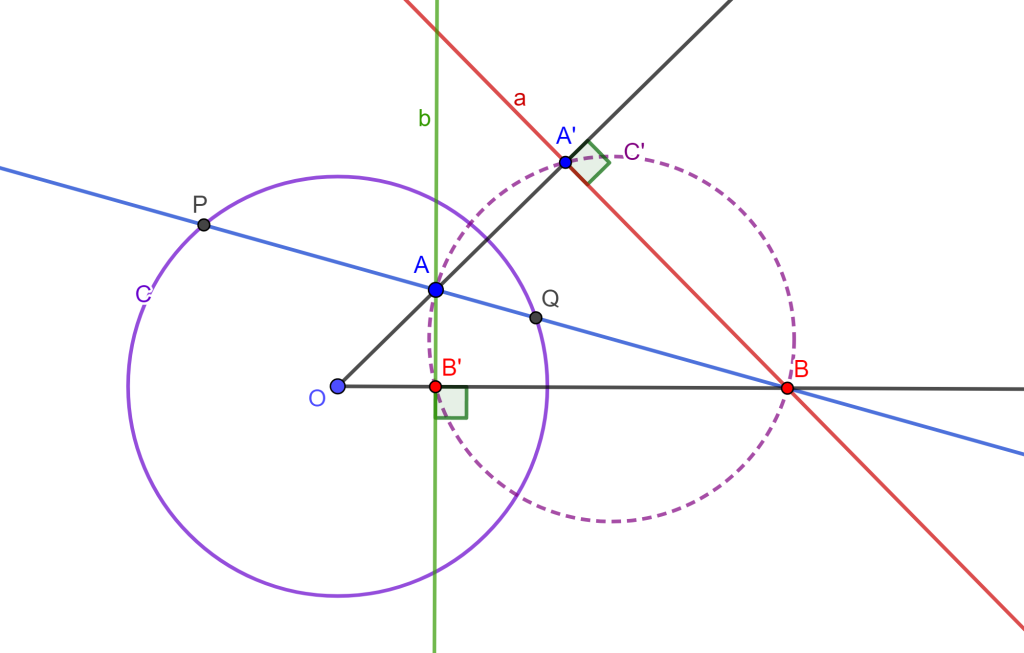
Dada una circunferencia $C(O,r)$ y dos puntos $A$ dentro de $C$ y $B$ fuera de $C$. La recta $AB$ corta a $C$ en dos puntos $P$ y $Q$, sea $a$ la polar de $A$ y $b$ la polar de $B$, por lo cual $b$ pasa por $A$ y $a$ pasa por $B$.
Ahora se tienen los inversos de $A$ y $B$ que son $A’$ y $B’$ correspondientemente, se tiene que $a$ es perpendicular a $OA’$ por $A’$ y $b$ es perpendicular a $OB’$ por $B’$, de esta forma el cuadrilátero $B’BA’A$ es cíclico y su circunferencia es perpendicular a $C(O,r)$, y se sigue que $AB$ es diámetro de $C(O,r)$. Por lo tanto, $A$ y $B$ son armónicos respecto a $P$ y $Q$. $_\blacksquare$
Teorema
Sea $C(O,r)$ una circunferencia dada, dos líneas conjugadas se intersecan fuera de $C$, están separadas armónicamente por las tangentes de sus puntos de intersección.
Demostración
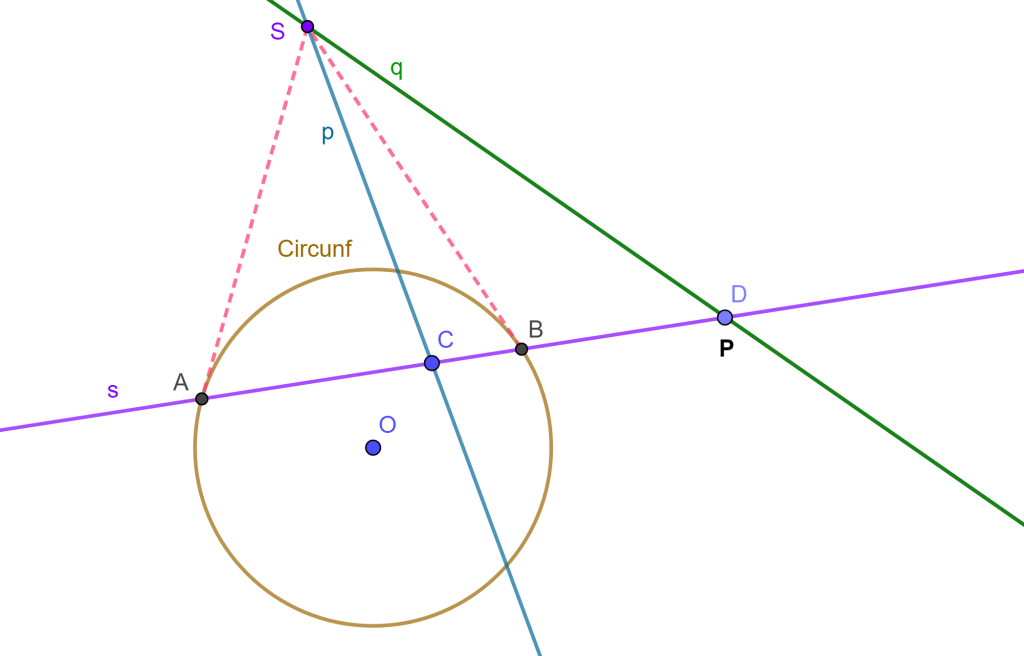
Sean $p$ y $q$ las dos rectas conjugadas, tal que $p$ corta a $C(O,r)$ y $q$ no corta a $C(O,r)$. El punto de intersección de $p$ y $q$ es $S$ fuera de $C(O,r)$.
Sea $P$ el punto de $p$ donde $P$ pertenece a $q$, la polar de $S$ es $s$ que pasa por $C$ donde $C$ es la intersección de $p$ y $s$, entonces la polar de $C$ pasa por $S$. También la polar de $P$ es $p$ que pasa por $C$ entonces la polar de $C$ pasa por $P$, entonces su polar es $q$ y también la polar de $C$ pasa por $D$, por lo cual la polar de $D$ pasa por $C$.
Por lo cual $C$ y $D$ son conjugados respecto a $C(O,r)$, entonces $C$ y $D$ son conjugados respecto a $A$ y $B$. Por lo tanto, $p$ y $q$ son armónicos respecto a $SA$ y $SB$. $_\blacksquare$
Teorema
Sea $C(O,r)$ una circunferencia, $p$ una recta y sean $A,B,C,D$ cuatro puntos armonicos sobre la recta, $p$, si $a,b,c,d$ son las polares respecto a $C(O,r)$ de $A,B,C,D$ entonces $a,b,c,d$ son líneas armónicas, entonces el haz $P{a,b,c,d}$ es armónico.
Demostración
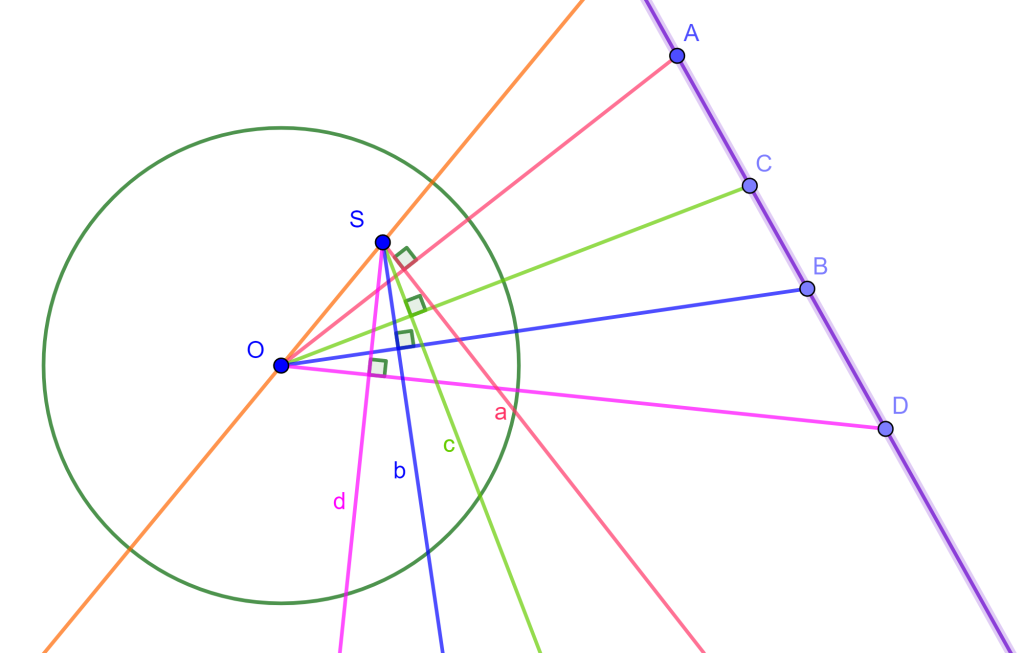
Se tienen $A,B,C,D$ puntos armónicos dados, con sus respectivas polares $a,b,c,d$ las cuales pasan por un punto $S$, el cual es el polo de la recta en la cual están los puntos. Ahora cada polar es perpendicular a la recta que une su polo con el centro de la circunferencia $C(O,r)$, y además el ángulo entre dos líneas cualesquiera del haz $O(ABCD)$ es igual al ángulo entre las rectas correspondientes del haz $a,b,c,d$. Por lo cual el haz $P{a,b,c,d}$ es armónico. $_\blacksquare$
Más adelante…
Se abordará el tema de dualidad desde un punto de vista teórico, y también se analizará los triángulos autopolares.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Unidad 3 Polos y Polares
- Siguiente entrada del curso: Principio de Dualidad y Triángulo Autopolar
