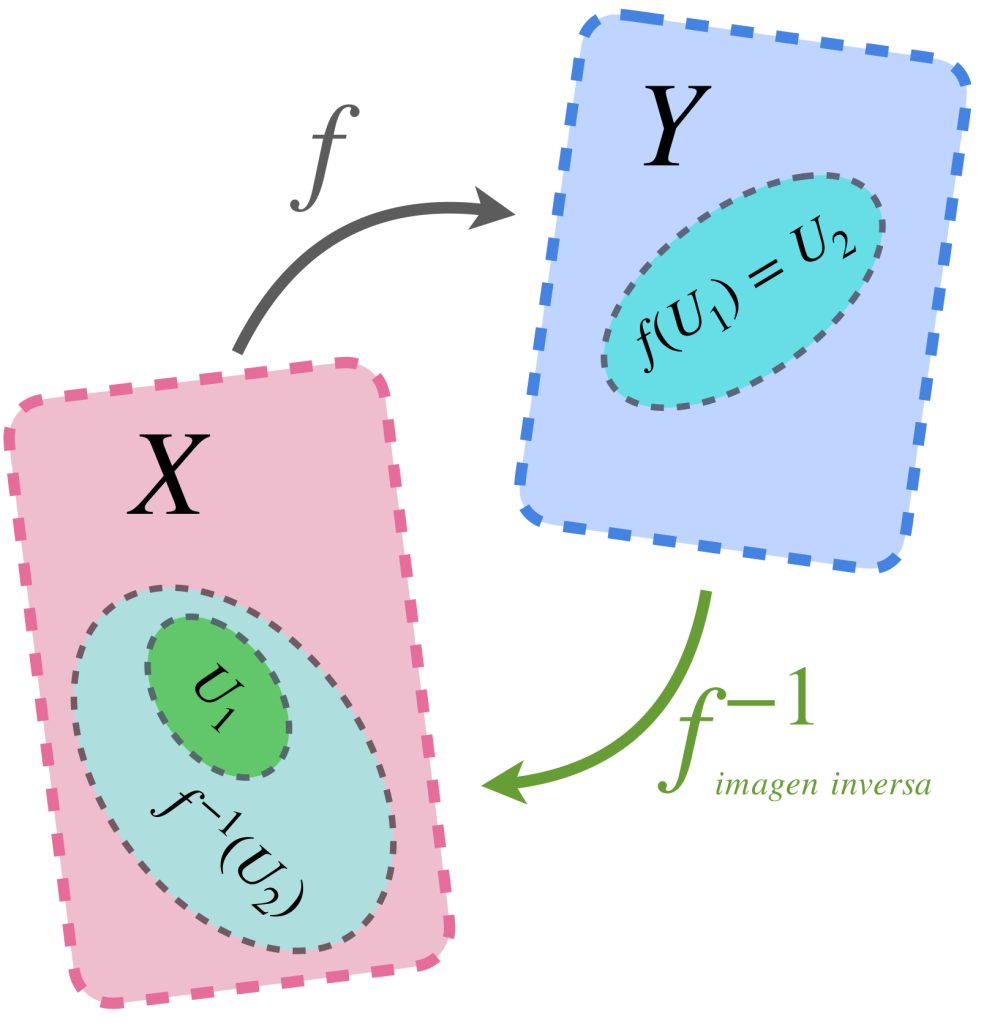
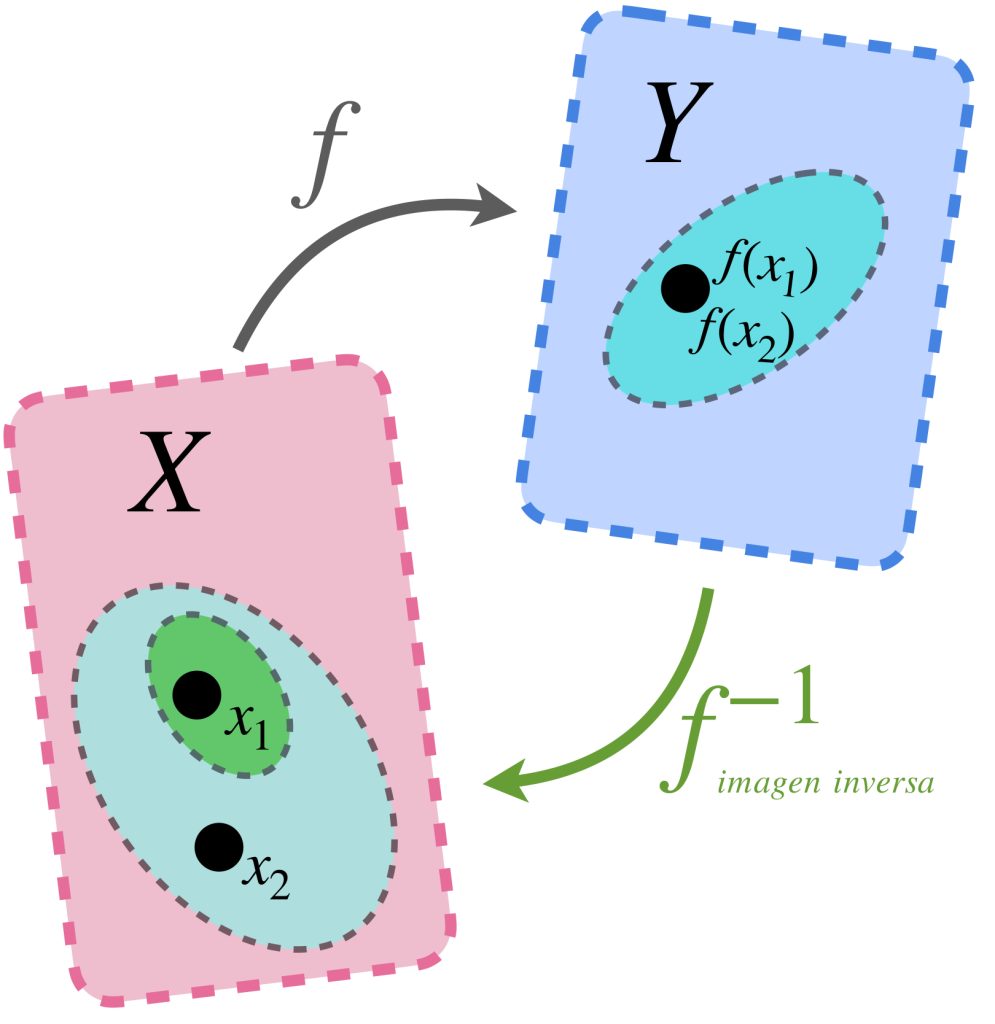
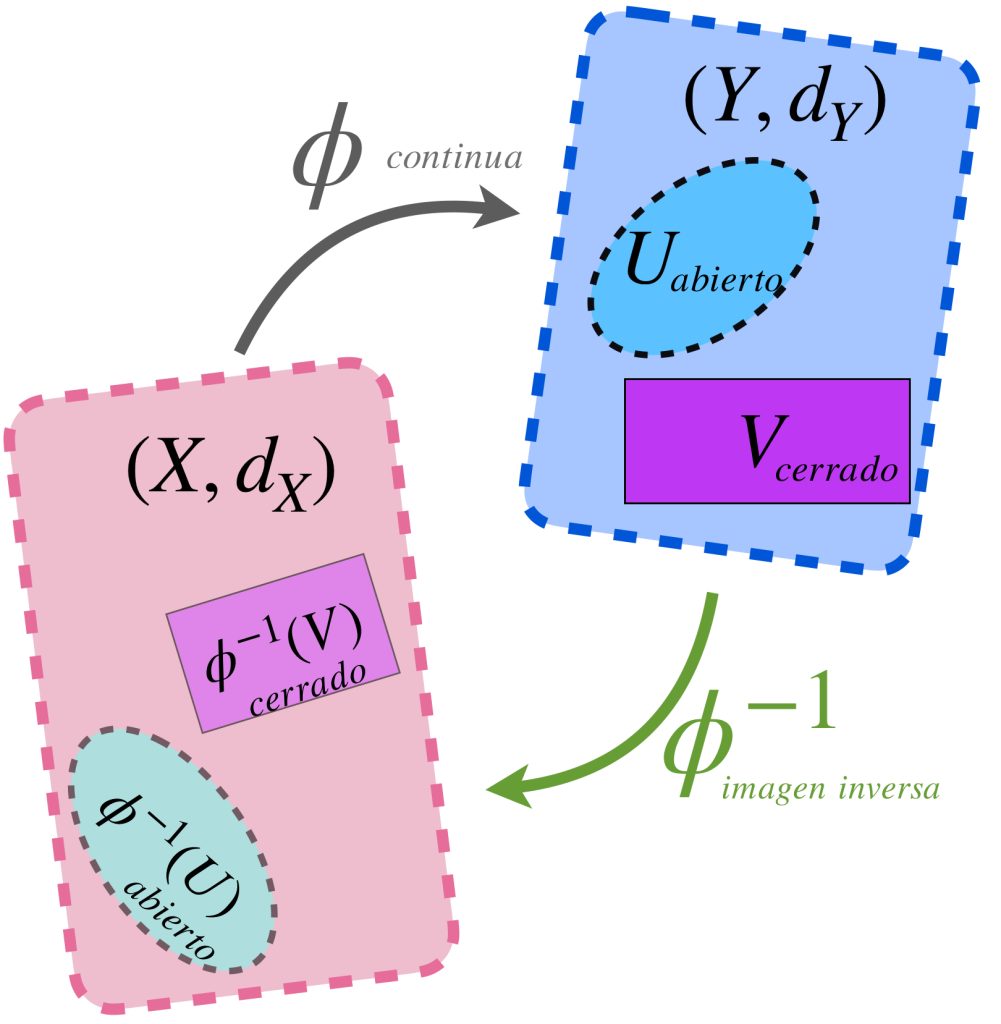
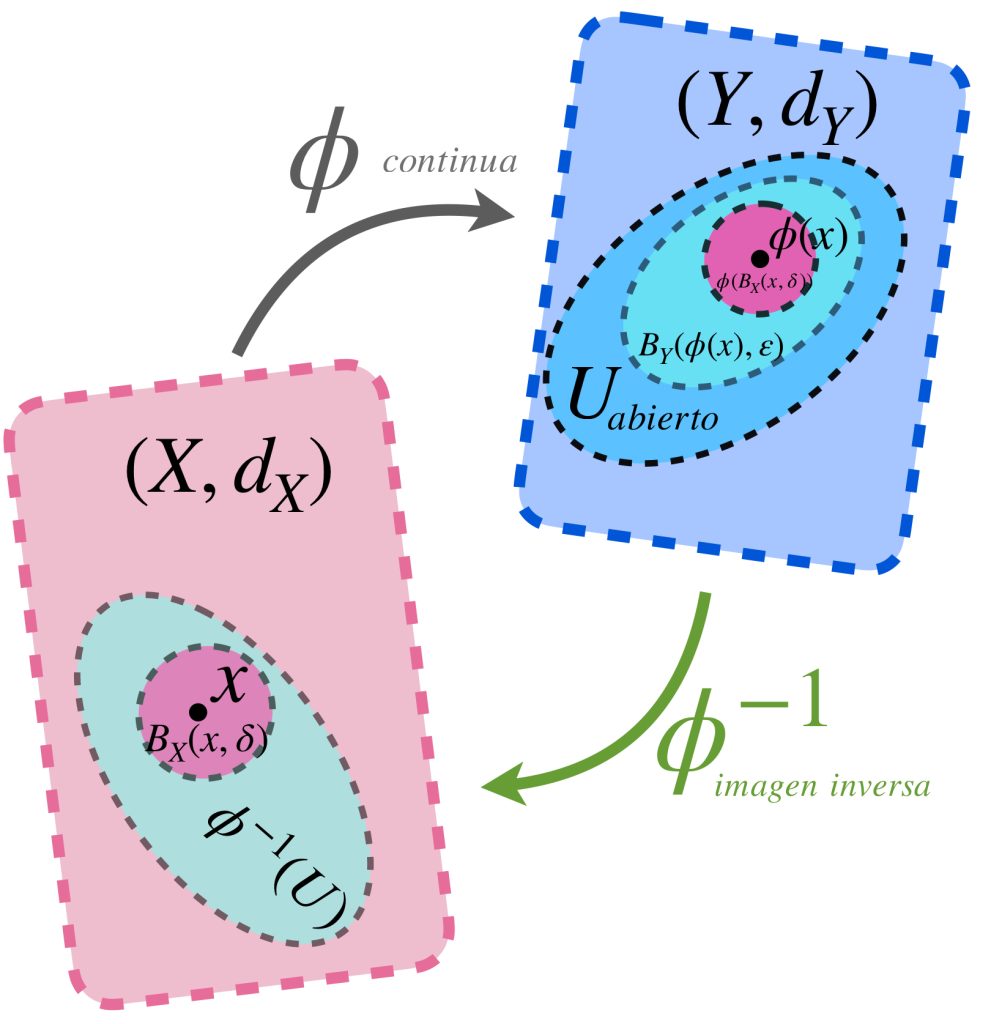
$ \textit{ MATERIAL EN REVISIÓN}$
El contenido de esta sección corresponde al artículo
Solís, DA, et.al, Abstraction and Application de la Universidad Autónoma de Yucatán, De la Geometría Riemanniana a los Espacios de Alexandrov I. Estructuras por Caminos y Métricas Inducidas: UADY, Mérida, 2015, págs 18-41.
Introducción
En las ideas más abstractas de espacios métricos, se relacionan dos puntos con un número mayor o igual que cero en los reales. Si bien, este número representa la distancia entre dos puntos, puede que en principio no esté muy claro cómo se originó esa distancia, o bien, qué camino se recorrió para llegar de un punto al otro y entonces sí, justificar de alguna forma, qué tan cerca o lejos están los puntos entre sí.
No obstante, hemos visto ejemplos de espacios métricos en los que sí fue un desplazamiento lo que inspiró la métrica definida, (como en la métrica del taxista, la del ascensor o la de las piezas de ajedrez). En esta sección observaremos que es posible definir una métrica en un conjunto a partir de la existencia de caminos que «conecten» a sus puntos. Comenzamos presentando una definición más general que la de los abiertos generados por una métrica:
Definición. Topología. Sea $X$ un conjunto, diremos que $\tau$ es una topología de $X$ si es una familia de subconjuntos de $X$ (que llamaremos abiertos) que satisface lo siguiente:
1) Los conjuntos $X$ y $\emptyset$ son abiertos.
2) La unión arbitraria de conjuntos abiertos $\underset{\alpha \in \mathbb{A}} {\cup} \, U_{\alpha}$ es un conjunto abierto.
3) La intersección finita de conjuntos abiertos $\underset{1\leq i \leq n}{\cap}U_i$ es un conjunto abierto.
Al conjunto $(X,\tau)$ lo llamaremos espacio topológico.
Ya que los abiertos de un espacio métrico satisfacen las condiciones anteriores, se puede concluir que un espacio métrico es también un espacio topológico.
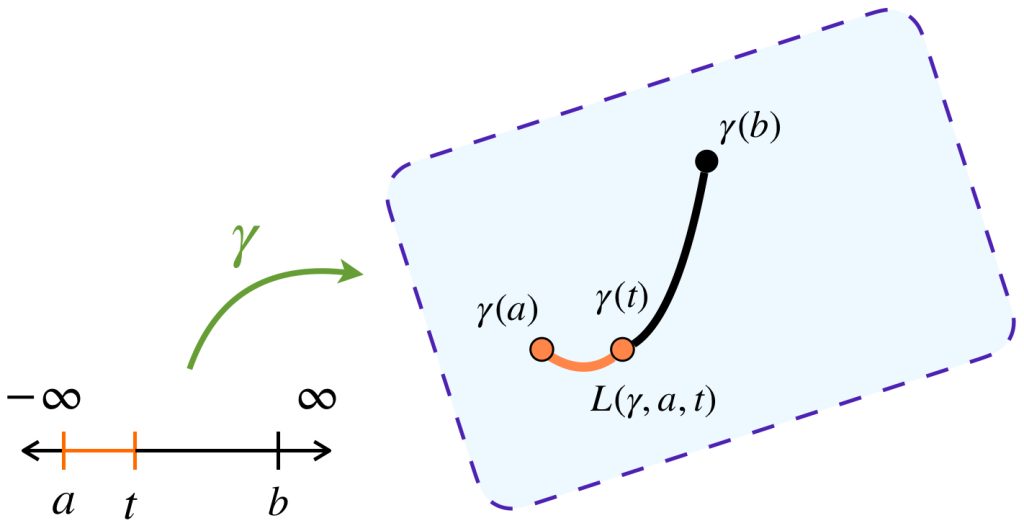
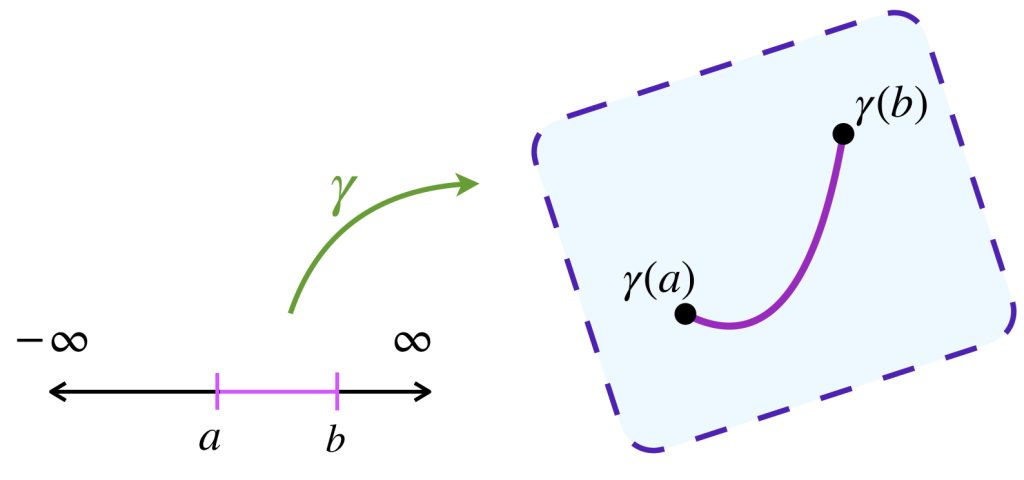
Definición. Camino. Un camino en un espacio topológico $(X, \tau)$ es una función continua $\gamma: I \to X$ donde $I=[a,b] \subset \mathbb{R}$.
Definición. Estructura por caminos. Sea $(X, \tau)$ un espacio topológico. Una estructura por caminos $(\mathcal{C},L)$ en $X$ es una clase $\mathcal{C}$ de caminos en $X$, que llamaremos admisibles. Se les asocia una función $L: \mathcal{C} \to [0, \infty]$ que llamaremos longitud de caminos.
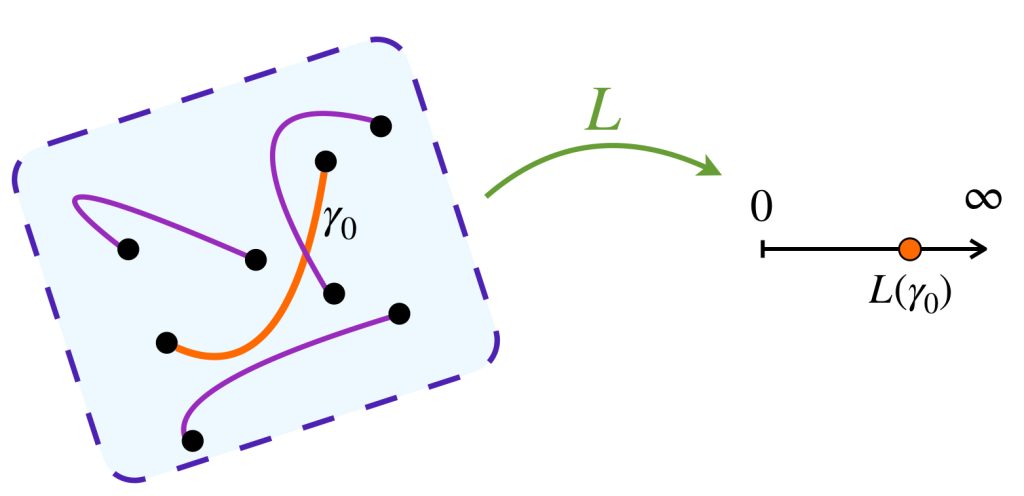
La clase $\mathcal{C}$ satisface las siguientes condiciones:
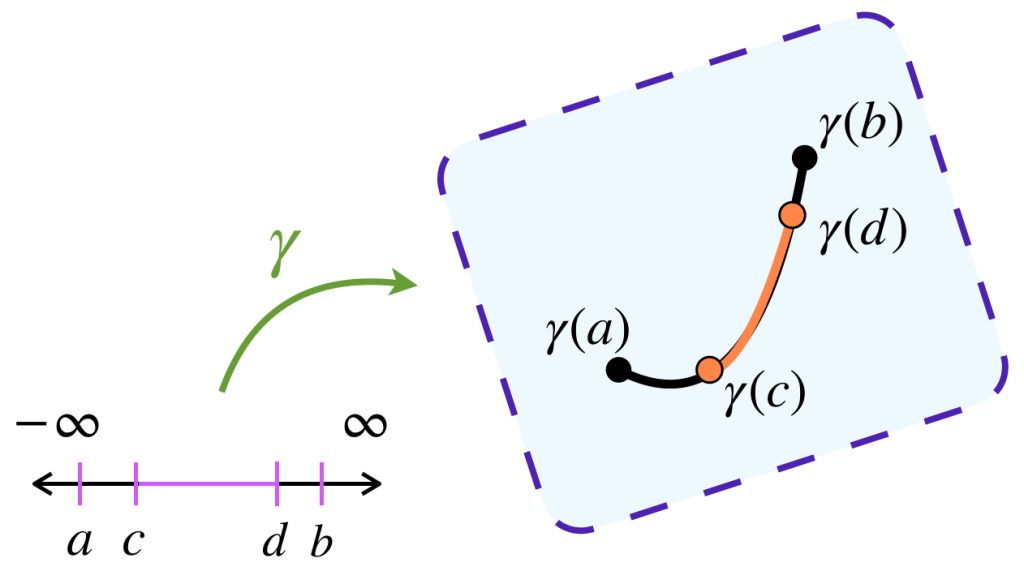
1. $\mathcal{C}$ es cerrado bajo restricciones: Si $\gamma: [a,b] \to X$ es un camino admisible y $a \leq c \leq d \leq b,$ entonces la restricción de $\gamma$ en $[c,d]$, denotada como $\gamma |_{[c,d]} \,$ también es un camino admisible.
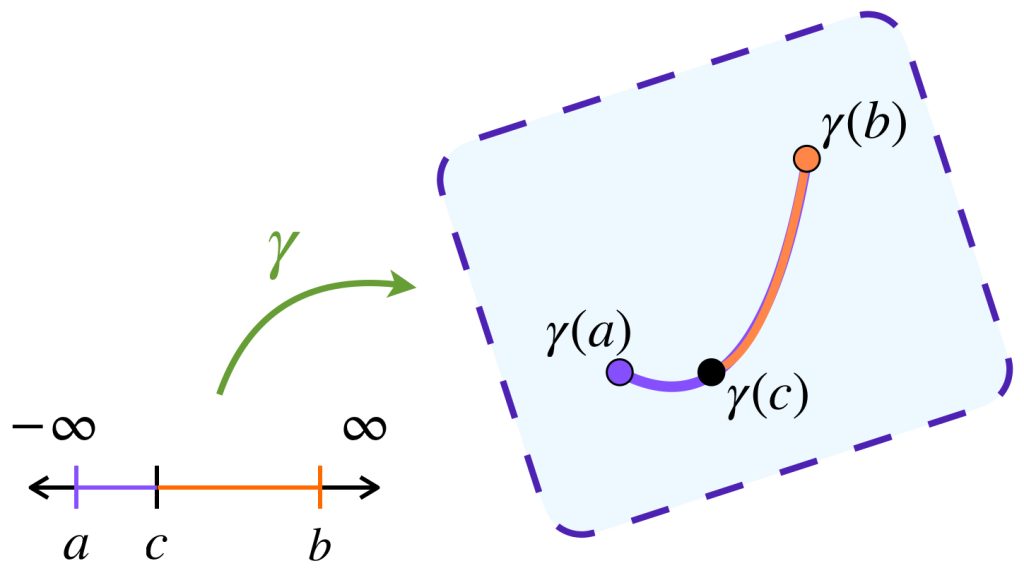
2. $\mathcal{C}$ es cerrado bajo concatenaciones de caminos: Si $\gamma: [a,c] \to X$ y $\gamma: [c,b] \to X$ son caminos admisibles, entonces también lo es $\gamma:[a,b] \to X =: \gamma |_{[a,c]} \cdot \gamma |_{[c,b]}$
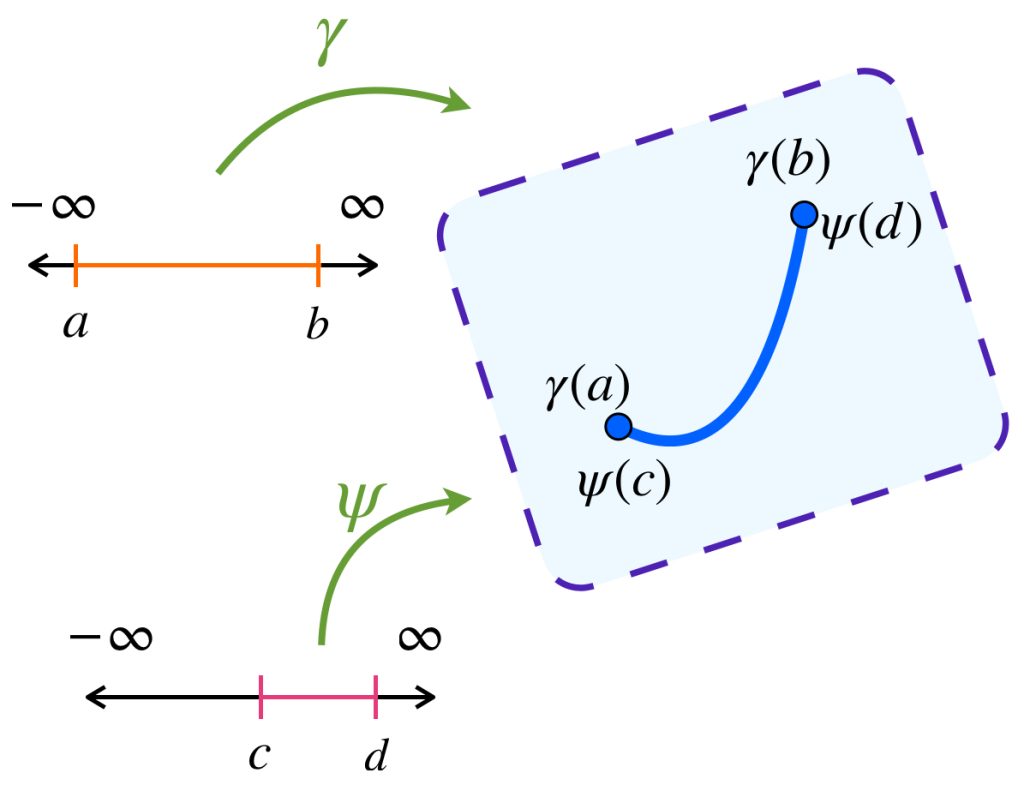
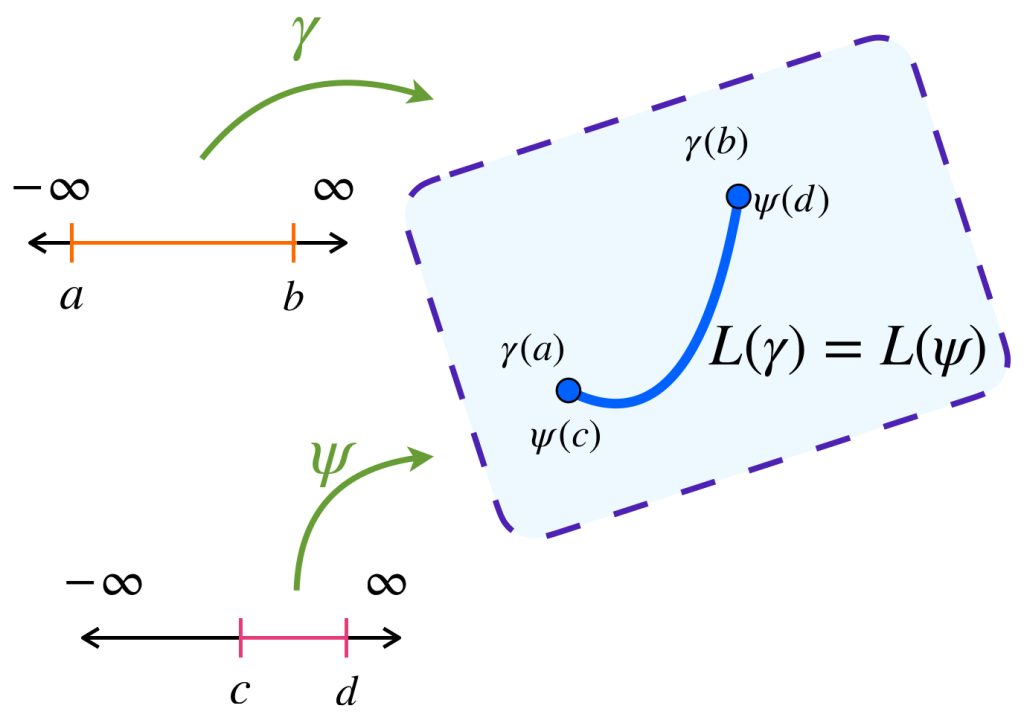
3. $A$ es cerrado bajo reparametrizaciones lineales. Si $\gamma:[a,b] \to X$ es un camino admisible, una reparametrización $\psi:[c,d] \to X$ que represente la curva de la misma forma, también será un camino admisible.
Mientras que la función $L$ cumple que:
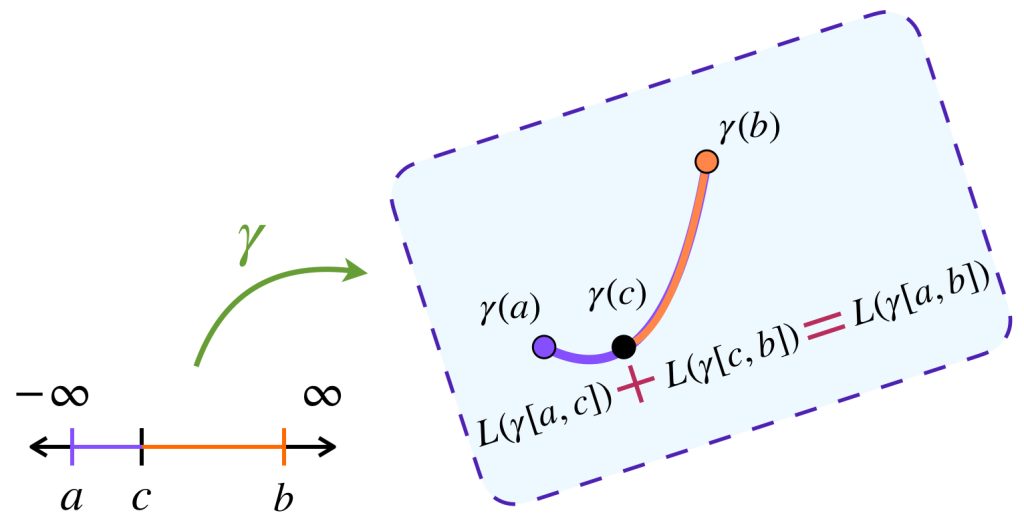
1. La longitud de caminos es aditiva: $$L(\gamma|[a,b])=L(\gamma|[a,c])+L(\gamma|[c,b])$$ para cualquier $c \in [a,b].$
2. Para un camino de longitud finita $\gamma:[a,b] \to X$ definimos $L(\gamma,a,t):= L(\gamma|[a,t])$. Entonces esta función es continua en $[a,b].$
3. Si $\gamma:[a,b] \to X$ es un camino admisible y $\phi:[c,d] \to X$ es una reparametrización de $\gamma$ entonces $L(\gamma)=L(\psi).$
Ahora definamos una distancia en el conjunto $X$ a partir de una estructura por caminos $(\mathcal{C},L)$. Para cualesquiera dos puntos $x,y \in X$ consideremos la longitud de todos los caminos que conectan a $x$ con $y$. El ínfimo de esas longitudes será la distancia entre ambos puntos, es decir:
$$d_L(x,y):=inf\{L(\gamma): \gamma:[a,b] \to X, \gamma \in \mathcal{C}, \gamma (a)=x , \gamma (b) =y \}$$
Si no existe un camino que conecte a $x$ con $y$ se define $d_L(x,y) = \infty$
Entonces $(X,d_L)$ es un espacio métrico, siendo $d_L$ la métrica inducida por la estructura por caminos $(\mathcal{C},L)$.
Definición. Espacio métrico de caminos. Un espacio métrico cuya métrica puede ser obtenida como la función distancia de una estructura por caminos es llamado espacio métrico de caminos. La distancia asociada recibe el nombre de métrica intrínseca.
Ejemplos
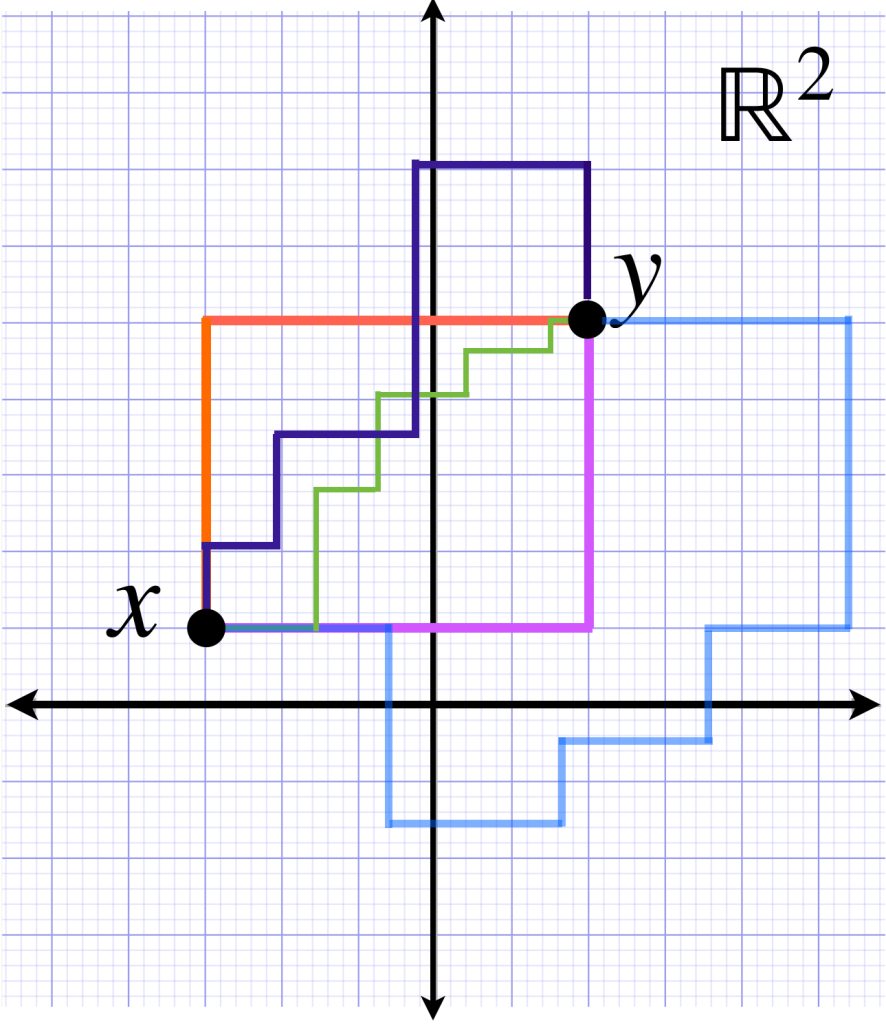
En el conjunto $\mathbb{R}^2$ considera los caminos que unen a cualesquiera dos puntos $x,y \in \mathbb{R}^2$ a través de la concatenación de segmentos que son paralelos a los ejes coordenados. Como ejemplo presentamos la siguiente imagen:
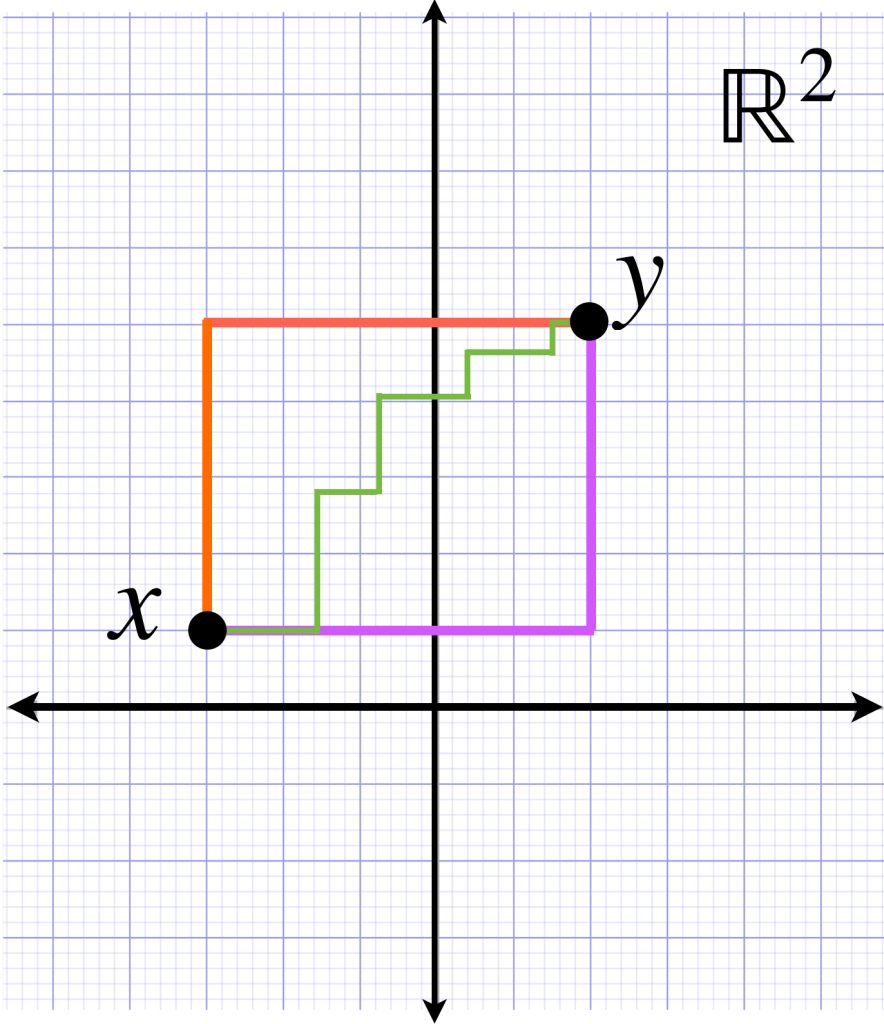
Eso significa que la distancia $d_L(x,y)$ corresponderá al ínfimo de las longitudes de estos caminos. En este caso, el valor del ínfimo coincide con la longitud de los caminos que son de este estilo:
En la entrada Otros ejemplos de espacios métricos vimos que esta métrica es conocida como métrica del taxista.
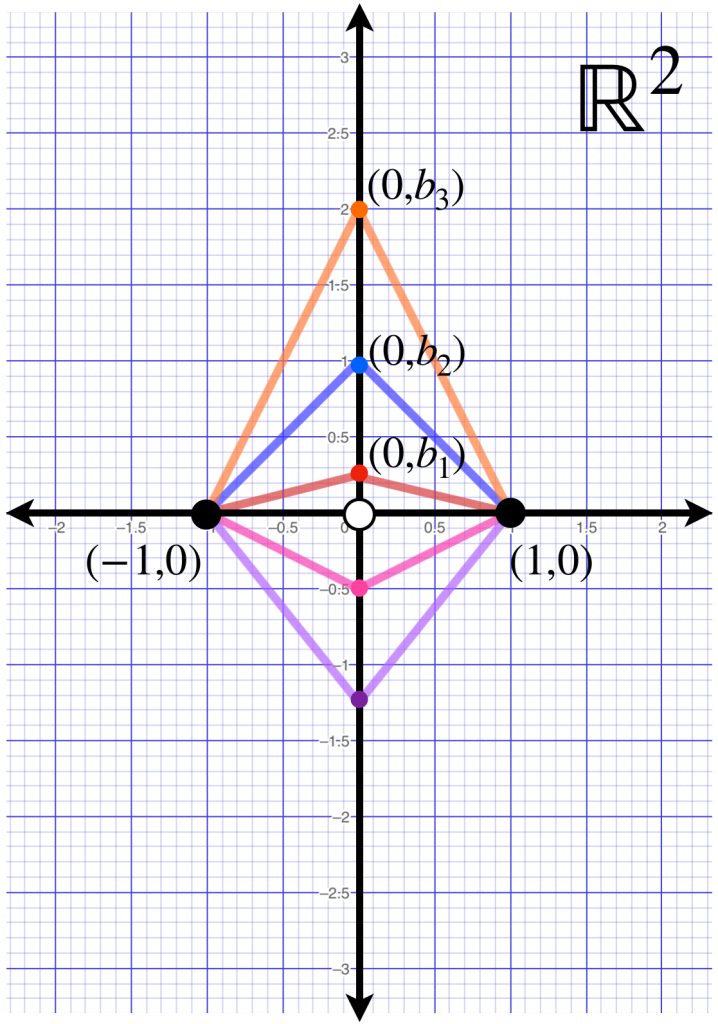
No todos los espacios métricos de caminos tendrán siempre un camino cuya longitud coincida con la distancia de los puntos que une. Por ejemplo, considera el espacio $\mathbb{R}^2 \setminus \{(0,0)\}$ Si los caminos que conectan a los puntos $(-1,0)$ y $(1,0)$ están dados por la unión de los segmentos $\overline{(-1,0),(0,b)}$ y $\overline{(0,b),(1,0)}$ como muestra la siguiente imagen:
Es posible probar que el ínfimo de estas longitudes es $2$, sin embargo, no existe un camino que tenga a $2$ como longitud. La justificación de esta conclusión se deja como ejercicio al final de esta sección.
Definición. Estructura por caminos completa. Cuando para cualesquiera puntos $x,y \in X$ sí existe un camino admisible cuya longitud coincide con $d_L(x,y)$ diremos que tenemos una estructura por caminos completa. La métrica que induce recibe el nombre de métrica estrictamente intrínseca.
Un subespacio que es posible deducir de un espacio métrico de caminos es uno restringido a los caminos en un conjunto. Lo expresamos en la siguiente:
Definición. Estructura restringida. Sea $(\mathcal{C},L)$ una estructura por caminos de $X,$ entonces induce una estructura por caminos $(\mathcal{C}|_A,L|_A)$ en un conjunto $A \subset X$ donde $\mathcal{C}|_A$ consiste de todos los caminos de $\mathcal{C}$ cuya imagen está totalmente contenida en $A$ y la función $L|_A$ es la restricción de de $L$ en $\mathcal{C}|_A$.
Es posible que en la estructura restringida las distancias entre dos puntos no se preserven.
Ejemplo
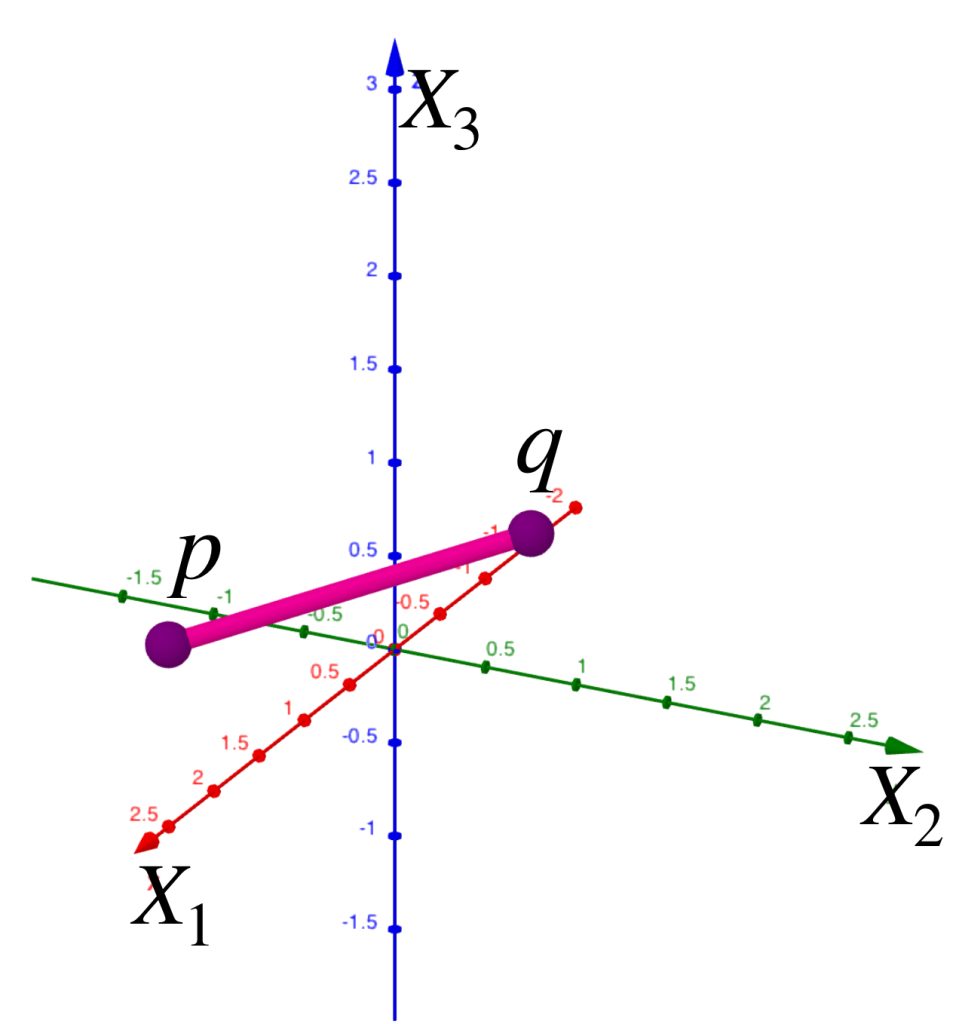
La distancia usual $\mathbb{R}^3$ puede verse como un espacio métrico de caminos donde la distancia entre dos puntos $p$ y $q$ está dada por la longitud del segmento que los une.
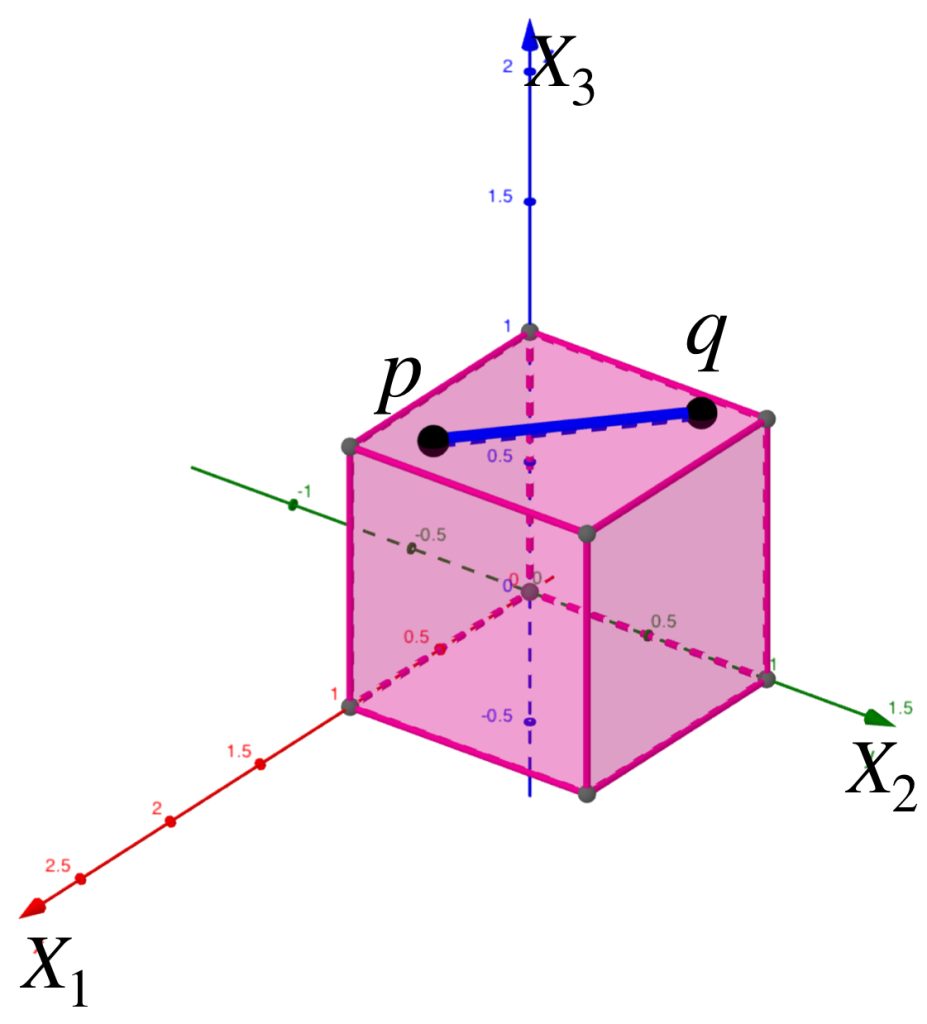
Si restringimos este espacio al conjunto $A= \partial([0,1]\times [0,1] \times [0,1])$ representado por las caras de un cubo de aristas de medida $1$, podemos verificar que cuando dos puntos $p,q \in A$ están en la misma cara del cubo, la distancia restringida coincide con la de la métrica usual.
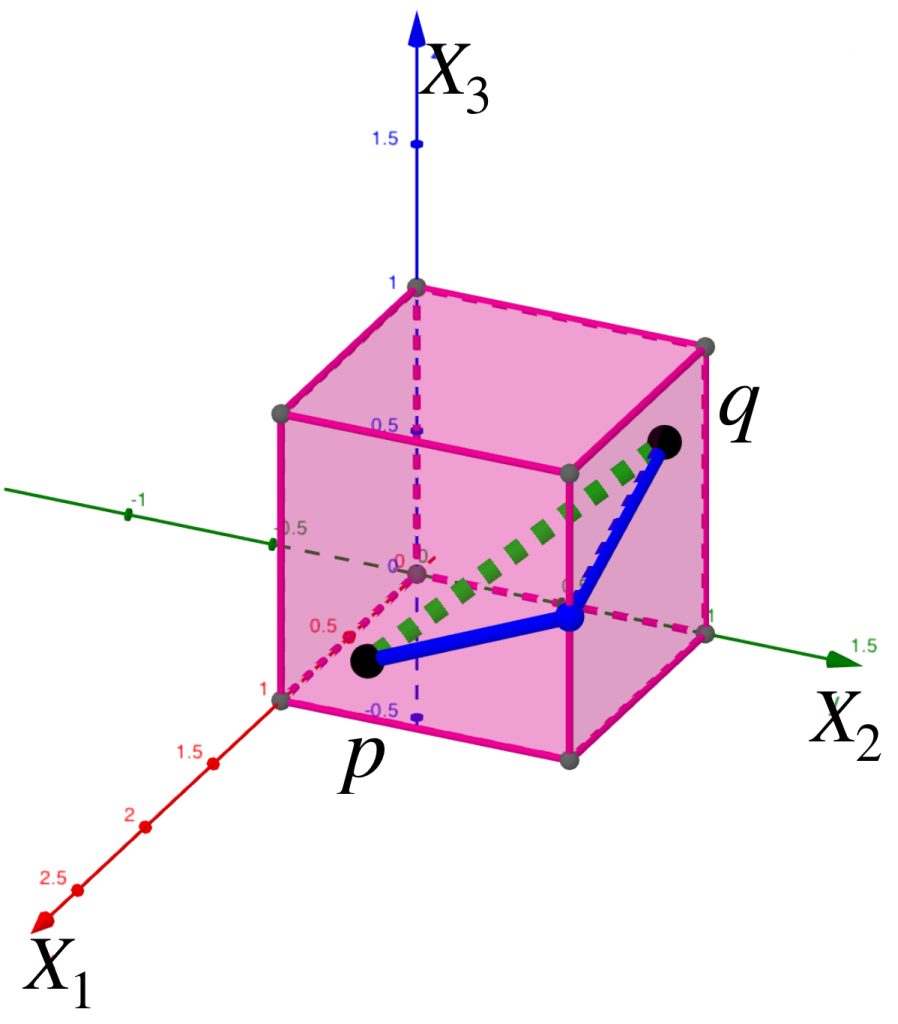
Pero cuando no es así, el segmento que los conecta no pertenece a $\mathcal{C}|_A$. En esta situación el “camino más corto” en $\mathbb{R}^3$ está dentro de las caras del cubo. Un camino que conecte a $p$ con $q$ tendrá distancia mayor. Se concluye que $d_{L_A}(x,y) \geq d_{L}(x,y).$
Más adelante…
Conoceremos sucesiones cuyos elementos se van aproximando de manera arbitraria pero que no necesariamente convergen. Veremos bajo qué condiciones sí se puede asegurar la convergencia. Esto incentivará un nuevo concepto, el de los espacios métricos completos.
Tarea moral
- En el espacio $\mathbb{R}^2 \setminus \{(0,0)\}$ del ejemplo anterior, donde los caminos que conectan a los puntos $(-1,0)$ y $(1,0)$ están dados por la unión de los segmentos $\overline{(-1,0),(0,b)}$ y $\overline{(0,b),(1,0)}$. Prueba que el ínfimo de las longitudes de estos caminos es $2$ y que no existe un camino que cuya longitud sea $2.$
- Demuestra que las piezas de ajedrez vista en la entrada Otros ejemplos de espacios métricos inducen una métrica de caminos.
- ¿Es la métrica del ascensor, vista en Otros ejemplos de espacios métricos, una métrica de caminos?