Introducción
Las funciones continuas resultan muy útiles al relacionar espacios métricos. Propiedades identificadas en el dominio pueden conservarse también en el contradominio y viceversa.
En esta sección presentaremos definiciones más específicas para funciones continuas que reúnen ciertas características. Si una función es aplicada a dos puntos, ¿qué ocurre con la distancia en los puntos del espacio en el que caen? Ya sabemos que podemos hacer la distancia muy cercana si se toma como referencia un punto donde la función es continua pero, ¿habrá casos donde existan funciones que restrinjan la distancia de un modo más general, para todos los puntos? Comencemos con la siguiente:
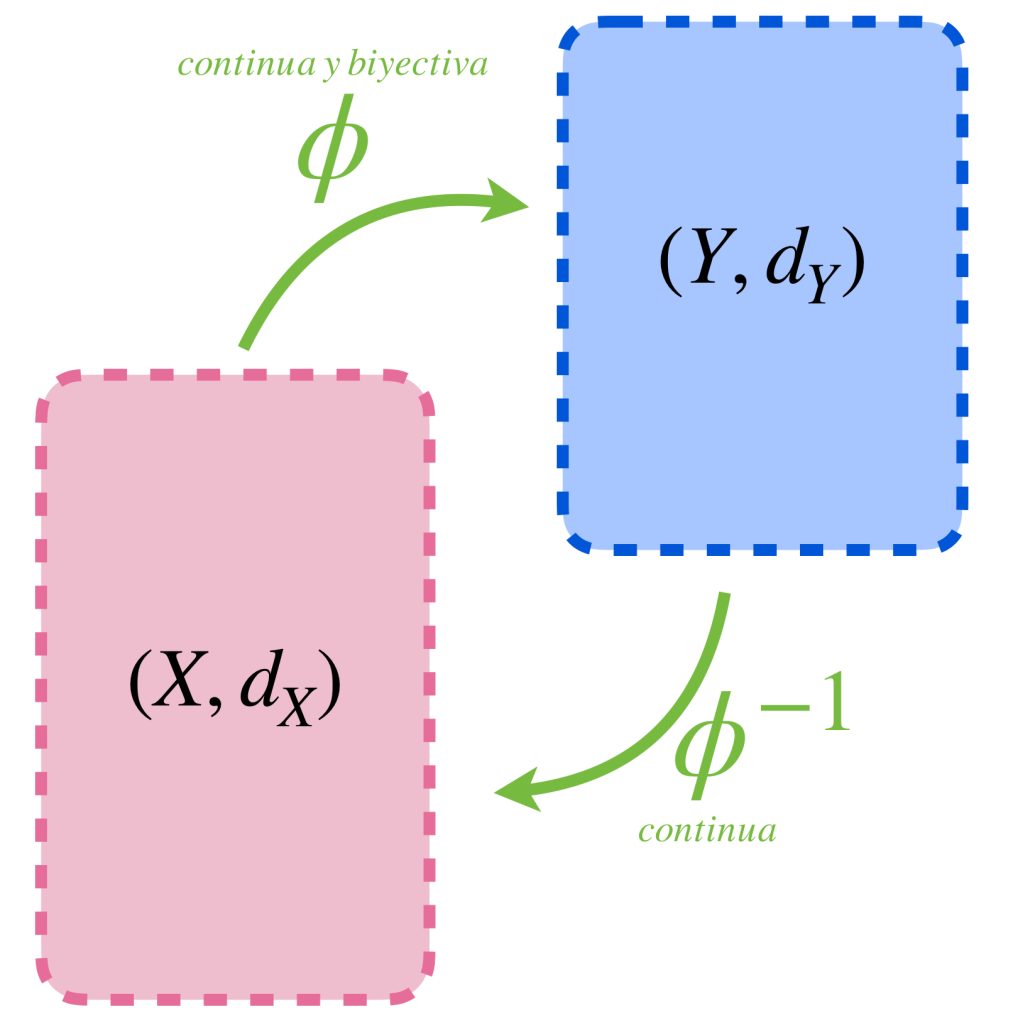
Definición homeomorfismo: Sea $\phi: X \to Y$ una función continua. Si además $\phi$ es biyectiva y su inversa $\phi^{-1}: Y \to X$ es continua, diremos que $\phi$ es un homeomorfismo. Dos espacios métricos $X$ y $Y$ son homeomorfos si existe un homeomorfismo entre ellos.
Dos espacios homeomorfos tienen, en principio, la misma cardinalidad. Como existe una función continua y de inversa continua, puntos que están cerca en un espacio métrico se conservarán cerca en el otro. Podemos pensar que los espacios homeomorfos tienen la misma forma, en el sentido de que es posible modificar continuamente uno para convertirlo en el otro.
Ejemplos:
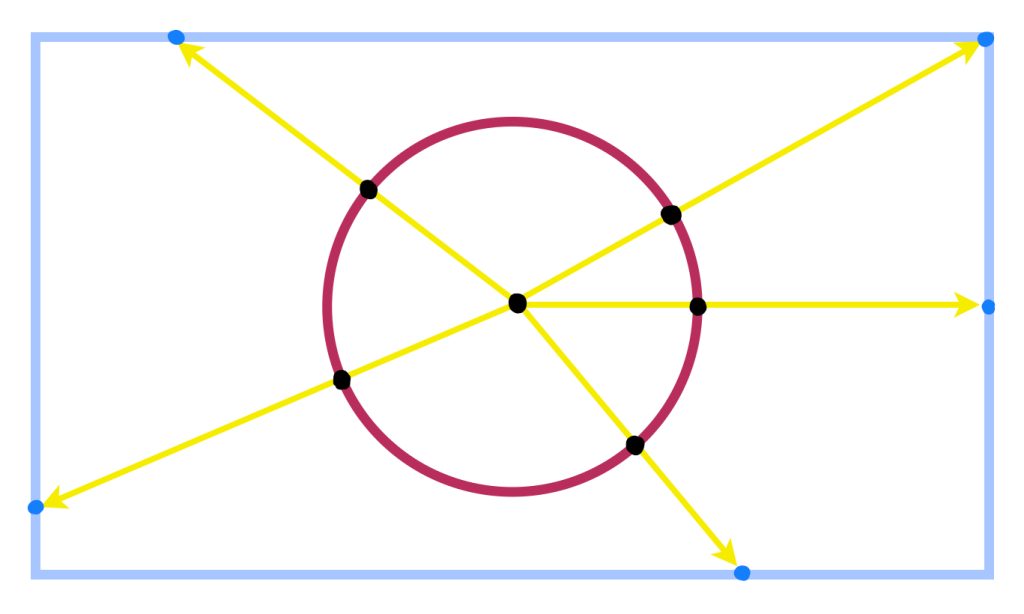
Una circunferencia y el perímetro de un rectángulo son homeomorfos. Un homeomorfismo entre estos espacios está dado por la proyección (que es una función continua) de los puntos de la circunferencia en el rectángulo.
Una taza de café y una dona son homeomorfos en $\mathbb{R}^3.$ La siguiente imagen nos muestra la transformación de un espacio al otro a través de la aplicación de homeomorfismos.
Proposición: Sean $(X,d_X), (Y,d_Y), (Z,d_Z)$ espacios métricos con $\phi: X \to Y$ y $\, \psi: Y \to Z$ funciones entre ellos. Las siguientes son propiedades de la composición de funciones:
a) Si $\phi$ y $\psi$ son continuas, entonces la composición $\psi \circ \phi: X \to Z$ es una función continua.
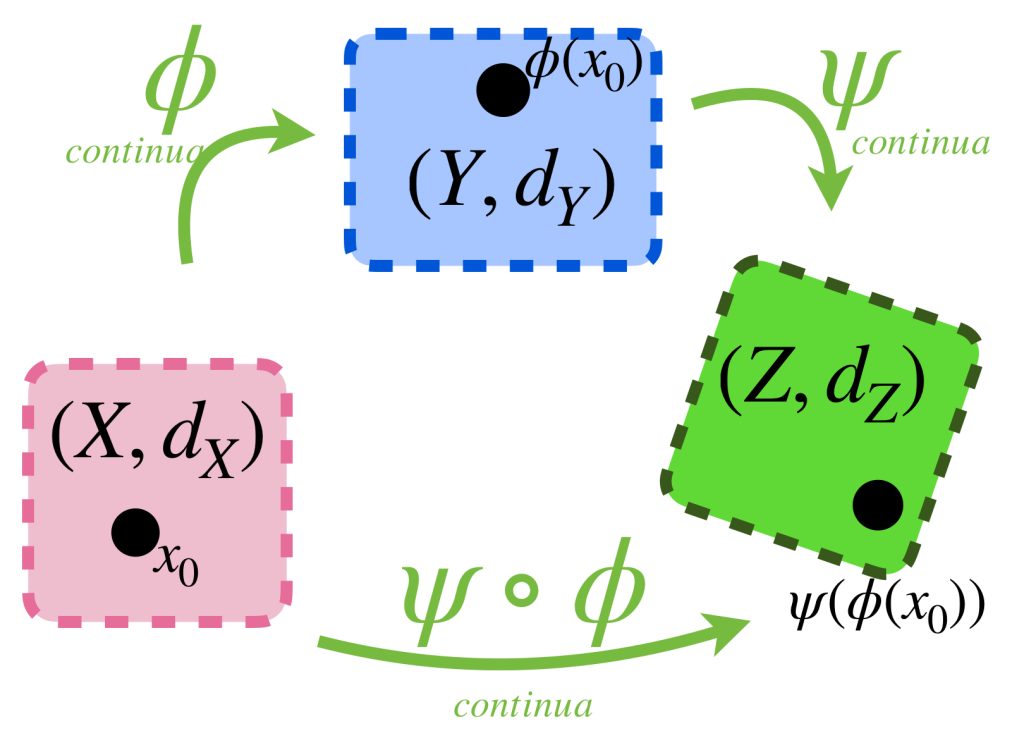
b) Si $\phi$ es un homeomorfismo, entonces $\psi$ es continua si y solo si la composición $\psi \circ \phi$ es continua.
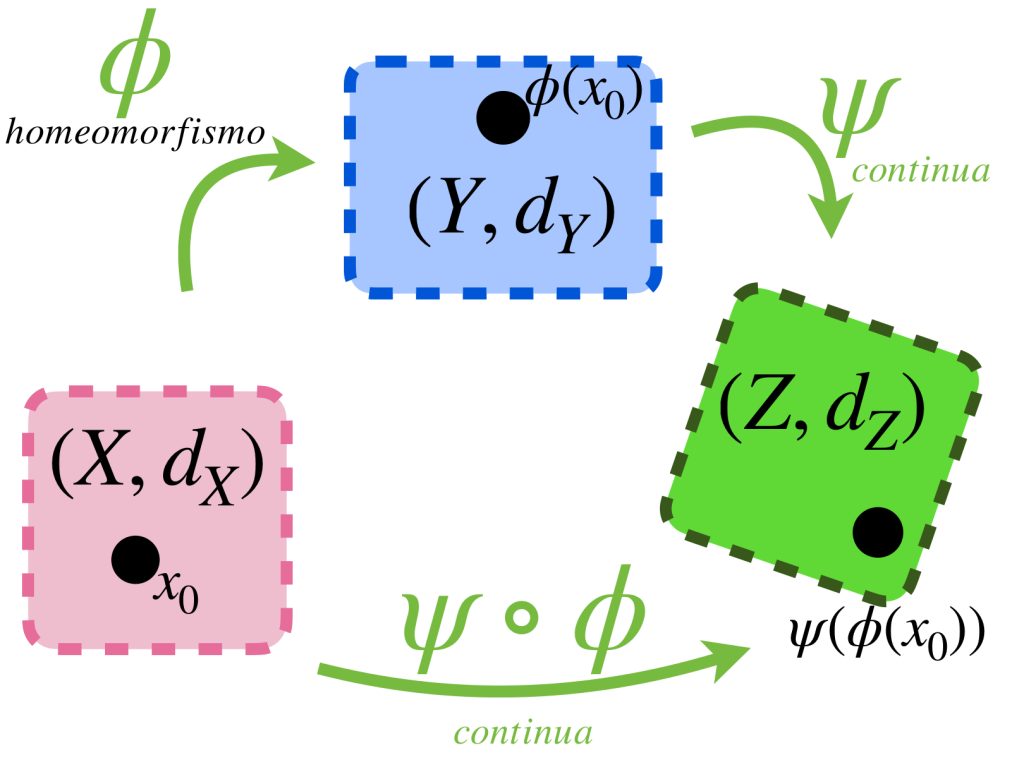
c) Si $\psi$ es un homeomorfismo, entonces $\phi$ es continua si y solo si la composición $\psi \circ \phi$ es continua.
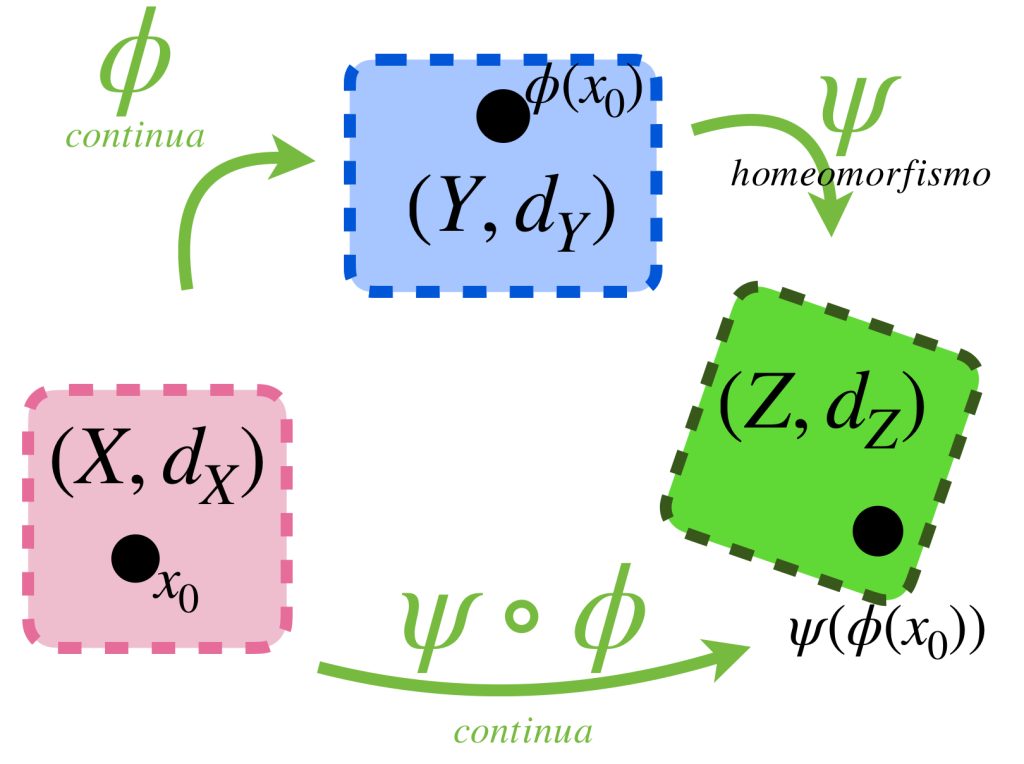
Demostración:
La prueba de a) se dejará como ejercicio al final de esta sección. Por lo pronto ya lo asumiremos válido.
Para probar b) nota que si $\phi$ es homeomorfismo entonces es continua y su función inversa $\phi^{-1}$ también lo es. A partir de a) concluimos que $\psi \circ \phi$ es continua si y solo si $(\psi \circ \phi)\circ\phi^{-1}= \psi$ es continua.
Para probar c) nota que si $\psi$ es homeomorfismo entonces es continua y su función inversa $\psi^{-1}$ también lo es. A partir de a) concluimos que $\psi \circ \phi$ es continua si y solo si $\psi^{-1}\circ(\psi \circ \phi)= \phi$ es continua.
Definición isometría. Sean $(X,d_X)$ y $(Y,d_Y)$ dos espacios métricos. Decimos que $\phi: X \to Y$ es una isometría si preserva distancias entre espacios, es decir, para toda $x,y \in X:$
$$d_X(x,y) = d_Y(\phi(x), \phi(y))$$
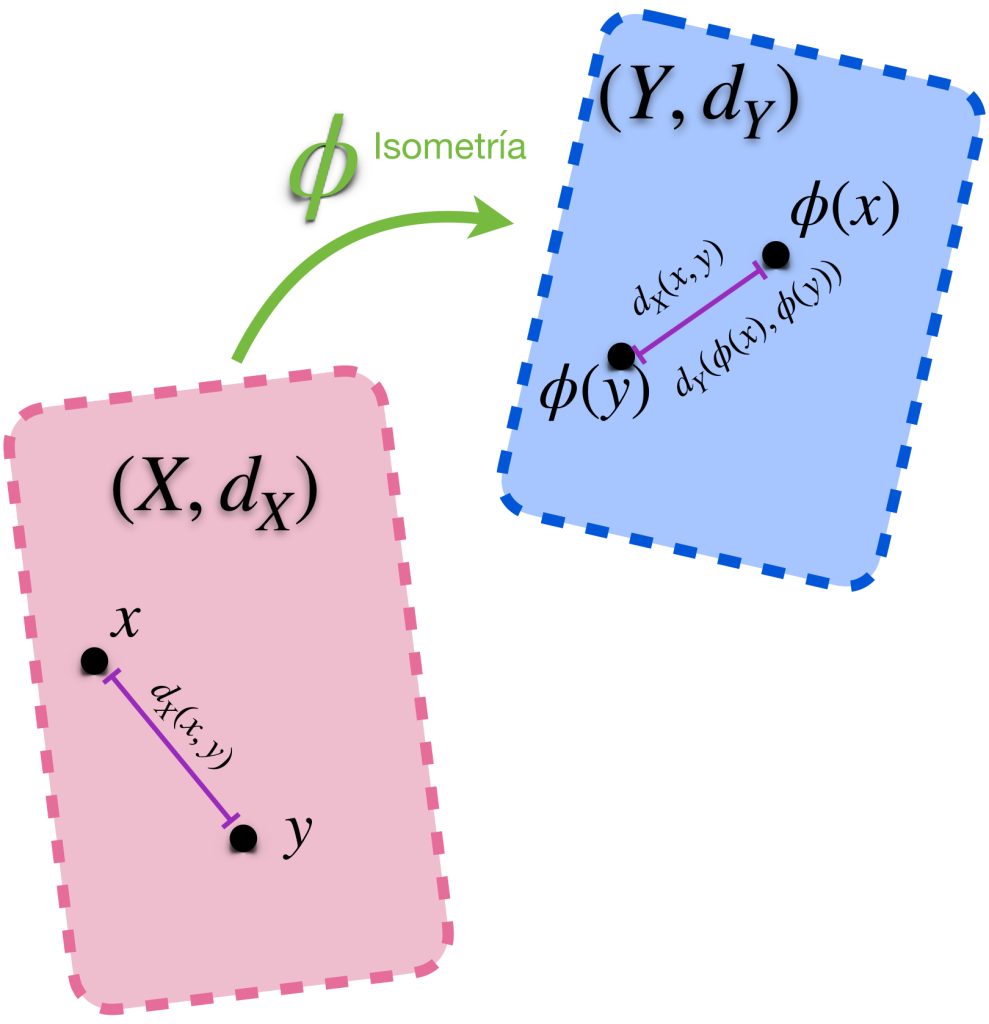
¿Puede una isometría ser un homeomorfismo? En principio sería necesario que sea biyectiva.
Proposición: Una isometría es una función inyectiva.
Demostración:
Sea $\phi: X \to Y$ una isometría y $x,y \in X$ tales que $\phi(x) = \phi(y)$ entonces $d_Y(\phi(x),\phi(y)) = 0$. Como $\phi$ es isometría, $d_X(x,y) = d_Y(\phi(x),\phi(y)) = 0$ por lo tanto $x = y.$
Se deja como ejercicio argumentar que si una isometría es suprayectiva, entonces es un homeomorfismo. Particularmente, en este caso diremos que los espacios son isométricos.
En la siguiente función las distancias en el espacio del contradominio estarán limitadas por las distancias del espacio del dominio y una constante $c \in \mathbb{R}:$
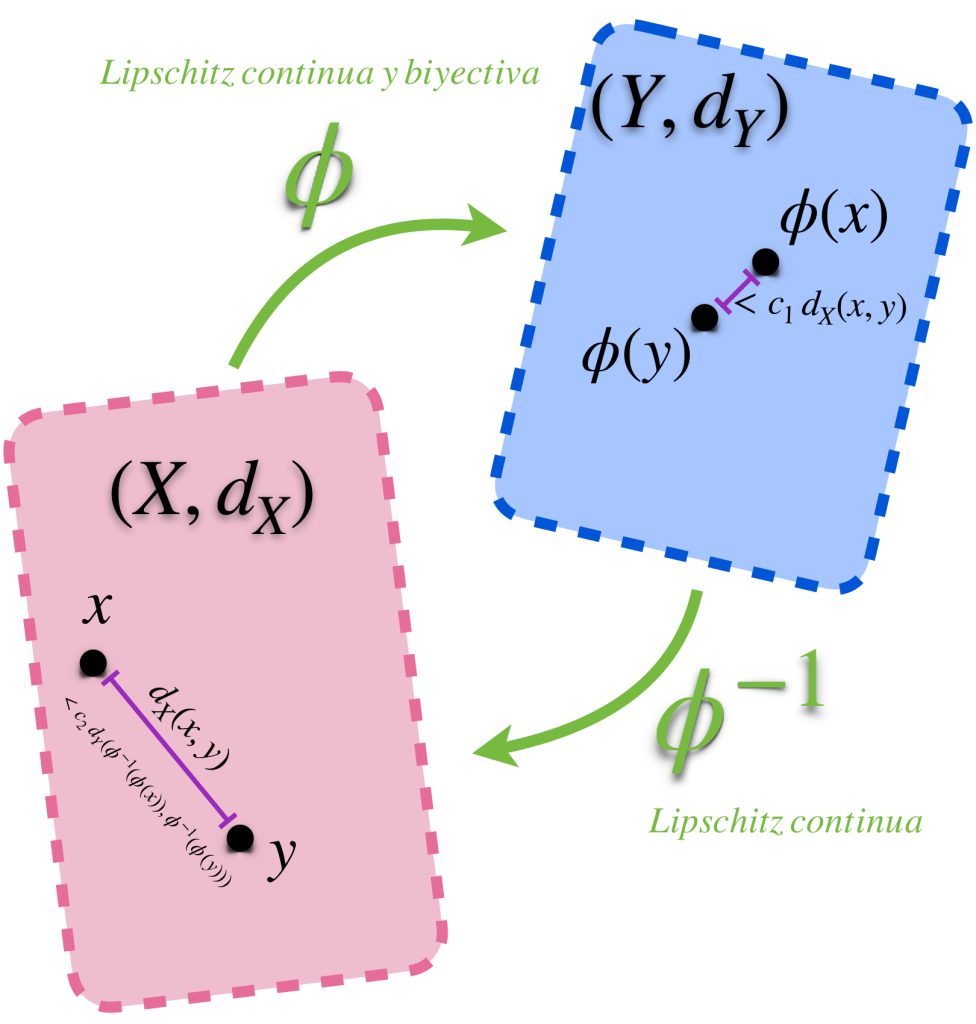
Definición función Lipschitz continua: Sea $\phi: X \to Y$. Si existe $c>0$ tal que para todo $x,y \in X, \,$ $d_Y(\phi(x), \phi(y)) \leq c \, d_X(x,y)$ diremos que $\phi$ es Lipschitz continua y que $c$ es constante de Lipschitz para $\phi$.
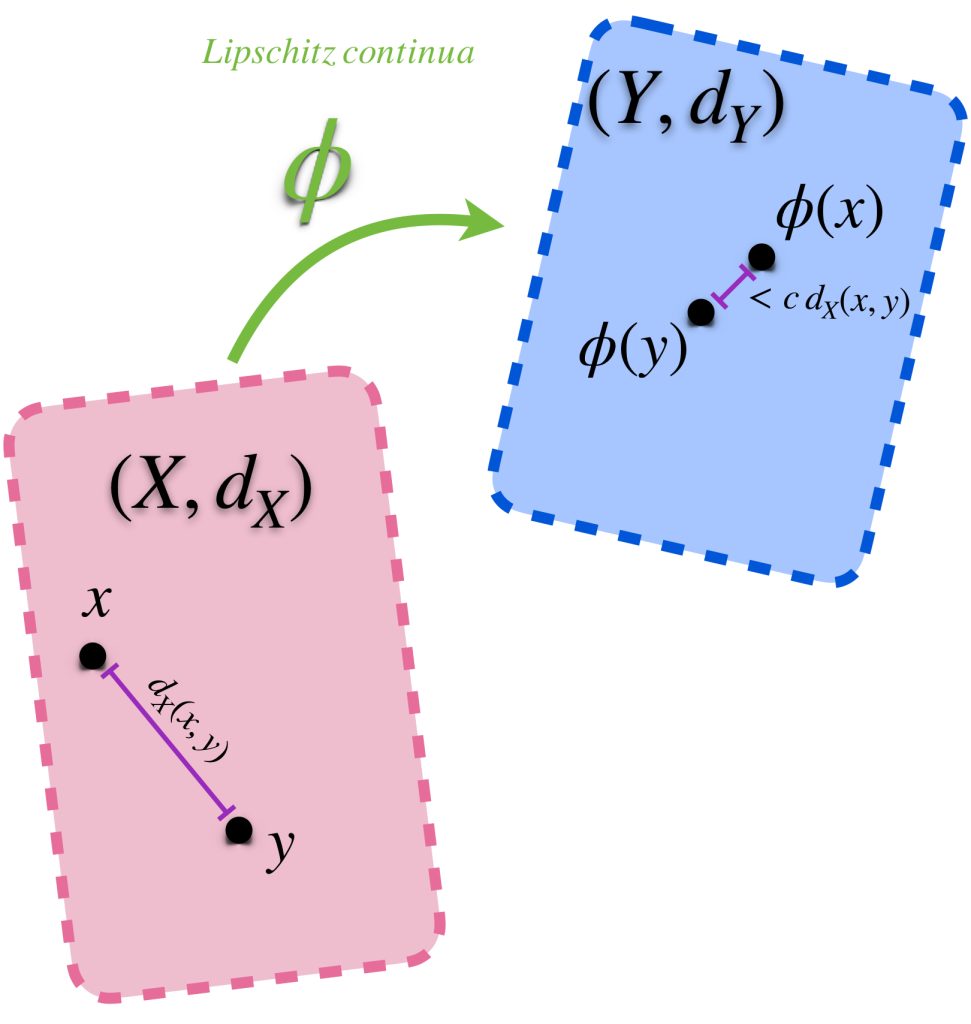
Proposición: Si la función $\phi$ es Lipschitz continua, entonces es continua.
Demostración:
Sea $\phi :X \to Y$ Lipschitz continua con constante de Lipschitz $c$, $x_0 \in X$ y $\varepsilon >0$. Si $\delta = \frac{\varepsilon}{c}$ entonces si $x$ es tal que $d_X(x,x_0) \leq \frac{\varepsilon}{c}$ se sigue que $d_Y(\phi(x_0), \phi(x)) \leq c \, d_X(x,x_0) \leq c \frac{\varepsilon}{c} = \varepsilon .$
El recíproco no es cierto. Se deja como ejercicio.
Definición equivalencia: Diremos que $\phi: X \to Y$ es una equivalencia si es Lipschitz continua y biyectiva y su inversa $\phi^{-1}:Y \to X$ también es Lipschitz continua.
Definición métricas equivalentes: Sean $d_1$ y $d_2$ dos métricas en el espacio métrico $X$. Diremos que $d_1$ y $d_2$ son equivalentes si la función identidad $I:(X,d_1) \to (X,d_2)$ es una equivalencia.
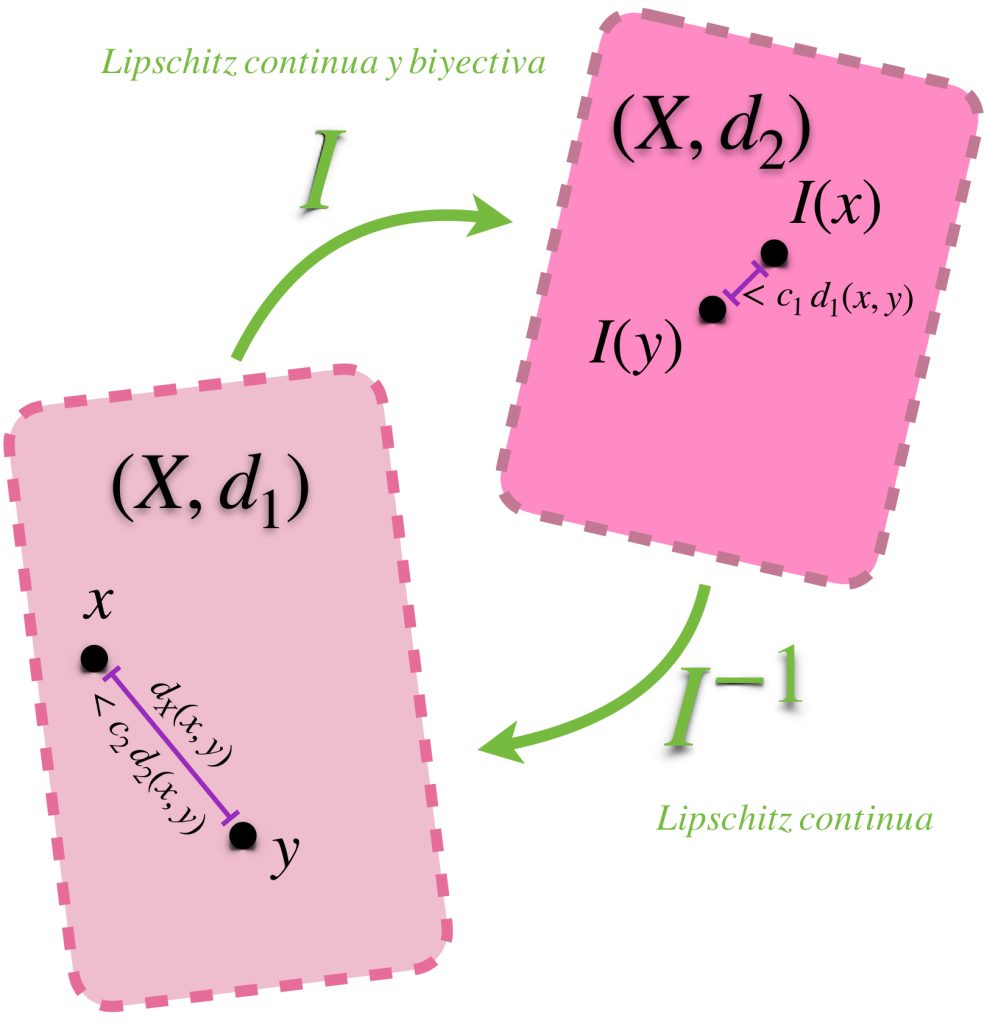
Asímismo, dos normas son equivalentes si las métricas inducidas por ellas son equivalentes. Podemos concluir también que si dos métricas son equivalentes, entonces ambas métricas generan los mismos conjuntos abiertos en el conjunto $X$, esto es, $A$ es abierto en $(X,d_1)$ si y solo si $A$ es abierto en $(X,d_2).$ ¿Por qué?
Ejemplos
En el conjunto $\mathbb{R}^n$ considera los puntos $x,y,z \in \mathbb R^n$, con $x=(x_{1},…,x_{n})$ y $y=(y_{1},…,y_{n}).$ Las siguientes métricas son equivalentes:
a) $d_{2}(x,y) = \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}$
b) $d_{\infty}(x,y) = max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}$
c) $d_{1}(x,y) = |x_{1}-y_{1}|+…+|x_{n}-y_{n}|$
Demostración:
Demostremos que $d_{2}$ y $d_{\infty}$ son métricas equivalentes.
\begin{align*}
(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2 &\leq n^2(max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\})^2\\
\sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2} &\leq n \, max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}\\
d_{2}(x,y) &\leq n \, d_{\infty}(x,y)
\end{align*}
Por otro lado
\begin{align*}
(max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\})^2 &\leq (x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2\\
max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\} &\leq \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}\\
d_{\infty}(x,y) &\leq d_{2}(x,y)
\end{align*}
Por lo tanto $d_{2}$ y $d_{\infty}$ son métricas equivalentes.
Ahora demostraremos que las métricas $d_{1}$ y $d_{\infty}$ son equivalentes.
\begin{align*}
d_1(x,y) &= |x_{1}-y_{1}|+…+|x_{n}-y_{n}| \\
&\leq n \, max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}\\
&= n \, d_{\infty}
\end{align*}
Por otro lado
\begin{align*}
d_{\infty} &= max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}\\
&\leq |x_{1}-y_{1}|+…+|x_{n}-y_{n}| \\
&= d_{1}(x,y)
\end{align*}
Por lo tanto las métricas $d_{1}$ y $d_{\infty}$ son equivalentes. Queda como ejercicio al lector demostrar que las métricas $d_1$ y $d_2$ son equivalentes. Nota que es posible concluirlo a partir de las equivalencias demostradas y la composición de funciones.
Para finalizar esta sección, presentamos dos normas no equivalentes:
Considera el espacio de funciones continuas $C^0[0,1]$, (que van del intervalo $[0,1] \subset \mathbb{R} \to \mathbb{R})$ con las normas:
\begin{align*}
\norm{f}_1&:= (\int_{0}^{1} |f(x)| \,dx), \\
\norm{f}_\infty&:= máx\{|f(x)|:0\leq x \leq 1 \}
\end{align*}
Veremos que no existe una función Lipschitz continua $\phi:(C^0[0,1],\norm{f}_\infty) \to (C^0[0,1],\norm{f}_1).$
Para cada $n \in \mathbb{N}$ considera la función $f_n(x) \in C^0[0,1]$ que a cada $x \in [0,1]$ asigna el punto $f_n(x) = x^{n-1}.$ La distancia que hay entre estas funciones y la función constante $0$ está dada por:
\begin{align*}
\norm{f_n}_1&:= (\int_{0}^{1} |f_n| \,dx) = \frac{1}{n}, \\
\norm{f_n}_\infty&:= máx\{|f_n|:0\leq x \leq 1 \} = 1
\end{align*}
No existe $c>0$ que satisfaga que para toda $n \in \mathbb{N}, \, \norm{f_n}_1 \leq c\norm{f_n}_\infty$ pues no es cierto que $\frac{1}{n}\leq c(1) =c$ para toda $n$. Por lo tanto no existe una función Lipschitz continua $\phi:(C^0[0,1],\norm{f}_\infty) \to (C^0[0,1],\norm{f}_1)$ y en conclusión, estas normas no son equivalentes
Más adelante…
Veremos que es posible definir un espacio métrico a partir de una familia de caminos que conecte puntos y de la longitud que estos caminos tienen. Observaremos la posibilidad de que varios caminos distintos conecten a los mismos dos puntos y si es posible rescatar alguna aproximación en funciones no continuas a través de un nuevo concepto: la semicontinuidad.
Tarea moral
- Demuestra que si $\phi$ y $\psi$ son continuas, entonces la composición $\psi \circ \phi: X \to Z$ es una función continua.
- Sea $\phi$ una isometría tal que es suprayectiva. Prueba que es también un homeomorfismo.
- Da un ejemplo de una función continua que no sea Lipschitz continua.
- Demuestra que una isometría es una equivalencia.
- Demuestra que las métricas $d_1(x,y) = |x_{1}-y_{1}|+…+|x_{n}-y_{n}|$ y $d_{2}(x,y) = \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}$ son equivalentes.