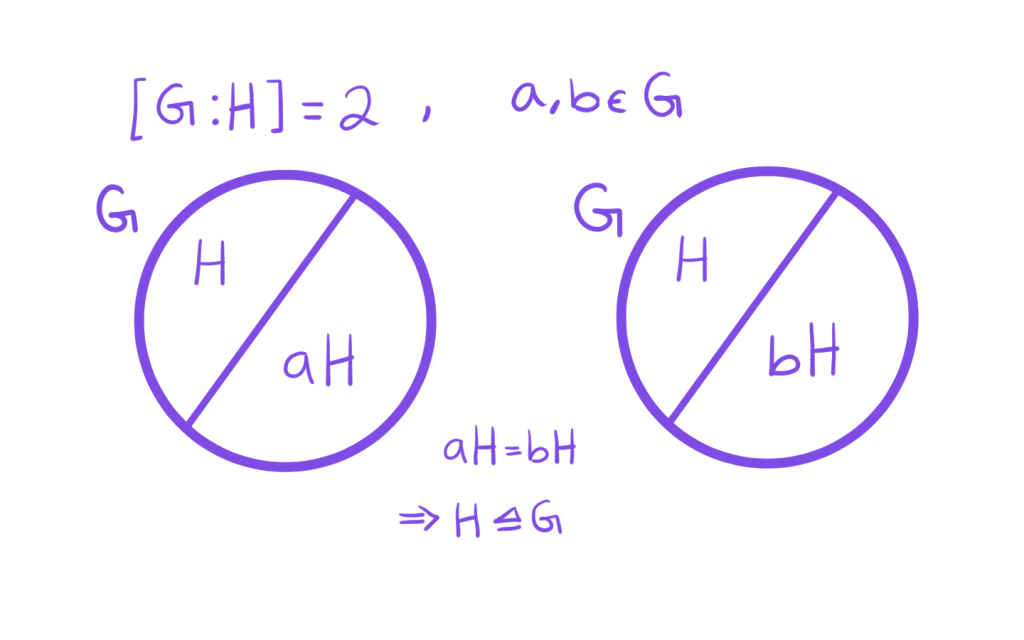Archivo del Autor: Cecilia del Carmen Villatoro Ramos

Álgebra Moderna I: Subgrupo Conmutador

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Vamos a ver una aplicación importante del grupo cociente. Sabemos que podemos dividir a los enteros en impares e impares. Esto se representa con Z2={0¯,1¯}, donde todos los pares quedan identificados por 0¯ y los impares por 1¯. Esto es el objetivo del grupo cociente que definimos en la entrada anterior, identificar elementos en una misma clase lateral.

Ahora, si queremos traducir esto a un grupo general G, necesitamos sacar el cociente módulo un subgrupo H, entonces cada h∈H es un representante de esta clase de equivalencia, de modo que todos los elementos de H se identificarán entre sí, en particular, todos los elementos de H quedarán identificados con el neutro e de H ya que hH=eH.

Por otro lado, recordemos que en general el grupo no es abeliano, es decir no sucede que ab=ba para a,b∈G. Pero si tomamos H⊴G de modo que ab∈H y ba∈H, entonces abH=baH y las clases representadas por ab y ba serán la misma, por lo que aH y bH conmutarán en el cociente. Si recordamos la relación de equivalencia definida en entradas anteriores podemos obtener las siguientes equivalencias,
abH=baH⇔(ab)−1ba=b−1a−1ba∈H.

Como nos interesa que G/H sea abeliano, necesitamos que la palabra b−1a−1ba∈H para toda a,b∈G. Esto nos obliga a que el conjunto {b−1a−1ba|a,b∈G} esté contenido en H. En general, este conjunto no es necesariamente un grupo, pero podemos considerar el generado y así, nos interesaría que el generado esté contenido en H:
⟨b−1a−1ba|a,b∈G⟩⊆H.

El objetivo de esta entrada es definir primero al conmutador de a y b. Luego, definir al generado por la colección de todos los conmutadores en el grupo. Todo esto con el objetivo de construir un grupo cociente abeliano, aunque G no lo sea.

Subgrupo conmutador de G

Definción. Sea G un grupo, a,b∈G. El conmutador de a y b es [a,b]=aba−1b−1.

El subgrupo conmutador de G es G′=⟨[a,b]|a,b∈G⟩.

Observación 1. G′={e} si y sólo si G es abeliano.

Demostración.

G′={e}⇔[a,b]=e∀a,b∈G⇔aba−1b−1=e∀a,b∈G⇔ab=ba∀a,b∈G⇔G es abeliano.

◼

Esa observación nos dice intuitivamente que entre más grande sea el conmutador, G está más alejado de ser abeliano.

Observación 2. El inverso de un conmutador es un conmutador.

La demostración queda como tarea moral.

Observación 3. El conmutador es un subgrupo normal de G, es decir, G′⊴G.

Demostración.
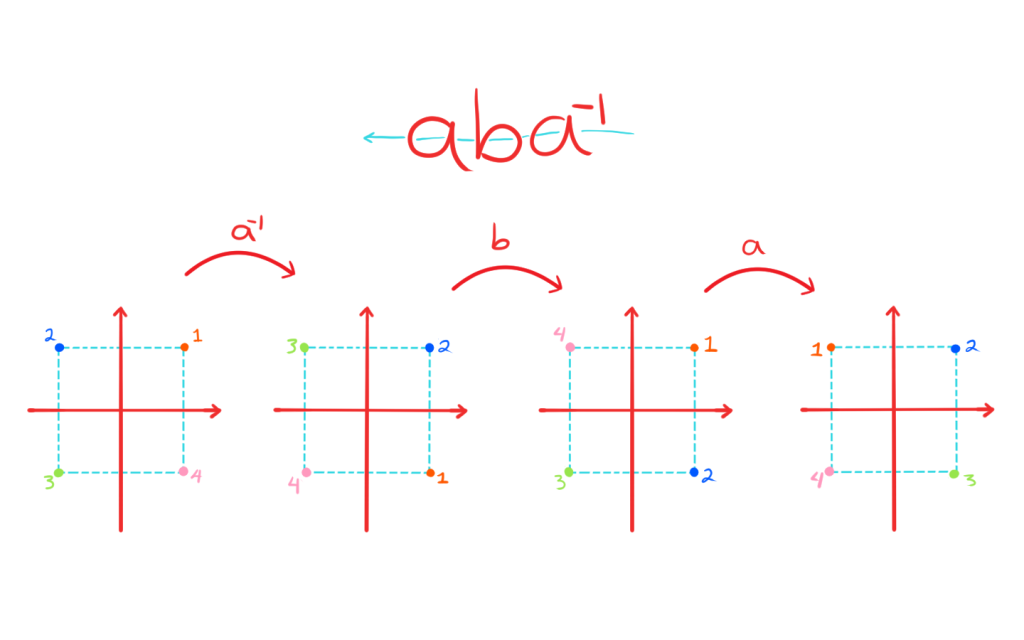
Para probar que el conmutador es un subgrupo normal, necesitamos ver que G′ es cerrado bajo conjugación. Pero como los elementos de G′ son palabras donde las letras son conmutadores o sus inversos, y por la observación anterior son palabras donde las letras son conmutadores, entonces basta ver que al conjugar un conmutador obtenemos un elemento en G′, es decir que g[a,b]g−1∈G′ para todos g,a,b∈G.

Sean a,b,g∈G.

g[a,b]g−1=gaba−1b−1g−1.
Para ver que este elemento está en G′ debemos ver a gaba−1b−1g−1 como un producto de conmutadores, para eso agregaremos al neutro antes de b−1g−1, con el neutro expresado como g−1b−1bg. Luego, nos fijamos qué términos dan lugar a conmutadores y obtenemos lo siguiente:
g[a,b]g−1=gaba−1b−1g−1=gaba−1(g−1b−1bg)b−1g−1=(ga)b(ga)−1b−1bgb−1g−1=[ga,b]|[b,g]∈G′

Por lo tanto G′⊴G.

◼

Condiciones sobre un subgrupo para que el cociente sea abeliano

Teorema. Sea G un grupo, H un subgrupo de G. Tenemos que

G′⊆H si y sólo si, H⊴G y G/H es abeliano.

Demostración.
Sea G un grupo H≤G.

|⇒] Supongamos que G′⊆H.

P.D. H⊴G.
Sean h∈H, g∈G.
P.D. ghg−1∈H

Sabemos que ghg−1h−1=[g,h]∈G′ por definición de conmutador, y por hipótesis G′⊆H. Así, ghg−1h−1∈H.

Luego, nombremos ghg−1h−1=h~ con h~∈H. Despejando lo que nos interesa, obtenemos ghg−1=h~h∈H. Con esto probamos que todo conjugado de H sigue viviendo en H.

Por lo tanto H⊴G.


P.D. G/H es abeliano.

Sean a,b∈G.

a−1b−1ab=a−1b−1(a−1)−1(b−1)−1=⌈a−1,b−1⌉∈G′⊆H⇒a−1b−1ab∈H⇒(ba)−1ab∈H⇒baH=abH⇒bHaH=aHbH.

Como aH y bH son clases arbitrarias en G/H, concluimos que G/H es abeliano.

[⇐| Supongamos que H⊴G y G/H es abeliano.

Tomemos a,b∈G arbritrarios.

Como G/H es abeliano, entonces a−1Hb−1H=b−1Ha−1H, es decir a−1b−1H=b−1a−1H. Entonces (b−1a−1)−1a−1b−1∈H, pero (b−1a−1)−1a−1b−1=aba−1b−1=[a,b], entonces [a,b]∈H para todos a,b∈G.

Así G′⊆H.

◼

Ejemplo

Para terminar, veamos un ejemplo sencillo pero importante.

Tomemos S3 y A3.

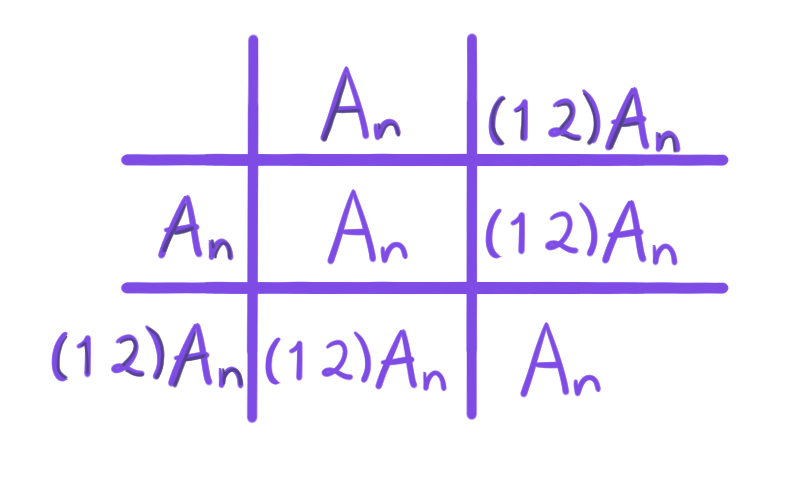
Sabemos que A3⊴S3 y S3/A3={A3,(12)A3} que es abeliano. De hecho, en la entrada anterior analizamos el caso general, puedes verificar cómo es la operación del grupo cociente con la tabla que dimos y verificar que S3/A3 que es abeliano.

Entonces S3′⊆A3={(1),(123),(132)}.

Como S3 no es abeliano, por la observación que dimos S3′≠{(1)}. Concluimos que S3′=A3.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba que el inverso de un conmutador también es un conmutador.
  2. Sea D2(4)={id,a,a2,a3,b,ab,a2b,a3b} el grupo diédrico formado por las simetrías de un cuadrado, con a la rotación de π2 y b la reflexión con respecto al eje x.
    1. Calcula el cociente de D2(4) módulo ⟨a2⟩.
    2. Encuentra D2(4)′.
  3. Sea G un grupo, H y K subgrupos normales de G tales que G/H y G/K son abelianos, ¿es entonces G/H∩K abeliano?

Más adelante…

¡Felicidades! Esta es la última entrada de la unidad 2. Esta unidad se trató de definir nuevas estructuras que nos ayudan para describir mejor a los grupos y subgrupos. Hablamos sobre el orden del grupo y extendimos propiedades de los enteros hacia la generalidad de los grupos, como separar un grupo en clases de equivalencia. La siguiente entrada introduce la tercera unidad de este curso y presenta un tema nuevo: unas funciones que «respetan» o «abren» operaciones.

Entradas relacionadas

Álgebra Moderna I: Grupo Cociente

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

La definición de subgrupos normales fue motivada porque queremos extraer las propiedades de los enteros a grupos más generales. Recordemos que en los enteros se define una relación de equivalencia (módulo n) de donde obtenemos clases de equivalencia. Estas clases no sólo inducen una partición, si no que conforman un subgrupo de Z. En esta entrada queremos generalizar esta idea y buscamos dar una operación en ciertas clases de equivalencia de modo que éstas formen también un grupo.

Grupo cociente G módulo N

Teorema. Sea G un grupo, N un subgrupo normal de G.

El conjunto
G/N={aN|a∈G}.
con la operación (aN)(bN)=abN∀a,b∈G
es un grupo de orden [G:N].

Definición. Al conjunto G/N de arriba se le conoce como el grupo cociente G módulo N.

Demostración del teorema.

Sea G un grupo, N un subgrupo normal de G.

En {aN|a∈G} consideremos la operación (aN)(bN)=abN∀a,b∈G.

Primero veamos que está bien definida.
Sean a,a′,b,b′∈G con aN=a′N, bN=b′N.
P.D. abN=a′b′N.

Como aN=a′N, a′∈aN entonces a′=an con n∈N.

Como bN=b′N, b′∈bN entonces b′=bn~ con n~∈N.

Sustituyendo a′ y b′ en a′b′ tenemos que a′b′=(an)(bn~)=a(nb)n~.

Como N⊴G, por la conmutatividad parcial, nb=bn^ con n^∈N.
Entonces a′b′=a(bn^)n~=ab(n^n~)∈abN.

Por lo tanto a′b′N=abN.

Veamos ahora que con esta operación, G/N es un grupo.

P.D. La operación es asociativa.
Sean aN,bN,cN∈G/N con a,b,c∈G.

aN(bNcN)=aN(bcN)=a(bc)NDefinición del producto de clases=(ab)cNAsociatividad en G=(abN)cN=(aNbN)cN.

Por lo tanto la operación en G/N es asociativa.

P.D. El neutro de la operación existe y está en G/N.
Sea aN∈G/N,
N(aN)=(eN)(aN)=eaN=aNNeutro en G(aN)N=(aN)(eN)=aeN=aNNeutro en G

Por lo tanto N es neutro en G/N.

P.D. Para cada elemento en G/N existe un inverso bajo la operación y este inverso está en G/N.
Dado aN∈G/N, como a∈G consideremos a−1∈G su inverso en G.

(aN)(a−1N)=aa−1N=eN=N(a−1N)(aN)=a−1aN=eN=N.

Así a−1N es inverso de aN. Por lo tanto G/N es un grupo.

Finalmente,
|G/N|=#{aN|a∈G}=[G:N].

◼

Notemos que en la demostración de que G/N con el producto es un grupo, usamos solamente las propiedades de que G es grupo.

Primer y segundo ejemplo

Ahora veremos algunos ejemplos de grupo cociente.

El primer ejemplo es justo el que motivó la idea de grupo cociente.
Tomemos (Z,+) y H={m|4 divide a m}=4Z⊴Z. 4Z es normal porque Z es abeliano.
Entonces, vamos describiendo el grupo cociente paso por paso:
Z/4Z=Z/H={H,1+H,2+H,3+H}={{4k|k∈Z},{4k+1|k∈Z},{4k+2|k∈Z},{4k+3|k∈Z}}={0¯,1¯,2¯,3¯}=Z4. La suma se realiza a partir de la suma de los representantes del siguiente modo: (a+H)+(b+H)=(a+b)+H, es decir a¯+b¯=a+b―, para cualesquiera a,b∈Z.

Ahora, para el segundo ejemplo, consideremos n≥2 y tomamos An⊴Sn. En la entrada anterior vimos por qué An es un subgrupo normal de Sn.
De nuevo, vamos describiendo el grupo cociente.
Sn/An={An,(12)An}={{α|α es par},{(12)α|α es par}}={{α|α es par},{β|β es impar}}.

En la tabla se muestra el resultado del producto de los elementos de Sn/An. Podemos observar que An funge como neutro.

Representación gráfica de la partición de Sn en permutaciones pares e impares.
Tabla que muestra el producto de los conjuntos de Sn/An.

Así, estamos partiendo a Sn en permutaciones pares (representadas por (1)) e impares (representadas por (12)). De esta manera, podemos decir que multiplicar dos permutaciones pares o dos impares resulta en una permutación par, pero multiplicar una par con una impar resulta en una permutación impar.

Tercer y cuarto ejemplo

A continuación, para nuestro tercer ejemplo, tomamos N={±1}⊴Q.
Para obtener una nueva clase lateral, escogemos un elemento de los cuaternios que no esté en N. El cociente se vería de la siguiente manera:
Q/N={N,iN,jN,kN}={{±1},{±i},{±j},{±k}}.
De nuevo, en las imágenes podemos ver una tabla que expresa el resultado de multiplicar distintas clases y una representación gráfica de las clases que obtenemos en el cociente.
Podemos verificar algunas de las operaciones de la tabla, hacemos el producto de Q/N usando el producto en Q. Recordemos que −kN=kN y −iN=iN, pues k y −k viven en una misma clase, y −i e i también son parte de una misma clase.

jNiN=jiN=−kN=kNjNkN=kjN=−iN=iN.

Partición de Q inducida por N.
Tabla que muestra los resultados de las operaciones de los elementos de Q/N.

Si ahora consideramos ⟨k⟩≤Q, ⟨k⟩={±1,±k}.
Entonces [Q:⟨k⟩]=|Q||⟨k⟩|=84=2, y así, ⟨k⟩⊴Q.
Así Q/⟨k⟩={⟨k⟩,i⟨k⟩}.

Tabla de las operaciones de los elementos de Q/⟨k⟩.
Partición de Q inducida por ⟨k⟩.

Para nuestro último ejemplo, consideremos Z×Z={(a,b)|a,b∈Z}, con la operación (a,b)+(c,d)=(a+c,b+d).
Sea H={(a,a)|a∈Z}.
(a,b)+H=(c,d)+H⇔−(a,b)+(c,d)∈H⇔(c−a,d−b)∈H⇔c−a=d−b⇔c=d+(a−b).
Recordemos que −(a,b) es el inverso de (a,b).
Así,
(a,b)+H={(d+(a−b),d)|d∈Z}={(a−b,0)+(d,d)|d∈Z}.
En particular (a,b)+H=(a−b,0)+H. Las clases laterales se muestran mejor gráficamente en la imagen.
Tomemos los puntos enteros del eje x como representantes de las clases laterales:
Z×Z/H={(a,0)+H|a∈Z}.((a,0)+H)+((c,0)+H)=(a+c,0)+H.

En esta imagen representamos a cada clase lateral (a,b)+H de un color distinto. Claramente son las diagonales discretas en el plano. También se muestra que los representantes de la clase son puntos en la misma diagonal.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea G un grupo, H un subgrupo de G tal que el producto de dos clases laterales izquierdas de H en G es de nuevo una clase lateral izquierda de H en G ¿es entonces H normal en G?
  2. Sea G un grupo, H un subgrupo normal de G de índice finito con m=[G:H]. Dada a∈G ¿qué podemos decir del elemento am? ¿Y si H no es normal en G?
  3. Sea G un grupo finito, N un subgrupo normal de G. Dada a∈G. Analiza cómo es el orden de a en relación al orden de aN.
  4. Considera el grupo aditivo R2 y el subgrupo N={(x,0)|x∈R}.
    1. Determina qué deben cumplir (a,b),(c,d)∈R2 para que (a,b)N=(c,d)N.
    2. Describe al grupo R2/N.
  5. Sea G un grupo, N un subgrupo normal de G de índice finito con p=[G:N] primo. Dada a∈G ¿qué podemos decir de ⟨aN⟩ y de G/N?
  6. Si quieres profundizar un poco más sobre Grupos cocientes, puedes revisar el video de Mathemaniac sobre el tema. El video está en inglés.

Más adelante…

En pocas palabras, un subgrupo normal induce una partición del grupo y ésta es el grupo cociente. Esta idea surge de lo que ocurre en los enteros. En la siguiente entrada usaremos el grupo cociente para crear, a partir de un grupo no abeliano, otro que sea abeliano.

Entradas relacionadas

Álgebra Moderna I: Teoremas y Proposiciones relacionadas con subgrupos normales y grupo Alternante.

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En entradas anteriores definimos el índice de H en G con H un subgrupo del grupo G. Además, dimos la definición de subgrupo normal, y demostramos equivalencias usando clases laterales izquierdas y derechas.

Cuando sólo hay dos clases laterales en G, es muy fácil concluir esa equivalencia, es decir, es fácil verificar que toda clase lateral derecha es una clase lateral izquierda y viceversa. Digamos, si [G:H]=2 y tomamos a,b∈G. Por un lado tenemos que se crea una partición P1={H,aH} de G y por otro lado tenemos P2={H,Hb}. Como ambas particiones tienen H, entonces necesariamente aH=Hb. Así, concluimos que H⊴G.

Lo anterior lo demostraremos de manera formal en esta entrada.

Representación gráfica de qué sucede cuando [G:H]=2.

Proposición sobre subgrupos

Proposición. Sean G un grupo y H un subgrupo de G.

  1. Si [G:H]=2, entonces g2∈H para toda g∈G.
  2. Si [G:H]=2, entonces H es normal en G.

Demostración.
Sea G un grupo, H≤G con [G:H]=2.

1. P.D. g2∈H para toda g∈G.

Sea g∈G. Como [G:H]=2 hay dos clases laterales izquierdas, H y aH para alguna a∈G∖H, y G=H∪˙aH, donde ∪˙ en este caso es una unión disjunta.

Como g∈G, entonces g∈H ó g∈aH.

Si g∈H, al ser H un subgrupo, g2∈H.
Si g∈aH, g=ah para alguna h∈H.
Por lo tanto g2=ahah.

Pero también, g2∈G=H∪˙aH. Por un lado, si g2∈aH, g2=ah~ con h~∈H.
⇒ah~=g2=ahah⇒h~=hahCancelamos la a que se repite⇒a=h−1h~h−1Despejando a.

Pero cada uno de h,h~,h−1∈H. Por lo que a∈H y esto sería una contradicción.
Por lo tanto g2∈H.

2. Como [G:H]=2 hay dos clases laterales izquierdas H y aH con a∈G∖H. Hay también dos clases laterales derechas H y Hb con b∈G∖H y además
H∪˙aH=G=H∪˙Hb.

Si g∈aH, entonces g∉H, así g∈G=H∪˙Hb pero g∉H, y entonces g∈Hb. Por lo que aH⊆Hb.

Si g∈Hb, entonces g∉H, así g∈G=H∪˙aH pero g∉H, y entonces g∈aH. Por lo que Hb⊆aH.

Así, aH=Hb y toda clase lateral izquierda es una clase lateral derecha.
Por lo tanto, podemos concluir que H⊴G.

◼

Ejemplos.

Enunciamos dos ejemplos sencillos:

Ejemplo 1. Como [Sn:An]=2, entonces An⊴Sn.

Ejemplo 2. En D2n=⟨a,b⟩ con a la rotación 2πn y b la reflexión con respecto al eje x.
Sea H=⟨a⟩.
[D2n:H]=|D2n||H|=2nn=2.
Por lo tanto H⊴D2n.

Más teoremas de subgrupos

Veamos que el hecho de que un número divida al orden de un grupo, no implica que haya un subgrupo de ese tamaño. Esto se puede ilustrar con un ejemplo.

Teorema. Sea A4 el subgrupo alternante de S4.
A4 no tiene subgrupos de orden 6.

Demostración.
Consideremos el subgrupo A4 de S4.

Sabemos que
|A4|=|S4|2=4!2=242=12.

Así, 6||A4|.

P.D. A4 no tiene subgrupos de orden 6.

Supongamos que existe H≤A4 con |H|=6.

⇒[A4:H]=A4H=126=2⇒H⊴A4Prop. anterior inciso 2.

Sea β=(abc)∈A4 un 3−ciclo.
Por el inciso 1 de la proposición anterior (β2)2∈H. Luego, β=β4=(β2)2∈H. Así, todo 3−ciclo está en H.

Pero en S4 hay exactamente ocho 3−ciclos. Entonces |H|≥8 y esto es una contradicción pues supusimos que |H|=6.

Por lo tanto A4 no tiene subgrupos de orden 6.

◼

Ahora veamos qué sucede si multiplicamos dos subgrupos. Esta multiplicación es posible y tiene sentido, pero esto no siempre nos da un subgrupo, aquí damos algunos casos en donde esto sí pasa.

Teorema. Sea G un grupo, H,K subgrupos de G.

  1. Si H⊴G ó K⊴G, entonces HK≤G.
  2. Si H⊴G y K⊴G, entonces HK⊴G.

Demostración.

Sea G un grupo, H y K subgrupos de G.

1. Supongamos que H⊴G.

P.D. HK≤G.
Por un resultado de una entrada previa, basta ver que HK=KH.

Si h∈H, k∈K, como H⊴G, entonces hk=kh~ con h~∈H por la conmutatividad parcial. Por lo tanto HK⊆KH.

Además kh=h¯k con h¯∈H, de nuevo, por la conmutatividad parcial ya que H⊴G. Por lo tanto KH⊆HK.

Así, HK=KH y HK≤G.

Para K⊴G se demuestra que HK=KH de forma análoga.

2. Supongamos que H⊴G, K⊴G.
Sean h∈H,k∈K y a∈G. Veamos que a(hk)a−1∈HK.

Agregando un neutro,
a(hk)a−1=ah(a−1a)ka−1=(aha−1)(aka−1).

Pero como H⊴G sabemos que aha−1∈H, y como K⊴G sabemos que aka−1∈K, entonces a(hk)a−1=(aha−1)(aka−1)∈HK.

Por lo tanto HK⊴G.

◼

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea G un grupo, H un subgrupo de G con 3=[G:H]. ¿Es H normal en G?
  2. Prueba que en S4 hay exactamente ocho 3-ciclos.
  3. Demuestra que A5 no tiene subgrupos de orden 20: Supón por contradicción que H es un subgrupo de de orden 20.
    1. Sea α∈A5 un 5-ciclo. Prueba que si α∉H entonces H,αH y α2H son las 3 clases laterales izquierdas de H en A5.
    2. Prueba que α3 no está en ninguna de esas tres clases laterales.
    3. Concluye que α∈H para todo α 5-ciclo, y así H tendría más de 20 elementos.
  4. Sea G un grupo, H y K subgrupos de G. Prueba o da un contraejemplo:
    1. Si HK es un subgrupo de G, entonces H es normal en G o K es normal en G.
    2. Si HK es un subgrupo normal de G, entonces H es normal en G y K es normal en G.

Más adelante…

Esta entrada es la última antes de comenzar un pequeño tema nuevo: el grupo cociente. Seguiremos viendo cómo se pueden generar particiones de los grupos y definiremos una operación entre los elementos de esta partición.

Entradas relacionadas

Álgebra Moderna I: Subgrupo Conjugado, Subgrupo Normal y Conmutatividad Parcial

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Hace algunas entradas, comenzamos dando una motivación usando a los enteros. En ésta, nos encontramos de nuevo con la necesidad de retomarlos para darle introducción al tema principal de la entrada. Sabemos que (Z,+) es un grupo, de ahí podemos considerar el subgrupo nZ formado por los múltiplos de n, y trabajar con las clases módulo n. Supongamos que tenemos a,b∈Z y las clases de equivalencia de a y b módulo n . Éstas se definen de la siguiente manera:
a¯=a+nZ,b¯=b+nZ.

Si queremos sumar dos clases de equivalencia, usamos la suma usual en Z. Digamos
a¯+b¯=a+b―.

Aunque lo escribamos así, en realidad lo que estamos haciendo, es definir la suma +n en Zn usando +Z que es la suma del grupo (Z,+). Entonces lo anterior quedaría:
a¯+nb¯=a+Zb―.

Resulta que +n es una operación bien definida y (Zn,+n) es un grupo.

Otra manera de escribirlo sería:
(a+Z)+n(b+Z)=(a+Zb)+Z.
Donde, en este caso estamos usando la notación aditiva.

Entonces, ahora nos preguntamos, ¿cómo podemos generalizar esta propiedad?

Tomemos G un grupo y H un subgrupo y consideremos dos clases laterales izquierdas de H, digamos aH y bH, lo que queremos es definir, en caso de ser posible, un producto entre clases del siguiente modo:
aH⋅HbH=abH.

donde ⋅H es el nuevo producto entre clases y ab se hace con el producto en G.

Sin embargo, debemos verificar que este producto ⋅H esté bien definido. Para ello tenemos que ver que no depende de los representantes elegidos. Tomemos entonces otros representantes de las clases, para simplificarlo, cambiemos sólo el representante de una de las dos clases, digamos a~∈G tal que a~H=aH.

Entonces, quisiéramos que abH=a~bH, pero esto sucedería sólo de la siguiente manera,
abH=a~bH⇔(ab)−1a~b∈H⇔b−1a−1a~b∈H.

Entonces, ¿cómo sabemos que b−1a−1a~b∈H? Lo que sí sabemos es que a−1a~∈H, pues a~H=aH. Entonces, bastaría pedir que si h∈H, al multiplicar a h a un lado por un elemento de G, y al otro por su inverso, sigamos obteniendo elementos en H.

En esta entrada usaremos la idea anterior para definir un producto entre dos clases izquierdas usando el producto en G.

Subgrupos normales

Primero necesitamos definir formalmente qué es un conjugado.

Definición. Sea G un grupo, b,c∈G. Decimos que b es conjugado de c si b=aca−1 para alguna a∈G.

Dado a∈G y H un subgrupo de G,el conjugado de H por el elemento a es
aHa−1={aha−1|h∈H}.

Observación. aHa−1 es un subgrupo de G, para toda a∈G.

La demostración de esta observación queda de tarea moral.

Definición. Sea G un grupo, N subgrupo de G. Decimos que N es normal en G si ana−1∈N para todas a∈G, n∈N.

Notación. N⊴G.

Ahora, veamos una proposición. Recordemos que en una entrada pasada vimos que las clases laterales izquierdas no siempre coinciden con las clases laterales derechas y dimos algunos ejemplos. La siguiente proposición nos dirá que con subgrupos normales, la igualdad de clases derechas e izquierdas siempre se da.

Proposición. Sea G un grupo, N subgrupo de G. Las siguientes condiciones son equivalentes:

  1. N⊴G.
  2. aNa−1=N para todo a∈G.
  3. Toda clase laterial izquierda de N en G es una clase lateral derecha de N en G.

Demostración. Sea G un grupo, N≤G.

|1)⇒2)] Supongamos que N⊴G. Sea a∈G.

P.D. aNa−1=N.
Probaremos esto por doble contención.

⊆] Como N⊴G, ana−1∈N para toda n∈N. Entonces el conjunto aNa−1={ana−1|n∈N} está contenido en N.

⊇] Sea n∈N, como N⊴G, a−1na=a−1n(a−1)−1∈N. Entonces n=a(a−1na)a−1∈aNa−1.

Por lo tanto aNa−1=N.

|2)⇒3)] Supongamos que para todo a∈G, entonces aNa−1=N. Sea a∈G.

P.D. aN=Na.
De nuevo, probaremos esto por doble contención.

⊆] Tomemos an∈aN con n∈N, como ana−1∈aNa−1, y aNa−1=N por hipótesis, entonces an=(ana−1)a∈Na.

⊇] Tomemos na∈Na con n∈N, como a−1na∈a−1Na, y a−1Na=N por hipótesis, entonces na=a(a−1na)∈aN.

Por lo tanto aN=Na.

|3)⇒1)] Supongamos que para todo a∈G, existe b∈G tal que aN=Nb. Sean a∈G y n∈N.

P.D. ana−1∈N.

Por hipótesis aN=Nb para alguna b∈G. Pero a∈aN=Nb, entonces a∈Nb, por lo que a es otro representante de la clase lateral Nb, y en consecuencia Na=Nb. Tenemos entonces que aN=Nb=Na

Así, an∈aN=Na y entonces an=n~a para alguna n~∈N. Entonces

ana−1=(an)a−1=(n~a)a−1=n~∈N.
Por lo tanto N⊴G.

Así 1), 2) y 3) son equivalentes.

◼

Observación. (Conmutatividad parcial)
Si N⊴G, dados n∈N y a∈G, tenemos que an=n~a para alguna n~∈N, también na=an^ para alguna n^∈N.

Ejemplos

  1. An⊴Sn ya que si β∈An y α∈Sn.
    sgn(αβα−1)=sgnαsgnβsgnα−1=sgnα(+1)sgnα=+1
    Por lo tanto αβα−1∈An.
  2. Consideremos
    Q={±1,±i,±j,±k}H={±1,±i}
    Las clases laterales izquierdas de H en Q son: H y jH.
    Las clases laterales derechas de H en Q son: H y Hj.
    Además jH={±j,±k}=Hj. Por lo tanto H⊴Q.
  3. Consideremos D2(4) las simetrías del cuadrado. Sea a la rotación π2, b la reflexión con respecto al eje x.
    Sea H={e,b}.
    Si tomamos la transformación aba−1 podemos desarrollarla algebraicamente y geométricamente. Primero lo haremos de manera algebraica y interpretación geométrica la podrás encontrar en una imagen más abajo.
    Así, como vimos cuando trabajamos con el grupo diédrico:
    aba−1=aab=a2b∉H
    con a2b la reflexión con respecto al eje y.
    Por lo tanto H⋬D2(4).
Representación gráfica de la transformación aba−1.

Tarea moral

  1. Sean W=⟨(12)(34)⟩, V={(1),(12)(34),(13)(24),(14)(23)}≤S4. Verifica si W es normal en V, si V es normal en S4 y si W es normal en S4 ¿qué puedes concluir con ello?
  2. Sea G un grupo, H y N subgrupos de G con N normal en G, prueba o da un contraejemplo:
    1. N∩H es normal en H.
    2. N∩H es normal en G.
  3. Demuestra o da un contraejemplo: Si G es un grupo tal que cada subgrupo de él es normal, entonces G es abeliano.
  4. Sea G un grupo finito con un único subgrupo H de orden |H|. ¿Podemos concluir que H es normal en G?

Más adelante…

Como ya es costumbre, después de dar las definiciones y de practicarlas un poco con ejemplos, toca profundizar y hablar más sobre las proposiciones y teoremas que involucran a los subgrupos normales. En la siguiente entrada veremos esto.

Entradas relacionadas

Álgebra Moderna I: Caracterización de grupos cíclicos

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Gracias al teorema de Lagrange sabemos que el orden de todo subgrupo divide al del grupo que lo contiene, pero no sabemos si para cada divisor del orden del grupo, existe un subgrupo de ese tamaño. El siguiente teorema nos da una respuesta positiva en el caso de los grupos cíclicos finitos.

En los grupos cíclicos, para cada divisor del orden del grupo existe un único subgrupo que tiene por orden dicho divisor. Eso es lo primero que veremos en esta entrada. Después, demostraremos un resultado de la teoría de los números, usando la teoría de los grupos para llegar a una caracterización de los grupos cíclicos. Esta caracterización y sus consecuencias en los campos finitos se basan en el material de los textos de Rotman y aparecen también en el libro de Avella, Mendoza, Sáenz y Souto, mencionados en la bibliografía.

Todo divisor tiene un subgrupo de ese orden

Teorema. Sea G un grupo finito cíclico de orden n. Para cada d∈Z+ divisor de n existe un único subgrupo de G de orden d.

Demostración.
Sea G un grupo finito cíclico de orden n y sea a∈G tal que G=⟨a⟩.

Sea d∈Z+ con d|n.

Veamos que existe un subgrupo de G de orden d.

P.D. Existe un subgrupo de G de orden d.
Como d|n, entonces n=dk con k∈Z.

Queda como ejercicio para la tarea moral verificar que
o(ak)=n(n;k)=nk=d.

Así, |⟨ak⟩|=o(ak)=d.

Veamos ahora que este subgrupo es único.

P.D. Que no hay otro subgrupo de orden d.
Sea H≤G con |H|=d. Como G es cíclico, H también es cíclico y, por ende, H=⟨am⟩ para alguna m∈Z, entonces

e=(am)|H|=(am)d=amd.
Como amd=e, podríamos pensar que o(a)=md, sin embargo eso no es siempre cierto, lo que sí es cierto es que n|md. Entonces, existe q∈Z tal que
md=nq⇒md=dkqSustituyendo n=dk⇒m=kq.

Así am=akq=(ak)q∈⟨ak⟩, entonces H=⟨am⟩≤⟨ak⟩. Pero |⟨am⟩|=|⟨ak⟩|=d, por lo tanto ⟨am⟩=⟨ak⟩.

◼

Demostrando resultados de teoría de números usando teoría de grupos

Para llegar a una caracterización de los grupos cíclicos, primero vamos a introducir alguna notación.

Notación. Sea C grupo cíclico, al conjunto de generadores del grupo cíclico C lo denotaremos por
gen C={a∈C|⟨a⟩=C}.

Recordatorio. Dado d∈Z+

φ(d)=#{m∈{1,2,…,d}|(m;d)=1}.
Es decir, φ(d) es la cantidad de primos relativos con d. A la función φ se le conoce como la función phi de Euler.

Ahora, veamos un resultado que se refiere más a asuntos de la teoría de los números, y se puede encontrar en el libro de Rotman An introduction to the theory of groups, Teorema 2.16, mencionado en la bibliografía:

Teorema. Sea n∈Z+. Entonces n=∑d|n1≤d≤nφ(d).

Demostración.
Sea G un grupo cíclico de orden n.

Por el teorema anterior, para cada d|n con 1≤d≤n existe un único subgrupo de G de orden d, digamos Cd.

P.D. G=⋃d|n1≤d≤ngen Cd.

Lo probaremos por doble contención.

⊆] Sea a∈G.

Sabemos que ⟨a⟩ es un subgrupo de G de orden o(a), con o(a)∣n. Entonces ⟨a⟩=Co(a) y además a∈gen Co(a) por construcción. Así, a∈⋃d|n1≤d≤ngen Cd.

⊇] Por construcción, se da que gen Cd⊆G para cada d|n, 1≤d≤n.

Por lo tanto, G=⋃d|n1≤d≤ngen Cd.

Ahora veamos que la unión es disjunta.

Sean d,d′∈{1,…,n} divisores de n.

P.D. Si gen Cd∩gen Cd′≠∅, entonces d=d′.

Sea a∈gen Cd∩gen Cd′.

Entonces
Cd=⟨a⟩=Cd′⇒d=|Cd|=|Cd′|=d′∴d=d′.

Así, tenemos una unión disjunta, y en consecuencia

|G|=|⋃d|n1≤d≤ngen Cd|=∑d|n1≤d≤n#gen Cd.

Luego, si Cd=⟨a⟩, queda como ejercicio para la tarea moral ver que Cd=⟨ak⟩ si y sólo si (k;d)=1. Por lo que tenemos tantos generadores como primos relativos haya con d. Así,
|G|=∑d|n1≤d≤n#gen Cd=∑d|n1≤d≤nφ(d).

Por último, como |G|=n, se sigue que
∑d|n1≤d≤nφ(d)=n.

◼

Ahora sí, la caracterización que todos esperábamos

Después de los resultados anteriores ya estamos listos para dar el siguiente teorema, (que aparece en el libro de Rotman An introduction to the theory of groups, Proposición 2.17, mencionado en la bibliografía) pero esta vez lo demostraremos usando la teoría de los grupos.

Teorema. Sea G un grupo finito de orden n. G es cíclico si y sólo si para cada d∈Z+ divisor de n, G tiene a lo más un subgrupo cíclico de orden d.

A pesar de que el enunciado dice que G tiene a lo más un subgrupo cíclico, al final resulta que existe un único. La redacción es adrede para que la demostración del regreso no sea trivial.

Demostración.
Sea G un grupo finito de orden n.

|⇒] Supongamos que G es cíclico, entonces, por un resultado previo, para cada d∈Z+ divisor de n, G tiene exactamente un subgrupo cíclico de orden d.

[⇐| Supongamos que para toda d∈Z+ divisor de n, G tiene a lo más un subgrupo cíclico de orden d; si éste existe lo denotaremos por Cd, si no existe definimos Cd=∅ y definimos también gen Cd=∅ en ese caso.

Por un argumento análogo al de la demostración del teorema anterior, se tiene que G es la siguiente unión disjunta:
G=⋃d|n1≤d≤ngen Cd.

Entonces, usando el teorema anterior,

n=|G|=∑d|n1≤d≤n#gen Cd≤∑d|n1≤d≤nφ(d)=n

(donde el teorema anterior se usa en la última igualdad.)

Entonces,

∑d|n1≤d≤n#gen Cd=∑d|n1≤d≤nφ(d).

Así, para toda d|n, con 1≤d≤n se tienen que #gen Cd=φ(d) de donde gen Cd≠∅.

Por lo tanto, para toda d|n con 1≤d≤n, G tiene exactamente un subgrupo cíclico de orden d. En particular G tiene exactamente un subgrupo cíclico de orden n que debe ser G mismo.

∴G es cíclico. ◼

Consecuencias

Veamos las siguientes consecuencias del resultado anterior (aparecen en el libro de Rotman A first course in abstract algebra mencionado en la bibliografía en el Teorema 2.18 y la observación previa):

Corolario 1. Sea G un grupo finito de orden n. Si para toda d∈Z+ divisor de n hay a lo más d soluciones de xd=e en G, entonces G es cíclico.

Demostración.
Sea G un grupo finito, |G|=n, tal que ∀d∈Z+ que d|n, existen a lo más d soluciones de xd=e en G.

P.D. G es cíclico.

Supongamos por contradicción que G no es cíclico, entonces, por el teorema anterior tenemos que para alguna d∈Z+ divisor de n existe más de un subgrupo cíclico de orden d, es decir, existen C,C′ con C≠C′ subgrupos cíclicos de G de orden d.

Por un lado, si a∈C, e=a|C|=ad. Por otro lado, si a∈C′, e=a|C′|=ad. Entonces para toda a∈C∪C′, a es solución de xd=e.

Pero como C≠C′, entonces #C∪C′>|C|=d, entonces habría más de d soluciones de xd=e en G. Esto es una contradicción.

Así, para toda d∈Z+ tal que d∈N existe a lo más un subgrupo cíclico de orden d.

Por el teorema anterior, G es cíclico.

◼

En realidad, nos interesa el corolario 1, para probar el corolario 2.

Corolario 2. Para todo campo finito K, el grupo K∗=K∖{0} con la multiplicación del campo, es cíclico.

Demostración.
Sea d∈Z+ tal que d||K∗|.

Ahora, nos fijamos en el polinomio f(x)=xd−1 que tiene a lo más d raíces en K∗. Pero las raíces de f(x) son precisamente las soluciones de la ecuación xd=1, con 1 es el neutro multiplicativo de K.
Por lo tanto, por el corolario 1, K∗ es cíclico.

◼

Tarea moral

1. Sea G un grupo finito cíclico de orden n y sea a∈G. Sea k∈Z+.

  • Demuestra que o(ak)=n(n;k)=nk.
  • Demuestra que G=⟨ak⟩ si y sólo si (n;k)=1.

2. Dada d∈Z+ definimos

ϕ(d)=#{m∈{1,2,…,d}|(m;d)=1}.

Donde (m,d) es máximo común divisor de m y d.

Encuentra ∑d|n1≤d≤nϕ(d) para n∈{5,8,9,12}.

3. Considera el conjunto
K={(abba+b)|a,b∈Z2}
con las operaciones usuales. Prueba que K es un campo con cuatro elementos y verifica que K∗ es cíclico.

Más adelante…

Con esta entrada concluimos por el momento los temas relacionados al orden de un grupo y de un subgrupo. En la próxima entrada comenzaremos una nueva tarea: encontrar una multiplicación apropiada entre dos clases laterales, para ello, regresaremos a estudiar un poco a los enteros.

Entradas relacionadas