(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
La definición de subgrupos normales fue motivada porque queremos extraer las propiedades de los enteros a grupos más generales. Recordemos que en los enteros se define una relación de equivalencia (módulo $n$) de donde obtenemos clases de equivalencia. Estas clases no sólo inducen una partición, si no que conforman un subgrupo de $\z$. En esta entrada queremos generalizar esta idea y buscamos dar una operación en ciertas clases de equivalencia de modo que éstas formen también un grupo.
Grupo cociente $G$ módulo $N$
Teorema. Sea $G$ un grupo, $N$ un subgrupo normal de $G$.
El conjunto
$$G/N = \{aN | a\in G\}.$$
con la operación $$(aN)(bN) = ab N \qquad \forall a,b \in G$$
es un grupo de orden $[G : N ].$
Definición. Al conjunto $G/N$ de arriba se le conoce como el grupo cociente $G$ módulo $N$.
Demostración del teorema.
Sea $G$ un grupo, $N$ un subgrupo normal de $G$.
En $\{aN|a\in G\}$ consideremos la operación $$(aN)(bN) = ab N \qquad \forall a,b \in G.$$
Primero veamos que está bien definida.
Sean $a,a’,b,b’\in G$ con $aN = a’N$, $bN = b’N$.
P.D. $abN = a’b’N.$
Como $aN = a’N$, $a’ \in aN$ entonces $a’ = an$ con $n\in \n$.
Como $bN = b’N$, $b’ \in bN$ entonces $b’=b\tilde{n}$ con $\tilde{n} \in N$.
Sustituyendo $a’$ y $b’$ en $a’b’$ tenemos que $a’b’ = (an)(b\tilde{n}) = a(nb)\tilde{n}$.
Como $N \unlhd G$, por la conmutatividad parcial, $nb = b\hat{n}$ con $\hat{n}\in N$.
Entonces $a’b’ = a(b\hat{n})\tilde{n} = ab(\hat{n}\tilde{n}) \in abN$.
Por lo tanto $a’b’N = abN.$
Veamos ahora que con esta operación, $G/N$ es un grupo.
P.D. La operación es asociativa.
Sean $aN, bN, cN \in G/N$ con $a,b,c \in G$.
\begin{align*}
aN\,(bN \,cN) &= aN(bcN) = a(bc)N & \text{Definición del producto de clases}\\
&=(ab)c N &\text{Asociatividad en } G \\
&= (abN)cN = (aNbN)cN.
\end{align*}
Por lo tanto la operación en $G/N$ es asociativa.
P.D. El neutro de la operación existe y está en $G/N$.
Sea $aN\in G/N$,
\begin{align*}
&N(aN) = (eN)(aN) = eaN = aN &\text{Neutro en } G\\
&(aN)N = (aN)(eN) = aeN = aN&\text{Neutro en } G
\end{align*}
Por lo tanto $N$ es neutro en $G/N$.
P.D. Para cada elemento en $G/N$ existe un inverso bajo la operación y este inverso está en $G/N$.
Dado $aN\in G/N$, como $a\in G$ consideremos $a^{-1} \in G$ su inverso en $G$.
\begin{align*}
(aN)(a^{-1} N) = a a^{-1} N = eN = N\\
(a^{-1}N)(aN) = a^{-1} a N = eN = N.
\end{align*}
Así $a^{-1}N$ es inverso de $aN$. Por lo tanto $G/N$ es un grupo.
Finalmente,
$$|G/N| = \#\{aN | a\in G\} = [G : N ].$$
$\blacksquare$
Notemos que en la demostración de que $G/N$ con el producto es un grupo, usamos solamente las propiedades de que $G$ es grupo.
Primer y segundo ejemplo
Ahora veremos algunos ejemplos de grupo cociente.
El primer ejemplo es justo el que motivó la idea de grupo cociente.
Tomemos $(\z, +)$ y $H = \{m | 4 \text{ divide a } m\} = 4\z \unlhd \z$. $4\z$ es normal porque $\z$ es abeliano.
Entonces, vamos describiendo el grupo cociente paso por paso:
\begin{align*}
\z/4\z &= \z/H = \{H, 1+ H, 2 + H, 3 + H\}\\
& = \{\{4k\,|k\in\z\}, \{4k + 1|k\in\z\}, \{4k+2|k\in\z\},\{4k+3|k\in\z\}\}\\
& = \{\bar{0},\bar{1},\bar{2}, \bar{3}\} = \z_4.
\end{align*} La suma se realiza a partir de la suma de los representantes del siguiente modo: $$(a+H)+(b+H)=(a+b)+H,$$ es decir $$\bar{a}+\bar{b}=\overline{a+b},$$ para cualesquiera $a,b\in\z$.
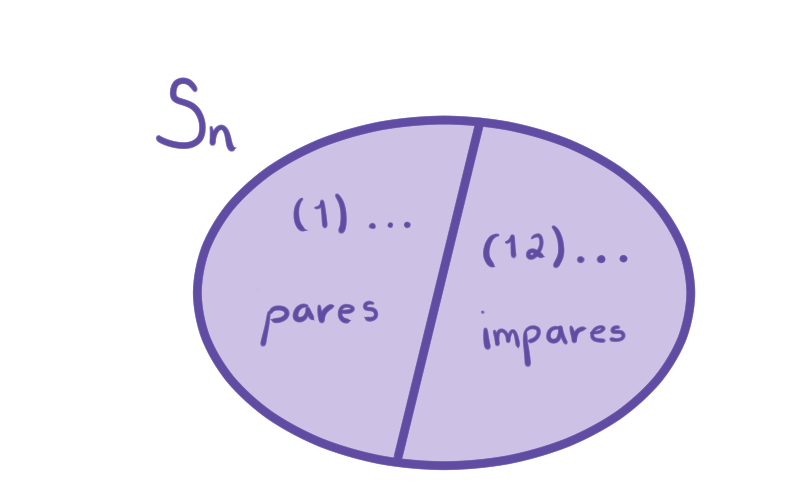
Ahora, para el segundo ejemplo, consideremos $n\geq2$ y tomamos $A_n \unlhd S_n$. En la entrada anterior vimos por qué $A_n$ es un subgrupo normal de $S_n$.
De nuevo, vamos describiendo el grupo cociente.
\begin{align*}
S_n/A_n &= \{A_n, (1\;2) A_n\}\\ &= \{\{\alpha\,|\alpha \text{ es par}\},\{(1\;2)\alpha\,|\alpha \text{ es par}\}\}\\
&= \{\{\alpha\,|\alpha \text{ es par}\},\{\beta\,|\beta \text{ es impar}\}\}.
\end{align*}
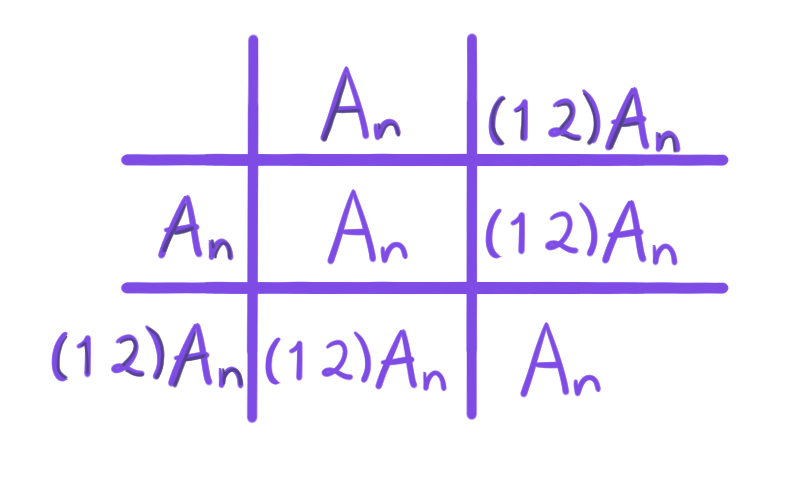
Así, estamos partiendo a $S_n$ en permutaciones pares (representadas por $(1)$) e impares (representadas por $(1\, 2)$). De esta manera, podemos decir que multiplicar dos permutaciones pares o dos impares resulta en una permutación par, pero multiplicar una par con una impar resulta en una permutación impar.
Tercer y cuarto ejemplo
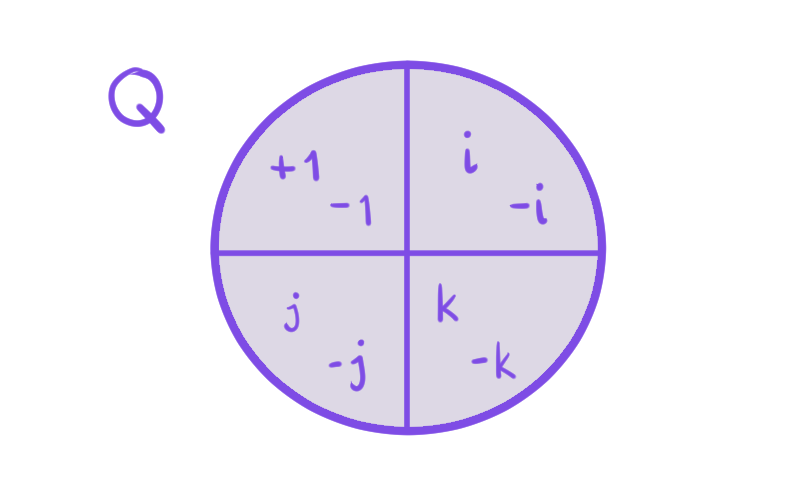
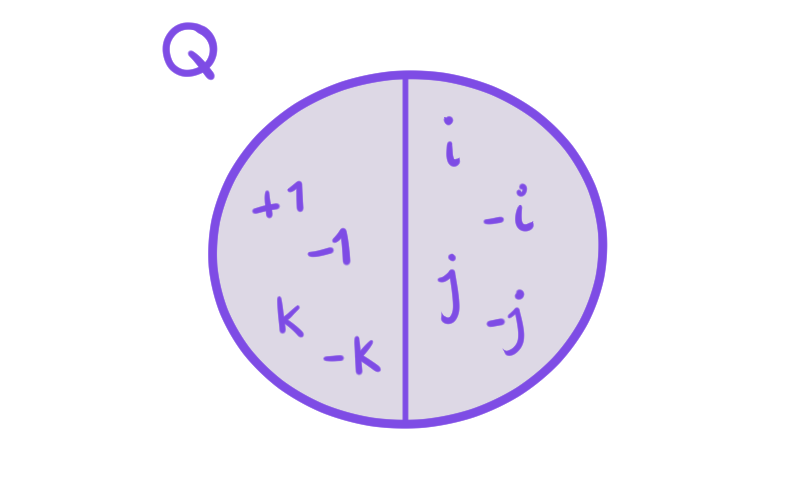
A continuación, para nuestro tercer ejemplo, tomamos $ N = \{\pm 1\} \unlhd Q$.
Para obtener una nueva clase lateral, escogemos un elemento de los cuaternios que no esté en $N$. El cociente se vería de la siguiente manera:
\begin{align*}
Q/N&=\{N, iN, jN, kN\}\\
&= \{\{\pm 1\},\{\pm i\},\{\pm j\},\{\pm k\}\}.
\end{align*}
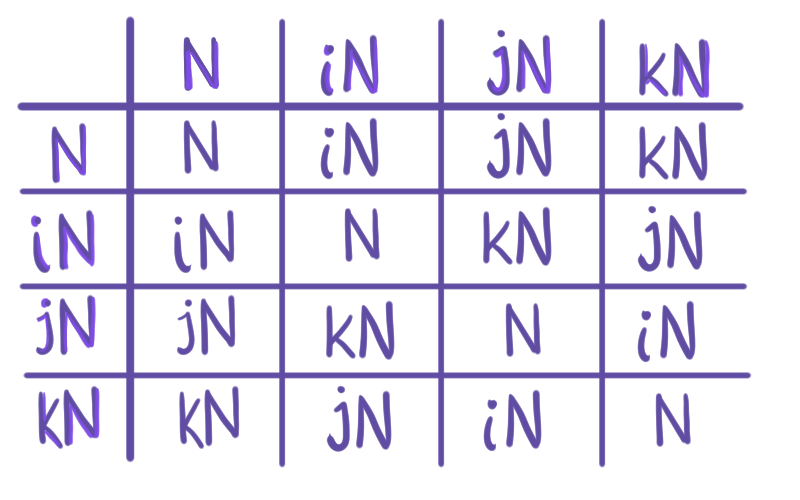
De nuevo, en las imágenes podemos ver una tabla que expresa el resultado de multiplicar distintas clases y una representación gráfica de las clases que obtenemos en el cociente.
Podemos verificar algunas de las operaciones de la tabla, hacemos el producto de $Q/N$ usando el producto en $Q$. Recordemos que $-kN = kN$ y $-iN = i N$, pues $k$ y $-k$ viven en una misma clase, y $-i$ e $i$ también son parte de una misma clase.
Si ahora consideramos $\left< k\right> \leq Q$, $\left< k\right> = \{\pm 1, \pm k\}$.
Entonces $\displaystyle [Q: \left< k\right> ]= \frac{|Q|}{|\left< k\right>|} = \frac{8}{4} = 2$, y así, $\left< k\right> \unlhd Q$.
Así $$Q/\left< k\right> = \{\left< k\right>, i \left< k\right>\}.$$
Para nuestro último ejemplo, consideremos $\z\times\z = \{(a,b) | a,b\in \z\}$, con la operación $(a,b)+(c,d) = (a+c, b+d)$.
Sea $H = \{(a,a) | a \in \z\}$.
\begin{align*}
(a,b) + H = (c,d) + H &\Leftrightarrow -(a,b) +(c,d) \in H \\
&\Leftrightarrow (c-a,d-b)\in H \Leftrightarrow c-a = d-b\\
&\Leftrightarrow c = d+ (a-b).
\end{align*}
Recordemos que $-(a,b)$ es el inverso de $(a,b)$.
Así,
\begin{align*}
(a,b) + H &= \{(d + (a-b), d) | d\in \z\}\\
&= \{(a-b, 0) + (d,d)| d \in \z\}.
\end{align*}
En particular $(a, b) + H = (a-b, 0) + H$. Las clases laterales se muestran mejor gráficamente en la imagen.
Tomemos los puntos enteros del eje $x$ como representantes de las clases laterales:
\begin{align*}
\z\times\z/H &= \{(a,0) + H | a\in \z\}.\\
((a,0) + H) + ((c,0) + H) &= (a + c, 0) + H.
\end{align*}

Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $G$ un grupo, $H$ un subgrupo de $G$ tal que el producto de dos clases laterales izquierdas de $H$ en $G$ es de nuevo una clase lateral izquierda de $H$ en $G$ ¿es entonces $H$ normal en $G$?
- Sea $G$ un grupo, $H$ un subgrupo normal de $G$ de índice finito con $m = [G:H]$. Dada $a\in G$ ¿qué podemos decir del elemento $a^m$? ¿Y si $H$ no es normal en $G$?
- Sea $G$ un grupo finito, $N$ un subgrupo normal de $G$. Dada $a\in G$. Analiza cómo es el orden de $a$ en relación al orden de $aN$.
- Considera el grupo aditivo $\r^2$ y el subgrupo $N = \{(x,0)|x\in \r\}.$
- Determina qué deben cumplir $(a,b), (c,d) \in \r^2$ para que $(a,b)N = (c,d)N$.
- Describe al grupo $\r^2/N$.
- Sea $G$ un grupo, $N$ un subgrupo normal de $G$ de índice finito con $p = [G:N]$ primo. Dada $a\in G$ ¿qué podemos decir de $\left< aN \right>$ y de $G/N$?
- Si quieres profundizar un poco más sobre Grupos cocientes, puedes revisar el video de Mathemaniac sobre el tema. El video está en inglés.
Más adelante…
En pocas palabras, un subgrupo normal induce una partición del grupo y ésta es el grupo cociente. Esta idea surge de lo que ocurre en los enteros. En la siguiente entrada usaremos el grupo cociente para crear, a partir de un grupo no abeliano, otro que sea abeliano.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Teoremas y Proposiciones relacionadas con subgrupos Normal y grupo Alternante.
- Siguiente entrada del curso: Subgrupo Conmutador.
- Resto de cursos: Cursos.