Archivo de la etiqueta: grupo alternante

Álgebra Moderna I: Teoremas y Proposiciones relacionadas con subgrupos normales y grupo Alternante.

Por Cecilia del Carmen Villatoro Ramos

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En entradas anteriores definimos el índice de $H$ en $G$ con $H$ un subgrupo del grupo $G$ . Además, dimos la definición de subgrupo normal, y demostramos equivalencias usando clases laterales izquierdas y derechas.

Cuando sólo hay dos clases laterales en $G$ , es muy fácil concluir esa equivalencia, es decir, es fácil verificar que toda clase lateral derecha es una clase lateral izquierda y viceversa. Digamos, si $[G : H] = 2$ y tomamos $a, b \in G$ . Por un lado tenemos que se crea una partición $P_{1} = {H, a H}$ de $G$ y por otro lado tenemos $P_{2} = {H, H b}$ . Como ambas particiones tienen $H$ , entonces necesariamente $a H = H b$ . Así, concluimos que $H ⊴ G$ .

Lo anterior lo demostraremos de manera formal en esta entrada.

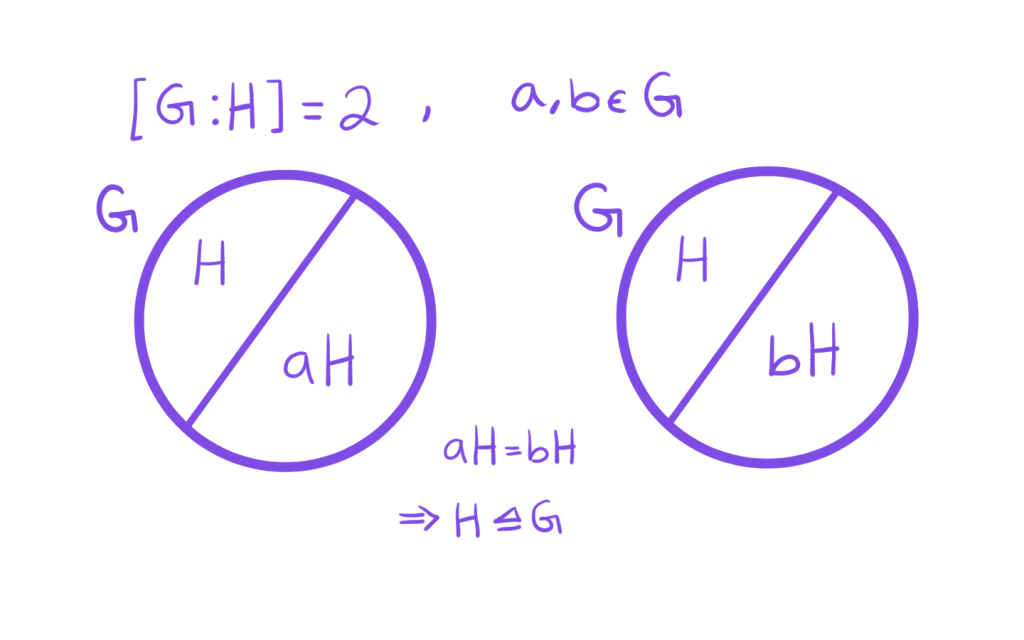
Representación gráfica de qué sucede cuando $[G : H] = 2$ .

Proposición sobre subgrupos

Proposición. Sean $G$ un grupo y $H$ un subgrupo de $G$ .

Si $[G : H] = 2$ , entonces $g^{2} \in H$ para toda $g \in G$ .
Si $[G : H] = 2$ , entonces $H$ es normal en $G$ .

Demostración.
Sea $G$ un grupo, $H \leq G$ con $[G : H] = 2$ .

$1.$ P.D. $g^{2} \in H$ para toda $g \in G$ .

Sea $g \in G$ . Como $[G : H] = 2$ hay dos clases laterales izquierdas, $H$ y $a H$ para alguna $a \in G ∖ H$ , y $G = H \dot{\cup} a H$ , donde $\dot{\cup}$ en este caso es una unión disjunta.

Como $g \in G$ , entonces $g \in H$ ó $g \in a H$ .

Si $g \in H$ , al ser $H$ un subgrupo, $g^{2} \in H$ .
Si $g \in a H$ , $g = a h$ para alguna $h \in H$ .
Por lo tanto $g^{2} = a h a h$ .

Pero también, $g^{2} \in G = H \dot{\cup} a H$ . Por un lado, si $g^{2} \in a H$ , $g^{2} = a \tilde{h}$ con $\tilde{h} \in H$ .
$\begin{aligned} \Rightarrow a \tilde{h} = g^{2} = a h a h \\ \Rightarrow \tilde{h} = h a h & Cancelamos la a que se repite \\ \Rightarrow a = h^{- 1} \tilde{h} h^{- 1} & Despejando a . \end{aligned}$

Pero cada uno de $h, \tilde{h}, h^{- 1} \in H$ . Por lo que $a \in H$ y esto sería una contradicción.
Por lo tanto $g^{2} \in H$ .

$2.$ Como $[G : H] = 2$ hay dos clases laterales izquierdas $H$ y $a H$ con $a \in G ∖ H$ . Hay también dos clases laterales derechas $H$ y $H b$ con $b \in G ∖ H$ y además
$H \dot{\cup} a H = G = H \dot{\cup} H b .$

Si $g \in a H$ , entonces $g \notin H$ , así $g \in G = H \dot{\cup} H b$ pero $g \notin H$ , y entonces $g \in H b$ . Por lo que $a H \subseteq H b$ .

Si $g \in H b$ , entonces $g \notin H$ , así $g \in G = H \dot{\cup} a H$ pero $g \notin H$ , y entonces $g \in a H$ . Por lo que $H b \subseteq a H$ .

Así, $a H = H b$ y toda clase lateral izquierda es una clase lateral derecha.
Por lo tanto, podemos concluir que $H ⊴ G$ .

Ejemplos.

Enunciamos dos ejemplos sencillos:

Ejemplo 1. Como $[S_{n} : A_{n}] = 2$ , entonces $A_{n} ⊴ S_{n}$ .

Ejemplo 2. En $D_{2 n} = ⟨ a, b ⟩$ con $a$ la rotación $\frac{2 π}{n}$ y $b$ la reflexión con respecto al eje $x$ .
Sea $H = ⟨ a ⟩$ .
$\begin{array}{r} [D_{2 n} : H] = \frac{| D_{2 n} |}{| H |} = \frac{2 n}{n} = 2. \end{array}$
Por lo tanto $H ⊴ D_{2 n}$ .

Más teoremas de subgrupos

Veamos que el hecho de que un número divida al orden de un grupo, no implica que haya un subgrupo de ese tamaño. Esto se puede ilustrar con un ejemplo.

Teorema. Sea $A_{4}$ el subgrupo alternante de $S_{4}$ .
$A_{4}$ no tiene subgrupos de orden $6$ .

Demostración.
Consideremos el subgrupo $A_{4}$ de $S_{4}$ .

Sabemos que
$| A_{4} | = \frac{| S_{4} |}{2} = \frac{4!}{2} = \frac{24}{2} = 12.$

Así, $6 | | A_{4} |$ .

P.D. $A_{4}$ no tiene subgrupos de orden $6$ .

Supongamos que existe $H \leq A_{4}$ con $| H | = 6$ .

$\begin{aligned} \Rightarrow & [A_{4} : H] = \frac{A_{4}}{H} = \frac{12}{6} = 2 \\ \Rightarrow & H ⊴ A_{4} & Prop. anterior inciso 2. \end{aligned}$

Sea $β = (a b c) \in A_{4}$ un $3 -$ ciclo.
Por el inciso 1 de la proposición anterior $(β^{2})^{2} \in H$ . Luego, $β = β^{4} = (β^{2})^{2} \in H$ . Así, todo $3 - c i c l o$ está en $H$ .

Pero en $S_{4}$ hay exactamente ocho $3 -$ ciclos. Entonces $| H | \geq 8$ y esto es una contradicción pues supusimos que $| H | = 6$ .

Por lo tanto $A_{4}$ no tiene subgrupos de orden 6.

Ahora veamos qué sucede si multiplicamos dos subgrupos. Esta multiplicación es posible y tiene sentido, pero esto no siempre nos da un subgrupo, aquí damos algunos casos en donde esto sí pasa.

Teorema. Sea $G$ un grupo, $H, K$ subgrupos de $G$ .

Si $H ⊴ G$ ó $K ⊴ G$ , entonces $H K \leq G$ .
Si $H ⊴ G$ y $K ⊴ G$ , entonces $H K ⊴ G$ .

Demostración.

Sea $G$ un grupo, $H$ y $K$ subgrupos de $G$ .

$1.$ Supongamos que $H ⊴ G$ .

P.D. $H K \leq G$ .
Por un resultado de una entrada previa, basta ver que $H K = K H$ .

Si $h \in H$ , $k \in K$ , como $H ⊴ G$ , entonces $h k = k \tilde{h}$ con $\tilde{h} \in H$ por la conmutatividad parcial. Por lo tanto $H K \subseteq K H$ .

Además $k h = \bar{h} k$ con $\bar{h} \in H$ , de nuevo, por la conmutatividad parcial ya que $H ⊴ G$ . Por lo tanto $K H \subseteq H K$ .

Así, $H K = K H$ y $H K \leq G$ .

Para $K ⊴ G$ se demuestra que $H K = K H$ de forma análoga.

$2.$ Supongamos que $H ⊴ G$ , $K ⊴ G$ .
Sean $h \in H, k \in K$ y $a \in G$ . Veamos que $a (h k) a^{- 1} \in H K .$

Agregando un neutro,
$a (h k) a^{- 1} = a h (a^{- 1} a) k a^{- 1} = (a h a^{- 1}) (a k a^{- 1}) .$

Pero como $H ⊴ G$ sabemos que $a h a^{- 1} \in H$ , y como $K ⊴ G$ sabemos que $a k a^{- 1} \in K$ , entonces $a (h k) a^{- 1} = (a h a^{- 1}) (a k a^{- 1}) \in H K .$

Por lo tanto $H K ⊴ G$ .

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sea $G$ un grupo, $H$ un subgrupo de $G$ con $3 = [G : H]$ . ¿Es $H$ normal en $G$ ?
Prueba que en $S_{4}$ hay exactamente ocho $3$ -ciclos.
Demuestra que $A_{5}$ no tiene subgrupos de orden 20: Supón por contradicción que $H$ es un subgrupo de de orden 20.
1. Sea $α \in A_{5}$ un $5$ -ciclo. Prueba que si $α \notin H$ entonces $H, α H$ y $α^{2} H$ son las 3 clases laterales izquierdas de $H$ en $A_{5}$ .
2. Prueba que $α^{3}$ no está en ninguna de esas tres clases laterales.
3. Concluye que $α \in H$ para todo $α$ 5-ciclo, y así $H$ tendría más de 20 elementos.
Sea $G$ un grupo, $H$ y $K$ subgrupos de $G$ . Prueba o da un contraejemplo:
1. Si $H K$ es un subgrupo de $G$ , entonces $H$ es normal en $G$ o $K$ es normal en $G$ .
2. Si $H K$ es un subgrupo normal de $G$ , entonces $H$ es normal en $G$ y $K$ es normal en $G$ .

Más adelante…

Esta entrada es la última antes de comenzar un pequeño tema nuevo: el grupo cociente. Seguiremos viendo cómo se pueden generar particiones de los grupos y definiremos una operación entre los elementos de esta partición.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Subgrupo Conjugado, Subgrupo Normal, Conmutatividad Parcial.
Siguiente entrada del curso: Grupo Cociente.
Resto de cursos: Cursos.

Álgebra Moderna I: Paridad de una permutación

Por Cecilia del Carmen Villatoro Ramos

4 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior descubrimos que toda permutación se puede factorizar en producto de transposiciones. Mas aún, el polinomio de Vandermonde nos permite saber que, aunque hayan varias factorizaciones, en realidad, todas siempre tienen una cantidad par (o un cantidad impar) de transposiciones. Con esto, podemos definir el signo de una permutación. La secuencia que se seguirá para abordar el signo de una permutación es la presentada en el libro Grupos I de Avella, Mendoza, Sáenz y Souto que se indica en la bibliografía, es decir se usarán los resultados de la entrada previa de acuerdo al enfoque de Herstein, para introducir la función signo y probar que es multiplicativa, y con ello obtener la fórmula del signo que aparece en el libro A first course in abstract algebra de Rotman (todos estos libros son los que se mencionan en la bibliografía).

Ya teniendo una noción de la paridad de una permutación podemos jugar con las consecuencias: podemos deducir qué pasa si multiplicamos dos permutación con la misma paridad, qué sucede cuando tienen distinta paridad y además, como es raro en los cursos de matemáticas… ¡podemos agrupar por paridad! En esta entrada, descubrimos que el conjunto de transposiciones con signo par, es en realidad un grupo con $\frac{n!}{2}$ elementos. Este conjunto es llamado el grupo alternante.

¿Pares o impares?

Definición. Sea $α \in S_{n}$ , $α$ es par si $α = id$ o si $α$ es un producto de un número par de transposiciones. Por otro lado, $α$ es impar si es un producto de un número impar de transposiciones.

La función signo es $s g n : S_{n} \to {+ 1, - 1}$ definida como
$\begin{array}{r} s g n α = {\begin{cases} + 1 & si α es par \\ - 1 & si α es impar \end{cases} \end{array}$

Observación. Sean $α = τ_{1} \dots τ_{r} \in S_{n}$ , con $τ_{1}, \dots, τ_{r}$ transposiciones. Entonces $s g n α = (- 1)^{r}$ .

Demostración.
La definición nos asegura que $s g n α = + 1$ si y sólo si $r$ es par.

Proposición. Sean $α, β \in S_{n}$ . Entonces $s g n (α β) = s g n α s g n β .$

Esto nos dice que la función signo ( $s g n$ ) es multiplicativa. Esto lo hace más sencilla de trabajar.

Demostración.

Esto es bastante fácil de demostrar, para usar lo que vimos tenemos que expresar a estas permutaciones como producto de transposiciones.

Sean $α, β \in S_{n}$ , con $α = τ_{1} \dots τ_{r}$ , $β = ρ_{1} \dots ρ_{t}$ . Donde, $τ_{1}, \dots, τ_{r}, ρ_{1}, \dots, ρ_{t}$ son transposiciones.

Si calculamos el signo del producto $α β$ y usando la observación anterior, obtenemos lo siguiente:
$\begin{aligned} s g n (α β) & = s g n (τ_{1} \dots τ_{r} ρ_{1} \dots ρ_{t}) \\ = (- 1)^{r + t} & Observación anterior \\ = (- 1)^{r} (- 1)^{t} & Propiedades de las potencias \\ = s g n α s g n β & Observación anterior \end{aligned}$

Esto es precisamente lo que queríamos probar.

Podemos concluir que para calcular el signo de un producto, basta entender el signo de cada uno de los factores.

Calculando el signo de una permutación

Seguiremos puliendo la idea que nos dio la proposición anterior hasta llegar a una fórmula para sacar el signo de una permutación. Pero por ahora, veamos qué sucede con los $r$ -ciclos.

Lema. Sea $σ = (i_{1} \dots i_{r}) \in S_{n}$ un $r$ -ciclo. Entonces $s g n σ = (- 1)^{r - 1}$ .

Demostración.
Recordemos que en la entrada anterior vimos que podemos escribir a $σ$ como un producto de transposiciones:
$\begin{aligned} σ & = (i_{1} \dots i_{r}) = (i_{1} i_{r}) \dots (i_{1} i_{2}) . \end{aligned}$
Intuitivamente, estamos intercambiando a $i_{1}$ con los elementos que le siguen, esto nos da $r - 1$ transposiciones. Por lo tanto, $σ$ es un producto de $r - 1$ transposiciones. De acuerdo con la observación, podemos concluir que $s g n σ = (- 1)^{r - 1}$ .

Estamos listos para enunciar y probar la fórmula del signo que aparece en el libro A first course in abstract algebra de Rotman que se menciona en la bibliografía, y que resulta muy útil para calcular el signo de una permutación.

Teorema. Sea $α \in S_{n}$ , $α = β_{1} \dots β_{t}$ una factorización completa de $α$ . Entonces $s g n α = (- 1)^{n - t}$ , donde $t$ es la cantidad de factores que tiene la factorización completa de $α$ .

Demostración.
Como el signo es multiplicativo,
$\begin{array}{r} s g n α = \prod_{i = 1}^{t} s g n β_{i} . \end{array}$
Estamos tomando una factorización completa de $α$ , entonces todos los $β_{i}$ son ciclos disjuntos. Así que su signo está dado por la longitud del ciclo (de acuerdo al lema dado):
$\begin{array}{r} s g n β_{i} = (- 1)^{long β_{i} - 1} \forall i \in {1, \dots, t} . \end{array}$
Juntando ambas ecuaciones y sumando los $t$ exponentes obtenemos las siguientes igualdades
$\begin{aligned} s g n α & = \prod_{i = 1}^{t} s g n β_{i} & Proposición \\ = \prod_{i = 1}^{t} (- 1)^{long β_{i} - 1} & Lema \\ = (- 1)^{(\sum_{i = 1}^{t} long β_{i}) - t} = (- 1)^{n - t} . & Leyes de exponentes \end{aligned}$

Como la factorización es completa, la siguiente igualdad se cumple: $\sum_{i = 1}^{t} long β_{i} = n .$

Por lo tanto $s g n α = (- 1)^{n - t}$ .

Esta forma resulta útil porque ya no se requiere descomponer una permutación en producto de transposiciones, basta con encontrar una factorización completa. Veamos esto con un ejemplo.

Ejemplo.
Consideremos $α \in S_{10}$ como
$\begin{array}{r} α = (\begin{array}{c} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 2 & 4 & 7 & 5 & 1 & 8 & 3 & 9 & 6 & 10 \end{array}) . \end{array}$

También podemos escribirla como $α = (1 2 4 5) (3 7) (6 8 9) (10)$ . Esta expresión es una factorización completa de $α$ con cuatro factores.

Entonces, de acuerdo con el teorema que acabamos de probar, $s g n α = (- 1)^{10 - 4} = (- 1)^{6} = + 1.$

Por otro lado mostremos una factorización de $α$ en transposiciones: $α = (1 5) (1 4) (1 2) (3 7) (6 9) (6 8)$ que tiene seis transposiciones. Entonces, efectivamente $α$ es un producto de un número par de transposiciones.

Hora de Agrupar

Hemos visto que la función $s g n$ es una función mutliplicativa. Esto nos da como consecuencia que al multiplicar dos permutaciones con la misma paridad, te da como resultado una permutación par. En caso contrario, el resultado es impar. Ahora nos fijaremos solamente en las permutaciones pares.

Definición. El grupo alternante para $n$ elementos está definido como

$A_{n} = {α \in S_{n} | s g n α = + 1} .$

Observación. $A_{n}$ efectivamente es un subgrupo de $S_{n}$ .

Demostración.
Si $α = id$ , por definición del signo, $s g n id = + 1$ . Así, $id \in A_{n}$ .

Sean $α, β \in A_{n}$ .
Como la función signo es multiplicativa:
$\begin{array}{r} s g n α β = s g n α s g n β = (+ 1) (+ 1) = + 1. \end{array}$
Así, $α β \in A_{n}$ . Es decir, $A_{n}$ es cerrada bajo el producto.

Por último, sea $α \in A_{n}$ .

Por un lado, usando la propiedad multiplicativa del signo obtenemos:
$\begin{array}{r} s g n (α α^{- 1}) = s g n α s g n α^{- 1} = (+ 1) s g n α^{- 1} . \end{array}$

Por otro lado, como $α α^{- 1} = id$ , tenemos:
$\begin{array}{r} s g n (α α^{- 1}) = s g n id = + 1. \end{array}$

Por lo tanto $s g n (α α^{- 1}) = + 1$ , así $α^{- 1} \in A_{n}$ . Es decir, $A_{n}$ es cerrada bajo inversos.

Por lo tanto $A_{n}$ es un subgrupo de $S_{n}$ .

El siguiente resultado nos muestra que el grupo alternante $A_{n}$ «parte en dos» a las permutaciones, es decir, la mitad de permutaciones son pares.

Proposición. Sea $n > 1$ , entonces $| A_{n} | = \frac{n!}{2}$ .

Demostración. Podemos ver a $S_{n}$ como la unión de las permutaciones pares e impares, esto se expresa así $S_{n} = A_{n} \cup (S_{n} ∖ A_{n}) .$
Pero, podemos dar una biyección definida como $ϕ : A_{n} \to S_{n} ∖ A_{n}$ , definida como $ϕ α = (1 2) α$ .

Entonces, $| A_{n} | = # S_{n} ∖ A_{n}$ .

Así, como dijimos que

$n! = | S_{n} | = | A_{n} | + # S_{n} ∖ A_{n} = 2 | A_{n} |$ .

Por lo tanto $| A_{n} | = \frac{n!}{2}$ .

Notación. Para denotar la cardinalidad u orden de un conjunto $A$ , usamos dos notaciones:
$\begin{aligned} | A | \to & Si A es un grupo. \\ # A \to & Si A no es un grupo (o si no sabemos si A es un grupo o no). \end{aligned}$

Tarea moral

Considera el elemento $α \in S_{12}$ como
$\begin{array}{r} α = (\begin{array}{c} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ 2 & 11 & 4 & 1 & 8 & 12 & 3 & 6 & 9 & 5 & 7 & 10 \end{array}) \end{array}$
1. Encuentra $α^{- 1}$ , el signo de $α$ y el de $α^{- 1}$ .
2. En general, ¿qué pasará con el signo de una permutación y de su inversa?
Sea $α$ un $r$ ciclo en $S_{n}$ . ¿Podemos determinar el signo de $α$ a partir de la paridad de $r$ ?
Dada $α \in S_{n}$ decimos que los números $i, j \in {1, 2, \dots, n}$ forman una inversión si $i < j$ pero $α (i) > α (j)$ . ¿Qué relación existe entre la paridad y el número de inversiones de $α$ ?
Encuentra todos los elementos de $A_{4}$ .

Más adelante…

Esta entrada nos sirvió para construir los cimientos, es importante que lo tengamos claro antes de avanzar. En la siguiente entrada definiremos el producto de $S$ con $T$ , veremos en qué situaciones el producto de los subconjuntos conmuta, cuándo se cumple que $S T$ es un subgrupo de $G$ . Esto nos ayudará para definir las clases laterales. Más adelante, estas clases nos ayudarán a definir una nueva relación de equivalencia.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Estructura Cíclica, Permutación Conjugada y Polinomio de Vandermonde.
Siguiente entrada del curso: Producto de subconjuntos y Clases Laterales.
Resto de cursos: Cursos.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: grupo alternante

Álgebra Moderna I: Teoremas y Proposiciones relacionadas con subgrupos normales y grupo Alternante.

Introducción

Proposición sobre subgrupos

Más teoremas de subgrupos

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Paridad de una permutación

Introducción

¿Pares o impares?

Calculando el signo de una permutación

Hora de Agrupar

Tarea moral

Más adelante…

Entradas relacionadas