círculo pedal archivos - El blog de Leo

Introducción

En esta ocasión hablaremos sobre un tipo mas general de pares de rectas que las medianas y simedianas, estas son las rectas isogonales, esto nos permitirá hablar sobre pares de puntos mas generales que el centroide y el punto simediano, nos referimos a los puntos conjugados isogonales y a sus triángulos pedales.

Rectas isogonales

Definición 1. Dos rectas que pasan por el vértice de un ángulo tales que una es la reflexión de la otra respecto a la bisectriz del ángulo, se llaman rectas isogonales.

Teorema 1. Las distancias a los lados de un ángulo desde dos puntos en dos rectas que pasan por el vértice del ángulo son inversamente proporcionales si y solo si las rectas son isogonales.

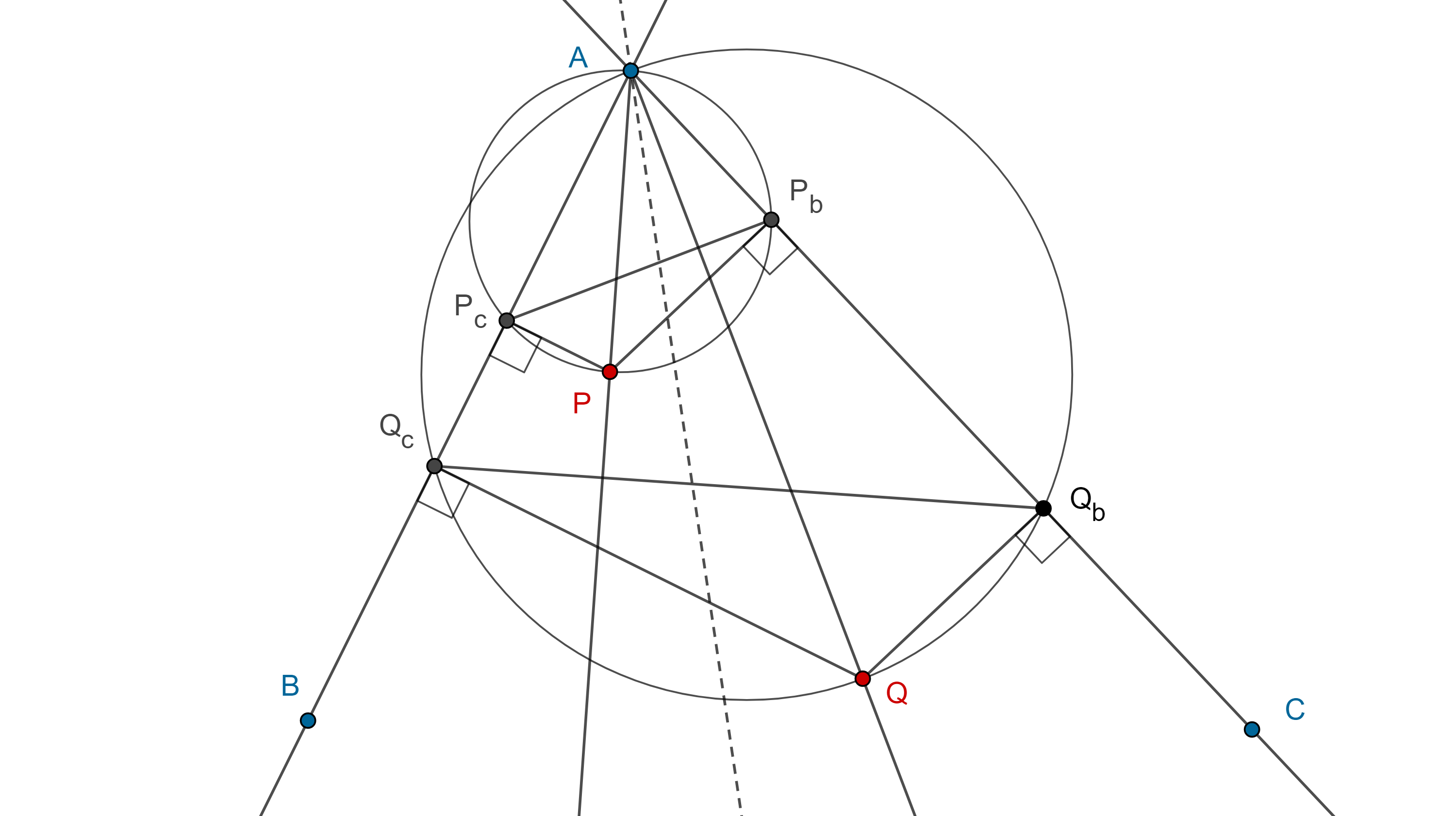
Demostración. Si $A P$ y $A Q$ son dos rectas isogonales respecto del ángulo $∠ B A C$ , considera $P_{c}$ , $Q_{c}$ , las proyecciones de $P$ y $Q$ en $A B$ , y $P_{b}$ , $Q_{b}$ , las proyecciones de $P$ y $Q$ en $A C$ .

Como $A P$ , $A Q$ son isogonales entonces $∠ B A P = ∠ Q A C$ y tenemos las siguientes semejanzas $△ A P P_{c} \sim △ A Q Q_{b}$ , $△ A P P_{b} \sim △ A Q Q_{c}$ por lo tanto,
$\frac{P P_{c}}{Q Q_{b}} = \frac{A P}{A Q} = \frac{P P_{b}}{Q Q_{c}}$ .

Ahora supongamos que las distancias a los lados del ángulo, desde $P$ y $Q$ , son inversamente proporcionales.

Notemos que los cuadriláteros $A P_{c} P P_{b}$ , $A Q_{c} Q Q_{b}$ son cíclicos, por lo tanto, los pares de ángulos $∠ B A C$ , $∠ P_{b} P P_{c}$ y $∠ B A C$ , $∠ Q_{b} Q Q_{c}$ son suplementarios, entonces $∠ P_{b} P P_{c} = ∠ Q_{b} Q Q_{c}$ .

Por hipótesis tenemos que $P P_{c} \times Q Q_{c} = P P_{b} \times Q Q_{b}$
$\Rightarrow \frac{P P_{c}}{Q Q_{b}} = \frac{P P_{b}}{Q Q_{c}}$ .

Por criterio de semejanza LAL, $△ P P_{b} P_{c} \sim △ Q Q_{c} Q_{b}$ , y como $A P_{c} P P_{b}$ , $A Q_{c} Q Q_{b}$ son cíclicos, entonces
$∠ B A P = ∠ P_{c} P_{b} P = ∠ Q Q_{c} Q_{b} = ∠ Q A C$ .

Por lo tanto $A P$ y $A Q$ son isogonales.

Puntos conjugados isogonales

Teorema 2. Si tres cevianas de un triángulo son concurrentes, entonces sus rectas isogonales respecto de los ángulos del triángulo son concurrentes, los puntos de concurrencia se llaman conjugados isogonales respecto al triángulo considerado.

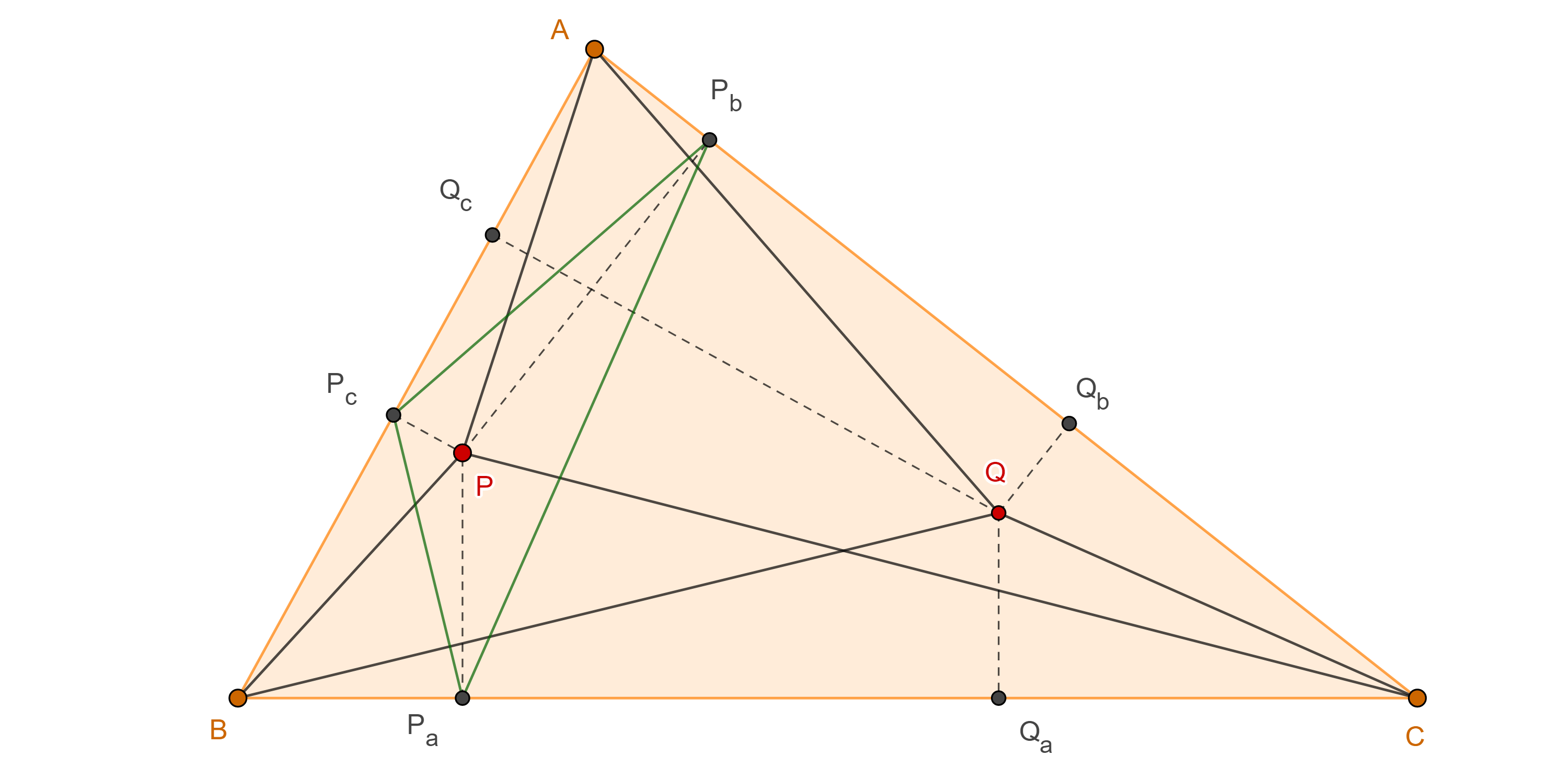
Si en $△ A B C$ , $A P$ , $B P$ , $C P$ son tres cevianas concurrentes, consideremos $Q$ la intersección de las isogonales $B Q$ , $C Q$ de $B P$ y $C P$ respectivamente, sean $P_{a}$ , $P_{b}$ , $P_{c}$ ; $Q_{a}$ , $Q_{b}$ , $Q_{c}$ , las proyecciones de $P$ y $Q$ en $B C$ , $C A$ y $A B$ respectivamente.

Por el teorema 1, $\frac{P P_{a}}{P P_{c}} = \frac{Q Q_{c}}{Q Q_{a}}$ y $\frac{P P_{b}}{P P_{a}} = \frac{Q Q_{a}}{Q Q_{b}}$ .

Como resultado, $P P_{c} \times Q Q_{c} = P P_{a} \times Q Q_{a} = P P_{b} \times Q Q_{b}$ .

Por el teorema 1, $P$ y $Q$ están sobre rectas isogonales repecto de $∠ B A C$ .

Proposición 1. Dados un ángulo y un punto, la recta que une las proyecciones del punto a los lados del ángulo, es perpendicular a la isogonal a la recta que une el vértice del ángulo con el punto dado.

Demostración. En la entrada simediana probamos la misma proposición, pero para simedianas y medianas, la demostración permanece igual para el caso general.

Corolario. Dados un triángulo $△ A B C$ y un punto $P$ , las perpendiculares desde los vértices del triángulo a los lados del triángulo pedal de $P$ respecto de $△ A B C$ , concurren en el conjugado isogonal de $P$ respecto de $△ A B C$ .

Demostración. Aplicamos la proposición anterior a los tres ángulos del triángulo y recordamos que las tres isogonales a $A P$ , $B P$ y $C P$ son concurrentes (figura 2).

Proposición 2. El conjugado isogonal de un punto respecto a un triángulo es un punto al infinito si y solo si el punto se encuentra en el circuncírculo del triángulo.

Demostración. Sean $△ A B C$ , y $P$ un punto, recordemos que el triángulo pedal de $P$ respecto de $△ A B C$ degenera en una recta, la recta de Simson, sí y solo si $P$ esta en el circuncírculo de $△ A B C$ .

Por la proposición 1, las rectas isogonales a $A P$ , $B P$ , $C P$ , respecto de los ángulos de $△ A B C$ son perpendiculares a los lados del triángulo pedal, por lo tanto estas rectas son paralelas si y solo si las proyecciones de $P$ en los lados de $△ A B C$ son colineales.

Ya que las rectas paralelas se intersecan en un punto ideal y las isogonales a $A P$ , $B P$ , $C P$ se intersecan en el conjugado isogonal a $P$ , se tiene el resultado.

Circulo pedal de conjugados isogonales

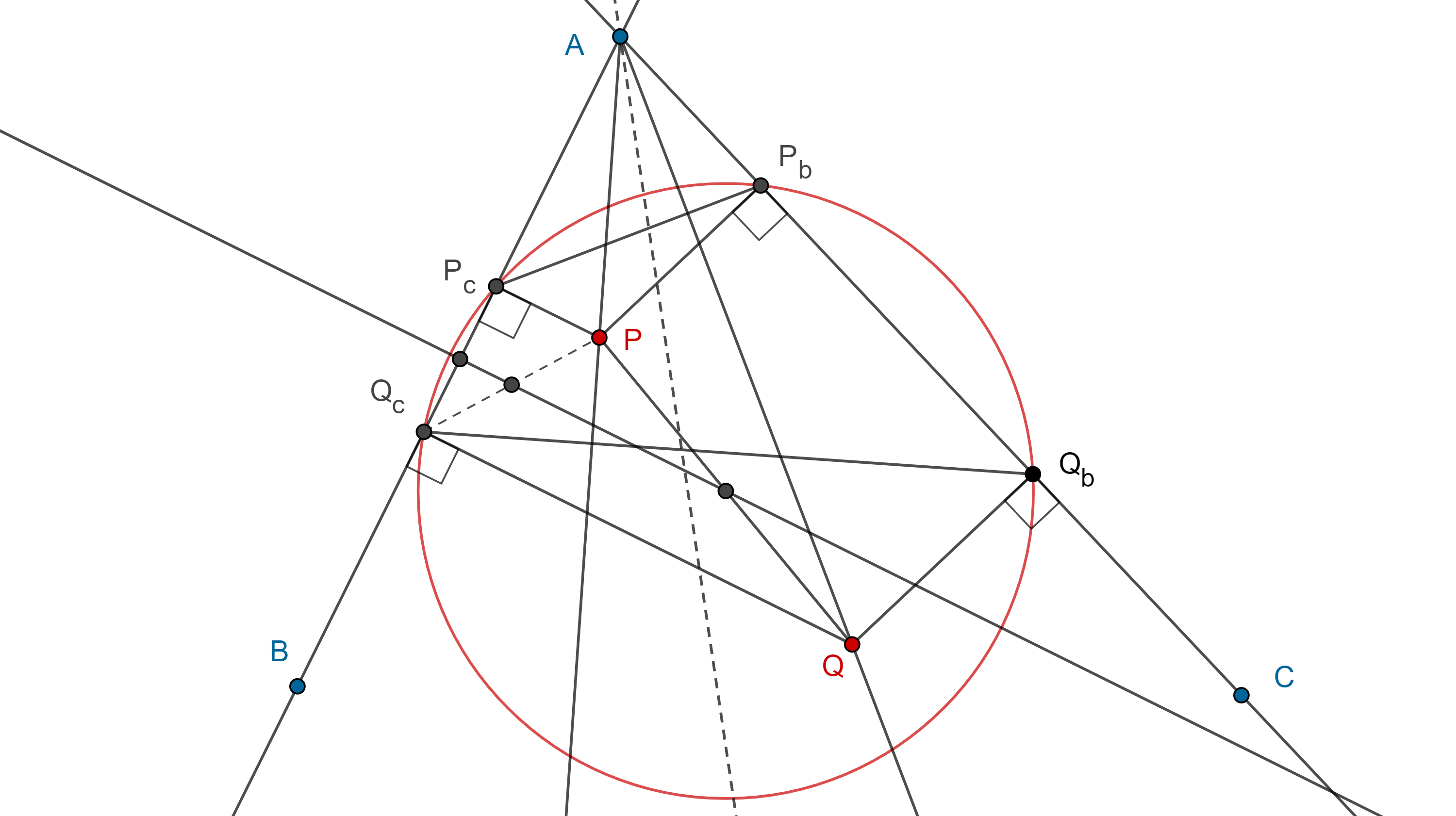
Proposición 3. Las proyecciones a los lados de un ángulo desde dos puntos en dos rectas isogonales son cíclicos y el centro de la circunferencia es el punto medio entre $P$ y $Q$ .

Demostración. En la demostración del teorema 1, vimos que se tienen la siguientes semejanzas, $△ A P P_{c} \sim △ A Q Q_{b}$ , $△ A P P_{b} \sim △ A Q Q_{c}$ , es decir,
$\frac{A P_{c}}{A Q_{b}} = \frac{A P}{A Q} = \frac{A P_{b}}{A Q_{c}}$
$\Rightarrow A P_{c} \times A Q_{c} = A P_{b} \times A Q_{b}$ .

Por el teorema de las cuerdas, $P_{c} Q_{b} P_{b} Q_{c}$ es un cuadrilátero cíclico.

Por otra parte, en $△ P_{c} Q_{c} P$ , la mediatriz de $P_{c} Q_{c}$ es paralela a $P_{c} P$ y pasa por el punto medio de $P_{c} Q_{c}$ , por lo tanto pasa por el punto medio de $P Q_{c}$ .

En $△ P Q_{c} Q$ la mediatriz de $P_{c} Q_{c}$ es paralela a $Q_{c} Q$ y pasa por el punto medio de $P Q_{c}$ por lo tanto pasa por el punto medio de $P Q$ .

Igualmente vemos que la mediatriz de $P_{b} Q_{b}$ pasa por el punto medio de $P Q$ .

Como $P_{c} Q_{c}$ y $P_{b} Q_{b}$ son cuerdas de la circunferencia sus mediatrices se intersecan en el centro, por lo tanto este coincide con el punto medio de $P Q$ .

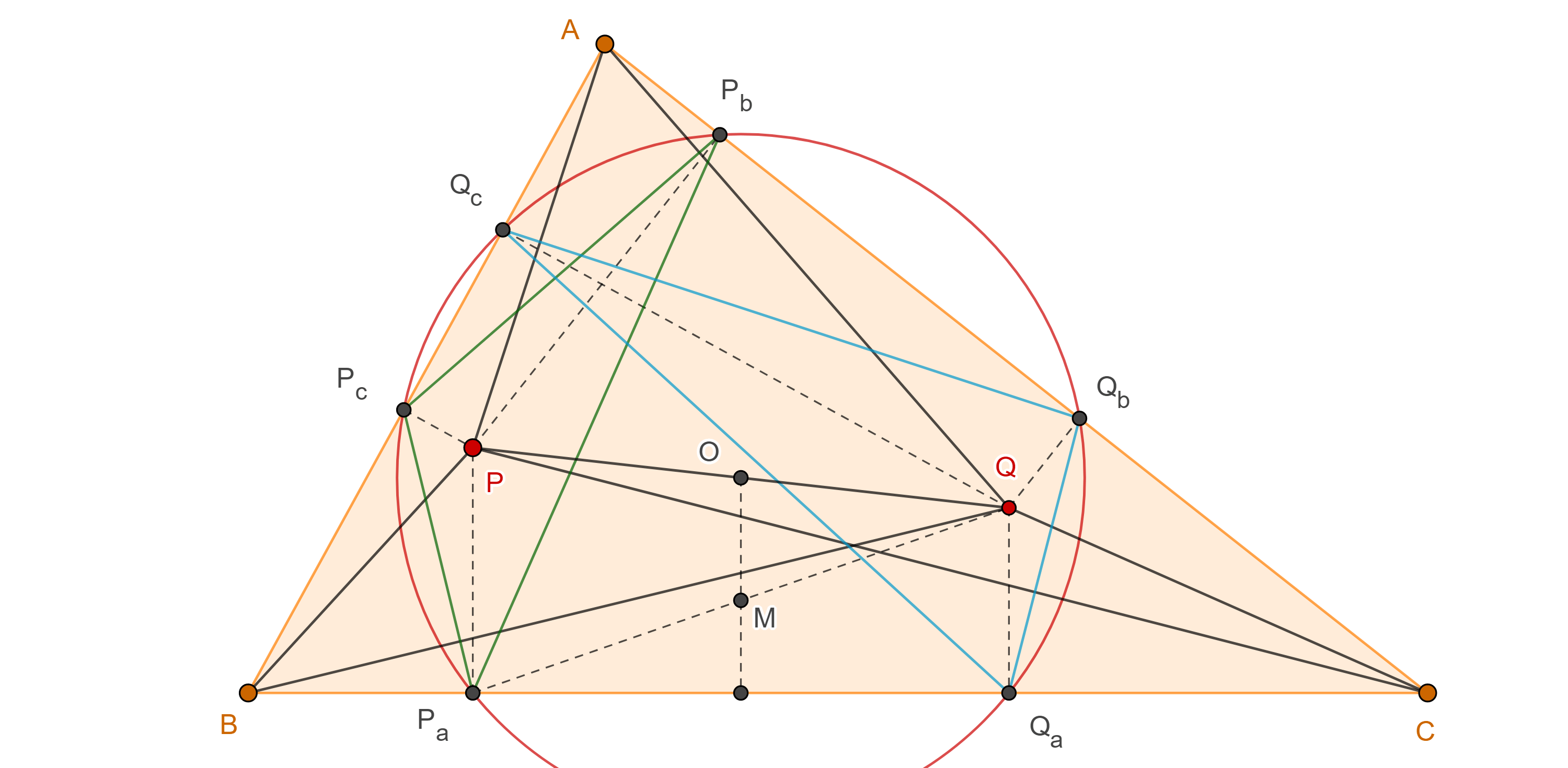
Teorema 3. Los triángulos pedales de dos puntos que son conjugados isogonales respecto a un triángulo tienen el mismo circuncírculo y su centro es el punto medio entre los puntos isogonales, esta circunferencia se conoce como circulo pedal de los puntos conjugados isogonales.

Demostración. Sean $O$ el punto medio de $P Q$ y $△ P_{a} P_{b} P_{c}$ , $△ Q_{a} Q_{b} Q_{c}$ , los triángulos pedales de $P$ y $Q$ .

Por la proposición anterior, $Q_{c} P_{C} Q_{b} P_{b}$ es cíclico, con centro en $O$ , $Q_{c} P_{c} P_{a} Q_{a}$ es cíclico con centro en $O$ , $P_{b} P_{a} Q_{a} Q_{b}$ es cíclico con centro en $O$ .

Como estas tres circunferencias son concéntricas y tienen el mismo radio, son la misma.

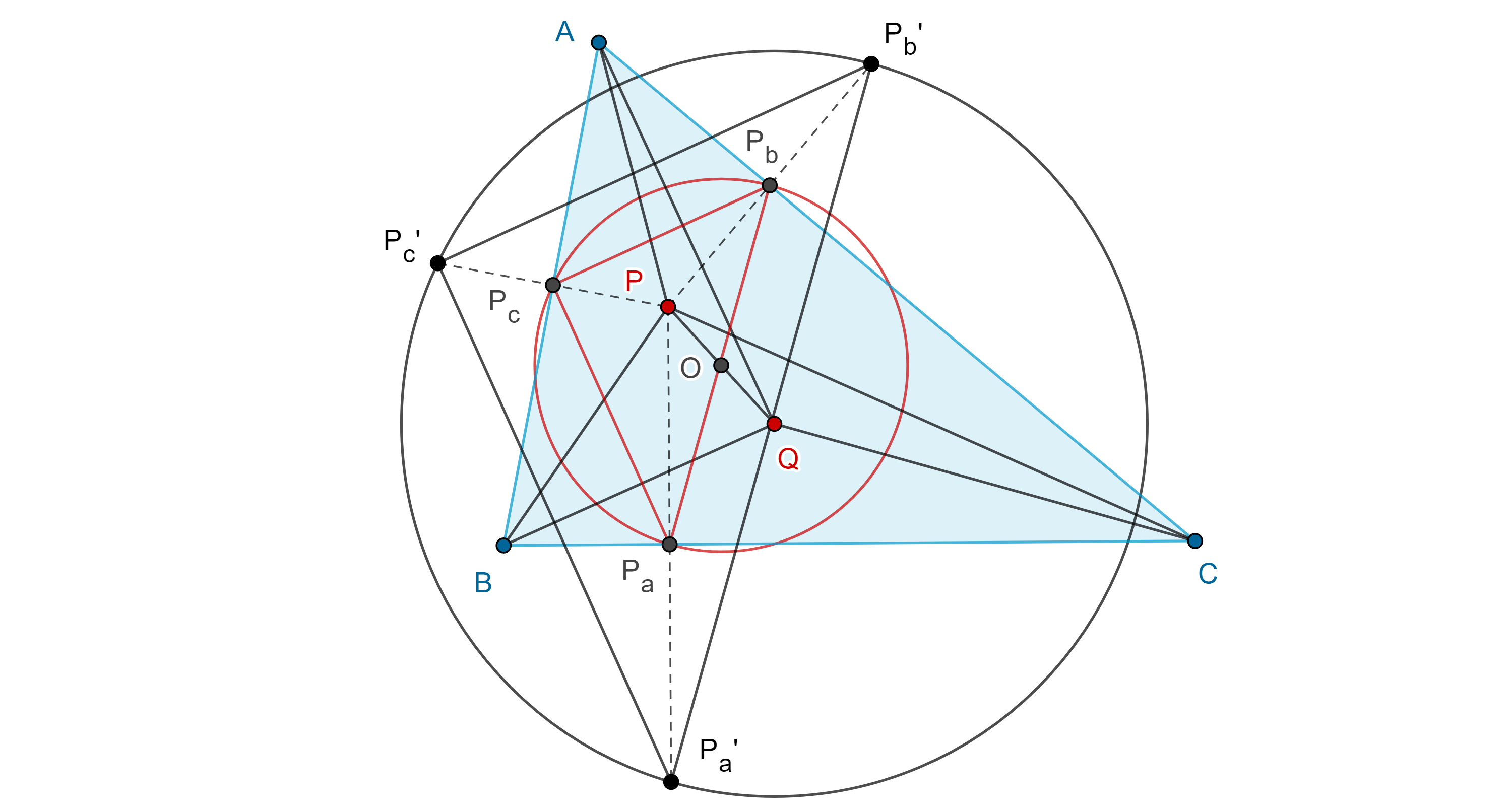
Teorema 4. Dado un triángulo $△ A B C$ y un punto $P$ , el circuncírculo del triángulo pedal de $P$ respecto de $△ A B C$ , corta a los lados de $△ A B C$ en los vértices del triángulo pedal del conjugado isogonal de $P$ respecto a $△ A B C$ .

Demostración. Si $△ P_{a} P_{b} P_{c}$ es el triángulo pedal de $P$ (figura 5), sean $Q_{a} \in B C$ , $Q_{b} \in C A$ , $Q_{c} \in A B$ , las otras tres intersecciones de $Γ (O)$ , el circuncírculo de $△ P_{a} P_{b} P_{c}$ con $△ A B C$ , consideremos $Q$ el conjugado isogonal de $P$ respecto $△ A B C$ y $O M ∥ P P_{a}$ , con $M \in P_{a} Q$ .

Como $O M ∥ P P_{a}$ y pasa por el punto medio de $P Q$ entonces $M$ es el punto medio de $P_{a} Q$ .

Como $O M ⊥ P_{a} Q_{a}$ y pasa por $O$ entonces es la mediatriz de $P_{a} Q_{a}$ y por lo tanto biseca a $P_{a} Q_{a}$ .

Ya que $O M$ biseca a $P_{a} Q_{a}$ y $P_{a} Q$ entonces $O M ∥ Q Q_{a}$ .

Por lo tanto, $Q Q_{a} ⊥ B C$ , igualmente vemos que $Q Q_{b} ⊥ C A$ , $Q Q_{c} ⊥ A B$ .

En consecuencia, $△ Q_{a} Q_{b} Q_{c}$ es el triángulo pedal de $Q$ .

Proposición 4. Dado un triángulo $△ A B C$ y un punto $P$ , el centro del circuncírculo del triángulo cuyos vértices son las reflexiones de $P$ respecto de los lados de $△ A B C$ , es el conjugado isogonal de $P$ respecto de $△ A B C$ .

Demostración. Sean $P_{a}^{'}$ , $P_{b}^{'}$ , $P_{c}^{'}$ , las respectivas reflexiones de $P$ respecto de $B C$ , $C A$ y $A B$ , considera $△ P_{a} P_{b} P_{c}$ el triángulo pedal de $P$ respecto de $△ A B C$ .

Por construcción, $P$ es el centro de homotecia entre $△ P_{a} P_{b} P_{c}$ y $△ P_{a}^{'} P_{b}^{'} P_{c}^{'}$ con razón de homotecia $2$ , por lo tanto, sus respectivos circuncírculos y sus circuncentros también están en homotecia con centro en $P$ y razón $2$ .

En consecuencia, si $O$ es el circuncentro de $△ P_{a} P_{b} P_{c}$ , entonces el circuncentro de $△ P_{a}^{'} P_{b}^{'} P_{c}^{'}$ se encuentra en la reflexión $Q$ , de $P$ respecto de $O$ .

Por el teorema 3, $Q$ el conjugado isogonal de $P$ respecto de $△ A B C$ .

Triángulo antipedal

Definición 2. Dado un triángulo $△ A B C$ y un punto $P$ , el triángulo $△ A^{'} B^{'} C^{'}$ formado por las perpendiculares a $A P$ , $B P$ , $C P$ , por los vértices de $△ A B C$ se llama triángulo antipedal de $P$ respecto de $△ A B C$

Notemos que $△ A B C$ es el triángulo pedal de $P$ respecto de $△ A^{'} B^{'} C^{'}$ .

Proposición 5. Sean $△ A B C$ y $P$ un punto, entonces el triángulo antipedal de $P$ respecto de $△ A B C$ y el triángulo pedal del conjugado isogonal de $P$ respecto de $△ A B C$ son homotéticos.

Demostración. Sea $Q$ el conjugado isogonal de $P$ respecto de $△ A B C$ , consideremos $Q_{a} \in B C$ , $Q_{b} \in C A$ , $Q_{c} \in A B$ , las proyecciones de $Q$ en lados de $△ A B C$ .

Por la proposición 1, la isogonal $C P$ , de $C Q$ , es perpendicular a $Q_{a} Q_{b}$ entonces $A^{'} B^{'} ∥ Q_{a} Q_{b}$ (figura 7).

Igualmente vemos que $B^{'} C^{'} ∥ Q_{b} Q_{c}$ y $C^{'} A^{'} ∥ Q_{c} Q_{a}$ .

Por lo tanto, existe una homotecia entre $△ A^{'} B^{'} C^{'}$ y $△ Q_{a} Q_{b} Q_{c}$ .

Área del triangulo pedal

Teorema 5, de Euler. Sean $△ A B C$ y $P$ un punto, considera $△ P_{a} P_{b} P_{c}$ el triángulo pedal de $P$ respecto de $△ A B C$ y $(O, R)$ el circuncírculo de $△ A B C$ , entonces podemos calcular el área de $△ P_{a} P_{b} P_{c}$ mediante la siguiente formula:
$(△ P_{a} P_{b} P_{c}) = \frac{| R^{2} - O P^{2} |}{4 R^{2}} (△ A B C)$ .

Demostración. Sean $D$ , $E$ , $F$ las segundas intersecciones de $A P$ , $B P$ , $C P$ con $(O, R)$ , veamos que $△ P_{a} P_{b} P_{c}$ y $△ D E F$ son semejantes.

Tomando en cuenta que $P P_{c} P_{b} A$ y $P B P_{a} P_{c}$ son cíclicos tenemos:
$∠ D F E = ∠ D F P + ∠ P F E$
$= ∠ D A C + ∠ C B E = ∠ P A P_{b} + ∠ P_{a} B P$
$= (π - ∠ P_{b} P_{c} P) + (π - ∠ P P_{c} P_{a})$
$= 2 π - ∠ P_{b} P_{c} P_{a} = ∠ P_{a} P_{c} P_{b}$ .

De manera similar vemos que $∠ E D F = ∠ P_{b} P_{a} P_{c}$ y $∠ F E D = ∠ P_{c} P_{b} P_{a}$ , $\Rightarrow △ P_{a} P_{b} P_{c} \sim △ D E F$ .

Al triángulo $△ D E F$ se le conoce como triángulo circunscrito de Ceva de $P$ respecto de $△ A B C$ .

Recordemos que podemos calcular el área de un triángulo como el producto de sus lados entre cuatro veces su circunradio, si $R_{p}$ es el circunradio de $△ P_{a} P_{b} P_{c}$ , entonces

$\begin{matrix} (1) & \frac{(△ P_{a} P_{b} P_{c})}{(△ A B C)} = \frac{P_{a} P_{b}}{A B} \times \frac{P_{b} P_{c}}{B C} \times \frac{P_{c} P_{a}}{C A} \times \frac{R}{R_{p}} . \end{matrix}$

Con el fin de calcular la última ecuación, consideremos los siguientes argumentos.

Como $△ P_{a} P_{b} P_{c} \sim △ D E F$ entonces $\frac{R}{R_{p}} = \frac{D E}{P_{a} P_{b}}$ .

Ya que $A B D E$ es cíclico, entonces $△ P A B \sim △ P E D$ , esto es
$\frac{P A}{P E} = \frac{A B}{E D}$ .

También, como $P P_{c} P_{b} A$ y $P B P_{a} P_{c}$ $P P_{a} C P_{b}$ son cíclicos y aplicando la ley extendida de los senos tenemos,
$P_{b} P_{c} = P A \sin ∠ A$ y $P_{c} P_{a} = P B \sin ∠ B$ .

Ahora, aplicamos la ley extendida de los senos en $△ A B C$ ,
$\frac{\sin ∠ A}{B C} = \frac{1}{2 R} = \frac{\sin ∠ B}{A C}$ .

Finalmente, la potencia de $P$ respecto de $(O, R)$ es $P B \times P E = | R^{2} - O P^{2} |$ .

Sustituyendo lo anterior en $(1)$ obtenemos:

$\frac{(△ P_{a} P_{b} P_{c})}{(△ A B C)} = \frac{P_{a} P_{b}}{A B} \times \frac{P A \sin ∠ A}{B C} \times \frac{P B \sin ∠ B}{C A} \times \frac{D E}{P_{a} P_{b}}$
$= \frac{P E}{P A} \times \frac{P A \times P B}{(2 R) (2 R)}$
$= \frac{| R^{2} - O P^{2} |}{4 R^{2}}$ .

Más adelante…

En la siguiente entrada hablaremos sobre un par de puntos conjugados isogonales en particular, se trata de los puntos de Brocard, que tienen algunas propiedades especiales dentro de un triángulo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que:
$i)$ el ortocentro y el circuncentro de un triángulo son conjugados isogonales,
$i i)$ el incentro y los excentros de un triángulo son sus propios conjugados isogonales.
Sea $P$ un punto dentro de un triangulo $△ A B C$ , considera a $Q$ su conjugado isogonal, muestra que $∠ B P C + ∠ B Q C = π + ∠ B A C$ .
Sean $P$ y $Q$ puntos conjugados isogonales respecto a un triangulo $△ A B C$ , prueba que $\frac{A P \times A Q}{A B \times A C} + \frac{B P \times B Q}{B A \times B C} + \frac{C P \times C Q}{C A \times C B} = 1$ .
Sean $△ A B C$ y $P$ un punto en su interior, considera $△ P_{a} P_{b} P_{c}$ el triángulo pedal de $P$ respecto $△ A B C$ , supón que $P_{a} P_{b} ⊥ P_{a} P_{c}$ , muestra que el conjugado isogonal de $P$ respecto de $△ A B C$ es el ortocentro de $△ A P_{b} P_{c}$ .
En la figura 7, muestra que el producto de los triángulos homotéticos es igual al cuadrado del área de $△ A B C$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Circunferencias de Lemoine.
Siguiente entrada del curso: Puntos de Brocard.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 267-273.
Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 95-108.
Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 169-176.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 153-157.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: círculo pedal

Geometría Moderna I: Rectas isogonales