La Olimpiada Mexicana de Matemáticas (OMM) se organiza en varios niveles: estatal, nacional y participación en concursos internacionales. Los estudiantes comienzan con la etapa estatal, en donde realizan varios exámenes y además se les prepara mediante entrenamientos. Después de repetir esto algunas veces, algunos estudiantes son elegidos para ir al Concurso Nacional de la OMM, para el cual se preparan adicionalmente.
A grandes rasgos, la forma en la que se organiza una olimpiada estatal se ve así:
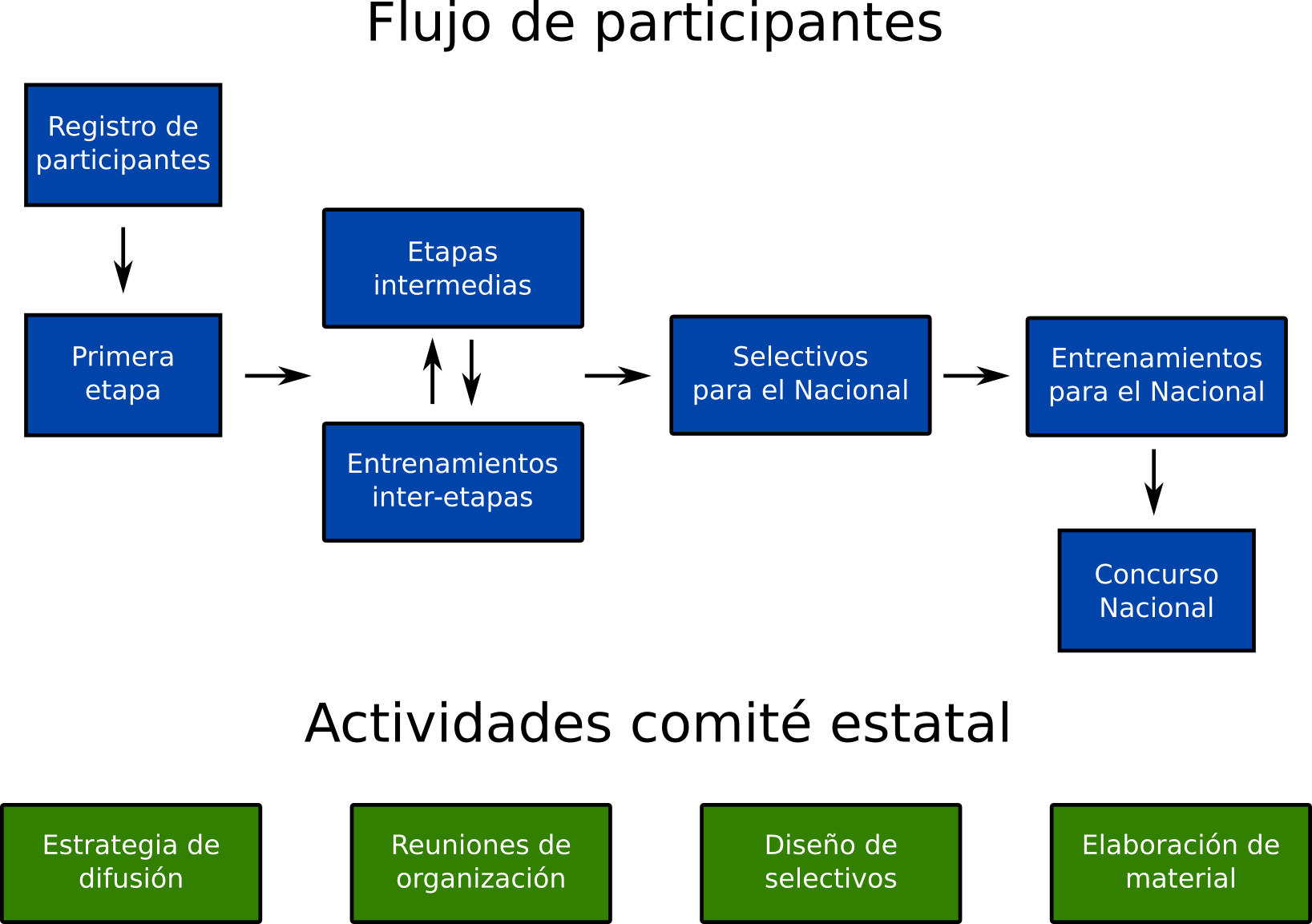
En la parte de arriba se ve el flujo de los estudiantes. En la parte de abajo se ven varias actividades que realizan los comités estatales.
En esta época de la pandemia de COVID19, es muy importante encontrar alternativas para realizar muchas de estas actividades de manera digital. La idea de esta entrada de blog es ser un mini-curso introductorio a material y tecnologías de educación a distancia que pueden ser usadas para realizar estas actividades. Si bien está pensada originalmente como una entrada para ayudar a la organización de los concursos estatales de la OMM, el contenido puede:
- Ser de utilidad incluso cuando salgamos de la pandemia, para tener más alcance.
- Apoyar a otros concursos de otras ciencias, y otros países, a encontrar alternativas.
Para cada tecnología también hay un video, para ver cada uno de los recursos más en acción. El video introductorio es el siguiente.
Página de la Olimpiada Mexicana de Matemáticas
La página de la Olimpiada Mexicana de Matemáticas es uno de los mejores lugares para encontrar material de entrenamiento gratuito, de calidad, de acceso libre y con soluciones. Además, en esta página están disponibles en versión digital todos los números de la revista Tzaloa, que tiene otro tanto de material.
Otras cosas que se pueden encontrar en la página son los datos de contacto de los organizadores, resultados históricos de México en las olimpiadas internacionales y un sistema para pedir libros de la serie Cuadernos de Olimpiada.
La página de la OMM es http://www.ommenlinea.org. En el siguiente video se exploran con más detalle las distintas secciones.
El blog de Leo
El blog de Leo es precisamente esta página, en donde está esta entrada de blog. Forma parte de los recursos que propongo pues aquí en el blog hay también bastante material para preparar a olímpicos y entrenadores de la Olimpiada. Algunas secciones que pueden ser de utilidad son:
- Videos: Material de entrenamiento en heurísticas y en áreas específicas
- Curso de heurísticas: Notas de un curso de técnicas de resolución de problemas que se ha impartido repetidas veces en la UNAM
- Material para olimpiadas universitarias: Exámenes selectivos, notas de entrenamiento, exámenes anteriores
- Cursos a nivel licenciatura: Notas de los cursos que impartí el semestre pasado en línea. Son se Álgebra Superior y de Álgebra Lineal
En el siguiente video se explora el blog más a detalle.
La red social más popular es Facebook, y una de sus misiones es conectar a las personas. Se puede aprovechar todo el potencial que tienen sus herramientas para dar difusión a los concursos de matemáticas, para estar en contacto con los concursantes y para entrar en contacto con otras comunidades.
Dentro de Facebook, los dos lugares más indicados para ir y estar cerca de la comunidad olímpica matemática de México son:
- La página de FB de la OMM: Página oficial, manejada por el Comité. Ahí se sube información de eventos, se publican resultados a nivel nacional y se informa de la participación de México en concursos internacionales.
- El grupo Insommnia: El ambiente es más relajado. Es un grupo extraoficial, pero con una comunidad enorme de olímpicos y ex-olímpicos. Hay chistes, problemas propuestos, videos, discusiones de mejora del proyecto, mini-exámenes, etc.
Cada Comité Estatal puede aprovechar que en Facebook se pueden hacer grupos privados para estar en contacto con organizadores, papás o concursantes.
Hablo más de Facebook y su papel en concursos matemáticos en el siguiente video.
Overleaf
LaTeX es un lenguaje para escribir matemáticas y que se produzca un documento en el cual las matemáticas se vean bonito. Con él se pueden hacer exámenes selectivos, notas de entrenamiento e incluso libros.
Típicamente, para usar LaTeX en una computadora es necesario instalar una distribución y un editor. Overleaf es una página de internet en la cual se puede escribir y compliar LaTeX sin necesidad de instalar nada adicional.
Una ventaja de Overleaf es que lo que se trabaja se queda en la nube, así que se puede acceder a los documentos desde cualqueir computadora con internet. Esto tiene la desventaja de que se necesita tener internet, pero es fácilmente arreglable ya que, de ser necesario, se pueden bajar a una computadora todos los archivos fuente.
Otra ventaja de Overleaf es que se puede hacer colaboración simultánea en un mismo documento. Esto es muy útil para cuando se tiene que escribir matemáticas con otras personas: al hacer notas, escribir artículos de investigación y textos más grandes como libros o tesis.
En el siguiente video hablo más acerca de Overleaf.
Moodle
Un LMS es una plataforma que tiene todo lo que necesita un curso a distancia: herramientas para hacer exámenes, definir actividades, calendarizar, contactar a estudiantes, etc. Uno de los LMS más importantes y de más uso en la docencia a distancia es Moodle.
La principal dificultad con usar Moodle reside en que es necesario descargar un software e instalarlo en un servidor. Esto puede ser muy difícil para alguien que no conoce del tema. Sin embargo, una vez que Moodle queda instalado, es muy facil de usar para profesores y estudiantes (o en este contexto, delegados, entrenadores y concursantes).
El tipo de cosas que se pueden hacer en Moodle incluyen:
- Tener un sistema de registro de nuevos concursantes
- Subir notas
- Subir mini-libros
- Crear exámenes con límites de tiempo
- Crear actividades de aprendizaje
- Hacer cuestionarios
- Tener foros personalizados
En el siguiente video hablo más a detalle de algunas de estas cosas.
Zoom, Hangouts y otras plataformas de videollamada
Finalmente, me gustaría platicar un poco acerca de opciones para tener videollamadas hoy en día. Sobre todo, me gustaría enfocarme en Zoom y en Hangouts. Ambas son buenas opciones para tener llamadas con grupos de varias personas.
Zoom agarró mucha popularidad en esta época de pandemia, y tiene sentido. Es una herramienta fácil de usar y de instalar que permite:
- Armar reuniones con muchas personas
- Compartir la pantalla con los asistentes (por ejemplo, puede servir para dar entrenamientos)
- Programar reuniones y avisar a los participantes
- Tener mecanismos de participación por chat, reacciones de «levantar la mano» o «aplaudir»
La versión gratuita de Zoom tiene algunas limitaciones, como que sólo se puede usar por 40 minutos de manera simultánea. La versión de paga permite hacer varias cosas como dividir a un grupo en sub-grupos.
Google Hangouts es una herramienta muy similar. También permite reuniones con muchas personas y compartir la pantalla. Se integra mejor con todo el ecosistema de Google y puede ser muy útil para quienes ya tengan una cuenta ahí.
En el siguiente video hablo de estas y un par de opciones más.
Reflexión final
Esta entrada fue un mini-curso al material y las tecnologías que se pueden usar para seguir organizando concursos matemáticos a distancia. El material que se presentó toma en mente el flujo de participantes en un modelo básico del concurso. También toma en cuenta el tipo de tecnología que podría necesitar un comité organizador local para hacer todas las actividades que se necesitan.
Hay una hipótesis muy fuerte que estamos haciendo: que los organizadores y participantes tienen acceso estable y bueno a internet. Al realizar actividades que aprovechen la tecnología hay que tener en cuenta que esta hipótesis es posible que no se cumpla. Puede suceder que:
- Haya personas sin acceso a internet
- Haya personas con acceso sólo con datos, para quienes ver videos es impermisiblemente caro
- Haya personas con computadora y acceso a internet en su casa, pero de los cuales no puedan disponer
- Haya personas con todos los recursos tecnológicos, pero viviendo muchas dificultades debido a la pandemia.
Así como muchos otros aspectos de la docencia, es importante tener empatía en el aspecto digital.