Archivo de la etiqueta: grupo diédrico

Álgebra Moderna I: Acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

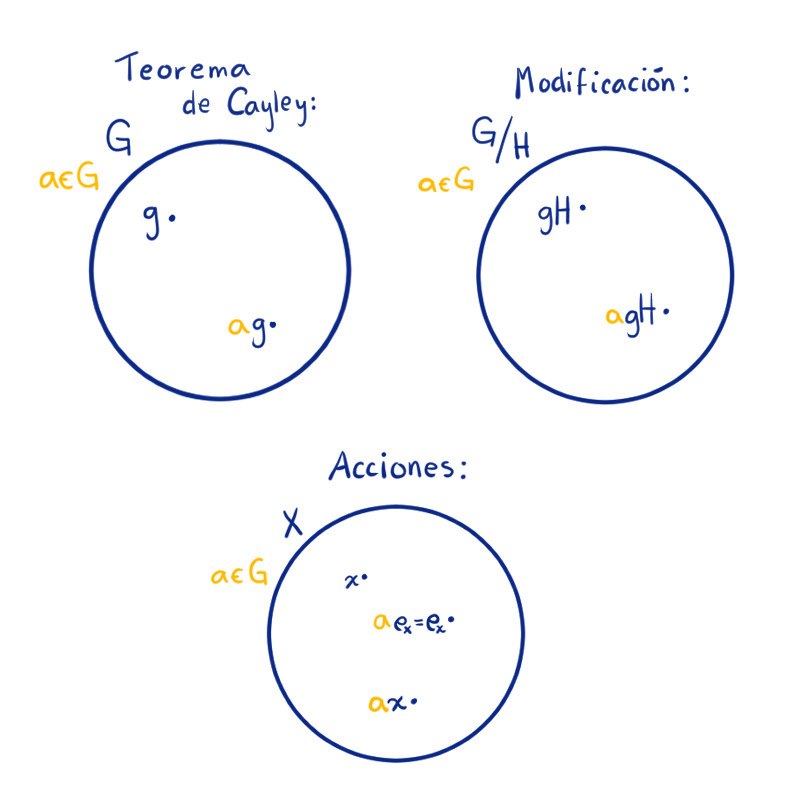
Antes de comenzar con el tema que nos compete, repasemos lo que hemos visto del Teorema de Cayley y su modificación de la entrada anterior. Primero, en el Teorema de Cayley, comenzamos tomando un grupo $G$, un $a$ en el grupo y actuamos con ese $a$ sobre el grupo, es decir multiplicamos los elementos. En resumen, nos permite mover los elementos del mismo grupo.

Con la modificación avanzamos en la abstracción. En el teorema nos tomamos el conjunto de clases laterales y ahora, $G$ actúa sobre las clases laterales. Detente un minuto para pensar, si cada vez somos más generales ¿cuál es el siguiente paso? ¿sobre quién queremos que actúe $G$ ahora?

La respuesta es: sobre un conjunto cualquiera $X$. Ahora queremos pensar que usamos los elementos de $G$ para mover elementos de $X$. Para eso necesitamos una especie de producto, además de algunos matices. Por ejemplo, para un $x\in X$ cuando $a = e$, el elemento $a\cdot x = x$ se quede fijo y que si se multiplica por $a$ y luego por $b$, que sea lo mismo que multiplicar por $ab$, es decir $a\cdot(b\cdot x) = ab\cdot x$. Si se cumplen estas dos condiciones diremos que $a$ es una acción de $G$ en el conjunto $X$.

Diagrama de qué es una acción.

Luces, cámara, ¡acción!

Como verás, hemos estado usando el verbo actuar para referirnos a esta transformación que sucede al operar un $a\in G$ y otro elemento, sea del mismo $G$ o de las clases laterales. Aunque no hayamos definido formalmente qué es una acción, la realidad es que ya usar actuar da una idea de lo que estamos queriendo decir. Estamos usando un elemento de un grupo para transformar un elemento de otro. A continuación definiremos formalmente a una acción.

Definición. Sea $G$ un grupo, $X$ un conjunto. Si existe una función:
\begin{align*}
G \times X &\to X\\
(a,x) &\mapsto a\cdot x
\end{align*}
para todos $a\in G, x\in X$, tal que:

  1. $e \cdot x = x$ para toda $x\in X$.
  2. $a \cdot (b\cdot x) = (ab)\cdot x $ para todas $a,b\in G, x\in X$,

decimos que la función es una acción de $G$ en $X$, y que $G$ actúa en $X$ o que $X$ es un $G$-conjunto.

Ejemplos.

Veamos algunos ejemplos nuevos y retomemos algunos otros, para verificar que esto es una generalización para lo que se hizo en el Teorema de Cayley y en su modificación.

Ejemplo 1. Sean $G$ grupo, $X=G$ definimos $a\cdot x = ax$ para todas $a\in G, x\in X$. Es decir, definimos una acción sobre sí mismo. Probemos las dos condiciones:

\begin{align*}
&e\cdot x = ex = x &\forall x\in X\\
&a\cdot(b\cdot x) = a\cdot(bx) = a(bx) = (ab)x = (ab)\cdot x &\forall a,b\in G,\; x\in X.
\end{align*}

Así, todo grupo $G$ actúa en sí mismo mediante su operación binaria. Como vimos en la entrada del Teorema de Cayley.

Ejemplo 2. Sean $G$ grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH)= agH$ para toda $a,g\in G$. Ahora, probemos las dos condiciones de una acción:

\begin{align*}
&e\cdot(gH) = egH = gH &\forall g\in G
\end{align*}
\begin{align*}
a\cdot(b\cdot(gH)) &= a\cdot(bgH) = a(bg)H = (ab)gH \\
&= ab\cdot (gH) &\forall a,b,g\in G
\end{align*}

Así se tiene una acción de $G$ en las clases laterales de $H$ en $G$. Este ejemplo lo vimos en la entrada de la modificación al Teorema de Cayley.

Por último, podemos ver un ejemplo nuevo.

Ejemplo 3. Sea $G = D_{2n}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices de polígono regular de $n$ lados.

Dados $g\in G, i\in X$ definimos $g\cdot i = j$ si $g$ manda el vértice $i$ en el vértice $j$. Recordemos que los elementos de un grupo diédrico son las simetrías del polígono regular de $n$ lados, es decir, son transformaciones lineales del plano que mandan del polígono en sí mismo. En particular, los vértices van a dar a vértices bajo estas transformaciones.

Representación de una grupo diédrico.

Entonces, como son transformaciones del plano nuestra acción quedaría como una evaluación $g \cdot i = g(i)$. Así, para todos $i\in X, g,h\in G$,
\begin{align*}
\text{id}\cdot i &= \text{id}(i) = i \\
g\cdot (h\cdot i )& = g\cdot (h(i)) = g(h(i)) = (gh) (i) = (gh) \cdot i.
\end{align*}

Así, $D_{2n}$ actúa en el conjunto de vértices.

Recordemos que al escribir $(gh)\cdot i$, la operación que ocurre entre $g$ y $h$ es la composición. En este momento se omitió el símbolo $\circ$ para evitar confusiones con el símbolo $\cdot$ de acción.

Otra definición de Acción

Anteriormente hemos visto la noción de que los elementos de un grupo dan lugar a permutaciones. Usaremos esta idea para dar una definición de acción equivalente a la definición que acabamos de dar.

Teorema. Sean $G$ un grupo, $X$ un conjunto. Toda acción de $G$ en $X$ induce un homomorfismo de $G$ en $S_X$ y viceversa.

Demostración.

Sean $G$ un grupo y $X$ un conjunto.
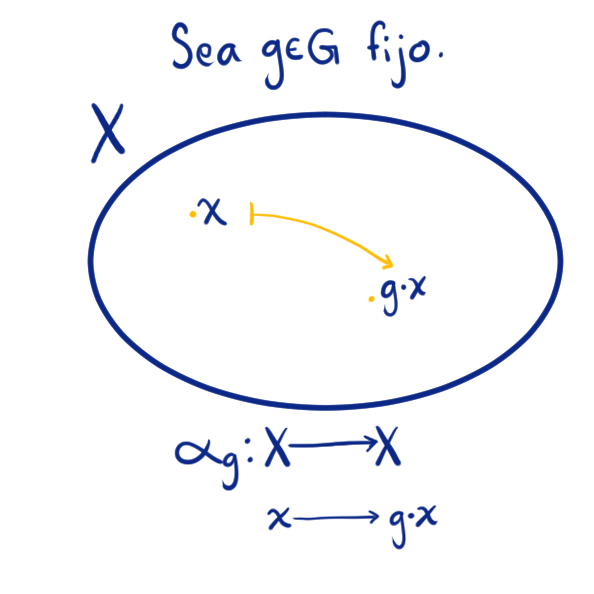
Supongamos que $G\times X \to X$ es una acción de $G$ en $X$ tal que $(g,x)\mapsto g\cdot gx$. Para cada $g\in G$ definimos $\alpha_g : X\to X$ dada por $\alpha_g(x) = g\cdot x$ para toda $x\in X$.

Ilustración del efecto de $\alpha_g$.

Analicemos las funciones $\alpha_g$, veamos que son biyectivas:

\begin{align*}
\alpha_g\circ\alpha_{g^{-1}}(x) & = \alpha_g(\alpha_{g^{-1}}) = \alpha_g(g^{-1}\cdot x) = g\cdot(g^{-1}\cdot x)\\
&= (gg^{-1})\cdot x &\text{Condición 2 de acción}\\
&= e\cdot x = x &\text{Condición 1 de acción}.
\end{align*}

Entonces $\alpha_g\circ\alpha_{g^{-1}} = \text{id}_X$.

Anáogamente $\alpha_{g^{-1}}\circ \alpha_g = \text{id}_X$, entonces $\alpha_g$ es biyectiva, es decir $\alpha_g \in S_X$.

Definimos $\psi: G \to S_X$ con $\psi (g) = \alpha_g$ para toda $g\in G$.

Veamos que $\psi$ es un homomorfismo. Tomemos $g,h\in G$,
\begin{align*}
\psi(gh)(x) &= \alpha_{gh}(x) = (gh)\cdot x = g\cdot(h\cdot x) = \alpha_g(\alpha_h(x)) & \text{Condición 2}\\
&= \alpha_g \circ \alpha_g(h) = \psi(g) \psi(h)(x) &\forall x\in X.
\end{align*}

Entonces $\psi(gh) = \psi(g)\psi(h)$ para todos $g,h\in G$.

Por lo tanto $\psi$ es un homomorfismo.

Ahora de regreso. Supongamos ahora que se tiene un homomorfismo $\psi: G\to S_X$. Entonces, para cada $g\in G, \psi(g) \in S_x$.

Definimos la función $G\times X \to X$ donde $(g,x)\mapsto g\cdot x$. Entonces $g\cdot x = \psi(g)(x)$ para toda $g\in G, x\in X$. Además, $\psi(g)(x) \in X$.

Ahora veamos que esta función es una acción. La primera condición para ser acción se cumple de la siguiente manera:

Como $\psi$ es un homomorfismo, $\psi(e) = \text{id}_X$. Así,
\begin{align*}
e\cdot x& = \psi(e)(x) = \text{id}_X(x) = x &\forall x\in X
\end{align*}

Probemos la segunda condición de acción:

\begin{align*}
g\cdot (h\cdot x) &= \psi(g) (\psi(h)(x)) = \psi(g)\circ \psi(h)(x) \\
&= \psi(gh)(x) = (gh) \cdot x & \psi\text{ es un homomorfismo}.
\end{align*}
Para todas $g,h\in G, x\in X$. Así $G$ actúa en $X$.

$\blacksquare$

Una relación de equivalencia

Si tenemos un grupo $G$ actuando sobre un conjunto $X$, entonces podemos considerar $g\in G$ y $x,y\in X$. Con los dos elementos $x,y$ de $X$, podemos preguntarnos ¿es posible llegar de $x$ a $y$ usando a $g$?, algo como $y = g\cdot x$. En realidad esto no es siempre posible, entonces podemos crear una relación de $x$ con $y$ si existe tal $g\in G$. Esto lo veremos en el siguiente resultado.

¿Es posible llegar de $x$ a $y$ usando a $g$?

Lema. Sean $G$ un grupo, $X$ un $G$-conjunto. Para todo $x,y\in X$, la relación en $X$: $x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$ es una relación de equivalencia.

Demostración.
Sean $G$ un grupo, $X$ un $G$-conjunto. Definimos la relación en $X$ donde para todo $x,y\in X$.
\begin{align*}
x\sim y \Leftrightarrow g\cdot x = y \text{ para algún }g\in G.
\end{align*}

Primero, por la condición 1 de acción, $e\cdot x = x$ para toda $x\in X$ con $e\in G$, entonces $x\sim x$ para toda $x\in X$. Por lo que nuestra relación es reflexiva.

Si $x,y\in X$ son tales que $x\sim y$, entonces existe $g\in G$ tal que $g\cdot x = y$. Así,
\begin{align*}
g^{-1} \cdot y &= g^{-1}\cdot (g\cdot x) \\
&= (g^{-1}g)\cdot x & \text{por condición } 2\\
&= (e\cdot x )\\
&= x & \text{por condición } 1
\end{align*}

con $g^{-1} \in G$, entonces $y\sim x$. Por lo que tenemos una relación simétrica.

Si $x,y,z\in X$ son tales que $x\sim y$ y $y\sim z$, entonces existen $g,h\in G$ tales que $g\cdot x = y$, $h\cdot y = z$. Así
\begin{align*}
(hg)\cdot x &= h\cdot (g\cdot x) &\text{condición } 2\\
&= h \cdot y = z
\end{align*}
con $hg\in G$. Entonces $x\sim z$. Así, nuestra relación es transitiva.

Por lo tanto $\sim$ es una relación de equivalencia.

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. En los siguientes incisos determina si la función dad es una acción de $G$ en $X$:
    • Considera un campo $K$ y $V$ un $K$-espacio vectorial. Sea $G= K^*$ con el producto y $X= V$. Definimos $\lambda\cdot v = \lambda v$ para cada $\lambda\in K^*$ y $v\in V$. (Nota que $K^*$ es el campo sin el neutro aditivo).
    • Sea $G$ un grupo y $X=G$. Definimos $g\cdot x = g^{-1}xg$ para cada $g\in G$ y cada $x\in X$.
    • Sea $G$ un grupo y $X = \{H|H\leq G\}$. Definimos $g\cdot H = gHg^{-1}$ para cada $g\in G$ y cada $H\in X$.
    • Sea $G$ un grupo y $X=N$ un subgrupo normal de $G$. Definimos $g\cdot n= gng^{-1}$ para cada $g\in G$ y cada $n\in N$.
  2. Sea $G$ un grupo y $X$ un $G$ conjunto. Considera el homomorfismo $\psi: G\to S_X$ asociado. ¿Es necesariamente $\psi$ un monomorfismo? Si lo es, pruébalo y si no, establece qué condiciones debería cumplir la acción para que lo sea.
  3. Para repasar lo que hemos visto desde el Teorema de Cayley, puedes consultar el video en inglés de Mathemaniac.

Más adelante…

Hemos expandido la idea de que un grupo puede mover a los elementos de otro hasta llamarlo una acción. Luego, encontramos una relación de equivalencia a partir de la acción. Como es usual en este tipo de cursos, estudiaremos la partición inducida por esta relación de equivalencia y a partir de estos conjuntos, definiremos otros tipos de acciones.

Entradas relacionadas

Álgebra Moderna I: Cuarto Teorema de Isomorfía

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta entrada veremos el Cuarto Teorema de Isomorfía, para entenderlo mejor es necesario ilustrarlo con diagramas de retícula.

Sean $G$ un grupo y $N$ un subgrupo normal de $G$. Recordemos que podemos escribir todos los subgrupos de $G$ en una retícula. Como estamos considerando a todos los subgruposde $G$, el subgrupo más pequeño es el conjunto que contiene sólo al neutro $\{e_G\}$. Así, $G$ va hasta arriba del diagrama y $\{e_G\}$ al final.

Por otro lado, como $H\unlhd G$, tiene sentido considerar otro diagrama, el del grupo $G/N$. De la misma manera que en el anterior, hasta abajo colocaríamos $\{e_{G/N}\}$ que es el conjunto unitario de $\{N\}$.

Diagramas de retícula de $G$ y de $G/N$.

Luego, como $N \unlhd G$. Podemos tomar un subgrupo $H$ de $G$ que contenga $N$ y colocarlos en el diagrama. Además, esto nos daría la existencia de $H/N \leq G/N$, entonces podríamos dar una correspondencia de $H \mapsto H/N$. Esto nos da una relación entre ambas retículas (la de $G$ y la de $G/N$):

\begin{align*}
G &\longmapsto G/N\\
H &\longmapsto H/N\\
N &\longmapsto \{e_G\} = \{N\}.
\end{align*}

La relación que existe entre la retícula desde $N$ a $G$ y la retícula de $G/N$ además de ser biyectica tiene otras propiedades, por ejemplo, si existe $N\leq K \unlhd H$, entonces $K/N \unlhd H/N$. Estas propiedades son las que veremos en el teorema que nos compete.

Diagramas de retícula de $G$ y de $G/N$ con correspondencia.

Enunciado y demostración del Teorema

A continuación veremos el Cuarto Teorema de Isomorfía (CTI), también conocido como Teorema de la Correspondencia.

Teorema. (Cuarto Teorema de Isomorfía)
Sea $G$ un grupo, $N$ subgrupo normal de $G$, $\pi: G \to G/N$ con $\pi(a) = aN$ (la proyección canónica) para toda $a\in G$. Consideremos

\begin{align*}
\text{Sub}_N^G &= \{H| N\leq H \leq G \}, \\
\text{Sub}_{ G/N} &= \{\mathcal{H} | \mathcal{H} \leq G/N\}.
\end{align*}

Entonces $\pi$ define una correspondencia biyectiva
\begin{align*}
F: \text{Sub}_N^G \to \text{Sub}_{ G/N}
\end{align*}
con $F(H) = \pi [H] = H/N$ para todo $H \in \text{Sub}_H^G$.

Además, si $H,K\in \text{Sub}_N^G$:

  1. $K\leq H$ si y sólo si $K/N \leq H/N$ y en este caso $[ H:K] = [H/N : K/N]$.
  2. $K \unlhd H$ si y sólo si $K/N \unlhd H/N$.
  3. $\left< H\cup K \right> / N = \left< H/N \cup K/N \right>$.
  4. $(H\cap K) / N = (H/ N) \cap (K/N)$.

Demostración.

Sean $G$ un grupo, $N\unlhd G$, $\pi:G\to G/N$ con $\pi(a) = aN$ para toda $a\in G$.
Sean
\begin{align*}
\text{Sub}_N^G &= \{H\,|\, N\leq H \leq G \}, \quad
\text{Sub}_{ G/N} = \{\mathcal{H} | \mathcal{H} \leq G/N\}.
\end{align*}

Definimos
\begin{align*}
F: \text{Sub}_N^G \to \text{Sub}_{ G/N}
\end{align*}
con $F(H) = \pi[ H] = H/N$ para todo $H \in \text{Sub}_H^G$. Donde $\pi[H]$ es la imagen directa de $H$ bajo $\pi$.

Como $\pi$ es un homomorfismo y $H\leq G$ entonces $\pi[H]\leq \pi[G ]$, es decir $H/N\leq G/N$, entonces $F$ está bien definida.

Veamos que $G$ es inyectiva, para ello probemos la primera parte del inciso 1.
Sean $H, K \in \text{Sub}_N^G$.
P.D. $K \leq H \Leftrightarrow K/N \leq H/N$.

$|\Rightarrow]$ Supongamos que $K \leq H$. Sea $x \in K/N, x = kN$ con $k\in K.$

Como $K\subseteq H$, $k\in H$ y así $x = kN \in H/N$. Por lo tanto $K/N \leq H/N$.

$[\Leftarrow|$ Supongamos que $K/N \leq H/N.$ Sea $k\in K$, tenemos las siguientes implicaciones:
\begin{align*}
k N \in K/N &\Rightarrow kN \in H/N &\text{pues } K/N \leq H/N \\
&\Rightarrow kN = hN \;\text{con } h\in H \\
& \Rightarrow k = hn\; \text{con } h\in H, n\in N &\text{por } k \in kN = hN\\
& \Rightarrow k \in H & \text{ya que } N \subseteq H.
\end{align*}

Por lo tanto $K \leq H$.

De este modo, si $H,K \in \text{Sub}_N^G $ son tales que $F(H) = F(K)$, entonces $H/N = K/N$, así
\begin{align*}
H/N \leq K/N &\Rightarrow H \leq K \\
K/N \leq H/N &\Rightarrow K \leq H,
\end{align*}

ambas implicaciones son consecuencia de lo que acabamos de probar del inciso 1 de CTI. Así, $H=K$.

Veamos que $F$ es suprayectiva. Se $\mathcal{H} \in \text{Sub}_{G/N}$, es decir $\mathcal{H} \leq G/N$. Como $\pi: G \to G/N$ es un homomorfismo y $\{N\}\leq \mathcal{H} \leq G/N$, entonces $N \leq \pi^{-1}[\mathcal{H}] \leq G$.

Diagrama de la imagen inversa de $\mathcal{H} = \pi^{-1}[\mathcal{H}]$.

Nos vamos a fijar en el subgrupo $\pi^{-1} [\mathcal{H}]$, porque nos va a servir para probar la suprayectividad que buscamos.
Entonces apliquemos $F$: $$F(\pi^{-1} [\mathcal{H} ]) = \pi [\pi^{-1}[\mathcal{H}]]= \mathcal{H}$$ pues $\pi$ es suprayectiva. Así, $F$ es suprayectiva.

Probaremos ahora la segunda parte del inciso 1).
Sean $H,K\in \text{Sub}_N^G$, con $K\leq H$.
P.D. $[H: K ] = [H/N: K/N]$.

Recordemos que $[H/N : K/N]$ es la cardinalidad de $\{(hN)K/N \,|\, hN \in H/N\}$.

Para simplificar, denotaremos a $K/N$ por $K^*$ y como $\pi (h) = hN$, entonces $[H/N : K/N ]$ es la cardinalidad de $\{\pi(h)K^* | h\in H\}.$

P.D. $\{hK | h \in H \}$ y $\{\pi(h)K^*|h\in H\}$ tienen la misma cardinalidad.

Sea $f: \{hK | h \in H\} \to \{\pi(h)K^*| h\in H\}$ definida por $f(hK) = \pi(h)K^*$ para toda $h\in H$. Demostraremos que es una función biyectiva.
Primero, veamos que $f$ está bien definida. Tomemos $h, \tilde{h} \in H$. Tenemos las siguientes implicaciones:

\begin{align*}
hK = \tilde{h}K &\Rightarrow h^{-1}\tilde{h} \in K \\
&\Rightarrow h^{-1}\tilde{h} N \in K/N = K^*\\
&\Rightarrow \pi(h^{–1}\tilde{h}) \in K^* & \text{definición de }\pi\\
&\Rightarrow \pi(h)^{-1} \pi(\tilde{h}) \in K^* & \pi\text{ es homomorfismo}\\
&\Rightarrow \pi(h)K^* = \pi(\tilde{h})K^*.
\end{align*}
Por lo tanto, $f$ está bien definida.

Ahora veamos que $f$ es inyectiva. Sean $hK,\tilde{h}K$ con $h,\tilde{h}\in H$, tales que $f(hK) = f(\tilde{h}K)$. Seguiremos las siguientes implicaciones,

\begin{align*}
f(hk) = f(\tilde{h}K) & \Rightarrow \pi(h)K^* = \pi(\tilde{h})K^* &\text{definición de }f \\
&\Rightarrow \pi(h)^{-1}\pi(\tilde{h}) \in K^* \\
&\Rightarrow \pi(h^{–1}\tilde{h}) \in K^* &\pi\text{ es homomorfismo}\\
&\Rightarrow h^{–1}\tilde{h}N\in K^*&\text{definición de }\pi\\
&\Rightarrow h^{-1}\tilde{h}N = kN \text{ con } k \in K & \text{porque }K^* = K/N\\
&\Rightarrow h^{-1}\tilde{h} = kn, k\in K, n\in N &\text{porque } h^{-1}\tilde{h}\in h^{-1}\tilde{h}N \\
&\Rightarrow h^{-1}\tilde{h}\in K &\text{pues } N\subseteq K \\
&\Rightarrow hK = \tilde{h}K.
\end{align*}
Por lo tanto $f$ es inyectiva.

Además, si tenemos $\pi(h)K^*$ con $h\in H$, entonces $\pi(h)K^* = f(hK) \in \text{Im}f$. Por lo tanto $f$ es suprayectiva.

Así,
\begin{align*}
[H:K] &= \# \{hK | h \in H\} \\
&= \#\{\pi(h)K^* | h \in H\} = [H/N:K/N].
\end{align*}

Ahora, demostraremos el inciso 2.

Sean $H,K\in \text{Sub}_N^G$.
P.D. $K \unlhd H \Leftrightarrow K/N \unlhd H/N.$

El inciso 1 (que acabamos de probar) ya nos da que $K \leq H \Leftrightarrow K/N \leq H/N.$ Entonces lo que nos resta probar es que son subgrupos normales.

$|\Rightarrow]$ Supongamos que $K\unlhd H$. Sean $x\in H/N, y \in K/N$, entonces $x = hN, y = kN$ con $h\in H, k\in K$.

Lo que queremos es considerar el conjugado $xyx^{-1}$, es decir, ver que si tomamos un elemento de $K$ módulo $N$ (al que llamamos $y$) y lo conjugamos con cualquier elemento de $H$ módulo $N$ (en este caso $x$), vuelvo a tener un elemento en $K$ módulo $N$. Esto se ve de la siguiente manera:
\begin{align*}
x y x^{-1} = (hN)(kN)(hN)^{-1} = (hN)(kN)(h^{-1}N) = hkh^{-1}N.
\end{align*}

Como $k \in K, h \in H$ y $K\unlhd H$, se tiene que $hkh^{-1} \in K$.

Así, $xyx^{-1} = hkh^{-1} N \in K/N$. Por lo que $K/N \unlhd H/N$.

$[\Leftarrow|$ Supongamos que $K/N \unlhd H/N$. Sean $k\in K, h\in H$.

Veamos qué sucede con la clase $hkh^{-1}N$:
\begin{align*}
hkh^{-1} N = (hN)(kN)(h^{-1}N) = (hN)(kN)(hN)^{-1}
\end{align*}

Es otras palabras, estamos conjugando un elemento de $kN\in K/N$ con un elemento de $kN\in K/N$. Luego, como sabemos que $K/N \unlhd H/N$ obtenemos que esta conjugación sigue estando en $K/N$. Es decir, $hkn^{-1}N\in K/N$.

Podríamos reescribir $hkh^{-1}N = \tilde{k}N$ con $\tilde{k} \in K$. Así,

\begin{align*}
hkh^{-1}N &= \tilde{k}N & \text{con }\tilde{k} \in K\\
\Rightarrow hkh^{-1} &= \tilde{k}n, \tilde{k}\in K, n\in N & \text{por } hkh^{-1} \in hkh^{-1}N = \tilde{k}N \\
\Rightarrow hkh^{-1}&\in K &\text{pues } N\subseteq K.
\end{align*}

Por lo tanto $K\unlhd H$.

$\blacksquare$

Ejemplo de CTI

Ejemplo. Tomemos el grupo diédrico (todas las simetrías de un cuadrado) $D_{2(4)} = \left<a,b \right>$, donde $a$ la rotación de $\frac{\pi}{2}$ y $b$ es la reflexión respecto al eje $x$.

Construyamos la retícula de $D_{2(4)}$: comenzamos con $D_{2(4)}$ hasta arriba, este tiene orden de 8. En el siguiente nivel colocamos los subgrupos:
\begin{align*}
\left<a^2,b\right> &= \{\text{id}, a^2, b, a^2b\}\\
\left<a\right> &= \{\text{id}, a, a^2, a^3\} \\
\left<a^2,ab\right> &= \{\text{id}, a^2, ab, a^3b\}.
\end{align*}

Cada uno de esos subgrupos tiene orden 4, en realidad esos son los únicos subgrupos de $D_{2(4)}$ que tienen orden 4. Siéntete libre de confirmar las cuentas.

Luego podemos colocar en el tercer nivel los subgrupos de orden 2:
\begin{align*}
\left< b\right> &= \{\text{id}, b\}\\
\left< a^2b\right> &= \{\text{id}, a^2b\}\\
\left< a^2\right> &= \{\text{id}, a^2\}\\
\left< ab\right> &= \{\text{id}, ab\}\\
\left< a^3b\right> &= \{\text{id}, a^3b\}.
\end{align*}

Por último, hasta abajo tenemos al unitario de la identidad $\{\text{id}\}$. Si verificamos las operaciones, nos daremos cuenta que hemos construido todo el diagrama de retícula de $D_{2(4)}$.

Para poder usar el CTI, consideremos $\left<a^2\right> \unlhd D_{2(4)}$ y concentremos nuestra atención en la parte de la retícula que se encuentra entre esos dos (marcada con rojo en la imagen).

Ahora, dibujaremos el diagrama de retícula de $D_{2(4)}/\left<a^2\right>$, éste va hasta arriba. Colocamos los cocientes respectivos en el siguiente nivel, siguiendo esta correspondencia:

\begin{align*}
\left<a^2,b\right> &\longmapsto \left<a^2,b\right> / \left<a^2\right>\\
\left<a\right> &\longmapsto \left<a\right>/ \left<a^2\right>\\
\left<a^2,ab\right> &\longmapsto \left<a^2,ab\right>/ \left<a^2\right>.
\end{align*}

Haciendo las cuentas veremos que:
\begin{align*}
\left<a^2,b\right> / \left<a^2\right> = \left<b \left<a^2\right>\right>\\
\left<a\right>/ \left<a^2\right> = \left<a \left<a^2\right>\right>\\
\left<a^2,ab\right>/ \left<a^2\right> = \left<ab \left<a^2\right>\right>.
\end{align*}

Construcción de los diagramas de retícula

Por último, haremos una observación. Si tomamos el subgrupos $\left< a^3b\right>$ de orden 2 igual podríamos aplicarle la regla de correspondencia de $F$ y seguirían cayendo en elementos de la retícula de $D_{2(4)}/\left<a^2\right>$ es decir:
\begin{align*}
F(\left< a^3b\right>)=\pi[\left< a^3b\right>] = \{\text{id}\left<a^2\right>, a^3b\left<a^2\right>\} = \left<ab\left<a^2\right>\right>.
\end{align*}

En ese contexto la función con la regla de correspondencia de $F$ no sería biyectiva ya que $F(\left< a^3b\right>)=F(\left< ab\right>)$, pero esto no contradice el Teorema de la Correspondencia porque en realidad $\left< a^3b\right>$ ni siquiera está contemplado en el dominio de $F$ porque no forma parte de la retícula entre $D_{2(4)}$ y $\left<a^2\right>$.

Diagrama de retícula completo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba los incisos 3 y 4 del Teorema de la correspondencia (Cuarto Teorema de Isomorfía).
  2. Encuentra la retícula de sugrupos de $\z$ que contienen a $24\z$.
    • Encuentra la retícula de subgrupos de $\z/24\z$.
    • Compara ambas retículas.
  3. Usando el diagrama reticular de subgrupos de $\z_{36}$ encuentra el de $\z_{36}/N$ donde $N = \{\bar{0}, \overline{12}, \overline{24}\}$.

Más adelante…

Con esta entrada concluimos la Unidad 3. En la siguiente unidad comenzaremos a ver cómo es posible ver a cualquier grupo como un subgrupo de permutaciones. ¿Puedes imaginártelo?

Entradas relacionadas

Álgebra Moderna I: Palabras

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

Introducción

En la entrada anterior tomamos un grupo $G$ y un subconjunto $X \subseteq G$ y, logramos encontrar al menor subgrupo de $G$ que contiene a $X$. Este conjunto resultó ser la intersección de todos los subgrupos contenidos en $G$ que, a su vez, contienen a $X$. Recordemos que se llama el subgrupo de $G$ generado por $X$ y se denota

\begin{align*}
\left< X\right> = \bigcap_{\substack{H \leq G \\ X \subseteq H}} H.
\end{align*}

Sin embargo, esto no nos dice mucho sobre los elementos de $X$. Ilustremos un poco lo que tenemos. Tomemos un grupo $G$, un subconjunto $X \subseteq G$ y al generado $ \left<X\right> \subset G$. Entonces, si tomamos $x_1,x_2,x_3 \in X$, sabemos que todas las potencias de esos elementos están en el generado de $X$. Es decir, para todas $q,r,s \in \z$, $x_1^q, x_2^r, x_3^s \in \left<X\right>$. Más aún, las diferentes multiplicaciones de esos elementos también están en $\left<X\right>$, por ejemplo, si consideramos $x_1^1, x_3^{-2}, x_2^{3}$ y $x_1^{-4}$, el elemento

\begin{align}\label{palabra}
x_1^{-4} x_3^{-2} x_1^1 x_2^{3}
\end{align}

está en $\left<X\right>$, por ser una multiplicación de elementos del subgrupo. Entonces, en el generado de $X$ estarán todos los elementos de $X$, las potencias de esos elementos y todas las multiplicaciones entre dichas potencias.

Al elemento \eqref{palabra} la llamamos una palabra en $X$ y es lo que estudiaremos en esta entrada. Además, las palabras nos permiten dar descripción del subgrupo generado. Esta idea es análoga a la que se estudia en álgebra lineal cuando se describe al subespacio generado por un conjunto como una colección de combinaciones lineales de vectores. Sin embargo, en el caso de subgrupos, esta descripción no es igual a la de álgebra lineal porque hay que recordar que un grupo en general no es abeliano. Esto influye en qué tanto se pueda simplificar una palabra.

Nuestra primera aproximación a las palabras

Definición. Sea $G$ un grupo, $X$ un subconjunto de $G$. Una palabra en $X$ es, o bien el neutro $e$, o bien un elemento de la forma

$x_1^{\alpha_1}, \dots, x_n^{\alpha_n}$

con $n \in \n^+$, $x_1,\dots, x_n\in X, \alpha_1, \dots, \alpha_n \in \z$.

Notación. Denotamos por $W_X$ al conjunto de todas las palabras en $X$.

Ejemplos

Ejemplo 1. Sea $G = D_{2(4)}$ el grupo diédrico formado por las simetrías de un cuadrado centrado en el origen. Sea $a$ la rotación de $\pi/2$ y $b$ la reflexión con respecto al eje $x$.
$ba^3 b a^{-1} b^{-4} a$ es una palabra en $\{a, b\}$.

En este caso, la palabra sí se puede simplificar como:
\begin{align*}
b a^3 b a^{-1}b^{-4} a &= ba^3ba^{-1} e a \\
& = b a^3 b a^{-1} a \\
& = ba^3 b
\end{align*}

Para la primera igualdad, recordemos que $b$ es la rotación por $\pi/2$, entonces al aplicar esa rotación $4$ veces, el cuadrado recupera su estado inicial, así por eso $ b^{4} = e$ y de forma análoga como $b^{-1}$ es la rotación por $-\pi/2$ se tiene que $b^{4} = e$.

Notación. Usaremos la notación $D_{2(4)}$ para denotar las simetrías del cuadrado (que tiene 4 vértices), este grupo diédrico tiene 8 elementos. Otros autores pueden escribir simplemente $D_8$, pero esto se puede confundir con el grupo de las simetrías de un octágono. De forma más general el grupo diédrico de un polígono de $n$ lados es el grupo de simetrías de un polígono regular de $n$ lados centrado en el origen, con la operación de composición. Lo denotatemos por $D_{2n}$ y tendrá $2n$ elementos.

Ejemplo 2. Consideremos el conjunto $ \{\pm 1, \pm i, \pm j, \pm k\}$. Este conjunto es llamado el grupo de los cuaterniones o cuaternios y se suele denotar por $Q$ o $Q_8$ porque tiene 8 elementos.

Las operaciones en el conjunto se definen como:
\begin{align*}
1 a &= a 1 = a &\forall a \in Q \\
(-1) a &= a (-1) = -a & \forall a \in Q
\end{align*}

Además, las multiplicaciones no son conmutativas y están definidas así:
$\begin{align*}
ij &= k, \quad &jk = i, \quad &ki =j, \\
ji &= -k, \quad &kj = -i, \quad &ik=-j, \\
i^2 &= j^2 = k^2 = -1.
\end{align*}$

Una palabra en $\{j\}$ es $j^5j^{-2} j^{3} j^{-4}$, resolviendo las potencias podemos concluir que esta palabra es igual a $-1$ (verificarlo quedará como ejercicio). Podemos ahora considerar el conjunto de todas las palabras formadas con el elemento $j$, es decir el conjunto de palabras en $\{j\}$. Se puede ver que:
\begin{align*}
W_{\{j\}} = \{j,-1,-j, +1\}.
\end{align*}

También podemos considerar el conjunto de palabras formadas con los elementos $j$ y $k$, es decir el conjunto de palabras en $\{j,k\}$. En este caso se tiene que:
\begin{align*}
W_{\{j,k\}} = \{\pm 1, \pm i, \pm j, \pm k \}=Q.
\end{align*}

Palabras y el subgrupo generado por $X$

Lema. Sea $G$ un grupo y $X$ un subconjunto de $G$. $W_X$ es un subgrupo de $G$ que contiene a $X$.

Demostración.
Caso 1, cuando $X = \emptyset$.
En este caso, $W_X = \{e\} \leq G$ y $X = \emptyset \subset \{e\} = W_X$.

Caso 2, cuando $X \neq \emptyset$.
P.D. $W_X \leq G$.
Por definición $e \in W_X$.
Sean $a, b \in W_X$, entonces

\begin{align*}
a &= x_1^{\alpha_1} \dots x_n^{\alpha_n} & \alpha_1, \dots, \alpha_n, \beta_1, \dots, \beta_m \in \z \\
b &= y_1^{\beta_1} \dots y_m^{\beta_m} & x_1, \dots, x_n, y_1, \dots, y_m \in X\\
&& n,m \in \n^+
\end{align*}

Entonces, podemos tomar $ab^{-1}$ y verificar quién es

\begin{align*}
a b^{-1} &= (a_1^{\alpha_1} \dots x_n^{\alpha_n})(y_1 \dots y_m^{\beta_m})^{-1} \\
& = x_1^{\alpha_1} \dots x_n^{\alpha_n}y_m^{-\beta} \dots y_1^{-\beta_1} \in W_X.
\end{align*}

Por lo tanto $W_X \leq G$.

P.D. $X \subseteq W_X$.
Sea $x \in X$,
\begin{align*}
x = x^1 \in W_X.
\end{align*}

Por lo tanto $X \subseteq W_X$.

En ambos casos $W_X$ es un subgrupo de $G$ que contiene a $X$.

$\blacksquare$

Teorema. Sea $G$ un grupo, $X$ un subconjunto de $G$. Entonces

$\left< X \right> = W_X$.

Demostración.
$\subseteq)$ Por el lema anterior, $W_X \in \{H \leq G : X \subseteq H\}$. Entonces, por nuestra definición del subgrupo generado,
\begin{align*}
\left< X \right> = \bigcap_{\substack{H \leq G \\ X \subseteq H}} H \subseteq W_X.
\end{align*}

$\supseteq)$ Sea $a \in W_X$, entonces $a = x_1^{\alpha_1} \cdots x_n^{\alpha_n}$ con, $n \in \n^+$, $\alpha_1, \dots, \alpha_n \in \z$ y $x_1, \dots, x_n \in X$.

Como cada $x_i \in X$, con $i \in \{1,..,n\}$, y $X \subseteq \left< X \right>$, entonces $x_i\in\left< X \right>$ para toda $i \in \{1, \dots ,n\}$.
Como el generado es un subgrupo de $G$, obtenemos que $x_i^{\alpha_i} \in \left< X \right>$ para toda $i \in \{1,\dots,n\}$. Usando nuevamente que el generado es un subgrupo de $G$ tenemos que $a = x_1^{\alpha_1} \dots x_n^{\alpha_n} \in \left<X\right>$.

Por lo tanto, $\left< X \right> = W_X$.

$\blacksquare$

¿Quién es el orden de un producto?

Ya hemos hablado del orden de un elemento. Si tenemos un grupo $G$ y $a, b \in G$ y sabemos quién es $o(a)$ y $o(b)$, ¿podemos saber cómo es $o(ab)$? En algunos casos podemos respuesta a esta pregunta dando una explicación más precisa de cómo es el orden de un producto en términos del orden de sus factores. El siguiente resultado aparece en el libro de Avella, Mendoza, Sáenz y Souto mencionado en la bibliografía, Teorema 3.3.12:

Teorema. Sea $G$ un grupo y $a, b \in G$.
Si $a$ y $b$ son de orden finito, sus ordenes son primos relativos y $ab = ba$, entonces

\begin{align*}
o(ab) &= o(a) o(b) \\
\text{y } \left< a,b \right> &= \left<ab\right>.
\end{align*}

Demostración.
Sea $G$ un grupo, $a,b \in G$ de orden finito con $n = o(a)$, $m = o(b)$. Supongamos que $(n;m) = 1$ y $ab = ba$.

P.D. $o(ab) = nm$.
Entonces

\begin{align*}
(ab)^{nm} & = a^{nm} b^{nm} & \text{ porque } ab = ba \\
& = (a^n)^m(b^m)^n & \text{ propiedades de los exponentes}\\
& = e^m e^n \\
& = e
\end{align*}

Ya teniendo que $(ab)^{nm} = e$, tenemos que ver que $nm$ es el menor exponente positivo tal que al elevar $ab$ a ese exponente nos da el neutro, o bien ver que divide a cualquier otro $k$ tal que $(ab)^k = e$. Procedamos de acuerdo a la segunda opción.

Sea $k\in\z$ tal que $(ab)^k = e$, y como $ab=ba$ esto implica que $a^k b^k = e$. Despejando, obtenemos $a^k = b^{-k}$.

Así $(a^k)^m = (b^{-k})^m = (b^m)^{-k} = e^{-k} = e$ (porque $o(b) = m$), es decir $a^{km} = e$. Dado que $o(a) = n$, entonces $n|km$ y como $(n;m) = 1$ entonces $n|k$.

Si consideramos ahora $(a^k)^n = (b^{-k})^n$ y seguimos un argumento análogo obtenemos que $m|k$.

Como $n|k$ y $m|k$ y $(n;m) = 1$, entonces $nm|k$.
Por lo tanto $o(ab) = nm$.

P.D. $\left< a,b \right> = \left< ab \right>$.
Como toda palabra en $\{ab\}$ es una palabra en $\{a, b\}$ entonces
\begin{align*}
\left< ab \right> \subseteq \left< a, b \right>.
\end{align*}

Por otro lado, como $ab = ba$, toda palabra en $\{a,b\}$ se reduce a una de la forma $a^{i}b^{j}$ con $i, j \in \z$, y como $o(a) = n$, $o(b) = m$, la expresión $a^{i}b^{j}$ se puede reducir aún más a una expresión de la forma $a^{i}b^{i}$ con $0 \leq i < n$ y $0 \leq j < m$.

Entonces $\left< a, b \right> = \{a^{i}b^{j}: 0 \leq i < n, 0 \leq j < m\}$. Luego, $|\left<a, b\right>| \leq nm$.
Pero $\left< ab \right> \subseteq \left<a,b\right>$, entonces $|\left< ab \right>| \leq |\left< a,b \right>|$.
Así,

\begin{align*}
nm = o(ab) = |\left< ab \right>| &\leq |\left< a,b \right>| \leq nm. \\
\end{align*}

Por lo tanto $\left<ab\right> = \left< a, b \right>$.

$\blacksquare$

Tarea moral

  1. En el grupo de los cuaternios definido anteriormente, verifica que $j^5j^{-2}j^3j^{-4} = -1$.
  2. Considera $Q$, el grupo de cuaternios. Reduce la siguiente palabra a uno de los elementos $\pm 1, \pm i, \pm j, \pm k$,
    $$\begin{align*}
    j^7k(-i)jki^2jk^{-6}
    \end{align*}$$
  3. Sea $D_{2n} = \{\text{ id }, a, \dots, a^{n-1}, ab, \dots, a^{n-1}b\}$ el grupo diédrico formado por las simetrías de un polígono regular de $n$ lados, con $a$ la rotación de $\displaystyle \frac{2\pi}{n}$ y $b$ la reflexión con respecto al eje $x$.
    1. Identifica geométricamente quiénes son $\text{ id }, a, \dots, a^{n-1}, ab, \dots, a^{n-1}b$.
    2. Determina quién es el elemento $bab$ y, de modo más general, quién es el elemento $ba^{i}b$ para toda $i\in\z$.
    3. Determina quién es el elemento $ba^i$ para toda $i\in\z$.
  4. Considera el grupo simétrico $S_5$, $\alpha$ la permutación que manda $1$ en $2$, $2$ en $3$ y $3$ en $1$, fija a $4$ y a $5$, y $\beta$ la permutación que intercambia $4$ y $5$.
    1. Encuentra $\beta \alpha$ y $\alpha \beta$.
    2. Encuentra el orden de $\alpha$, $\beta$, $\alpha\beta$ y $\beta\alpha$.
  5. Por último, te invitamos a que veas este video que habla sobre las aplicaciones tecnológicas del grupo de los cuaternios. El video está en inglés, pero tiene subtítulos en español.

Más adelante…

¡Felicidades por acabar la Unidad 1! Ya entiendes las bases de este curso, trata de recordarlas porque las estaremos usando implícitamente.
En la siguiente unidad estaremos viendo Permutaciones y Grupo Cociente, para no adelantar mucho, sólo diremos que ambas estructuras son grupos muy importantes en el álgebra y nuestros objetos de estudio en la siguiente unidad.

Entradas relacionadas

Álgebra Moderna I: Propiedades de grupos y Definición débil de grupo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Cuando se estudian campos vectoriales u otras estructuras algebraicas primero se definen ciertas propiedades básicas y después, otras propiedades importantes que se desprenden de las primeras. Ahora, vamos a ver propiedades de los grupos. Dentro de los grupos mencionamos la existencia de un neutro, asociatividad e inverso. Pero de ahí se desprenden otras propiedades que vamos a usar como la cancelación, la unicidad de los neutros, etc.

Propiedades de grupos

Propiedades. Sea $(G,*)$ un grupo, entonces

  1. Para cualesquiera $x, a, b \in G$, se tiene que $$x*a = x*b \Rightarrow a = b,$$ también se vale cancelar por la derecha, $$a*x = b*x \Rightarrow a = b.$$ Estas propiedades son conocidas como las leyes de cancelación.
  2. El neutro en $(G,*)$ es único.
  3. Cada $a \in G$ tiene un único inverso y se denota por $a^{-1}$.
  4. Para toda $a \in G$, $(a^{-1})^{-1} = a$.

Demostración. 1. Sean $x,a,b \in G$.
Supongamos que $x*b = x*b$. Sea $\tilde{x} \in G$ inverso de $x$. Tenemos que

$\begin{align*}
\text{ }\\
\Rightarrow \\
\Rightarrow\\
\Rightarrow
\end{align*}$

$\begin{align*}
\tilde{x} * (x * a) = \; & \tilde{x} * (x * b) & \text{ }\\
(\tilde{x} * x) * a = \; & (\tilde{x} * x) * b & \text{por la asociatividad}\\
e* a = \; & e * b & \text{por ser $\tilde{x}$ el inverso de $x$}\\
a = \;& b & \text{por ser $e$ el neutro}
\end{align*}$

La cancelación por la derecha es análoga y se deja como ejercicio.

2. Sean $e, e’ \in G$ neutros

$\begin{align*}
e \;{=}\; & e * e’ & \text{ por ser $e’$ un neutro}\\
{=}\; & e’ & \text{ por ser $e$ un neutro}\\
\end{align*}$

$\therefore \; e= \; e’$

3. Sea $a\in G$. Supongamos que $\hat{a}, \tilde{a} \in G$ son inversos de a, entonces:

$\begin{align*}
\hat{a} \;{=}\; & e * \hat{a} & \text{ por ser $e$ el neutro}\\
= \; &(\tilde{a} * a)* \hat{a} & \text{ por ser $\tilde{a}$ un inverso de $a$}\\
=\; & \tilde{a} * (a * \hat{a}) & \text{ por la asociatividad}\\
=\; & \tilde{a} * e & \text{por ser $\hat{a}$ un inverso de $a$}\\
=\; &\tilde{a} & \text{ por ser $e$ el neutro}
\end{align*}$

$\therefore \hat{a} = \tilde{a}$

4. Sea $a \in G$.
Como $(a^{-1})^{-1}$ es el inverso de $a^{-1}$ tenemos que

$a^{-1} * (a^{-1})^{-1} = e$

Como $a^{-1}$ es el inverso de $a$ tenemos que

$a^{-1} * a = e$

Así $a^{-1}*(a^{-1})^{-1} = a^{-1} *a$, entonces por la propiedad 1 podemos cancelar el elemento $a^{-1}$ por la izquierda y concluir que $(a^{-1})^{-1} = a$.

$\blacksquare$

Definición débil de grupo

Teorema. Sea $G$ un conjunto, $*$ una operación binaria en $G$. Supongamos que

  1. $*$ es asociativa,
  2. existe $e \in G$ tal que $e*a = a $ para toda $a \in G$ y
  3. $\forall a \in G$ existe $ \tilde{a} \in G$ tal que $\tilde{a}*a=e$,

entonces $(G,*)$ es un grupo. A partir de ahora, a las propiedades $2$ y $3$ de la definición débil de grupo las denotaremos como $2’$ y $3’$ respectivamente para dejar que los números $2$ y $3$ denoten las propiedades de la definición de grupo.

Demostración. Supongamos que $(G,*)$ cumple $1, 2’$ y $3’$.
Sea $a \in G$, por $3’$, existe $\tilde{a} \in G$ tal que $\tilde{a} * a = e$.
Tenemos que $\tilde{a}$ es un inverso izquierdo de $a$. Veamos primero que $\tilde{a}$ es también un inverso derecho de $a$, es decir que $a * \tilde{a} = e$.

$\begin{align*}
\tilde{a} * (a * \tilde{a}) \;=\;& (\tilde{a} * a) * \tilde{a} & \text{por la asociatividad}\\
= \; & e * \tilde{a} & \text{por la propiedad }3’\\
= \;& \tilde{a} & \text{ por la propiedad } 2’\\
\end{align*}$

$\Rightarrow \tilde{a} * (a * \tilde{a}) = \tilde{a}$.

Por $3’$ existe $b \in G$ tal que $b*\tilde{a}=e$. Multiplicando $ \tilde{a} * (a * \tilde{a}) = \tilde{a}$ a la izquierda por $b$ tenemos que

$\begin{align*}
\text{ }\\
\Rightarrow \\
\Rightarrow\\
\Rightarrow
\end{align*}$

$\begin{align*}
b * (\tilde{a} * (a * \tilde{a})) =\;& b * \tilde{a} & \text{ }\\
(b * \tilde{a}) * (a * \tilde{a}) = \;& b * \tilde{a} & \text{por la asociatividad}\\
e * (a * \tilde{a}) =\;& e & \text{ya que $b$ es un inverso izquierdo de $\tilde{a}$}\\
a * \tilde{a}=\;& e &\text{ya que $e$ es un neutro izquierdo.}
\end{align*}$

Así, $\tilde{a}$ es también un inverso derecho de $a$.

Por $2’$, $e*a=a$ para toda $a\in G$, es decir $e$ es un neutro izquierdo. Veamos ahora que $e$ también es un neutro derecho probando que $a * e = a$ para toda $a \in G$.

Sea $a \in G$, por $3’$ existe $\tilde{a} \in G$ tal que $\tilde{a} * a=e$, y por lo que acabamos de probar $a * \tilde{a} = e$. Usando estas igualdades y la propiedad asociativa tenemos que

$a * e = a * (\tilde{a} * a) = (a * \tilde{a}) * a = e * a$

y como $e$ es un neutro por la izquierda, $e * a = a$. Así $a * e = a$.

Por lo tanto $(G, *)$ es un grupo.

$\blacksquare$

Tarea moral

  1. Usando la Definición débil de grupo, determina cuáles de estos conjuntos son un grupo.
    • $G = \r \setminus \{-1\}$, $a*b := a+b+ab$.
    • $G = \r^*$, $a*b = |a|b$.
    • $G = \{r \in \mathbb{Q} \;|\; r = \frac{p}{q} \text{ con } (p,q)= 1 \text{ y } q \text{ impar}\}$, $a*b = a+b$ (la adición usual).
    • Sea $X$ un conjunto. Considera $G = \mathcal{P}(X)$ el conjunto potencia de $X$ con la operación binaria $A \triangle B = (A \cup B)\setminus (A \cap B)$ para todo $A,B \in \mathcal{P}(X)$.
  2. Muestra que $G = \r^*$ con la operación $a * b = |a| b$, tiene un neutro izquierdo $e$ y para cada elemento $a$ existe $\tilde{a}$ tal que $a * \tilde{a} = e$ ¿qué puedes concluir con respecto a la definición débil de un grupo?
  3. Para el conjunto $\mathcal{S}:= \{\bigstar, \blacktriangledown, \blacklozenge, \clubsuit \}$, considera las operaciones que creaste en la tarea moral de una entrada anterior.
    • Si definiste una operación tal que $(\cS, *)$ es un grupo, comprueba las propiedades vistas en esta entrada y verifica la definición débil.
    • Si no, observa si alguna de las propiedades analizadas se cumplen con tu operación.
  4. Si quieres conocer el grupo de transformaciones lee la sección 3.1.1 del libro Introducción analítica a la geometría de Javier Bracho (página 112 a la 115).
  5. Si quieres conocer el grupo diédrico puedes ver el video Dihedral Group de Socratica. El video está en inglés. De todas maneras, después usaremos el grupo diédrico, así que lo definiremos más adelante.

Más adelante…

En la siguiente entrada generalizaremos la propiedad de la asociatividad porque hasta ahora sólo la manejamos con tres elementos. Además, seguiremos formalizando conceptos que ya conocemos intuitivamente: definiremos qué es una potencia, escribiremos las leyes de los exponentes y las demostraremos.

Entradas relacionadas