Introducción

Hasta ahora hemos visto la definición de función compleja y hemos estudiado los conceptos de límite, continuidad y diferenciabilidad de dicho objeto matemático. En la entrada anterior, a través de las ecuaciones de Cauchy-Riemann, hemos caracterizado la diferenciabilidad compleja y probamos que no basta la diferenciabilidad de las funciones escalares reales para garantizar la diferenciabilidad compleja, aún cuando toda función compleja queda completamente determinada por dos funciones escalares reales a las que llamamos su parte real e imaginaria.

En esta entrada definiremos una de las funciones complejas más elementales, recordando que hemos hecho una extensión de los números reales $\mathbb{R}$ a través de la construcción del campo de los números complejos $\mathbb{C}$, por lo que nos gustaría que la función exponencial compleja preservará las propiedades de su versión real correspondiente. Motivados en este hecho procedemos a deducir una definición para la función exponencial compleja.

Queremos definir una función analítica $f$ tal que si $z_1,z_2\in \mathbb{C}$, entonces: $$f(z_1+z_2)=f(z_1)f(z_1),$$ además, que para toda $z=x\in \mathbb{R}$ cumpla que: $$f(z)=f(x)=e^x.$$

De acuerdo con estas propiedades, si $z=x+iy\in \mathbb{C}$ se debe cumplir que: $$\begin{array}{rl}f(z)& =f(x+iy)\\ & =f(x)f(iy)\\ & =e^{x}f(iy).\end{array}$$

Tomando $f(iy)=A(y)+iB(y)$, tenemos: $$\begin{array}{rl}f(z)& =e^x[A(y)+iB(y)]\\ & =e^{x}A(y)+i{e}^{x}B(y),\end{array}$$ de donde $u(x,y)=e^{x}A(y)$ y $v(x,y)=e^{x}B(y)$.

Para que $f$ sea una función analítica se deben satisfacer las ecuaciones de Cauchy-Riemann, es decir: $$u_x(x,y)=e^{x}A(y)=e^x{B}^{\prime }(y)=v_y(x,y)$$ $$u_y(x,y)=e^x{A}^{\prime }(y)=–e^{x}B(y)=–v_x(x,y),$$ por lo que las funciones reales $A(y)$ y $B(y)$ deben cumplir que:
$$\begin{array}{r}A(y)=B^{\prime }(y),\\ \text{(20.1)}& B(y)=-A^{\prime }(y),\end{array}$$ de donde: $$A^{‘‘}(y)=–A(y),B^{‘‘}(y)=–B(y).$$

Sean $\alpha ,\beta \in \mathbb{R}$. Tomando: $$A(y):=\alpha \cos (y)+\beta \mathrm{sen}(y),$$ tenemos que: $$A^{\prime }(y)=–\alpha \mathrm{sen}(y)+\beta \cos (y),$$ $$A^{‘‘}(y)=–[\alpha \cos (y)–\beta \mathrm{sen}(y)]=–A(y),$$ de donde: $$B(y):=-\beta \cos (y)+\alpha \mathrm{sen}(y),$$ $$B^{‘‘}(y)=[-\beta \cos (y)+\alpha \mathrm{sen}(y)]=-B(y).$$

Claramente las funciones reales $A(y)$ y $B(y)$ propuestas cumplen (20.1).

Entonces, para $z=x+iy\in \mathbb{C}$ tenemos que: $$\begin{array}{rl}f(z)& =e^x[A(y)+iB(y)]\\ & =e^x[(\alpha -i\beta )\cos (y)+(\beta +i\alpha )\mathrm{sen}(y)].\end{array}$$ Como $f(z)=e^x$ para $z=x+i0\in \mathbb{R}$, entonces: $$\begin{array}{rl}f(z)& =e^x[(\alpha -i\beta )\cos (0)+(\beta +i\alpha )\mathrm{sen}(0)]\\ & =e^x(\alpha -i\beta )\\ & =e^x,\end{array}$$ lo cual se cumple si y solo si $\alpha =1$ y $\beta =0$.

De acuerdo con lo anterior hemos motivado la siguiente:

Definición 20.1. (Exponencial compleja.)
Si $z=x+iy\in \mathbb{C}$, entonces se define a la función exponencial compleja, denotada por $\exp (z)$, como el número complejo: $$\exp (z)=e^x[\cos (y)+i\mathrm{sen}(y)],$$ donde $e^x$, $\cos (y)$ y $\mathrm{sen}(y)$ corresponden a las funciones reales exponencial, coseno y seno, respectivamente.

Observación 20.1.
La función exponencial compleja extiende a la exponencial real, por lo que se utilizarán de forma indistinta las expresiones $\exp (z)$ y $e^z$ para denotar a dicha función. La justificación de este hecho se dará más adelante al hablar de series de potencias, donde se verá que las definiciones de las funciones más elementales, en particular de la exponencial compleja, que veremos en esta unidad coinciden con las definiciones de nuestros cursos de Cálculo.

Ejemplo 20.1.
Obtengamos el valor de $f(z)=e^z$ para $z=3-i\frac{\pi }{3}$, $z=2+3\pi i$ y $z=-1+\pi i$.

Solución. De acuerdo con la definición de la función exponencial compleja tenemos que:
a) $f(3-i\frac{\pi }{3})=e^3[\cos (-\frac{\pi }{3})+i\mathrm{sen}(-\frac{\pi }{3})]=e^3\left(\frac{1}{2}–i\frac{\sqrt{3}}{2}\right)$.
b) $f(2+3\pi )=e^2[\cos (3\pi )+i\mathrm{sen}(3\pi )]=e^2(-1)=-e^2$.
c) $f(-1+\pi i)=e^{-1}[\cos (\pi )+i\mathrm{sen}(\pi )]=e^{-1}(-1)=-{\displaystyle \frac{1}{e}}$.

Proposición 20.1. (Analicidad de la exponencial compleja.)
La función exponencial compleja, $f(z)=e^z$, es una función entera y su derivada está dada por: $$\frac{d}{dz}{e}^z=e^z.$$

Demostración.
De acuerdo con la definición de la función exponencial compleja para $z=x+iy\in \mathbb{C}$ tenemos que: $$\begin{array}{r}\mathrm{Re}(e^z)=u(x,y)=e^x\cos (y),\\ \mathrm{Im}(e^z)=v(x,y)=e^x\mathrm{sen}(y).\end{array}$$

Es claro que las funciones $u(x,y)$ y $v(x,y)$ son continuas en ${\mathbb{R}}^2$ y que ambas tienen derivadas parciales de primer orden continuas para todo $(x,y)\in {\mathbb{R}}^2$. Notemos que: $$\begin{array}{r}\frac{\partial u}{\partial x}=e^x\cos (y)=\frac{\partial v}{\partial y},\\ \frac{\partial u}{\partial y}=-e^x\mathrm{sen}(y)=-\frac{\partial v}{\partial x},\end{array}$$ es decir que $u$ y $v$ satisfacen las ecuaciones de C-R para todo $z=x+iy\in \mathbb{C}$, por lo que de acuerdo con el teorema 18.1 (o el teorema 18.3) concluimos que la función $f(z)=e^z$ es analítica en $\mathbb{C}$, por lo que es una función entera.

Más aún, sabemos que la derivada de $f$ está dada por: $$\begin{array}{rl}\frac{d}{dz}{e}^z& =\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}\\ & =e^x\cos (y)+i{e}^x\mathrm{sen}(y)\\ & =e^x[\cos (y)+i\mathrm{sen}(y)]\\ & =e^z.\end{array}$$ para todo $z=x+iy\in \mathbb{C}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 20.1. (Continuidad de la exponencial compleja.)
La función exponencial compleja, $f(z)=e^z$, es continua en $\mathbb{C}$.

Demostración. Se sigue de la proposición 16.1.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 20.2.
Notemos que utilizando la proposición 20.1 y la regla de la cadena podemos deducir que si $f(z)$ es una función analítica en un dominio $D$, entonces la función $e^{f(z)}$ también será analítica en $D$ y su derivada está dada por: $$\frac{d}{dz}{e}^{f(z)}=f^{\prime }(z)e^{f(z)},\mathrm{\forall }z\in D.$$

Ejemplo 20.2.
Estudiemos la analicidad de las siguientes funciones y determinemos su derivada.
a) $f(z)=i{z}^3(z-e^{z^2})$.
b) $f(z)=e^{z^2-(1+i)z+3}$.

Solución.
a) Primeramente notemos que $f$ está dada como el producto de las funciones $h(z)=i{z}^3$ y $g(z)=z-e^{z^2}$. Claramente la función $h$ es entera pues es un polinomio complejo. Por otra parte, notemos que $h$ está dada como la resta de dos funciones, pero ambas son funciones enteras pues la primera función es un polinomio complejo y la segunda función es una composición entre las funciones $e^z$ y $z^2$ que sabemos son enteras, por tanto la función $f$ es entera y su derivada está dada por la regla del producto, es decir: $$\begin{array}{rl}{f}^{\prime }(z)& =h^{\prime }(z)g(z)+g^{\prime }(z)h(z)\\ & =3i{z}^2(z-e^{z^2})+(1-e{z}^2(2z))\left(i{z}^3\right)\\ & =i{z}^2\left(4z–e^{z^2}(2z^2+3)\right).\end{array}$$ b) Notemos que $f$ está dada por la composición de las funciones $h(z)=e^z$ y $g(z)=z^2-(1+i)z+3$ las cuales son enteras por tratarse de la exponencial compleja y de un polinomio complejo, por lo que considerando la regla de la cadena tenemos que su derivada es: $$\begin{array}{rl}{f}^{\prime }(z)& =h^{\prime }(g(z))g^{\prime }(z)\\ & =e^{z^2-(1+i)z+3}(2z-1-i).\end{array}$$

Ejemplo 20.3.
Veamos que al igual que en el caso real, para la función exponencial compleja se cumple que: $$\underset{z\to 0}{lim}\frac{e^z–1}{z}=1.$$

Solución. De acuerdo con la proposición 20.1 sabemos que la función $f(z)=e^z$ es entera. En particular notemos que: $$1=e^0=f^{\prime }(0)=\underset{z\to 0}{lim}\frac{f(z)–f(0)}{z-0}=\underset{z\to 0}{lim}\frac{e^z–1}{z}.$$

Ejemplo 20.4.
Estudiemos la analicidad de las siguientes funciones. Determinemos los puntos donde son al menos diferenciables y de existir obtengamos sus derivadas.
a) $f(z)=e^{|z{|}^2}$.
b) $f(z)=\bar{z}{e}^{-|z{|}^2}$.

Solución.
a) De acuerdo con el ejercicio 3(a) de la entrada 17, sabemos que la función $g(z)=|z{|}^2$ no es analítica para ningún $z\in \mathbb{C}$, pero que al menos es diferenciable en $z=0$. Considerando la observación 20.2 veamos que esto se mantiene para la función $f$.

Sea $z=x+iy\in \mathbb{C}$, entonces: $$f(z)=e^{|z{|}^2}=e^{x^2+y^2},$$ por lo que: $$u(x,y)=e^{x^2+y^2},v(x,y)=0.$$

Notemos que para todo $z=x+iy\in \mathbb{C}$ tenemos que: $$u_x(x,y)=2x{e}^{x^2+y^2},u_y(x,y)=2y{e}^{x^2+y^2},$$ $$v_x(x,y)=0,u_y(x,y)=0.$$

Entonces $u_x(x,y)=v_y(x,y)$ y $u_y(x,y)=–v_x(x,y)$ si y solo si $x=0=y$, es decir para $z=0$.

Puesto que las derivadas parciales existen y son continuas para todo $z=x+iy\in \mathbb{C}$, entonces $f$ solo es diferenciable en $z=0$ y como no existe disco abierto alrededor de $z=0$ donde $f$ sea diferenciable, entonces $f$ no es analítica en ningún punto en $\mathbb{C}$.

Por último, tenemos que: $$\begin{array}{rl}{f}^{\prime }(0)& =\underset{z\to 0}{lim}\frac{f(z)–f(0)}{z-0}\\ & =\underset{z\to 0}{lim}\frac{e^{|z{|}^2}–1}{z}\\ & =\underset{z\to 0}{lim}\bar{z}\left(\frac{e^{|z{|}^2}–1}{z\bar{z}}\right)\\ & =\left(\underset{z\to 0}{lim}\bar{z}\right)\left(\underset{z\to 0}{lim}\frac{e^{|z{|}^2}–1}{|z{|}^2}\right)\\ & =0(1)\\ & =0.\end{array}$$

b) Podemos proceder de manera similar que en el inciso anterior, sin embargo considerando los resultados de la entrada anterior, tenemos que: $$f(z)=\bar{z}{e}^{-|z{|}^2}=\bar{z}{e}^{-z\bar{z}}=g(z,\bar{z}).$$

Por los ejercicios 8 y 9 de la entrada anterior tenemos que: $$f_z=\frac{\partial g}{\partial z}=0+\bar{z}\left(e^{-z\bar{z}}(-\bar{z})\right)=–{\bar{z}}^2{e}^{-z\bar{z}}=–{\bar{z}}^2{e}^{-|z{|}^2}.$$ $$f_{\bar{z}}=\frac{\partial g}{\partial \bar{z}}=e^{-z\bar{z}}+\bar{z}\left(e^{-z\bar{z}}(-z)\right)=e^{-z\bar{z}}(1-z\bar{z})=e^{-|z{|}^2}(1-|z{|}^2).$$

Claramente $f_z$ y $f_{\bar{z}}$ existen y son continuas para todo $z\in \mathbb{C}$, por lo que las derivadas parciales $u_x,u_y,v_x$ y $v_y$ existen y son continuas para todo punto $z=x+iy\in \mathbb{C}$, es decir $f$ es de clase $C^1$.

Notemos que: $$f_{\bar{z}}=0⟺e^{-|z{|}^2}(1-|z{|}^2)=0⟺1-|z{|}^2=0⟺|z|=1.$$

Entonces, las ecuaciones de C-R solo la satisfacen los puntos $z=x+iy\in \mathbb{C}$ tales que $|z|=1$, es decir los puntos sobre la circunferencia unitaria $C(0,1)$, por lo que al existir y ser continuas las cuatro derivadas parciales en todo $\mathbb{C}$, en particular en $C(0,1)$, concluimos que $f$ solo es diferenciable en los puntos sobre la circunferencia unitaria. Más aún, para $z=x+iy\in C(0,1)$, es decir $|z|=1$, tenemos que: $$\begin{array}{rl}{f}^{\prime }(z)=f_z(z)& =–{\bar{z}}^2{e}^{-|z{|}^2}\\ & =-(\overline{x+iy}{)}^2{e}^{-(1^2)}\\ & =-e^{-1}{(x-iy)}^2\\ & =-e^{-1}(x^2-i2xy-y^2)\\ & =-e^{-1}(x^2-i2xy-(1-x^2))\\ & =e^{-1}(1-2x^2+i2xy).\end{array}$$

Dado que para ningún $z\in C(0,1)$ existe disco abierto, alrededor de dicho punto, donde $f$ sea diferenciable, entonces $f$ no es analítica en ningún punto en $\mathbb{C}$.

Ejemplo 20.5.
Determinemos dónde es analítica la función $f(z)=\sqrt{1+e^z}$ y obtengamos su derivada.

Solución. Recordemos que la función $F(w)=\sqrt{w}$ es multivaluada, por lo que si elegimos a la rama principal del argumento, es decir $-\pi <\mathrm{Arg}(w)\le \pi$ obtenemos a la rama principal de $F$, que de acuerdo con el ejemplo 16.5 sabemos que dicha rama es analítica en el dominio: $$D=\mathbb{C}\setminus (-\mathrm{\infty },0]=\mathbb{C}\setminus \{w\in \mathbb{C}:\mathrm{Re}(w)\le 0,\mathrm{Im}(w)=0\}.$$

Procedemos a determinar el corte de rama de la función $f$ restringida a la rama principal del argumento, es decir los puntos donde $f$ es discontinua, entonces para $w=1+e^z$ y $z=x+iy\in \mathbb{C}$ tenemos que: $$\{\begin{array}{l}\mathrm{Re}(1+e^z)=1+e^x\cos (y)\le 0,\\ \\ \mathrm{Im}(1+e^z)=e^x\mathrm{sen}(y)=0.\end{array}$$

Dado que para todo $x\in \mathbb{R}$ se cumple que $e^x>0$, entonces de la segunda condición se sigue que $y=k\pi$, con $k\in \mathbb{Z}$.

Notemos que si $k=2n$, con $n\in \mathbb{Z}$, entonces $\cos (2n\pi )=1$, por lo que de la primera condición se sigue que: $$1+e^x(1)\le 0⟺e^x\le -1,$$ lo cual claramente no es posible desde que $x\in \mathbb{R}$.

Entonces $k=2n+1$, con $n\in \mathbb{Z}$, por lo que de la primera condición se sigue que: $$1+e^x(-1)\le 0⟺-e^x\le -1⟺e^x\ge 1⟺x\ge 0.$$

Por lo que ambas condiciones se satisfacen si $z=x+i(2n+1)\pi$, con $x\ge 0$ y $k\in \mathbb{Z}$, es decir que $f$ es una función analítica en el dominio: $$A=\mathbb{C}\setminus \{z=x+iy\in \mathbb{C}:x\ge 0,y=(2n+1)\pi ,n\in \mathbb{Z}\}.$$

Por último, para determinar la derivada de $f$ en $A$ procedemos a utilizar la regla de la cadena.

Por el ejemplo 16.5, sabemos que la derivada de la rama principal de la función multivaluada $F(w)=\sqrt{w}$, es decir $f_0(w)=\sqrt{w}$ con $w\in \mathbb{C}\setminus (-\mathrm{\infty },0]$, es: $$f_0^{‘}(w)=\frac{1}{2\sqrt{w}}.$$

Notemos que $f=f_0\circ g$, con $g(z)=1+e^z$ una función entera, entonces por la regla de la cadena para $z\in A$ tenemos que: $$f^{\prime }(z)=f_0\prime (g(z))g^{\prime }(z)=\frac{e^z}{2\sqrt{1+e^z}}.$$

Proposición 20.2. (Propiedades exponencial.)
La función exponencial compleja satisface las siguientes propiedades:

1. $e^{z_1}\cdot e^{z_2}=e^{z_1+z_2}$, para todo $z_1,z_2\in \mathbb{C}$.
2. $e^0=1$.
3. ${\displaystyle \frac{e^{z_1}}{e^{z_2}}}=e^{z_1–z_2}$, para todo $z_1,z_2\in \mathbb{C}$. En particular $e^{-z}={\displaystyle \frac{1}{e^z}}$.
4. $|e^z|=e^x$ y $e^z\ne 0$, para todo $z=x+iy\in \mathbb{C}$.
5. $e^{i\theta }=\mathrm{cis}(\theta )=\cos (\theta )+i\mathrm{sen}(\theta )$, con $\theta \in \mathbb{R}$, fórmula de Euler.
6. Para todo $\theta \in \mathbb{R}$ se tiene que $|e^{i\theta }|=1$, en particular se cumple la identidad de Euler $e^{i\pi }=-1$ y $$e^{\pm i2\pi }=1,e^{i\frac{\pi }{2}}=i,e^{i\frac{3\pi }{2}}=-i.$$
7. ${\left(e^z\right)}^n=e^{nz}$, para todo $z\in \mathbb{C}$ y para todo $n\in \mathbb{Z}$.
8. $\overline{e^z}=e^{\bar{z}}$, para todo $z\in \mathbb{C}$.
9. $e^{z+i\pi }=–e^z$, para todo $z\in \mathbb{C}$.
10. $e^z=1$ si y solo si $z=i2k\pi$ para algún $k\in \mathbb{Z}$.

Demostración.

1. Sean $z_1,z_2\in \mathbb{C}$ tales que $z_1=x_1+i{y}_1$ y $z_2=x_2+i{y}_2$.
   Por definición tenemos que:$$\begin{array}{rl}{e}^{z_1}\cdot e^{z_1}& =e^{x_1}[\cos (y_1)+i\mathrm{sen}(y_1)]e^{x_2}[\cos (y_2)+i\mathrm{sen}(y_2)]\\ & =e^{x_1+x_2}([\cos (y_1)\cos (y_2)–\mathrm{sen}(y_1)\mathrm{sen}(y_2)]\\ & +i[\mathrm{sen}(y_1)\cos (y_2)+\mathrm{sen}(y_2)\cos (y_1)])\\ & =e^{x_1+x_2}[\cos (y_1+y_2)+i\mathrm{sen}(y_1+y_2)]\\ & =e^{z_1+z_2}\end{array}$$
2. Se deja como ejercicio al lector.
3. Se deja como ejercicio al lector.
4. Sea $z=x+iy\in \mathbb{C}$, entonces: $$\begin{array}{rl}|e^z|& =|e^x[\cos (y)+i\mathrm{sen}(y)]|\\ & =|e^x||\cos (y)+i\mathrm{sen}(y)|\\ & =e^x[{\cos }^2(y)+{\mathrm{sen}}^2(y)]\\ & =e^x.\end{array}$$ Dado que para todo $x\in \mathbb{R}$ se tiene que $e^x>0$, entonces: $$|e^z|=e^x\ne 0,$$ por lo que $e^z\ne 0$ para todo $z\in \mathbb{C}$.
5. Sea $z=iy$, con $y\in \mathbb{R}$, es decir $\mathrm{Re}(z)=x=0$, entonces: $$\begin{array}{rl}{e}^z=e^{0+iy}& =e^0[\cos (y)+i\mathrm{sen}(y)]\\ & =\cos (y)+i\mathrm{sen}(y).\end{array}$$
6. Por el inciso anterior sabemos que para $\theta \in \mathbb{R}$ se tiene que: $$e^{i\theta }=\cos (y)+i\mathrm{sen}(y),$$ por lo que: $$|e^{i\theta }{|}^2={\cos }^2(y)+{\mathrm{sen}}^2(y)=1,$$ de donde se sigue el resultado.
   Notemos que: $$e^{\pm i\pi }=\cos (\pm \pi )+i\mathrm{sen}(\pm \pi )=-1+i0=-1,$$ $$e^{\pm i2\pi }=\cos (\pm 2\pi )+i\mathrm{sen}(\pm 2\pi )=1+i0=1,$$ $$e^{i\frac{\pi }{2}}=\cos \left(\frac{\pi }{2}\right)+i\mathrm{sen}\left(\frac{\pi }{2}\right)=0+i(1)=i,$$ $$e^{i\frac{3\pi }{2}}=\cos \left(\frac{\pi }{2}\right)+i\mathrm{sen}\left(\frac{\pi }{2}\right)=0+i(-1)=-i.$$
7. Se deja como ejercicio al lector.
8. Se deja como ejercicio al lector.
9. Sea $z\in \mathbb{C}$, por (1) y (6) tenemos que: $$e^{z+i\pi }=e^z{e}^{i\pi }=–e^z.$$
10. $\Rightarrow )$
    Sea $z=x+iy\in \mathbb{C}$. Tenemos que: $$e^z=1⟺e^x\cos (y)+i{e}^x\mathrm{sen}(y)=1⟺\{\begin{array}{l}{e}^x\cos (y)=1\\ e^x\mathrm{sen}(y)=0.\end{array}$$ Dado que $e^x>0$ para todo $x\in \mathbb{R}$, entonces de la segunda ecuación tenemos que: $$\mathrm{sen}(y)=0⟺y=k\pi ,\text{para algún}k\in \mathbb{Z}.$$ Dado que $\cos (k\pi )=(-1{)}^k$, para $k\in \mathbb{Z}$, entonces: $$e^x\cos (k\pi )=1⟺e^x(-1{)}^k=1,$$ de donde $k=2n$, con $n\in \mathbb{Z}$. Por lo tanto, tenemos que $e^x=1$ si y solo si $x=0$. Entonces $z=x+iy=0+i2k\pi =i2k\pi$, para algún $k\in \mathbb{Z}$.
    
    $(\Leftarrow$
    Sea $z=i2k\pi$, con $k\in \mathbb{Z}$. Por (6) y (7) tenemos que: $$e^z=e^{i2k\pi }={\left(e^{i2\pi }\right)}^k={\left(1\right)}^k=1,$$ para todo $k\in \mathbb{Z}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 20.3.
De acuerdo con el ejercicio 2 de la entrada 15, notemos que la función compleja de variable real $f:\mathbb{R}\to \mathbb{C}$ dada por: $$f(\theta )=e^{i\theta }=\cos (\theta )+i\mathrm{sen}(\theta ),$$ es una función continua desde que las funciones $u(\theta )=\cos (\theta )$ y $v(\theta )=\mathrm{sen}(\theta )$ son continuas en $\mathbb{R}$.

Observación 20.4.
De la fórmula de Euler se sigue que, para $z\in \mathbb{C}$, podemos expresar a la función exponencial compleja como: $$f(z)=e^z=e^x[\cos (y)+i\mathrm{sen}(y)]=e^x{e}^{iy},$$ lo cual es consecuente con las propiedades de la exponencial compleja.

De esta última igualdad es claro que si $f(z)=e^z=w$, entonces: $$|w|=e^x,\arg w=y+2\pi k,k\in \mathbb{Z}.$$

Más aún, la fórmula de Euler resulta de mucha utilidad pues nos permite establecer una relación entre la forma polar de un número complejo $z\ne 0$ y la exponencial compleja, es decir: $$z=r\mathrm{cis}(\theta )=r{e}^{i\theta },$$ donde $r=|z|$ y $\theta =\arg z$.

Esta última expresión suele llamarse representación exponencial de un número complejo y nos permite aprovechar las propiedades de la exponencial compleja al trabajar con la forma polar de un número complejo, lo cual resulta de mucha utilidad pues simplifica muchos cálculos. Muestra de esto es que dada una función analítica, de acuerdo con la proposición 17.1, podemos obtener su derivada mediante las ecuaciones de C-R en su forma polar.

Ejemplo 20.6.
Sea $\theta \in \mathbb{R}$. Determinemos expresiones para $\mathrm{sen}(3\theta )$ y $\cos (3\theta )$ en términos de $\mathrm{sen}(\theta )$ y $\cos (\theta )$, respectivamente.

Solución. Notemos que: $$\begin{array}{rl}\cos (3\theta )+i\mathrm{sen}(3\theta )=e^{i3\theta }& ={\left(e^{i\theta }\right)}^3\\ & ={(\cos (\theta )+i\mathrm{sen}(\theta ))}^3\\ & ={\cos }^3(\theta )+i3{\cos }^2(\theta )\mathrm{sen}(\theta )-3\cos (\theta ){\mathrm{sen}}^2(\theta )-i{\mathrm{sen}}^3(\theta )\\ & ={\cos }^3(\theta )–3\cos (\theta ){\mathrm{sen}}^2(\theta )+i(3{\cos }^2(\theta )\mathrm{sen}(\theta )–{\mathrm{sen}}^3(\theta )).\end{array}$$

Igualando las partes real e imaginaria tenemos que: $$\begin{array}{rl}\cos (3\theta )& ={\cos }^3(\theta )–3\cos (\theta ){\mathrm{sen}}^2(\theta )\\ & ={\cos }^3(\theta )–3\cos (\theta )[1–{\cos }^2(\theta )]\\ & =4{\cos }^3(\theta )–3\cos (\theta ).\end{array}$$ $$\begin{array}{rl}\mathrm{sen}(3\theta )& =3{\cos }^2(\theta )\mathrm{sen}(\theta )–{\mathrm{sen}}^3(\theta )\\ & =3[1–{\mathrm{sen}}^2(\theta )]\mathrm{sen}(\theta )–{\mathrm{sen}}^3(\theta )\\ & =3\mathrm{sen}(\theta )-4{\mathrm{sen}}^3(\theta ).\end{array}$$

Ejemplo 20.7.
Sea $\alpha \in \mathbb{R}$ fijo y sea $I=(\alpha ,\alpha +2\pi ]$. Definimos: $$f(z)=\sqrt[3]{z}=\sqrt[3]{r}\exp \left(i\frac{\theta (z)}{3}\right),$$ con $z\in \mathbb{C}\setminus L_{\alpha }$, $r=|z|$ y $\theta (z)={\mathrm{Arg}}_I(z)$, donde $L_{\alpha }=\{r{e}^{i\alpha }:r\ge 0\}$.

Veamos que la función $f$ corresponde con una rama de la función multivaluada $F(z)=z^{1/3}$. Determinemos dónde es analítica $f$ y obtengamos su derivada.

Solución. Sabemos que el conjunto $L_{\alpha }$ corresponde con la semirrecta que parte del origen y que forma un ángulo $\alpha$ con el semieje real positivo, figura 77.

De acuerdo con la observación 15.4, sabemos que la función $\theta (z)={\mathrm{Arg}}_I(z)$ es continua en el dominio: $$D=\mathbb{C}\setminus L\alpha =\{z\in \mathbb{C}:|z|>0,\alpha <\arg z<\alpha +2\pi \},$$ por lo que la función $f(z)$ es continua en el mismo dominio, es decir para $z\in D$ tenemos que $f$ determina una rama de la función multivaluada $F(z)=z^{1/3}$.

Sea $z\in D$ dado por $z=r{e}^{i\theta }$, con $r=|z|$ y $\theta ={\mathrm{Arg}}_I(z)$ tal que $\alpha <\theta <\alpha +2\pi$, entonces: $$f(z)=\sqrt[3]{r}{e}^{i\frac{\theta }{3}}=\sqrt[3]{r}\cos \left(\frac{\theta }{3}\right)+i\sqrt[3]{r}\cos \left(\frac{\theta }{3}\right),$$ de donde:

$$u(r,\theta )=\sqrt[3]{r}\cos \left(\frac{\theta }{3}\right),v(r,\theta )=\sqrt[3]{r}\mathrm{sen}\left(\frac{\theta }{3}\right).$$

Es claro que para todo $z\in D$ existen y son continuas las derivadas parciales: $$\begin{array}{r}{u}_r(r,\theta )=\frac{\cos \left(\frac{\theta }{3}\right)}{3r^{2/3}},u_{\theta }(r,\theta )=-\frac{r^{1/3}}{3}\mathrm{sen}\left(\frac{\theta }{3}\right),\\ v_r(r,\theta )=\frac{\mathrm{sen}\left(\frac{\theta }{3}\right)}{3r^{2/3}},v_{\theta }(r,\theta )=\frac{r^{1/3}}{3}\cos \left(\frac{\theta }{3}\right).\end{array}$$

Notemos que para todo $z\in D$ se cumple que: $$\begin{array}{r}{u}_r(r,\theta )=\frac{\cos \left(\frac{\theta }{3}\right)}{3r^{2/3}}=\frac{1}{r}{v}_{\theta }(r,\theta ),\\ v_r(r,\theta )=\frac{\mathrm{sen}\left(\frac{\theta }{3}\right)}{3r^{2/3}}=-\frac{1}{r}{u}_{\theta }(r,\theta ),\end{array}$$ es decir que se satisfacen las ecuaciones de C-R en su forma polar en $D$, por lo que, de acuerdo con los ejercicios 1 y 2 de la entrada 17 y el teorema 18.1, tenemos que $f$ es una función analítica en $D$. Más aún, por la proposición 17.1 tenemos que la derivada de $f$ está dada por: $$\begin{array}{rl}{f}^{\prime }(z)& =e^{-i\theta }[u_r(r,\theta )+i{v}_r(r,\theta )]\\ & =e^{-i\theta }[\frac{\cos \left(\frac{\theta }{3}\right)}{3r^{2/3}}+i\frac{\mathrm{sen}\left(\frac{\theta }{3}\right)}{3r^{2/3}}]\\ & =\frac{1}{3r^{2/3}}{e}^{-i\theta }{e}^{i\frac{\theta }{3}}\\ & =\frac{1}{3r^{2/3}{e}^{i2/3\theta }}\\ & =\frac{1}{3{\left(\sqrt[3]{r}{e}^{i\frac{\theta }{3}}\right)}^2}\\ & =\frac{1}{3z^{2/3}},\end{array}$$ para todo $z\in D$.

Definición 20.2. (Función periódica.)
Sea $f:S\subset \mathbb{C}\to \mathbb{C}$ una función. Diremos que $f$ es una función periódica con período $T$ si para todo $z\in S$ se tiene que: $$f(z+T)=f(z).$$

Observación 20.5.
Una diferencia importante entre la función exponencial real y la exponencial compleja es que la exponencial compleja es periódica. Este hecho se justifica en que la exponencial compleja está definida en términos de las funciones reales trigonométricas seno y coseno, las cuales son periódicas.

Proposición 20.3. (Periodicidad de la función exponencial.)
La función exponencial compleja, $f(z)=e^z$, es periódica con periodo imaginario $2\pi i$. En consecuencia la exponencial compleja no es una función inyectiva. Además es una función suprayectiva en $\mathbb{C}\setminus \{0\}$.

Demostración. Sea $z\in \mathbb{C}$. De acuerdo con la proposición 20.2 tenemos que:
$$\begin{array}{rl}f(z+2\pi i)& =e^{z+2\pi i}\\ & =e^z{e}^{2\pi i}\\ & =e^z\\ & =f(z).\end{array}$$

Dado que $z+2\pi i\ne z$ para todo $z\in \mathbb{C}$, entonces la exponencial compleja no es una función inyectiva.

Por último, veamos que $f(z)=e^z$ es una función suprayectiva en $\mathbb{C}\setminus \{0\}$. Sea $w\in \mathbb{C}\setminus \{0\}$ tal que: $$w=r_0\mathrm{cis}({\theta }_0)=r_0{e}^{i{\theta }_0},$$ donde $r_0=|w|>0$ y ${\theta }_0=\mathrm{Arg}w$, es decir ${\theta }_0\in (-\pi ,\pi ]$.

Queremos ver que existe $z=x+iy\in \mathbb{C}$ tal que $e^z=w$. Sea $z=\ln (r_0)+i({\theta }_0)$, tenemos que: $$e^z=e^{\ln (r_0)}{e}^{i{\theta }_0}=r_0{e}^{i{\theta }_0}=w,$$ donde $\ln (x)$ corresponde con la función real logaritmo natural.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 20.2.
Sean $z_1,z_2\in \mathbb{C}$, entonces $e^{z_1}=e^{z_2}$ si y solo si $z_2=z_1+i2\pi n$ para algún entero $n$.

Demostración. Sean $z_1,z_2\in \mathbb{C}$.

$\Rightarrow )$
Supongamos que $e^{z_1}=e^{z_2}$. Considerando las propiedades de la exponencial, lo anterior implica que: $$\frac{e^{z_2}}{e^{z_1}}=e^{z_2}{e}^{-z_1}=e^{z_2-z_1}=1.$$

Entonces, de acuerdo con la proposición 20.2(10), tenemos que $z_2–z_1=i2\pi n$ para algún $n\in \mathbb{Z}$, de donde se sigue el resultado.

$(\Leftarrow$
Supongamos que $z_2=z_1+i2\pi n$, para algún $n\in \mathbb{Z}$, entonces: $$e^{z_2}=e^{z_1+i2\pi n}=e^{z_1}{e}^{i2\pi n}=e^{z_1}.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Debido a la periodicidad de la función exponencial compleja, $f(z)=e^z$, tenemos que:
$$f(z)=e^z=e^{z+i2\pi }=e^{(z+i2\pi )+i2\pi }=f(z+i4\pi ).$$

Procediendo de manera similar podemos concluir que: $$f(z)=e^z=e^{z+i2\pi n}=f(z+i2\pi n),n\in \mathbb{Z},$$ es decir que $\pm i2\pi ,\pm i4\pi ,\pm i6\pi ,\dots$, son también periodos de la función exponencial compleja.

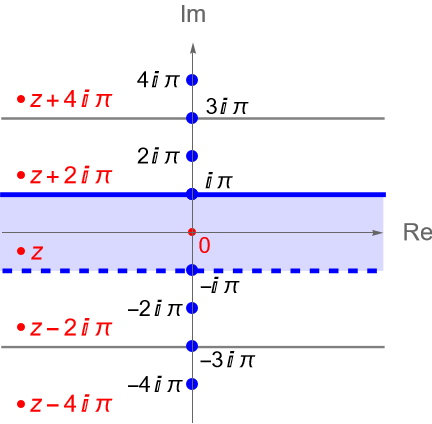
Más aún, dado que $f$ no es inyectiva, tenemos que si $z\in \mathbb{C}$ es tal que $f(z)=w$, es decir si $z$ se mapea bajo $f$ en un punto $w$, entonces bajo $f$ los puntos $z\pm i2\pi ,z\pm i4\pi ,z\pm i6\pi ,\dots$, también serán mapeados al punto $w$. Por lo que, podemos restringir los valores de $z$ que toma $f$ a una banda horizontal infinita de ancho $2\pi$ en el plano complejo $z$, figura 78, para garantizar que los valores $w$ que asigna $f$ sean distintos. Es decir, para $y_0\in \mathbb{R}$ fijo, todos los valores $w$ distintos que toma la función exponencial compleja $f$, estarán dados por los $z$ en la banda: $$S_{y_0}=\{z=x+iy\in \mathbb{C}:-\mathrm{\infty }<x<\mathrm{\infty },y_0<y\le y_0+2\pi \}.$$

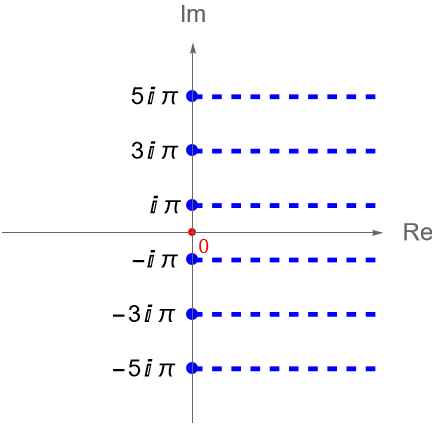
En la figura 78 hemos divido el plano complejo en bandas horizontales, de ancho $2\pi$, fijando el valor de $y_0$ a múltiplos impares de $\pi$. En general, podemos dividir el plano complejo en bandas horizontales infinitas, de ancho $2\pi$, considerando solo múltiplos de impares de $\pi$, es decir, para $n\in \mathbb{Z}$ definimos a las bandas: $$S_n=\{z=x+iy\in \mathbb{C}:-\mathrm{\infty }<x<\mathrm{\infty },(2n-1)\pi <y\le (2n+1)\pi \}.$$

En cualquiera de estas bandas la función exponencial compleja tendrá el mismo comportamiento.

Si tomamos $y_0=-\pi \in \mathbb{R}$ ó $n=0$, entonces obtenemos la banda: $$S_0=\{z\in \mathbb{C}:-\mathrm{\infty }<\mathrm{Re}(z)<\mathrm{\infty },-\pi <\mathrm{Im}(z)\le \pi \},$$ a la cual llamaremos la región fundamental de la función exponencial compleja y se representa en color azul en la figura 78.

Proposición 20.4.
La función exponencial compleja es inyectiva si se restringe su dominio a la región fundamental.

Demostración. Sea $f(z)=e^z$ definida sobre el dominio $S_0$ y sean $z_1=x_1+i{y}_1,z_2=x_2+i{y}_2\in S_0$.

Supongamos que $e^{z_1}=e^{z_2}$, entonces: $$\begin{array}{}\text{(20.2)}& |e^{z_1}|=|e^{z_2}|,\arg \left(e^{z_1}\right)=\arg \left(e^{z_2}\right).\end{array}$$

De acuerdo con la observación 20.4, de (20.2) tenemos que: $$\begin{array}{}\text{(20.3)}& e^{x_1}=e^{x_2},y_2=y_1+2\pi n,n\in \mathbb{Z}.\end{array}$$

Como $z_1,z_2\in S_0$, entonces $x_1,x_2\in \mathbb{R}$ y $y_1,y_2\in (-\pi ,\pi ]$. Por lo que, se sigue de (20.3) que $x_1=x_2$ y $y_1=y_2$, de donde $z_1=z_2$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 20.8.
Determinemos las soluciones de la ecuación $e^z=i$.

Solución. Sea $z=x+iy\in \mathbb{C}$. Por la observación 20.4 y la proposición 20.2(6) tenemos que: $$\begin{array}{rl}{e}^z=i⟺e^x{e}^{iy}=1e^{i\frac{\pi }{2}}& ⟺\{\begin{array}{c}|e^z|=|i|,\\ \arg \left(e^z\right)=\arg \left(i\right).\end{array}\\ & ⟺\{\begin{array}{c}{e}^x=1,\\ y+2\pi n_1={\displaystyle \frac{\pi }{2}}+2\pi n_2,n_1,n_2\in \mathbb{Z}.\end{array}\end{array}$$

De la primera ecuación es claro que $x=0$. Por otra parte, de la segunda ecuación tenemos que: $$y={\displaystyle \frac{\pi }{2}}+2\pi \left(n_2–n_1\right)={\displaystyle \frac{\pi }{2}}(4k+1),k=n_2–n_1\in \mathbb{Z}.$$

Por lo que, las soluciones de la ecuación $e^z=i$ son:
$$z=x+iy=0+i(4k+1)\frac{\pi }{2}=i\frac{\pi }{2}+2k\pi i,k\in \mathbb{Z}.$$

Es interesante notar que todas las soluciones difieren por $2k\pi i$, con $k\in \mathbb{Z}$.

Observación 20.6 (Condición función univaluada.)
Notemos que a través de la representación exponencial de un número complejo podemos caracterizar a las funciones multivaluadas y univaluadas.

Sea $z\in \mathbb{C}\setminus \{0\}$, escribiendo a $z$ en su representación exponencial tenemos: $$z=z(r,\theta )=r{e}^{i\theta },$$ donde $r=|z|$ y $\theta =\mathrm{Arg}z\in (-\pi ,\pi ]$.

Si aumentamos de $\theta$ a $\theta +2\pi$, entonces: $$\begin{array}{rl}z(r,\theta +2\pi )& =r{e}^{i(\theta +2\pi )}\\ & =r{e}^{i\theta }{e}^{i2\pi }\\ & =r{e}^{i\theta }\\ & =z(r,\theta ),\end{array}$$ es decir, al aumentar el argumento principal de $z$ en $2\pi$ tenemos que $z$ regresa a su valor original.

Definición 20.3. (Funciones univaluadas y multivaluadas.)
Diremos que una función compleja $f$ es una función univaluada si $f$ es tal que: $$\begin{array}{rl}f(z)& =f(z(r,\theta ))\\ & =f(z(r,\theta +2\pi )),\end{array}$$ para todo $z$ en el dominio de $f$. Si $f$ no es univaluada, entonces diremos que $f$ es una función multivaluada.

Ejemplo 20.9.
Sea $f(z)=z^n$, con $z\in \mathbb{C}$, tenemos que:

a) Si $n\in \mathbb{Z}$, entonces $f$ es simple.
Solución. Sabemos que para todo $n\in \mathbb{Z}$ se cumple que: $$e^{i2\pi n}=1.$$ Considerando a $z$ en su representación exponencial, observación 20.4, tenemos que: $$\begin{array}{rl}f(z(r,\theta +2\pi ))& ={\left[r{e}^{i(\theta +2\pi )}\right]}^n\\ & =r^n{e}^{in(\theta +2\pi )}\\ & =r^n{e}^{in\theta }{e}^{i2\pi n}\\ & =r^n{e}^{in\theta }\\ & ={\left[r{e}^{i\theta }\right]}^n\\ & =f(z(r,\theta )).\end{array}$$

b) Si $n\notin \mathbb{Z}$, entonces $f$ es multivaluada.
Solución. Dado que $e^{i2\pi n}\ne 1$ para $n\notin \mathbb{Z}$, entonces: $$f(z(r,\theta ))\ne f(z(r,\theta +2\pi )),$$ por lo que, en tal caso, $f$ es una función multivaluada.

Tarea moral

1. Completa la demostración de la proposición 20.1.
2. Determina las funciones $u(x,y)$ y $v(x,y)$, correspondientes con la parte real e imaginaria, de las siguientes funciones y en cada caso expresa a $f$ como $f(z)=u(x,y)+iv(x,y)$.
   a) $f(z)=e^{2\bar{z}+1}$.
   b) $f(z)=e^{1/z}$.
   c) $f(z)=z^2{e}^{z+i}$.
   d) $f(z)=\overline{i{e}^z+1}$.
3. Para cada una de las siguientes funciones determina su dominio de analicidad y encuentra su derivada.
   a) $f(z)={\displaystyle \frac{3e^{2z}–i{e}^{-z}}{z^3-1+i}}$.
   b) $f(z)=i{e}^{1/z}$.
   c) $f(z)={\displaystyle \frac{e^z-1}{e^z+1}}$.
   d) $f(z)=e^{\bar{z}}$.
   e) $f(z)=e^{2\bar{z}+1}$.
   f) $f(z)=e^{z^2}$.
4. Determina todas las soluciones para las siguientes ecuaciones.
   a) $e^z=1+i\sqrt{3}$.
   b) $e^{1/z}=-1$.
   c) $e^{2z}=1+i$.
   d) $(1-i)e^z=1+i$.
5. Considera los siguientes planteamientos, en cada caso da una prueba o un contraejemplo.
   a) Sabemos que la función exponencial real es una función creciente, es decir si $x_1<x_2$ entonces $e^{x_1}<e^{x_2}$. Considera la función exponencial compleja, ¿si $|z_1|<|z_2|$ entonces $|e^{z_1}|<|e^{z_2}|$?
   b) Sabemos que la función exponencial real siempre es positiva, es decir si $x\in \mathbb{R}$ entonces $e^x>0$. Considera la función exponencial compleja, ¿siempre es positiva o existe $z\in \mathbb{C}$ tal que $e^z<0$?
6. Muestra que para todo $z=x+iy\in \mathbb{C}$ se cumple que:
   a)] $|e^z|\le 1$ si y solo si $\mathrm{Re}(z)\le 0$. ¿Para qué valores se da la igualdad?
   b) $|e^z|\le e^{|z|}$ si y solo si $\mathrm{Re}(z)\le 0$. ¿Para qué valores se da la igualdad?
   c) $|1+e^z|\le 1+e^x$.
   d) Determina para qué valores se cumple la igualdad en $|e^{-iz}|\le 1$.
7. Supón que $f(z)=f(x+iy)=R{e}^{i\varphi }$ es una función analítica. Muestra que: $$\frac{\partial R}{\partial x}=R\frac{\partial \varphi }{\partial y}.$$ Toma $a,b\in \mathbb{R}$ constantes y $z=r{e}^{i\theta }$, con $r=|z|$ y $\theta =\arg z$. Considera a los dominios: $$\begin{array}{r}{D}_a=\{z\in \mathbb{C}:a<|z|<1\},D_b=\{z\in \mathbb{C}:b<|z|<1\}.\end{array}$$ Define la función $f:D_a\to D_b$ dada por: $$f\left(r{e}^{i\theta }\right)=[\left(\frac{1-b}{1-a}\right)r+\frac{b-a}{1-a}]e^{i\theta }.$$ Muestra que $f$ es una función biyectiva y prueba que $f$ es analítica si y solo si $a=b$.
8. Verifica que la función: $$f(z)=\{\begin{array}{lcc}{e}^{-1/z^4}& \text{si}& z\ne 0,\\ 0& \text{si}& z\ne 0,\end{array}$$ satisface las ecuaciones de C-R en todo punto del plano complejo $\mathbb{C}$, pero que la función no es analítica en todo $\mathbb{C}$. ¿Cuál es su dominio de analicidad? Donde exista, obtén su derivada.
   Hint: Estudia la continuidad de $f$ en $z=0$.
9. Escribe cada una de las siguientes expresiones considerando su representación exponencial, es decir, en la forma $e^{i\alpha }$, con $\alpha \in \mathbb{R}$.
   a) ${\displaystyle \frac{\cos (\theta )–i\mathrm{sen}(\theta )}{\cos (3\theta )+i\mathrm{sen}(3\theta )}}$.
   b) ${\left({\displaystyle \frac{1}{\cos (\theta )–i\mathrm{sen}(\theta )}}\right)}^8$.
   c) ${\displaystyle \frac{1}{{(\frac{\sqrt{2}}{2}\cos (\theta )–i\frac{\sqrt{2}}{2}\mathrm{sen}(\theta ))}^3}}$.
   d) $[\cos (\theta )+i\mathrm{sen}(\theta )][\cos (2\theta )–i\mathrm{sen}(2\theta )]$.
10. Muestra que: $$\begin{array}{rl}\cos (\theta +\beta +\alpha )& =\cos (\theta )\cos (\beta )\cos (\alpha )–\cos (\theta )\mathrm{sen}(\beta )\mathrm{sen}(\alpha )\\ & –\cos (\beta )\mathrm{sen}(\theta )\mathrm{sen}(\alpha )–\cos (\alpha )\mathrm{sen}(\theta )\mathrm{sen}(\alpha ).\end{array}$$ Determina una expresión similar para $\mathrm{sen}(\theta +\beta +\alpha )$.

Más adelante…

En esta entrada hemos definido la función exponencial compleja, de tal modo que garantizamos que sea una función entera. A través de esta función hemos extendido a la exponencial real y algunas de sus propiedades.

Es importante recordar que esta nueva función tiene propiedades muy particulares que no se cumplen en su versión real, algunas de ellas son que la exponencial compleja puede tomar valores reales negativos y que es una función
periódica. Este último hecho nos llevo a concluir que la función exponencial compleja no es inyectiva, aunque podemos garantizar esta propiedad al restringir el dominio de dicha función a una banda horizontal infinita de ancho $2\pi$.

La función exponencial compleja juega un papel fundamental en el estudio de las funciones complejas, pues además de ser una función elemental, podemos definir al resto de las funciones complejas elementales en términos de la exponencial compleja, hecho que veremos en las siguientes entradas.

La siguiente entrada definiremos al logaritmo complejo, motivados en determinar una solución a la ecuación $e^w=z$, que como veremos nos llevará a concluir que el logaritmo complejo, es decir la solución a esta ecuación, será una función multivaluada. Veremos que a través del concepto de rama podremos definir una función univaluada que corresponda con una de las inversas de la función exponencial compleja y que nos permita caracterizar a la función logaritmo complejo.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Consecuencias de las ecuaciones de Cauchy-Riemann.
• Siguiente entrada del curso: Logaritmo complejo y potencias complejas.