Archivo de la etiqueta: diferenciabilidad

Cálculo Diferencial e Integral III: Divergencia, laplaciano y rotacional

Por Alejandro Antonio Estrada Franco

2 respuestas

Introducción

Después de algunas entradas muy técnicas, en las que hemos demostrado dos resultados sumamente importantes (el teorema de la función inversa y el teorema de la función implícita), pasaremos brevemente a una entrada un poco más ligera en términos de teoría, pero también relevante. En esta entrada nos volcaremos a una cara más práctica del cálculo diferencial e integral.

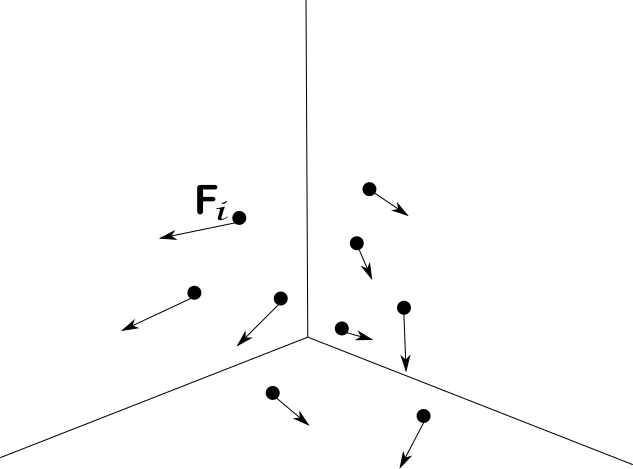
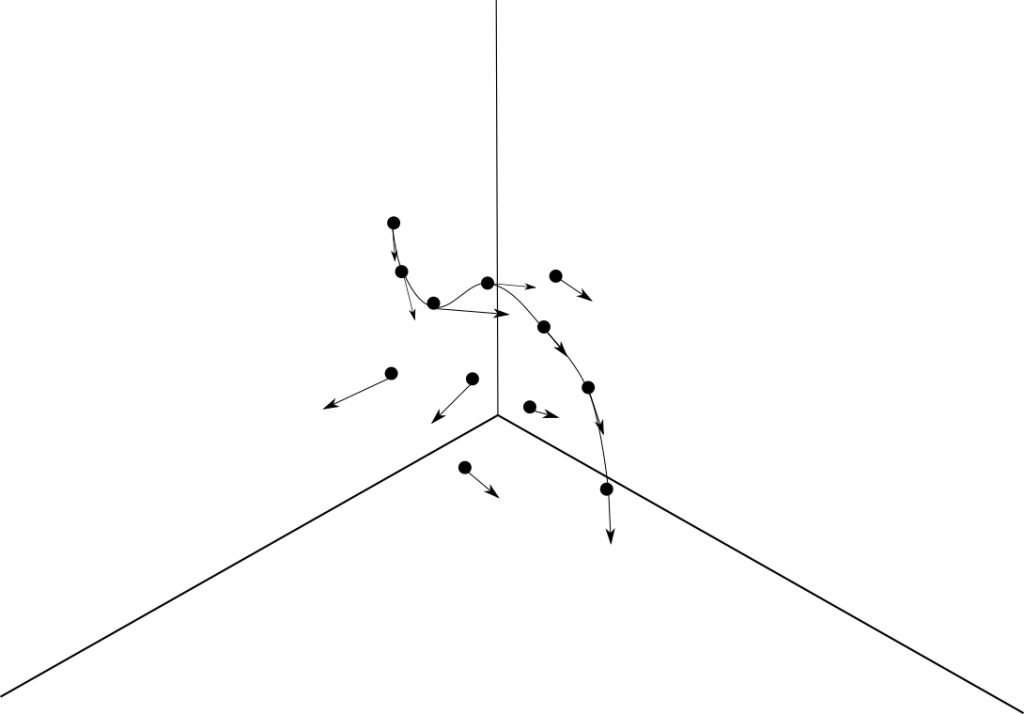
Recordemos que un campo vectorial es una función $F:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$. El nombre de campo vectorial está justificado con que a cada punto de un espacio base $\mathbb{R}^n$, estamos asignando otro vector, en $\mathbb{R}^m$. Si pegamos a cada vector del dominio el vector que le corresponde en a partir de $F$, podemos tener otra intuición geométrica de lo que hacen estas funciones. En la figura 1 apreciamos un ejemplo de esto, donde tenemos un campo vectorial $F$ de $\mathbb{R}^{3}$ en $\mathbb{R}^{3}$ y entonces a cada vector de $\mathbb{R}^3$ le estamos «pegando una flecha».

Figura 1

Esta manera de pensar a los campos vectoriales se presta mucho para entender propiedades físicas de los objetos: flujo eléctrico, flujo de calor, fuerza, trabajo, etc. Si pensamos en esto, otros conceptos que hemos estudiado también comienzan a tener significado. Por ejemplo, el gradiente de un campo escalar está íntimamente relacionado a otras propiedades físicas descritas por el campo escalar. Un ejemplo que hemos discutido es que el gradiente, por ejemplo, nos da la dirección de cambio máximo.

Un ejemplo más concreto sería el siguiente. Pensemos en $\mathbb{R}^{3}$ en un sólido $S$ y un campo escalar $T:S\rightarrow \mathbb{R}$ que da la temperatura de cada punto del sólido. Si consideramos la expresión $\textbf{J}=-k\triangledown T$, obtenemos lo que se conoce como el flujo de calor. Tiene sentido. Por lo que aprendemos en educación elemental, el calor va de los puntos de mayor temperatura a los de menor temperatura. El gradiente $\triangledown T$ da la dirección de máximo crecimiento. Pero entonces $-\triangledown T$ da la dirección de máximo descenso (así como su magnitud). La $k$ que aparece tiene que ver con qué tan bien el material del que hablamos transmite el calor.

Notación tradicional de los campos vectoriales

En el ámbito de las aplicaciones generalmente se usa la notación con gorros. Veamos un ejemplo de cómo escribir con esta notación. En vez de escribir para $\bar{v}\in \mathbb{R}^{3}$ la expresión $\bar{v}=(x,y,z)$, escribimos $$\bar{v}=x\hat{\imath}+y\hat{\jmath}+z\hat{k},$$ es decir, podemos pensar que $\hat{\imath}=(1,0,0)$, $\hat{\jmath}=(0,1,0)$, $\hat{k}=(0,0,1)$.

Si $F:\mathbb{R}^3\to \mathbb{R}^3$ es un campo vectorial, escribimos $$F=P\hat{\imath}+Q\hat{\jmath}+R\hat{k},$$ donde $P$, $Q$ y $R$ son los campos escalares componente, que cada uno de ellos va de $\mathbb{R}^3$ a $\mathbb{R}$.

Generalmente escribimos también $$F(x,y,z)=P(x,y,z)\hat{\imath}+Q(x,y,z)\hat{\jmath}+R(x,y,z)\hat{k}$$ tras evaluar.

Con esta notación también podemos escribir al gradiente y pensarlo como un «operador» que manda campos escalares a campos vectoriales. A este operador se le llama operador nabla. Lo escribimos de la siguiente manera:

\[ \triangledown =\frac{\partial}{\partial x}\hat{\imath}+\frac{\partial}{\partial y}\hat{\jmath}+\frac{\partial}{\partial z}\hat{k}. \]

Si tenemos un campo escalar $\phi:\mathbb{R}^3\to \mathbb{R}$, entonces el operador hace lo siguiente

\[ \triangledown \phi (x,y,z)=\frac{\partial \phi (x,y,z)}{\partial x}\hat{\imath}+\frac{\partial \phi (x,y,z)}{\partial y}\hat{\jmath}+\frac{\partial \phi (x,y,z)}{\partial z}\hat{k}.\]

Es decir, a partir de $\phi$ obtenemos su gradiente.

Líneas de flujo

Ahora introducimos el concepto de línea de flujo el cual es muy usado para campos vectoriales en el modelado fenómenos físicos.

Definición. Si $F:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es un campo vectorial, una línea de flujo para $F$ es una función $\alpha :U\subseteq \mathbb{R}\rightarrow \mathbb{R}^{n}$ tal que $\alpha^{\prime}(t)=F(\alpha(t))$ para todo $t\in U$.

Es decir una línea de flujo es una trayectoria sobre la cual $F$ asigna en cada punto de ella su correspondiente vector tangente. En la Figura 2 tenemos una ilustración de una línea de flujo en un campo vectorial.

Figura 2

Divergencia

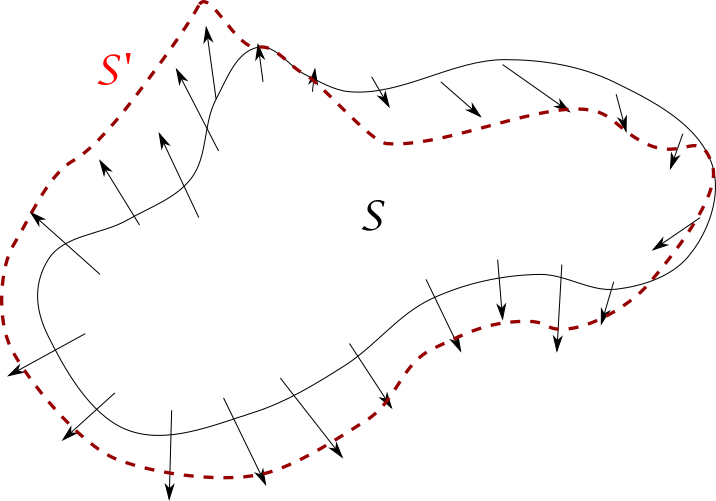
Supongamos que tenemos en el plano (o el espacio) una región $S$. Para cada punto $\bar{x}$ de $S$ sea $\textbf{x}(t)$ una línea de flujo que parte de $\bar{x}$ bajo el campo vectorial $F$. El conjunto de líneas $\textbf{x}(t)$ describe cómo cambia el conjunto $S$ bajo la acción de $F$ a través del tiempo. Formalizando esto un poco, en el caso del plano tomemos $F:S\subseteq \mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$. Para cada $\bar{x}\in S$ podemos considerar $\gamma_x:I_{x}\subset \mathbb{R}\rightarrow \mathbb{R}^{2}$, como la trayectoria $\textbf{x}(t)$ y que es línea de flujo bajo $F$. Estas trayectorias van mostrando «cómo se va deformando $S$ a causa del campo vectorial $F$». También, consideremos al conjunto $S’=\{\bar{x}+F(\bar{x})|\bar{x}\in S \}$, al cual pensaremos como el conjunto resultante de aplicar a $S$ el campo vectorial $F$.

Estas nociones se pueden analizar a través de una herramienta llamada divergencia. La definimos a continuación, pero una demostración formal de que el operador divergencia mide la expansión del efecto de un campo vectorial es un tema que se estudia en un cuarto curso de cálculo diferencial e integral.

Figura 3. Aquí se ilustra el efecto de un campo vectorial sobre una sección $S$ del plano.

Damos la definición en $\mathbb{R}^3$, pero podrías dar una versión análoga para $\mathbb{R}^2$.

Definición. Si $F=P\hat{\imath}+Q\hat{\jmath}+R\hat{k}$ es un campo vectorial definimos la divergencia de $F$ como:

\[ \triangledown \cdot F=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}.\]

En dimensiones más altas, si $F=(F_{1},\dots ,F_{n})$, entonces $\triangledown \cdot F=\sum_{i=1}^{n}\frac{\partial F_{i}}{\partial x_{i}}$.

Rotacional

Figura 4

Pensemos en un fluido que se mueve de acuerdo con el flujo marcado por el campo vectorial $F$. Tenemos una forma de determinar la rotación que el fluido imprimiría sobre un sólido llevado por él. Imaginemos un remolino y una pequeña esfera solida llevada por el remolino. Lo que llamaremos el rotacional del vector nos proporcionará la información sobre las rotaciones sobre su eje que el fluido imprime a la pequeña esfera (Figura 4).

Definición. Sea $$F(x,y,z)=F_{1}(x,y,z)\hat{\imath}+F_{2}(x,y,z)\hat{\jmath}+F_{3}(x,y,z)\hat{k}.$$ Entonces definimos al rotacional de $F$ como el siguiente campo vectorial:

\[ \triangledown \times F(x,y,z)=\left( \frac{\partial F_{3}}{\partial y} – \frac{\partial F_{2}}{\partial z} \right)\hat{\imath}+\left( \frac{\partial F_{1}}{\partial z}-\frac{\partial F_{3}}{\partial x} \right)\hat{\jmath}+\left( \frac{\partial F_{2}}{\partial x}-\frac{\partial F_{1}}{\partial y} \right)\hat{k}.\]

También suele representarse por el siguiente determinante:

\[ \triangledown \times F=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ {\large \frac{\partial}{\partial x}} & {\large \frac{\partial}{\partial y}} & {\large \frac{\partial}{\partial z}} \\ F_{1} & F_{2} & F_{3} \end{vmatrix}. \]

Una visión mas clara de por qué esta expresión calcula lo que queremos se puede aprender en un cuarto curso de cálculo diferencial e integral, o bien en algún curso de aplicaciones del cálculo a la física. Por ahora veremos en los ejemplos solamente la parte operativa.

Laplaciano

Hay un operador más que surge naturalmente en las ecuaciones que involucran al gradiente y a la divergencia.

Definición. Sea $f:\mathbb{R}^3\to \mathbb{R}$ un campo escalar. El operador laplaciano se establece de la siguiente manera:

\[ \triangledown ^{2}f=\frac{\partial ^{2}f}{\partial x^{2}}\hat{\imath}+\frac{ \partial^{2}f}{\partial y^{2}}\hat{\jmath}+\frac{\partial ^{2}f}{\partial z^{2}}\hat{k}. \]

Es decir, el laplaciano consiste en aplicar el operador divergencia al gradiente de un campo escalar.

Ejemplos de problemas de los conceptos anteriores

Revisemos algunos problemas que tienen que ver con estos operadores. Esto nos permitirá ampliar nuestra visión en cuanto a la practicidad de esta herramienta matemática.

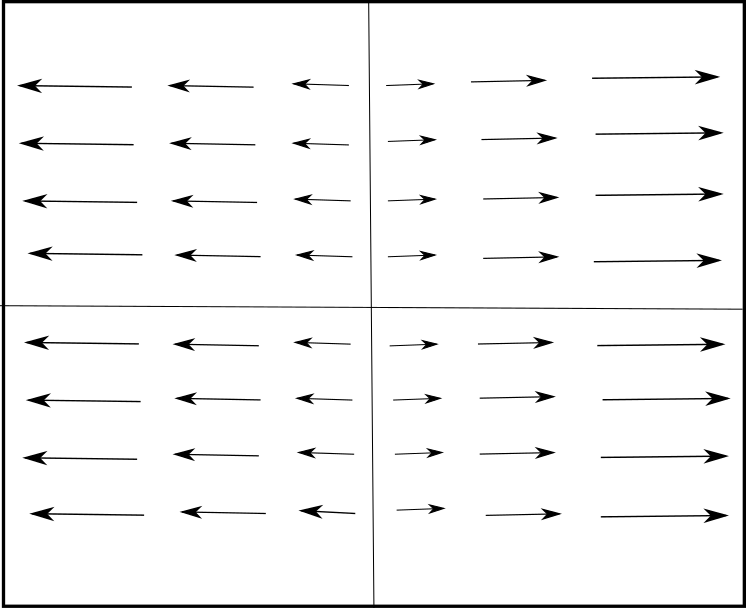
Consideremos el siguiente campo vectorial en el plano $F(x,y)=x\hat{\imath}$. Pensaremos el signo de la divergencia de $F$ como la razón del cambio de áreas bajo este campo. Interpretaremos a $F$ como aquel que asigna a cada punto del plano un vector velocidad de un fluido en el plano.

Para $x>0$ el campo apunta hacia la derecha con vectores paralelos al eje $x$ con tamaño $|x|$, para $x<0$ los vectores apuntan a la izquierda paralelamente al eje $x$ con tamaño $|x|$ (Figura 5). Por ello las longitudes de las flechas de $F$ son mas cortas en torno al origen; así cuando el fluido se mueve, se expande. Y esto coincide con el hecho de que $\triangledown \cdot F=1$.

Figura 5

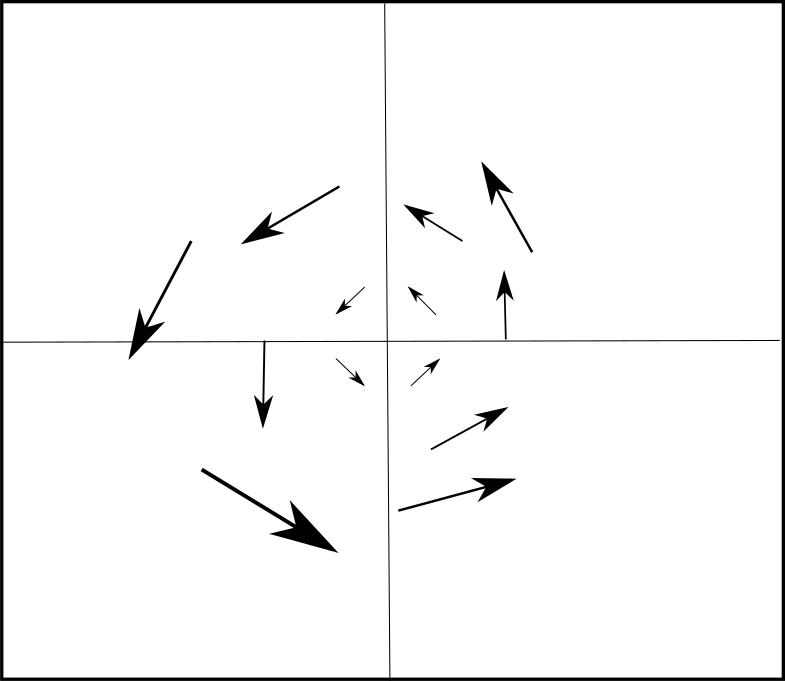
En el siguiente ejemplo consideremos el campo vectorial $F(x,y)=-y\hat{\imath}+x\hat{\jmath}$. Las líneas de flujo de $F$ siguen circunferencias concéntricas centradas al origen en dirección contrarias a las manecillas del reloj. Al calcular la divergencia tenemos lo siguiente:

\[ \triangledown \cdot F=\frac{\partial }{\partial x}(-y)+\frac{\partial}{\partial y}(x)=0. \]

En la figura 6 tenemos la ilustración de cómo se ve el campo de este ejemplo. Suena razonable. En este caso el fluido no se está expandiendo, sino que más bien está rotando.

Figura 6

En el laplaciano aplicamos la divergencia a un gradiente. Pero, ¿qué pasa cuando aplicamos el rotacional a un gradiente? Consideremos una función $f$ con derivadas parciales diferenciables continuas es decir, de clase $C^{2}$. Para una función así tenemos

\[ \triangledown f(x,y,z)=(\partial f/\partial x,\partial f/ \partial y,\partial f/\partial z). \]

De acuerdo con la definición de rotacional, tenemos:

\begin{align*} \triangledown \times (\triangledown f)&= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & \frac{\partial f}{\partial z} \end{vmatrix}\\ &= \left( \frac{\partial ^{2}f}{\partial y\partial z}-\frac{\partial ^{2}f}{\partial z\partial y} \right)\hat{\imath}+\left( \frac{\partial ^{2}f}{\partial z\partial x}-\frac{\partial ^{2}f}{\partial x \partial z} \right)\hat{\jmath}+\left( \frac{\partial ^{2}f}{\partial x\partial y}-\frac{\partial ^{2}f}{\partial y\partial x} \right)\hat{k}\\ &=\bar{0} \end{align*}

por la igualdad de las parciales mixtas. Es decir; si $f$ es un campo escalar cuyas derivadas parciales son diferenciables con derivada continua tenemos $\triangledown \times \triangledown f=0$.

Esto nos puede ayudar a saber si una cierta función puede obtenerse como gradiente de otra. Tomemos $G(x,y,z)= y\hat{\imath}-x\hat{\jmath}$. Notemos que las funciones en $\hat{\imath}$ y en $\hat{\jmath}$ son diferenciables con derivada continua. Entonces nos preguntaremos ¿$G$ es gradiente de un campo escalar? Para ello calculemos $\triangledown \times G$ cuyo resultado en caso afirmativo debería ser igual a cero. Sin embargo,

\[ \triangledown \times G=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ y & -x & 0 \end{vmatrix}=-2\hat{k}\neq 0,\]

por lo tanto $G$ no es un gradiente.

También tenemos que la divergencia de un rotacional es igual a cero, es decir si $F$ es un campo vectorial $\triangledown \cdot (\triangledown \times F)=0$. Queda como tarea moral demostrar este hecho.

Mas adelante…

Con esta entrada terminamos nuestro estudio de conceptos relacionados con campos vectoriales. Sin embargo, aún no los descartaremos por completo. Retomaremos a los campos vectoriales en la última unidad del curso. En ella, retomaremos varias partes de la teoría para establecer resultados de optimización de campos escalares, y de funciones bajo restricciones.

Tarea moral

  1. Para los siguientes campos vectoriales, halla su divergencia
    • $F(x,y)=x^{3}\hat{\imath}+x\hspace{0.1cm}sen\hspace{0.1cm}(xy)\hat{\jmath}$
    • $G(x,y,z)=e^{xy}\hat{\imath}+e^{xy}\hat{\jmath}+e^{yz}\hat{k}$.
  2. Obtén el rotacional de los siguientes campos vectoriales:
    • $F(x,y,z)=(x^{2}+y^{2}+z^{2})(3\hat{\imath}+4\hat{\jmath}+5\hat{k})$
    • $G(x,y,z)=yz\hat{\imath}+xz\hat{\jmath}+xy\hat{k}$.
  3. Dibuja algunas líneas de flujo del campo $F(x,y)=-3x\hat{\imath}-y\hat{\jmath}$. Calcula $\triangledown \cdot F$ y explica el significado del resultado de la divergencia en su relación con las líneas de flujo.
  4. Demuestra que $\triangledown \cdot (\triangledown \times F)=0$
  5. Sean $f$ y $g$ dos campos escalares diferenciables, y $F$, y $G$ dos campos vectoriales diferenciables. Demuestra las siguientes identidades (solo usa la parte operativa, piensa que todos los campos tanto los vectoriales como los escalares tienen el mismo dominio):
    1. $\triangledown \cdot gG =g(\triangledown \cdot G) + G\cdot (\triangledown g)$
    2. $\triangledown (fg)=f(\triangledown g) +g (\triangledown f)$
    3. $\triangledown \cdot (F\times G)= G\cdot (\triangledown \times F)-F\cdot (\triangledown \times G)$

Entradas relacionadas

Cálculo Diferencial e Integral III: Regla de la cadena para campos vectoriales

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Tenemos ya la definición de diferenciabilidad, y su versión manejable: la matriz jacobiana. Seguiremos construyendo conceptos y herramientas del análisis de los campos vectoriales muy importantes e interesantes. A continuación, enunciaremos una nueva versión de la regla de la cadena, que nos permitirá calcular las diferenciales de composiciones de campos vectoriales entre espacios de dimensión arbitraria. Esta regla tiene numerosas aplicaciones y es sorprendentemente fácil de enunciar en términos de producto de matrices.

Primeras ideas hacia la regla de la cadena

La situación típica de regla de la cadena es considerar dos funciones diferenciables que se puedan componer. A partir de ahí, buscamos ver si la composición también es diferenciable y, en ese caso, intentamos dar la derivada de la composición en términos de las derivadas de las funciones. Veamos qué pasa en campos vectoriales.

Pensemos en $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ y en su composición $h=f\circ g$ definida sobre alguna vecindad $V\subseteq S_g$ de $\bar{a}$ y tal que $g(V)\subseteq S_f$. Pensemos que $g$ es diferenciable en $\bar{a}$ con derivada $G_\bar{a}$ y que $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$.

Exploremos la diferenciabilidad de la composición $h$ en el punto $\bar{a}$. Para ello, tomemos un $\bar{y}\in \mathbb{R}^{l}$ tal que $\bar{a}+\bar{y}\in V$ y consideremos la siguiente expresión:

\begin{align*}
h(\bar{a}+\bar{y})-h(\bar{a})=f(g(\bar{a}+\bar{y}))-f(g(\bar{a})).
\end{align*}

Tomando $\bar{v}=g(\bar{a}+\bar{y})-g(\bar{a})$, tenemos $\bar{b}+\bar{v}=g(\bar{a})+\bar{v}=g(\bar{a}+\bar{y})$. De esta forma,

\begin{align*}
f(g(\bar{a}+\bar{y}))-f(g(\bar{a}))=f(\bar{b}+\bar{v})-f(\bar{b}).
\end{align*}

Por la diferenciabilidad de $g$ en $\bar{a}$, tenemos que podemos escribir

$$\bar{v}=G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}),$$ con $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$.

Usando la diferenciabilidad de $f$ en $\bar{b}$, y la linealidad de su derivada $F_\bar{b}$, tenemos entonces que:

\begin{align*}
f(\bar{b}+\bar{v})-f(\bar{b})&=F_\bar{b}(\bar{v})+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=F_\bar{b}(G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=(F_{b}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||(F_{\bar{b}}\circ E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_{f}(\bar{b};\bar{v}),
\end{align*}

con $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b};\bar{v})=0$.

Concatenando nuestras igualdades, podemos reescribir esto como

\[ h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),\] en donde hemos definido

\[ E_{h}(\bar{a};\bar{y})=(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})+\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b};\bar{v}).\] Si logramos demostrar que $\lim\limits_{\bar{y}\to \bar{0}}E_{h}(\bar{a};\bar{y})=0$, entonces tendremos la diferenciabilidad buscada, así como la derivada que queremos. Dejemos esto en pausa para enunciar y demostrar un lema auxiliar.

Un lema para acotar la norma de la derivada en un punto

Probemos el siguiente resultado.

Lema. Sea $\phi:S\subseteq \mathbb{R}^l\to \mathbb{R}^m$ un campo vectorial diferenciable en un punto $\bar{c}\in S$ y $T_\bar{c}$ su derivada. Entonces, para todo $\bar{v}\in \mathbb{R}^{l}$, se tiene:

$$||T_{\bar{c}}(\bar{v})||\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||.$$

Donde $\phi(\bar{v})=\left( \phi_{1}(\bar{v}),\dots ,\phi_{m}(\bar{v})\right)$

Demostración. Procedemos con desigualdad del triángulo como sigue:

\begin{align*}
||T_{\bar{c}}(\bar{v})||&=\left|\left|\sum_{k=1}^{m}(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_{k}\right|\right|\\
&\leq \sum_{k=1}^{m}||(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_k||\\
&=\sum_{k=1}^{m}|\triangledown \phi_{k}(\bar{c})\cdot \bar{v}|
\end{align*}

y luego usamos la desigualdad de Cauchy-Schwarz en cada sumando para continuar como sigue

\begin{align*}
\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||,
\end{align*}

que es lo que buscábamos.

$\square$

Conclusión del análisis para regla de la cadena

Retomando el análisis para $E_{h}(\bar{a};\bar{y})$, dividamos el límite en los dos sumandos.

Primer sumando:

Como $F_{\bar{b}}$ es lineal, entonces es continua. También, sabemos que $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$. Así,

\begin{align*}
\lim\limits_{\bar{y}\to \bar{0}}(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})&=F_{\bar{b}}\left(\lim\limits_{\bar{y}\to \bar{0}} E_{g}(\bar{a};\bar{y})\right)\\
&=F_\bar{b}(\bar{0})\\
&=0.
\end{align*}

Segundo sumando:

Retomando la definición de $\bar{v}$, aplicando desigualdad del triángulo y el lema que demostramos,

\begin{align*}
||\bar{v}||&=||G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y})||\\
&\leq ||G_{\bar{a}}(\bar{y})||+||\bar{y}||||E_{g}(\bar{a};\bar{y})||\\
&\leq \left(\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||||\bar{y}||\right)+||\bar{y}||||E_{g}(\bar{a};\bar{y})||.
\end{align*}

Dividiendo ambos lados entre $||\bar{y}||$, obtenemos entonces que

$$ \frac{||\bar{v}||}{||\bar{y}||}\leq \sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||+||E_{g}(\bar{a};\bar{y})||. $$

De aquí se ve que conforme $\bar{y}\to \bar{0}$, la expresión $\frac{||\bar{v}||}{||\bar{y}||}$ está acotada superiormente por la constante $A:=\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||.$ Además, si $\bar{y}\to \bar{0}$, entonces $\bar{v}\to \bar{0}$. Así,

\[0\leq \lim\limits_{\bar{y}\to \bar{0}}\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b},\bar{v})\leq A\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})=0 \] pues $\lim\limits_{\bar{y}\to \bar{0}}\bar{v}=\bar{0}$ implica $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})$.

Hemos concluido que $$h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),$$

con $\lim_{\bar{y}\to \bar{0}} E_h(\bar{a};\bar{y})=0$. Esto precisamente es la definición de $h=f\circ g$ es diferenciable en $\bar{a}$, y su derivada en $\bar{a}$ es la transformación lineal dada por la composición de transformaciones lineales $F_\bar{b}\circ G_\bar{a}$.

Recapitulación de la regla de la cadena

Recapitulamos toda la discusión anterior en el siguiente teorema.

Teorema (Regla de la cadena). Sean $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ campos vectoriales. Supongamos que la composición $f\circ g$ está definida en todo un abierto $S\subseteq S_g$. Supongamos que $g$ es diferenciable en un punto $\bar{a}\in S$ con derivada $G_\bar{a}$ y $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$. Entonces, $h$ es diferenciable en $\bar{a}$ con derivada $F_\bar{b}\circ G_\bar{a}$.

Dado que la representación matricial de la composición de dos transformaciones lineales es igual al producto de estas, podemos reescribir esto en términos de las matrices jacobianas como el siguiente producto matricial: $$Dh(\bar{a})=Df(\bar{b})Dg(\bar{a}).$$

Usos de la regla de la cadena

Hagamos algunos ejemplos de uso de regla de la cadena. En el primer ejemplo que veremos a continuación, la función $f$ es un campo escalar.

Ejemplo 1. Tomemos $g:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ campo vectorial, y $f:U\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}$ campo escalar. Consideremos $h=f\circ g$ y supongamos que se satisfacen las hipótesis del teorema de la regla de la cadena. Tenemos: \[ Df(\bar{b})=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix} \] y \[ Dg(\bar{a})=\begin{pmatrix}\frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix} . \]

Por la regla de la cadena tenemos $Dh(\bar{a})=Df(\bar{b})Dg(\bar{a})$ esto implica \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix}\begin{pmatrix} \frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

Así \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}= \begin{pmatrix} \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{1}}(\bar{a}) & \dots & \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

En otras palabras, tenemos las siguientes ecuaciones para calcular cada derivada parcial de $h$: \[ \frac{\partial h}{\partial x_{j}}(\bar{a})=\sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{j}}(\bar{a}).\]

$\triangle$

Ejemplo 2. Sean $\bar{a}=(s,t)$ y $\bar{b}=(x,y)$ puntos en $\mathbb{R}^{2}$. Pensemos que las entradas de $\bar{b}$ están dadas en función de las entradas de $\bar{a}$ mediante las ecuaciones $x=g_{1}(s,t)$ y $y=g_{2}(s,t)$. Pensemos que tenemos un campo escalar $f:\mathbb{R}^2\to \mathbb{R}$, y definimos $h:\mathbb{R}^2\to \mathbb{R}$ mediante $$h(s,t)=f(g_{1}(s,t),g_{2}(s,t)).$$

Por el ejemplo anterior \[ \frac{\partial h}{\partial s}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial s} \] y \[ \frac{\partial h}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}. \] Como tarea moral queda que reflexiones qué significa $\partial x$ cuando aparece en el «numerador» y qué significa cuando aparece en el «denominador».

$\triangle$

Ejemplo 3. Para un campo escalar $f(x,y)$ consideremos un cambio de coordenadas $x=rcos\theta$, $y=rsen\theta$ es decir tomemos la función $\phi (r,\theta)=f(rcos\theta ,rsen\theta )$.

Por el ejemplo anterior tenemos \[ \frac{\partial \phi }{\partial r}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial r} \] y \[ \frac{\partial \phi }{\partial \theta }=\frac{\partial f}{\partial x}\frac{\partial x}{\partial \theta }+\frac{\partial f}{\partial y}\frac{\partial y}{\partial \theta } \] donde, haciendo las derivadas parciales tenemos: \[ \frac{\partial x}{\partial r}=cos\theta ,\hspace{1cm}\frac{\partial y}{\partial r}=sen\theta \] y \[ \frac{\partial x}{\partial \theta }=-rsen\theta,\hspace{1cm}\frac{\partial y}{\partial \theta }=-rcos\theta. \] Finalmente obtenemos: \[ \frac{\partial \phi }{\partial r }=\frac{\partial f }{\partial x }cos\theta +\frac{\partial f }{\partial y }sen\theta \] y \[ \frac{\partial \phi }{\partial \theta }=-\frac{\partial f }{\partial x }rsen\theta +\frac{\partial f }{\partial y }rcos\theta \] que son las derivadas parciales del cambio de coordenadas en el dominio de $f$.

$\triangle$

Mas adelante…

En la siguiente entrada comenzaremos a desarrollar la teoría para los importantes teoremas de la función inversa e implícita si tienes bien estudiada esta sección disfrutaras mucho de las siguientes.

Tarea moral

  1. Considera el campo escalar $F(x,y,z)=x^{2}+y sen(z)$. Imagina que $x,y,z$ están dados por valores $u$ y $v$ mediante las condiciones $x=u+v$, $y=vu$, $z=u$. Calcula $\frac{\partial F}{\partial u}$, $\frac{\partial F}{\partial v}$.
  2. Sea $g(x,y,z)=(xy,x)$, y $f(x,y)=(2x,xy^{2},y)$. Encuentra la matriz jacobiana del campo vectorial $g\circ f$. Encuentra también la matriz jacobiana del campo vectorial $f\circ g$.
  3. En la demostración del lema que dimos, hay un paso que no justificamos: el primero. Convéncete de que es cierto repasando el contenido de la entrada anterior Diferenciabilidad.
  4. Imagina que sabemos que la función $f:\mathbb{R}^n\to \mathbb{R}^n$ es invertible y derivable en $\bar{a}$ con derivada $T_\bar{a}$. Imagina que también sabemos que su inversa $f^{-1}$ es derivable en $\bar{b}=f(\bar{a})$ con derivada $S_\bar{b}$. De acuerdo a la regla de la cadena, ¿Qué podemos decir de $T_\bar{a}\circ S_\bar{b}$? En otras palabras, ¿Cómo son las matrices jacobianas entre sí, en términos de álgebra lineal?
  5. Reflexiona en cómo todas las reglas de la cadena que hemos estudiado hasta ahora son un corolario de la regla de la cadena de esta entrada.

Entradas relacionadas

Cálculo Diferencial e Integral III: Derivadas parciales de segundo orden

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En las entradas anteriores definimos qué quiere decir que un campo escalar sea diferenciable. Así mismo, definimos las derivadas parciales y el gradiente. Ya usamos estas herramientas para hablar de dirección de cambio máximo y de puntos críticos. Además demostramos una versión del teorema del valor medio para este caso, lo que nos permitió poner un poco de orden a nuestra teoría: una función es diferenciable en un punto cuando existen sus parciales en ese punto y son continuas. Es momento de hablar de derivadas parciales de segundo orden. Cualquiera de las derivadas parciales es por sí misma un campo escalar, así que podemos preguntarnos si tiene o no sus propias derivadas parciales. Exploraremos esta idea.

Derivadas parciales de segundo orden

Las derivadas parciales de un campo escalar $f$ nos originan nuevos campos escalares. Supongamos que $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ es un campo escalar para el cual existe la $k$-ésima derivada parcial en un conjunto abierto $S’\subseteq S$. Entonces, obtenemos un nuevo campo escalar $\frac{\partial f}{\partial x_{k}}:S’\rightarrow \mathbb{R}$.

Este campo escalar puede o no tener $j$-ésima derivada parcial. Suponiendo que la tiene en algún $U\subseteq S’$ podríamos escribirla como

$$\frac{\partial\left(\frac{\partial f}{\partial x_k}\right)}{\partial x_j}.$$

Sin embargo, esta notación es engorrosa, y por ello optamos o bien por escribir la expresión como sigue

\[ \frac{\partial}{\partial x_{j}}\left( \frac{\partial f}{\partial x_{k}}\right)\]

o todavía más compacto, como

\[ \frac{\partial ^{2}f}{\partial x_{j}\partial x_{k}}.\]

A esto le llamamos una derivada parcial de segundo orden. Si $j=k$, introducimos la notación

\[ \frac{\partial ^{2}f }{\partial x_{k}^{2}}.\]

Las derivadas parciales de segundo orden vuelven a ser, una vez más, cada una de ellas un campo escalar. Esto permite seguir iterando la idea: podríamos hablar de derivadas parciales de segundo, tercero, cuarto, … , $k$-ésimo, … orden. Daremos una definición un poco más formal en una siguente entrada, pero por ahora trabajemos en entender a las derivadas parciales de segundo orden.

Un ejemplo de derivadas parciales de segundo orden

Ejemplo. Consideremos el campo escalar $f(x,y,z)=x^{2}yz$. Para este campo escalar tenemos que sus derivadas parciales con respecto a $x$, $y$ y $z$ son:

\begin{align*}
\frac{\partial f}{\partial x}(x,y,z)&=2xyz,\\
\frac{\partial f}{\partial y}(x,y,z)&=x^{2}z\\
\frac{\partial f}{\partial z}(x,y,z)&=x^{2}y.
\end{align*}

Cada una de estas expresiones es a su vez un campo escalar. Cada una de ellas es derivable con respecto a $x$ en todo $\mathbb{R}^3$. Al derivarlas con respecto a $x$ obtenemos:

\begin{align*}
\frac{\partial ^{2}f}{\partial x^{2}}(x,y,z)&=2yz,\\
\frac{\partial ^{2}f}{\partial x\partial y}(x,y,z)&=2xz,\\
\frac{\partial ^{2}f}{\partial x\partial z}(x,y,z)&=2xy.
\end{align*}

Por otro lado, las derivadas parciales de primer orden también podríamos haberlas derivado con respecto a $y$. En este caso, hubieramos obtenido.

\begin{align*}
\frac{\partial ^{2}f}{\partial y \partial x}(x,y,z)&=2xz,\\
\frac{\partial ^{2}f}{\partial y ^2}(x,y,z)&=0,\\
\frac{\partial ^{2}f}{\partial y\partial z}(x,y,z)&=x^2.
\end{align*}

También podríamos derivar a las derivadas parciales de primer orden con respecto a $z$ para obtener las tres derivadas de orden dos faltantes. En total tenemos tres derivadas parciales de primer orden y nueve derivadas parciales de segundo orden.

$\triangle$

Igualdad de las derivadas parciales de segundo orden mixtas

En numerosos campos escalares de interés tenemos una propiedad muy peculiar: que los operadores «obtener la derivada parcial con respecto a $x$» y «obtener la derivada parcial con respecto a $y$» conmutan. Es decir, varias veces podemos intercambiar el orden de derivación de las parciales y obtener el mismo resultado. En el ejemplo anterior quizás hayas notado que

\[ \frac{\partial ^{2}f}{\partial y\partial x}=2xz=\frac{\partial ^{2}f}{\partial x\partial y}.\]

Esto no siempre pasa, pero hay criterios de suficiencia sencillos de verificar. Por ejemplo, basta que las parciales mixtas existan y sean continuas para que sean iguales. El siguiente teorema formaliza el resultado.

Teorema. Sea $f:S\subseteq \mathbb{R}^{2}\rightarrow \mathbb{R}$ un campo escalar tal que las derivadas parciales $\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial^{2} f}{\partial y\partial x}$, $\frac{\partial ^{2}f}{\partial x\partial y}$ existen en un conjunto abierto $U$. Si $(a,b)\in U$ es tal que $\frac{\partial^{2} f}{\partial y\partial x}$, $\frac{\partial ^{2}f}{\partial x\partial y}$ son continuas en $(a,b)$, entonces dichas derivadas mixtas de segundo orden son iguales en $(a,b)$.

Demostración. Sean $h,k\neq 0$ suficientemente chicos para que los puntos en el plano $(a,b)$, $(a,b+k)$, $(a+h,b)$, y $(a+h,b+k)$ estén en $U$.

Definamos la función $\Gamma (x)=f(x,b+k)-f(x,b)$ para $x\in [a,a+h]$ y definamos

\begin{equation} \Delta (h,k)=\Gamma (a+h)-\Gamma (a).\end{equation}

Notemos que $\Gamma$ es una función de $\mathbb{R}$ en $\mathbb{R}$ cuya derivada es $$\Gamma'(x)=\frac{\partial f}{\partial x}(x,b+k)-\frac{\partial f}{\partial x}(x,b).$$ Así, se le puede aplicar el teorema del valor medio con extremos en $a$ y $a+h$ para concluir que existe $\xi _{1}\in [a,a+h]$ que nos permite escribir $\Delta(h,k)$ de la siguiente manera:

\begin{align*}
\Delta(h,k)&=\Gamma (a+h)-\Gamma (a)\\
&= h\Gamma'(\xi _{1})\\
&=h\left[ \frac{\partial f}{\partial x}(\xi _{1},b+k)-\frac{\partial f}{\partial x}(\xi _{1},b) \right]
\end{align*}

Ahora podemos aplicar el teorema del valor medio en la función $y\mapsto \frac{\partial f}{\partial x} (\xi _{1},y)$ con extremos $b$ y $b+k$. Esto nos permite continuar la cadena de igualdades anterior mediante un $\eta _{1}\in [b,b+k]$ que cumple

\begin{equation}\label{eq:primerdelta} \Delta (h,k)=hk\frac{\partial ^{2}f}{\partial y\partial x}(\xi _{1},\eta _{1}).\end{equation}

Como $(\xi _{1},\eta _{1})\in [a,a+h]\times[b,b+k]$, se tiene que $(\xi _{1},\eta _{1})\to (a,b)$ conforme $(h,k)\to \bar{0}$.

Ahora consideremos análogamente a la función $\varLambda (y)=f(a+h,y)-f(a,y)$. Mediante un procedimiento similar al que acabamos de hacer, pero aplicado a $\varLambda$ en vez de a $\Gamma$, se tiene otra forma de expresar a $\Delta(h,k)$:

\begin{equation}\label{eq:segundodelta}\Delta(h,k)=hk\frac{\partial ^{2} f}{\partial x\partial y}(\xi _{2},\eta _{2}),\end{equation} donde $(\xi _{2},\eta _{2})\in [a,a+h]\times[b,b+k]$. Nuevamente, $(\xi _{2},\eta _{2})\to (a,b)$ conforme $(h,k)\to (0,0)$.

Igualando las expresiones en \eqref{eq:primerdelta} y \eqref{eq:segundodelta}, tenemos lo siguiente:

\[ \frac{\partial f}{\partial y\partial x}(\xi _{1},\eta _{1})=\frac{\partial f}{\partial x\partial y}(\xi _{2},\eta _{2}).\]

El resultado se sigue de hacer tender $(h,k)\to (0,0)$, ya que dado que las derivadas parciales les estamos pidiendo que sean continuas, tenemos que:

\begin{align*}
\frac{\partial ^{2} f}{\partial y\partial x}(a,b)&=\lim\limits_{(h,k)\to (0,0)}\frac{\partial ^{2} f}{\partial y\partial x}(\xi _{1},\eta _{1})\\
&=\lim\limits_{(h,k)\to (0,0)}\frac{\partial ^{2}f}{\partial x\partial y}(\xi _{2},\eta _{2})\\
&=\frac{\partial ^{2}f}{\partial x\partial y}(a,b).
\end{align*}

Así concluimos nuestro resultado.

$\square$

Más adelante…

En esta entrada hablamos de las derivadas parciales de segundo orden y vimos que bajo condiciones razonables podemos elegir las variables de derivación en el orden que queramos. Estas ideas son más generales, y a continuación nos llevarán a definir las derivadas parciales de cualquier orden $k$. Después, usaremos estas derivadas parciales para generalizar otro de los teoremas de cálculo unidimensional: el teorema de Taylor.

Tarea moral

  1. Para las siguientes funciones calcula $\frac{\partial ^{2}f}{\partial x^{2}}$:
    • $f(x,y)=x^{2}+y^{2}cos(xy)$
    • $f(x,y)=e^{x}cos(y)$
    • $f(x,y,z)=\textup{log}(x^{2}+2y^{2}-3z^{2})$
  2. En el teorema que afirma que las derivadas parciales mixtas son iguales usamos cuatro veces el teorema del valor medio (¿cuáles 4 son?). Asegúrate de que en verdad lo podamos usar.
  3. Calcula $\frac{\partial ^{2}f}{\partial y^{2}}$, y $\frac{\partial ^{2}f}{\partial x\partial y}$ para las funciones del punto 1. Explica por qué no es necesario calcular de manera separada $\frac{\partial ^{2}f}{\partial y\partial x}$
  4. Investiga de un ejemplo en el que las derivadas parciales $\frac{\partial ^{2}f}{\partial x\partial y}$ y $\frac{\partial ^{2}f}{\partial y\partial x}$ no sean iguales. Realiza las cuentas para verificar que en efecto tienen valores distintos en algún punto.
  5. El teorema que enunciamos está muy limitado. Sólo nos habla de campos escalares de $\mathbb{R}^2$ en $\mathbb{R}$. Sin embargo, debería también funcionar si $f:\mathbb{R}^n\to \mathbb{R}$. Enuncia y demuestra un resultado similar que te permita garantizar que $$\frac{\partial^{2} f}{\partial x_i\partial x_j}=\frac{\partial ^{2}f}{\partial x_j\partial x_i}.$$

Entradas relacionadas

Cálculo Diferencial e Integral III: Teorema del valor medio para campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Ya hemos definido qué es el gradiente $\nabla f$ de un campo escalar $f$. Hemos visto cómo está relacionado con las derivadas direccionales. Así mismo, mostramos que conocer este gradiente nos permite dar información sobre los máximos y mínimos del campo escalar. En esta entrada mostraremos una propiedad más del gradiente: que nos ayuda a dar una generalización del teorema del valor medio de Cálculo I, pero para campos escalares. Este será un resultado fundamental para demostrar otras propiedades de los campos escalares. Como ejemplo, también damos en esta entrada un criterio suficiente para que un campo escalar sea diferenciable.

Teorema del valor medio para funciones de $\mathbb{R}$ en $\mathbb{R}$

Para facilitar la lectura de este material, recordemos lo que nos dice el teorema del valor medio sencillo, es decir, el de $\mathbb{R}$ en $\mathbb{R}$.

Teorema. Sean $a<b$ reales. Sea $f:[a,b]\to\mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe algún punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

Una vez que uno interpreta el teorema gráficamente, se vuelve muy intuitivo. Considera la siguiente figura.

Intuición geométrica del teorema del valor medio

El término $$\frac{f(b)-f(a)}{b-a}$$ es la pendiente del segmento que une los puntos $(a,f(a))$ y $(b,f(b))$ El término $f'(c)$ va marcando la pendiente de la recta tangente a $f$ en cada punto $c$. En términos geométricos, lo que nos dice este teorema es que para algún valor de $c$, la pendiente de la recta tangente en $c$ es la pendiente del segmento entre los extremos.

Lo que haremos a continuación es dar una generalización apropiada para funciones de $\mathbb{R}^n$ a $\mathbb{R}$.

Teorema del valor medio para funciones de $\mathbb{R}^n$ en $\mathbb{R}$

Para generalizar el teorema del valor medio a funciones de $\mathbb{R}^n$ a $\mathbb{R}$, necesitaremos cambiar un poco las hipótesis. El segmento $[a,b]$ que usábamos ahora será un segmento (multidimensional) que conecte a dos vectores $\bar{x}$ y $\bar{y}$ en $\mathbb{R}^n$. La diferenciabilidad la pediremos en todo un abierto que contenga al segmento. El enunciado apropiado se encuentra a continuación.

Teorema (del valor medio para campos escalares). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar diferenciable. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

En este caso no podemos «pasar dividiendo $\bar{y}-\bar{x}$» pues no tiene sentido dividir entre vectores. Pero en el caso $n=1$ sí se puede, y justo obtenemos de vuelta el teorema del valor medio de $\mathbb{R}$ en $\mathbb{R}$. Uno podría pensar que entonces esta es una manera alternativa de demostrar el teorema para funciones de $\mathbb{R}$ en $\mathbb{R}$. Sin embargo, como veremos a continuación, la demostración de la versión para campos escalares usa la versión para funciones reales.

Demostración. Consideremos la función $\gamma:[0,1] \to \mathbb{R}^{n}$ dada $\gamma (t)=(1-t)\bar{x}+t\bar{y}$. Notemos que $\gamma$ es diferenciable, con $\gamma’ (t)=\bar{y}-\bar{x}$. Además, por hipótesis $f$ es diferenciable en $S$. Así, $f\circ \gamma:[0,1]\to \mathbb{R}$ también es diferenciable, y por regla de la cadena

\begin{align*}
(f\circ \gamma)'(t)&=\nabla f(\gamma(t))\cdot \gamma'(t)\\
&=\nabla f(\gamma(t))\cdot (\bar{y}-\bar{x}).
\end{align*}

¡Pero $f\circ \gamma$ ya es una función de $\mathbb{R}$ en $\mathbb{R}$! Así, podemos aplicarle el teorema del valor medio real (verifica las hipótesis como tarea moral). Al hacer esto, obtenemos que existe una $c\in (0,1)$ tal que
\begin{align*}
(f\circ \gamma)'(c) &= \frac{(f\circ \gamma)(1)-(f\circ \gamma)(0)}{1-0}\\
&=f(\bar{y})-f(\bar{x}).
\end{align*}

Usando la fórmula que obtuvimos por regla de la cadena para $(f\circ \gamma)’$ y la definición de $\gamma$ obtenemos que

$$ \nabla f((1-c)\bar{x}+c\bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}),$$

tal y como buscábamos.

$\square$

En el teorema anterior estamos pidiendo que $f$ sea diferenciable. Sin embargo, basta con que exista la derivada de la composición en el segmento que nos interesa y el resultado también se sigue. Es decir, tenemos la siguiente versión con una hipótesis más débil. La enunciamos pues la usaremos en la siguiente sección.

Teorema (del valor medio para campos escalares, hipótesis debilitada). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$ y tales que para toda $c\in[0,1]$ se cumple que la derivada (real) de $f((1-c)\bar{x}+c\bar{y}))$ existe. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

La demostración es exactamente la misma.

Aplicación del teorema del valor medio

Como primera aplicación del teorema del valor medio para campos escalares mostraremos un criterio de diferenciabilidad muy útil, al que llamaremos el teorema de diferenciabilidad y derivadas parciales.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Supongamos que para cierto punto $\bar{a}\in S$ y cierta vecindad $B_r(\bar{a})\subset S$ existen las derivadas parciales $\frac{\partial f}{\partial x_{1}},\dots ,\frac{\partial f}{\partial x_{n}}$ y son continuas en $\bar{a}$. Entonces $f$ es diferenciable en $\bar{a}$.

Demostración. Elijamos un vector $\bar{u}=u_1\hat{e}_1+\dots +u_n\hat{e}_n$ de norma $1$ y tomemos $\bar{v}=\lambda \bar{u}$ con $\lambda$ suficientemente chico como para que $\bar{a}+\bar{v}$ esté en $B_{r}(\bar{a})$. Definamos los siguientes vectores:

\begin{align*}
\bar{v}_0&=\bar{0}\\
\bar{v}_1&=u_1\hat{e}_1\\
\bar{v}_2&=u_1\hat{e}_1+u_2\hat{e}_2\\
&\vdots\\
\bar{v}_n&=u_1\hat{e}_1+u_2\hat{e}_2+\ldots+u_n\hat{e}_n=\bar{u}.
\end{align*}

Con ellos creamos la siguiente suma telescópica para expresar a $f(\bar{a}+\bar{v})-f(\bar{a})$

\begin{align}
f(\bar{a}+\bar{v})-f(\bar{a})&=f(\bar{a}+\lambda \bar{u})-f(\bar{a}) \nonumber\\
&=\sum_{k=1}^{n}[f(\bar{a}+\lambda \bar{v}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1})] \label{eq:telescopica}
\end{align}

Notemos que el $k$-ésimo término de esta suma puede ser escrito como $$f(\bar{a}+\lambda \bar{v}_{k-1}+\lambda u_{k}\hat{e}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1}).$$ Para simplificar, definimos $\bar{b}_{k}=\bar{a}+\lambda \bar{v}_{k-1}$ y reescribiendo el $k$-ésimo término tenemos $$f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k}).$$

Aplicando el teorema del valor medio con hipótesis debilidada para campos escalares a los puntos $\bar{b}_{k}$ y $\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}$ (verifica las hipótesis), tenemos que para cada $k$ existe $\xi_k \in (0,1)$ tal que

\begin{align*}
f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})&=\triangledown f((1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}))\cdot (\lambda u_{k}\hat{e}_{k})\\
&=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}),
\end{align*}

en donde hemos definido $\bar{c}_k:=(1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})$, que es un punto en el segmento que une a $\bar{b}_k$ con $\bar{b}_k+\lambda u_k\hat{e}_k$.

Tenemos pues que podemos escribir al $k$-ésimo término como:

$$f(\hat{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}).$$

Notemos además que si $\lambda \to 0$, entonces $\bar{b}_{k}\to \bar{a}$, $\bar{c}_{k} \to a$ y $\bar{v}\to \bar{0}$.

Escribimos entonces la ecuación \eqref{eq:telescopica} como:

\begin{equation}
\label{eq:resumen}
f(\bar{a}+\bar{v})-f(\bar{a})=\lambda \sum_{k=1}^{n}u_k\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})
\end{equation}

En unos momentos usaremos esta expresión. Antes de ello, estudiemos otro de los términos involucrados en la diferenciabilidad. Tenemos que:

\begin{align}
\triangledown f(\bar{a})\cdot \bar{v}&=\triangledown f(\bar{a})\cdot \lambda u \nonumber\\
&=\lambda \triangledown f(\bar{a})\cdot u \nonumber\\
&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a}) \label{eq:ppunto}.
\end{align}

Empecemos entonces a combinar lo visto hasta ahora para entender los términos en la definición de diferenciabilidad. Tenemos juntando \eqref{eq:resumen} y \eqref{eq:ppunto} que

\begin{align*}
f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot v&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a})\\&=\lambda \sum_{k=1}^{n}u_{k}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right].
\end{align*}

Como mencionamos, si $\lambda \to 0$ entonces $\bar{v}\to \bar{0}$. Además, $||\bar{v}||=|\lambda|$. Así:

\[ \lim\limits_{\bar{v}\to \bar{0}} \frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=\lim\limits_{\lambda \to 0} \left|\sum_{k=1}^{n}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|.\]

Veamos qué más sucede cuando $\lambda \to 0$. Ya notamos que $\bar{c}_k\to \bar{a}$, así que usando la continuidad de las derivadas parciales tenemos:

\[ \lim\limits_{\lambda \to 0}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\lim\limits_{\bar{c}_{k}\to \bar{a}}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\frac{\partial f}{\partial x_{k}}(\bar{a}).\]

Aplicando desigualdad del trángulo en la suma, el límite buscado es menor o igual a

\[ \lim\limits_{\lambda \to 0}\sum_{k=1}^{n}\left|\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|=0.\]

Y aquí cada sumando se va a $0$. La conclusión final es que

\[ \lim\limits_{\bar{v}\to \bar{0}}\frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=0,\]

de modo que $f$ es diferenciable en $\bar{a}$.

$\square$

El regreso del teorema anterior no se vale

El teorema de diferenciabilidad nos dice que si las derivadas parciales existen y son continuas, entonces la función es diferenciable. Sin embargo, el regreso de este teorema no se vale, en el sentido de que existen funciones diferenciables cuyas derivadas parciales no son continuas. En otras palabras, si las derivadas parciales no son continuas, no podemos descartar la diferenciablidad de una función.

A continuación esbozamos un ejemplo que deberás completar como tarea moral.

Ejemplo. Consideremos la función

$$f(x,y)=\begin{cases} (x^2+y^2)\sin\left(\frac{1}{\sqrt{x^2+y^2}}\right) &\text{si $(x,y)\neq (0,0)$}\\ 0 & \text{si $(x,y)=(0,0)$}\end{cases}$$

Se puede demostrar que $f$ es diferenciable en $(0,0)$. De manera intuitiva, la función queda entre las funciones $(x,y)\to x^2+y^2$ y $(x,y)\to -x^2-y^2$. Se puede usar un argumento de acotamiento para mostrar que el plano tangente coincide entonces con el de estas funciones en $(0,0)$ que es el plano $z=0$. Verifica los detalles de tarea moral.

Así mismo, se puede ver que las derivadas parciales en $(0,0)$ existen y que de hecho se satisface $$\frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 0.$$

Finalmente, se puede ver que las derivadas parciales no convergen a $0$. Fuera del $(0,0)$, tenemos por reglas de derivación que

\begin{align*} \frac{\partial f}{\partial x}(x,y) &= 2 x \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{x \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}\\ \frac{\partial f}{\partial y}(x,y) &= 2 y \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{y \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}. \end{align*}

Una manear de ver que estas no son contínuas es aproximándonos por un eje. Por ejemplo, puedes verificar que sobre el eje $x$, conforme $x\to 0$, tenemos que la primera parcial oscila entre $-1$ y $1$.

$\triangle$

Más adelante…

Hemos enunciado y demostrado una versión del teorema del valor medio para campos escalaras. Gracias a ella hemos podido mostrar que si un campo escalar tiene derivadas parciales continuas, entonces es diferenciable. Las aplicaciones del teorema del valor medio para campos escalares van más allá. En la siguiente entrada hablaremos de las derivadas parciales de orden superior. El teorema del valor medio para campos escalares nos permitirá demostrar que bajo ciertas condiciones, en cierto sentido estas derivadas parciales «conmutan».

Tarea moral

  1. ¿Qué dice el teorema del valor medio para campos escalares para la función $f(x,y)=\sin(x)\cos(y)$ tomando como extremos los puntos $\left(0,\frac{\pi}{2}\right)$ y $\left(\frac{\pi}{2},0\right)$? Verifica si puedes aplicar las hipótesis.
  2. En la demostración del teorema del valor medio que dimos, verifica que la función $f\circ \gamma$ dada en efecto satisface las hipótesis del teorema del valor medio real.
  3. Supongamos que $f:\mathbb{R}^n\to \mathbb{R}$ es diferenciable en un abierto $S$ que contiene al segmento cuyos extremos son ciertos vectores $\bar{x}$ y $\bar{y}$ de $\mathbb{R}^n$. Supongamos que $f(\bar{x})=f(\bar{y})$. ¿Será cierto siempre que $\nabla f$ se anula en algún vector del segmento que une $x$ con $y$? Ten cuidado, pues hay un producto escalar involucrado. En caso de que no siempre sea cierto, ¿Qué es lo que sí puedes garantizar?
  4. En la demostración del teorema de diferenciabilidad, verifica que se pueden usar las hipótesis del teorema del valor medio para campos escalares con hipótesis debilitada. Necesitarás ver que la derivada real que tiene que existir es justo una parcial de las que suponemos que existen, completa los detalles. Luego, verifica que en efecto la conclusión que obtuvimos es justo la que se obtiene. Observa además que no podemos usar el teorema del valor medio para campos diferenciables con la hipótesis usual pues necesitaríamos saber que $f$ es diferenciable, lo cual es justo lo que queremos mostrar.
  5. Completa el contraejemplo al regreso del teorema de diferenciabilidad. Entre otras cosas, tienes que hacer lo siguiente:
    • Verificar que en efecto la función es diferenciable en $(0,0)$. Puedes proceder por definición o acotando como se sugiere.
    • Revisar que las parciales en $(0,0)$ en efecto existen y coinciden con lo que sabemos a partir de que el plano tangente en el origen es $(0,0)$.
    • Obtener paso a paso la fórmula que dimos para las parciales, usando lo que sabes de regla de la cadena, derivadas en $\mathbb{R}$, etc.
    • Verificar que ninguna de las dos derivadas parciales es continua, completando el argumento de que al acercarnos por los ejes tenemos oscilaciones.

Entradas relacionadas

Cálculo Diferencial e Integral III: Polinomio de Taylor para campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Una intuición que se obtiene de un primer curso de cálculo diferencial e integral es que las funciones que tienen muchas derivadas «se parecen mucho a polinomios», en el sentido de que podemos aproximarlas apropiadamente con este tipo de expresiones. Esta intuición nos las da el teorema del polinomio de Taylor. En muchas aplicaciones, es conveniente estudiar polinomios en vez de funciones en general, así que sería ideal tener una versión de este mismo resultado para cálculo de varias variables. En esta entrada recordaremos un poco del caso unidimensional y luego enunciaremos la teoría correspondiente para el polinomio de Taylor.

Recordatorio de polinomio de Taylor en $\mathbb{R}$

Recordemos qué es lo que dice el teorema del polinomio de Taylor para el caso unidimensional. Esto nos ayudará pues lo usaremos posteriormente para enunciar una versión para varias variables.

Teorema. Sea $f:S\subseteq \mathbb{R}\to \mathbb{R}$ una función y $a\in int(S)$ de tal manera que existen $f^{\prime}(a),\dots ,f^{(k)}(a)$. Sea $$a_{\ell}=\frac{f^{(\ell)}(a)}{\ell!}$$ con $0\leq \ell \leq k$ y definamos a partir de esto $$T_{k,a}(x)=a_{0}+a_{1}(x-a)+\dots +a_{k}(x-a)^k,$$

al que llamamos el polinomio de Taylor de $f$ de grado $k$ alrededor de $a$.

Entonces $$\lim_{x \to a}\frac{f(x)-T_{k,a}(x)}{(x-a)^k}=0.$$

La demostración de este teorema la puedes encontrar en la entrada El Polinomio de Taylor (Parte 1) del curso de Cálculo I. Es recomendable que consultes esta entrada para recordar todo lo referente a este tema en una variable real.

Pidiendo un poco más de regularidad, se puede estudiar el residuo $$R_{k,a}(x):=f(x)-T_{k,a}(x).$$

Por ejemplo, se puede demostrar el siguiente teorema.

Teorema. Sea $f:S\subseteq \mathbb{R}\to\mathbb{R}$. Supongamos que $f^{\prime},\dots ,f^{(k+1)}$ están definidas sobre $[a,x]$. Entonces, se puede expresar el residuo del teorema de Taylor como

\begin{equation}
\label{eq:residuo}
R_{k,a}(x)=\frac{f^{(k+1)}(\xi)}{(k+1)!}(x-a)^{k+1}.
\end{equation}

para algún $\xi\in[a,x]$.

Para la demostración de este teorema y otras expresiones del residuo (por ejemplo, una expresión en términos de integrales), puedes visitar el curso de Cálculo II, en particular la entrada Series de Taylor y de Maclaurin.

Pensemos de momento que $f$ tiene derivadas parciales de todos los órdenes (es decir, que es $C^\infty$). En este caso, $f$ tiene polinomios de Taylor de todos los grados. De entrada, no tendría por qué suceder que $\lim_{k\to \infty} T_{k,a}(x)=f(x)$, y de hecho hay contraejemplos para ello. Pero si además tenemos que se tiene $\lim_{k \to \infty}R_{k,a}(x)=0$, entonces la igualdad anterior sí se cumple. En este caso, verdaderamente $f$ se puede expresar como un polinomio infinito (una serie de potencias) alrededor de $a$ de la siguiente manera:

\begin{equation}\label{eq:taylor-inf}f(x)=\sum_{i=0}^{\infty}\frac{f^{(i)}(a)}{i!}(x-a)^{i}.\end{equation}

Ejemplo. Calculemos en $0$ el polinomio de Taylor de $f(x)=e^x$. Para cada entero positivo $k$ se tiene:

$$\frac{f^{(k)}(0)}{k!}x^{k}=\frac{e^0}{k!}x^{k}=\frac{x^{k}}{k!}.$$

De aquí, por la forma que toma el residuo, existe $\xi\in [0,x]$ para el cual

$$R_{k,0}(x)=\frac{e^\xi}{(k+1)!}x^{k+1}.$$

aquí $e^\xi$ está acotado y el cociente $\frac{x^{k+1}}{(k+1)!}$ se va a cero conforme $k\to \infty$. De este modo, tenemos la igualdad

$$e^x=1+\frac{x}{1}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\dots.$$

$\triangle$

Preliminares para polinomio de Taylor para campos escalares

La manera en la cual generalizaremos el teorema del polinomio de Taylor será a través de evaluar nuestro campo escalar sobre un segmento, muy parecido a como generalizamos el teorema del valor medio. Pongamos la situación en contexto.

Tomemos un abierto $S\subseteq \mathbb{R}^n$ y un campo escalar $f:S\to \mathbb{R}$. Tomemos vectores
\begin{align*}
\bar{a}=(a_1,\ldots,a_n)\\
\bar{v}=(v_1,\ldots,v_n),
\end{align*}

y $t$ en el intervalo $[0,1]$. Supondremos además que para todo dicho $t$ se cumple $\bar{a}+t\bar{v}\in S$.

Podemos recorrer el segmento de $\bar{a}$ a $\bar{a}+\bar{v}$ mediante la trayectoria $\gamma : [0,1] \to \mathbb{R}^{n}$ dada por $\gamma (t)=\bar{a}+t\bar{v}$. Si componemos a esta trayectoria con la función $f$, obtenemos una función $G: [0,1] \to \mathbb{R}$ dada por $$G(t)=(f\circ \gamma )(t)=f(\bar{a}+t\bar{v}).$$

Por la hipótesis de diferenciabilidad de $f$, es una función derivable de una variable real. Por la regla de la cadena su derivada está dada por la siguiente expresión:

\begin{align*}
G^{\prime}(t)&=v_{1}\frac{\partial f}{\partial x_{1}}(\bar{a}+t\bar{v})+\dots +v_n\frac{\partial f}{\partial x_n}(\bar{a}+t\bar{v})
\end{align*}

Vamos a introducir una notación muy usada y útil para el desarrollo que estamos haciendo. Definiremos un operador con la expresión anterior simplemente como

\[ G^{\prime}(t)=(\bar{v}\cdot \triangledown )f(\bar{a}+t\bar{v}).\]

Esta expresión no se sigue de manera tan formal de cosas que hemos hecho antes, pero observa que tiene sentido. En la expresión $\bar{v}\cdot \triangledown$ estamos haciendo algo así como un «producto punto de operadores». En el fondo, este operador manda a cada función diferenciable $f$ a su derivada direccional en la dirección de $\bar{v}$.

Para poder hablar de Taylor, necesitamos derivar iteradamente. Podemos entonces tomar ahora $G’$ y derivarla nuevamente, de donde obtendríamos

\begin{align*}
G^{\prime \prime} (t) &= (\bar{v}\cdot \triangledown) G'(\bar{a}+t\bar{v})\\
&=(\bar{v}\cdot \triangledown)\left((\bar{v}\cdot \triangledown)f(\bar{a}+t\bar{v})\right)\\
&=\left((\bar{v}\cdot \triangledown)(\bar{v}\cdot \triangledown)\right) f(\bar{a}+t\bar{v}).
\end{align*}

Es importante que medites en por qué se da la redistribución de paréntesis que hicimos en la última igualdad. Simplificaremos la expresión $(\bar{v}\cdot \triangledown)(\bar{v}\cdot \triangledown )$ como $(\bar{v}\cdot \triangledown)^2$, y de manera similar definimos $(\bar{v}\cdot \triangledown)^k$ como componer el operador $k$ veces. Continuando como arriba, bajo las hipótesis adecuadas de diferenciabilidad llegamos al siguiente resultado.

Proposición. Sea $k$ un entero positivo y $f:S\subseteq \mathbb{R}^{n}\to \mathbb{R}$ con $S$ abierto y derivadas parciales continuas de orden $1,2,\ldots,k$. Sea $\bar{a}\in S$, y $\bar{v}$ un vector tal que $\bar{a}+t\bar{v}\in S$ para todo $t\in [0,1]$. Entonces:

\begin{equation}\label{eq:iteradas}\left( \frac{d}{dt} \right)^{k}f(\bar{a}+t\bar{v})=(\bar{v}\cdot \triangledown )^{k}f(\bar{a}+t\bar{v}).\end{equation}

Demostración. Queda como tarea moral. Se sugiere hacerlo por inducción.

$\square$

Algo sorprendente y curioso que sucede con las expresiones del estilo $(\bar{v}\cdot \triangle)^k$ es que «se vale el binomio de Newton» para ellas, o en general, cualquier fórmula para elevar a la $k$-ésima potencia. Esto se ve muy claro en el caso de $f:S\subset \mathbb{R}^2\to \mathbb{R}$ y derivadas de orden $2$. Si tenemos $\bar{v}=(v_1,v_2)$, entonces $\bar{v}\cdot \triangledown=v_1\frac{\partial}{\partial x} + v_2\frac{\partial}{\partial y}$. Se puede demostrar, por ejemplo, que si las $k$-ésimas parciales son continuas entonces

\[ \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y}\right)^{k}=\sum_{i
=0}^{k}\binom{k}{i}v_1^iv_2^{k-i}\frac{\partial ^{i}}{\partial x^{i}}\frac{\partial^{k-i}}{\partial y^{k-i}}.\]

Un caso particular sería el de $n=2$ y $k=2$, en el que se obtiene que:

\begin{equation} \label{eq:binomio} \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{2}=v_1^{2}\frac{\partial ^{2}}{\partial x^{2}}+2{v_1}{v_2}\frac{\partial ^{2}}{\partial x\partial y}+v_2^{2}\frac{\partial ^{2}}{\partial y^{2}}.\end{equation}

En la práctica esto nos permitirá encontrar las expresiones que necesitamos para el polinomio de Taylor para campos escalares. Observa que estas expresiones son también las que nos confirman que la expresión que obtendremos será un polinomio en $v_1,v_2$ (en general, en las entradas de $\bar{v}$), pues tras aplicar el operador en $f$ y evaluar en un punto, finalmente \eqref{eq:binomio} quedará escrito para ciertas constantes $A,B,C$ como $$Av_1^2+2Bv_1v_2+Cv_2^2,$$ lo cual en efecto es un polinomio (en este caso de grado $2$ y dos variables).

Polinomio de Taylor para campos escalares

Con la notación que hemos introducido, ahora sí podemos enunciar apropiadamente el polinomio de Taylor. Pensemos en que $f$ es $k+1$ veces diferenciable y que todas esas derivadas son continuas. En la sección anterior vimos que $G=f\circ \gamma$ también sería $k+1$ veces diferenciable y dimos fórmulas para sus derivadas en términos de la notación $\bar{v}\cdot \triangledown$.

Aplicando el teorema de Taylor con la versión de residuo dada en la ecuación \eqref{eq:residuo}, para la función $G$, en los puntos $a=0$, $x=1$, tenemos que existe $\xi\in[0,1]$ tal que se satisface lo siguiente:

\[ G(1)=G(0)+G^{\prime}(0)+\frac{G^{(2)}(0)}{2!}+\dots +\frac{G^{(k)}(0)}{k!}+\frac{G^{(k+1)}(\xi)}{(k+1)!}.\]

Al usar las fórmulas dadas por la ecuación \eqref{eq:iteradas}, obtenemos que

\begin{align*}
G^{(s)}(0)&=(\bar{v}\cdot \triangledown )^{s}f(\bar{a}) & \text{para $s\leq k$}\\
G^{(k+1)}(\xi)&=(\bar{v}\cdot \triangledown )^{k+1}f(\bar{a}+\xi \bar{v}).
\end{align*}

Así, reescribiendo todo en términos de $f$ obtenemos que:

\begin{equation}\label{eq:prepoly}f(\bar{a}+\bar{v})=f(\bar{a})+\frac{(\bar{v}\cdot \triangledown )f(\bar{a})}{1!}+\dots +\frac{(\bar{v}\cdot \triangledown)^{k}f(\bar{a})}{k!}+\frac{(\bar{v}\cdot \triangledown )^{k+1}f(\bar{a}+\tau \bar{v})}{(k+1)!}.\end{equation}

Si de esta expresión quitamos el último término (el correspondiente al residuo) y hacemos la sustitución $\bar{w}=\bar{a}+\bar{v}$, obtenemos la siguiente expresión:

\begin{equation} \label{eq:poltaylor}T_{k,\bar{a}}(\bar{w}):=f(\bar{a})+\frac{((\bar{w}-\bar{a})\cdot \triangledown )f(\bar{a})}{1!}+\dots +\frac{((\bar{w}-\bar{a})\cdot \triangledown)^{k}f(\bar{a})}{k!}\end{equation}

le llamamos el polinomio de Taylor de $f$ de grado $k$ alrededor de $\bar{a}$ y converge a $f(\bar{a})$ conforme $\bar{w}\to \bar{a}$.

Ejemplo de polinomio de Taylor para campos escalares

Ejemplo. Determinemos el polinomio de Taylor de grado 3 de la expresión $f(x,y)=e^{5x+3y}$ alrededor del punto $(0,0)$. Para ello, usaremos la expresión de la fórmula \eqref{eq:prepoly} quitando el residuo y fórmulas tipo «binomio de Newton» como la de la ecuación \eqref{eq:binomio}.

Comencemos con el término de grado $1$. Está dado por el operador

$$\left(v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y}\right)$$

que aplicado a nuestra función es

$$((v_1,v_2)\cdot \triangledown)f(x,y)=5v_1e^{5x+3y}+3v_2e^{5x+3y}.$$

Necesitaremos su evaluación en $(x,y)=(0,0)$, que es $5v_1+3v_2$.

Para pasar al término de segundo grado, necesitamos

\[\left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{2}=v_1^{2}\frac{\partial ^{2}}{\partial x^{2}}+2{v_1}{v_2}\frac{\partial ^{2}}{\partial x\partial y}+v_2^{2}\frac{\partial ^{2}}{\partial y^{2}}.\]

Al aplicar este operador en nuestra $f$, se obtiene:

$$((v_1,v_2)\cdot \triangledown)^2f(x,y)=25v_1^2e^{5x+3y}+30{v_1}{v_2}e^{5x+3y}+9v_2^2 e^{5x+3y}$$

Lo necesitaremos evaluado en $(0,0)$, que es $25v_1^2+30v_1v_2+9v_2^2$.

Finalmente, también requeriremos del término de orden $3$, para el cual es necesario calcular el siguiente operador

\[ \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{3}=v_1^{3} \frac{\partial}{\partial x^3}+3v_1^{2}{v_2}\frac{\partial}{\partial x^{2}\partial y}+3v_1v_2^{2}\frac{\partial}{\partial x \partial y^2}+v_2^3\frac{\partial}{\partial y^3},\]

y aplicarlo a nuestra $f$ para obtener

$$((v_1,v_2)\cdot \triangledown)^3f(x,y)=125v_1^3e^{5x+3y}+225v_1^2v_2e^{5x+3y}+135v_1v_2^2 e^{5x+3y}+27v_2^3e^{5x+3y}.$$

Una vez más, requerimos la evaluación en $(0,0)$, la cual es $125v_1^3+225v_1^2v_2+135v_1v_2^2+27v_2^3$.

Juntando todo esto, obtenemos que

\begin{align*}
f(v_1,v_2)&=f(0,0)+\frac{((x,y)\cdot \triangledown )f(0,0)}{1!}+\frac{((x,y)\cdot \triangledown )^{2}f(0,0)}{2!}+\frac{((x,y)\cdot \triangledown)^{3}f((0,0))}{3!}\\
&=1+5v_1+3v_2+\frac{25v_1^2+30v_1v_2+9v_2^2}{2}+\frac{125v_1^3+225v_1^2v_2+135v_1v_2^2+27v_2^3}{6}.
\end{align*}

$\square$

Observa que, en efecto, obtenemos un polinomio en dos variables y de grado tres.

Los casos especiales para grado $1$ y grado $2$

Las presentaciones más clásicas del polinomio de Taylor para campos escalares de varias variables son las versiones de primero y segundo grado. Para el polinomio de primer grado, tenemos la siguiente expresión:

$$T_{1,\bar{a}}(\bar{a}+\bar{v})=f(\bar{a})+\sum_{i=1}^{n}(v_i)\frac{\partial f}{\partial x_{i}}(\bar{a}).$$

En el caso de la presentación clásica para la fórmula de segundo orden tenemos

$$\frac{(\bar{v}\cdot \triangledown)^{2}f}{2!}(\bar{a})=\sum_{i=1}^n\sum_{j=1}^nv_{i}v_{j}\frac{\partial ^{2}f}{\partial x_{j}\partial x_{i}}(\bar{a})$$

Donde

$$T_{2,\bar{a}}(\bar{a}+\bar{v})=f(\bar{a})+\sum_{i=1}^{n}v_{i}\frac{\partial f}{\partial x_{i}}(\bar{a})+\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^{n}v_{i}v_{j}\frac{\partial ^{2}f}{\partial x_{j}\partial x_{i}}(\bar{a}).$$

Esta suma tendrá utilidad especial hacia el final del curso, cuando hablemos de optimización. La expresión también puede ponerse en términos de otro objeto matemático que se llama la matriz Hessiana, la cual definiremos más adelante una vez que hayamos hecho un repaso de álgebra lineal, matrices y formas cuadráticas.

Mas adelante…

Con lo que hemos trabajado hasta ahora hemos desarrollado un muy buen entendimiento de las curvas y de los campos escalares, que respectivamente son funciones $f:\mathbb{R}\to \mathbb{R}^m$ y $f:\mathbb{R}^n\to \mathbb{R}$. Sin embargo, nos gustaría ahora poder hablar con mucha mayor generalidad y entender a las funciones del estilo $f:\mathbb{R}^n\to \mathbb{R}^m$. Ya entendimos un poco de cómo son en términos de continuidad, cuando hablamos de la topología de $\mathbb{R}^n$. Sin embargo, para poder hablar de su diferenciabilidad y de otros resultados teóricos será necesario hacer un repaso de algunos conceptos adicionales de álgebra lineal. Por esta razón, en la siguiente unidad hablaremos de temas como transformaciones lineales, matrices, sistemas de ecuaciones, formas lineales y bilineales.

Tarea moral

  1. Encuentra el polinomio de Taylor de primer grado para las siguientes funciones:
    • $f(x,y)=e^(x+y)$
    • $f(x,y)=e^{sen(x+y)}$
    • $f(x,y)=x^2y^2+x+y$
  2. Calcula el polinomio de Taylor de segundo grado para los siguientes campos escalares en el punto dado:
    • $f(x,y)=x^2+xy$ en el punto $(1,1)$.
    • $f(x,y,z)=xsen(yz)$ alrededor del punto $(\pi ,\pi ,\pi)$.
  3. Demuestra por inducción la fórmula \[\left( \frac{d}{dt} \right)^{k}f(\bar{a}+t\bar{v})=(\bar{v}\cdot \triangledown )^{k}f(\bar{a}+t\bar{v}).\]
  4. Demuestra por inducción \[ \left( x\frac{\partial}{\partial x}+y\frac{\partial}{\partial y}\right)^{k}=\sum_{i=1}^{k}\binom{k}{i}x^{i}y^{k-i}\frac{\partial ^{i}}{\partial x^{i}}\frac{\partial^{k-i}}{\partial y^{k-i}}.\]
  5. En esta entrada sólo discutimos con detalle lo que pasa con el polinomio de Taylor «hasta cierto grado $k$». Sin embargo, no dimos una versión que generalice el polinomio de Taylor para cuando usamos todos los términos posibles (como en la ecuación \eqref{eq:taylor-inf}). Observa que en el recordatorio de una variable real sí pusimos el resultado para la serie de Taylor. Enuncia y demuestra una versión para campos escalares.

Entradas relacionadas