Archivo de la etiqueta: bimediana

Geometría Moderna I: Cuadrilátero ortodiagonal

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Decimos que un cuadrilátero convexo es ortodiagonal si sus diagonales son perpendiculares. En esta entrada veremos algunas propiedades del cuadrilátero ortodiagonal.

Dos caracterizaciones para el cuadrilátero ortodiagonal

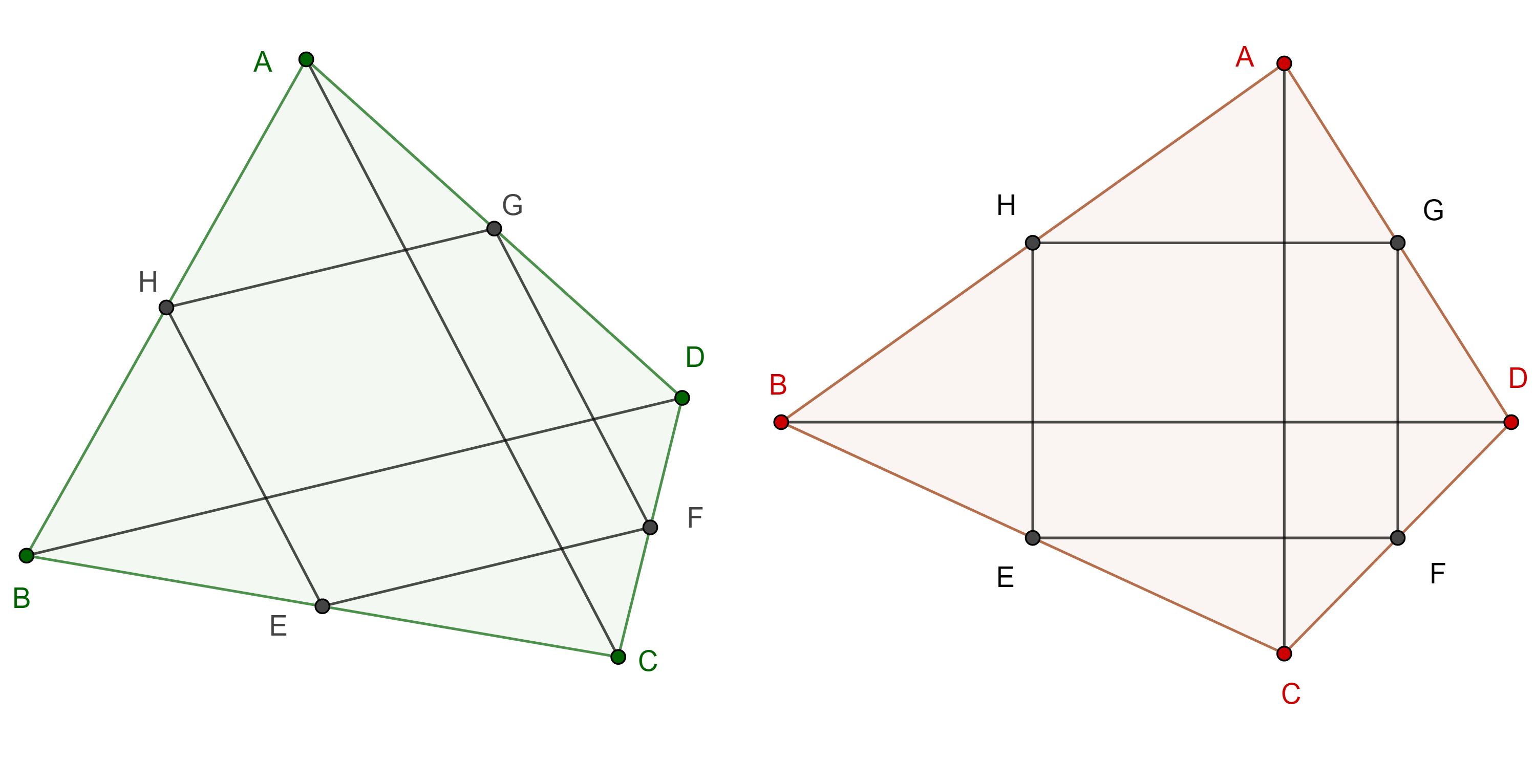
Teorema 1. Un cuadrilátero convexo es ortodiagonal si y solo si la suma de los cuadrados de dos lados opuestos es igual a la suma de los cuadrados de los restantes lados opuestos.

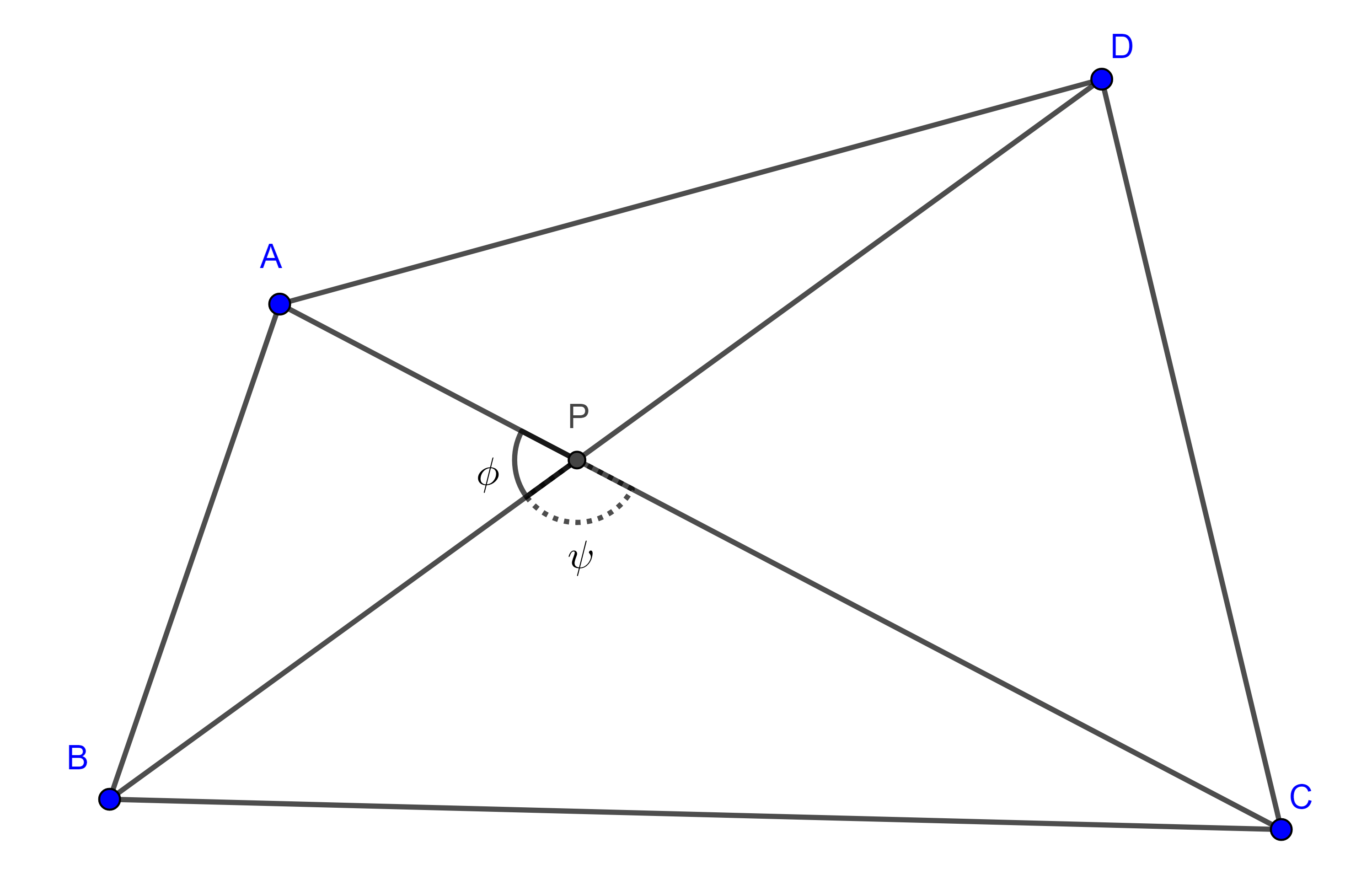
Demostración. Sea $\square ABCD$ convexo, consideremos $P$ la intersección de las diagonales, $\phi = \angle APB$, $\psi = \angle BPC$.

Como $\phi + \psi = \pi$ entonces $\cos \phi = – \cos \psi$.

Figura 1

Aplicando la ley de los cosenos a los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ obtenemos,
$AB^2 = AP^2 + BP^2 – 2AP \times BP \cos \phi$,
$BC^2 = BP^2 + CP^2 – 2BP \times CP \cos \psi$,
$CD^2 = CP^2 + DP^2 – 2CP \times DP \cos \phi$,
$AD^2 = AP^2 + DP^2 – 2AP \times DP \cos \psi$.

Por lo tanto,
$AB^2 + CD^2 – BC^2 – AD^2 $
$= (AP^2 + BP^2 + 2AP \times BP \cos \psi) + (CP^2 + DP^2 + 2CP \times DP \cos \psi)$
$- (BP^2 + CP^2 – 2BP \times CP \cos \psi) – (AP^2 + DP^2 – 2AP \times DP \cos \psi)$
$= 2 \cos \psi (AP \times BP + CP \times DP + BP \times CP + AP \times DP)$.

Notemos que $0 < \psi < \pi$, por lo tanto,
$\overline{AC} \perp \overline{BD} \Leftrightarrow  \psi = \dfrac{\pi}{2} \Leftrightarrow  \cos \psi = 0$
$\Leftrightarrow  AB^2 + CD^2 = BC^2 + AD^2$.

$\blacksquare$

Proposición 1. Sean $\square ABCD$ convexo, $P$ la intersección de las diagonales, $m_{i}$ con $i = 1, 2, 3, 4$ las medianas de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$, que pasan por $P$, entonces $\square ABCD$ es ortodiagonal si y solo si $m_{1}^2 + m_{3}^2 = m_{2}^2 + m_{4}^2$.

Figura 2

Demostración. Aplicando el teorema de Apolonio para calcular la longitud de las medianas en términos de los lados de sus respectivos triángulos obtenemos,

$m_{1}^2 + m_{3}^2 = m_{2}^2 + m_{4}^2$
$\Leftrightarrow  4m_{1}^2 + 4m_{3}^2 = 4m_{2}^2 + 4m_{4}^2$
$\Leftrightarrow  2(AP^2 + BP^2) – AB^2 + 2(CP^2 + DP^2) – CD^2$
$ = 2(BP^2 + CP^2) – BC^2 + 2(AP^2 + DP^2) – AD^2$
$\Leftrightarrow  AB^2 + CD^2 = BC^2 + AD^2$.

La última doble implicación es cierta por el teorema 1.

$\blacksquare$

Circunferencia de los 8 puntos del cuadrilátero ortodiagonal

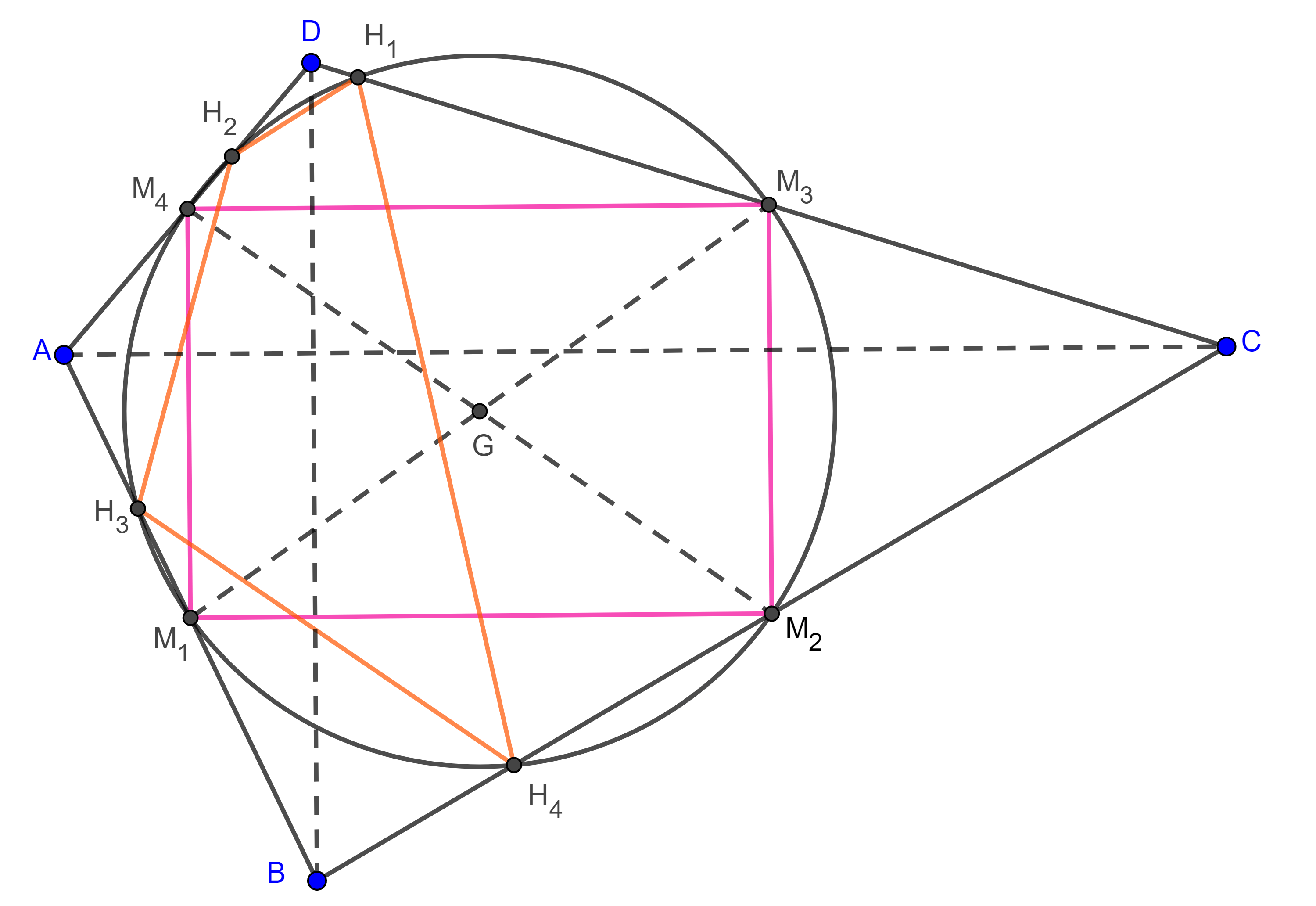
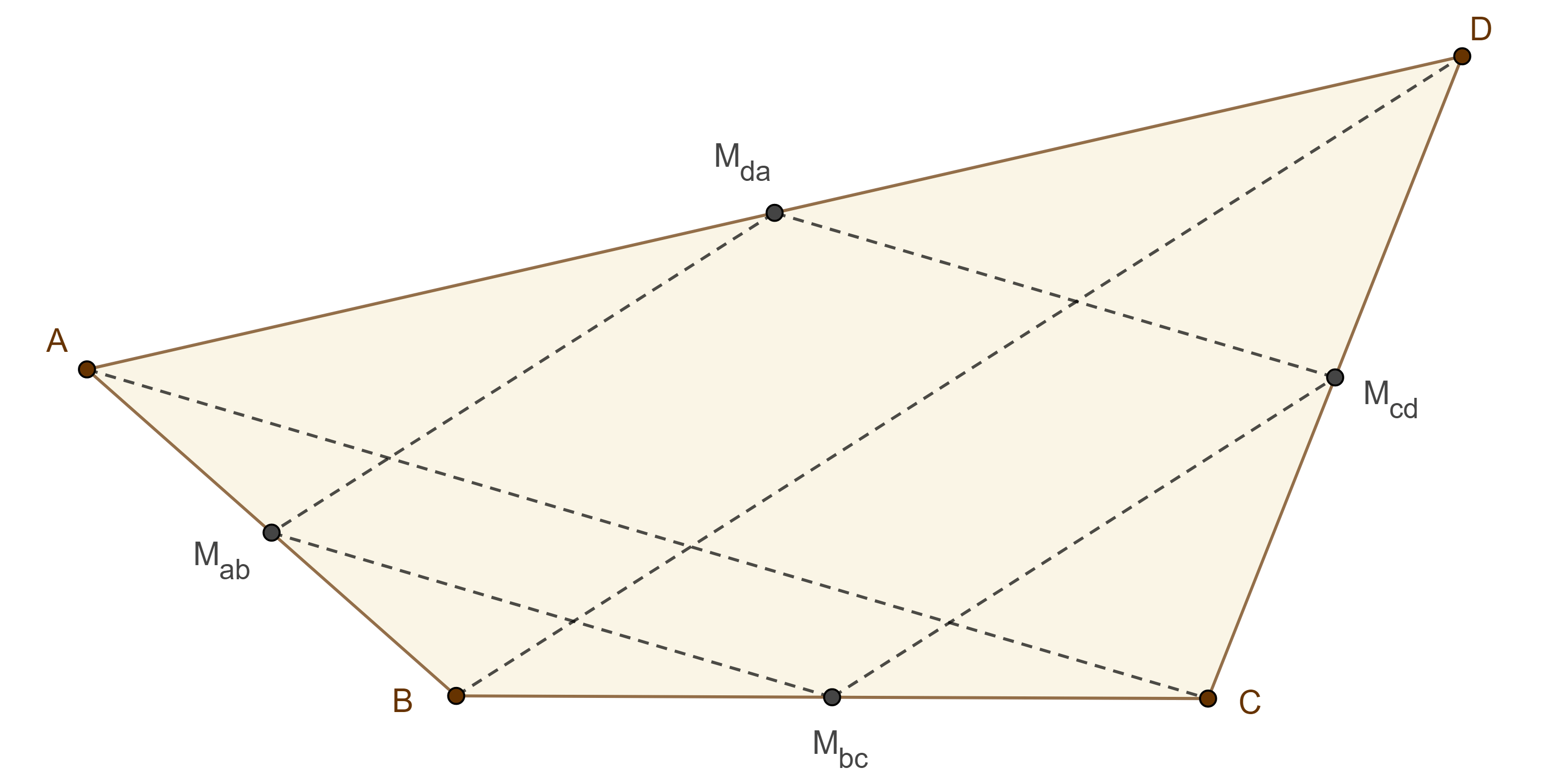
Definición. Al cuadrilátero formado por los pies de las $m$-alturas de un cuadrilátero convexo se le conoce como cuadrilátero principal órtico.

Lema 1. Los vértices del paralelogramo de Varignon y los vértices del cuadrilátero principal órtico de un cuadrilátero convexo que se encuentran sobre lados opuestos, están en dos circunferencias con centro en $G$, el centroide del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo $M_{1}$, $M_{2}$, $M_{3}$ y $M_{4}$ los puntos medios de $AB$, $BC$, $CD$ y $AD$ respectivamente.

Recordemos que las diagonales del cuadrilátero de Varignon, es decir, las bimedianas $M_{1}M_{3}$ y $M_{2}M_{4}$, se intersecan en su punto medio, $G$, al que llamamos centroide.

Figura 3

Sean $M_{1}H_{1}$, $M_{2}H_{2}$, $M_{3}H_{3}$ y $M_{4}H_{4}$ las $m$-alturas de $\square ABCD$.

Por construcción $\angle M_{3}H_{1}M_{1} = \angle M_{1}H_{3}M_{3} = \dfrac{\pi}{2}$, por lo tanto, $M_{1}M_{3}$ es el diámetro de una circunferencia con centro en $G$ y que pasa por $H_{1}$ y $H_{3}$.

De manera análoga podemos ver que los puntos $H_{2}$ y $H_{4}$ están en una circunferencia de diámetro $M_{2}M_{4}$ con centro en $G$.

$\blacksquare$

Teorema 2. Los vértices del paralelogramo de Varignon y los vértices del cuadrilátero principal órtico de un cuadrilátero convexo están en una misma circunferencia con centro en el centroide del cuadrilátero si y solo si el cuadrilátero es ortodiagonal.

A dicha circunferencia se le conoce como primera circunferencia de los ocho puntos del cuadrilátero ortodiagonal.

Demostración. El lema anterior nos dice que los puntos ${M_{1}, H_{1}, M_{3}, H_{3}}$ y ${M_{2}, H_{2}, M_{4}, H_{4}}$ están en dos circunferencias con centro en $G$, el centroide de $\square ABCD$.

Figura 4

Además, las bimedianas de un cuadrilátero se bisecan en el centroide del cuadrilátero.

Por lo tanto, el paralelogramo de Varignon y el cuadrilátero principal órtico son ambos cíclicos y comparten la misma circunferencia si y solo si $M_{1}M_{3} = M_{2}M_{4}$, es decir, las bimedianas tienen la misma longitud, si y solo si el paralelogramo de Varignon es un rectángulo si y solo si $\square ABCD$  es ortodiagonal.

$\blacksquare$

Teorema de Brahmagupta

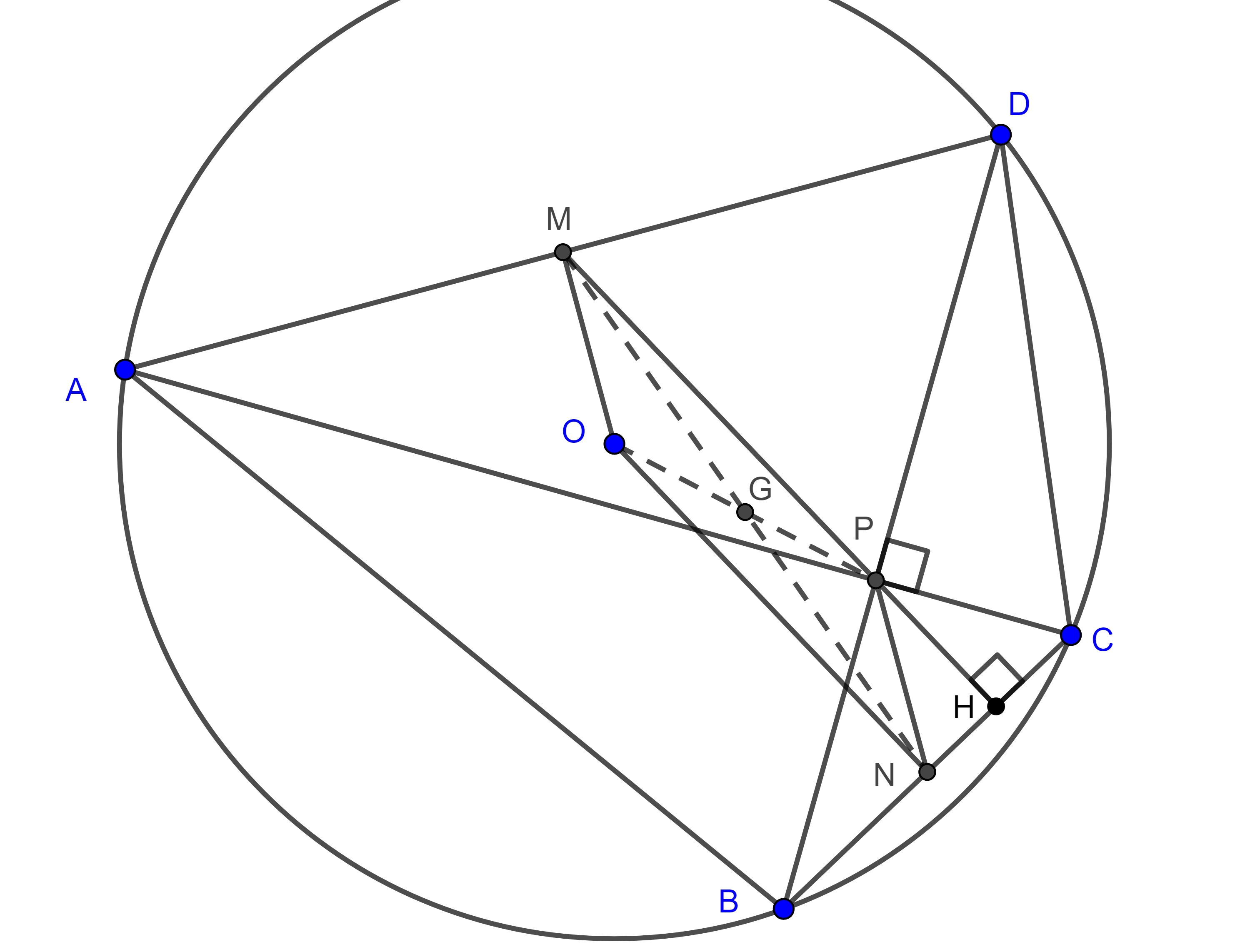
Teorema 3. de Brahmagupta. En un cuadrilátero ortodiagonal y cíclico, el anticentro coincide con la intersección de las diagonales del cuadrilátero.

Demostración. Recordemos que en un cuadrilátero cíclico las $m$-alturas son concurrentes y definimos al punto de concurrencia como el anticentro, el cual tiene la propiedad de ser simétrico al circuncentro respecto a $G$, el centroide del cuadrilátero.

Sea $\square ABCD$ ortogonal y cíclico, tracemos el segmento $MP$ que pasa por el punto medio de $AB$ y la intersección de las diagonales $P$, consideremos $H = MP \cap BC$.

Figura 5

En un triángulo rectángulo la distancia del punto medio de la hipotenusa a los tres vértices del triángulo es la misma, por lo tanto, $\triangle AMP$ es isósceles pues $\angle DPA = \dfrac{\pi}{2}$.

Esto implica que $\angle PAM = \angle MPA = \angle HPC$.

Donde la última igualdad se debe a que los ángulos considerados son opuestos por el vértice, además $\angle ADP = \angle PCH$.

Como consecuencia de las últimas dos igualdades tenemos $\triangle APD \sim \triangle PHC$, por criterio de semejanza AA.

Entonces $\angle CHP = \angle DPA = \dfrac{\pi}{2}$, por lo tanto, $MH$ es una $m$-altura de $\square ABCD$.

De manera análoga podemos ver que las otras $m$-alturas pasan por $P$ y como todas las $m$-alturas de un cuadrilátero cíclico concurren en el anticentro entonces este coincide con $P$.

$\blacksquare$

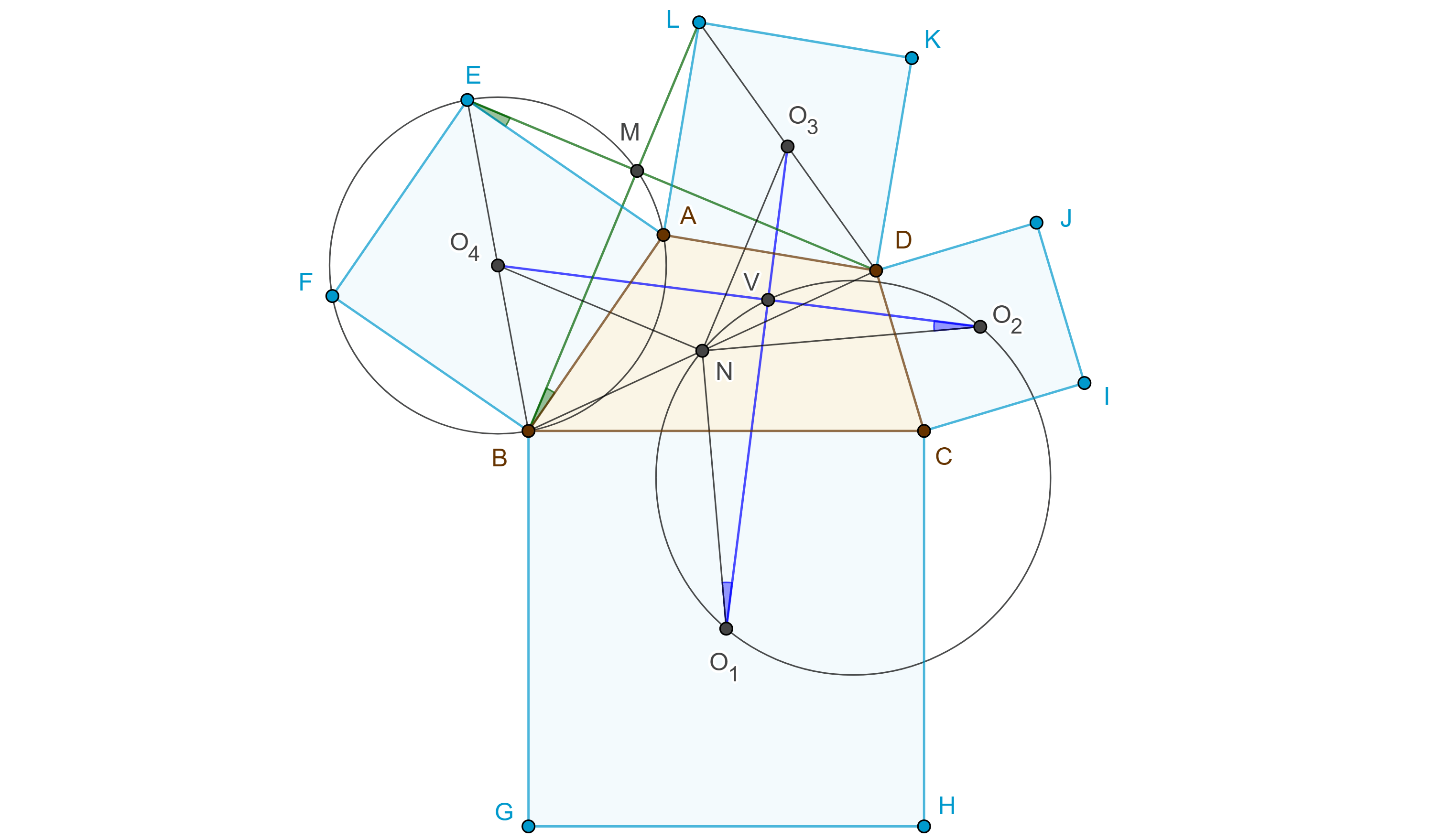
Proposición 2. En un cuadrilátero cíclico y ortodiagonal la distancia desde el circuncentro a uno de los lados del cuadrilátero es igual a la mitad del lado opuesto.

Demostración. Sea $G$ el centroide del cuadrilátero $\square ABCD$ (figura 5) y $N$ el punto medio de $BC$.

Sabemos que $G$ biseca a $MN$ y a $OP$, por lo tanto, $\square MONP$ es un paralelogramo, en consecuencia, la distancia de $O$ a $BC$ es $ON = MP = \dfrac{AD}{2}$.

Donde la primera igualdad se da porque $\square MONP$ es paralelogramo y la segunda porque $M$ es el punto medio de la hipotenusa en $\triangle APD$.

$\blacksquare$

Corolario 1. El circunradio de un cuadrilátero cíclico y ortodiagonal $\square ABCD$ con lados $a = AB$, $b = BC$, $c = CD$ y $d = AD$ cumple la siguiente igualdad, $4R^2 = a^2 + c^2 = b^2 + d^2$.

Demostración. Por la prueba de la proposición anterior sabemos que $\angle ONB = \dfrac{\pi}{2}$ (figura 5), por lo tanto podemos aplicar el teorema de Pitágoras a $\triangle ONB$.

$R^2 = OB^2 = ON^2 + BN^2 = (\dfrac{AD}{2})^2 + (\dfrac{BC}{2})^2$
$\Leftrightarrow  4R^2 = d^2 + b^2$.

De manera análoga se ve que $4R^2 = a^2 + c^2$.

$\blacksquare$

Circunferencia de Droz-Farny

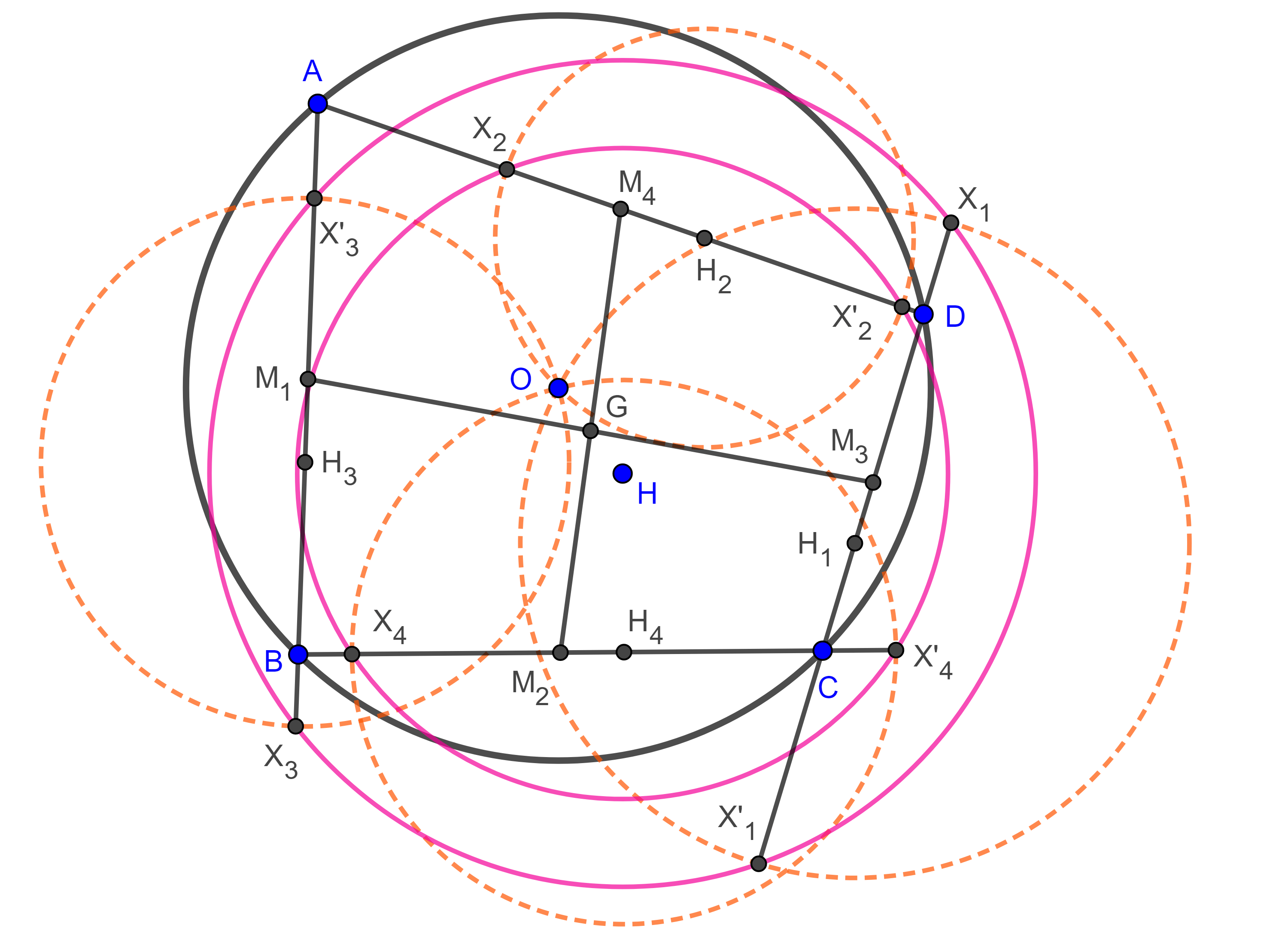
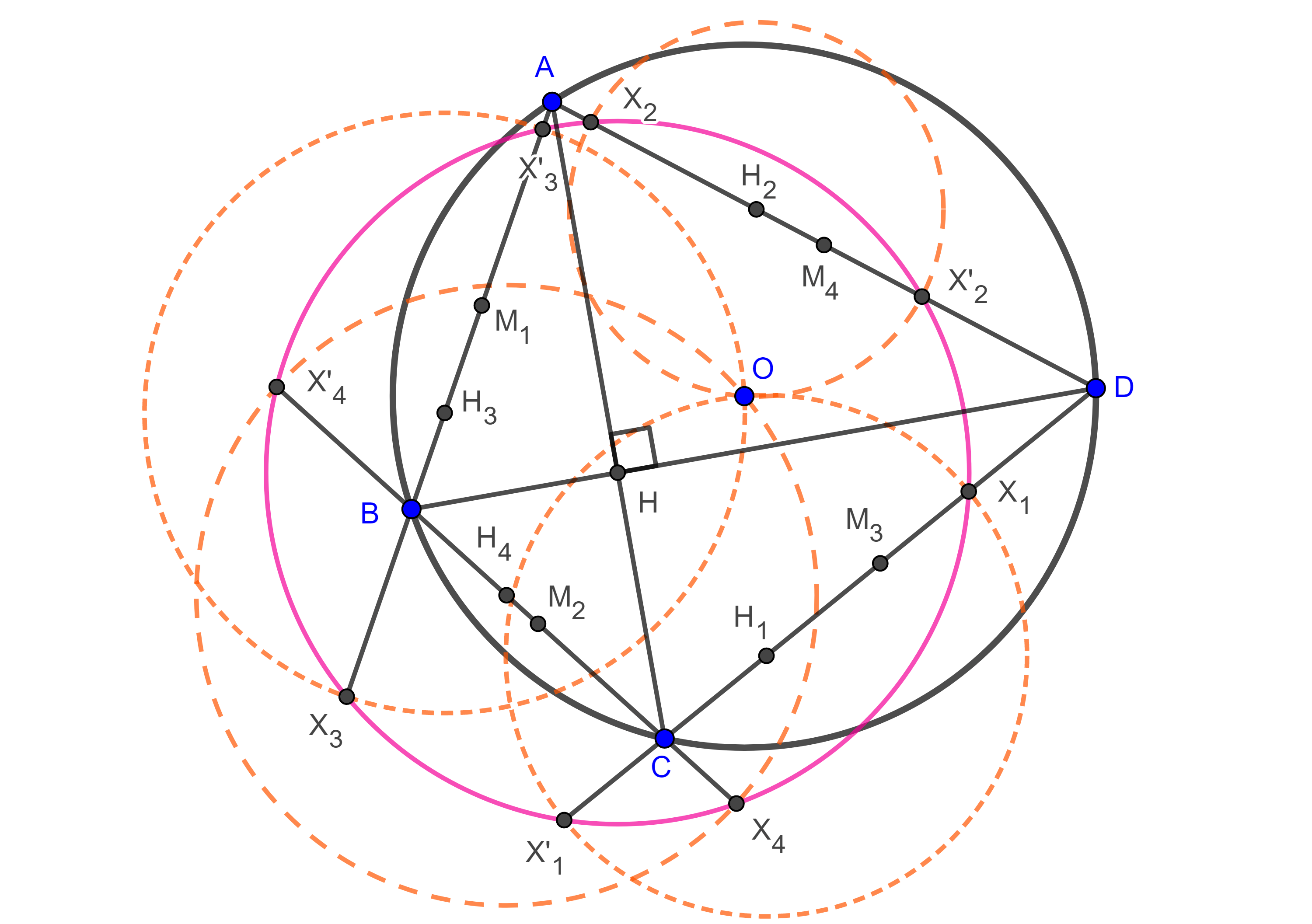
Lema 2. Sean $\square ABCD$ cíclico $O$ y $H$ el circuncentro y el anticentro respectivamente, consideremos el cuadrilátero principal órtico con vértices $H_{1} \in CD$, $H_{2} \in AD$, $H_{3} \in AB$, $H_{4} \in BC$, sean $X_{i}$, $X’_{i}$ las intersecciones de $(H_{i}, H_{i}O)$ (la circunferencia con centro en $H_{i}$ y radio $H_{i}O$) con el lado de $\square ABCD$ al que pertenece $H_{i}$. Entonces los puntos ${X_{1}, X’_{1}, X_{3}, X’_{3}}$ y los putos ${X_{2}, X’_{2}, X_{4}, X’_{4}}$ pertenecen a dos circunferencias con centro en $H$.

Figura 6

Demostración. Veamos que $\square X_{1}X’_{1}X_{3}X’_{3}$ es cíclico.

Dado que $HH_{1}$ es la mediatriz de $X_{1}X’_{1}$ entonces $HX_{1} = HX’_{1}$, de manera similar vemos que $HX_{3} = HX’_{3}$.

Por otra parte, como $X_{1} \in (H_{1}, H_{1}O)$, entonces $H_{1}X_{1} = H_{1}O$.

Sea $G$ el centroide del cuadrilátero $\square ABCD$ y recordemos que $G$ biseca a $OH$.

Aplicando el teorema de Pitágoras a $\triangle HH_{1}X_{1}$ y el teorema de Apolonio a la mediana $H_{1}G$ en $\triangle HH_{1}O$ obtenemos,
$HX_{1}^2 = HH_{1}^2 + H_{1}X_{1}^2 = HH_{1}^2 + H_{1}O^2$
$\begin{equation} = 2H_{1}G^2 + 2OG^2. \end{equation}$

De manera análoga calculamos
$\begin{equation} HX_{3}^2 = 2H_{3}G^2 + 2OG^2. \end{equation}$

Por el lema 1, $H_{1}$ y $H_{3}$ están en una misma circunferencia con centro en $G$ por lo tanto $H_{1}G = H_{3}G$,  de $(1)$ y $(2)$ se sigue que $HX’_{1} = HX_{1} = HX_{3} = HX’_{3}$.

Así, $X_{1}$, $X’_{1}$, $X_{3}$ y $X’_{3}$ están en una misma circunferencia con centro en $H$.

De manera análoga se ve que $X_{2}$, $X’_{2}$, $X_{4}$, $X’_{4}$ están en una misma circunferencia concéntrica con la anterior.

$\blacksquare$

Teorema 4. Sea $\square ABCD$ cíclico entonces los 8 puntos $X_{i}$, $X’_{i}$ con $i = 1, 2, 3, 4$ se encuentran en una misma circunferencia con centro en $H$, el anticentro del cuadrilátero cíclico, si y solo si $\square ABCD$ es ortodiagonal, esta es la primera circunferencia de Droz-Farny del cuadrilátero.

Demostración. Los puntos consideraos son concíclicos si y solo si las dos circunferencias a las que pertenecen tienen el mismo radio es decir $HX_{1} = HX_{2} = HX_{3} = HX_{4}$.

Figura 7

En la demostración del lema anterior vimos que $HX_{i}^2 = 2H_{i}G^2 + 2OG^2$.

Esto implica que $HX_{1} = HX_{2} = HX_{3} = HX_{4} \Leftrightarrow  H_{1}G = H_{2}G = H_{3}G = H_{4}G$, esto quiere decir que los vértices del cuadrilátero principal órtico de $\square ABCD$  están en una misma circunferencia con centro en $G$.

Por el teorema 3, esto ocurre si y solo si $\square ABCD$  es ortodiagonal.

$\blacksquare$

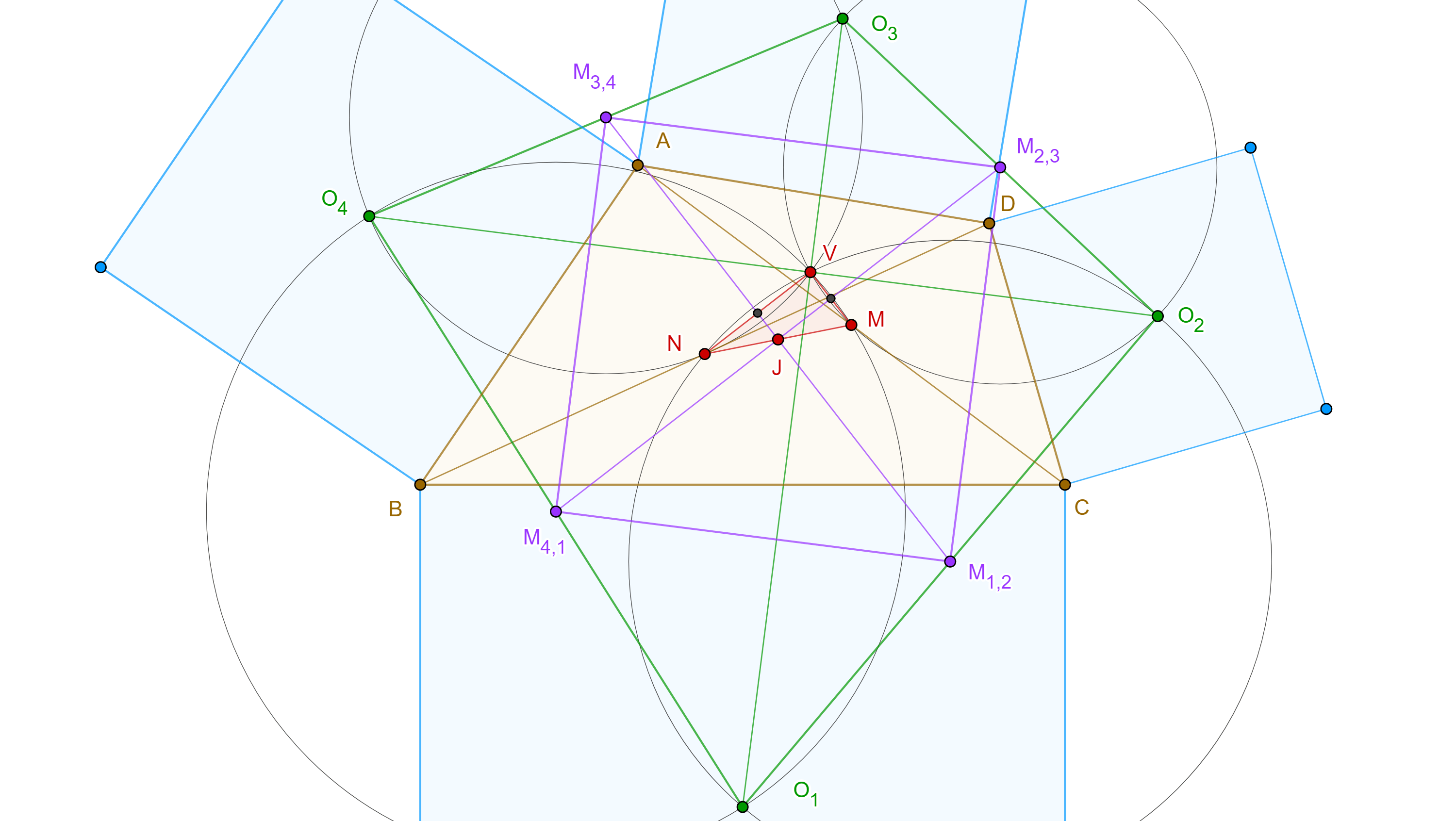
Proposición 3. Sea $\square ABCD$ cíclico y ortodiagonal entonces el radio de la primera circunferencia de Droz-Farny es igual al circunradio de $\square ABCD$.

Demostración. Por la prueba de lema 2 sabemos que
$\begin{equation} HX_{1}^2 = 2H_{1}G^2 + 2OG^2. \end{equation}$

El teorema 3 nos dice que el anticentro $H$ coincide con $P$, la intersección de las diagonales, por lo tanto $\triangle CHD$ es rectángulo (figura 7). Si $M_{3}$ es el punto medio de $CD$, la hipotenusa, entonces $M_{3}H = M_{3}C$.

Como $O$ esta en la mediatriz de $CD$, entonces $OM_3 \perp CD$.

Aplicando el teorema de Pitágoras a $\triangle OM_{3}C$ y el teorema de Apolonio a la mediana $M_{3}G$ en $\triangle OHM_{3}$ tenemos,

$\begin{equation} OC^2 = M_{3}O^2 + M_{3}C^2 = M_{3}O^2 + M_{3}H^2 = 2M_{3}G^2 + 2OG^2. \end{equation}$

Por el teorema 3, $M_{3}$ y $H_{1}$ están en una misma circunferencia con centro en $G$, por lo tanto $H_{1}G = M_{3}G$.

De $(3)$ y $(4)$ se sigue que $R = OC = HX_{1}$.

$\blacksquare$

Más adelante…

En la siguiente entrada hablaremos sobre cuadriláteros que tienen un incírculo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que de todos los cuadriláteros convexos con diagonales dadas los ortodiagonales son los de mayor área y calcula el área en función de las diagonales.
  2.  Sea $\square ABCD$ un cuadrilátero convexo y $P$ la intersección de las diagonales, consideremos los circunradios $R_{1}$, $R_{2}$, $R_{3}$ y $R_{4}$ de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, demuestra que
    $i)$ $\square ABCD$ es ortodiagonal si y solo si $R_{1}^2 + R_{3}^2 = R_{2}^2 + R_{4}^2$
    $ii)$ $\square ABCD$ es ortodiagonal si y solo si los circuncentros de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ son los puntos medios de los lados del cuadrilátero.
  3. Sea $\square ABCD$ un cuadrilátero convexo y $P$ la intersección de las diagonales, considera las alturas $h_{1}$, $h_{2}$, $h_{3}$ y $h_{4}$, de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ trazadas desde $P$, muestra que $\square ABCD$ es ortodiagonal si y solo si $\dfrac{1}{h_{1}^2} + \dfrac{1}{h_{3}^2} = \dfrac{1}{h_{2}^2} + \dfrac{1}{h_{4}^2}$.
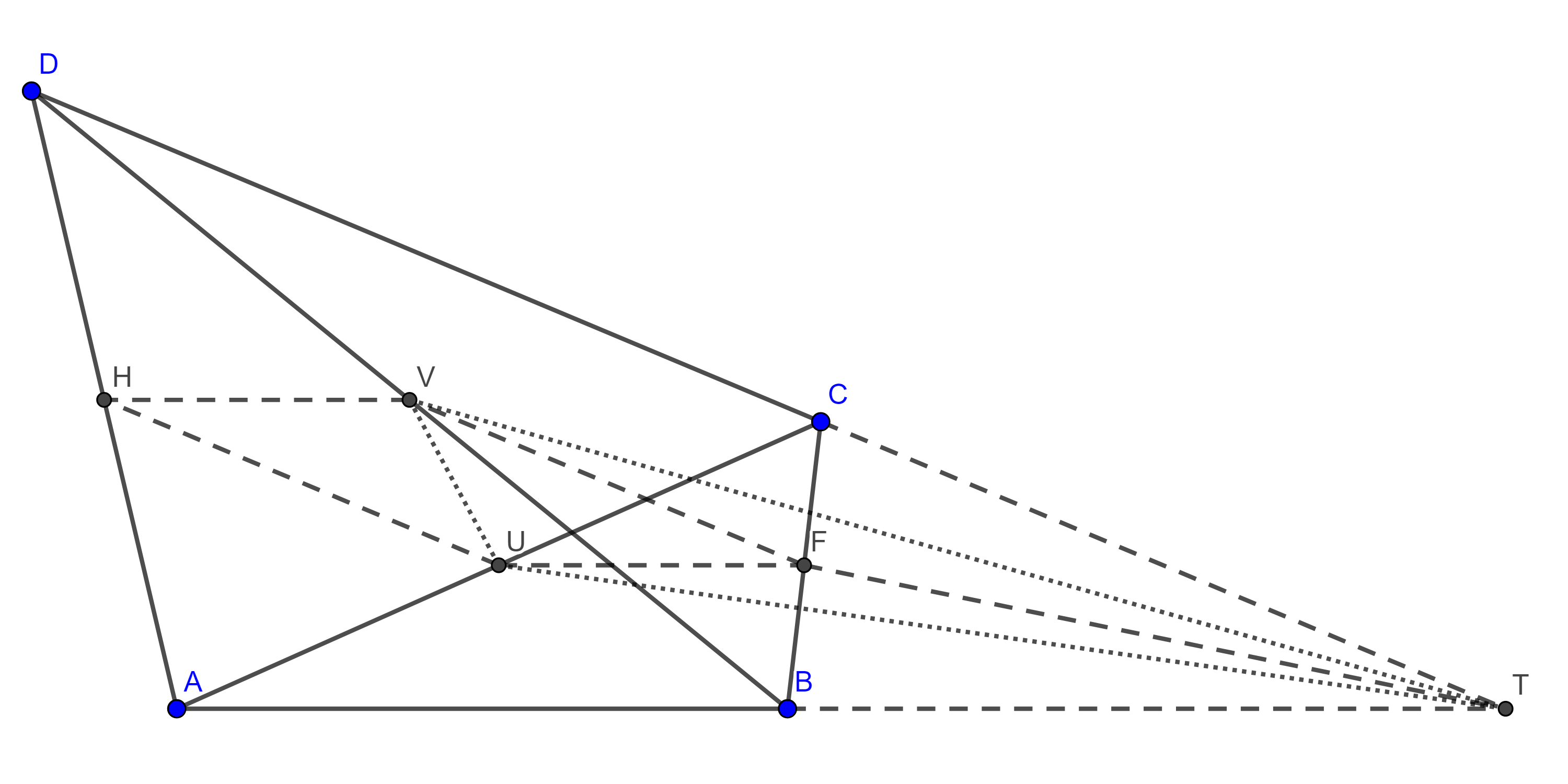
  4. Sean $\square ABCD$ un cuadrilátero convexo, $P$ la intersección de las diagonales, $P_{1}$, $P_{2}$, $P_{3}$ y $P_{4}$ las proyecciones trazadas desde $P$ a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, y considera los puntos $P’_{i}$ con $i = 1, 2, 3, 4$ como las intersecciones de $PP_{i}$ con el lado opuesto al que pertenece $P_{i}$ prueba que
    $i)$ $\square ABCD$ es ortodiagonal si y solo si $\angle CBP + \angle PCB + \angle PAD + \angle ADP = \pi$
    $ii)$ $\square ABCD$ es ortodiagonal si y solo si $\square P_{1}P_{2}P_{3}P_{4}$ es cíclico.
    $iii)$ $\square ABCD$ es ortodiagonal si y solo si los 8 puntos $P_{i}$, $P’_{i}$ con $i = 1, 2, 3, 4$ son cíclicos, a esta circunferencia se le conoce como segunda circunferencia de los ocho puntos del cuadrilátero ortodiagonal.
    $iv)$ La primera y la segunda circunferencias de los ocho puntos de un cuadrilátero ortodiagonal son la misma si y solo si el cuadrilátero es cíclico.
Figura 8
  1. Muestra que un cuadrilátero convexo $\square ABCD$ es ortodiagonal si y solo si el cuadrilátero $\square P’_{1}P’_{2}P’_{3}P’_{4}$, definido en el ejercicio anterior (figura 8), es un rectángulo cuyos lados son paralelos a las diagonales de $\square ABCD$.
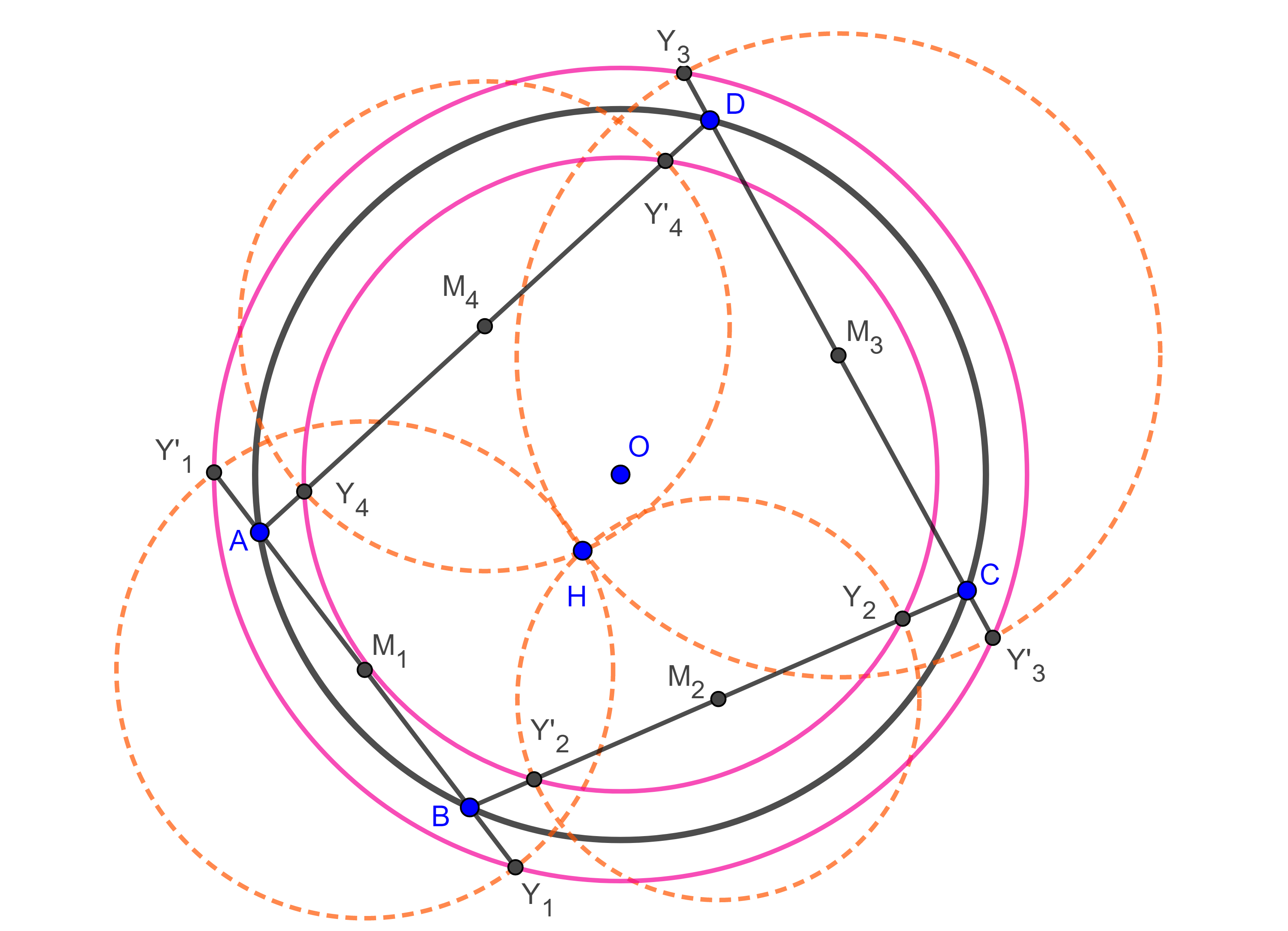
  2. Sean $\square ABCD$ cíclico, $O$ el circuncentro, $H$ el anticentro y considera los puntos medios $M_{i}$ con $i = 1, 2, 3, 4$ del cuadrilátero (figura 9), define $Y_{i}$, $Y’_{i}$ como las intersecciones de $(M_{i}, M_{i}H)$ (la circunferencia con centro en $M_{i}$ y radio $M_{i}H$) con el lado de $\square ABCD$ al que biseca $M_{i}$.
    $i)$ Muestra que los puntos ${Y_{1}, Y’_{1}, Y_{3}, Y’_{3}}$ y los putos ${Y_{2}, Y’_{2}, Y_{4}, Y’_{4}}$ están en dos circunferencias con centro en $O$
    $ii)$ Dichas circunferencias son la misma si y solo si $\square ABCD$ es ortodiagonal, esta es la segunda circunferencia de Droz-Farny del cuadrilátero.
Figura 9

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teoremas de Varignon y Van Aubel

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Con esta entrada damos inicio a la cuarta unidad que tratará sobre cuadriláteros. Comenzaremos hablando sobre el paralelogramo de Varignon y el teorema de Van Aubel.

Área del cuadrilátero

A partir de la ubicación de las diagonales de un cuadrilátero podemos establecer una clasificación de estos.

Un cuadrilátero es convexo si sus dos diagonales se encuentran dentro de él, es cóncavo si tiene una diagonal dentro y otra fuera de él, y es cruzado si las dos diagonales se ubican fuera del cuadrilátero.

El teorema de Varignon nos habla sobre el área de un cuadrilátero en general y ya que no es tan intuitivo definir el área de un cuadrilátero cruzado es necesario introducir el concepto de área orientada.

Consideraremos el área de un triángulo como positiva si recorremos sus vértices en el sentido opuesto a las manecillas del reloj y como negativa en caso contrario.

De esta manera tenemos que para un triángulo $\triangle ABC$,
$(\triangle ABC) = (\triangle BCA) = (\triangle CAB) $
$= – (\triangle CBA) = – (\triangle ACB) = – (\triangle BAC)$.

Figura 1

Definición 1. Definimos el área de un cuadrilátero $\square ABCD$ como la suma de las áreas de los triángulos que se forman al considerar una de sus diagonales, esto es,
$(\square ABCD) = (\triangle ABC) + (\triangle CDA)$.

Notemos que como resultado de esta definición el área del cuadrilátero cruzado resulta ser la diferencia de las áreas de los triángulos que se forman al considerar la intersección cruzada de los lados.

Paralelogramo de Varignon

Teorema 1, de Varignon.
$i)$ Los puntos medios de los lados de un cuadrilátero convexo son los vértices de un paralelogramo, conocido como paralelogramo de Varignon, cuyo perímetro es la suma de las diagonales del cuadrilátero,
$ii)$ el área del paralelogramo de Varignon es la mitad del área del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$ y $M_{da}$ los puntos medios de $AB$, $BC$, $CD$ y $DA$ respetivamente.

Figura 2

Notemos que $M_{ab}M_{bc}$ y $M_{cd}M_{da}$ son segmentos medios de $\triangle ABC$ y $\triangle DAC$ por lo que $M_{ab}M_{bc} \parallel CA \parallel M_{cd}M_{da}$ y $2M_{ab}M_{bc} = CA = 2M_{cd}M_{da}$.

De manera análoga podemos ver que $M_{ab}M_{da} \parallel DB \parallel M_{bc}M_{cd}$ y $2M_{ab}M_{da} = BD = 2M_{bc}M_{cd}$.

Por lo tanto los lados opuestos de $\square M_{ab}M_{bc}M_{cd}M_{da}$ son paralelos y $M_{ab}M_{bc} + M_{bc}M_{cd} + M_{cd}M_{da} + M_{da}M_{ab} = \dfrac{CA + BD + CA +BD}{2} = CA + BD$.

Para calcular el área de  $\square M_{ab}M_{bc}M_{cd}M_{da}$ primero notemos que $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ son semejantes pues $M_{ab}M_{da} \parallel BD$.

También sabemos que $M_{ab}M_{da} = \dfrac{BD}{2}$, por lo que las alturas desde $A$, $h$ y $h’$ de $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ respectivamente, también cumplirán que $h = \dfrac{h’}{2}$.

Por lo tanto,
$(\triangle AM_{ab}M_{da}) = \dfrac{M_{ab}M_{da} \times h}{2}$
$= \dfrac{\frac{1}{2}DBD \times \frac{1}{2}h’}{2} = \dfrac{1}{4} \dfrac{BD \times h’}{2} $
$= \dfrac{1}{4} (\triangle ABD)$.

De manera similar podemos encontrar las áreas de $\triangle BM_{bc}M_{ab}$, $\triangle CM_{cd}M_{bc}$ y $\triangle DM_{da}M_{cd}$.

En consecuencia,
$(\square M_{ab}M_{bc}M_{cd}M_{da}) = (\square ABCD) – (\triangle AM_{ab}M_{da}) – (\triangle BM_{bc}M_{ab}) – (\triangle CM_{cd}M_{bc}) – (\triangle DM_{da}M_{cd})$
$= (\square ABCD) – \dfrac{1}{4} ((\triangle ABD) + (\triangle BCD) + (\triangle CDB) + (\triangle DAC))$
$= (\square ABCD) – \dfrac{2}{4}(\square ABCD) $
$ = \dfrac{(\square ABCD)}{2}$.

$\blacksquare$

Corolario. Sea $\square ABCD$ un cuadrilátero convexo, entonces su cuadrilátero de Varignon
$i)$ es un rombo si y solo si $AC = BD$,
$ii)$ es un rectángulo si y solo si $AC \perp BD$,
$iii)$ es un cuadrado si y solo si $AC = BD$ y $AC \perp BD$.

Demostración. Sean $E$, $F$, $G$, $H$, los puntos medios de $BC$, $CD$, $DA$, $AB$, respectivamente como $EF$ y $FG$ son segmentos medios de $\triangle DBC$ y $\triangle ADC$, entonces, $2EF = BD$, $EF \parallel BD$ y $2FG = AC$, $FG \parallel AC$.

Figura 3

$i)$ $\square EFGH$ es un rombo, entonces por definición $EF = FG \Leftrightarrow AC = BD$.

$ii)$ $\square EFGH$ es un rectángulo, entonces por definición $EF \perp FG \Leftrightarrow AC \perp BD$.

$iii)$ Es consecuencia de $i)$ y $ii)$.

$\blacksquare$

Centroide de un cuadrilátero

Definición 2. Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se llaman bimedianas.

Al segmento que une los puntos medios de las diagonales de un cuadrilátero se le conoce como recta de Newton.

Teorema 2. Las bimedianas de un cuadrilátero convexo y su recta de Newton son concurrentes y se bisecan entre sí, el punto de concurrencia es el centroide del cuadrilátero.

Demostración. Sea $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$, $M_{da}$, $M$, $N$, los puntos medios de $AB$, $BC$, $CD$, $DA$, $AC$, $BD$, respectivamente.

$M_{ab}M_{cd}$ y $M_{bc}M_{da}$ son las diagonales del paralelogramo de Varignon, por lo tanto, se intersecan en $J$ su punto medio.

Figura 4

Por otra parte, $M_{ab}M$ es un segmento medio de $\triangle ABC$, por lo que $M_{ab}M \parallel BC$; $NM_{cd}$ es un segmento medio de $\triangle DBC$, por lo tanto, $NM_{cd} \parallel BC$, y así $NM_{cd} \parallel M_{ab}M$.

Igualmente vemos que $M_{ab}N \parallel MM{cd}$.

Por lo tanto, $\square M_{ab}NM_{cd}M$ es un paralelogramo, en consecuencia las diagonales $M_{ab}M_{cd}$ y $NM$ se intersecan en $J$ su punto medio.

En conclusión, $J$ es el punto medio de $M_{ab}M_{cd}$, $M_{bc}M_{da}$ y $NM$.

$\blacksquare$

Construcción de un cuadrilátero

Problema. Construye un cuadrilátero $\square ABCD$ conociendo $AB$, $BC$, $CD$, $DA$ y $M_{ab}M_{cd}$ donde $M_{ab}$ y $M_{cd}$ son los puntos medios de $AB$ y $CD$ respectivamente.

Solución. Primero construimos el paralelogramo $\square M_{ab}NM_{cd}M$, donde $M$ y $N$ son los puntos medios de las diagonales $AC$ y $BD$, de la siguiente manera.

De la demostración del teorema 2 sabemos que $M_{ab}M = NM_{cd} = \dfrac{BC}{2}$ y $M_{ab}N = MM_{cd} = \dfrac{AD}{2}$ (figura 4).

También sabemos que la diagonal de un paralelogramo lo divide en dos triángulos congruentes, por lo que basta construir un triángulo de lados $M_{ab}M_{cd}$, $\dfrac{BC}{2}$  y $\dfrac{AD}{2}$ y luego trazar paralelas por $M_{ab}$ y $M_{cd}$ a los lados del triángulo construido completando así el paralelogramo.

De manera similar construimos el paralelogramo $\square M_{ab}M_{bc}M_{cd}M_{da}$ donde $M_{bc}$ y $M_{da}$ serían los puntos medios de $BC$ y $AD$ respectivamente.

Sabemos también que $M_{bc}M \parallel AB$ por lo que trazamos la paralela $AB$ a $M_{bc}M$ por $M_{ab}$ tal que $AM_{ab} = M_{bc}B = \dfrac{AB}{2}$.

Con $A$ y $B$ construidos, por $M_{bc}$ trazamos $ABC$ tal que $BM_{bc} = M_{bc}C = \dfrac{BC}{2}$, similarmente construimos $D$.

$\blacksquare$

Teorema de Van Aubel

Teorema 3, de Van Aubel. Los segmentos que unen los centros de cuadrados construidos externamente sobre lados opuestos de un cuadrilátero convexo son perpendiculares y tienen la misma longitud.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $\square EFBA$, $\square BGHC$, $\square DCIJ$, $\square LADK$, cuadrados construidos externamente sobre los lados de $\square ABCD$ y $O_1$, $O_2$, $O_3$, $O_4$, sus respectivos centros.

Figura 5

Sea $M = LB \cap ED$, como $AL = AD$ y $AB = AE$ y $\angle LAB = \angle DAE$, por criterio de congruencia LAL, $\triangle LAB \cong \triangle DAE$,
$\Rightarrow LB = DE$ y $\angle AEM = \angle ABM$.

Por lo tanto, $\square MEBA$ es cíclico, así, $\angle EMB = \angle EAB$, es decir $LB \perp DE$.

Considera $N$ el punto medio de $BD$, $NO_4$ y $NO_3$ son segmentos medios de $\triangle BDE$ y $\triangle DBL$ respectivamente.

Esto implica que $2NO_4 = DE$ y $NO_4 \parallel DE$ y $2NO_3 = LB$ y $NO_4 \parallel LB$.

Por lo tanto, $NO_4 = NO_3$ y $NO_4 \perp NO_3$.

Igualmente vemos que $NO_1 = NO_2$ y $NO_1 \perp NO_2$.

Sea $V = O_1O_3 \cap O_2O_4$, por criterio de congruencia LAL, $NO_1O_3 \cong NO_2O_4$,
$\Rightarrow O_1O_3 = O_2O_4$ y $\angle VO_1N = \angle VO_2N$.

Por lo tanto, $\square VNO_1O_2$ es cíclico, y así $O_1O_3 \perp O_2O_4$.

$\blacksquare$

Definición 3. Nos referiremos al cuadrilátero $\square O_1O_1O_3O_4$ como cuadrilátero externo de Van Aubel y a la intersección de sus diagonales como punto externo de Van Aubel.

Centroide del cuadrilátero de Van Aubel

Teorema 4. Un cuadrilátero y su cuadrilátero externo de Van Aubel tienen el mismo centroide.

Demostración. Sean $\square ABCD$ y $\square O_1O_2O_3O_4$ su cuadrilátero externo de Van Aubel, $M$ y $N$ los puntos medios de $AC$ y $BD$, y $V$ el punto externo de Van Aubel.

Figura 6

En el teorema anterior vimos que $NV$ es una cuerda común a las circunferencias cuyos diámetros son $O_1O_2$ y $O_3O_4$, por lo tanto la línea que une sus centros $M_{1,2}M_{3,4}$ biseca a $NV$ y $M_{1,2}M_{3,4} \perp NV$.

De manera análoga podemos ver que $MV$ es una cuerda común a las circunferencias cuyos diámetros son $O_2O_3$ y $O_4O_1$ y por lo tanto la línea que une sus centros $M_{2,3}M_{4,1}$ biseca a $MV$ y $M_{2,3}M_{4,1} \perp MV$.

Por otra parte, por el teorema de Van Aubel las diagonales del cuadrilátero de Van Aubel son perpendiculares y tienen la misma longitud. Entonces por el corolario, su paralelogramo de Varignon $\square M_{1,2}M_{2,3}M_{3,4}M_{4,1}$ es un cuadrado, en particular, $M_{1,2}M_{3,4} \perp M_{2,3}M_{4,1}$.

En consecuencia, en $\triangle MNV$, $M_{1,2}M_{2,3} \parallel MV$ y $M_{1,2}M_{2,3}$ pasa por el punto medio de $NV$, por lo tanto $M_{1,2}M_{2,3}$ biseca a $MN$.

Igualmente podemos ver que $M_{2,3}M_{4,1}$ biseca a $MN$.

Por el teorema 2 sabemos que el punto medio $J$ de $MN$ es el centroide de $\square ABCD$ y que la intersección de las bimedianas $M_{1,2}M_{3,4}$ y $M_{2,3}M_{4,1}$ es el centroide de $\square O_1O_2O_3O_4$.

$\blacksquare$

Más adelante…

En la siguiente entrada continuaremos el estudio de los cuadriláteros cíclicos que comenzamos en la entada teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que un cuadrilátero es dividido por una de sus diagonales en dos triángulos de igual área si y solo si la diagonal biseca a la otra diagonal.
  2.  Verifica que el teorema de Varignon se cumple para los cuadriláteros cóncavo y cruzado.
  3. Sean $\square ABCD$ un cuadrilátero $U$ y $V$ los puntos medios de $\overline{AC}$ y $\overline{BD}$ respectivamente y $T$ la intersección de $\overline{AB}$ con $\overline{CD}$. Prueba que $(\triangle TUV) = \dfrac{(\square ABCD)}{4}$.
    Sugerencia. Considera $H$ y $F$ los puntos medios de $\overline{AD}$ y $\overline{BC}$ y los cuadriláteros $\square ACBD$, $\square CUFT$ y $\square BVFT$ para calcular el área de los triángulos $\triangle UVF$, $\triangle UFT$ y $\triangle VFT$.
Figura 7
  1. Construye un cuadrilátero dados dos ángulos opuestos, la longitud de las diagonales y el ángulo entre las diagonales.
  2. Verifica que el teorema de Van Aubel se cumple cuando los cuadrados son construidos internamente, y también para los para los cuadriláteros cóncavo y cruzado.
  3. Muestra que en un cuadrilátero convexo los puntos medios de sus diagonales y los puntos medios de las diagonales de su cuadrilátero externo de Van Aubel, forman un cuadrado, y que el punto externo de Van Aubel pertenece al circuncírculo de este cuadrado.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»