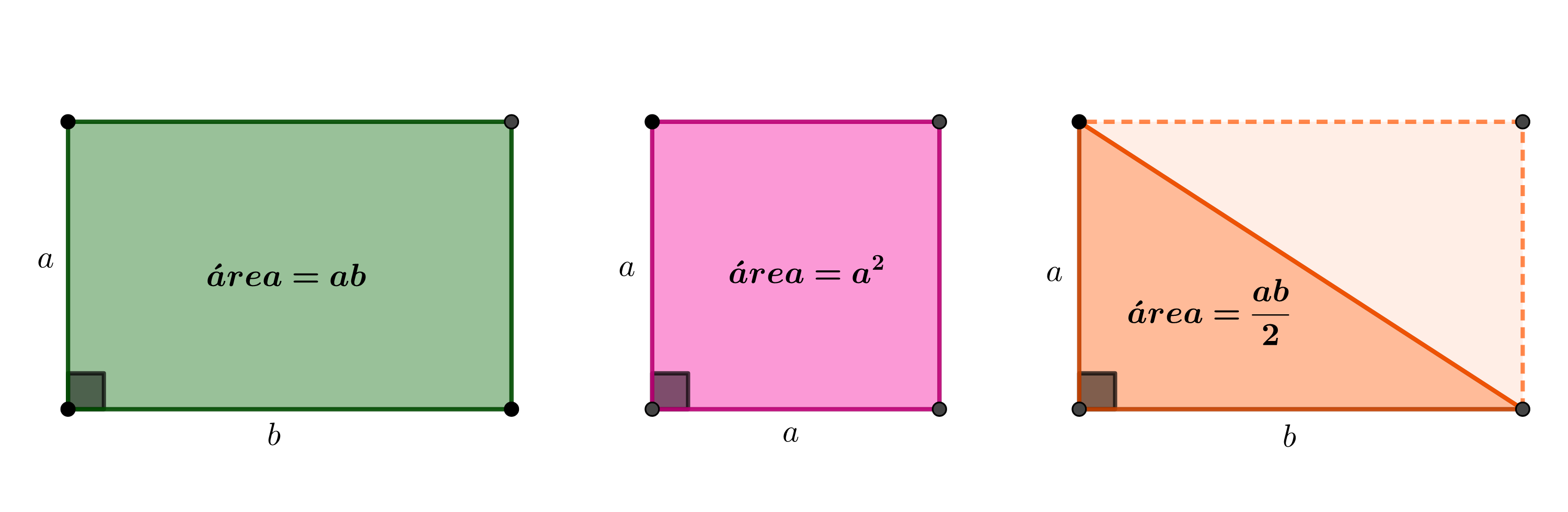Introducción

En esta ocasión veremos el teorema de Pitágoras que relaciona la hipotenusa de un triangulo rectángulo con la longitud de sus catetos, esta propiedad permite definir una métrica en el espacio euclidiano, en particular, con esto podemos calcular la longitud de un segmento si conocemos un triángulo rectángulo que tenga como hipotenusa dicho segmento.

Geométricamente el teorema de Pitágoras nos habla sobre el área de cuadrados construidos sobre los lados de un triángulo rectángulo, así que necesitamos presentar un concepto nuevo.

Definición. Definimos el área de un rectángulo como el producto de dos de sus lados adyacentes. De esta manera el área de un cuadrado será su lado al cuadrado.

Como las diagonales de todo rectángulo lo dividen en dos triángulos rectángulos congruentes, de la definición se sigue que el área de un triángulo rectángulo es el semiproducto de sus catetos.  

Teorema de Pitágoras

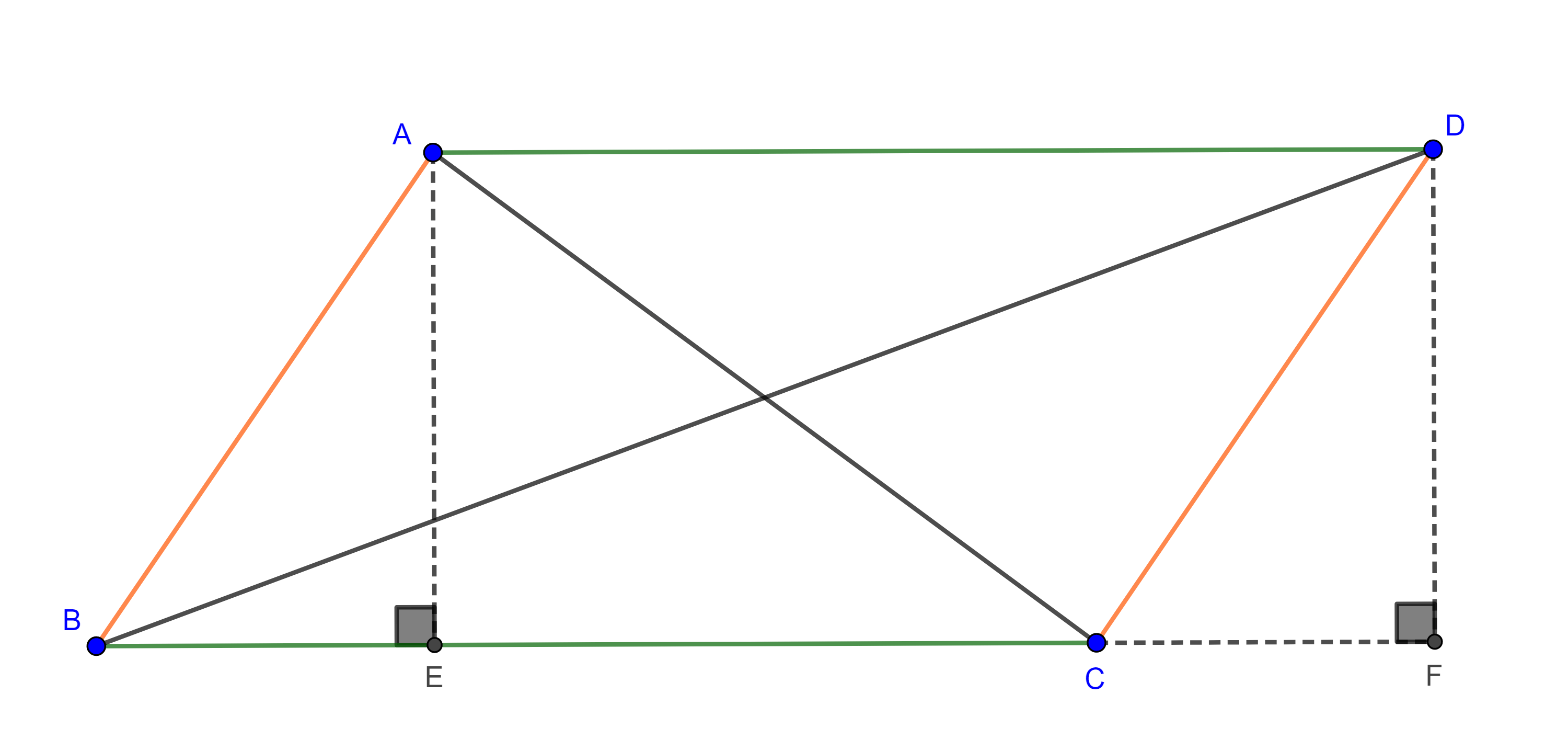
Teorema 1, de Pitágoras. El área de un cuadrado de lado igual a la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de cuadrados de lados igual a los catetos del triángulo rectángulo.

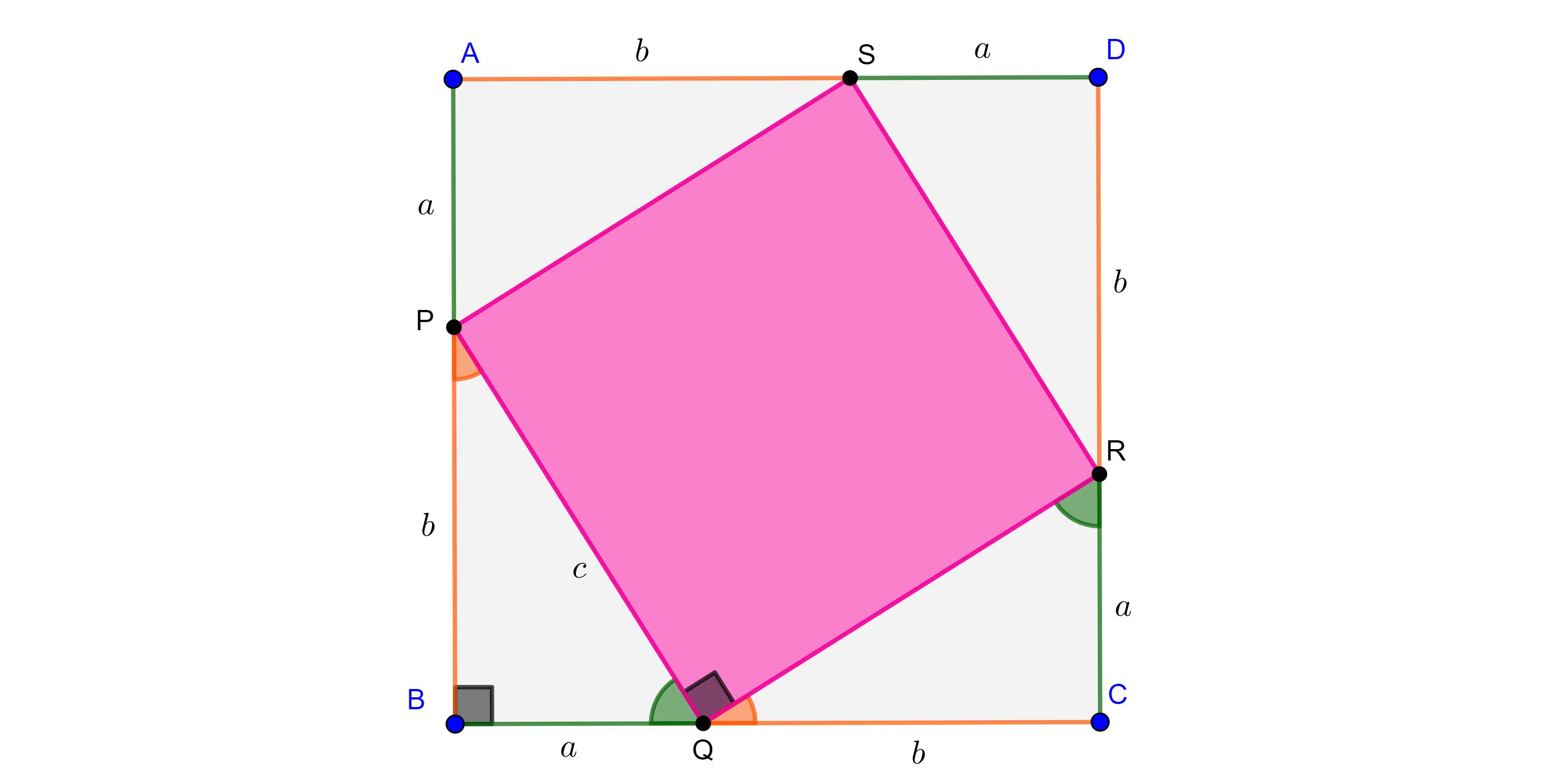
Demostración. Consideremos un triángulo rectángulo de catetos $a$, $b$ e hipotenusa $c$.

Construimos un cuadrado $\square ABCD$ de lados $a + b$, y puntos $P \in AB$, $Q \in BC$, $R \in CD$ y $S \in AD$, tales que $AP = BQ = CR = DS = a$ y $BP = CQ = DR = AS = b$.

Como los ángulos en las esquinas son rectos entonces por criterio LAL
$\begin{equation} \triangle ASP \cong \triangle BPQ \cong \triangle CQR \cong \triangle DRS, \end{equation}$
en particular $PQ = QR = RS = SP$.

Por $(1)$, $\angle CQR$ y $\angle PQB$ son complementarios en consecuencia $\angle RQP = \dfrac{\pi}{2}$.

De manera análoga se ve que
$\angle SRQ = \angle QPS = \angle PSR = \angle RQP = \dfrac{\pi}{2}$.

Por lo tanto, $\square PQRS$ es un cuadrado de lado $c$.

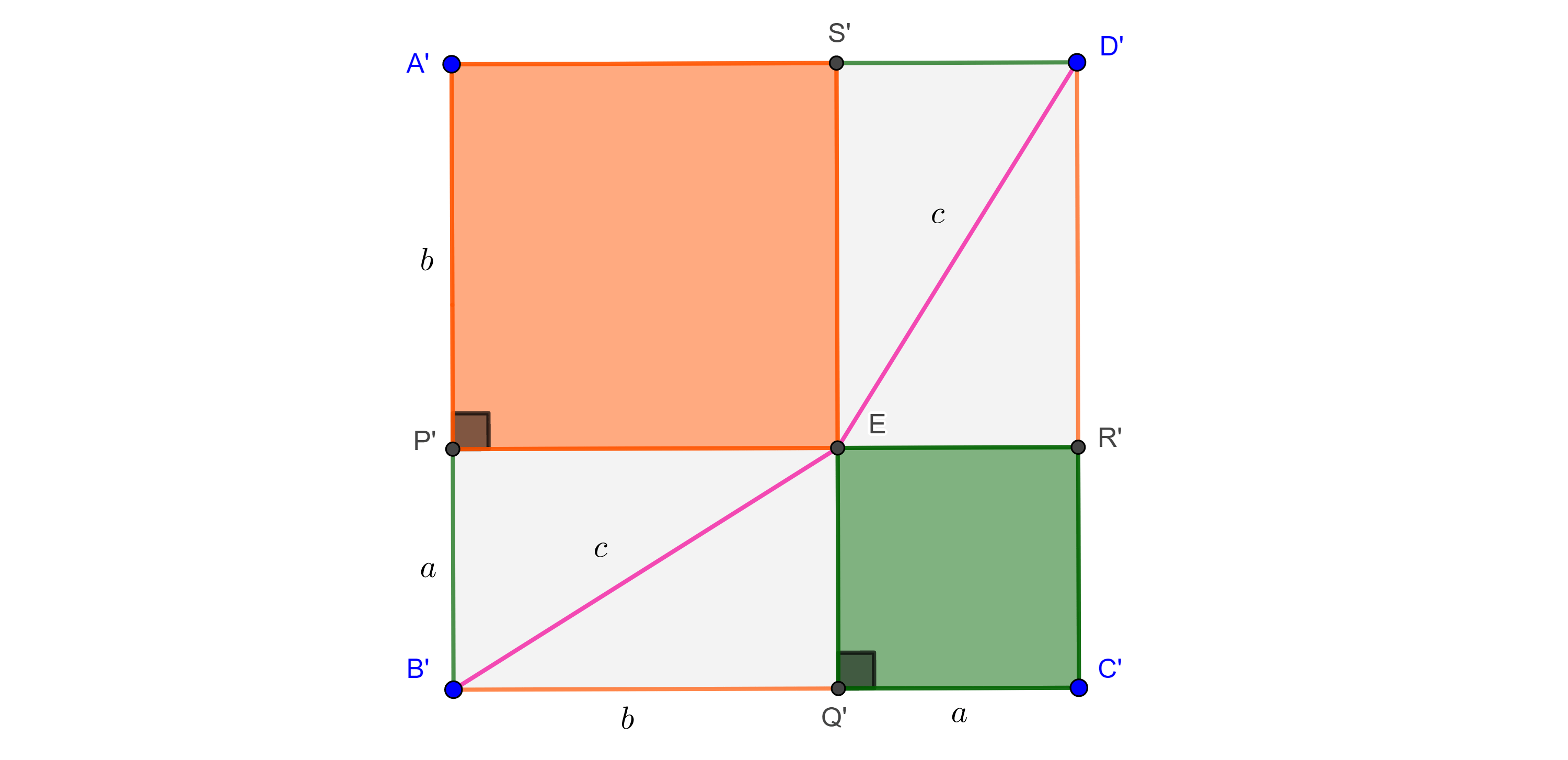
Ahora construimos otro cuadrado $\square A’B’C’D’$ de lados $a + b$, y puntos $P’ \in A’B’$ y $Q’ \in B’C’$ tales que $A’P’ = B’Q’ = b$ y $B’P’ = C’Q’ = a$.

Trazamos una perpendicular a $A’B’$ por $P’$ que interseca a $C’D’$ en $R’$, y una perpendicular a $B’C’$ por $Q’$ que interseca a $A’D’$ en $S’$.

Como $A’B’ \parallel C’D’$ entonces $P’R’ \perp C’D’$, análogamente $Q’S’ \perp A’D’$ y entonces $P’R’ \perp Q’S’$.

Por lo tanto, $\square A’P’ES’$, $\square EQ’C’R’$, $\square P’B’Q’E$ y $\square S’ER’D’$ son rectángulos.

Como los lados opuestos de todo rectángulo son iguales, concluimos que $\square A’P’ES’$ y $\square EQ’C’R’$ son cuadrados de lados $b$ y $a$ respectivamente.

$B’E$ y $ED’$ dividen a $\square P’B’Q’E$ y $\square S’ER’D’$ en cuatro triángulos rectángulos congruentes entre si pues los rectángulos son congruentes.

Pero al mismo tiempo los triángulos en $\square A’B’C’D’$ son congruentes con los triángulos en $\square ABCD$, pues tienen los mismos lados $a$ y $b$, y todos son triángulos rectángulos.

Finalmente, como $\square ABCD$ y $\square A’B’C’D’$ son congruentes entonces sus áreas son iguales y podemos sustraer a cada uno el área de los cuatro triángulos resultando así que el área del cuadrado rosa es igual a la suma de las áreas de los cuadrados verde y naranja.

Por lo tanto, $c^2 = a^2 + b^2$.

$\blacksquare$

Reciproco del Teorema de Pitágoras

Teorema 2. Reciproco del teorema de Pitágoras. Si en un triángulo el cuadrado de uno de sus lados es igual a la suma de los cuadrados de los otros dos lados entonces el triángulo es rectángulo.

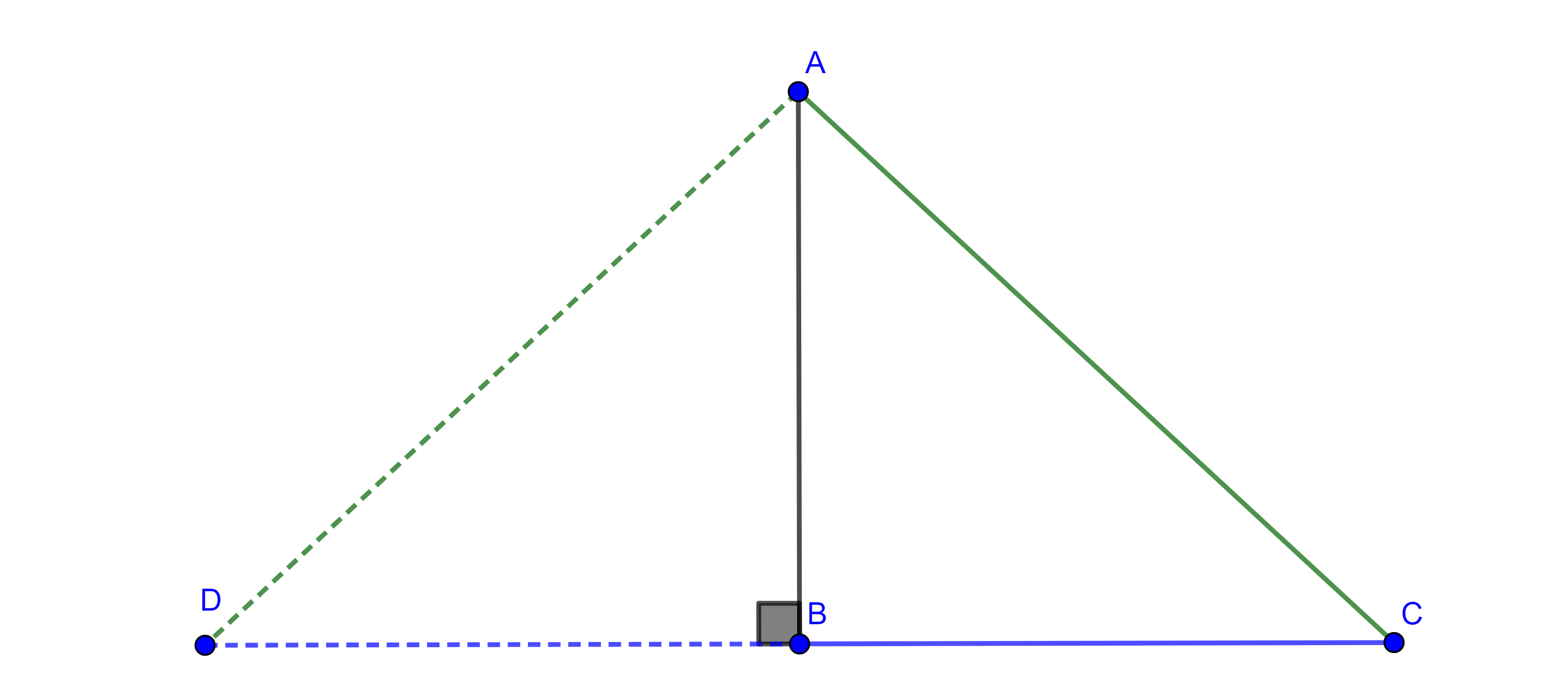
Demostración. Sea $\triangle ABC$ un triángulo tal que $AC^2 = AB^2 + BC^2$.

Construimos un punto $D$ del lado opuesto a $C$ respecto de $AB$ tal que $BD = BC$ y $BD \perp AB$.

Por construcción $\triangle ABD$ es rectángulo, por el teorema de Pitágoras, $AD^2 = AB^2 + BD^2$.

Como $BD = BC$ $\Rightarrow BD^2 = BC^2$, por lo tanto, $AD^2 = AB^2 + BC^2 = AC^2$.

Por hipótesis, $AC^2 = AB^2 + BC^2 \Rightarrow AD^2 = AC^2 \Rightarrow AD = AC$.

Por criterio LLL, $\triangle ABC \cong \triangle ADC$, en particular $\angle CBA = \angle ABC = \dfrac{\pi}{2}$.

$\blacksquare$

Caracterización de un ángulo interior

Sea $\triangle ABC$ entonces por los teoremas 1 y 2
$\angle B = \dfrac{\pi}{2} \Leftrightarrow AC^2 = AB^2 + BC^2$.

Ahora consideremos un triángulo $\triangle A’B’C’$ con $A’B’ = AB$ y $B’C’ = BC$ pero $\angle B’ > \dfrac{\pi}{2}$, entonces por la proposición 2 de la entrada desigualdad del triángulo y su reciproco, esto ocurre si y solo si $A’C’ > AC$
$\Leftrightarrow A’C’^2 > AC^2 = AB^2 + BC^2 = A’B’^2 + B’C’^2$

Por otra parte, si tenemos $\triangle A’’B’’C’’$ tal que $A’’B’’ = AB$ y $B’’C’’ = BC$ pero $\angle B’’ < \dfrac{\pi}{2}$, por el resultado antes mencionado, esto ocurre si y solo si $A’’C’’ < AC$
$\Leftrightarrow A’’C’’^2 < AC^2 = AB^2 + BC^2 = A’’B’’^2 + B’’C’’^2$

Resumiendo, tenemos lo siguiente para cualquier triángulo $\triangle ABC$, $\angle B$ es:

• recto $\Leftrightarrow AC^2 = AB^2 + BC^2$,
• obtuso $\Leftrightarrow AC^2 > AB^2 + BC^2$,
• agudo $\Leftrightarrow AC^2 < AB^2 + BC^2$.

Ley del paralelogramo

Teorema 3, ley del paralelogramo. La suma de los cuadrados de los lados de un paralelogramo es igual a la suma de los cuadrados de sus diagonales.

Demostración. Sean $\square ABCD$ un paralelogramo, $E$ y $F$ los pies de las perpendiculares a $BC$ trazadas desde $A$ y $D$ respectivamente.

Recordemos que los lados opuestos de un paralelogramo son iguales, por lo que $AB = CD$ y $AD = BC$, además $\square AEFD$ es un rectángulo y todo rectángulo es paralelogramo, por lo tanto, $AE = DF$ y $EF = AD = BC$, $\Rightarrow BE = CF$.

Aplicando el teorema de Pitágoras a los triángulos $\triangle ABE$, $\triangle DBF$ y $\triangle AEC$ obtenemos:

$\begin{equation} AB^2 = AE^2 + BE^2. \end{equation}$

$DB^2 = DF^2 + BF^2$
$= AE^2 + (BC + CF)^2 = AB^2 – BE^2 + (BC + BE)^2$
$= AB^2 – BE^2 +BC^2 + 2BC \times BE + BE^2$
$\begin{equation} = AB^2 + BC^2 + 2BC \times BE. \end{equation}$

$AC^2 = AE^2 + EC^2$
$= AE^2 + (BC – BE)^2 = AB^2 – BE^2 + BC^2 -2BC \times BE + BE^2$
$\begin{equation} = AB^2 + BC^2 -2BC \times BE. \end{equation}$

Sumamos $(3)$ y $(4)$ para obtener
$AC^2 + BD^2 = 2AB^2 + 2BC^2$.

$\blacksquare$

Teorema de Apolonio

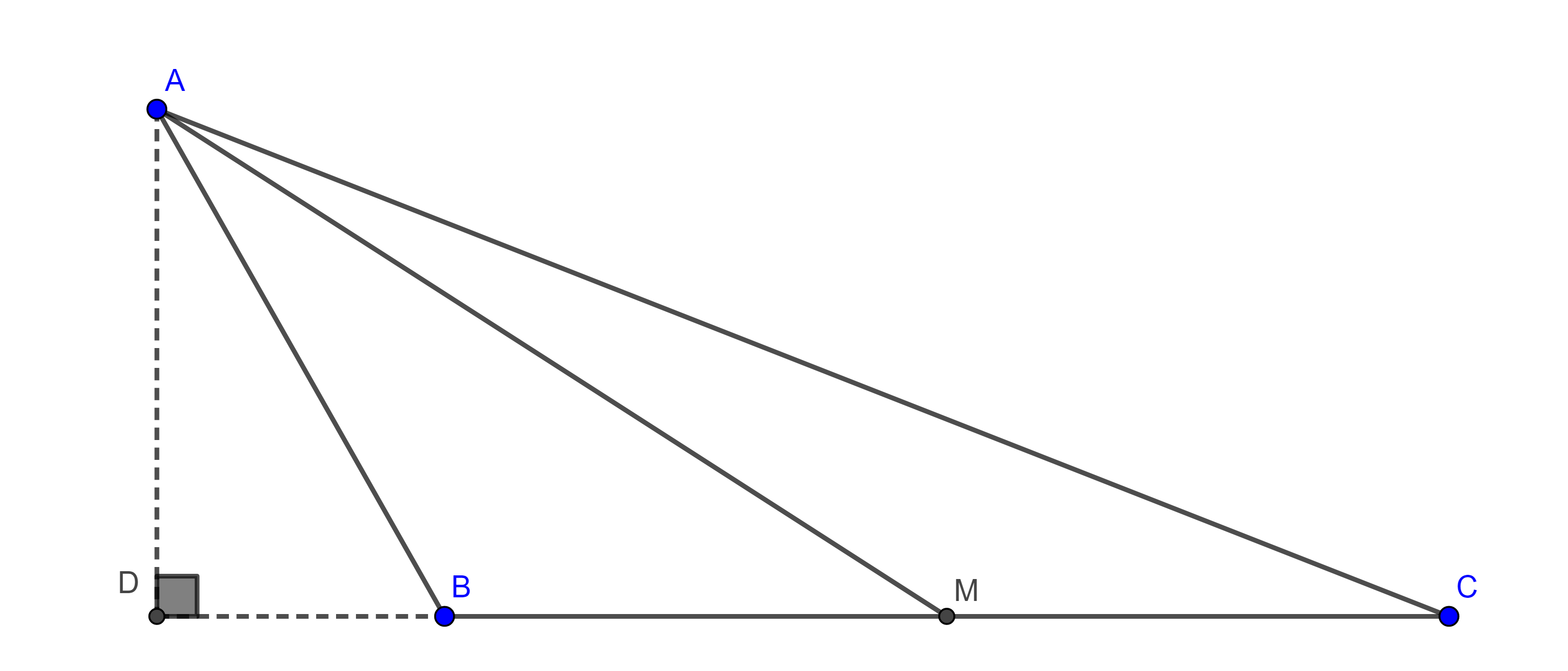
Teorema 4, de Apolonio. En todo triangulo la suma de los cuadrados de dos lados es igual a dos veces el cuadrado de la mitad del tercer lado más dos veces el cuadrado de la mediana que biseca al tercer lado.

Demostración. Sean $\triangle ABC$ y $M$ el punto medio de $BC$. Por demostrar que $AB^2 + AC^2 = 2(BM^2 + AM^2)$.

Sea $D$ el pie de la perpendicular a $BC$ trazada desde $A$, aplicamos el teorema de Pitágoras a los triángulos $\triangle ADM$, $\triangle ADB$ y $\triangle ADC$.

$\begin{equation} AM^2 = AD^2 + DM^2. \end{equation}$

$AB^2 = AD^2 + BD^2$
$= AM^2 – DM^2 + (DM – BM)^2 = AM^2 – DM^2 + DM^2 – 2DM \times BM + BM^2$
$\begin{equation} = AM^2 + BM^2 – 2DM \times BM. \end{equation}$

$AC^2 = AD^2 + DC^2$
$= AM^2 – DM^2 + (DM + MC)^2 = AM^2 – DM^2 +DM^2 + 2DM \times MC + MC^2$
$\begin{equation} = AM^2 + 2DM \times MC + MC^2. \end{equation}$

Como $BM = MC$ sumando $(6)$ y $(7)$ obtenemos
$AB^2 + AC^2 = 2AM^2 + 2MC^2$.

$\blacksquare$

Caracterización de las alturas de un triángulo

Proposición. Sean $BC$ un segmento y $P$ un punto en el plano, considera $D$ el pie de la perpendicular a $BC$ trazada desde $P$, entonces $PB^2 – PC^2 = DB^2 – DC^2$.

Demostración. Los triángulos $\triangle PDB$ y $\triangle PDC$ son rectángulos, por el teorema de Pitágoras tenemos que $PB^2 = PD^2 + DB^2$ y $PC^2 = PD^2 + DC^2$.

Despejando $PD^2$ de ambas ecuaciones e igualando tenemos que $PB^2 – DB^2 = PC^2 – DC^2$
$\Rightarrow PB^2 – PC^2 = DB^2 – DC^2$.

$\blacksquare$

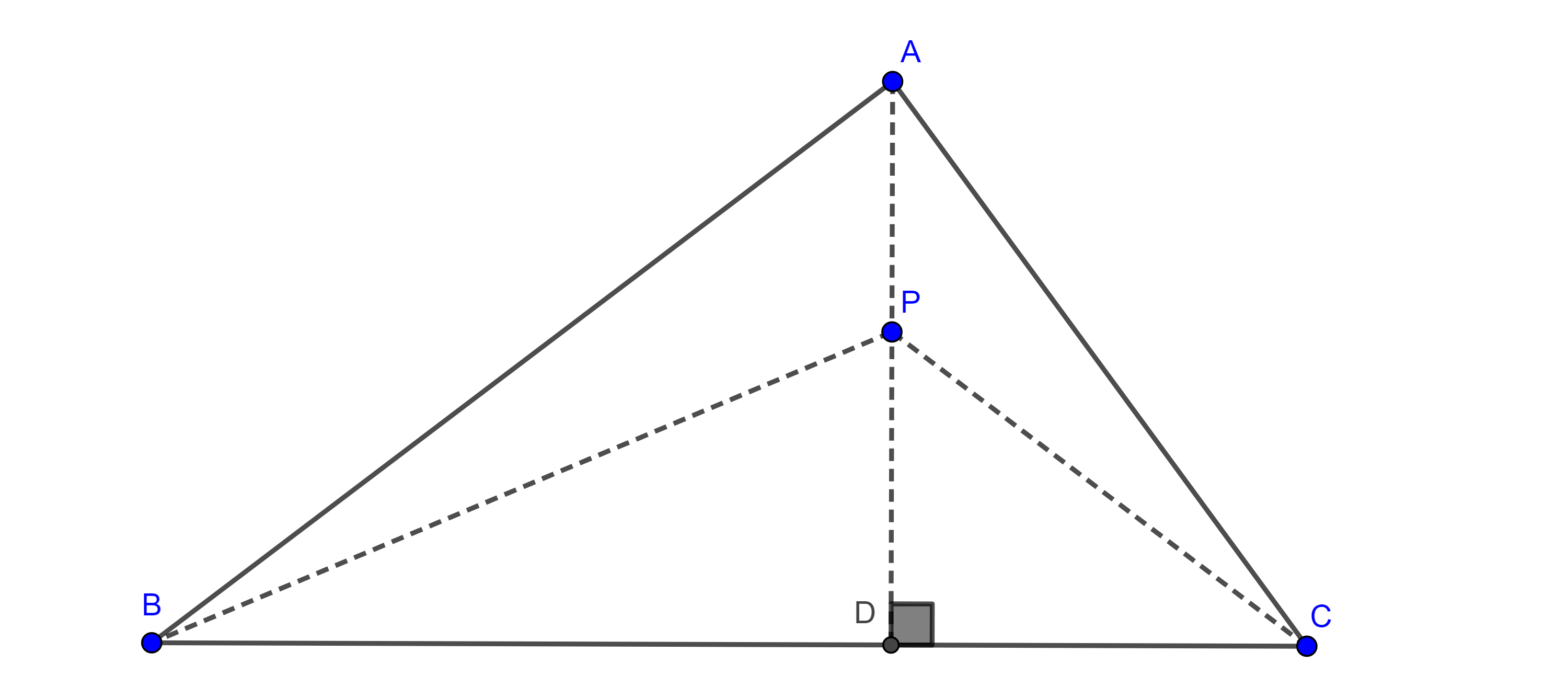
Teorema 5. Sea $\triangle ABC$ un triángulo entonces un punto $P$ está en la altura por $A$ si y solo si $PB^2 – PC^2 = AB^2 – AC^2$.

Demostración. Supongamos que $P$ es un punto en la altura desde $A$ entonces podemos considerar el triángulo $\triangle PBC$.

Por la proposición tenemos que los puntos $P$ y $A$ cumplen que $PB^2 – PC^2 = DB^2 – DC^2$ y $AB^2 – AC^2 = DB^2 – DC^2$ donde $D$ es el pie de la altura.

Por lo tanto $PB^2 – PC^2 = AB^2 – AC^2$.

$\blacksquare$

Ahora supongamos que $P$ es un punto en el plano tal que $PB^2 – PC^2 = AB^2 – AC^2$ por la proposición sabemos que $AB^2 – AC^2 = DB^2 – DC^2$, con $D$ el pie de la altura desde $A$.

Por transitividad se tiene que $PB^2 – PC^2 = DB^2 – DC^2$.

Sea $E$ el pie de la perpendicular a $BC$ trazada desde $P$, nuevamente por la proposición tenemos que $PB^2 – PC^2 = EB^2 – EC^2$ $\Rightarrow DB^2 – DC^2 = EB^2 – EC^2$

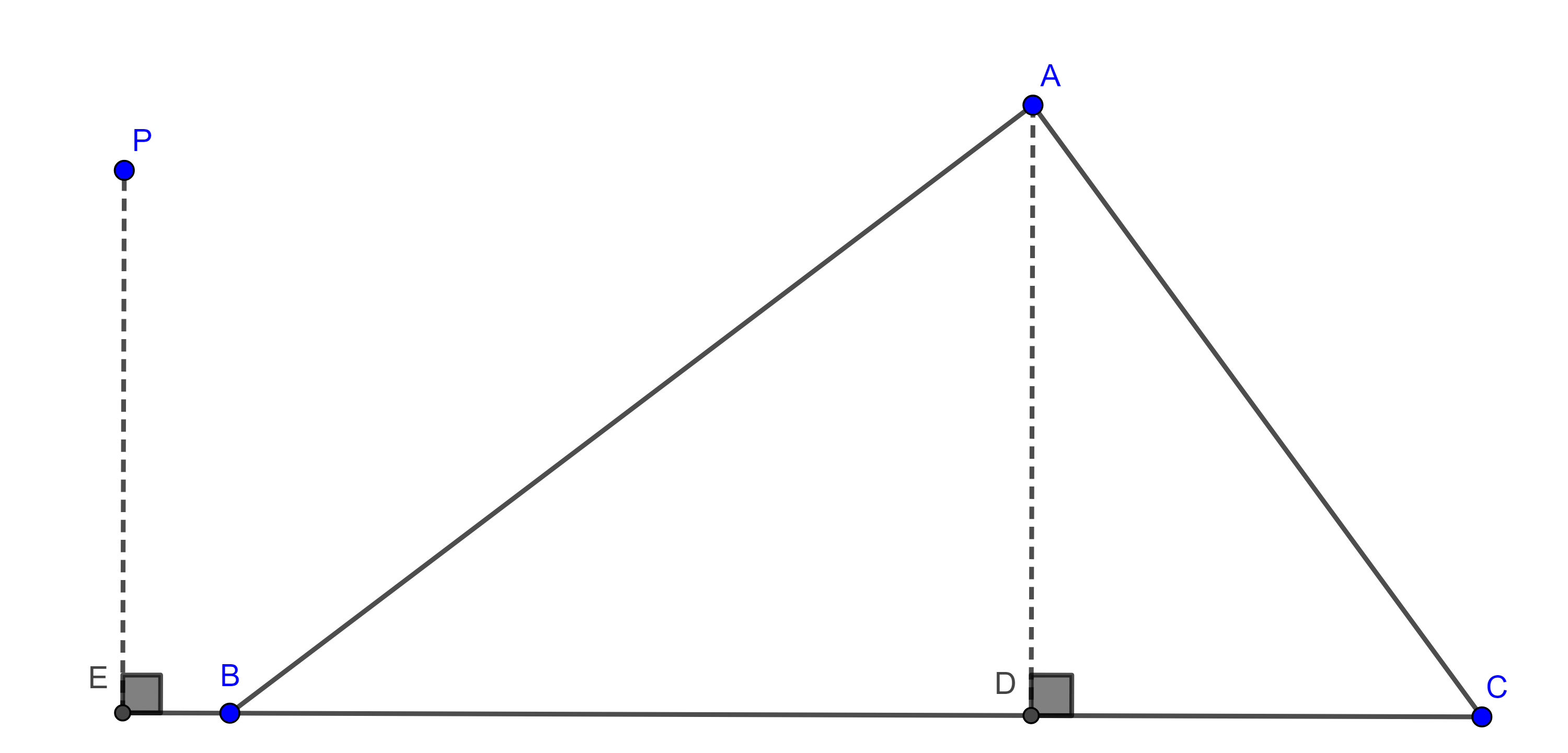
Supongamos que $D$ está en el segmento $BC$ y $E$ fuera del segmento y del lado de $B$ (figura 9), otros casos se muestran de manera similar, entonces $EB = ED – BD$ y $EC = ED + DC$.

$\Rightarrow DB^2 – DC^2 = (ED – BD)^2 – (ED + DC)^2$
$= ED^2 – 2ED \times BD + BD^2 – ED^2 – 2ED \times DC – DC^2$
$\Rightarrow 0 = ED \times BD + ED \times DC = ED(BD + DC)$

Como $BD + DC \neq 0 \Rightarrow ED = 0$
$\Rightarrow E = D$

De esto se concluye que $P$ está en la altura trazada desde $A$.

$\blacksquare$

Más adelante…

En la siguiente entada estudiaremos el teorema de Tales también conocido como teorema de la proporcionalidad.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Dado un segmento unitario construye un segmento de longitud $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$ …
2. Si $a$, $b$, $c$, $d$, y $e$ son las longitudes de cinco segmentos tales que con cualesquiera tres de ellos es posible construir un triángulo, muestra que al menos uno de los triángulos es acutángulo.
3. Sea $P$ un punto en el interior de $\triangle ABC$, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, expresa $AE$ en términos de $AF$, $FB$, $BD$, $DC$ y $CE$.
4. Muestra que en un triángulo con ángulos interiores iguales a $\dfrac{\pi}{2}$, $\dfrac{\pi}{3}$ y $\dfrac{\pi}{6}$, se tiene que el cateto opuesto al ángulo de $\dfrac{\pi}{6}$ es igual a la mitad de la hipotenusa y el cateto opuesto al ángulo de $\dfrac{\pi}{3}$ es igual a $\dfrac{\sqrt{3}}{2}$ veces la hipotenusa.
5. Si dos de los lados de un triángulo miden $a$ y $b$ y el ángulo entre ellos mide $\dfrac{3\pi}{4}$ encuentra la longitud del segmento medio entre los lados dados.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Paralelogramos.
• Siguiente entrada del curso: Teorema de Tales.

Fuentes

• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 22-27, 43-44.
• Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 11-14.
• Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 39-41.
• Wikipedia
• Geometría interactiva
• Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»