Introducción

Ya hemos cubierto varios temas de cálculo y resolución de problemas. Comenzamos platicando acerca de continuidad y de dos teoremas importantes para funciones continuas: el teorema del valor intermedio y el teorema del valor extremo. Después, hablamos acerca de derivadas y de dos teoremas importantes para funciones diferenciables: el teorema de Rolle y el teorema del valor medio. Luego, vimos que la diferenciabilidad también nos ayuda a encontrar límites de cocientes y potencias de formas indefinidas mediante la regla de L’Hôpital. En esta entrada y la siguiente hablaremos de la integral y cómo las ideas detrás de su construcción, así como sus propiedades, pueden ayudar a resolver problemas.

Para entender esta sección bien, es importante que conozcas la construcción de la integral de Riemann en una variable, así como sus propiedades principales. También supondremos que conoces las técnicas usuales para resolver integrales. Esto se hace durante el primer año de un curso de cálculo a nivel licenciatura. También puedes revisarlo en la literatura clásica, como el libro de Cálculo de Spivak.

Usar la integral como un área

La integral es por definición un límite de sumas superiores o inferiores. Hay problemas en los que podemos aprovechar esto para entender una suma o una sucesión. A grandes rasgos lo que hacemos es:

• Interpretar la sucesión o serie como una suma de areas correspondiente a una suma superior o inferior de cierta integral $\int f(x)dx$.
• Usar lo que sabemos de integración para poder decir algo del área dada por $\int f(x)dx$
• Regresar esta información al problema original.

Veamos un ejemplo de esto.

Problema. Calcula el siguiente límite $$\underset{n\to \mathrm{\infty }}{lim}(\frac{1}{n}+\frac{1}{n+1}+\dots +\frac{1}{2n-1}).$$

La cantidad de términos de este límite depende de $n$, así que no podemos hacerlos uno por uno. No hay una forma sencilla de hacer la suma. Tampoco parece que podamos usar la regla de L’Hôpital. Lo que haremos es entender a la expresión dentro del límite de manera geométrica.

Sugerencia pre-solución. Haz una figura con la que puedas relacionar el límite que buscamos con cierta área que puedas expresar en términos de una integral.

Solución. Consideremos la gráfica de la función $f(x)=\frac{1}{x}$ en el intervalo $[n,2n]$ y el área debajo de esta gráfica, que mostramos en verde a continuación.

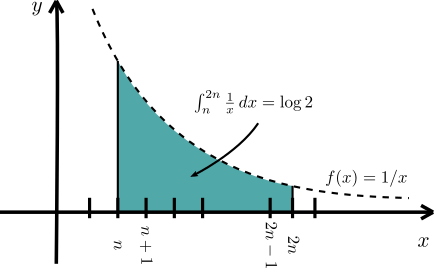
Notemos que la suma que aparece en el problemas corresponde a sumar las áreas de los rectángulos de base $1$ y alturas $\frac{1}{n}$, $\frac{1}{n+1}$, $\dots$, $\frac{1}{2n-1}$, que podemos encontrar en azul en la siguiente figura.

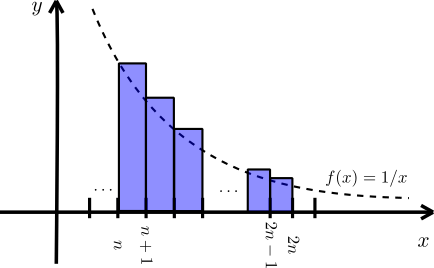
Así, obtenemos que podemos acotar inferiormente nuestra suma de la siguiente manera:

$$\begin{array}{rl}\frac{1}{n}+\dots +\frac{1}{2n-1}& >{\int }_n^{2n}\frac{1}{x}dx\\ & =(\log x){|}_n^{2n}\\ & =\log 2.\end{array}$$

De manera similar, podemos pensar ahora en rectángulos que queden por debajo de la gráfica de la función, y que en total su area es menor que el valor de la integral. Los mostramos a continuación en color rojo:

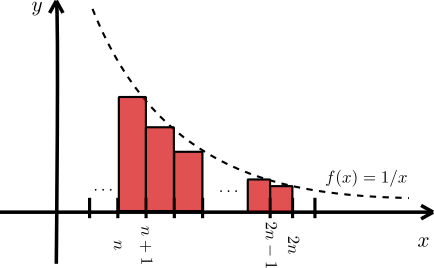
De aquí, podemos dar la siguiente cota:

$$\begin{array}{rl}\frac{1}{n+1}+\dots +\frac{1}{2n}& <{\int }_n^{2n}\frac{1}{x}dx\\ & =(\log x){|}_n^{2n}\\ & =\log 2.\end{array}$$

Si juntamos ambas desigualdades, deducimos que $$\log 2<\frac{1}{n}+\dots +\frac{1}{2n-1}<(\frac{1}{n}-\frac{1}{2n})+\log 2.$$

Ahora sí podemos hacer $n\to \mathrm{\infty }$. Como ambos lados de la desigualdad convergen a $\log 2$, tenemos que la sucesión que nos interesa también debe converger a $\log 2$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Traducir a una integral y usar técnicas de integración

Hay varias técnicas que podemos usar para realizar integrales: cambio de variable, integración trigonométrica, integración por partes, integración por fracciones parciales, etc. En algunas ocasiones podemos transformar un problema a una integral, aplicar una de estas técnicas, y luego regresar al contexto original. Veamos un ejemplo de esto.

Problema. Demuestra que para cualquier par de enteros positivos $m$ y $n$ tenemos que $$\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})\frac{1}{k+m+1}=\sum _{k=0}^m(-1{)}^k(\genfrac{}{}{0ex}{}{m}{k})\frac{1}{k+n+1}.$$

Sugerencia pre-solución. Intenta formular un problema equivalente aprovechando que para cualquier entero no negativo $r$ se tiene que $\frac{1}{r+1}={\int }_0^1{t}^{r}dt$. Tendrás que usar esto varias veces, usar la fórmula de binomio de Newton y después aprovechar una simetría para hacer un cambio de variable.

Solución. Notemos que $$\frac{1}{k+m+1}={\int }_0^1{t}^{k+m}dt.$$ Substituyendo en la expresión de la izquierda, obtenemos que la suma buscada es $$\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k}){\int }_0^1{t}^{k+m}dt.$$ Usando la linealidad de la integral y la fórmula del binomio de Newton tenemos que esta suma es igual a
$$\begin{array}{rl}& {\int }_0^1\sum _{k=1}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})t^{k+m}dt\\ =& {\int }_0^1{t}^m(1-t{)}^{n}dt.\end{array}$$

Con el cambio de variable $s=1-t$, la integral anterior es igual a $${\int }_0^1{s}^n(1-s{)}^m.$$ Pero por un argumento inverso al que hicimos para llegar a la primer integral, esta segunda integral es igual a $$\sum _{k=0}^m(-1{)}^k(\genfrac{}{}{0ex}{}{m}{k})\frac{1}{k+n+1}.$$

Esto es justo el lado derecho en la identidad que queríamos.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

El teorema de Lebesgue

No todas las funciones son integrables con la definición de Riemann (que aquí simplemente llamaremos «ser integrable»), pues puede ser que el límite de las sumas superiores no sea igual al de las sumas inferiores. Un resultado profundo en cálculo es el criterio de Lebesgue, que caracteriza aquellas funciones acotadas que tienen integral de Riemann en un intervalo.

Teorema (criterio de Lebesgue). Una función acotada $f:[a,b]\to \mathbb{R}$ es integrable si y sólo si su conjunto de discontinuidades tiene medida $0$.

El teorema de Lebesgue da una prueba sencilla de que si $f$ y $g$ son integrables, entonces su producto también, lo cual no es fácil de probar a partir de la definición. A continuación esbozamos esta prueba.

Las discontinuidades de $f^2$ están contenidas en las de $f$, de modo que si $f$ es integrable, por el teorema de Lebesgue $f^2$ también. Además, suma y resta de integrables es sencillo ver que es integrable, de modo que $(f+g{)}^2$ también lo es. Para concluir, notamos que $$fg=\frac{(f+g{)}^2-f^2-g^2}{2},$$ de modo que $fg$ es integrable.

Veamos un problema que combina varias de las ideas de cálculo que hemos visto.

Problema. Si $f:[a,b]\to \mathbb{R}$ es una función tal que $f+\sin (f)$ es integrable, entonces $f$ también es integrable.

Sugerencia pre-solución. Usa el criterio de Lebesgue. Necesitarás estudiar las discontinuidades con cuidado, para lo cual es útil recordar cómo interactúan las funciones continuas con las sucesiones convergentes.

Solución. Como $f+\sin (f)$ es integrable, entonces es acotada. Así, $f$ también lo es. La función $g(x)=x+\sin (x)$ tiene derivada $1+\cos (x)\ge 0$ y que es $0$ sólo en un conjunto discreto de puntos, de modo que es estrictamente creciente. Además, los límites en $-\mathrm{\infty }$ y $\mathrm{\infty }$ son $-\mathrm{\infty }$ e $\mathrm{\infty }$ respectivamente. Por el teorema del valor intermedio, pasa por todos los reales. Así, $g$ es una función biyectiva.

Mostraremos que las discontinuidades de $f$ están contenidas en las de $f+\sin (f)$, o bien, dicho de otra forma, que si $f+\sin (f)$ es continua en $x$, entonces $f$ también. Tomemos una sucesión $\{x_n\}$ que converge a $x$. Como $f+\sin (f)$ es continua en $x$, tenemos que $\{f(x_n)+\sin (f(x_n))\}$ converge a $f(x)+\sin (f(x))=g(f(x))$.

Como $f$ es una función acotada, la sucesión $\{f(x_n)\}$ es acotada, y para ver que converge a un límite, basta ver que toda subsucesión convergente converge al mismo límite. Tomemos una subsucesión convergente digamos, al límite $L$. Tendríamos que $g(L)=g(f(x))$, y como $g$ es biyectiva tendríamos que $L=f(x)$. En otras palabras, toda subsucesión convergente de $\{f(x_n)\}$ converge a $f(x)$. De esta forma, $\{f(x_n)\}$ converge a $f(x)$. Con esto concluimos que $f$ es continua en $x$.

Concluimos que el conjunto de discontinuidades de $f$ está contenido en el de $f+\sin (f)$, el cual tiene medida $0$. De este modo, el de $f$ también tiene medida $0$ y por el criterio de Lebesgue, es integrable.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más problemas

Hay más ejemplos de problemas relacionados con la integral en la Sección 6.8 del libro Problem Solving through Problems de Loren Larson.