Introducción
En esta y las siguientes entradas platicaremos varios temas relacionados con sucesiones, y cómo se aplican a la resolución de problemas matemáticos. Comenzaremos recordando qué es una sucesión y estudiando a las sucesiones aritméticas y geométricas. Más adelante, platicaremos de los siguientes tipos de sucesiones:
- Periódicas
- Acotadas
- Recursivas
- Con recursiones lineales
- Monótonas
- Convergentes
Supondremos que el que lee estas notas está al menos un poco familiarizado con estos conceptos. De cualquier forma, recordaremos las definiciones que vayamos necesitando.
Recordatorio de sucesiones
Una sucesión formalmente es una función de los naturales a un conjunto $X$. Aunque esta es la definición formal, es bastante más práctico pensar a una sucesión como ciertos elementos de $X$ en donde hay uno que es el primero, después del cual aparecen más, uno tras otro.
En muchos problemas, $X$ es un conjunto de números, como los naturales, enteros, racionales o reales. Sin embargo, $X$ también puede ser un conjunto de funciones, de polinomios, de figuras geométricas o de prácticamente cualquier otra cosa. Por ejemplo, en topología algebraica son de interés ciertas sucesiones de grupos.
Usaremos la notación $\{x_n\}$ para referirnos a una sucesión. Aunque usa llaves (como si fuera conjunto), en realidad los elementos están «ordenados de izquierda a derecha», entonces se tiene que pensar como $$\{x_n\}=(x_0,x_1,x_2,x_3,\ldots).$$ El término $x_n$ es el $n$-ésimo término de la sucesión.
Podemos definir a una sucesión de manera implícita mediante una fórmula, o mediante forma explícita escribiendo algunos de sus términos cuando el patrón que sigue es muy claro (lo cual no siempre pasa). Por ejemplo, la sucesión $\{x_n\}$ tal que para todo $n\geq 0$, tenemos $x_n=1$ es explícitamente la sucesión $$1,1,1,1,1,\ldots,$$ mientras que la sucesión $\{y_n\}$ tal que para todo $n\geq 0$ se tiene $y_n=n(n+1)$ es explícitamente la sucesión $$0, 2, 6, 12, 20, \ldots.$$
A partir de la forma implícita podemos dar tantos términos como queramos de la forma explícita, pero lo contrario no es cierto. Algunos acertijos se tratan de tomar pocos términos de una sucesión dada de manera explícita, y preguntar cuál es el siguiente término, o bien cuál es la regla general.
En términos formales, la respuesta no es única, pues la sucesión, en teoría, podría continuar como sea. Sin embargo, como acertijo es divertido encontrar una regla fácil de enunciar y que funcione siempre. Algunas sucesiones en las que se puede hacer esto son las siguientes:
- $1,1,1,1,1,1,1,\ldots$
- $1,2,3,4,5,6,7,\ldots$
- $2,4,6,8,10,12,14,\ldots$
- $1,\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{32}, \frac{1}{64},\ldots$
- $i, 1, 2, 3i, 5, 8i, 13, 21i, \ldots$
- $1,\sqrt{2},\sqrt{3},2,\sqrt{5},\sqrt{6},\sqrt{7},\ldots$
- $4,3,2,1,4,3,2,1,4,3,\ldots$
En todos estos ejemplos, la sucesión tiene cierto patrón u orden. Pero hay muchas otras sucesiones que no tienen un patrón claro para enunciarlas de forma implícita, o bien en las que este patrón es más difícil de encontrar:
- $3,1,4,1,5,9,2,6,5,\ldots$
- $4,13,0,1,7,18,54,\ldots$
- $2,1,24,6,720,120,40320,5040,\ldots$
Como ya comentamos, la forma explícita de una sucesión tiene el problema de que no sabemos cuáles términos siguen. Si en un problema aplicamos la heurística de buscar un patrón y tenemos que los primeros términos de una sucesión son $$2,4,6,8,10,12$$ por muy tentador que sea no podemos garantizar que el siguiente será $14$, hasta que no tengamos una demostración para ello.
Es posible que resolviendo problemas, o en otro quehacer matemático, encuentres los primeros términos de una sucesión de enteros y quieras saber cuál es. Una herramienta muy útil para ello es Enciclopedia en Línea de Sucesiones en Enteros (OEIS). Tiene un buscador en el que pones los primeros términos, y de ahí te sugiere algunas sucesiones que pueden ser la que estás buscando.
Problema. Para un entero $n\geq 1$, se toman $n$ puntos distintos sobre la orilla de una circunferencia. Se dibujan todos los segmentos entre pares de esos puntos. Se sabe que no hay tres de esos segmentos que coincidan en el interior de la circunferencia. ¿En cuántas regiones queda dividida el área de la circunferencia?
Sugerencia pre-solución. Haz varias figuras para hacer casos pequeños y buscar un patrón. Ten cuidado, pues el patrón no es el que puedes deducir inmediatamente.
Solución. Veamos qué sucede con casos pequeños. Cuando tenemos un punto, no hay segmentos y sólo queda $1$ región. Si tenemos dos puntos, se hace un segmento y tenemos $2$ regiones. Para tres puntos, queda un triángulo y tres regiones a sus lados, así que son $4$ regiones en total. Las siguientes figuras muestran que para cuatro y cinco puntos tenemos $8$ y $16$ regiones en total:
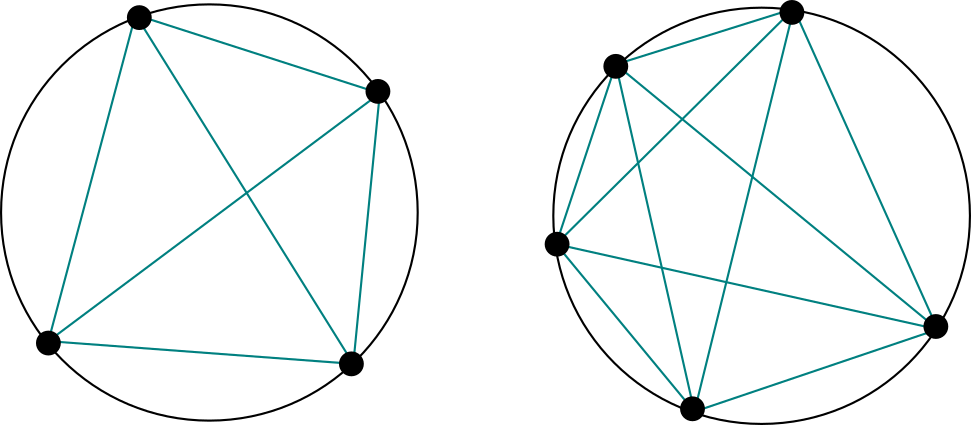
Así, la sucesión de cuántas regiones hay hasta ahora va así de manera explícita: $$1,2,4,8,16$$
Parecería que es la sucesión de potencias de dos, y que la respuesta sería entonces $2^{n-1}$. Pero esto es incorrecto. Al hacer un caso más, nos damos cuenta de esto, pues para seis puntos tenemos únicamente $31$ regiones:
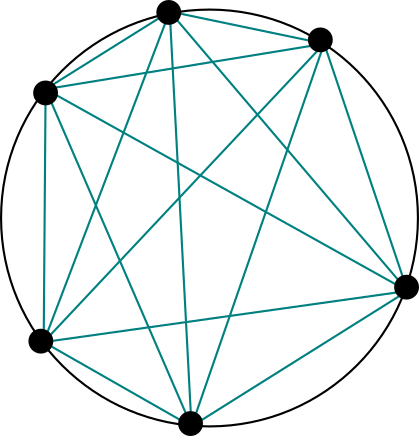
Cuando estamos haciendo matemáticas, o resolviendo un problema con acceso a internet, podemos poner esta sucesión en la OEIS para ver si hay algo que nos pueda ayudar.
Realizando la búsqueda, obtenemos varios resultados, y el segundo resultado tiene exactamente la descripción que queremos. La OEIS tiene una sección de fórmulas que podemos usar.
Ahí, dice que la cantidad de regiones es $$\binom{n-1}{0}+\binom{n-1}{1}+\binom{n-1}{2}+\binom{n-1}{3}+\binom{n-1}{4},$$ (lo cual se puede probar usando inducción) y de hecho, usando la definición de coeficientes binomiales, se puede ver que la expresión anterior es igual a $$\frac{n^4 – 6n^3 + 23n^2 – 18n + 24}{24}.$$
$\square$
Sucesiones aritméticas
Una sucesión aritmética es una sucesión en la cual de un término al siguiente siempre hay una misma diferencia. Un ejemplo es la sucesión $$1,4,7,10,13,16,19,\ldots,$$ que construimos de modo que la diferencia de un término al siguiente siempre sea $3$.
Si conocemos el término inicial $a_0=a$ de una sucesión aritmética y la diferencia $d$, entonces conocemos todos los términos. En efecto, se puede probar inductivamente que $a_n=a+nd$.
Esta fórmula es muy útil para trabajar con sucesiones aritméticas. Por ejemplo, si sabemos que $\{a_n\}$ es una sucesión aritmética tal que $a_5=30$ y $a_7=48$, entonces por un lado $$a_7-a_5=48-30=18,$$ y por otro $$a_7-a_5=(a+7d)-(a+5d)=2d.$$ De este modo, la diferencia es $d=9$, y el término inicial es $a=a_7-7\cdot 9=48-63=-15$.
Problema. Muestra que en cualquier sucesión aritmética de enteros con diferencia $d>0$ que tenga al menos un número al cubo $k^3$, tiene una infinidad de cubos.
Sugerencia pre-solución. Usa una identidad algebraica.
Solución. Podemos suponer sin perder generalidad que $k>0$. Para que una sucesión aritmética sea de enteros, su diferencia tiene que ser un número entero. Así, $d$ es un entero positivo.
Como $k^3$ es uno de los términos y la diferencia es $d$, entonces $k^3+nd$ también es un término para cualquier entero positivo $n$. En particular, lo es para los enteros de la forma $n=3mk^2+3m^2dk+m^3d^2$, con $m$ un entero positivo. De esta forma, $$k^3+3mdk^2+3m^2d^2k+m^3d^3=(k+md)^3$$ es un término de la sucesión para todo entero positivo $m$, así que la sucesión tiene una infinidad de cubos.
$\square$
Una observación sencilla, pero útil, es que si $\{a_n\}$ es una sucesión aritmética de enteros con término inicial $a$ y diferencia $d>0$, entonces los términos de $a$ son exactamente los números $m\geq a$ tales que $m\equiv a \pmod d$. Las sucesiones aritméticas juegan un papel importante en algunos resultados de teoría de números, por ejemplo, el siguiente teorema.
Teorema de Dirichlet. Sean $a$ y $b$ enteros primos relativos. En la sucesión de enteros $\{a+bn\}$ hay una infinidad de primos. De manera equivalente, hay una infinidad de primos $p$ tales que $p\equiv a \pmod b$.
Sucesiones geométricas
Si tenemos una sucesión en la cual para pasar de un término al siguiente siempre multiplicamos por un mismo número, entonces tenemos una sucesión geométrica. Estos son tres ejemplos:
- $1,2,4,816,32,64,\ldots$
- $2020,0,0,0,0,0,\ldots$
- $64,96,144,216,324,486,729,\ldots$
La primera está construida de modo que hay que multiplicar por $2$ para pasar de un término al siguiente. La segunda de modo que hay que multiplicar por $0$. En la última se multiplica por $\frac{3}{2}$. Parece que la última sucesión es de enteros, pero el siguiente término ya no es entero, pues es $\frac{2187}{2}$.
De nuevo, si el término inicial es $a_0=a$ y la razón (el número por el que se multiplica en cada paso) es $r$, entonces una sencilla inducción muestra que el término $a_n$ es $ar^n$. Si $a=0$, la sucesión es toda igual a $0$. Si $r=0$, a partir del segundo término la sucesión es $0$. En otro caso, conociendo dos valores de una sucesión geométrica podemos conocer información acerca de $r$.
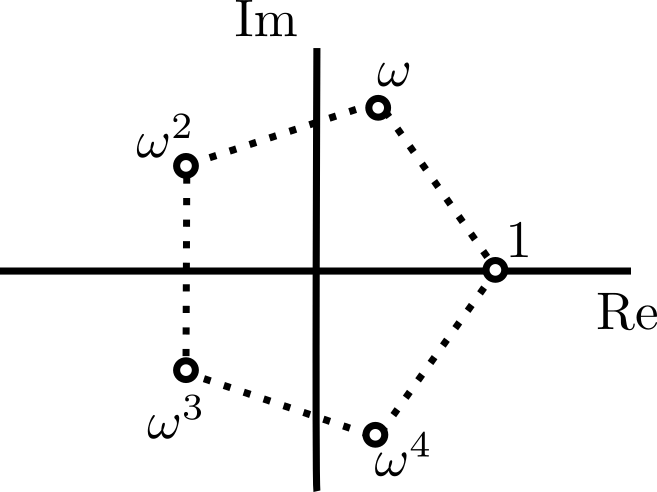
Problema. La sucesión de números complejos $\{a_n\}$ es geométrica y cumple que $a_6=a_{24}=2020$. ¿Qué posibles valores puede tener $a_0$?
Sugerencia pre-solución. Usa la fórmula para sucesiones geométricas. Como estás trabajando en $\mathbb{C}$, recuerda considerar todas las posibilidades que te da la aritmética de complejos.
Solución. Si el término inicial de la sucesión es $a_0=a$ y la razón es $r$, sabemos que $ar^6=2020=ar^{24}$. La primer igualdad implica $r\neq 0$ y $a=2020r^{-6}\neq 0$. La igualdad entre la primera y última igualdad implica que $r^{18}=1$, que podemos escribir como $(r^6)^3=1$. De aquí, $r^6$ puede ser cualquier cúbica de la unidad, y por lo tanto $r^{-6}$ también. De esta forma, $a=2020\omega$, con $\omega$ cualquier raíz cúbica de la unidad.
$\square$
Un problema de sucesiones geométricas y aritméticas
En el siguiente problema se mezclan los dos tipos de sucesiones de los que hemos hablado.
Problema. La sucesión $\{x_n\}$ es aritmética. La sucesión $\{y_n\}$ es geométrica. Tenemos que
\begin{align*}
x_1+y_1&=1\\
x_2+y_2&=8\\
x_3+y_3&=10\\
x_4+y_4&=32.
\end{align*}
Determina el valor de $x_5+y_5$.
Sugerencia pre-solución. Modifica el problema a encontrar los términos iniciales, diferencia y razón de las sucesiones. Usa las fórmulas para cada tipo de sucesión.
Solución. Supongamos que $\{x_n\}$ tiene término inicial $x_0=a$ y diferencia $d$. Supongamos que $\{y_n\}$ tiene término inicial $y_0=s$ y razón $r$. Vamos a determinar $a,d,r,s$. Usando las fórmulas para sucesiones aritmétricas y geométricas, las ecuaciones de la hipótesis se pueden reescribir como sigue:
\begin{align*}
a+d + rs&=1\\
a+2d + r^2s&=8\\
a+3d + r^3s&=10\\
a+4d + r^4s&=32.
\end{align*}
Restando la primera ecuación de la segunda, la segunda de la tercera, y la tercera ecuación de la cuarta, tenemos las siguientes tres ecuaciones:
\begin{align*}
d + r(r-1) s &= 7\\
d+r^2(r-1)s &= 2\\
d + r^3(r-1)s &= 22.
\end{align*}
Restando la primer ecuación de la segunda, y la segunda ecuación de la tercera, tenemos las siguientes dos ecuaciones:
\begin{align*}
r(r-1)^2 s &= -5\\
r^2(r-1)^2 s &= 20.
\end{align*}
De aquí, $s\neq 0$, $r\neq 0$ y $r\neq 1$. Multiplicando la primer ecuación por $-4$, tenemos que $$-4r(r-1)^2s=20=r^2(r-1)^2s.$$ Cancelando $r(r-1)^2s$ (pues no es cero) de ambos lados, obtenemos que $r=-4$. Así, la primera ecuación se transforma en $-4(25)s=-5$, por lo que $s=1/20$.
De la ecuación $d+r(r-1)s=7$, obtenemos entonces $d=7-1=6$. Finalmente, de la ecuación $a+d+rs=1$, obtenemos $a=1-6+1/5=-\frac{24}{5}$.
En resumen, $$a=-\frac{24}{5}, d=6, s=\frac{1}{20}, r=-4.$$
De esta forma,
\begin{align*}
x_5+y_5&=a+5d+rs^5\\
&=-\frac{24}{5}+30-\frac{4^5}{20}\\
&=-26.
\end{align*}
$\square$
Más problemas
Esta entrada es una extensión de las secciones 1, 2 y 3 del curso de sucesiones que impartí para los entrenadores de la Olimpiada Mexicana de Matemáticas. Puedes consultar las notas de este curso en el siguiente PDF, en donde hay más problemas de práctica: