Introducción
En la unidad anterior se revisó el concepto de función, sus características y diversas clasificaciones, los conocimientos adquiridos nos ayudarán a dar inicio a esta nueva unidad referente a un tipo especial de funciones que tienen como domino los números naturales y codominio los números reales, éstas son llamadas sucesiones.
En esta entrada nos enfocaremos en entender la definición y estudiar algunos ejemplos que nos permitan familiarizarnos de forma adecuada con este nuevo concepto.
Sucesiones
Es probable que recuerdes ejercicios del tipo «Encuentra el siguiente término de la sucesión 1.1, 4.2, 9.3, 16.4, __, 36.6». Para resolver estos problemas, hacíamos uso de nuestra creatividad con el fin de poder encontrar el patrón que nos permitiera generar cada uno de los números y, para lograrlo, resultaba fundamental establecer una especie de orden: el primer término, luego el segundo, seguido del tercero, etc. En nuestro ejemplo tenemos lo siguiente:
Primer término: 1.1.
Segundo término: 4.2.
Tercer término: 9.3.
Cuarto término: 16.4.
Quinto término: __.
Sexto término: 36.6.
Considerando esto, es que podíamos notar que la sucesión está determinada por $n^2 + \frac{n}{10}$ donde $n$ hace referencia al término $n$-ésimo. Finalmente, calculábamos el término faltante, en nuestro caso el quinto, que sería $5^2+\frac{5}{10} = 25.5$. Sin embargo, ahora estudiaremos las sucesiones desde una perspectiva distinta donde conoceremos desde un inicio esta regla de asignación que nos permite generar la sucesión y más bien nos importará determinar las características que ésta posea.
Definición. Una sucesión de números reales o sucesión en $\RR$ es una función $f$ definida en el conjunto de los números naturales $\mathbb{N}$ con codominio en los reales $\RR$, es decir, $f: \mathbb{N} \to \RR$.
Dada una sucesión $f: \mathbb{N} \to \RR$, los términos de la misma se obtendrán evaluando la función $f$ en elementos de su dominio. Es decir, el primer término de la sucesión es $f(1) = a_1$, el segundo $f(2)=a_2$, y así sucesivamente. De esta manera, identificamos al $n$-ésimo término mediante $a_n$ y denotamos a la sucesión en sí como $\{ a_n \}$.
Es importante destacar que en la definición especificamos que estamos hablando de una sucesión de números reales, pues, en principio, podemos definir funciones de $\mathbb{N}$ a cualquier otro conjunto $A$, sin embargo, en este curso sólo trataremos el caso donde tal conjunto $A$ es el conjunto de los números reales.
Retomando el ejemplo anterior y considerando la definición dada, podemos ser más formales y establecer que la anterior sucesión es una función $f: \mathbb{N} \to \RR$ donde $f(n) = n^2 + \frac{n}{10}$, o bien, podemos denotarla simplemente como $\{ n^2 + \frac{n}{10} \}$.
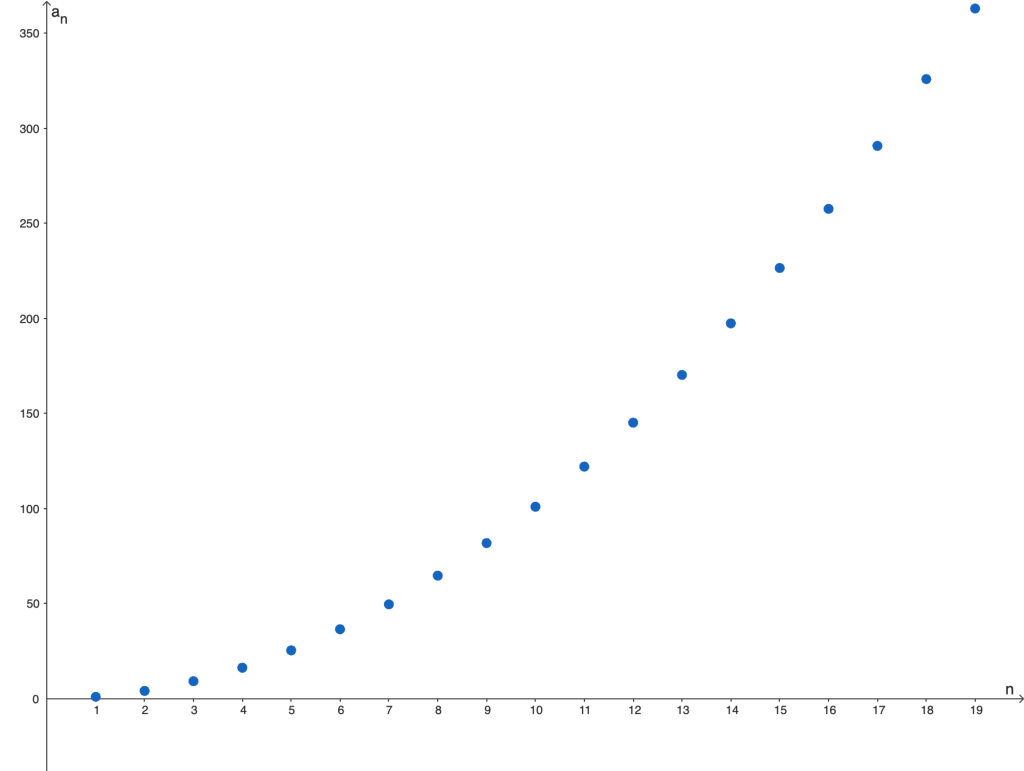
De esta forma, el primer término de nuestro ejemplo es $a_1 = 1^2+\frac{1}{10} =1.1$, el segundo término es $a_2 = 2^2+\frac{2}{10} =4.2$ y así sucesivamente. De forma más general, el $n$-ésimo término de la sucesión es $a_n = n^2 + \frac{n}{10}$. A continuación mostramos la gráfica de la sucesión:
Ejemplos de sucesiones
Ahora revisaremos algunos ejemplos de sucesiones.
Ejemplo 1. Sea $c \in \mathbb{R}$, la sucesión $\{a_n \}$ generada por $a_n = c$ para todo $n \in \mathbb{N}$, la llamamos sucesión constante. Así, la sucesión constante siempre toma el mismo valor y es de la forma $$\{ c, c, \ldots, c, \ldots \}.$$
Ejemplo 2. La sucesión $\{a_n\}$ generada por $a_n = 2n$ es la sucesión de los números pares positivos. Donde sus términos son $$\{ 2, 4, 6, \ldots, 2k, \ldots \}.$$
Ejemplo 3. Sea $\{a_n\}$ la sucesión generada por $a_n = (-1)^n$. Los términos de la sucesión son $$\{ -1,1,-1,\ldots, -1^k, \ldots \}.$$
Ejemplo 4. Sea $\{a_n\}$ la sucesión generada por $a_n =\frac{1}{n}$. De esta forma, sus términos son $$\left\{ 1, \frac{1}{2}, \frac{1}{3}, \ldots, \frac{1}{k}, \ldots \right\}.$$
Ejemplo 5. Sea $\{a_n\}$ la sucesión generada por $a_n = 2^n$. Con lo cual sus términos son $$\{ 2, 4, 8, 16, \ldots, 2^k \ldots \}.$$
Ejemplo 6. Una de las sucesiones más famosas es la sucesión de Fibonacci $\{f_n\}$ la cual se define de forma inductiva, es decir, cada término se define con base en los anteriores.
\begin{align*}
f_1 & = 1, \\
f_2 & = 1, \\
f_{n+1} & = f_{n-1}+f_{n} \quad \forall n \geq 3.
\end{align*}
A modo ilustrativo, calcularemos los primeros 5 elementos de la sucesión $\{f_n\}$.
$$f_1 = 1, \quad f_2 = 1, \quad f_3 = 1+1 = 2, \quad f_4 = 1+2 = 3, \quad f_5 = 2+3 = 5.$$
Ejemplo 7. Sea $\{a_n\}$ una sucesión definida inductivamente de la siguiente forma:
\begin{align*}
a_1 & = 1, \\
a_n & = n \cdot a_{n-1} \quad \forall n \geq 2.
\end{align*}
De esta forma, los primeros 5 términos de la sucesión son $$\{ 1, 2, 6, 24, 120 \}.$$
Al $n$-ésimo término de esta sucesión se le denota comúnmente como $n!$ y su valor está dado por $$n! = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1.$$ Adicionalmente, se define $0! = 1$.
Operaciones con sucesiones
Las reglas de la suma, la resta, el producto y el cociente de funciones particularmente aplican a las sucesiones, pues éstas también son funciones. Considerando esto, dadas dos sucesiones $\{a_n\}$, $\{b_n\}$ y si $c \in \mathbb{R}$, definimos:
- La suma: $\{a_n\} + \{b_n\} = \{a_n + b_n\}.$
- La resta: $\{a_n\} – \{b_n\} = \{a_n – b_n\}.$
- La multiplicación: $\{a_n\} \cdot \{b_n\} = \{a_n \cdot b_n\}.$
- La multiplicación por un escalar: $ c \cdot \{a_n\} = \{ c \cdot a_n \}.$
- El cociente: Si además $b_n \neq 0$ para todo $n \in \mathbb{N}$, entonces $$\frac{ \{a_n\} }{ \{b_n\} } = \left\{ \frac{a_n}{b_n} \right\}.$$
A continuación veremos algunos ejemplos.
Ejemplo 8. Sean $\{ a_n \} = \{ n^2 \}$ y $\{ b_n \}= \{ \frac{n}{10} \}$, entonces $\{a_n\} + \{b_n\} = \{ n^2 + \frac{n}{10} \}$. Denotamos a la sucesión generada como $\{ c_n \} = \{ n^2 + \frac{n}{10} \}$. A continuación se calculan los primeros tres términos:
\begin{align*}
c_1 =1^2 + \frac{1}{10} = 1.1, \\ \\
c_2 =2^2 + \frac{2}{10} = 4.2, \\ \\
c_3 =3^2 + \frac{3}{10} = 9.3.
\end{align*}
Así, los términos de la sucesión son: $$\left\{ 1.1, 4.2, 9.3, \ldots, k^2 + \frac{k}{10}, \ldots \right\}.$$
Ejemplo 9. Sean $\{ a_n \} = \{ n \} $ y $\{ b_n \}= \{ n+1 \}$, entonces $\{a_n\} – \{b_n\} = \{ -1 \}$. Denotamos a la sucesión generada como $\{ c_n \} = \{ -1 \}$. Los primeros tres términos son:
\begin{align*}
c_1 = -1, \\ \\
c_2 = -1, \\ \\
c_3 = -1.
\end{align*}
Así, los términos de la sucesión son: $$\{ -1, -1, -1, \ldots, -1, \ldots \}.$$
Ejemplo 10. Sean $\{ a_n \} = \{n-1\} $ y $\{ b_n \}= \{n+1\}$, entonces $\{a_n\} \cdot \{b_n\} = \{n^2-1\}$. Denotamos a la sucesión generada como $\{ c_n \} = \{n^2-1\}$. Los primeros tres términos son:
\begin{align*}
c_1 = 1^2-1 = 0, \\ \\
c_2 = 2^2-1 = 3, \\ \\
c_3 = 3^2-1 = 8.
\end{align*}
Así, los términos de la sucesión son: $$\{ 0, 3, 8, \ldots, k^2-1, \ldots \}.$$
Ejemplo 11. Sean $c = 5 $ y $\{ a_n \}= \{n \}$, entonces $5 \cdot \{a_n\} = \{5n\}$. Denotamos a la sucesión generada como $\{ c_n \} = \{5n\}$. Los primeros tres términos son:
\begin{align*}
c_1 = 5(1) = 5, \\ \\
c_2 = 5(2) = 10, \\ \\
c_3 = 5(3) = 15.
\end{align*}
Así, los términos de la sucesión son: $$\{ 5, 10, 15, \ldots, 5k, \ldots \}.$$
Ejemplo 12. Sean $\{ a_n \} = \{ n \} $ y $\{ b_n \}= \{ (-1)^n \}$, entonces $\frac{ \{a_n\} }{ \{b_n\}} = \left\{ \frac{ n }{ (-1)^n } \right\}$. Denotamos a la sucesión generada como $\{ c_n \} = \left\{ \frac{ n }{ (-1)^n } \right\}$. Los primeros tres términos son:
\begin{align*}
c_1 = \frac{1}{(-1)^1} = -1, \\ \\
c_2 = \frac{2}{(-1)^2} = 2, \\ \\
c_3 = \frac{3}{(-1)^3} = -3.
\end{align*}
Así, los términos de la sucesión son: $$\left\{-1, 2, -3, \ldots, \frac{k}{(-1)^k}, \ldots \right\}.$$
Más adelante…
En la siguiente entrada se hará la revisión del concepto de sucesión convergente. Para este propósito, revisaremos la definición de límite aplicado a sucesiones, que será clave para el estudio de todos los temas subsecuentes en el curso dado que es el antecesor de la definición del límite de una función.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Considera la sucesión de Fibonacci definida en esta entrada. Encuentra $f_8$.
- Consideremos las sucesiones $\{ a_n \}$ y $\{b_n\}$ donde $a_n = n^2-5n+10$ y $b_n = \frac{1}{n}$. Determina los primeros 8 términos de las siguientes sucesiones:
- $\{ a_n \} \cdot \{b_n\}.$
- $\{ a_n \} + \{b_n\}.$
- $\frac{\{ a_n \}}{\{b_n\}}.$
- $8 \cdot \{ a_n \} – 10 \cdot \{ \frac{1}{b_n}\}.$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Funciones exponenciales y logarítmicas
- Siguiente entrada del curso: Sucesiones convergentes
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»