Archivo de la etiqueta: ejemplos de sucesiones

Cálculo Diferencial e Integral I: Sucesiones de números reales

Por Juan Manuel Naranjo Jurado

Introducción

En la unidad anterior se revisó el concepto de función, sus características y diversas clasificaciones, los conocimientos adquiridos nos ayudarán a dar inicio a esta nueva unidad referente a un tipo especial de funciones que tienen como domino los números naturales y codominio los números reales, éstas son llamadas sucesiones.

En esta entrada nos enfocaremos en entender la definición y estudiar algunos ejemplos que nos permitan familiarizarnos de forma adecuada con este nuevo concepto.

Sucesiones

Es probable que recuerdes ejercicios del tipo «Encuentra el siguiente término de la sucesión 1.1, 4.2, 9.3, 16.4, __, 36.6». Para resolver estos problemas, hacíamos uso de nuestra creatividad con el fin de poder encontrar el patrón que nos permitiera generar cada uno de los números y, para lograrlo, resultaba fundamental establecer una especie de orden: el primer término, luego el segundo, seguido del tercero, etc. En nuestro ejemplo tenemos lo siguiente:

Primer término: 1.1.
Segundo término: 4.2.
Tercer término: 9.3.
Cuarto término: 16.4.
Quinto término: __.
Sexto término: 36.6.

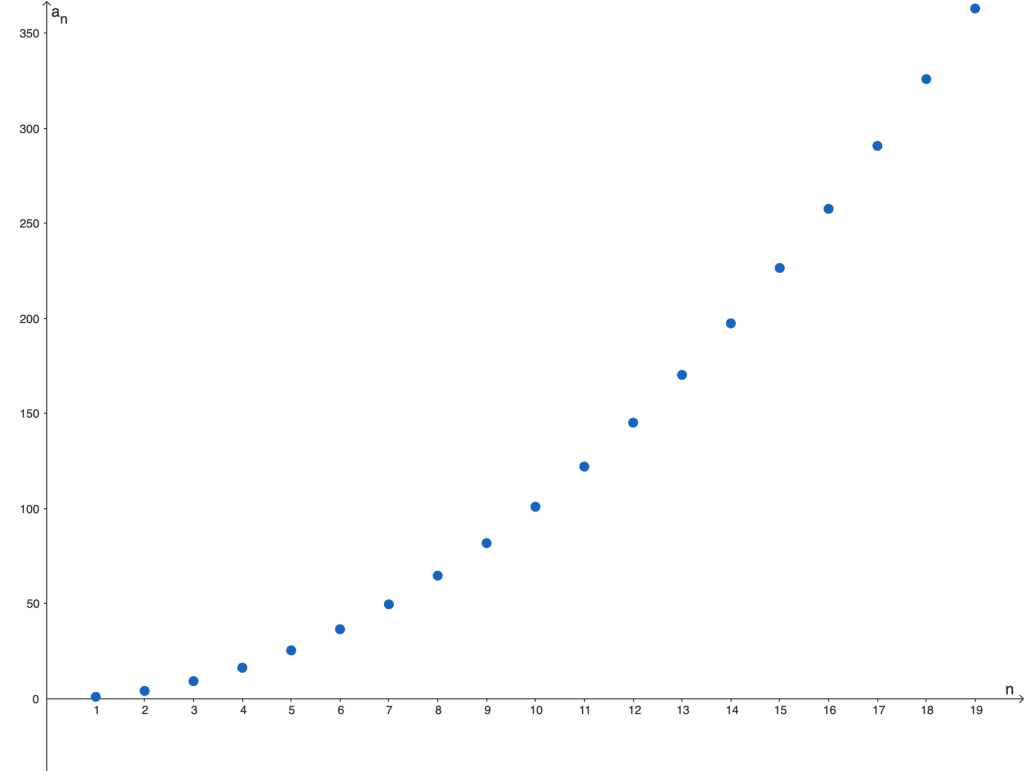
Considerando esto, es que podíamos notar que la sucesión está determinada por $n^{2} + \frac{n}{10}$ donde $n$ hace referencia al término $n$ -ésimo. Finalmente, calculábamos el término faltante, en nuestro caso el quinto, que sería $5^{2} + \frac{5}{10} = 25.5$ . Sin embargo, ahora estudiaremos las sucesiones desde una perspectiva distinta donde conoceremos desde un inicio esta regla de asignación que nos permite generar la sucesión y más bien nos importará determinar las características que ésta posea.

Definición. Una sucesión de números reales o sucesión en $R$ es una función $f$ definida en el conjunto de los números naturales $N$ con codominio en los reales $R$ , es decir, $f : N \to R$ .

Dada una sucesión $f : N \to R$ , los términos de la misma se obtendrán evaluando la función $f$ en elementos de su dominio. Es decir, el primer término de la sucesión es $f (1) = a_{1}$ , el segundo $f (2) = a_{2}$ , y así sucesivamente. De esta manera, identificamos al $n$ -ésimo término mediante $a_{n}$ y denotamos a la sucesión en sí como ${a_{n}}$ .

Es importante destacar que en la definición especificamos que estamos hablando de una sucesión de números reales, pues, en principio, podemos definir funciones de $N$ a cualquier otro conjunto $A$ , sin embargo, en este curso sólo trataremos el caso donde tal conjunto $A$ es el conjunto de los números reales.

Retomando el ejemplo anterior y considerando la definición dada, podemos ser más formales y establecer que la anterior sucesión es una función $f : N \to R$ donde $f (n) = n^{2} + \frac{n}{10}$ , o bien, podemos denotarla simplemente como ${n^{2} + \frac{n}{10}}$ .

De esta forma, el primer término de nuestro ejemplo es $a_{1} = 1^{2} + \frac{1}{10} = 1.1$ , el segundo término es $a_{2} = 2^{2} + \frac{2}{10} = 4.2$ y así sucesivamente. De forma más general, el $n$ -ésimo término de la sucesión es $a_{n} = n^{2} + \frac{n}{10}$ . A continuación mostramos la gráfica de la sucesión:

Ejemplos de sucesiones

Ahora revisaremos algunos ejemplos de sucesiones.

Ejemplo 1. Sea $c \in R$ , la sucesión ${a_{n}}$ generada por $a_{n} = c$ para todo $n \in N$ , la llamamos sucesión constante. Así, la sucesión constante siempre toma el mismo valor y es de la forma ${c, c, \dots, c, \dots} .$

Ejemplo 2. La sucesión ${a_{n}}$ generada por $a_{n} = 2 n$ es la sucesión de los números pares positivos. Donde sus términos son ${2, 4, 6, \dots, 2 k, \dots} .$

Ejemplo 3. Sea ${a_{n}}$ la sucesión generada por $a_{n} = (- 1)^{n}$ . Los términos de la sucesión son ${- 1, 1, - 1, \dots, - 1^{k}, \dots} .$

Ejemplo 4. Sea ${a_{n}}$ la sucesión generada por $a_{n} = \frac{1}{n}$ . De esta forma, sus términos son ${1, \frac{1}{2}, \frac{1}{3}, \dots, \frac{1}{k}, \dots} .$

Ejemplo 5. Sea ${a_{n}}$ la sucesión generada por $a_{n} = 2^{n}$ . Con lo cual sus términos son ${2, 4, 8, 16, \dots, 2^{k} \dots} .$

Ejemplo 6. Una de las sucesiones más famosas es la sucesión de Fibonacci ${f_{n}}$ la cual se define de forma inductiva, es decir, cada término se define con base en los anteriores.

$\begin{aligned} f_{1} & = 1, \\ f_{2} & = 1, \\ f_{n + 1} & = f_{n - 1} + f_{n} \forall n \geq 3. \end{aligned}$

A modo ilustrativo, calcularemos los primeros 5 elementos de la sucesión ${f_{n}}$ .
$f_{1} = 1, f_{2} = 1, f_{3} = 1 + 1 = 2, f_{4} = 1 + 2 = 3, f_{5} = 2 + 3 = 5.$

Ejemplo 7. Sea ${a_{n}}$ una sucesión definida inductivamente de la siguiente forma:

$\begin{aligned} a_{1} & = 1, \\ a_{n} & = n \cdot a_{n - 1} \forall n \geq 2. \end{aligned}$

De esta forma, los primeros 5 términos de la sucesión son ${1, 2, 6, 24, 120} .$

Al $n$ -ésimo término de esta sucesión se le denota comúnmente como $n!$ y su valor está dado por $n! = n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot 2 \cdot 1.$ Adicionalmente, se define $0! = 1$ .

Operaciones con sucesiones

Las reglas de la suma, la resta, el producto y el cociente de funciones particularmente aplican a las sucesiones, pues éstas también son funciones. Considerando esto, dadas dos sucesiones ${a_{n}}$ , ${b_{n}}$ y si $c \in R$ , definimos:

La suma: ${a_{n}} + {b_{n}} = {a_{n} + b_{n}} .$
La resta: ${a_{n}} - {b_{n}} = {a_{n} - b_{n}} .$
La multiplicación: ${a_{n}} \cdot {b_{n}} = {a_{n} \cdot b_{n}} .$
La multiplicación por un escalar: $c \cdot {a_{n}} = {c \cdot a_{n}} .$
El cociente: Si además $b_{n} \neq 0$ para todo $n \in N$ , entonces $\frac{{a_{n}}}{{b_{n}}} = {\frac{a_{n}}{b_{n}}} .$

A continuación veremos algunos ejemplos.

Ejemplo 8. Sean ${a_{n}} = {n^{2}}$ y ${b_{n}} = {\frac{n}{10}}$ , entonces ${a_{n}} + {b_{n}} = {n^{2} + \frac{n}{10}}$ . Denotamos a la sucesión generada como ${c_{n}} = {n^{2} + \frac{n}{10}}$ . A continuación se calculan los primeros tres términos:

$\begin{array}{r} c_{1} = 1^{2} + \frac{1}{10} = 1.1, \\ c_{2} = 2^{2} + \frac{2}{10} = 4.2, \\ c_{3} = 3^{2} + \frac{3}{10} = 9.3 . \end{array}$
Así, los términos de la sucesión son: ${1.1, 4.2, 9.3, \dots, k^{2} + \frac{k}{10}, \dots} .$

Ejemplo 9. Sean ${a_{n}} = {n}$ y ${b_{n}} = {n + 1}$ , entonces ${a_{n}} - {b_{n}} = {- 1}$ . Denotamos a la sucesión generada como ${c_{n}} = {- 1}$ . Los primeros tres términos son:

$\begin{array}{r} c_{1} = - 1, \\ c_{2} = - 1, \\ c_{3} = - 1. \end{array}$
Así, los términos de la sucesión son: ${- 1, - 1, - 1, \dots, - 1, \dots} .$

Ejemplo 10. Sean ${a_{n}} = {n - 1}$ y ${b_{n}} = {n + 1}$ , entonces ${a_{n}} \cdot {b_{n}} = {n^{2} - 1}$ . Denotamos a la sucesión generada como ${c_{n}} = {n^{2} - 1}$ . Los primeros tres términos son:

$\begin{array}{r} c_{1} = 1^{2} - 1 = 0, \\ c_{2} = 2^{2} - 1 = 3, \\ c_{3} = 3^{2} - 1 = 8. \end{array}$
Así, los términos de la sucesión son: ${0, 3, 8, \dots, k^{2} - 1, \dots} .$

Ejemplo 11. Sean $c = 5$ y ${a_{n}} = {n}$ , entonces $5 \cdot {a_{n}} = {5 n}$ . Denotamos a la sucesión generada como ${c_{n}} = {5 n}$ . Los primeros tres términos son:

$\begin{array}{r} c_{1} = 5 (1) = 5, \\ c_{2} = 5 (2) = 10, \\ c_{3} = 5 (3) = 15. \end{array}$
Así, los términos de la sucesión son: ${5, 10, 15, \dots, 5 k, \dots} .$

Ejemplo 12. Sean ${a_{n}} = {n}$ y ${b_{n}} = {(- 1)^{n}}$ , entonces $\frac{{a_{n}}}{{b_{n}}} = {\frac{n}{(- 1)^{n}}}$ . Denotamos a la sucesión generada como ${c_{n}} = {\frac{n}{(- 1)^{n}}}$ . Los primeros tres términos son:

$\begin{array}{r} c_{1} = \frac{1}{(- 1)^{1}} = - 1, \\ c_{2} = \frac{2}{(- 1)^{2}} = 2, \\ c_{3} = \frac{3}{(- 1)^{3}} = - 3. \end{array}$
Así, los términos de la sucesión son: ${- 1, 2, - 3, \dots, \frac{k}{(- 1)^{k}}, \dots} .$

Más adelante…

En la siguiente entrada se hará la revisión del concepto de sucesión convergente. Para este propósito, revisaremos la definición de límite aplicado a sucesiones, que será clave para el estudio de todos los temas subsecuentes en el curso dado que es el antecesor de la definición del límite de una función.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Considera la sucesión de Fibonacci definida en esta entrada. Encuentra $f_{8}$ .
Consideremos las sucesiones ${a_{n}}$ y ${b_{n}}$ donde $a_{n} = n^{2} - 5 n + 10$ y $b_{n} = \frac{1}{n}$ . Determina los primeros 8 términos de las siguientes sucesiones:
- ${a_{n}} \cdot {b_{n}} .$
- ${a_{n}} + {b_{n}} .$
- $\frac{{a_{n}}}{{b_{n}}} .$
- $8 \cdot {a_{n}} - 10 \cdot {\frac{1}{b_{n}}} .$

Entradas relacionadas

Ir a Cálculo Diferencial e Integral I
Entrada anterior del curso: Funciones exponenciales y logarítmicas
Siguiente entrada del curso: Sucesiones convergentes
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Sucesiones convergentes

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Anteriormente se dio la definición de sucesión y revisamos algunos ejemplos. En esta entrada, se definirá la convergencia para una sucesión y se darán varios ejemplos de sucesiones convergentes y no convergentes.

Límite de una sucesión

A continuación daremos la definición de límite de una sucesión:

Definición. Sea ${a_{n}}$ una sucesión en $R$ . Sea $L \in R$ , decimos que $L$ es el límite de la sucesión ${a_{n}}$ si para todo $ε > 0$ existe un número natural $n_{0}$ tal que para todo $n \geq n_{0}$ se satisface $| a_{n} - L | < ε$ .

Si una sucesión tiene como límite a $L$ , también decimos que converge a $L$ y lo denotamos como $lim_{n \to \infty} a_{n} = L .$

En términos más simples, la definición nos indica que una sucesión es convergente a $L$ si a partir de cierto elemento en la sucesión, $a_{n_{0}}$ , los términos están lo suficientemente cerca, $ε$ , de $L$ . Para ilustrar estos elementos, a continuación se presenta la gráfica de la sucesión ${a_{n}} = {\frac{1}{n}}$ , y más adelante probaremos que converge a $L = 0$ .

Observación. Cada punto de la gráfica está determinado por las coordenadas $(i, a_{i})$ con $i \in N$ , pero por simplicidad, se denotan únicamente como $a_{i}$ .

Ejemplos de sucesiones convergentes

Ahora continuaremos con algunos ejemplos de sucesiones convergentes. Es importante recalcar que para demostrar que una sucesión converge a $L$ , deberemos especificar las condiciones que $n_{0}$ debe cumplir tal que para un $ε > 0$ arbitrario dado, $| a_{n} - L | < ε$ para todo $n \geq n_{0}$ .

Ejemplo 1. Sea $k$ un número real y consideremos la sucesión ${a_{n}} = {k}$ , entonces $lim_{n \to \infty} k = k .$

Demostración.

Sea $ε > 0$ (establecemos el valor arbitrario de un épsilon positivo).
Para esta sucesión cualquier valor de $n_{0}$ sirve, en particular consideremos $n_{0} = 1$ (en este caso se puede dar $n_{0}$ explícitamente).
Si $n \geq n_{0} = 1$ , entonces

$\begin{matrix} | a_{n} - k | = | k - k | = 0 < ε . \\ ∴ lim_{n \to \infty} k = k . \end{matrix}$

El ejemplo anterior es uno sencillo, sin embargo, como lo podemos ver en los comentarios entre paréntesis, están presentes los pasos relevantes para demostrar la convergencia. En este caso, dado que nuestra sucesión era un valor constante, el valor de $n_{0}$ que funcionaba era cualquier número natural, pero, en la mayoría de los casos, su valor estará definido en términos de épsilon.

Ejemplo 2. Consideremos la sucesión ${\frac{1}{n}}$ , entonces $lim_{n \to \infty} \frac{1}{n} = 0.$

Demostración.

Sea $ε > 0$ .

Dado que el valor de $ε$ es positivo, por la propiedad Arquimediana, existe $n_{0} \in N$ tal que $1 < n_{0} \cdot ε$ , es decir, $\frac{1}{n_{0}} < ε$ . Así, para cualquier $n \geq n_{0}$ se tiene que $\frac{1}{n} \leq \frac{1}{n_{0}} < ε$ . De lo anterior se sigue que

$| \frac{1}{n} - 0 | = \frac{1}{n} < ε .$

$∴ | \frac{1}{n} - 0 | < ε$ para todo $n \geq n_{0} .$

$∴ lim_{n \to \infty} = 0.$

En este último ejemplo podemos observar cómo se establecen condiciones que $n_{0}$ debe cumplir en función de $ε$ , así como la relevancia de la propiedad Arquimediana que estará constantemente presente al momento de demostrar convergencia mediante su definición.

Ejemplo 3. Demuestra que

$lim_{n \to \infty} \frac{8 n - 5}{3 n} = \frac{8}{3} .$

Demostración.

Sea $ε > 0$ .
Notemos que

$| \frac{8 n - 5}{3 n} - \frac{8}{3} | = | \frac{8 n - 5 - 8 n}{3 n} | = | \frac{- 5}{3 n} | = \frac{5}{3 n} .$

$\begin{array}{r} (1) & ∴ | \frac{8 n - 5}{3 n} - \frac{8}{3} | = \frac{5}{3 n} . \end{array}$

Consideremos $n_{0} \cdot ε > \frac{5}{3}$ , que sabemos que existe gracias a la propiedad Arquimediana. De esta forma, se tiene que

$ε > \frac{5}{3 n_{0}} .$

Si $n \geq n_{0}$ , entonces tenemos

$\begin{aligned} | \frac{8 n - 5}{3 n} - \frac{8}{3} | = & \frac{5}{3 n}, por (1) \\ \leq & \frac{5}{3 n_{0}}, pues n \geq n_{0} \\ < & ε . \end{aligned}$

$∴ | \frac{8 n - 5}{3 n} - \frac{8}{3} | < ε .$

$∴ lim_{n \to \infty} \frac{8 n - 5}{3 n} = \frac{8}{3} .$

Ejemplo 4. $lim_{n \to \infty} (\sqrt{n + 1} - \sqrt{n}) = 0.$

Demostración.

Sea $ε > 0$ . Para simplificar la expresión, multiplicaremos por un uno haciendo uso del conjugado de la expresión anterior.

$\begin{aligned} \sqrt{n + 1} - \sqrt{n} = & (\sqrt{n + 1} - \sqrt{n}) \cdot \frac{\sqrt{n + 1} + \sqrt{n}}{\sqrt{n + 1} + \sqrt{n}} \\ = & \frac{{\sqrt{n + 1}}^{2} - {\sqrt{n}}^{2}}{\sqrt{n + 1} + \sqrt{n}} \\ = & \frac{n + 1 - n}{\sqrt{n - 1} + \sqrt{n}} \\ = & \frac{1}{\sqrt{n - 1} + \sqrt{n}} \\ \leq & \frac{1}{\sqrt{n}} . \end{aligned}$

$∴ \sqrt{n - 1} - \sqrt{n} \leq \frac{1}{\sqrt{n}} .$

Consideremos $n_{0} > \frac{1}{ε^{2}} \Rightarrow \frac{1}{\sqrt{n_{0}}} < ε$ . Entonces tenemos

$\begin{aligned} | \sqrt{n - 1} - \sqrt{n} - 0 | = & \frac{1}{\sqrt{n - 1} + \sqrt{n}}, por la observación anterior \\ \leq & \frac{1}{\sqrt{n}} \\ \leq & \frac{1}{\sqrt{n_{0}}}, pues n \geq n_{0} \\ < & ε . \end{aligned}$

$∴ | \sqrt{n - 1} - \sqrt{n} - 0 | < ε .$

$∴ lim_{n \to \infty} (\sqrt{n + 1} - \sqrt{n}) = 0.$

Los dos ejemplos de arriba hacen uso de manipulaciones algebraicas que nos permiten simplificar nuestro problema; esta técnica de simplificación de expresiones, cuyo fin es llevarlas a otras más sencillas, es ampliamente usada para demostrar la convergencia de sucesiones.

Ejemplos de sucesiones no convergentes

Después de haber revisado ejemplos de sucesiones convergentes, vale la pena conocer sucesiones que no convergen, es decir, que su límite no existe.

Ejemplo 5. Consideremos la sucesión ${a_{n}} = {(- 1)^{n}}$ . Probaremos que el límite de ${a_{n}}$ no existe.

Demostración.

Procederemos a hacer esta demostración por contradicción. Supongamos que existe $L \in R$ tal que $lim_{n \to \infty} (- 1)^{n} = L .$

Consideremos $ε = 1 / 2 > 0$ . Por definición, existe $n_{0} \in N$ tal que si $n \geq n_{0}$ entonces $| (- 1)^{n} - L | < \frac{1}{2} .$

Como $2 n_{0} > n_{0}$ y $2 n_{0} + 1 > n_{0}$ , entonces
$\begin{matrix} (1) & | (- 1)^{2 n_{0}} - L | < \frac{1}{2} \Rightarrow | 1 - L | < \frac{1}{2} . \\ (2) & | (- 1)^{2 n_{0} + 1} - L | < \frac{1}{2} \Rightarrow | - 1 - L | = | 1 + L | < \frac{1}{2} . \end{matrix}$

Y notemos que

$\begin{aligned} 2 = | 1 + 1 | = & | 1 - L + L + 1 | \\ \leq & | 1 - L | + | 1 + L | \\ < & \frac{1}{2} + \frac{1}{2}, por (1) y (2). \end{aligned}$

Lo anterior implica que $2 < 1$ y esto es una contradicción.
Por tanto, podemos concluir que tal límite no existe.

Ahora estudiaremos una nueva definición para un tipo particular de sucesiones que no tienen como límite a un número real $L$ .

Definición. Sea ${a_{n}}$ una sucesión en $R$ . Decimos que ${a_{n}}$ diverge a infinito si $\forall M \in R$ existe $n_{0} \in N$ tal que si $n \geq n_{0}$ entonces $M < a_{n}$ .

La definición anterior nos indica que una sucesión diverge a infinito si para cualquier número real $M$ , existe un término de la sucesión $a_{n_{0}}$ a partir del cual todos los valores subsecuentes en la sucesión son mayores que $M$ . Cuando una sucesión ${a_{n}}$ diverja a infinito lo denotaremos como $lim_{n \to \infty} a_{n} = \infty .$

Ejemplo 6. La sucesión ${a_{n}} = {n}$ diverge a infinito.

Demostración.

Sea $M \in N$ . Sabemos que $N$ no está acotado superiormente, entonces existe $n_{0} \in N$ tal que $M < n_{0}$ , de esta forma, si $n \geq n_{0}$ , se tiene que $M < n$ .

Ejemplo 7. $lim_{n \to \infty} n^{2} = \infty .$

Demostración.

Procederemos a hacer la prueba por contradicción. Supongamos que para todo $n \in N$ se tiene que $n^{2} \leq M$ para algún $M \in R$ . Se sigue que

$\sqrt{n^{2}} \leq \sqrt{M} .$

Es decir,

$n \leq \sqrt{M} .$

Lo cual es una contradicción pues sabemos que el conjunto de los números naturales no está acotado superiormente.

$∴ {n^{2}}$ diverge a infinito.

Más adelante…

Se han revisado las definiciones de convergencia y divergencia a infinito, hemos visto diversos ejemplos de ambas definiciones. En las siguientes entradas se revisarán criterios para la convergencia de sucesiones, así como sus propiedades y teoremas con lo cual podremos determinar si una sucesión es convergente o no de manera más rápida.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Prueba que el límite de una sucesión convergente ${a_{n}}$ es único.
Sugerencia:
1. Proceder por contradicción y asumir que existen dos números reales distintos $L$ y $L^{'}$ tales que
$lim_{n \to \infty} a_{n} = L y lim_{n \to \infty} a_{n} = L^{'} .$
2. Utilizar la definición de límite de una sucesión empleando el siguiente valor de épsilon: $ε = \frac{| L - L^{'} |}{2} .$
$ε > 0$ , ¿por qué?
Demuestra lo siguiente:
a) $lim_{n \to \infty} \frac{(- 1)^{n}}{n} = 0.$
b) $lim_{n \to \infty} \sqrt{n} = \infty .$
c) $lim_{n \to \infty} \sqrt{12 + \frac{1}{n}} = \sqrt{12} .$
Sea ${a_{n}}$ una sucesión en $R$ y sea $L \in R$ . Prueba que $lim_{n \to \infty} a_{n} = L \Leftrightarrow lim_{n \to \infty} a_{n} - L = 0.$
Una sucesión también puede ser divergente a $- \infty$ . Propón una definición análoga a la de divergencia a infinito y prueba que $lim_{n \to \infty} - \sqrt{n} = - \infty .$

Entradas relacionadas

Ir a Cálculo Diferencial e Integral I
Entrada anterior del curso: Sucesiones de números reales
Siguiente entrada del curso: Operaciones con sucesiones convergentes
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: ejemplos de sucesiones

Cálculo Diferencial e Integral I: Sucesiones de números reales

Introducción

Sucesiones

Ejemplos de sucesiones

Operaciones con sucesiones

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Cálculo Diferencial e Integral I: Sucesiones convergentes

Introducción

Límite de una sucesión

Ejemplos de sucesiones convergentes

Ejemplos de sucesiones no convergentes

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos