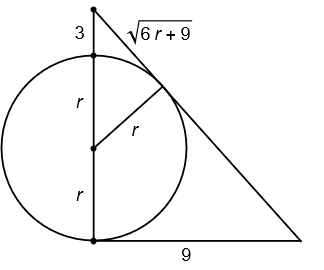Introducción
A lo largo del tiempo el desarrollo de las Matemáticas ha sido una constante abstracción entre lo real y lo necesario. Es claro que la necesidad de resolver distintas problemáticas ha sido la motivación para dar soluciones que a su vez permitan desarrollar nuevas teorías que den sustento y validez a dichos planteamientos. Muchos de los resultados y de las teorías que tenemos actualmente parecen haber sido trabajados de manera consecutiva, sin embargo hoy sabemos que se han dado de forma independiente, y que algunas de las ramas de las Matemáticas que convergen en teorías más generales fueron, en principio, abordadas en distinto tiempo y con distinto enfoque. El hecho de que hoy podamos entender conceptos que parecen evidentes es gracias a todo este desarrollo.
Tanto la definición como el concepto que tenemos hoy en día sobre lo que es un número complejo han cambiado durante el desarrollo de la teoría de los Números Complejos. Con ánimos de plantear soluciones a problemas como ecuaciones cuadráticas y cubicas, pero sobre todo de entender y explicar expresiones que requerían hablar de algunas “cantidades sofisticadas”, como les llamó Cardano, se ha desarrollado la teoría que hoy conocemos como Variable Compleja. Aunque estos números estuvieron presentes en problemas matemáticos desde el primer siglo, como en cálculos de volúmenes de pirámides hechos por Herón de Alejandría alrededor del año 75 D.C., este concepto se tuvo que abstraer primero para poder comprender expresiones en las que se tenían raíces de números negativos. Del mismo modo en que el concepto de número negativo en principio parecía inconcebible, tanto que se les llego a llamar “falsos números”, los números complejos fueron tratados en ocasiones como “cantidades imposibles”, ya que no eran aceptados por estar fuera de lo real.
Antecedentes
En la historia de los números complejos aparecen nombres de grandes matemáticos que en su tiempo hicieron algún aporte en la teoría y comprensión de estos números, por lo que es importante mencionar algunos de sus resultados con la finalidad de entender un poco mejor el origen de la Variable Compleja.
Aunque los primeros resultados trascendentes al trabajar con números complejos se dieron durante el siglo XVI, desde los primeros siglos algunos matemáticos hindúes como Bhaskara Acharya (486 D.C.) y Mahavira Acharya (850 D.C.) tenían en sus trabajos escritos como “el cuadrado tanto de un número positivo como de un número negativo es positivo y la raíz cuadrada de un número positivo es doble: positiva y negativa, mientras que no existe la raíz cuadrada de un número negativo, porque no existen números negativos al elevarlos al cuadrado” y “como es natural, una cantidad negativa no es una cantidad al cuadrado, por lo que no tiene raíz cuadrada”. Estas ideas nos dejan claro que el contexto para hablar de un número complejo, tal y como lo conocemos ahora, no era favorable. Fue hasta el año de 1545 cuando el matemático italiano Girolamo Cardano, publicó su libro Ars Magna (El Gran Arte), en el cual describía métodos algebraicos para resolver ecuaciones cuadráticas y cúbicas, cuando los números complejos comenzaron a ser necesarios.
La importancia del trabajo de Cardano está en que reconoce la necesidad de trabajar con “cantidades sofisticadas” para dar solución a ecuaciones que se habían catalogado como “imposibles”. Es quizás la sutileza que observó Cardano en sus soluciones la que abre un nuevo capítulo para los números complejos.
Si deseas conocer más acerca de la historia de los números complejos y los resultados de Cardano puedes consultar los libros An Introduction to Complex Analysis de Agarwal, Ravi P., Numbers de Ebbinghaus, H.D., y Ars Magna or the Rules of Algebra by Girolamo Cardano traducido al inglés por Richard Witmer.
- https://www.springer.com/gp/book/9781461401940
- https://www.springer.com/gp/book/9780387974972
- https://www.amazon.com/-/es/dp/B01K16HOC4
Fórmula de Cardano
Antes de presentar el resultado de Cardano, consideremos el siguiente:
Lema 1.
Dada una ecuación de la forma:
\begin{equation*}
ax^3 + bx^2 + cx + d = 0, \tag{1.1}
\end{equation*}
con $a, b, c, d \in \mathbb{C}$ y $a \neq 0$, podemos reducirla a una ecuación sin el término cuadrático de la forma:
\begin{equation*}
x^3 + px + q = 0,
\end{equation*}
donde $p= – \frac{b^2}{3a^2} + \frac{c}{a}$ y $q = \frac{2b^3}{27a^3} – \frac{bc}{3a^2} + \frac{d}{a}$.
Demostración. Dadas las hipótesis, primeramente hagamos al polinomio (1.1) un polinomio mónico:
\begin{equation*}
x^3 + Bx^2 + Cx + D = 0, \quad \text{donde} \quad B=\frac{b}{a}, \, C = \frac{c}{a}, \, D = \frac{d}{a}.
\end{equation*}
Consideremos ahora el cambio de variable $x = y + e$. Entonces:
\begin{equation*}
(y+e)^3 + B(y+e)^2 + C(y+e) + D = 0.
\end{equation*}
Desarrollando y agrupando tenemos que:
\begin{equation*}
y^3 + (B+3e)y^2 + (3e^2 + 2Be + C)y + (e^3 + Be^2 + Ce + D) = 0,
\end{equation*}
Si hacemos $B+3e=0$, entonces $e = \frac{-B}{3}$. Por lo que, definiendo:
\begin{equation*}
p:= 3e^2 + 2Be + C = – \frac{B^2}{3} + C,
\end{equation*}
\begin{equation*}
q:= e^3 + Be^2 + Ce + D = \frac{2B^3}{27} – \frac{BC}{3} + D,
\end{equation*}
se sigue el resultado haciendo las sustituciones correspondientes:
\begin{equation*}
y^3 + py + q = 0 \quad \text{o simplemente} \quad x^3 + px + q = 0,
\end{equation*}
con $p= – \frac{b^2}{3a^2} + \frac{c}{a}$ y $q = \frac{2b^3}{27a^3} – \frac{bc}{3a^2} + \frac{d}{a}$.
$\blacksquare$
De acuerdo con el resultado anterior, dada una ecuación cúbica como en (1.1), para reducirla a una ecuación sin el término cuadrático basta con usar un cambio de variable de la forma $x=y-\frac{b}{3a}$.
Teorema 1. (Fórmula de Cardano.)
Sean $a, b, c, d \in \mathbb{R}$ con $a \neq 0$. Las raíces de la ecuación cúbica:
\begin{equation*}
ax^3 + bx^2 + cx + d = 0, \tag{1.2}
\end{equation*}
están dadas por:
\begin{equation*}
x = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} + \sqrt[3]{-\frac{q}{2} – \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} – \frac{b}{3a}. \tag{1.3}
\end{equation*}
Donde $p= – \dfrac{b^2}{3a^2} + \dfrac{c}{a}$ y $q = \dfrac{2b^3}{27a^3} – \dfrac{bc}{3a^2} + \dfrac{d}{a}$.
Demostración. Dadas las hipótesis, de acuerdo con el Lema 1 tenemos que la ecuación (1.2), utilizando el cambio de variable $x=y-\frac{b}{3a}$, se puede simplificar como:
\begin{equation*}
y^3 + py + q = 0, \tag{1.4}
\end{equation*}
donde $p= – \dfrac{b^2}{3a^2} + \dfrac{c}{a}$ y $q = \dfrac{2b^3}{27a^3} – \dfrac{bc}{3a^2} + \dfrac{d}{a}$.
Notemos que:
\begin{align*}
\left(\alpha + \beta\right)^3 & = \alpha^3 + \beta^3 + 3\alpha^2 \beta + 3\alpha \beta^2\\
& = \alpha^3 + \beta^3 + 3\alpha\beta \left(\alpha + \beta\right),
\end{align*}
de donde obtenemos:
\begin{align*}
\left(\alpha + \beta\right)^3 – 3\alpha\beta \left(\alpha + \beta\right) – \left(\alpha^3 + \beta^3\right) = 0. \tag{1.5}
\end{align*}
Si definimos $q = – \left(\alpha^3 + \beta^3\right)$ y $p = – 3\alpha\beta$ en (1.5), entonces $y = \alpha + \beta$ es una solución de (1.4). Tenemos entonces que:
\begin{align*}
p = -3 \alpha \beta \quad \Longrightarrow \quad \left(\alpha \beta\right)^3 = -\left(\frac{p}{3}\right)^3.\\ \tag{1.6}
q = – \left(\alpha^3 + \beta^3\right) \quad \Longrightarrow \quad \alpha^3 + \beta^3 = -q.
\end{align*}
De (1.6) se sigue que $\beta^3 = -\frac{p^3}{27 \alpha^3}$, por lo que podemos obtener la siguiente ecuación en términos de $\alpha^3$:
\begin{align*}
-q &= \alpha^3 + \beta^3\\
&= \alpha^3 -\frac{p^3}{27 \alpha^3},
\end{align*}
o equivalentemente:
\begin{equation*}
\left( \alpha^3 \right)^2 + q \alpha^3 – \frac{p^3}{27} = 0. \tag{1.7}
\end{equation*}
Resolviendo (1.7) para $\alpha^3$ tenemos que las soluciones son:
\begin{align*}
\alpha^3 & = \frac{-q \pm \sqrt{q^2 + 4\left(\frac{p}{3}\right)^3}}{2}\\
& = -\frac{q}{2} \pm \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}
\end{align*}
Notemos que el mismo resultado se obtiene para $\beta^3$. De acuerdo con (1.6), como $\alpha^3 + \beta^3 = -q$, entonces sin pérdida de generalidad:
\begin{equation*}
\alpha^3 = -\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3} \quad \Longrightarrow \quad \alpha = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}.
\end{equation*}
\begin{equation*} \beta^3 = -\frac{q}{2} – \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3} \quad \Longrightarrow \quad \beta = \sqrt[3]{-\frac{q}{2} – \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}.
\end{equation*}
Considerando que tenemos 2 raíces cuadradas y 3 raíces cúbicas, entonces hay en total 6 raíces, pero dadas las condiciones en (1.6), tenemos que fijado un valor de $\alpha$, entonces el valor de $\beta$ está determinado por la igualdad $p = – 3\alpha \beta$, lo cual nos garantiza que (1.4) tiene solo 3 soluciones, que de acuerdo con lo anterior son de la forma:
\begin{align*}
x & = y \,-\, \frac{b}{3a}\\
& = \left(\alpha + \beta\right) \,-\, \frac{b}{3a}\\
& = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} + \sqrt[3]{-\frac{q}{2} – \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} \,-\, \frac{b}{3a},
\end{align*}
donde $p= – \dfrac{b^2}{3a^2} + \dfrac{c}{a}$ y $q = \dfrac{2b^3}{27a^3} – \dfrac{bc}{3a^2} + \dfrac{d}{a}$.
$\blacksquare$
Corolario 1.
Las raíces de la ecuación cúbica:
\begin{equation*}
x^3 + px + q = 0.
\end{equation*}
están dadas por:
\begin{equation*}
x = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} + \sqrt[3]{-\frac{q}{2} – \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}.
\end{equation*}
$\blacksquare$
Observación 1.1.
El resultado de Cardano parecía no tener sentido en el caso en que $\left(\dfrac{q}{2}\right)^2 + \left(\dfrac{p}{3}\right)^3< 0$, sin embargo fue la sutileza de Cardano la que le permitió asumir que trabajar con «cantidades sofisticadas», a decir expresiones donde aparecían números negativos dentro de raíces cuadradas, daba resultados útiles aunque fuera de lo real. Cardano mostró que las ecuaciones cúbicas con ésta condición tenían soluciones reales dadas como suma de raíces cúbicas imaginarias.
Ejemplo 1.
Consideremos las siguientes ecuaciones:
- a) $ \quad x^3 – 30x -36 =0$.
- b) $ \quad x^3 – 15x – 4 = 0$.
Es claro que estas ecuaciones no eran consideradas “imposibles” desde que $x = 6$ es solución de a) y $x = 4$ es solución de b). Sin embargo usando la fórmula de Cardano obtenemos las siguientes soluciones:
- a) Tenemos que $p = -30 $ y $q = -36$, entonces sustituyendo en la solución del Corolario 1 tenemos que:
\begin{align*}
x & = \sqrt[3]{18 + \sqrt{-676}} + \sqrt[3]{18 – \sqrt{-676}}\\
& = \sqrt[3]{18 + \sqrt{-1} \, 26} + \sqrt[3]{18 – \sqrt{-1} \, 26}.
\end{align*} - b) Tenemos que $p = -15 $ y $q = -4$, entonces sustituyendo en la solución del Corolario 1 tenemos que:
\begin{align*}
x & = \sqrt[3]{2 + \sqrt{-121}} + \sqrt[3]{2 – \sqrt{-121}}\\
& = \sqrt[3]{2 + \sqrt{-1} \, 11} + \sqrt[3]{2 – \sqrt{-1} \, 11}.
\end{align*}
Lo que observó Cardano claramente era cuestionable, aunque fue hasta 1572 que el matemático italiano Rafael Bombelli en su libro «L’Algebra» desarrolló las reglas básicas del álgebra de los números complejos. Usando la notación moderna para $\sqrt{-1}$, es decir la letra $i$, misma que fue usada por primera vez por el matemático Leonhard Euler, Bombelli estableció que:
- $(\pm 1)i = \pm i $.
- $(\pm 1)(-i) = \mp i $.
- $(+i)(+i) = -1$.
- $(-i)(+i) = (+i)(-i) = +1$.
Es entonces cuando los resultados que aparentemente no tenían sentido alguno lo cobran gracias a Bombelli, quien estableció la forma correcta de operar con estos números, tanto que mediante el uso de las propiedades de los números reales manipula las expresiones obtenidas por Cardano resolviendo así que:
- Para la ecuación a):
\begin{align*}
x & = \left(\sqrt[3]{18 + \sqrt{-1} \, 26}\right) + \left(\sqrt[3]{18 – \sqrt{-1} \, 26}\right)\\
& = \left(a + \sqrt{-1} \, b\right) + \left( a – \sqrt{-1} \, b \right).
\end{align*}
Que equivalentemente podemos expresar como:
\begin{align*}
18 + \sqrt{-1} \, 26 & = \left(a + \sqrt{-1} \, b\right)^3\\
& = \left(a^3 -3ab^2\right) + \sqrt{-1}\left( 3a^2b – b^3\right).
\end{align*}
\begin{align*}
18 – \sqrt{-1} \, 26 & = \left(a – \sqrt{-1} \, b\right)^3\\
& = \left(a^3 -3ab^2\right) – \sqrt{-1}\left(3a^2b-b^3\right).
\end{align*}
Entonces:
\begin{align*}
18 = a^3 -3ab^2\\
26 = 3a^2b – b^3.
\end{align*}
Por lo que para $a = 3$ y $b=1$ notamos que se satisface el sistema, entonces:
\begin{equation*}
x = \left(3 + \sqrt{-1} \right) + \left( 3 – \sqrt{-1} \right) = 6.
\end{equation*}
- Para la ecuación b):
\begin{align*}
x & = \left(\sqrt[3]{2 + \sqrt{-1} \, 11}\right) + \left(\sqrt[3]{2 – \sqrt{-1} \, 11}\right)\\
& = \left(a + \sqrt{-1} \, b\right) + \left( a – \sqrt{-1} \, b \right).
\end{align*}
Que equivalentemente podemos expresar como:
\begin{align*}
2 + \sqrt{-1} \, 11 & = \left(a + \sqrt{-1} \, b\right)^3\\
& = \left(a^3 -3ab^2\right) + \sqrt{-1}\left( 3a^2b – b^3\right).
\end{align*}
\begin{align*}
2 – \sqrt{-1} \, 11 & = \left(a – \sqrt{-1} \, b\right)^3\\
& = \left(a^3 -3ab^2\right) – \sqrt{-1}\left( 3a^2b – b^3\right).
\end{align*}
Entonces:
\begin{align*}
2 = a^3 -3ab^2\\
11 = 3a^2b – b^3.
\end{align*}
Por lo que para $a = 2$ y $b=1$ notamos que se satisface el sistema, entonces:
\begin{equation*}
x = \left(2 + \sqrt{-1} \right) + \left( 2 – \sqrt{-1} \right) = 4.
\end{equation*}
Todo el desarrollo anterior fue posible gracias al trabajo hecho por Bombelli. Después de Cardano y Bombelli hubo aportaciones de grandes matemáticos como Descartes, Leibniz, Euler, Wallis, Wessel, Argand, Gauss, Cauchy, Hamilton, entre otros, quienes colaboraron en el desarrollo y comprensión de estos números y su teoría, la construcción moderna que tenemos hoy en día de los números complejos, su operabilidad, interpretación geométrica, incluso su mismo nombre, es sin duda el resultado de la abstracción y unificación de todas estas ideas.
Observación 1.2.
Es importante mencionar que a lo largo de este curso haremos uso de las siguientes notaciones para referirnos a los distintos conjuntos:
- Números naturales y naturales positivos:
\begin{align*}
\mathbb{N} = \{0,1,2,\ldots\},\\
\mathbb{N}^+ = \{1,2,\ldots\}.
\end{align*}
- Números enteros, enteros positivos y enteros negativos:
\begin{align*}
\mathbb{Z} = \{\ldots, -2, -1, 0, 1 , 2,\ldots\},\\
\mathbb{Z}^+ = \{1 , 2,\ldots\},\\
\mathbb{Z}^- = \{-1, -2, \ldots\}.
\end{align*}
- Números racionales:
\begin{equation*}
\mathbb{Q} = \left\{ \frac{p}{q} \, : \, p,q\in\mathbb{Z}, \, q\neq 0 \right\}.
\end{equation*}
- Números reales $\mathbb{R} = (-\infty,\infty)$ y reales positivos $\mathbb{R}^+ = (0,\infty)$.
Tarea Moral
- Encuentra las otras dos raíces cúbicas de las ecuaciones a) y b) del ejemplo 1. ¿También son reales?
- Consideremos al discriminante $\triangle = \left( \dfrac{q}{2} \right)^2 + \left( \dfrac{p}{3} \right)^3$. De acuerdo con los ejemplos, notamos que las raíces reales estaban dadas como suma de raíces cúbicas complejas en el caso en que $\triangle<0$. ¿Qué pasa cuando $\triangle = 0$ y $\triangle>0$?.
- Considera las siguientes ecuaciones:
- a) $ \quad x^3 + 6x + 20 = 0$.
- b) $ \quad x^3 -6x – 4 = 0 $.
Utilizando la fórmula de Cardano encuentra la solución y de ser necesario realiza un poco de álgebra para simplificar los resultados, observa que $x=-2$ es una solución para ambas ecuaciones ¿Cómo es su discriminante $\triangle$ ?
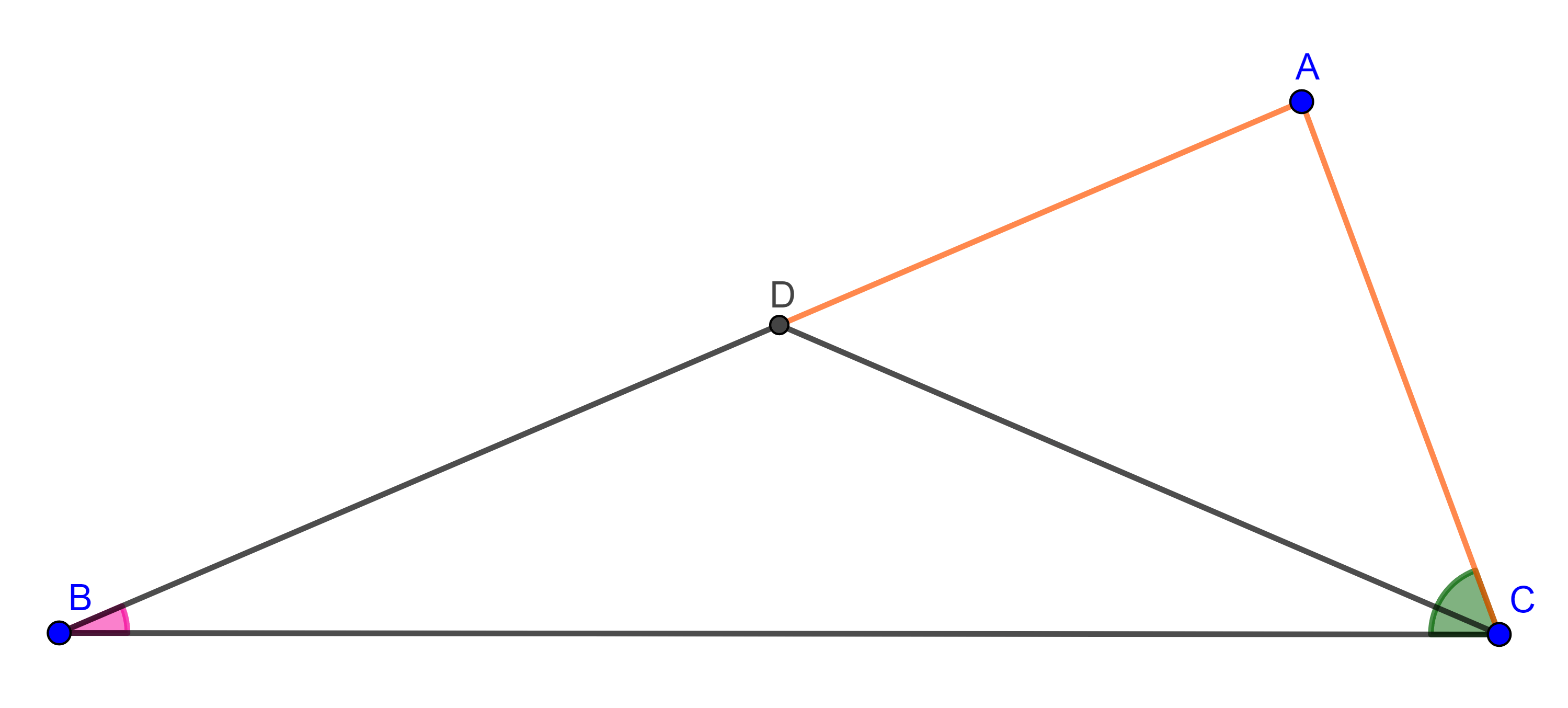
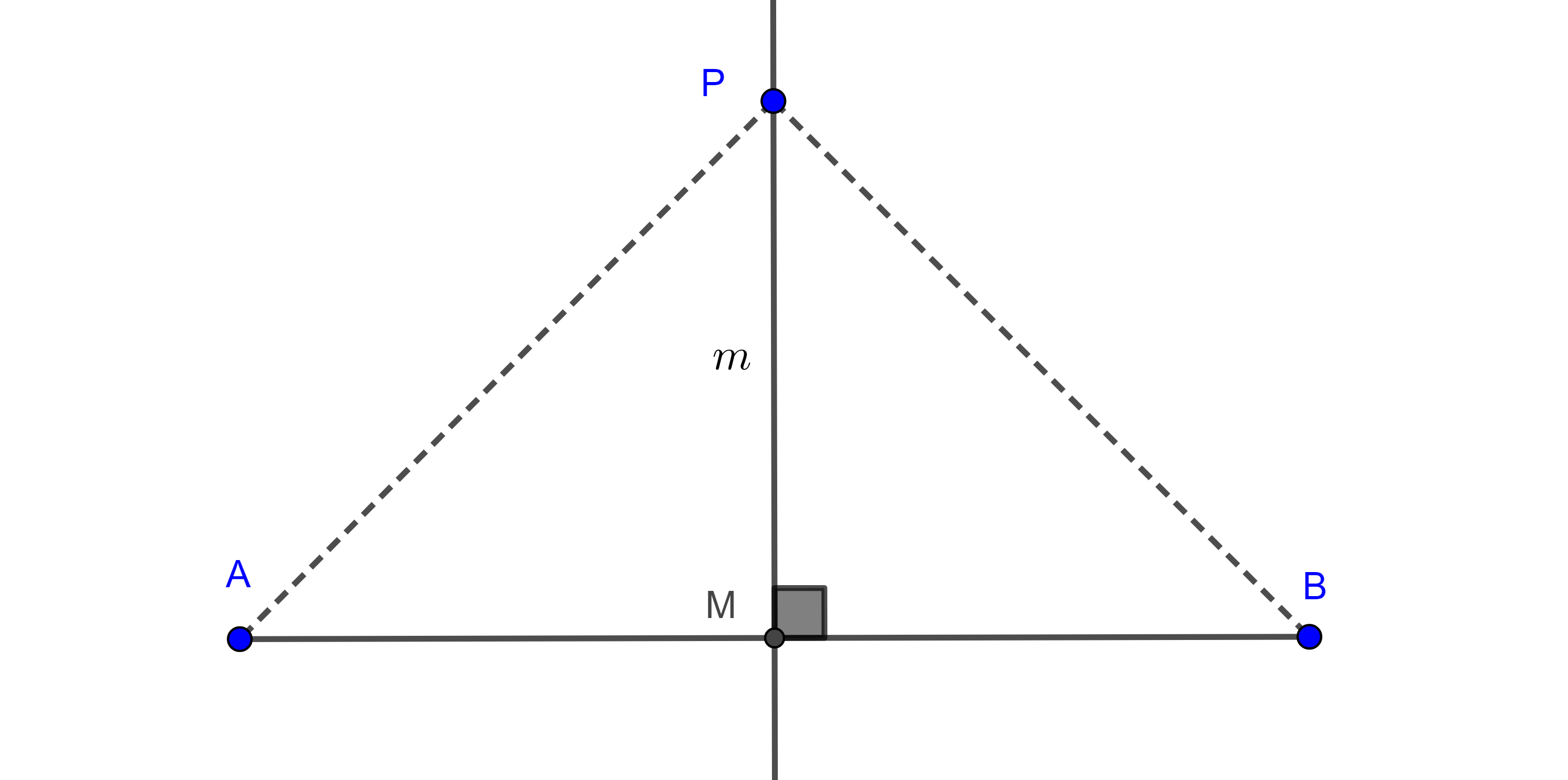
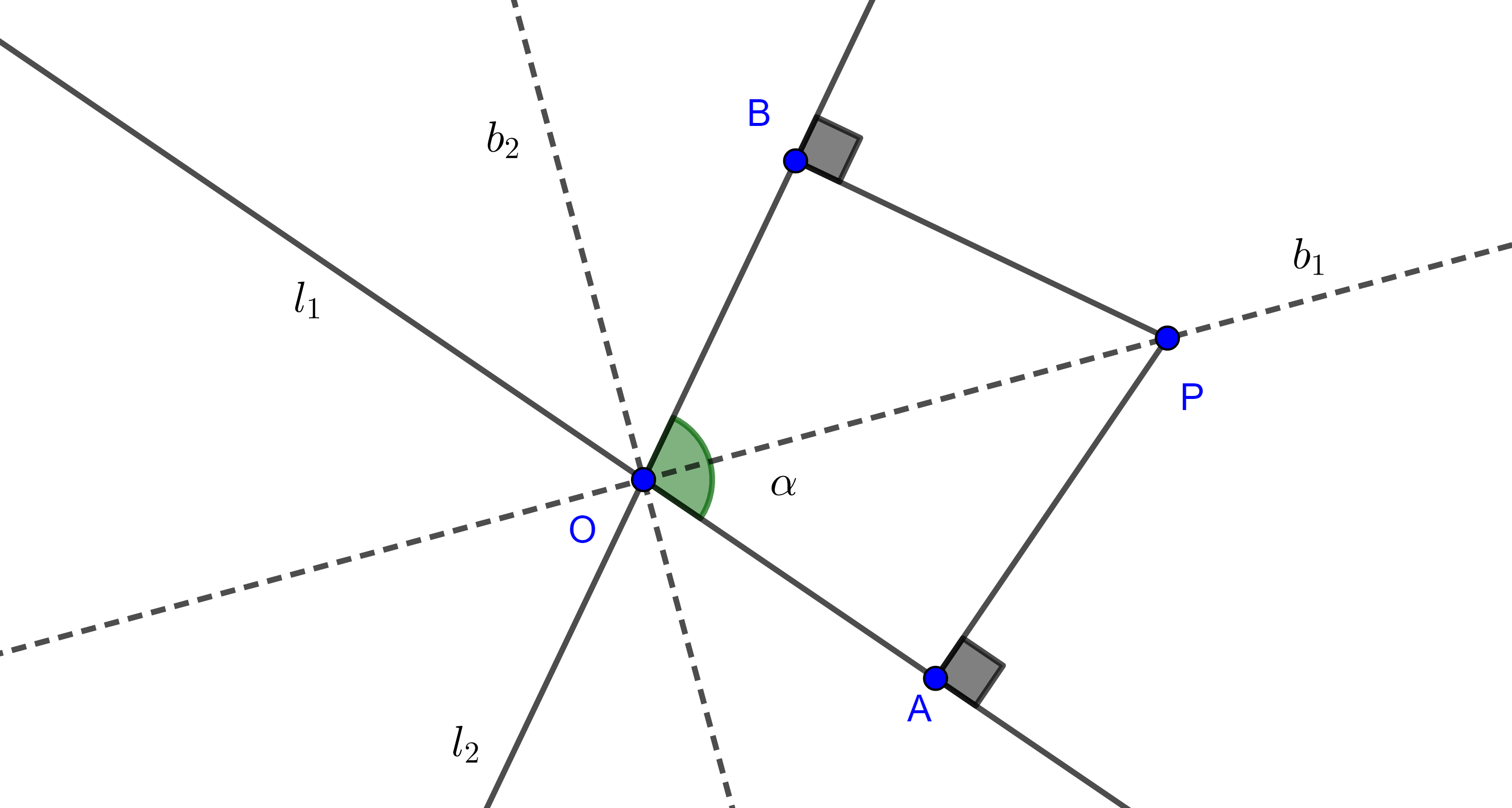
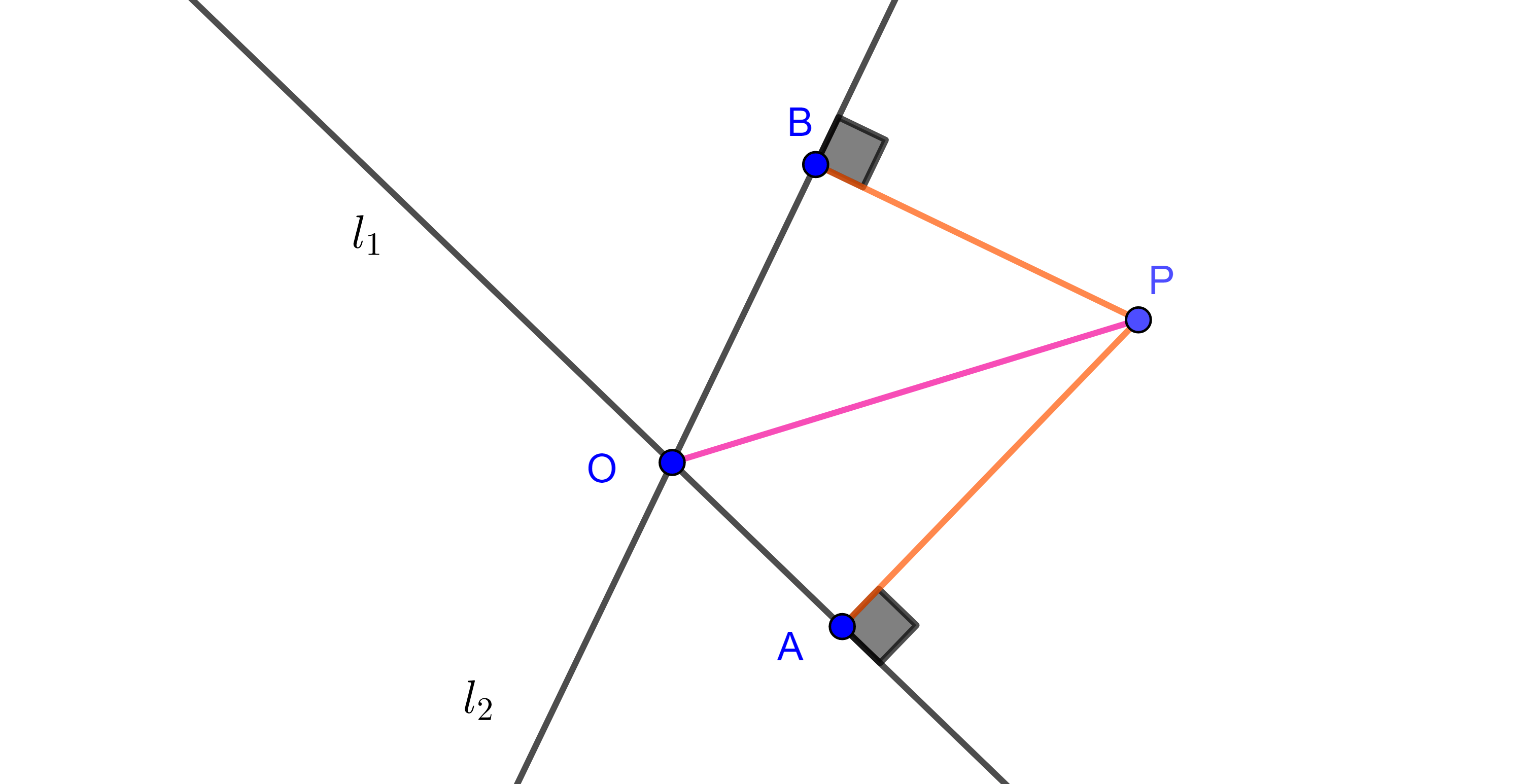
- Resuelve el siguiente problema planteado por el matemático chino Qin Jinshao en el siglo XIII:
Una ciudad está rodeada por una muralla circular con dos puertas, una al norte y otra al sur. Saliendo por la puerta norte y caminando 3 li hacia el norte se llega hasta un árbol. Saliendo por la puerta sur, hay que caminar 9 li hacia el este para ver el mismo árbol. Calcular el diámetro de la ciudad.
Hint: considera que ambos triángulos del esquema anterior son semejantes.
- Considera el siguiente problema, el cual llegó a considerarse insoluble:
Divide 10 en dos partes, tales que su producto sea igual a 40.
Es decir, encuentra los números $x, y$ tales que:
\begin{align*}
x+y = 10,\\
xy = 40.
\end{align*}
Es fácil ver que no existen soluciones reales para este problema. Sin embargo, haciendo un poco de cuentas obtendríamos que $x=5+\sqrt{-15}$ y $y=5-\sqrt{-15}$ son las soluciones a nuestro problema. ¿Consideras entonces que $\sqrt{-1}$ es un factor clave en las soluciones de algunas ecuaciones insolubles en los reales?
Más adelante…
Hasta ahora hemos motivado la necesidad de trabajar con números complejos. Es posible realizar un análisis más exhaustivo de la solución para ecuaciones cúbicas, considerando casos particulares y determinando las condiciones necesarias para la existencia de raíces reales e imaginarias, pero esto se escapa de los objetivos del curso, por lo que dejaremos hasta aquí este pequeño resumen histórico de la construcción y desarrollo de los números complejos.
En la siguiente entrada haremos la construcción formal de los números complejos como un campo, definiremos propiamente lo que entenderemos por un número complejo, así como sus operaciones algebraicas y algunas propiedades importantes que nos permitirán ir trabajando con estos números e interpretarlos mejor desde una perspectiva geométrica.
Entradas relacionadas
- Ir a Variable Compleja I.
- Siguiente entrada del curso: El campo de los números complejos.