Introducción

En la entrada antepasada definimos lo que es una medida de probabilidad. Esto es, dimos una lista de propiedades que debe de cumplir una función para llamarla «medida de probabilidad». Como en toda teoría matemática, esto da lugar a más propiedades. Por ello, en esta entrada veremos varios resultados que se desprenden de la definición de medida de probabilidad.

Regla de complementación

Dado $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad, puede pasarnos que obtener la probabilidad de un evento es muy difícil. Sin embargo, quizás calcular la probabilidad de su complemento sea más fácil. Por ello, veamos primero una propiedad que relaciona la probabilidad de un evento con la de su complemento.

---

Proposición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Para cualquier evento $A \in \mathscr{F}$ se cumple que

\[ \mathbb{P}(A^{\mathsf{c}}) = 1 − \mathbb{P}(A). \]

---

Demostración. Sea $A \in \mathscr{F}$ un evento. Nuestro objetivo es demostrar que $\mathbb{P}(A^{\mathsf{c}}) = 1 − \mathbb{P}(A)$. Para hacerlo, recuerda que en la entrada antepasada vimos que una medida de probabilidad es finitamente aditiva. Además, nota que $A \cap A^{\mathsf{c}} = \emptyset$; es decir, $A$ y $A^{\mathsf{c}}$ son ajenos. En consecuencia, se cumple que

\[ \mathbb{P}(A \cup A^{\mathsf{c}}) = \mathbb{P}(A) + \mathbb{P}(A^{\mathsf{c}}). \]

Por otro lado, por la definición del complemento relativo se tiene que $A \cup A^{\mathsf{c}} = \Omega$, con lo que $\mathbb{P}(A \cup A^{\mathsf{c}}) = \mathbb{P}(\Omega) = 1$. Por lo tanto, se sigue que

\[ \mathbb{P}(A) + \mathbb{P}(A^{\mathsf{c}}) = 1. \]

Finalmente, despejando a $\mathbb{P}(A^{\mathsf{c}})$, obtenemos que $\mathbb{P}(A^{\mathsf{c}}) = 1 − \mathbb{P}(A)$, que es justamente lo que queríamos demostrar.

$\square$

Esta propiedad será útil en numerosos ejemplos de conteo que veremos más adelante.

¿Qué pasa con la probabilidad de la unión de dos eventos?

En la entrada antepasada nos encontramos con un problema. Al momento de obtener la suma de las probabilidades de dos eventos $A$ y $B$ que no son ajenos, podía salirnos más de $1$. Sin embargo, había una pista de qué podíamos hacer al respecto. Notamos que contábamos algo más de una vez. Más precisamente, contamos $A \cap B$ más de una vez. Además, en la tarea moral te sugerimos que pensaras qué hacerle a $\mathbb{P}(A) + \mathbb{P}(B)$ para que coincida con $\mathbb{P}(A\cup B)$. La siguiente proposición nos da la respuesta.

---

Proposición. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Sean $A$, $B \in \mathscr{F}$ eventos cualesquiera. Entonces se cumple que

\[ \mathbb{P}(A \cup B) + \mathbb{P}(A \cap B) = \mathbb{P}(A) + \mathbb{P}(B). \]

---

Demostración. Sean $A$, $B \in \mathscr{F}$ eventos. Primero, aplicando algunas propiedades de las operaciones de conjuntos, podemos ver lo siguiente:

\begin{align*}
A &= A \cap \Omega \\
&= A \cap (B \cup B^{\mathsf{c}}) \\ &= (A \cap B) \cup (A \cap B^{\mathsf{c}}) \\ &= (A \cap B) \cup (A \smallsetminus B).
\end{align*}

Además, observa que $(A \cap B) \cap (A \smallsetminus B) = \emptyset$. De manera similar, se tiene que

\[ B = (A \cap B) \cup (B \smallsetminus A), \]

y además, $(A \cap B) \cap (B \smallsetminus A) = \emptyset$. En consecuencia, por la aditividad finita de $\mathbb{P}$, podemos ver que

\begin{align*}
\mathbb{P}(A) &= \mathbb{P}(A \cap B) + \mathbb{P}(A \smallsetminus B), \\
\mathbb{P}(B) &= \mathbb{P}(A \cap B) + \mathbb{P}(B \smallsetminus A),
\end{align*}

Sumando estas dos expresiones obtenemos que

\begin{equation}
\label{sum}
\mathbb{P}(A) + \mathbb{P}(B) = \mathbb{P}(A \cap B) + \mathbb{P}(A \smallsetminus B) + \mathbb{P}(A \cap B) + \mathbb{P}(B \smallsetminus A).
\end{equation}

Ahora, observa que $A \cup B = (A \smallsetminus B) \cup (A \cap B) \cup (B \smallsetminus A)$, y que los tres conjuntos en esta unión son ajenos entre sí. Por la aditividad finita de $\mathbb{P}$, esto implica que

\begin{equation}
\label{partition}
\mathbb{P}((A \smallsetminus B) \cup (A \cap B) \cup (B \smallsetminus A)) = \mathbb{P}(A \smallsetminus B) + \mathbb{P}(A \cap B) + \mathbb{P}(B \smallsetminus A).
\end{equation}

Luego, sustituyendo \eqref{sum} en \eqref{partition} y utilizando que $A \cup B = (A \smallsetminus B) \cup (A \cap B) \cup (B \smallsetminus A)$,

\begin{align*}
\mathbb{P}(A) + \mathbb{P}(B) &= \mathbb{P}(A \cap B) + \mathbb{P}((A \smallsetminus B) \cup (A \cap B) \cup (B \smallsetminus A)) \\ &= \mathbb{P}(A \cap B) + \mathbb{P}(A \cup B).
\end{align*}

En conclusión, hemos llegado a que

\begin{align*}
\mathbb{P}(A) + \mathbb{P}(B) &= \mathbb{P}(A \cap B) + \mathbb{P}(A \cup B),
\end{align*}

que es justamente lo que queríamos demostrar.

$\square$

Alternativamente, la expresión que obtuvimos en esta proposición puede escribirse como sigue.

\[ \mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) − \mathbb{P}(A \cap B), \]

que corresponde a «quitar» la parte que contamos más de una vez en la probabilidad de $A \cup B$. En resumen, esta proposición nos da una expresión para calcular la probabilidad de cualquier unión de dos eventos sin necesidad de que estos sean ajenos. Esta propiedad es conocida como el principio de inclusión-exclusión para $2$ eventos.

Interpretación visual del principio de inclusión-exclusión

En el caso para $2$ eventos, podemos representar visualmente los eventos $A$ y $B$ mediante un diagrama de Venn-Euler. En la siguiente figura están representados $A$ y $B$.

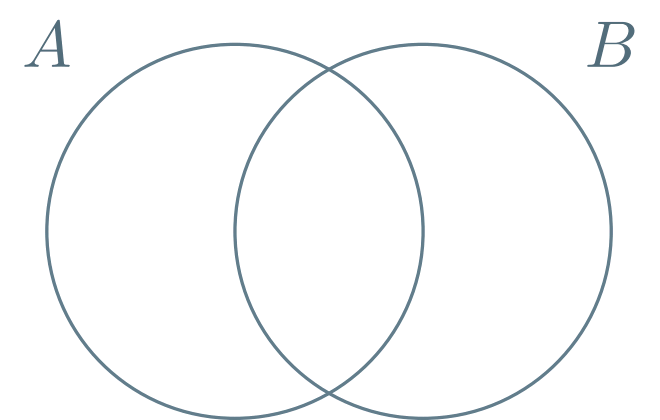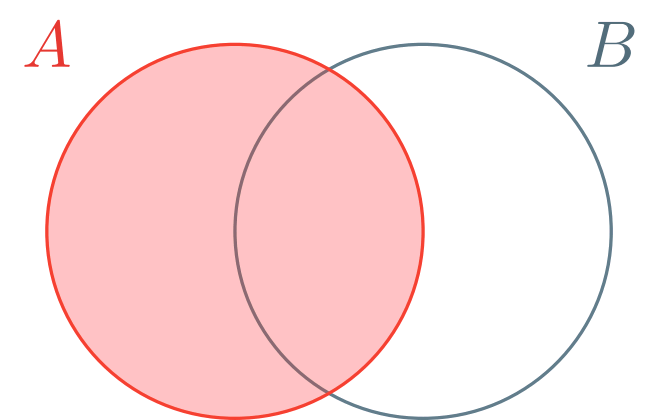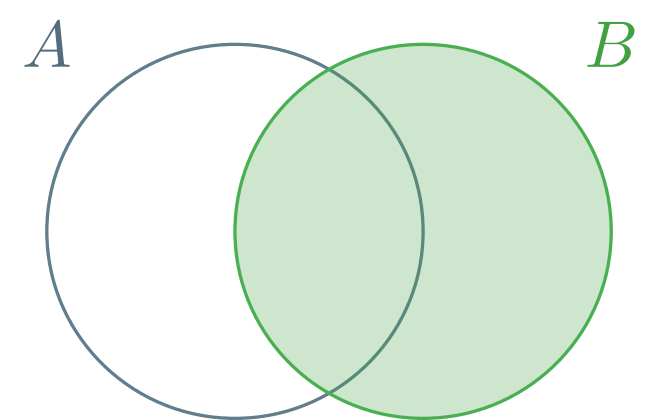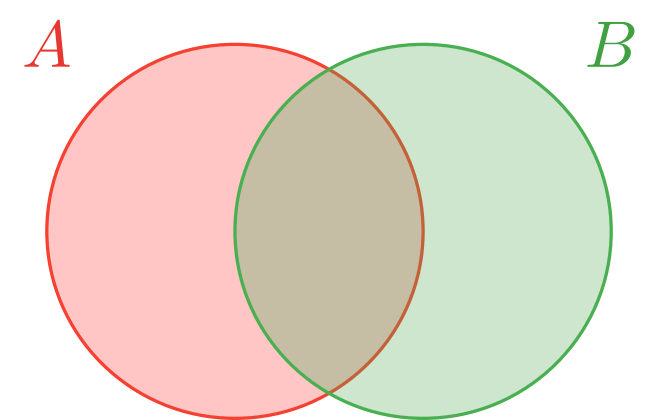
Al colorearlos, estamos pensando que lo coloreado de color rojo representa a $\mathbb{P}(A)$, y lo de color verde representa a $\mathbb{P}(B)$. Además, los coloreamos con una opacidad baja para que se note que la parte en donde se traslapan, que es $A \cap B$, se colorea dos veces cuando sumamos las áreas sombreadas por separado: esto lo comentamos previamente, en $\mathbb{P}(A) + \mathbb{P}(B)$ se cuenta $2$ veces a $A \cap B$. Por ello, para obtener $\mathbb{P}(A \cup B)$ se le resta $\mathbb{P}(A \cap B)$ a $\mathbb{P}(A) + \mathbb{P}(B)$.

En la figura anterior resaltamos con la misma opacidad a todo $A \cup B$ con azul. Al restarle $\mathbb{P}(A \cap B)$ a $\mathbb{P}(A) + \mathbb{P}(B)$ aseguramos que $A \cap B$ no se contabiliza $2$ veces.

Principio de inclusión-exclusión para más eventos

El principio de inclusión-exclusión aplica para cualquier familia finita de eventos. Por ejemplo, sean $A_{1}$, $A_{2}$ y $A_{3}$ eventos. Podemos aplicar el principio de inclusión-exclusión (al cual abreviaremos P.I.E. por ahora) para $2$ eventos a $A_{1} \cup A_{2}$ y $A_{3}$. Es decir, se tiene que

\[ \mathbb{P}((A_{1} \cup A_{2}) \cup A_{3}) = \mathbb{P}(A_{1} \cup A_{2}) + \mathbb{P}(A_{3}) − \mathbb{P}((A_{1} \cup A_{2}) \cap A_{3}). \]

Aplicamos nuevamente el P.I.E. para $2$ eventos para optener $\mathbb{P}(A_{1} \cup A_{2})$, por lo que nos queda

\begin{equation}
\label{pie0}
\mathbb{P}((A_{1} \cup A_{2}) \cup A_{3}) = \mathbb{P}(A_{1}) + \mathbb{P}(A_{2}) − \mathbb{P}(A_{1} \cap A_{2}) + \mathbb{P}(A_{3}) − \mathbb{P}((A_{1} \cup A_{2}) \cap A_{3}).
\end{equation}

Luego, podemos aplicar la distributividad a $(A_{1} \cup A_{2}) \cap A_{3}$ y obtener que

\[(A_{1} \cup A_{2}) \cap A_{3} = (A_{1}\cap A_{3}) \cup (A_{2} \cap A_{3})). \]

Aplicando nuevamente el P.I.E. para $2$ eventos obtenemos $\mathbb{P}((A_{1}\cap A_{3}) \cup (A_{2} \cap A_{3}))$. Esto es,

\begin{equation}
\label{pie1}
\mathbb{P}((A_{1}\cap A_{3}) \cup (A_{2} \cap A_{3})) = \mathbb{P}(A_{1} \cap A_{3}) + \mathbb{P}(A_{2} \cap A_{3}) − \mathbb{P}((A_{1}\cap A_{3}) \cap (A_{2} \cap A_{3})),
\end{equation}

y recordando que la intersección de conjuntos es conmutativa y asociativa, podemos reacomodar el último término de \eqref{pie1} como

\begin{align*}
(A_{1}\cap A_{3}) \cap (A_{2} \cap A_{3}) &= A_{1} \cap (A_{3} \cap A_{2} \cap A_{3}) \\
&= A_{1} \cap (A_{2} \cap A_{3} \cap A_{3}) \\ &= A_{1} \cap (A_{2} \cap A_{3}) \\ &= A_{1} \cap A_{2} \cap A_{3},
\end{align*}

y así, la igualdad \eqref{pie1} puede reescribirse como

\begin{equation}
\label{pie2}
\mathbb{P}((A_{1}\cap A_{3}) \cup (A_{2} \cap A_{3})) = \mathbb{P}(A_{1} \cap A_{3}) + \mathbb{P}(A_{2} \cap A_{3}) − \mathbb{P}(A_{1} \cap A_{2} \cap A_{3}).
\end{equation}

Finalmente, sustituimos \eqref{pie2} en \eqref{pie0} para obtener

\begin{align*}
\mathbb{P}((A_{1} \cup A_{2}) \cup A_{3}) = \mathbb{P}(A_{1}) + \mathbb{P}(A_{2}) − \mathbb{P}(A_{1} \cap A_{2}) + \mathbb{P}(A_{3}) − (\mathbb{P}(A_{1} \cap A_{3}) + \mathbb{P}(A_{2} \cap A_{3}) − \mathbb{P}(A_{1} \cap A_{2} \cap A_{3})),
\end{align*}

que puede reescribirse como

\begin{align*} \mathbb{P}(A_{1} \cup A_{2} \cup A_{3}) = \mathbb{P}(A_{1}) + \mathbb{P}(A_{2}) + \mathbb{P}(A_{3}) − \mathbb{P}(A_{1} \cap A_{2}) − \mathbb{P}(A_{1} \cap A_{3}) − \mathbb{P}(A_{2} \cap A_{3}) + \mathbb{P}(A_{1} \cap A_{2} \cap A_{3}).
\end{align*}

En conclusión, obtuvimos una fórmula para el cálculo de la probabilidad de la unión de cualesquiera $3$ eventos.

Interpetación visual del P.I.E. para tres eventos

Nuevamente podemos auxiliarnos de un diagrama de Venn-Euler para representar visualmente a los $3$ eventos.

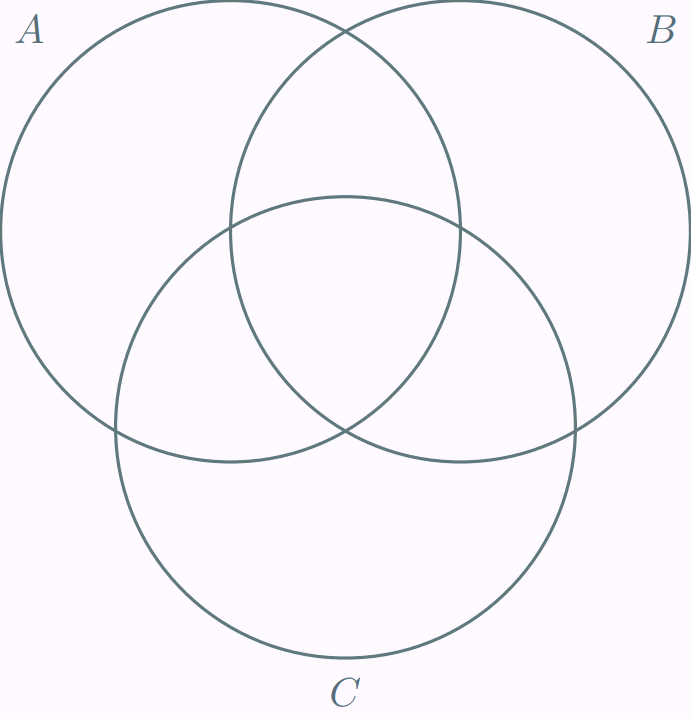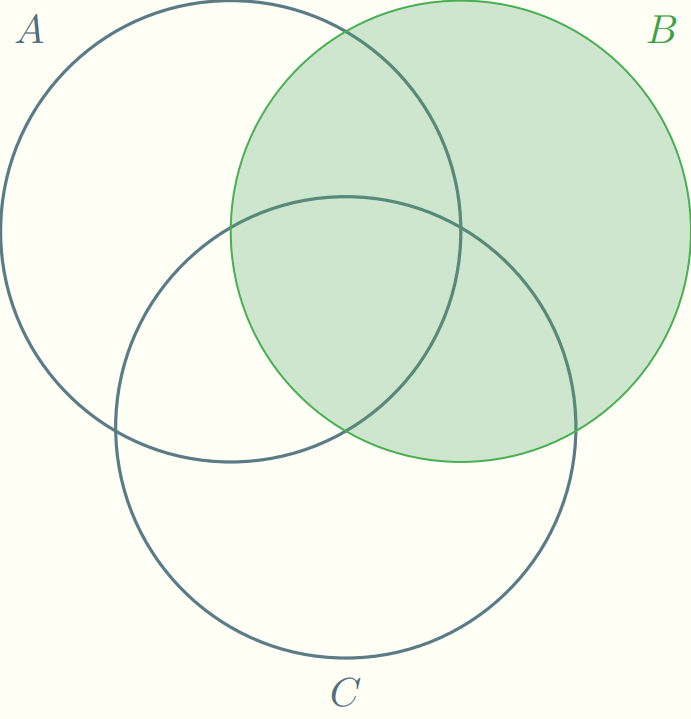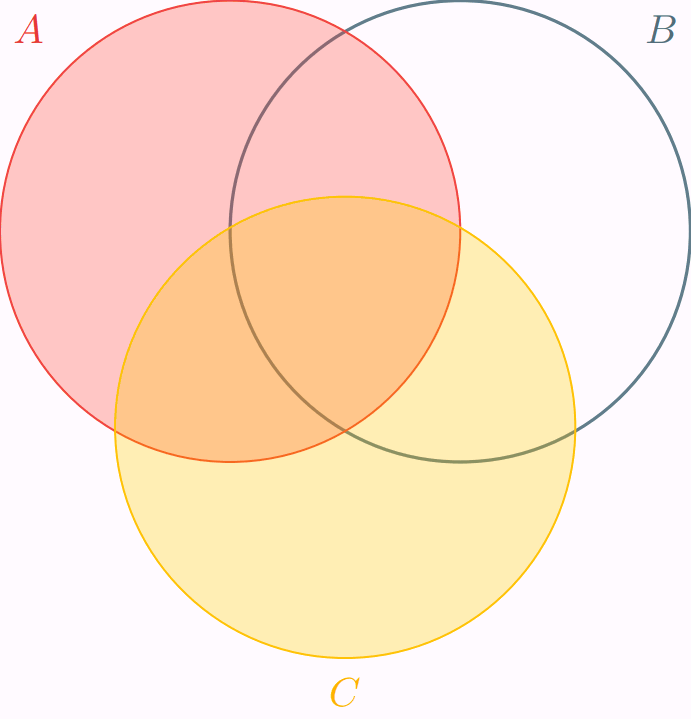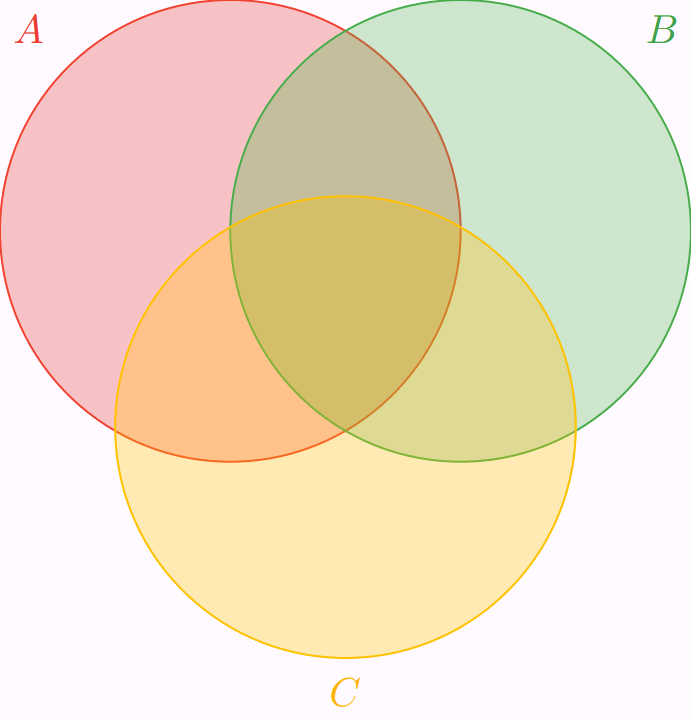
Con rojo representamos a $\mathbb{P}(A)$, con verde a $\mathbb{P}(B)$ y con ámbar a $\mathbb{P}(C)$. En la animación anterior se muestra cada una de las regiones por separado, luego dos a dos, y luego las tres juntas. Así, se exhibe que estamos contabilizando más de una vez algunas de las regiones del diagrama, y pone en evidencia cuáles son las que deberíamos de quitar.

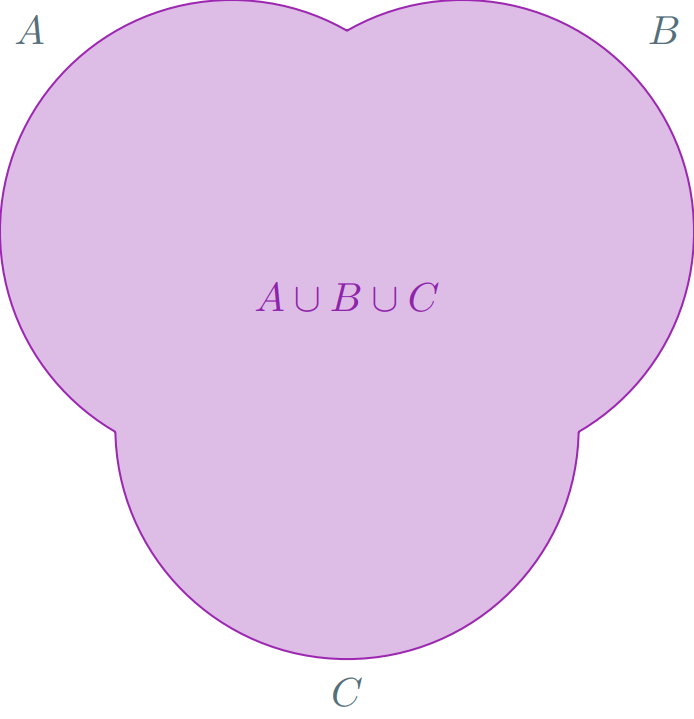
En esta última figura, representamos el valor $\mathbb{P}(A \cup B \cup C)$ con el área de color morado. Aquí pasan más cosas que en el caso de $2$ eventos. Recuerda que la expresión que obtuvimos para $\mathbb{P}(A \cup B \cup C)$ es

\begin{align*}
\mathbb{P}(A \cup B \cup C) = \mathbb{P}(A) + \mathbb{P}(B) + \mathbb{P}(C) − \mathbb{P}(A \cap B) − \mathbb{P}(A \cap C) − \mathbb{P}(B \cap C) + \mathbb{P}(A \cap B \cap C).
\end{align*}

Al sumar $\mathbb{P}(A) + \mathbb{P}(B) + \mathbb{P}(C)$, las intersecciones dos a dos de los eventos se contabilizan una vez más de lo que deberían, es lo mismo lo que nos pasó con el caso para $2$ eventos. Por ello, restamos la probabilidad de cada intersección dos a dos. Sin embargo, observa que esto provoca un daño colateral: quitamos $3$ veces a $\mathbb{P}(A \cap B \cap C)$, porque $A \cap B$, $A \cap C$ y $B \cap C$ contienen a $A \cap B \cap C$. Pero en $\mathbb{P}(A) + \mathbb{P}(B) + \mathbb{P}(C)$ también lo contabilizamos $3$ veces. Así que estamos omitiendo $\mathbb{P}(A \cap B \cap C)$, razón por la que se le suma $\mathbb{P}(A \cap B \cap C)$ a la expresión.

Generalización del P.I.E.

El principio de inclusión-exclusión puede generalizarse para cuando se tienen $n \in \mathbb{N}^{+}$ eventos. Esto lo pondremos como un teorema, aunque omitiremos su demostración.

---

Teorema. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Entonces para cualquier $n \in \mathbb{N}^{+}$ y cualesquiera eventos $A_{1}$, $A_{2}$, …, $A_{n} \in \mathscr{F}$, se cumple que

\begin{align*}
\mathbb{P}{\left( \bigcup_{i=1}^{n} A_{i} \right)} = \sum_{i=1}^{n}\mathbb{P}(A_{i}) − \sum_{i < j} \mathbb{P}(A_{i} \cap A_{j}) + \sum_{i < j < k} \mathbb{P}(A_{i} \cap A_{j} \cap A_{k}) + \cdots + (-1)^{n+1} \mathbb{P}{\left( \bigcap_{i=1}^{n} A_{i} \right)},
\end{align*}

que puede escribirse de forma cerrada como sigue:

\begin{align*}
\mathbb{P}{\left( \bigcup_{i=1}^{n} A_{i} \right)} = \sum_{k=1}^{n}{\left[ (-1)^{k+1} \sum_{\substack{I \subseteq \{1, \ldots, n\} \\ |I| = k}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \right]}.
\end{align*}

---

La segunda fórmula se ve un poco fea, pero en realidad no es tan horrible. Observa que se trata de una «suma de sumas». Es decir, para cada $k \in \{1, \ldots, n\}$, el $k$-ésimo término de esa suma es una suma. Lo más complicado está en cada una de estas sumas: están indicadas por $I$, que se refiere a que el índice es un subconjunto de $\{1, \ldots, n\}$. Lo importante de este índice es que $|I| = k$, es decir, hay un término por cada subconjunto de $\{1, \ldots, n\}$ de cardinalidad $k$. Además, cada uno de estos términos es la probabilidad de la intersección sobre todos los $A_{j}$ para los cuales $j \in I$.

Ejemplo. Obtengamos la expresión para $3$ eventos a partir de la segunda fórmula. Sean $A_{1}$, $A_{2}$ y $A_{3}$ eventos. Entonces

\begin{align*}
\mathbb{P}{\left( \bigcup_{i=1}^{3} A_{i} \right)} = \sum_{k=1}^{3}{\left[ (-1)^{k+1} \sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = k}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \right]}.
\end{align*}

La suma de afuera cuenta con $3$ términos, porque es la suma de $1$ a $3$. Cada uno de sus términos es una suma, en la que hay que sustituir los respectivos valores de $k$. Así que nos queda:

\begin{align*} \sum_{k=1}^{3}\left[ (-1)^{k+1} \sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = k}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \right] =&\, (-1)^{1+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 1}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \\ & + (-1)^{2+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 2}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \\ & + (-1)^{3+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 3}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)}. \end{align*}

Veamos el primer término. Este corresponde a la suma sobre todos los $I \subseteq \{1,2,3\}$ tales que $|I| = 1$. Los subconjuntos de cardinalidad $1$ de $\{1,2,3\}$ son $3$: $\{1\}$, $\{2\}$ y $\{3\}$, por lo que hay un término en esa suma por cada uno de ellos. Es decir,

\[ (-1)^{1+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 1}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} = (-1)^{2} {\left[ \mathbb{P}{\left( \bigcap_{j \in \{1\}} A_{j} \right)} + \mathbb{P}{\left( \bigcap_{j \in \{2\}} A_{j} \right)} + \mathbb{P}{\left( \bigcap_{j \in \{3\}} A_{j} \right)} \right]}, \]

y observa que las intersecciones en cada término son simplemente $A_{1}$, $A_{2}$ y $A_{3}$, porque la intersección es únicamente sobre $\{1\}$, $\{2\}$ y $\{3\}$, respectivamente. Así,

\[ (-1)^{1+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 1}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} = (-1)^{2} {\left[ \mathbb{P}\left(A_{1}\right) + \mathbb{P}{\left(A_{2} \right)} + \mathbb{P}{\left(A_{3} \right)} \right]} = \mathbb{P}\left(A_{1}\right) + \mathbb{P}{\left(A_{2} \right)} + \mathbb{P}{\left(A_{3} \right)}. \]

Para el segundo término, el índice $I$ son todos los subconjuntos de $\{ 1, 2, 3\}$ de cardinalidad $2$, que nuevamente son $3$: $\{ 1, 2 \}$, $\{1,3\}$ y $\{2,3\}$. Por lo tanto,

\[ (-1)^{2+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 2}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} = (-1)^{3} {\left[ \mathbb{P}{\left( \bigcap_{j \in \{1,2\}} A_{j} \right)} + \mathbb{P}{\left( \bigcap_{j \in \{1,3\}} A_{j} \right)} + \mathbb{P}{\left( \bigcap_{j \in \{2,3\}} A_{j} \right)} \right]}. \]

Ahora, cada una de las intersecciones en la expresión anterior queda como sigue:

\begin{align*} \bigcap_{j \in \{1,2\}} A_{j} &= A_{1} \cap A_{2}, \\ \bigcap_{j \in \{1,3\}} A_{j} &= A_{1} \cap A_{3}, \\ \bigcap_{j \in \{2,3\}} A_{j} &= A_{2} \cap A_{3}, \end{align*}

por lo que

\begin{align*} (-1)^{2+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 2}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} &= (-1)^{3} {\left[ \mathbb{P}{\left(A_{1} \cap A_{2}\right)} + \mathbb{P}{\left(A_{1} \cap A_{3}\right)} + \mathbb{P}{\left(A_{2} \cap A_{3}\right)} \right]} \\ &= − {\left[ \mathbb{P}{\left(A_{1} \cap A_{2}\right)} + \mathbb{P}{\left(A_{1} \cap A_{3}\right)} + \mathbb{P}{\left(A_{2} \cap A_{3}\right)} \right]}. \end{align*}

Finalmente, para el último término, el índice corre por todos los subconjuntos de $\{1,2,3\}$ de cardinalidad $3$, y sólamente hay uno de estos: $\{1,2,3\}$. Por ello, se tiene que

\begin{align*} (-1)^{3+1}\sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = 3}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} &= (-1)^{4}{\left[ \mathbb{P}{\left( \bigcap_{j \in \{1,2,3\}} A_{j}\right)} \right]} \\ &= \mathbb{P}{\left(A_{1} \cap A_{2} \cap A_{3}\right)}, \end{align*}

por lo que podemos concluir que

\begin{align*} \sum_{k=1}^{3}\left[ (-1)^{k+1} \sum_{\substack{I \subseteq \{1, \ldots, 3\} \\ |I| = k}} \mathbb{P}{\left( \bigcap_{j \in I} A_{j} \right)} \right] =&\, \mathbb{P}\left(A_{1}\right) + \mathbb{P}{\left(A_{2} \right)} + \mathbb{P}{\left(A_{3} \right)} \\ &\, − {\left[ \mathbb{P}{\left(A_{1} \cap A_{2}\right)} + \mathbb{P}{\left(A_{1} \cap A_{3}\right)} + \mathbb{P}{\left(A_{2} \cap A_{3}\right)} \right]} \\ &\, + \mathbb{P}{\left(A_{1} \cap A_{2} \cap A_{3}\right)}, \end{align*}

que es justamente la expresión que habíamos obtenido previamente.

---

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

• Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad, y sean $A$, $B$, $C$ y $D$ eventos. Obtén una fórmula para obtener $\mathbb{P}(A \cup B \cup C \cup D)$. Para ello, te proponemos dos caminos:
  • Sugerencia 1. Sigue un camino similar al que seguimos para obtener el P.I.E. para $3$ eventos. Es decir, aplica los P.I.E. que ya tienes (para $2$ y para $3$ eventos) de manera conveniente. Como pista, aplica el P.I.E. para $3$ eventos a $(A \cup B)$, $C$ y $D$.
  • Sugerencia 2. Utiliza cualquiera de las fórmulas del último teorema de esta entrada para $n = 4$ y haz el desarrollo correctamente.
• Intenta demostrar el último teorema de esta entrada. Esto puede hacerse por inducción sobre $n$, el número de elementos en la familia finita de eventos.
  • Sugerencia. Utiliza inducción fuerte. Es decir, primero observa que la igualdad es cierta para $1$. Luego, demuestra que para cualquier $n$, si la igualdad es verdadera para cada $k \in \{1,\ldots, n\}$, entonces es cierta para $n+1$. En este paso será necesario que uses la de $2$ eventos y la de $n$ eventos para proceder.

Más adelante…

En esta entrada vimos dos propiedades muy importantes de una medida de probabilidad: la regla de complementación y el principio de inclusión-exclusión. La primera será de mucha utilidad cuando veamos algunos ejercicios de conteo, en donde buscaremos calcular la probabilidad de eventos que parecen muy complicados en principio, pero que esta regla facilitará el cálculo. Por otro lado, el principio de inclusión-exclusión es una herramienta un poco complicada, pero que permite el cálculo de la probabilidad de la unión de cualesquiera $n$ eventos, sin importar si son ajenos o no.

En la siguiente entrada veremos algunas propiedades más de una medida de probabilidad. Una vez que terminemos con las propiedades que tiene cualquier medida de probabilidad, centraremos nuestra atención en nuestros primeros ejemplos concretos de medida de probabilidad, cuya relevancia histórica los hace destacables.

Entradas relacionadas

• Ir a Probabilidad I
• Entrada anterior del curso: Interpretación de las Operaciones con Eventos
• Siguiente entrada del curso: Propiedades de una Medida de Probabilidad, parte 2