Introducción

Son el tipo de tasas de interés que tienen una estrecha relación con los periodos anuales, ya que el periodo anual es de suma importancia en una gran variedad de fenómenos económicos, financieros, así como en muchas actividades del ser humano.

Tasas nominales de interés

Dichas tasas de interés se caracterizan por:

a) Hacen referencia al año, sin embargo no son tasas efectivas anuales
b) Permiten conocer cada cuándo, se van a pagar los intereses de dicha tasa y a cuánto ascienden dentro del periodo de un año.
c) Muestran la tasa de interés que se recibirá dentro del transcurso de un año, si los intereses no se reinvierten. (Esto aplica porque el inversionista puede decidir si retira sus intereses o los deja para que se reinviertan.
d) Se denotan como: $i^{(m)}$ y se lee «$i$ de $m$»para que no se confunda cuando se esté trabando con alguna potencia. En dicha expresión $m$ representa el apellido de la tasa, además de ser la variable que nos indicará el número de veces que se paga la tasa, (a este proceso será también mencionado como: pagadera, convertible o capitalizable) dentro del periodo de un año.

Por ejemplo, una tasa $i^{(2)}$ será pagadera semestralmente, una tasa $i^{(12)}$ será capitalizable mensualmente, $i^{(6)}$ bimestralmente, etc., todo dependerá del periodo que esté indicado. Nótese que $m$ puede tomar cualquier número entero. Éste tipo de tasas fueron creadas para hacer más fácil la comprensión de la forma en que se realiza el pago o cobro de los intereses dentro de una operación.

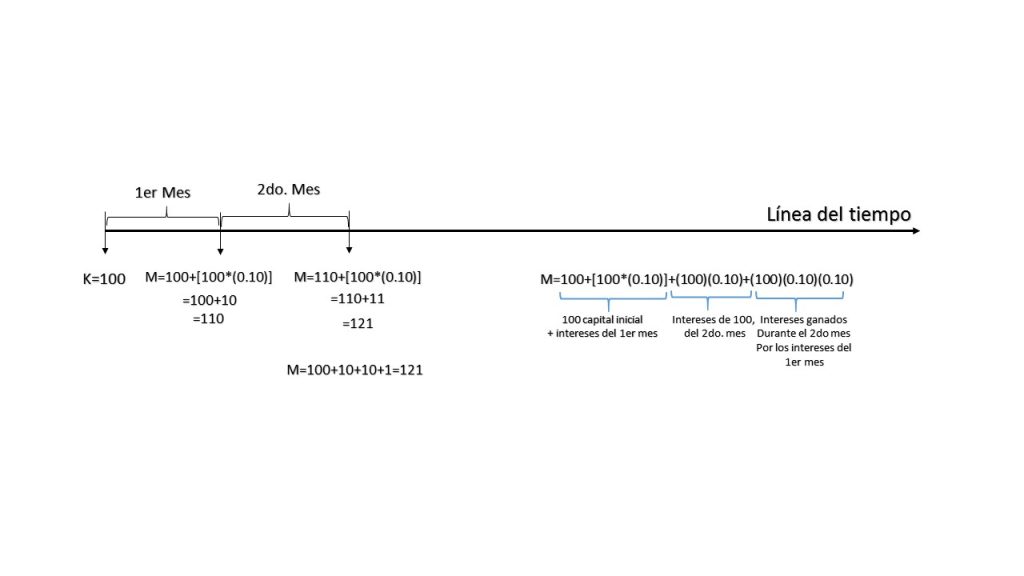
Ejemplo. Una persona desea invertir en un banco que le ofrece pagar una tasa del 24% pagadero 12 veces al año, lo que implica que los pagos serán de forma mensual.
Para poder saber cuál es la tasa mensual que le estará pagando el banco al inversionista se hace lo siguiente:
$\frac{i^{12}}{12}=\frac{24%}{12}=.02$.
lo cual implica que la tasa que el banco pagará de forma mensual es del 2%. Cabe hacer mención que con esto, no se debe interpretar que una tasa del 24%, con una tasa $i^{12}$, implica que el banco no va a pagar el 24% de interés cada mes, sino más bien el interés «real» que estará pagando el banco será del 2% mensual. Aunado a lo anterior si el inversionista desea al término de cada mes hacer el retiro de sus intereses, al término del año pactado el inversionista habrá recibido el 24% de intereses prometido por el banco. Y como es de esperarse, dicha operación que se acaba de calcular corresponde al modelo de interés simple, así tal cual estuvo descrita. Ahora bien, recordando que el modelo que se utiliza para hacer cualquier transacción es el modelo de interés compuesto, entonces se van a estar reinvirtiendo los intereses.
Por otra parte, para fines prácticos se estará manejando la siguiente notación:

$${\frac{i^{(m)}}{m}=i_{m}}.$$

Retomando el ejemplo anterior, si ahora el inversionista desea no retirar los intereses y reinvertirlos, en tal caso se estaría usando el modelo de interés compuesto, y la tasa se estaría tomando efectiva, por lo que tomando en cuenta un capital de \$3000, y reinvertir sus intereses por un periodo de 7 meses, entonces tendrá un capital acumulado de:

\begin{align*}
M&=3000\left(1+\frac{i^({12})}{12}\right)^7\\
&=3000\left(1+\frac{0.24}{12}\right)^7\\
&=3000(1+0.02)^7=3446.0570.
\end{align*}
Lo anterior, muestra que al estar utilizando el modelo de interés simple, si el inversionista tiene un capital de \$1, sólo obtendrá con una $i^{(12)}$ un rendimiento del 1% mensual, lo que vendría a ser la suma aritmética, sin embargo; al usar el modelo de interés compuesto, estará ganando un rendimiento de $12.68%$, éste resultado es obtenido de la siguiente forma:

\begin{align*}
M&=1.00\left(1+\frac{i^(12)}{12}\right)^{12}\\
&=1.00\left(1+\frac{0.01}{12}\right)^{12}\\
&=1.00(1+0.01)^{12}=1.1268.
\end{align*}
De esta forma, se está introduciendo un nuevo concepto, que se llama tasas de equivalencia, su nombre se debe a que a partir de una tasa nominal se puede obtener su tasa equivalente mensual, como fue calculado en el ejemplo anterior. Siguiendo ésta idea, se puede incorporar al modelo de interés compuesto las tasas nominales, proceso que será expuesto en el siguiente gráfico.

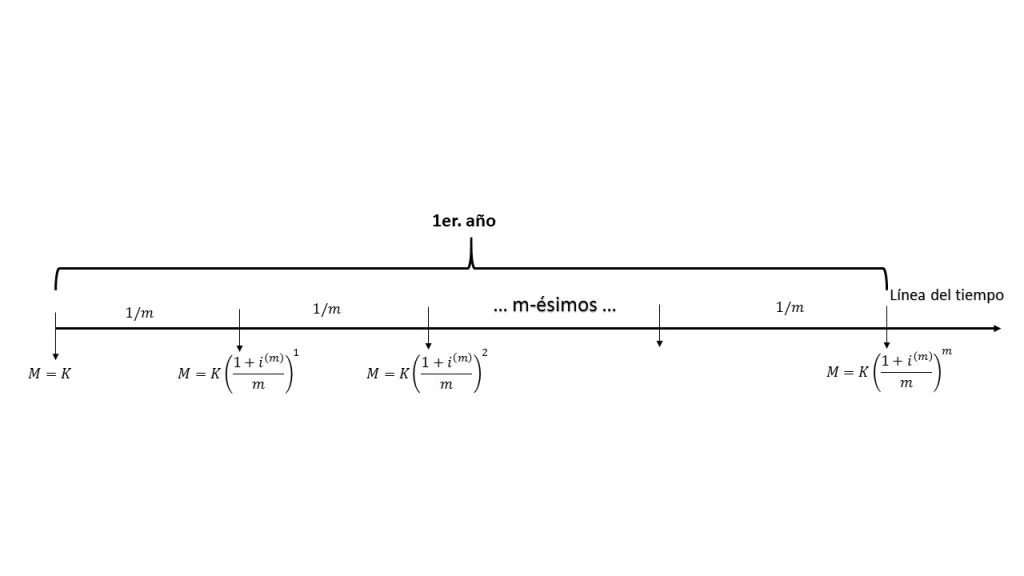
Tomando como base el modelo anterior, se obtiene el monto alcanzado del m-ésimo periodo, se calcula para el segundo año, los siguiente:

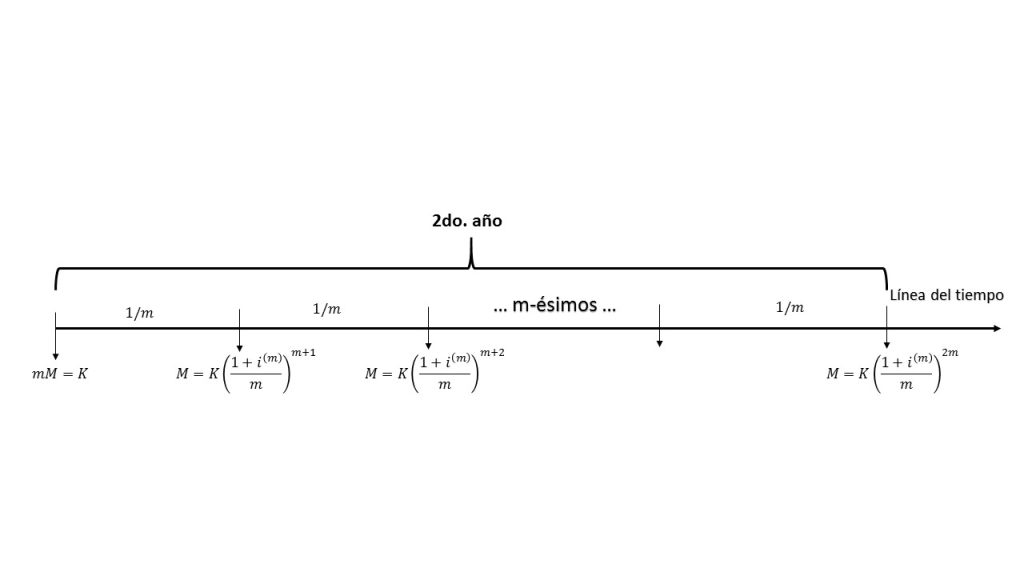
De forma análoga, observando el último término del primer año, con el último término del segundo año, se puede obtener la expresión para el periodo t-ésimo año, el cual queda:
$$M=K\left(1+\frac{i^{(m)}}{m}\right)^{mt}.$$

Para éste modelo es necesario establecer que la unidad de medición de $t$ es en años, debido a la forma en que se construyó, lo anterior es de suma importancia ya que recordemos que el modelo de interés compuesto, $t$ se medía de acuerdo al «apellido» de la tasa, el cual no necesariamente eran años.
$m$ indica el número de veces que la tasa se va a pagar durante el año.

Ejemplo. Suponga que en una operación se está trabajando con una tasa nominal $i^{12}=60\%$, lo que equivales a decir:
$i_{12}=\frac{i^{12}}{12}=\frac{0.60}{12}=0.05.$

Esto es una tasa efectiva mensual del 5%.
Por lo tanto, si tenemos un capital de \$1 y se quiere calcular el monto a dicha tasa, después de un año y 6 meses, esto es un plazo de 18 meses, el monto será de:
$M=1.00(1+i_m)^{18}=1.00(1+0.05)^{18}=\$2.4066.$
Es pertinente hacer mención que la tasa $i_m$ es mensual, por ése motivo $t$ debe de ser escrito de en meses, que en este caso son 18.

Ejercicios resueltos

Ejercicio. Un banco ofrece un rendimiento con una tasa de interés del 4.68% pagadera diariamente. Calcular el monto de que se obtendrá luego de haber transcurrido cinco meses, con un capital inicial de \$1500.

Ejercicio. Una persona tiene 2 tarjetas de crédito; una bancaria con un saldo a la fecha de \$30,000 y la otra emitida por una tienda de ropa con un saldo de \$25,000. La tarjeta bancaria está cobrando comisión con una tasa de interés del 25% pagadero mensualmente, mientras que la tarjeta de ropa maneja una tasa del 4% efectivo mensual. Al día siguiente ésta persona se entera que una tienda de autoservicio está manejando una tarjeta de crédito con una tasa del 20% anual pagadero diariamente. Se desea saber si conviene o no adquirirla. Explique el ¿por qué?

Es importante resaltar que las tasas pueden ser pactadas fijas durante la duración de la operación, sin embargo; también hay ocasiones en las que algunos contratos de crédito, por ejemplo, manejan tasas de referencias, en México, dichas tasas pueden ser la Tasa de Interés Interbancaria de Equilibrio (TIIE), la tasa que da los Certificados de la Tesorería (CETES), el Costo Porcentual Promedio (CPP), etc., todas ellas regularmente son tasas nominales pagaderas diariamente.

Más adelante…

Se abordarán temas en los que se analiza cómo se va dando la relación de las tasas de interés, incluso se estudiarán los métodos en que pueden ser equivalentes aunque sean de distinta periodicidad.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

Introducción

Es de vital importancia conocer el modelo de interés compuesto, así como su fenómeno de acumulación que es el que lo caracteriza, pero también es igual de importante poder conocer la forma en que se puede calcular el valor de hoy, el valor presente de una obligación futura, saber cuánto se deberá pagar en un futuro cierta deuda adquirida el día de hoy, nos permite conocer cuánto se debe de ahorrar el día de hoy para garantizar el pago de dicha obligación. Por ejemplo, si una persona desea adquirir algún bien, una casa, por ejemplo, o una empresa si desea después de cierto tiempo hacer cambio de su mobiliario o de su maquinaria, o de su equipo de cómputo. Todo lo anterior son ejemplo de la utilidad que tiene el saber calcular el valor presente, que como se observa a simple vista, permite encontrar una solución ante todas éstas situaciones.

Valor Presente

Aunque anteriormente ya se había hecho uso, el modelo que describe el fenómeno de valor presente, es el siguiente:

$K=\frac{M}{(1+i)^t}=M(1+i)^{-t}.$
Lo anterior se puede expresar de esa forma porque, recordando una de las leyes de los exponentes $\frac{1}{a^x}=a^{-x}.$
Por lo tanto, el modelo que se va a estudiar es:

$$K=M(1+i)^{-t}.$$

Es una ecuación que ya había sido deducida directamente del modelo de interés compuesto, en el tema anterior, y al ser parte de dicho modelo, las reglas que rigen a la fórmula de interés compuesto, rigen de igual forma a ésta expresión. Es importante señalar que la expresión que se acaba de presentar como Valor Presente, es fundamental en muchos cálculos que se estarán obteniendo, es por ésa razón que a continuación se va a establecer una forma más simplificada de expresarla, la cual es la siguiente:

$$v_1=\frac{1}{1+i}$$

esto es una expresión cuando $t=1.$

Ahora cuando expresamos $t$ de forma general, la expresión queda:
$v_i^t=\frac{1}{(1+i)^t}=(1+i)^{-t}.$

Por último, sustituyendo dicha expresión en el modelo de valor presente:
$$K=Mv_i^{t}.$$

El motivo de usar una $v.$

De acuerdo con la imagen, el valor presente es la función inversa del proceso de acumulación de capital, de manera tal que, mantienen una relación que consiste en, que a mayor tasa de interés corresponde una mayor disminución del valor presente del monto. Además, la imagen anterior muestra el proceso de acumulación en comparación al del valor presente, cada una con sus respectivas expresiones algebraicas que los definen.

Tabla de equivalencias entre periodos

A lo largo de estos temas, se puede hacer notar que cada uno de los negocios, convenios, pactos, préstamos, inversiones, etc. tienen en común que tienen una fecha de vencimiento, una fecha de pago, una fecha de cobro, etc. Entre otras cosas, también aparecen las condiciones en las que se realizará sea cual sea la operación, que como ya se ha visto son: tasa de interés, monto inicial, periodo de tiempo, cada cuando se realizaran los pagos. Debido a lo anterior, es necesario establecer ciertos «convenios» en lo que se refiere a la periodicidad de los pagos, con la finalidad de hacer los cálculos de la forma consistente y que sea aplicable a la realidad que describe el fenómeno que se está estudiando.
Con base a lo ya dicho, se presenta a continuación, la siguiente tabla:

En la tabla anterior, se establece de forma general el tiempo, para dar a conocer la forma en que se van a estar usando con fines prácticos, sin embargo; es pertinente señalar que cuando se trate de inversiones, por ejemplo, las que manejan los bancos, es necesario hacer uso del total de días que tiene el mes, esto es, 30 o 31 días en algunos meses, ó 28 o 29 en el caso del mes de febrero, esto debido a que los tipos de inversión consideran el pago de intereses el último día de cada mes.

También, es necesario establecer el número de decimales con el cual se estará realizando los cálculos, estos son al menos 5 decimales, con éste último redondeado. Y el resultado final se deberá ser presentado sólo con dos decimales.

Ejercicios resueltos

Ejercicio. Calcular el valor presente o traer a valor presente, a la fecha de hoy, la cantidad de \$2000 que deberán pagarse dentro de un año a una tasa de interés efectiva semestral del 7%.

Ejercicio. Para este ejemplo, se va a suponer que el día de hoy es 2 de octubre, y una empresa de ropa tiene contemplado saldar la deuda de un pagaré con un valor de \$85000, con fecha de vencimiento 30 de mayo, del siguiente año. En dicha deuda se acordó una tasa efectiva del 10% anual. Dicha empresa se propone saldar su deuda, aprovechando la temporada decembrina que tiene ventas e ingresos extras, para el día 30 de diciembre.

Ejercicio. Se quiere calcular el monto de una cantidad $X$ durante un tiempo cero, $t=0$ con una tasa de interés $i.$

Más adelante…

A lo largo de estos temas se ha estudiado cómo el dinero modifica su valor con el paso del tiempo, en particular los dos casos que acaban se ser abordados, proceso de acumulación y valor presente. Se ha visto el comportamiento de las tasas efectivas de interés, dentro del modelo de interés simple como de interés compuesto. Un aspecto importante que no se debe de restar importancia, es al fenómeno en el que queremos calcular el valor presente en un tiempo cero, esto es, el mismo día que se emite el préstamo, fecha en la que cual el monto y el valor presente son el mismo. Lo anterior adquiere mucha importancia sobre todo, cuando se construya una ecuación de valor, tema que pronto será abordado.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

Introducción

Siguiendo una estructura análoga a la anterior, procederemos a desarrollar la ecuación que describe la característica central del modelo de interés compuesto: la capacidad de generar intereses adicionales. Además, sentaremos las bases para abordar la aplicación de tasas de interés y establecer relaciones entre ellas, con el propósito de calcular tasas equivalentes.

El interés compuesto representa la segunda modalidad de pago de intereses. Su rasgo distintivo es la generación de nuevos intereses a medida que transcurre el tiempo o cada período específico. Estos intereses recién generados se suman al capital original, que luego comienza a generar intereses por sí mismo, repitiendo este proceso según lo establecido. Similar al modelo de interés simple, los intervalos de tiempo pueden ser mensuales, anuales, trimestrales, semanales, entre otros.

Interés compuesto

El modelo de interés compuesto es ampliamente empleado en contratos comerciales y operaciones financieras en todo el mundo, e incluso está respaldado por la legislación vigente en nuestro país, como lo establece la Ley Federal de Protección al Consumidor.

Para comenzar con su construcción, se propone el siguiente ejemplo:

A una persona les prestan \$100, con una tasa de interés efectiva mensual del 10%, dicho monto al término del primer mes estaría generando \$10 por concepto de interés más los \$100 pesos originales. La parte interesante comienza a ocurrir a partir del segundo mes, en el que los intereses que ya se habían generado durante el primer mes comienzan a generar nuevos intereses invertidos a la misma tasa, esto es:

Monto del periodo anterior $=\$110$

Intereses del segundo periodo $=(\$110)(0.10)=\$11$

Lo que nos da un monto total al final del segundo periodo de \$121. Es importante hacer mención que el $1 que aparece en nuestro último resultado, representa los intereses generados por los nuevos intereses. En la siguiente gráfica se representa con detalle este proceso.

Ahora bien, se va a construir el modelo general de Interés compuesto:

El primer periodo comienza con un capital $K$, con una tasa de interés $i$, de tal manera que al final del primer periodo tenemos el capital inicial más los intereses generados durante ése periodo, y nos quedaría una expresión como la siguiente: $M=K+Ki$.

Por consiguiente, el monto del segundo periodo queda como el capital inicial más los intereses obtenidos en el 1er y 2do periodo.

Es importante recalcar que los intereses se calculan multiplicando el capital por la tasa de interés. Si los intereses generados en el 1er periodo fueron $Ki$, entonces los intereses generados en el segundo periodo se calcularon a partir de la expresión $Kii$. De esta forma, el monto obtenido al final del segundo periodo se representa con la expresión: $M=K+Ki+Ki+Kii$, la cual se reduce a la expresión señalada en la figura 1.5> $M=K(1+i)^2$.

Generalizando la fórmula queda lo siguiente: $M=K(1+i)^t$. En ésta expresión la variable $t$, es la que va a estar representando el número de periodos, el cual va a estar ligados siempre con el «apellido» de la tasa de interés, este es mensual, semanal, diario, etc. como ya en algunos párrafos anteriores se ha hecho mención.

Las reglas para aplicar correctamente este modelo son semejantes a la del modelo de interés simple, con algunas variantes, pero para no dejar ambigüedad alguna se enuncian a continuación:

• El valor de las variables $K$ y $M$ se escriben en unidades monetarias, siendo la primera que representa el capital inicial ($K$), mientras que la segunda representa el monto ($M$).
• $i$ es la tasa de interés efectiva por periodo, expresada en %, y al realizar cálculos usada al tanto por uno, es decir ya dividida entre 100.
• La periodicidad de la tasa determina la unidad de tiempo con la que se va a utilizar la variable $t$, esto es, en años, meses, bimestres, durante el lapso de tiempo acordado que dure la operación.

Siguiendo una lógica similar al modelo de interés simple, en el caso del modelo de interés compuesto, tenemos la capacidad de expresar cualquier variable en función de las otras tres. Es decir, podemos despejar y expresar cualquier variable en términos de las demás.

Por lo anterior podemos establecer que, partiendo del modelo de interés compuesto, $K$ se puede calcular a partir de la siguiente expresión:

$$K=M\frac{1}{(1+i)^t}=M(1+i)^{-t}.$$

Para obtener $i$, se divide entre $K$ la ecuación de interés compuesto, luego se eleva a la potencia $\frac{1}{t}$ y por último se le resta uno, con lo que se llega a:

$$i=\frac{(M)}{(K)}^{\frac{1}{t}}-1.$$

Finalmente, para expresar $t$ es necesario usar algunas propiedades de los logaritmos, como se observa a continuación:

$$t=\frac{\log M-\log K}{\log(1+i)}.$$

Es fundamental destacar una diferencia significativa en comparación con el modelo de interés simple, que, como ya hemos visto, exhibe un comportamiento lineal. Por otro lado, el modelo de interés compuesto muestra un comportamiento geométrico, como se puede apreciar en el siguiente gráfico:

En la figura 1.6, se muestra un ejemplo de cómo se comporta el modelo de interés compuesto, bajo una inversión de un capital de \$1700 invertido durante 3 años, a una tasa mensual del $12\%$.

Ejercicios resueltos

Ejercicio. ¿Cuál es el monto que se genera, con un capital inicial de \$2500 y lo queremos invertir con las siguientes tasas de interés, durante los periodos que se indican:

1. A una tasa del 6.5% anual, durante tres años y 6 meses.
2. 2.4% mensual, luego de haber transcurrido dos años y 8 meses.
3. 5.8% semestral, después de un periodo de 10 meses.
4. 0.04% diario, después de un año con 23 días.

Ejercicio. Calcula la tasa de interés anual, que se necesita calcular para los siguientes incisos:

1. Monto inicial de \$1 500, durante un año genera un monto de \$1 800.
2. Monto inicial de \$27 500, que durante un lapso de un año y cinco meses genera \$30500.
3. Monto inicial de \$22 000, durante un lapso de 7 semestres con 5 meses, genera un monto total de \$25 000.

Ejercicio. Dado un capital inicial de \$1200 pesos, un monto total de \$3500, con una tasa efectiva trimestral de 3.77%, calcular $t$.

Más adelante…

En este tema, se abordó el modelo de Interés compuesto, mediante el cual se observa el fenómeno mediante el cual, una cantidad de dinero invertida, prestada o depositada en alguna institución bancaria, nos genera intereses con el paso del tiempo, y no sólo eso, sino que, en el caso particular del interés compuesto, los intereses generan más intereses. Éste proceso que se acaba de estudiar de forma implícita es conocido también como acumulación. Con éste modelo nos da una herramienta muy importante para poder tomar mejores decisiones respecto al uso de los recursos que se tienen de manera personal, comercial, social, etc. porque nos sirve para saber cuánto se puede llegar a ahorrar en el caso de querer adquirir un bien o servicio, o unas vacaciones, o comprar un vehículo. En otro caso, cuánto se va a tener que pagar por un cierto préstamo, o incluso cuánto se requiere tener para llevar a cabo un proyecto que requiere cierto financiamiento (es un tipo de préstamo que permite tener recursos, por ejemplo, inversionistas) para conocer cuánto es lo que se va a deber en el futuro.

En el siguiente capítulo, se abordará el proceso inverso que acabamos de estudiar, esto es, describir la metodología que nos permita conocer el valor que al día de hoy tiene una obligación futura, fenómeno que dentro de las Matemáticas Financieras se le conoce como Valor Presente.

• Ir a Matemáticas Financieras
• Entrada anterior: Historia, antecedentes, interés simple
• Entrada siguiente