Introducción
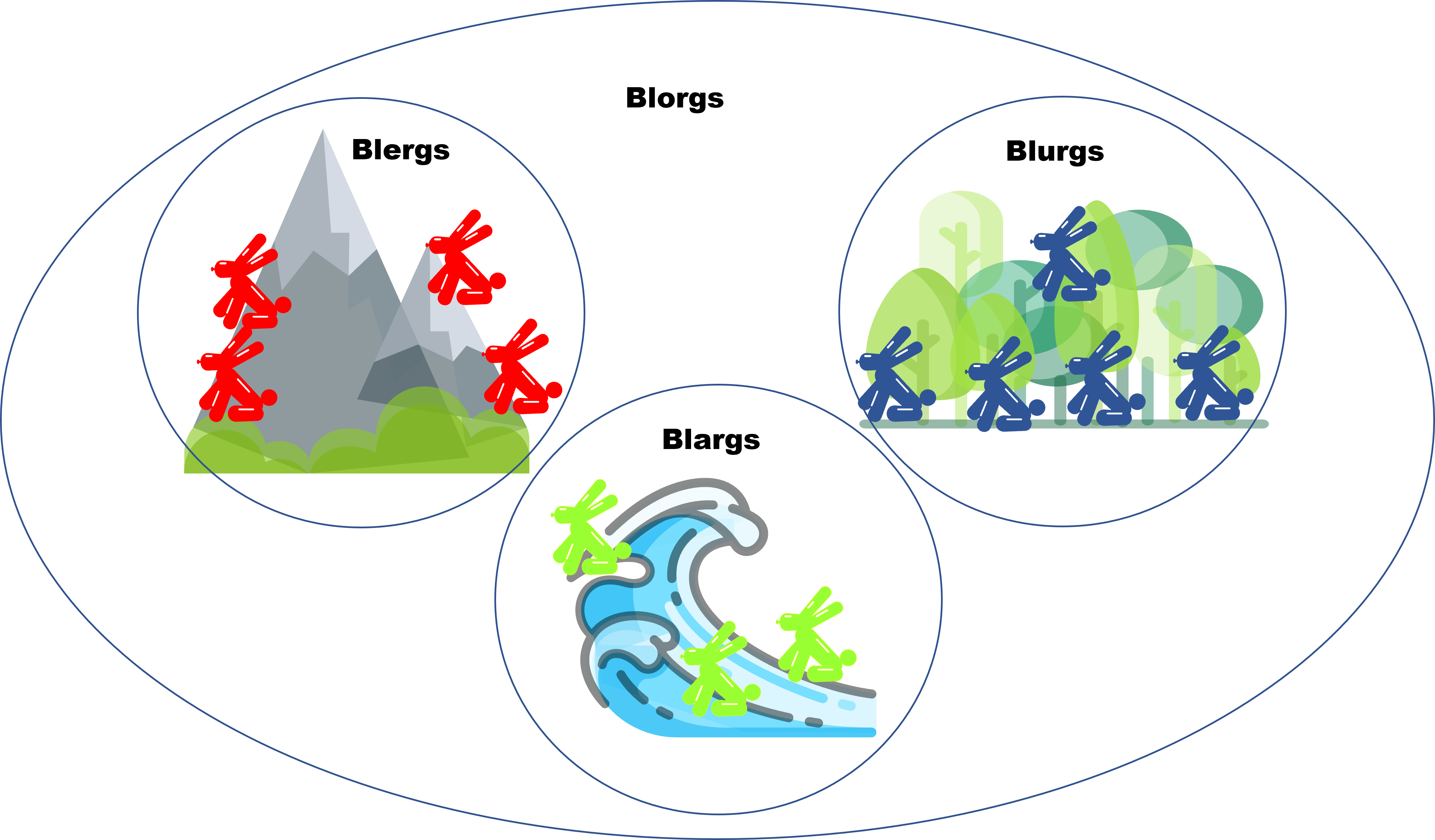
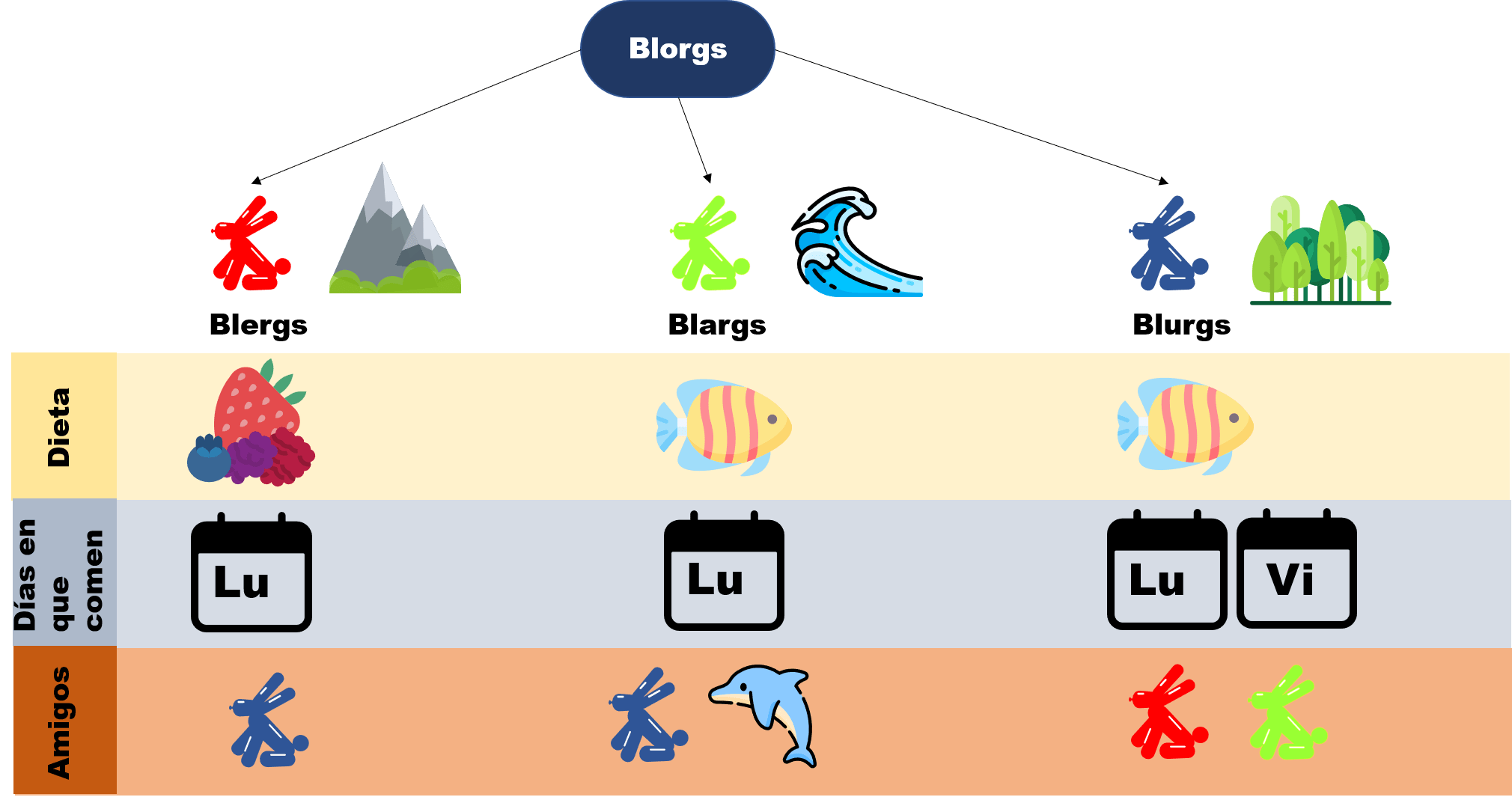
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de condicionales y dobles condicionales. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.
Para terminar nuestra sección de demostraciones (no significa que terminamos de demostrar, para nada, apenas es el comienzo), vamos a ver el caso en donde tengamos la doble implicación. Esto no va a ser difícil, pues hemos desarrollado suficientes estrategias para ello, y solo verás que la forma de demostrar estas proposiciones, es ver la doble implicación de otra manera.
La suficiencia y necesidad
Es común ver proposiciones matemáticas de la forma
$$\forall x (P(x) \Leftrightarrow Q(x)) $$
Como por ejemplo
Proposición. Un blorg come dos veces a la semana si y solo si tiene amigos amarillos y rojos.
Para este tipo de demostraciones, lo que haremos será demostrar dos cosas: la suficiencia y la necesidad. Recordemos que la doble implicación puede escribirse de la siguiente manera:
$$\forall x (P(x) \Leftrightarrow Q(x)) = \forall x ((P(x) \Rightarrow Q(x)) \land (Q(x) \Rightarrow P(x) )) $$
Es decir, para demostrar la condición, es necesario demostrar que si un blorg come dos veces a la semana entonces tiene amigos amarillos y rojos, y también será necesario mostrar que si un blorg tiene amigos amarillos y rojos come dos veces a la semana. Esto es, demostrar que las condiciones son equivalentes: un blorg solo tiene amigos amarillos y rojos si y solo si come dos veces por semana.
Demostración. Para esto, consideremos primero a un blorg $x$, para demostrar la doble implicación, es común dividir el problema en dos partes que podrás encontrar como «la ida» y «el regreso», esto hace referencia a que al demostrar la ida, demostraras que $P(x) \Rightarrow Q(x)$ y el regreso demuestra que $P(x) \Leftarrow Q(x)$. No dejes que te confunda la dirección de la flecha, simplemente es otra forma de demostrar que $Q(x) \Rightarrow P(x)$ (mira la dirección de la flecha).
Y comúnmente encontrarás en las demostraciones las notaciones de $\Rightarrow$ y $\Leftarrow$ haciendo referencia a si demostrarán la ida o el regreso, justo como lo haremos a continuación.
$\Rightarrow$
Primero demostraremos que si un $x$ come dos veces a la semana, entonces tiene amigos rojos y amarillos.
Como $x$ come dos veces a la semana, entonces es un blurg, pues es la única especie que come los Lunes y Viernes, mientras que los Blargs y Blergs comen solo los Lunes. Ahora, notemos que un blurg es amigo de los Blergs y los Blargs, cuyos respectivos colores son rojos y amarillos. Así hemos demostrado que si un $x$ come dos veces a la semana, entonces tiene amigos rojos y amarillos.
$\Leftarrow$
Ahora, para demostrar el regreso, supongamos que $x$ tiene amigos rojos y amarillos y lleguemos a la conclusión de que come dos veces a la semana.
Notemos a los amigos de cada especie de blorg. Los Blargs son amigos de los Blurgs y de los delfines, los cuales son azules, entonces no tienes amigos amarillos y rojos, por otro lado los Blergs son amigos de los Blurgs, que son azules, por lo que tampoco cumplen la condición. Mientras que los Blurgs son amigos de los Blergs y Blargs, que cumplen con ser rojos y amarillos. Entonces $x$ tiene que se un blurg. A continuación, notemos que los Blurgs comen los Lunes y Viernes, esto es, que comen dos veces por la semana, cumpliendo la proposición.
De esta forma hemos demostrado que un blorg come dos veces a la semana si y solo si tiene amigos amarillos y rojos.
Otro vistazo a la doble implicación
Para que te des una idea mejor sobre el poder de este tipo de proposiciones, recuerda lo siguiente: «La doble implicación es la forma de decir que dos cosas son equivalentes». Esto no es algo nuevo, pues ya hemos mencionado esto antes. La diferencia es que ahora ya tenemos aplicaciones prácticas de esto, ve el siguiente ejemplo:
Proposición. Un blorg come dos veces por semana si y solo si tiene un amigo de otra especie que puede comer fresas.
Demostración. Ahora, no solo vamos a usar la doble implicación para la demostración, sino que juntaremos proposiciones que hemos demostrado anteriormente. Primero que nada, notemos que la proposición se parece en parte a la pasada. Usaremos lo que sabemos de la proposición pasada. Como un blorg come dos veces por semana si y solo si tiene amigos amarillos y rojos. Ahora veamos cómo podemos usarla para demostrar esto.
Considera las proposiciones:
$$ P(x) = \text{ x come dos veces por semana},$$
$$ Q(x) = \text{ x tiene amigos rojos y amarillos},$$
$$ R(x) = \text{ x tiene un amigo de otra especie que puede comer fresas}.$$
Lo que nos pide demostrar la proposición es que
$$\forall x (P(x) \Leftrightarrow R(x)). $$
Pero sabemos que
$$\forall x (P(x) \Leftrightarrow Q(x)). $$
Y notemos que la siguiente regla de inferencia es válida
$$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$
Entonces podemos reducir esta proposición a demostrar «Un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas». Entonces demostremos esto.
Afirmación. Un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas.
Demostración de la afirmación.
$\Rightarrow$
Sea $y$ un blorg con amigos amarillos y rojos. Basta exhibir a algún amigo que pueda comer fresas, así que ingeniosamente decimos: sea $x$ un amigo rojo de $y$ (esto lo podemos hacer, ya que suponemos que el blorg tiene amigos amarillos y rojos). Como $x$ es rojo, entonces es un blerg. Además, sabemos por una proposición de la entrada anterior que existe una única raza de Blorgs que pueden comer fresas, y son precesiamente los Blergs. De esta manera $x$ puede comer fresas.
Por lo tanto $y$ tiene un amigo que puede comer fresas. Como además tiene amigos de dos colores, y la única especie que puede tener amigos amarillos y rojos son los Blurgs, entonces $y$ es un blurg. Así, $y$ tiene un amigo de otra especie que puede comer fresas.
$\Leftarrow$
Ahora supongamos que $y$ es un blorg y tiene un amigo $x$ de otra especie que puede comer fresas. Como la única especie vegetariana son los Blergs, entonces $x$ es un Blerg (supongamos que esto es cierto por ahora, más adelante lo demostrarás). De esta manera, $y$ es un blarg o blurg (pues recordemos que $x$ y $y$ son de diferentes especies). Veamos que si $y$ fuera un blarg, tendría únicamente amigos Blurgs y delfines, y no de Blergs, mientras que los Blurgs sí son amigos de los Blergs, por lo tanto $y$ es blurg.
Finalmente, nota que los Blurgs tienen amigos Blargs y Blergs, los cuales son amarillos y rojos.
De esta manera, hemos demostrado que un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas.
$\square$
Habiendo demostrado la afirmación, y sabiendo que $$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$ Entonces se cumple que Un blorg come dos veces por semana si y solo si tiene un amigo de otra especie que puede comer fresas.
$\square$
Más adelante…
El mundo de los Blorgs nos ayudó a poner un paso dentro del pensamiento matemático. Nos acompañarán solo un poco más, pero ya no estaremos enfocados en las demostraciones. Daremos pasos hacia un camino que puede resultar un poco distinto, pero verás que se parece mucho a la lógica proposicional. Algunos dicen que no puede haber una sin otra. Y este tema es la teoría de conjuntos. Si pudiéramos poner las matemáticas como un edificio, algunos dirían que la estructura estaría hecha de lógica y conjuntos. Así que exploraremos este otro «ingrediente» de las matemáticas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que la siguiente regla de inferencia es válida: $$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$
- Demuestra que un blorg es vegetariano si y solo si es un blerg.
- Usando la última proposición de la entrada, demuestra que Un blorg come dos veces por semana si y solo si tiene un amigo que puede comer alimentos con semillas.
- Demuestra que un blorg no es amigo de los Blergs si y solo si come los mismos días que los Blergs y es amigo de un animal marino.
Entradas relacionadas
- Ir a Álgebra Superior I
- Entrada anterior del curso: Problemas de demostraciones con conectores y cuantificadores
- Siguiente entrada del curso: Problemas de demostraciones de condicionales y dobles condicionales.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»