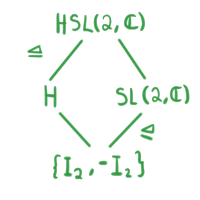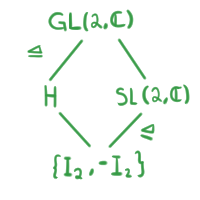(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
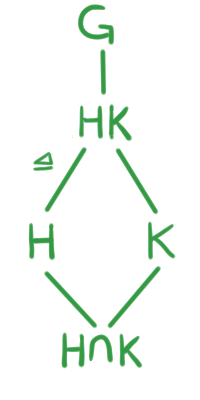
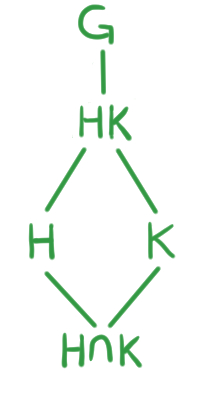
Comencemos introduciendo la idea del Segundo Teorema de Isomorfía. Para ello tomemos $H,K$ dos subgrupos de $G$ tales que $H\unlhd G$. Por favor, apóyate en el diagrama de retícula.
Observemos el cociente $HK/H$, este es posible porque $H\unlhd HK$ (como se hizo notar en la entrada anterior y esto se indica en el diagrama). Por nuestra experiencia manejando fracciones, podríamos pensar que es posible cancelar la $H$ y obtener que $HK/H \cong K$. Sin embargo, esto no es cierto porque $K$ puede tener elementos en común con $H$. Por ejemplo, si tomamos el caso cuando $H=K$ el isomorfismo $HK/H \cong K$ ya no se cumple.
¡Pero no temais! porque sí existe un isomorfismo para $HK/H$, en esta entrada el Segundo Teorema de Isomorfía nos dice que $$HK/H \cong K/(H\cup K).$$
Cabe notar que en la literatura suelen mezclarse el Segundo y el Tercer Teorema de Isomorfía entre sí. El Primer Teorema de Isomorfía siempre es el que enunciamos en la entrada pasada, pero a veces el Segundo puede ser el Tercero y viceversa. Esto lo aclaramos por si el teorema que tratamos en esta entrada no es el que te esperabas.
Segundo Teorema de Isomorfía
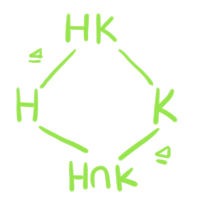
El segundo Teorema de isomorfía también es llamado del Teorema del Diamante por la forma del diagrama de retícula asociado.
Teorema. (2do Teorema de Isomorfía)
Sean $G$ un grupo, $H,K$ subgrupos de $G$ con $H\unlhd G$. Entonces $HK\leq G$, $H \unlhd HK$, $H\cap K \unlhd K$ y
\begin{align*}
HK/H \cong K/(H\cap K).
\end{align*}
Demostración.
Sean $G$ un grupo, $H \unlhd G$, $K \leq G$.
Como $H \unlhd G$, entonces $HK \leq G$. Tenemos que $H\leq HK$ y como $H \unlhd G$, entonces $H \unlhd HK$.
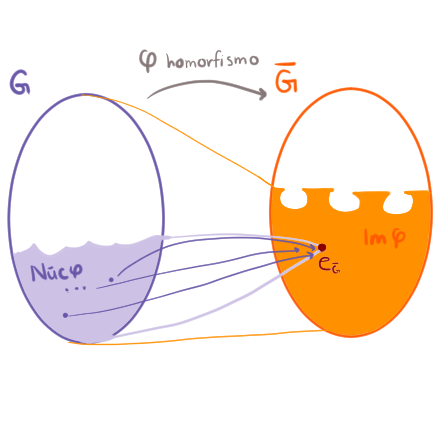
En esta demostración queremos usar el Primer Teorema de Isomorfía. Para ello bastaría construir un homomorfismo cuyo núcleo sea $H\cap K$ y cuya imagen sea $HK/H$. Comencemos definiendo dicho homomorfismo:
Sea
\begin{align*}
\varphi: K \to HK/H
\end{align*}
con $\varphi(k) = kH, \forall k\in K$.
P.D. $\varphi$ es un homomorfismo.
Sean $k, \tilde{k} \in K$,
\begin{align*}
\varphi(k\tilde{k}) = k\tilde{k}H = kH\tilde{k}H = \varphi(k)\varphi(\tilde{k}).
\end{align*}
Así, $\varphi$ es un homomorfismo.
Ahora veamos quién es el núcleo de $\varphi$:
\begin{align*}
\text{Núc }\varphi &= \{ k\in K | \varphi(k) = e_{HK/H} \} \\
&= \{k \in K | kH = H\} \\ &= \{k\in K|k\in H\} = H\cap K.
\end{align*}
De este modo, $H\cap K = \text{Núc }\varphi \unlhd K$.
Veamos ahora que $\varphi$ es suprayectiva.
Sea $x\in HK/H$, $x = hk H$ con $h\in H, k \in K$.
\begin{align*}
x = hk H = (kk^{-1})hk H = k(k^{-1}hk) H = kH
\end{align*}
ya que $k^{-1}hk\in H$ pues $H\unlhd G$.
Entonces $x = kH = \varphi(k) \in \text{Im }\varphi$. Por lo que $\varphi$ es suprayectiva y además, $\text{Im }\varphi = HK/H$.
Por el 1er Teorema de Isomorfía,
\begin{align*}
K/\text{Núc }\varphi \cong \text{Im }\varphi
\end{align*}
entonces
\begin{align*}
K/(H\cap K) \cong HK/H.
\end{align*}
$\blacksquare$
Un ejemplo para reforzar del STI
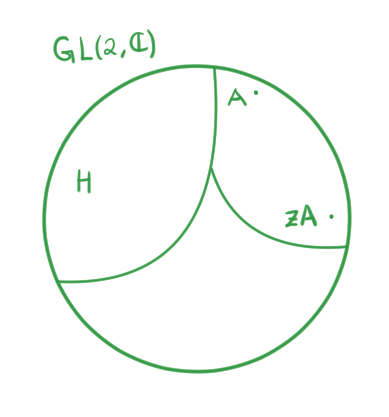
Consideremos $G = GL(2,\c), H = \{zI_2| z \in\c^*\}$ y $K = SL(2,\c)$. Recordemos que $K$ es el grupo lineal especial.
Dado $z \in\c^*$ y $A\in GL(2,\c)$,
\begin{align*}
A(zI_2)A^{-1} = zAI_2A^{-1} = zI_2.
\end{align*}
Así $H \unlhd G$.
Además,
\begin{align*}
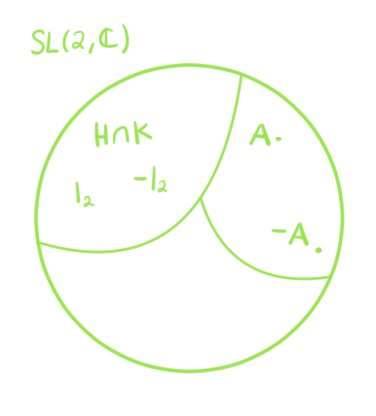
H\cap K &= \{zI_2|\det(zI_2) = 1\}\\ &= \left\{ \begin{pmatrix}
z & 0\\0 & z \end{pmatrix} : z^2 = 1\right\}\\
& = \left\{\left( \begin{array}{rr}1 & 0\\0 & 1 \end{array}\right), \left( \begin{array}{rr}
-1 & 0\\0 & -1 \end{array}\right) \right\} = \{I_2, -I_2\}.
\end{align*}
Por el Segundo Teorema de Isomofía,
\begin{align*}
HSL(2,\c)/ H \cong SL(2,\c)/ \{I_2, -I_2\}.
\end{align*}
Analicemos qué pasa con $HSL(2,\mathbb{C})$. Primero $HSL(2,\c) \leq GL(2, \mathbb{C})$, y si $A \in GL(2,\mathbb{C})$.
\begin{align*}
A = \left(\sqrt{\det A} \;I_2 \right) \left(\frac{1}{\sqrt{\det A}}\right)A.
\end{align*}
Como el primer término está en $H$ y el segundo está en $SL(2,\c)$, entonces $A \in H\,SL(2,\c)$.
Así, tenemos que $H\,SL(2,\c) = GL(2,\mathbb{C})$.
Reescribiendo lo que nos dice el Segundo Teorema de Isomorfía obtenemos:
\begin{align*}
GL(2,\mathbb{C})/H \cong SL(2,\mathbb{C})/\{I_2, -I_2\}.
\end{align*}
Analicemos ahora cómo es $GL(2,\c)/H$. Tomemos $A,B \in GL(2,\mathbb{C})$,
\begin{align*}
AH = BH &\Leftrightarrow A^{-1}B\in H\\ &\Leftrightarrow A^{-1}B = \begin{pmatrix}z & 0 \\ 0 & z\end{pmatrix} \quad \text{con }z\in \c^* \\
&\Leftrightarrow B = A \begin{pmatrix} z & 0 \\ 0 & z \end{pmatrix} = z A \quad \text{con }z\in \c^*
\end{align*}
es decir, en el cociente identificamos a matrices que difieren por un escalar no nulo.
Ahora, analicemos el cociente $SL(2,\c)/\{I_2, -I_2\}$. Tomemos $A,B\in SL(2,\c)$,
\begin{align*}
A\{I_2, -I_2\} = B\{I_2,-I_2\} &\Leftrightarrow A^{-1}B \in \{I_2, -I_2\}\\ &\Leftrightarrow A^{-1}B = \pm I_2 \\
&\Leftrightarrow B = \pm A
\end{align*}
es decir, identificamos a los matrices que difieren a lo mucho por su signo.
Versión intuitiva del ejemplo
Veamos ahora el ejemplo de una manera más intuitiva (con dibujos) para entender por qué esos cocientes son isomorfos.
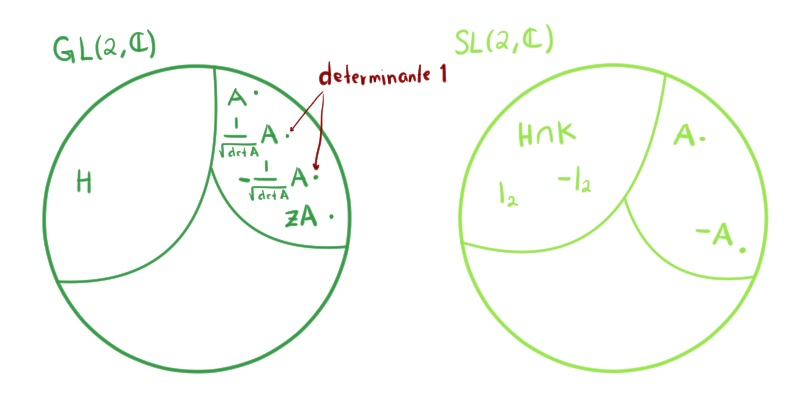
Lo que hicimos fue tomar el grupo general lineal $GL(2,\c)$ y hacer un cociente respecto a $H$, que consiste en todas las matrices escalares con escalares no nulos. Esto hace que cada matriz $A$ se identifique con cualquier otra de la forma $zA$, con $z$ un escalar no nulo.
En el caso del grupo especial lineal $SL(2,\c)$, hicimos un cociente con $H\cap K$ que consta solamente de la identidad $I_2$ y de su inverso aditivo $-I_2$. De acuerdo con lo que analizamos, las clases de equivalencia tienen 2 elementos. Cada matriz $A$ se identifica con su inverso aditivo $-A$.
Luego, regresando a $GL(2,\c)$, si nos tomamos la matriz dada por $\frac{1}{\sqrt{\text{det }A}} A$, ésta está en la misma clase de equivalencia que $A$ ya que es de la forma $zA$ con $z=\frac{1}{\sqrt{\text{det }A}}$ un escalar no nulo. Pero además, $\frac{1}{\sqrt{\text{det }A}} A$ es de determinante igual a 1. Entonces, en la misma clase de equivalencia dos matrices con determinante 1:
\begin{align*}
\frac{1}{\sqrt{\text{det }A}} A, \quad -\frac{1}{\sqrt{\text{det }A}} A.
\end{align*}
Además, éstas son las únicas dos opciones con determinante 1. Esto sucede porque ya $\text{det}(zA) = z^2 \text{det }A$ debido a las propiedades del determinante. Entonces si queremos que $zA$ sea de determinante uno, obtendríamos:
\begin{align*}
1 = \text{det}(zA) = z^2 \text{det }A &\Leftrightarrow z^2 = \frac{1}{\text{det }A} \\
&\Leftrightarrow z = \pm \frac{1}{\sqrt{\text{det }A}}.
\end{align*}
Entonces, podemos usar alguna de esas dos matrices de determinante uno como representante de la clase de equivalencia de $A$. De la misma manera $I_2, -I_2 \in H$ tienen determinante uno, por lo que podríamos usar alguna de ellas como representante de la clase $H$.
Al trabajar en el contexto de $SL(2,\c)$ consideraríamos sólo las matrices con determinante uno, así que en la clase $H\cap K$ sólo quedarían $I_2$ y $-I_2$. De modo más general, en $GL(2,\c)$ módulo $H$ cada matriz $A$ se identifica con cualquiera de la forma $zA$, y sabemos que sólo $\pm \frac{1}{\sqrt{\text{det }A}} A$ tienen determinante uno, así que al trabajar ahora en $SL(2,\c)$ la clase de cada matriz $A$ en $SL(2,\c)$ consistirá sólo de $\pm \frac{1}{\sqrt{\text{det }A}} A$, y como $\text{det }A=1$, en cada clase tendríamos sólo a la matriz y a su inverso aditivo $\pm A$ .
Esto es lo hay de fondo cuando decimos que los cocientes son isomorfos:
\begin{align*}
GL(2,\mathbb{C})/H \cong SL(2,\mathbb{C})/\{I_2, -I_2\}.
\end{align*}
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $G$ un grupo finito, $H$ y $K$ subgrupos de $G$ con $H$ normal en $G$. ¿Cuál es la cardinalidad de $HK$ en términos de la de $H$ y de la de $K$? ¿Qué sucede si $H$ no es normal?
- Sea $G$ un grupo finito, $S$ y $T$ subconjuntos de $G$. ¿Cuál es la cardinalidad de $ST$ en términos de la de $S$ y la de $T$?
- Da otra prueba del 2do Teorema de Isomorfía encontrando un homomorfismo adecuado $\varphi: HK \to K/(H\cap K)$.
- Sean $G= Q$ el grupo de los cuaternios, $H = \left< i \right>$, $K = \left< k \right>$. Calcula los cocientes $HK/H$ y $K/(H\cap K)$ encontrando explícitamente su orden, el orden de sus elementos y su tabla de multiplicar, y a partir de ello compara ambos cocientes.
- Sean $G = \z \times \z \times \z$ con la suma entrada a entrada, $H = \z\times\z\times \{0\}$, $K = \{0\}\times\z\times\z$.
- Analiza cómo es el cociente $(H+K)/H$ entendido qué se requiere para que $(a,b,c) + H = (d,f,g) + H$.
- Analiza cómo es el cociente $K/(H\cap K)$ entendiendo qué se requiere para que $(a,b,c)+H\cap K = (d,f,g)+ H\cap K$.
- Encuentra un homomorfismo $\varphi: \{0\}\times\z\times\z \to \z$ que te permita entender cómo es el cociente $K/(H\cap K)$.
Más adelante…
Ahora ya conocemos al que llamaremos el Segundo Teorema de Isomorfía, a diferencia del PTI, éste no se usa para probar el Tercero, pero igual lo ocupando en las unidades siguientes.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Primer Teorema de Isomorfía.
- Siguiente entrada del curso: Tercer Teorema de Isomorfía.
- Resto de cursos: Cursos.