Archivo del Autor: Cecilia del Carmen Villatoro Ramos

Álgebra Moderna I: Clase de Conjugación, Centro de $G$, Ecuación de Clase y $p$-Grupo

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Esta entrada es una caja de herramientas. Continuamos sobre la línea de estudiar las propiedades de una órbita y de su orden. Primero, nos vamos a enfocar en grupos actuando sobre sí mismos, a partir de esto definiremos un nuevo conjunto al que llamamos el centro de $G$ y daremos algunas observaciones al respecto.

El segundo bloque importante de la entrada es probar la llamada ecuación de clase, una ecuación que nos permite calcular el orden de un $G$-conjunto usando otros conjuntos relacionados. Uno de estos conjuntos lo definiremos como $X_G$, el conjunto de todos los elementos de $X$ que quedan fijos sin importar el elemento de $G$ que actúa sobre ellos. Volveremos a encontrar a la órbita de los elementos en la demostración de esta ecuación.

Por último, comenzaremos a trabajar con $p$-grupos, es decir grupos de orden una potencia de un número primo y usaremos la ecuación de clase para demostrar una propiedad de los $p$-grupos.

Decimos que esta entrada es una caja de herramientas, porque no estamos introduciendo temas que vayamos a estudiar a profundidad, más bien son conceptos que nos ayudarán a llegar al tema principal de esta unidad: los Teoremas de Sylow.

Clases de conjugación, centralizadores y centro de $G$

La acción de un grupo actuando en sí mismo por conjugación es muy importante y debido a ello daremos nombres y notaciones específicas para las órbitas y estabilizadores correspondientes (que fueron estudiados de manera general en la entrada Órbita de $x$ y tipos de acciones).

Definición. Sea $G$ es un grupo actuando en sí mismo por conjugación, es decir $g\cdot x = g x g^{-1}$ para todos $g,x\in G$. Dado $x\in G$ la órbita del elemento $x$ bajo esta acción se llama la clase de conjugación de $x$ y se denota por $x^G$, esto es:
\begin{align*}
x^G=\mathcal{O}(x) &= \{g\cdot x | g\in G \} = \{gxg^{-1} | g\in G\}.
\end{align*}

Por otro lado el estabilizador de $x$ se llama el centralizador de $x$ en $G$ y se denota por $C_G(x)$, es decir:

\begin{align*}
C_G(x)=G_x &= \{g\in G|g\cdot x = x\} = \{g\in G | gxg^{-1} = x\}\\
&= \{g\in G | gx = xg\} ,
\end{align*}

siendo entonces el conjunto de todos los elementos del grupo que conmutan con $x$.

Otra colección que resultará clave en el material que desarrollaremos más adelante es el llamado centro de un grupo:

Definición. Sea $G$ un grupo, el centro de $G$, denotado por $Z(G)$, es
\begin{align*}
Z(G) = \{x\in G | xg = gx \quad \forall g\in G\}.
\end{align*}

Es decir, el centro es la colección de todos los elementos de $G$ que conmutan con todos los demás.

Observación 1. $Z(G)$ es subgrupo normal de $G$.

Demostración.
Primero, tomemos el neutro $e\in G$ y veamos que está en $Z(G)$. Como estamos hablando del neutro, se cumple que $eg = g = ge$ para toda $g\in G$, entonces $e\in Z(G)$.

Ahora, tomamos $x\in Z(G)$ entonces $xg = gx$ para toda $g\in G$. Así $g=x^{-1}gx$ para toda $g\in G$, lo que implica que $gx^{-1} = x^{-1}g$ para toda $g\in G$ por lo que $x^{-1} \in Z(G)$.

Luego, si tomamos $x,y\in Z(G)$, se tienen las siguientes igualdades por la definición del centro $(xy)g = x(yg) = x(gy) = (xg)y = (gx)y = g(xy)$ para todo $g\in G$. Así, $xy \in Z(G)$.

Concluimos que el centro es un subgrupo.

Por último, probemos que es un subgrupo normal. Sean $x\in Z(G)$, $g\in G$, al conjugar $x$ con $g$ podemos usar la asociatividad y la definición de centro para concluir que $$gxg^{-1} = (gx)g^{-1} = (xg)g^{-1} = x(gg^{-1}) = xe = x \in Z(G).$$

Por lo tanto $Z(G)\unlhd G$.

$\blacksquare$

Observación 2. Sean $G$ un grupo y $x\in G$. Entonces $x\in Z(G)$ si y sólo si $x^G = \{x\}$.

Demostración. Sean $G$ un grupo y $x\in G$. Tenemos que
\begin{align*}
x^G = \{x\} &\Leftrightarrow gxg^{-1} = x \quad \forall g\in G &\\
&\Leftrightarrow gx = xg &\text{Multiplicamos por $g$ a la derecha}\\
&\Leftrightarrow x\in Z(G).
\end{align*}

$\blacksquare$

La observación anterior nos dice entonces que los elementos del centro son precisamente aquellos cuya clase de conjugación es trivial.

Ecuación de Clase

Para poder enunciar la ecuación de clase, que describe la carnalidad de un $G$-conjunto $X$ en términos de los índices de ciertos estabilizadores, definamos primero un cierto subconjunto de $X$:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto finito,
\begin{align*}
X_G = \{x\in X | g\cdot x = x \; \forall g\in G\}.
\end{align*}

Es decir, $X_G$ es el conjunto de elementos de $X$ que quedan fijos sin importar qué elemento de $G$ actúe sobre ellos.

Notemos que dado $x\in X$ se tiene que $x\in X_G$ si y sólo si $g\cdot x = x$ para toda $g\in G$ y esto sucede si y sólo si $\mathcal{O}(x) = \{x\}.$ Entonces se cumple lo siguiente:

Observación 3. $x\in X_G$ si y sólo si $\mathcal{O}(x) = \{x\}.$

Así, el conjunto $X_G$ consiste de los elementos cuya órbita es trivial.

Proposición. (Ecuación de Clase)
Sea $G$ un grupo, $X$ un $G$-conjunto finito. Tenemos que
\begin{align*}
\#X = \#X_G + \sum_{j=1}^k [ G : G_{x_j}]
\end{align*}
con $x_1, \cdots x_k$ representantes de las distintas órbitas con más de un elemento.

En particular, si $G$ es finito y actúa en $G$ por conjugación
\begin{align*}
|G| = |Z(G)| + \sum_{j= i}^{k} [ G: C_G(x_j) ]
\end{align*}
con $x_1,\cdots x_k$ representantes de las distintas clases de conjugación con más de un elemento.

Demostración.
Sea $G$ un grupo, $X$ un $G$-conjunto finito.

Sabemos que las órbitas son una partición de $X$. Sean $x_1,\cdots,x_k, x_{k+1},\cdots, x_t$ representantes de las distintas órbitas, donde $\#\mathcal(x_j) > 1$ si $j\in \{1,\cdots, k \}$ y $\#\mathcal{O}(x_j) = 1$ si $j\in \{k+1,\cdots , t\}.$ Entonces por un lado tenemos a las órbitas que tienen un sólo elemento y, por otro lado, las demás.

Por la observación 3, $X_G = \{x\in X| \# \mathcal{O}(x) = 1\} = \{x_{k+1},\cdots, x_t\}$.

Así,
\begin{align*}
\# X &= \sum_{j=1}^t \#\mathcal{O}(x_j) \\
&= \sum_{j= 1}^k \#\mathcal{O}(x_j) + \sum_{j= k+1}^t \#\mathcal{O}(x_j) &\text{Separamos la suma}\\
&= \sum_{j= 1}^k \#\mathcal{O}(x_j) + \sum_{j = k+1}^t 1 & \#\mathcal{O}(x_j) = 1 \text{ para } j \geq k+1\\
&= \sum_{j= 1}^k [ G : G_{x_j} ] + \# X_G & \text{Por la observación 3.}
\end{align*}

Si $G$ es finito y actúa en $G$ por conjugación, $X_G = Z(G)$, $\mathcal{O}(x_j) = x_j^G$ son las clases de conjugación y $G_{x_j} = C_G(x_j)$. Así
\begin{align*}
|G| = \sum_{j= 1}^k \lceil G: C_G(x_j) \rceil + |Z(G)|.
\end{align*}

$\blacksquare$

$p$-grupo

Hemos tratado con grupos finitos de orden primo, de ellos sabemos propiedades importantes como el hecho de que son cíclicos. El siguiente paso en nuestro estudio, es enfocarnos en los grupos cuyo orden es una potencia de algún primo. No todos los grupos finitos cumplen esta característica, pero los que sí, nos permiten entender a los demás.

Definición. Sea $G$ un grupo, $p\in\z^+$ un primo. Decimos que $G$ es un $p$-grupo si $|G| = p^t$ para alguna $t\in \n$.

Teorema. Sean $p\in \z^+$ un primo, $G$ un $p$-grupo, $X$ un $G$-conjunto finito. Entonces $$\#X \equiv \# X_G ( \text{mód } p).$$

Demostración.
Sean $p\in \z^+$ un primo, $G$ un $p$-grupo, $X$ un $G$-conjunto finito. Por la ecuación de clase,
\begin{align*}
\#X = \#X_G + \sum_{j=1}^k [G: G_{x_j} ]
\end{align*}
con $x_1,\cdots, x_k$ representantes de las distintas órbitas con más de un elemento. Como $G$ es un $p$-grupo, $|G| = p^t$ con $t\in \n$. Dado que el orden de los estabilizadores divide al orden de $G$ tenemos que $|G_{x_j}| \mid p^t$ y por lo tanto $|G_{x_j}| = p^{m_j}$ con $m_j\in \n, m_j \leq t.$

Entonces

\begin{align*}
1< \# \mathcal{O}(x_j) &= [G: G_{x_j} ] & \text{Por lo visto anteriormente}\\
&= \frac{|G|}{|G_{x_j}|} & \text{Propiedad del índice}\\
&= \frac{p^t}{p^{m_j}} & \text{Consecuencia de la hipótesis}\\
&= p^{t-m_j}.
\end{align*}

Así, $p$ divide a $[G: G_{x_j}]$ para toda $j\in \{1,\cdots, k\}.$ Por lo que

\begin{align*}
p \text{ divide a } \sum_{j=1}^k [G:G_{x_j}].
\end{align*}

Pero por la ecuación de clase $ \displaystyle \sum_{j=1}^k [G:G_{x_j}]= \# X – \# X_G.$

Entonces
\begin{align*}
p \text{ divide a } \# X – \# X_G.
\end{align*}

En consecuencia $\# X \equiv \#X_G( \text{mód } p).$

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Considera el grupo $S_4$ actuando sobre sí mismo por conjugación.
    • Determina las clases de conjugación de $S_4$.
    • Escribe la ecuación de clase de $S_4$.
    • Deduce el orden de cada uno de los estabilizadores $G_x$, donde $x\in S_4$.
  2. Encuentra todos los $p$-subgrupos de $S_4$.
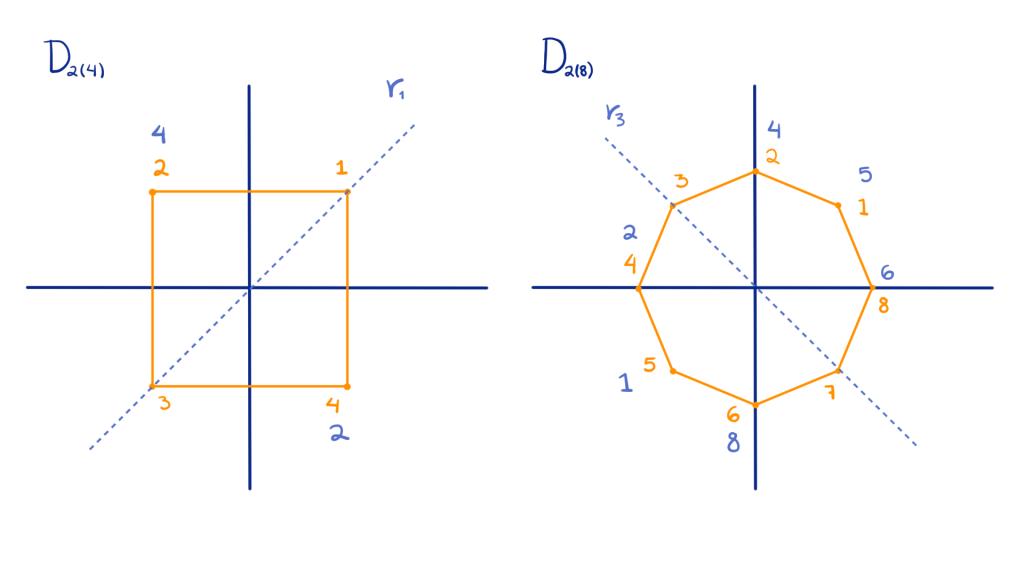
  3. Sean $X = \{H \,|\, H \leq D_{2(4)}\}$, $G = \left< a \right>$ con $a$ la rotación de $\displaystyle \frac{\pi}{2}$. Considera la acción de $G$ en $X$ dada por $g \cdot H = gHg^{-1}$ para todo $g\in G$, $H \in X$. Encuentra $X_G$ y verifica que $\#X \equiv \# X_G (\text{mód }2)$.

Más adelante…

Ahora nuestro interés está puesto en los números primos o más bien, en la relación de los números primos con el orden de los grupos. Esta entrada te da lo que tienes que saber de $p$-grupos y más adelante veremos cómo mediante ellos se pueden estudiar otros grupos. Además, eventualmente veremos un caso especial de los $p$-grupos, llamados $p$-subgrupos de Sylow, que nos llevará (para sorpresa de nadie) a los Teoremas de Sylow.

Entradas relacionadas

Álgebra Moderna I: Tamaño de una órbita y de un estabilizador

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta entrada repasaremos lo que vimos en la entrada anterior. Primero, veremos unos ejemplos que ilustran las definiciones de órbita y estabilizadores. A partir de estos ejemplos podremos observar ciertos patrones que se repiten y los analizaremos formalmente en una proposición. Por último, daremos un último ejemplo para ilustrar dicha proposición.

Ejemplos de Acciones

Repasemos lo que hemos visto con los siguientes ejemplos. En cada ejemplo describimos el grupo $G$, la órbita y los estabilizadores de los elementos.

Ejemplo 1. Consideremos la permutación $\alpha = (1\,2\,3\,4) \in S_6$. Sean $G = \left<\alpha\right>$ y $X = \{1,2,3,4,5,6\}$ con la acción dada por $\alpha^k \cdot i = \alpha^k(i)$ para toda $k\in \z, i\in X.$

Este diagrama nos ayuda a entender cómo funciona $\alpha$ y qué sucede cuando aplicamos $\alpha^2$, $\alpha^3$, $\dots$. Los elementos del círculo van cambiando en el orden indicado por las flechas.
Además, $\alpha$ deja fijos al 5 y al 6.

Comencemos describiendo a las órbitas de los elementos:
\begin{align*}
\mathcal{O}(1) &= \{1,2,3,4\}\\
&= \mathcal{O}(2) = \mathcal{O}(3) = \mathcal{O}(4)\\
\mathcal{O}(5) &= \{5\}\\
\mathcal{O}(6) &= \{6\}.
\end{align*}

Observemos que las órbitas de $1, 2, 3$ y $4$ son iguales porque $\alpha$ es una permutación cíclica que mueve esos elementos, pero como $\alpha$ deja fijos a $5$ y a $6,$ sus órbitas son distintas y consisten solamente de sí mismos.

Ahora, podemos describir mejor a $G = \left< \alpha \right>$. Como $\alpha$ tiene orden 4, $G$ quedaría:

$$G = \{(1), \alpha, \alpha^2,\alpha^3\}.$$

Por último, describamos los estabilizadores. De acuerdo a la definición de la entrada previa el estabilizador de un objeto son los elementos del grupo que fijan al objeto, en este caso las potencias de $\alpha$ que dejan fijo al objeto. En el caso del $1$ la única potencia de $\alpha$ que lo fija es la identidad y análogamente para $2,3$ y $4$. Por otro lado en el caso de $5$ y $6$, como $\alpha$ no los mueve en absoluto, cualquier potencia de $\alpha$ forma parte de sus respectivos estabilizadores. Esto quedaría escrito de la siguiente manera:
\begin{align*}
G_1 &= \{\alpha^k \in G | \alpha^k \cdot 1 = 1\} = \{(1)\}\\
&= G_2 = G_3 = G_4. \\\\
G_5 &= \{\alpha^k \in G | \alpha^k \cdot 5 = 5\} = G = \{(1), \alpha, \alpha^2,\alpha^3\} \\&= \{\alpha^k \in G | \alpha^k \cdot 6 = 6\}= G_6.
\end{align*}

Ejemplo 2. Consideremos ahora la permutación $\beta = (1\,2\,3)(4\,5)\in S_5$. Sean $G = \left< \beta \right>$ y $X= \{1,2,3,4,5\}$ con la acción dada por $\beta^k \cdot i = \beta^k(i)$ para todas $k\in\z$ y $i\in X.$

Este diagrama ilustra el efecto de $\beta$ en los elementos de $X$. Podemos ver como $1, 2$ y $3$ forman un ciclo y, $4$ y $5$ forman otro.

Primero, describamos las órbitas de los elementos:

\begin{align*}
\mathcal{O}(1) &= \{1,2,3\} = \mathcal{O}(2) = \mathcal{O}(3).\\
\mathcal{O}(4) &= \{4,5\} = \mathcal{O}(5).
\end{align*}

Ahora, describamos mejor a $G$. Observemos que $\beta$ está compuesta por dos ciclos disjuntos: $(1\, 2\, 3)$ con orden $3$ y $(4\,5)$ con orden $2$, es decir es el producto de dos ciclos que conmutan y que tienen órdenes primos relativos entre sí. Por el último teorema de la entrada Palabras, el orden de $\beta$ es entonces $6$. Así, $G$ quedaría descrito como:
$$G = \{(1), \beta, \beta^2, \beta^3, \beta^4,\beta^5\}.$$

Por último, describamos los estabilizadores de cada elemento.

\begin{align*}
G_1 &= \{\beta^k \in G | \beta^k(1) = 1\} = \{(1),\beta^3\}\\
&= G_2 = G_3. \\\\
G_4 &= \{\beta^k\in G | \beta^k(4) = 4\} = \{(1), \beta^2, \beta^4\}\\
&= \{\beta^k\in G | \beta^k(5) = 5\} = G_5.
\end{align*}

Antes de avanzar a la siguiente sección, considera los ejemplos estudiados e intenta determinar si existe alguna relación entre $\#\mathcal{O}(x)$, $|G_x|$ y $|G|$.

¿Qué relación existe entre el tamaño de la órbita y el tamaño del estabilizador de un elemento?

Los ejemplos que trabajamos al inicio de esta entrada nos pueden dar la idea de que existe algún tipo de relación entre los tamaños de la órbita y del estabilizador para cada elemento.

Proposición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$.
\begin{align*}
\#\mathcal{O}(x) = [ G:G_x].
\end{align*}

Demostración.

Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. Dado que $[ G:G_x]=\# \{gG_x| g\in G\}$ bastaría con encontrar una biyección entre $\mathcal{O}(x)$ y $\{gG_x| g\in G\}.$
Proponemos $\varphi : \mathcal{O}(x) \to \{gG_x| g\in G\}$ tal que $g\cdot x \mapsto gG_x$ para todo $g\in G.$

Debemos probar que $\varphi$ es una biyección.

Primero, veamos que está bien definida. Tomemos $g,h\in G$, y supongamos que $g\cdot x = h\cdot x$.

Entonces

Esto implica,
\begin{align}\label{ec1}
h^{-1}\cdot (g\cdot x) &= h^{-1}\cdot (h\cdot x)
\end{align}

Por las propiedades de acción, al desarrollar la parte derecha de la igualdad \ref{ec1} obtenemos
\begin{align*}
h^{-1}\cdot (h\cdot x) &= (h^{-1}h)\cdot x\\
&= e\cdot x = x.
\end{align*}

Por otro lado al desarrollar la parte izquierda de la igualdad \ref{ec1} obtenemos que,
\begin{align*}
h^{-1}\cdot(g\cdot x) = (h^{-1}g)\cdot x,
\end{align*}

así, $ (h^{-1}g)\cdot x=x$ y esto por definición quiere decir que $h^{-1}g\in G_x$.
Por lo que estudiamos en clases laterales, esto implica que $gG_x = hG_x$, es decir que $\varphi(g\cdot x)=\varphi(h\cdot x)$.
Así, concluimos que $\varphi$ está bien definida.

Ahora, probaremos que $\varphi$ es unyectiva.
Sean $g, h \in G$, tales que $\varphi(g\cdot x) = \varphi(h\cdot x)$, es decir tales que $g G_x = hG_x.$ Pero
\begin{align*}
g G_x &= hG_x\\
\Rightarrow &h^{-1} g\in G_x &\text{Por lo que sabemos de clases laterales}\\
\Rightarrow &(h^{-1}g)\cdot x = x & \text{Por estar en el estabilizador}\\
\Rightarrow &h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Haciendo actuar $h$}\\ \Rightarrow &g\cdot x=((hh^{-1})g)\cdot x =(h(h^{-1}g))\cdot x =h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Por las propiedades de acción.}\\
\end{align*}

Así $\varphi$ es inyectiva.

Por construcción podemos observar que $\varphi$ es suprayectiva.

Por lo tanto $\#\mathcal{O} = [ G:G_x]$.

$\blacksquare$

Como consecuencia de lo anterior obtenemos el siguiente corolario.

Corolario. Sea $G$ un grupo finito, $X$ un $G$-conjunto, $x\in X.$ Entonces, $\# \mathcal{O}(x)$ divide a $|G|.$

Ejemplo del Dodecaedro

Veamos un ejemplo en el que apliquemos lo que acabamos de ver.

Consideremos el dodecaedro $D$.

Si pensamos en todas las simetrías en $\r^3$ que mandan el dodecaedro en sí mismo, podemos tomar las rotaciones y así definir $G = \{\varphi \text{ rotación en }\r^3 | \varphi[D]= D\}$.

¿Cuál es el orden de $G$?

Sea $X$ el conjunto de caras de $D$, $G$ actúa en $X$ ya que manda caras de $D$ en caras de $D$. La acción es transitiva ya que cada cara se puede llevar a cualquier cara contigua mediante una rotación de $\displaystyle\frac{2\pi}{3}.$

Si el eje de rotación va del origen a un vértice, las caras rotarán tomando el lugar de otras caras. En cambio, si el eje de rotación cruza del origen al centro de una cara, esa cara rotará sobre sí misma y cada que rote $\displaystyle r = \frac{2\pi}{5}$ seguirá en su lugar.

Rotación de $\frac{2\pi}{5}$ del dodecaedro cuando el eje pasa por el centro de una cara. Las caras superiores e inferiores rotan sobre sí mismo.
Rotación de $\frac{2\pi}{3}$ del dodecaedro cuando el eje pasa por un vértice.

Así, dado $x\in X$, habrá exactamente cinco rotaciones que mandan la cara $x$ en sí misma (aquellas rotaciones de ángulo $ \frac{2\pi}{5}$ cuyo eje de rotación cruza del origen al centro de una cara), por lo cual $|G_x| = 5$. Además, como la acción es transitiva $\# X = \#\mathcal{O}(x)$. Luego, $\#X = 12$ y $\#\mathcal{O}(x) = [G:G_x ]$. Pero $\displaystyle [G:G_x ] = \frac{|G|}{5}$. Si juntamos todo eso, obtenemos:
$$12 = \# X = \#\mathcal{O}(x) = [G:G_x ]= \frac{|G|}{5}.$$

Despejando, $|G| = 12\cdot 5 = 60.$ Es decir, tenemos 60 rotaciones en $\r^3$ que son simetrías del dodecaedro.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $G$ un grupo finito actuando sobre sí mismo:
    • Determina si el hecho de que exista $x\in G$ y tal que $G_x =\{e\}$ implica que la acción es transitiva.
    • Determina si el hecho de que la acción sea transitiva implica que exista $x\in G$ tal que $G_x =\{e\}$.
  2. Encuentra el orden del grupo de simetrías de cada sólido platónico (recuerda que hay algunos que son duales y por lo tanto tienen el mismo grupo de simetrías).

Más adelante…

Ya casi acabamos de estudiar la órbita, todavía nos queda analizar con ás detalle el caso cuando $X=G$, es decir cuando $G$ actúa sobre sí mismo. También podemos preguntarnos qué sucede con el conjunto de elementos de $X$ que se quedan fijos ante cualquier elemento de $G$ que actúe sobre ellos. Esto nos servirá para llegar a una importante ecuación llamada la ecuación de clase.

Además, en la siguiente entrada definiremos un nuevo tipo de grupo conocido como $p$-grupo y esto nos perfilará para llegar a los Teoremas de Sylow.

Entradas relacionadas

Álgebra Moderna I: Órbita de $x$ y tipos de acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Tomemos un grupo $G$ y $X$ un $G$-conjunto. A lo largo de esta entrada consideraremos la relación de equivalencia en $X$ inducida por esta acción y que fue definida en la entrada anterior de la siguiente manera:

$x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$.

Continuemos entonces con esta idea, comenzando por definir las clases de equivalencia inducidas por esa relación.

Después, definiremos nuevos tipos de acciones, por ejemplo, ¿qué pasa si la relación sólo induce una clase de equivalencia? o ¿qué sucede con el conjunto de objetos que dejan fijo a los elementos de $G$?

Órbita de un elemento de $X$

Dada la importancia de esta manera de relacionar a los elementos de un grupo de acuerdo a una acción, daremos un nombre a sus clases de equivalencia.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Para cada $x\in X$, la órbita de $x$ es
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g \in G\},
\end{align*}

es decir, todos los objetos que podemos obtener haciendo actuar a $G$ sobre $x$.

Observación. Sean $G$ un grupo, $X$ un $G$-conjunto. Tenemos que $\mathcal{O}(x)$ es la clase de equivalencia de $x$ con respecto a la relación inducida por la acción de $G$ en $X$.

Demostración.

Sea $x\in G$. Sabemos que la clase de equivalencia de $x$, denotada por $[x]$, se define como:
\begin{align*}
[ x ] &= \{y\in X |x\sim y\} &\text{Definición de clase de equivalencia} \\
&= \{y\in X|\exists g\in G \text{ con }g\cdot x = y\} &\text{Definición de la relación }\sim\\
&= \{g\cdot x| g\in G\} = \mathcal{O}(x) &\text{Definición de órbita.}
\end{align*}

$\blacksquare$

De cursos anteriores sabemos que la colección de clases de equivalencia inducidas por una relación es una partición del conjunto. El siguiente teorema se da como consecuencia de las propiedades de una partición.

Teorema. Sean $G$ un grupo, $X$ un $G$-conjunto. Entonces

  1. $\mathcal{O}(x) \neq \emptyset $ para toda $x\in X$.
  2. Sean $x,y\in X$. Si $\mathcal{O}(x)\cap \mathcal{O}(y)\neq \emptyset$, entonces $\mathcal{O}(x) = \mathcal{O}(y)$.
  3. $\displaystyle X = \bigcup_{x\in X}\mathcal{O}(x)$.

Este teorema sólo enlista las propiedades de una partición en el caso particular en el que estamos trabajando, por lo que no hay nada nuevo que demostrar.

Una acción transitiva

Las órbitas están determinadas por varios factores: el conjunto $X$, el grupo $G$ y la acción de $G$ en $X$. En algunos casos existe una única órbita.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Si $\mathcal{O}(x) = X$ para alguna $x\in X$, decimos que la acción es transitiva.

Esta definición nos dice que podemos obtener cualesquier elemento de $X$ haciendo actuar algún elemento del grupo en el objeto $x$.

Ejemplos de acciones transitivas

Ejemplo 1. Dado $G$ un grupo, $X=G$ definimos la acción de $G$ en sí mismo mediante la operación de $G$, es decir $a\cdot x = a x$ para todas $a\in G$, $x\in X.$

Consideremos cualquier $x\in X$. Sea $y\in X$. Siempre tenemos una manera de obtener $y$ a través de $x$:
\begin{align*}
y = y(x^{-1}x) = (yx^{-1})x = (yx^{-1})\cdot &x \in \mathcal{O}(x). \\
\text{Entonces } &y \in \mathcal{O}(x).
\end{align*}

Por lo tanto $\mathcal{O}(x) = X$ y así la acción es transitiva.

Ejemplo 2. Sean $G$ un grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH) = agH$ para todas $a,g\in G.$

Consideremos cualquier $gH \in X.$ Sea $tH \in X$ con $t\in G.$ Podemos reescribir al representante como:
\begin{align*}
t H &= t(g^{-1}g) H = (tg^{-1})gH \\
&= (tg^{-1})\cdot gH \in \mathcal{O}(gH).
\end{align*}

Por lo tanto $\mathcal{O}(gH) = X$. Así, la acción es transitiva.

Ejemplo 3. Sea $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

La acción que ya habíamos trabajado: dados $g\in G$, $i\in X$ definimos $g\cdot i = g(i)$.

Dada $a\in G$ la rotación $\displaystyle\frac{2\pi}{n}$ y $1\in X$, tenemos que
\begin{align*}
\text{id}\cdot 1 &= 1, \\
a\cdot 1 = a(1) &= 2,\\
a^2 \cdot 1 = a^2(1) &= 3, \\
&\vdots \\
a^{n-1} \cdot 1 = a^{n-1} (1) &= n.
\end{align*}

Entonces $X = \{1,2,\cdots,n\}\subseteq \mathcal{O}(1) \subseteq X$. Así, $\mathcal{O}(1) = X$. Por lo tanto la acción es transitiva.

Ejemplo 4. Ahora veamos un ejemplo nuevo.

Sea $G$ un grupo, $X= G$. Dados $a\in G$, $x\in X$ definimos
\begin{align*}
a\cdot x &= a x a^{-1}.
\end{align*}

Demostremos que es una acción:
\begin{align*}
e\cdot x &= exe^{-1} = x &\forall x\in X.\\
a\cdot(b\cdot x) &= a(b\cdot x)a^{-1} = a(bxb^{-1})a^{-1} = (ab)x(ab)^{-1}& \text{Asociando diferente}\\
&= (ab)\cdot x &\forall a,b\in G, \forall x\in X.
\end{align*}

Así, $G$ actúa en sí mismo por conjugación.

Dado $x\in X$,
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g\in G\} = \{gxg^{-1}| g\in G\}
\end{align*}
que son todos los conjugados de $x$.

En este caso, la acción no siempre es transitiva: Si $ G\neq \{e\}$ consideremos $x\in G\setminus\{e\}.$ Si $e\in \mathcal{O}(x)$ entonces $e = g\cdot x = gxg^{-1}$ para algún $g\in G$ y entonces $e = x$, esto es una contradicción porque $x\in G\setminus\{e\}$. Así, $\mathcal{O}(x)\neq X$ y la acción no es transitiva.

Más definiciones de acciones

En toda acción el neutro del grupo actúa de forma trivial en todos los elementos del conjunto pero puede ser que existan otros elementos del grupo con esa propiedad. Si no es el caso decimos que la acción es fiel:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto. Decimos que la acción es fiel si $g\cdot x = x$, con $g\in G$, para todo $x\in X$, implica que $g=e.$

Consideremos ahora los elementos del grupo que fijan a algún elemento específico del conjunto:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. El estabilizador de $x$ es
\begin{align*}
G_x = \{g\in G | g\cdot x = x\}.
\end{align*}

Es decir, la colección de todos los elementos de $G$ que dejan fijo a $x$.

Ejemplos de acción fiel y estabilizador

Ejemplo 1. Sea $G$ un grupo, $X = G$ y $g\cdot x = gx$ para todo $g,x \in G.$

Si $g\in G$ es tal que $g\cdot x = x$ para toda $x\in X$, entonces $gx = x$ para toda $x\in X$, en particular $g = ge = e.$

Así $g=e$ y la acción es fiel.

Dado $x\in X$,
\begin{align*}
G_x = \{g\in G | g\cdot x = x\} = \{g\in X| gx = x\}.
\end{align*}

Pero si $gx = x$,por cancelación $g=e$. Así $G_x = \{e\}$ para toda $x\in X,$ de modo que los estabilizadores son triviales.

Ejemplo 2. Sean $G$ grupo, $H$ subgrupo de $G$, $X = \{xH | x\in G\}$ con $g\cdot(xH) = gx H$ para toda $g,x\in G.$

Si $g\in G$ es tal que $g\cdot (xH) = xH$ para toda $x\in G$, entonces
\begin{align*}
gxH &= xH &\forall x\in G\\
\Rightarrow \, x^{-1} g x &\in H & \forall x\in G\\
\Rightarrow \, g&\in xHx^{-1} & \forall x\in G.
\end{align*}

Si $H\unlhd G$ esto se cumple para toda $g\in H$. Por lo tanto la acción no necesariamente es fiel.

Ahora, dada una clase lateral $xH \in X$.
\begin{align*}
G_{xH} &= \{g\in G | g\cdot (xH) = xH\}\\
&= \{g\in G| gxH = xH\}\\
&= \{g\in G | x^{-1}gx\in H\} \\
&= \{g\in G | g\in xHx^{-1}\}\\
&= xHx^{-1}.
\end{align*}

Así $G_{xH} = xHx^{-1}$ para toda $x\in G.$

Ejemplo 3. Sean $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

Dados $g\in G, i \in X$ definimos $g\cdot i = g(i)$.

Si $g\in G$ es tal que $g\cdot i = i$ para toda $i \in X$, entonces $g(i) = i$ para toda $i\in X$. Así, $g$ sería una transformación lineal en el plano, que fija a los vértices $1$ y $2,$ los cuales forman una base del plano. Por lo tanto $g = \text{id}$ y la acción es fiel.

Dado $i\in X$,
\begin{align*}
G_i &= \{g \in G | g\cdot i = i\}\\
&= \{g\in G | g(i) = i\}\\
&= \{\text{id},r_i\}
\end{align*}
con $r_i$ la reflexión con respecto a la recta que pasa por $(0,0)$ y $i.$

Por último, veremos una observación.

Ilustración de lo que sucede con $r_i$ de $D_{2(n)}.$ Usamos $D_{2(4)}$ representado con un cuadrado y $D_{2(8)}$ representado con un octágono. En el dibujo, $r_1$ mantiene fijo a 1 y 3, y $r_3$ mantiene fijo a 3 y 7.

Observación. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. $G_x$ es un subgrupo de $G$.

Demostración.
Sean $G$ grupo, $X$ un $G$-conjunto, $x\in X.$

El neutro de $G$ siempre está en el estabilizador porque:
\begin{align*}
e\cdot x = x \quad \forall x\in X,
\end{align*}

entonces $e\in G_x.$

Si $a,b\in G_x$, entonces $(ab)\cdot x = a\cdot (b\cdot x) = a\cdot x = x = x$. Así, $ab\in G_x$. Es decir, el estabilizador es cerrado bajo producto.

Finalmente si $a\in G_x$, $a\cdot x = x$, entonces $a^{-1}\cdot x = a^{-1}\cdot (a\cdot x) = (a^{-1}a)\cdot x = e\cdot x = x$, así $a^{-1} \in G_x$.

Por lo tanto $G_x \leq G$.

$\blacksquare$

Tarea moral

  1. En cada uno de los incisos del ejercicio 1 de la entrada de acciones, en donde haya una acción, describe cómo son las órbitas y determina si se trata de una acción transitiva.
  2. Considera el conjunto $X = \{1,2,3,4,5,6,7,8\}$ y el grupo $G = \left< a \right>$ con $a\in S_8$. Define $a^{i}\cdot j = a^{i}(j)$ para cada $a^{i} \in G$ y cada $j\in X$.
    • Verifica que es una acción de $G$ en $X$.
    • Si $a = (2 \; 4 \; 1 \; 7 \; 8)$ describe las órbitas y determina si se trata de una acción transitiva.
    • Si $a = (6 \; 1 \; 5 \; 8)(3 \; 4)$ describe órbitas y determina si se trata de una acción transitiva.
  3. Sea $G$ un grupo y $X$ un $G$-conjunto. Si la acción de transitiva prueba o da un contraejemplo para las siguientes afirmaciones:
    • $\mathcal{O}(x) = X$ para todo $x\in X$.
    • Para cada $x,y \in X$ existe $g\in G$ tal que $g\cdot x = y$.
  4. Considera el grupo diédrico $D_{2(n)}$ actuando sobre sí mismo con conjugación.
    • Determina si la acción es fiel.
    • Encuentra el estabilizador de $a$, con $a$ la rotación de $\displaystyle\frac{2\pi}{n}$, y el de $b$ con $b$ la reflexión con respecto al eje $x$.
  5. Sea $G$ un grupo y $X$ un $G$-conjunto.
    • Determina si el hecho de que exista $x\in G$ tal que $G_x = \{e\}$ implica que la acción es fiel.
    • Determina si el hecho de que la acción sea fiel implica que exista $x\in G$ tal que $G_x=\{e\}$.

Más adelante…

Continuaremos estudiando las propiedades de las órbitas, en particular, el orden de las órbitas, ¿cómo se relaciona éste con el orden del grupo $G$? Daremos respuesta a ello en la siguiente entrada.

Entradas relacionadas

Álgebra Moderna I: Acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Antes de comenzar con el tema que nos compete, repasemos lo que hemos visto del Teorema de Cayley y su modificación de la entrada anterior. Primero, en el Teorema de Cayley, comenzamos tomando un grupo $G$, un $a$ en el grupo y actuamos con ese $a$ sobre el grupo, es decir multiplicamos los elementos. En resumen, nos permite mover los elementos del mismo grupo.

Con la modificación avanzamos en la abstracción. En el teorema nos tomamos el conjunto de clases laterales y ahora, $G$ actúa sobre las clases laterales. Detente un minuto para pensar, si cada vez somos más generales ¿cuál es el siguiente paso? ¿sobre quién queremos que actúe $G$ ahora?

La respuesta es: sobre un conjunto cualquiera $X$. Ahora queremos pensar que usamos los elementos de $G$ para mover elementos de $X$. Para eso necesitamos una especie de producto, además de algunos matices. Por ejemplo, para un $x\in X$ cuando $a = e$, el elemento $a\cdot x = x$ se quede fijo y que si se multiplica por $a$ y luego por $b$, que sea lo mismo que multiplicar por $ab$, es decir $a\cdot(b\cdot x) = ab\cdot x$. Si se cumplen estas dos condiciones diremos que $a$ es una acción de $G$ en el conjunto $X$.

Diagrama de qué es una acción.

Luces, cámara, ¡acción!

Como verás, hemos estado usando el verbo actuar para referirnos a esta transformación que sucede al operar un $a\in G$ y otro elemento, sea del mismo $G$ o de las clases laterales. Aunque no hayamos definido formalmente qué es una acción, la realidad es que ya usar actuar da una idea de lo que estamos queriendo decir. Estamos usando un elemento de un grupo para transformar un elemento de otro. A continuación definiremos formalmente a una acción.

Definición. Sea $G$ un grupo, $X$ un conjunto. Si existe una función:
\begin{align*}
G \times X &\to X\\
(a,x) &\mapsto a\cdot x
\end{align*}
para todos $a\in G, x\in X$, tal que:

  1. $e \cdot x = x$ para toda $x\in X$.
  2. $a \cdot (b\cdot x) = (ab)\cdot x $ para todas $a,b\in G, x\in X$,

decimos que la función es una acción de $G$ en $X$, y que $G$ actúa en $X$ o que $X$ es un $G$-conjunto.

Ejemplos.

Veamos algunos ejemplos nuevos y retomemos algunos otros, para verificar que esto es una generalización para lo que se hizo en el Teorema de Cayley y en su modificación.

Ejemplo 1. Sean $G$ grupo, $X=G$ definimos $a\cdot x = ax$ para todas $a\in G, x\in X$. Es decir, definimos una acción sobre sí mismo. Probemos las dos condiciones:

\begin{align*}
&e\cdot x = ex = x &\forall x\in X\\
&a\cdot(b\cdot x) = a\cdot(bx) = a(bx) = (ab)x = (ab)\cdot x &\forall a,b\in G,\; x\in X.
\end{align*}

Así, todo grupo $G$ actúa en sí mismo mediante su operación binaria. Como vimos en la entrada del Teorema de Cayley.

Ejemplo 2. Sean $G$ grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH)= agH$ para toda $a,g\in G$. Ahora, probemos las dos condiciones de una acción:

\begin{align*}
&e\cdot(gH) = egH = gH &\forall g\in G
\end{align*}
\begin{align*}
a\cdot(b\cdot(gH)) &= a\cdot(bgH) = a(bg)H = (ab)gH \\
&= ab\cdot (gH) &\forall a,b,g\in G
\end{align*}

Así se tiene una acción de $G$ en las clases laterales de $H$ en $G$. Este ejemplo lo vimos en la entrada de la modificación al Teorema de Cayley.

Por último, podemos ver un ejemplo nuevo.

Ejemplo 3. Sea $G = D_{2n}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices de polígono regular de $n$ lados.

Dados $g\in G, i\in X$ definimos $g\cdot i = j$ si $g$ manda el vértice $i$ en el vértice $j$. Recordemos que los elementos de un grupo diédrico son las simetrías del polígono regular de $n$ lados, es decir, son transformaciones lineales del plano que mandan del polígono en sí mismo. En particular, los vértices van a dar a vértices bajo estas transformaciones.

Representación de una grupo diédrico.

Entonces, como son transformaciones del plano nuestra acción quedaría como una evaluación $g \cdot i = g(i)$. Así, para todos $i\in X, g,h\in G$,
\begin{align*}
\text{id}\cdot i &= \text{id}(i) = i \\
g\cdot (h\cdot i )& = g\cdot (h(i)) = g(h(i)) = (gh) (i) = (gh) \cdot i.
\end{align*}

Así, $D_{2n}$ actúa en el conjunto de vértices.

Recordemos que al escribir $(gh)\cdot i$, la operación que ocurre entre $g$ y $h$ es la composición. En este momento se omitió el símbolo $\circ$ para evitar confusiones con el símbolo $\cdot$ de acción.

Otra definición de Acción

Anteriormente hemos visto la noción de que los elementos de un grupo dan lugar a permutaciones. Usaremos esta idea para dar una definición de acción equivalente a la definición que acabamos de dar.

Teorema. Sean $G$ un grupo, $X$ un conjunto. Toda acción de $G$ en $X$ induce un homomorfismo de $G$ en $S_X$ y viceversa.

Demostración.

Sean $G$ un grupo y $X$ un conjunto.
Supongamos que $G\times X \to X$ es una acción de $G$ en $X$ tal que $(g,x)\mapsto g\cdot gx$. Para cada $g\in G$ definimos $\alpha_g : X\to X$ dada por $\alpha_g(x) = g\cdot x$ para toda $x\in X$.

Ilustración del efecto de $\alpha_g$.

Analicemos las funciones $\alpha_g$, veamos que son biyectivas:

\begin{align*}
\alpha_g\circ\alpha_{g^{-1}}(x) & = \alpha_g(\alpha_{g^{-1}}) = \alpha_g(g^{-1}\cdot x) = g\cdot(g^{-1}\cdot x)\\
&= (gg^{-1})\cdot x &\text{Condición 2 de acción}\\
&= e\cdot x = x &\text{Condición 1 de acción}.
\end{align*}

Entonces $\alpha_g\circ\alpha_{g^{-1}} = \text{id}_X$.

Anáogamente $\alpha_{g^{-1}}\circ \alpha_g = \text{id}_X$, entonces $\alpha_g$ es biyectiva, es decir $\alpha_g \in S_X$.

Definimos $\psi: G \to S_X$ con $\psi (g) = \alpha_g$ para toda $g\in G$.

Veamos que $\psi$ es un homomorfismo. Tomemos $g,h\in G$,
\begin{align*}
\psi(gh)(x) &= \alpha_{gh}(x) = (gh)\cdot x = g\cdot(h\cdot x) = \alpha_g(\alpha_h(x)) & \text{Condición 2}\\
&= \alpha_g \circ \alpha_g(h) = \psi(g) \psi(h)(x) &\forall x\in X.
\end{align*}

Entonces $\psi(gh) = \psi(g)\psi(h)$ para todos $g,h\in G$.

Por lo tanto $\psi$ es un homomorfismo.

Ahora de regreso. Supongamos ahora que se tiene un homomorfismo $\psi: G\to S_X$. Entonces, para cada $g\in G, \psi(g) \in S_x$.

Definimos la función $G\times X \to X$ donde $(g,x)\mapsto g\cdot x$. Entonces $g\cdot x = \psi(g)(x)$ para toda $g\in G, x\in X$. Además, $\psi(g)(x) \in X$.

Ahora veamos que esta función es una acción. La primera condición para ser acción se cumple de la siguiente manera:

Como $\psi$ es un homomorfismo, $\psi(e) = \text{id}_X$. Así,
\begin{align*}
e\cdot x& = \psi(e)(x) = \text{id}_X(x) = x &\forall x\in X
\end{align*}

Probemos la segunda condición de acción:

\begin{align*}
g\cdot (h\cdot x) &= \psi(g) (\psi(h)(x)) = \psi(g)\circ \psi(h)(x) \\
&= \psi(gh)(x) = (gh) \cdot x & \psi\text{ es un homomorfismo}.
\end{align*}
Para todas $g,h\in G, x\in X$. Así $G$ actúa en $X$.

$\blacksquare$

Una relación de equivalencia

Si tenemos un grupo $G$ actuando sobre un conjunto $X$, entonces podemos considerar $g\in G$ y $x,y\in X$. Con los dos elementos $x,y$ de $X$, podemos preguntarnos ¿es posible llegar de $x$ a $y$ usando a $g$?, algo como $y = g\cdot x$. En realidad esto no es siempre posible, entonces podemos crear una relación de $x$ con $y$ si existe tal $g\in G$. Esto lo veremos en el siguiente resultado.

¿Es posible llegar de $x$ a $y$ usando a $g$?

Lema. Sean $G$ un grupo, $X$ un $G$-conjunto. Para todo $x,y\in X$, la relación en $X$: $x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$ es una relación de equivalencia.

Demostración.
Sean $G$ un grupo, $X$ un $G$-conjunto. Definimos la relación en $X$ donde para todo $x,y\in X$.
\begin{align*}
x\sim y \Leftrightarrow g\cdot x = y \text{ para algún }g\in G.
\end{align*}

Primero, por la condición 1 de acción, $e\cdot x = x$ para toda $x\in X$ con $e\in G$, entonces $x\sim x$ para toda $x\in X$. Por lo que nuestra relación es reflexiva.

Si $x,y\in X$ son tales que $x\sim y$, entonces existe $g\in G$ tal que $g\cdot x = y$. Así,
\begin{align*}
g^{-1} \cdot y &= g^{-1}\cdot (g\cdot x) \\
&= (g^{-1}g)\cdot x & \text{por condición } 2\\
&= (e\cdot x )\\
&= x & \text{por condición } 1
\end{align*}

con $g^{-1} \in G$, entonces $y\sim x$. Por lo que tenemos una relación simétrica.

Si $x,y,z\in X$ son tales que $x\sim y$ y $y\sim z$, entonces existen $g,h\in G$ tales que $g\cdot x = y$, $h\cdot y = z$. Así
\begin{align*}
(hg)\cdot x &= h\cdot (g\cdot x) &\text{condición } 2\\
&= h \cdot y = z
\end{align*}
con $hg\in G$. Entonces $x\sim z$. Así, nuestra relación es transitiva.

Por lo tanto $\sim$ es una relación de equivalencia.

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. En los siguientes incisos determina si la función dad es una acción de $G$ en $X$:
    • Considera un campo $K$ y $V$ un $K$-espacio vectorial. Sea $G= K^*$ con el producto y $X= V$. Definimos $\lambda\cdot v = \lambda v$ para cada $\lambda\in K^*$ y $v\in V$. (Nota que $K^*$ es el campo sin el neutro aditivo).
    • Sea $G$ un grupo y $X=G$. Definimos $g\cdot x = g^{-1}xg$ para cada $g\in G$ y cada $x\in X$.
    • Sea $G$ un grupo y $X = \{H|H\leq G\}$. Definimos $g\cdot H = gHg^{-1}$ para cada $g\in G$ y cada $H\in X$.
    • Sea $G$ un grupo y $X=N$ un subgrupo normal de $G$. Definimos $g\cdot n= gng^{-1}$ para cada $g\in G$ y cada $n\in N$.
  2. Sea $G$ un grupo y $X$ un $G$ conjunto. Considera el homomorfismo $\psi: G\to S_X$ asociado. ¿Es necesariamente $\psi$ un monomorfismo? Si lo es, pruébalo y si no, establece qué condiciones debería cumplir la acción para que lo sea.
  3. Para repasar lo que hemos visto desde el Teorema de Cayley, puedes consultar el video en inglés de Mathemaniac.

Más adelante…

Hemos expandido la idea de que un grupo puede mover a los elementos de otro hasta llamarlo una acción. Luego, encontramos una relación de equivalencia a partir de la acción. Como es usual en este tipo de cursos, estudiaremos la partición inducida por esta relación de equivalencia y a partir de estos conjuntos, definiremos otros tipos de acciones.

Entradas relacionadas

Álgebra Moderna I: Una modificación al Teorema de Cayley

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior aprendimos que el Teorema de Cayley es muy útil porque nos permite visualizar a un grupo $G$ como un subgrupo del grupo de permutaciones. Si el grupo es de orden $n$, se puede visualizar como un subgrupo del grupo $S_n$ que tiene orden $n!$, entonces hemos visualizado a $G$ como parte de un grupo de permutaciones $S_n$ que es realmente mucho más grande que $G$. Lo que haremos en esta entrada es relacionar al grupo $G$ con un grupo simétrico pero más pequeño que $S_n$. Utilizaremos los elementos de $G$ no para mover sus propios elementos, si no, para mover clases laterales.

Después de probar este resultado, veremos una aplicación de esta modificación del Teorema de Cayley para trabajar con clase laterales. Esta aplicación generaliza el resultado que se probó para grupos normales, anteriormente establecimos que todo subgrupo de índice 2 es un subgrupo normal. Probaremos que si tomamos el menor primo que divide al orden de un grupo y tenemos un subgrupo ese índice, entonces este subgrupo tiene que ser normal.

Para esta entrada, es recomendable que repases los grupos de permutaciones.

Relacionemos a $G$ con un grupo simétrico más pequeño

En el siguiente teorema relaciona a $G$ con un grupo simétrico, pero en este caso $n$ no es el orden de $G$, si no el índice de $G$ con respecto a un subgrupo $H$.

Teorema. Sea $G$ un grupo, $H$ subgrupo de $G$ de índice finito, $[ G:H ] = n.$
Existe un homomorfismo $\phi: G \to S_n$ con $\text{Núc }\phi \leq H$.

Observemos que el Teorema de Cayley nos da un isomorfismo y este teorema sólo nos da un homomorfismo (no necesariamente inyectivo). De todas maneras, se puede usar este teorema para probar otros resultados.

Demostración.

Sea $G$ un grupo, $H\leq G$ de índice finito, digamos $[ G:H ] = n$. Para cada $a \in G$ definimos $\tau_a : G/H \to G/H$ con $\tau_a(gH) = agH$ para toda $g\in G$.

Para esta demostración, como $H$ no es necesariamente normal, $G/N$ no es un grupo. Sólo lo estamos pensando como la colección de todas las clases laterales de $G$ con respecto a $H$.

Dada $g\in G$,
\begin{align*}
\tau_a \circ \tau_{a^{-1}} (gH) &= \tau_a(\tau_{a^{-1}}(gH)) = a(a^{-1}g)H = gH\\
\tau_{a^{-1}} \circ \tau_a (gH)&= \tau_{a^{-1}} (\tau_a(gH)) = a^{-1}(ag)H = gH.
\end{align*}

Así, $\tau_{a^{-1}}$ es la inversa de $\tau_a$ y $\tau_a$ es biyectiva.

Definimos entonces $\psi: G \to S_{G/H}$ con $\psi(a) = \tau_a$ para todo $a\in G$. Tomemos $a,b\in G$ y $g\in G$. A continuación demostraremos que $\psi$ es un homomorfismo:
\begin{align*}
\psi(ab) (gH) &= \tau_{ab}(gH) = (ab)gH = a(bg)H = \tau_a(\tau_b(gH))\\
&= \tau_a \circ \tau_b(gH) = \psi (a) \circ \psi(b) (gH)
\end{align*}

Observemos que las igualdades son producto exclusivamente de las definiciones de $\psi$ y de $\tau_a$. Así, $\psi(ab) = \psi(a)\circ\psi(b)$ para todo $a,b\in G$. Por lo que $\psi$ es un homomorfismo.

Ahora pasemos a la segunda parte del teorema.

Sí $a\in\text{Núc }\psi$, $\psi(a) = \text{id}_{G/N}$ y entonces, para todo $g\in G$ obtenemos,
\begin{align*}
\psi(a)(gH) = gH &\Rightarrow \tau_a(gH) = gH & \text{definición de }\psi\\
&\Rightarrow agH= gH & \text{pues } \psi(a) = \text{id}_{G/N} \\
&\Rightarrow aH = H &\text{en particular, cuando } g=e\\
&\Rightarrow a \in H.
\end{align*}

Por lo tanto $\text{Núc }\psi \leq H$.

Como $\#G/N = n$, sabemos que $S_{G/N}\cong S_n$ y existe $\rho: S_{G/H}\to S_n$ un isomorfismo. Así $\rho\circ\psi: G\to S_n$ es el homomorfismo buscado.

$\blacksquare$

Observación. Si $H = \{e\}$ se tienen el Teorema de Cayley.

Ilustremos lo aprendido

Veamos un ejemplo.

Ejemplo. Tomemos el grupo simétrico $G = S_3$, el subgrupo $H = \left<(1,2)\right>$ y el cociente $G/H = \{H, (1\;3)H, (2\;3)H\}$.

Retomemos la función de la demostración: $\psi: S_3 \to S_{G/H}$, $\psi(a) = \tau_a$ para toda $a \in S_3$. Entonces,

\begin{align*}
a \in \text{Núc }\psi &\Leftrightarrow \psi(a) = \text{id}_{G/N} \\ &\Leftrightarrow \tau_a(gH) = gH \;\; \forall g\in S_3\\
&\Leftrightarrow agH = gH \;\; \forall g\in S_3.
\end{align*}

Así, en este caso si $a\in \text{Núc }\psi$,
\begin{align*}
a(1\;3)H = (1\;3)H &\Rightarrow (1\;3) a (1\;3) \in H = \{(1), (1\;2)\}.
\end{align*}
Recordemos que dos clases laterales $aH, bH$ son iguales si y sólo si $b^{-1}ab\in H$. En este caso, el inverso de $(1\;3)$ es él mismo.
\begin{align*}
&\Rightarrow a = (1) \text{ ó } a = (1\; 3) (1\; 2)(1\;3) = (3\;2).
\end{align*}

Sin embargo, como $a\in\text{Núc }\psi$, no sólo deja fijo a $(1\;3)$, si no también a $(2\;3)$, siguiendo un razonamiento similar obtenemos:
\begin{align*}
a(2\;3)H = (2\; 3)H &\Rightarrow (2\; 3)a(2\; 3) \in H = \{(1), (1\;2)\}\\
&\Rightarrow a = (1) \text{ ó } a = (2\; 3) (1\; 2) (2\; 3) = (1\; 3).
\end{align*}

Entonces, por un lado tenemos que $a = (1) \text{ ó } a = (3\;2)$ y por el otro, tenemos que $a = (1) \text{ ó } a = (1\; 3)$. Así, $a = (1)$.

Por lo tanto, $\text{Núc }\psi = \{(1)\}\leq H.$

Aplicación de la modificación

A continuación veremos la aplicación de la modificación del Teorema de Cayley que mencionamos en la introducción. La aplicación consiste en una generalización de un resultado visto previamente. En entradas anteriores, vimos que todo subgrupo de índice 2 es un subgrupo normal. Ahora veremos que si hay un subgrupo de orden el menor primo que divide al orden de un grupo, este subgrupo será normal.

Corolario. Si $G$ es un grupo finito y $p\in \z^+$ es el menor primo positivo que divide al orden de $G$, entonces todo subgrupo de $G$ de índice $p$ es normal en $G$.

Demostración.

Sea $G$ un grupo finito, $|G|= n$, $p\in\z^+$ el menor primo positivo que divide a $n$.

Supongamos que $H\leq G$ con $[ G:H ] = p$. Probaremos que $H$ es normal.

Sea $\psi:G\to S_{G/H}$ con $\psi(a) = \tau_a$ para toda $a\in G$ como en el teorema anterior. Sabemos que $\text{Núc } \psi \leq H \leq G$, como secuencia del Teorema de Lagrange tenemos
\begin{align} \label{eq:orden}
[ G: \text{Núc }\psi] = [ G:H ] [ H: \text{Núc }\psi ] = p [ H:\text{Núc } \psi].
\end{align}

Por el Primer Teorema de Isomorfía, $$G/\text{Núc }\psi\cong \text{Im }\psi \leq S_{G/H}\cong S_p,$$

\begin{align*}
\Rightarrow& [ G: \text{Núc }\psi ] = \left|G/\text{Núc }\psi \right|\Big| |S_p|\\
\Rightarrow& p [ H: \text{Núc }\psi ] \Big| p! & \text{porque } |S_p| = p! \text{ y } (\ref{eq:orden})\\
\Rightarrow &[ H: \text{Núc }\psi ] \Big| (p-1)!
\end{align*}

Si $[ H: \text{Núc }\psi ] > 1$, existiría $q\in\z^+$ un primo que lo divide, entonces $q\Big| a$ con $a \in \{1,2,\dots,p-1\}$. Por lo tanto $q<p.$

Pero, por el Teorema de Lagrange, $$|G| = [ G:\text{Núc }\psi ] |\text{Núc }\psi| = [ G:H] [ H: \text{Núc }\psi] |\text{Núc }\psi|.$$ Entonces $[ H: \text{Núc }\psi] \Big| |G|.$

Y como $q| [ H : \text{Núc }\psi ]$, entonces $q\Big||G|$.

Entonces, $q$ sería un divisor primo positivo de $n$, menor que $p$. Esto es una contradicción.

Así $[ H: \text{Núc }\psi ] = 1$, de donde $|H| = |\text{Núc }\psi|$ y como $ \text{Núc }\psi \leq H$ concluimos que $H = \text{Núc }\psi \unlhd G.$

Por lo tanto $H\unlhd G$.

$\blacksquare$

Observación. No siempre existe dicho subgrupo, por ejemplo $A_4$ no tiene subgrupos de índice 2.

Esto sucede porque $A_4$ tiene 12 elementos, el menor primo que divide a 12 es 2. Pero, de acuerdo a lo que estudiamos, $A_4$ no tiene subgrupos de orden 6, entonces no existen subgrupos de índice 2.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra la observación: Si $H = \{e\}$ se tienen el Teorema de Cayley.
  2. Sea $V$ el grupo de Klein. $H = \left< (1,0) \right>$. Determina cómo son las funciones $\tau_a$ para cada $a\in V$ y describe cómo se puede visualizar a cada elemento $a\in V$ como una permutación en $\{(a,b) + H\,|\, (a,b) \in V \}$, y como una permutación en $S_2$.
  3. Dado $G$ un grupo y $H$ un subgrupo de $G$ de índice finito $n$, sabemos que existe un homomorfismo $\phi$ de $G$ en $S_n$ con $\text{Núc }\phi \leq H.$ Da una condición necesaria y suficiente para que $\text{Núc }\phi = H.$
  4. Sea $G$ un grupo finito de orden $n$ y $H$ un subgrupo de de índice primo $p$. ¿Es $H$ normal en $G$? Prueba o da un contraejemplo.

Más adelante…

Con este teorema hemos avanzado un pasito en la idea de usar elementos de un grupo para modificar otro, ahora usando clases laterales. El Teorema de Cayley y su modificación son importantes para el tema que veremos en la siguiente entrada, donde ahora sí, usaremos un grupo cualquiera para actuar sobre otro grupo cualquiera.

Entradas relacionadas