Archivo del Autor: Rubén Alexander Ocampo Arellano

Geometría Moderna I: Circunferencia de Apolonio

Por Rubén Alexander Ocampo Arellano

Introducción

En esta entrada veremos dos lugares geométricos importantes, uno es la caracterización de arco de circunferencia y el otro la circunferencia de Apolonio.

Arco de circunferencia

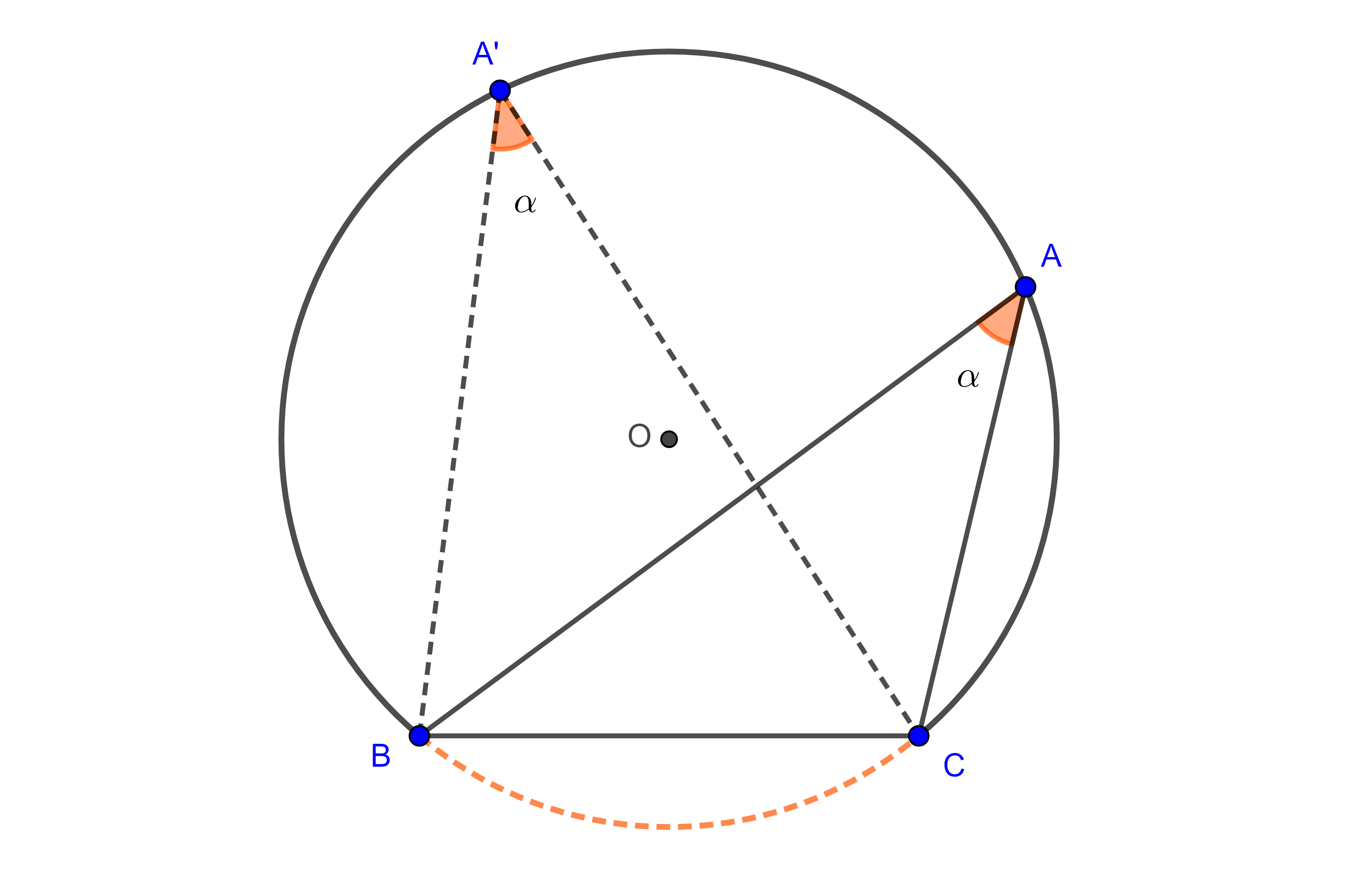
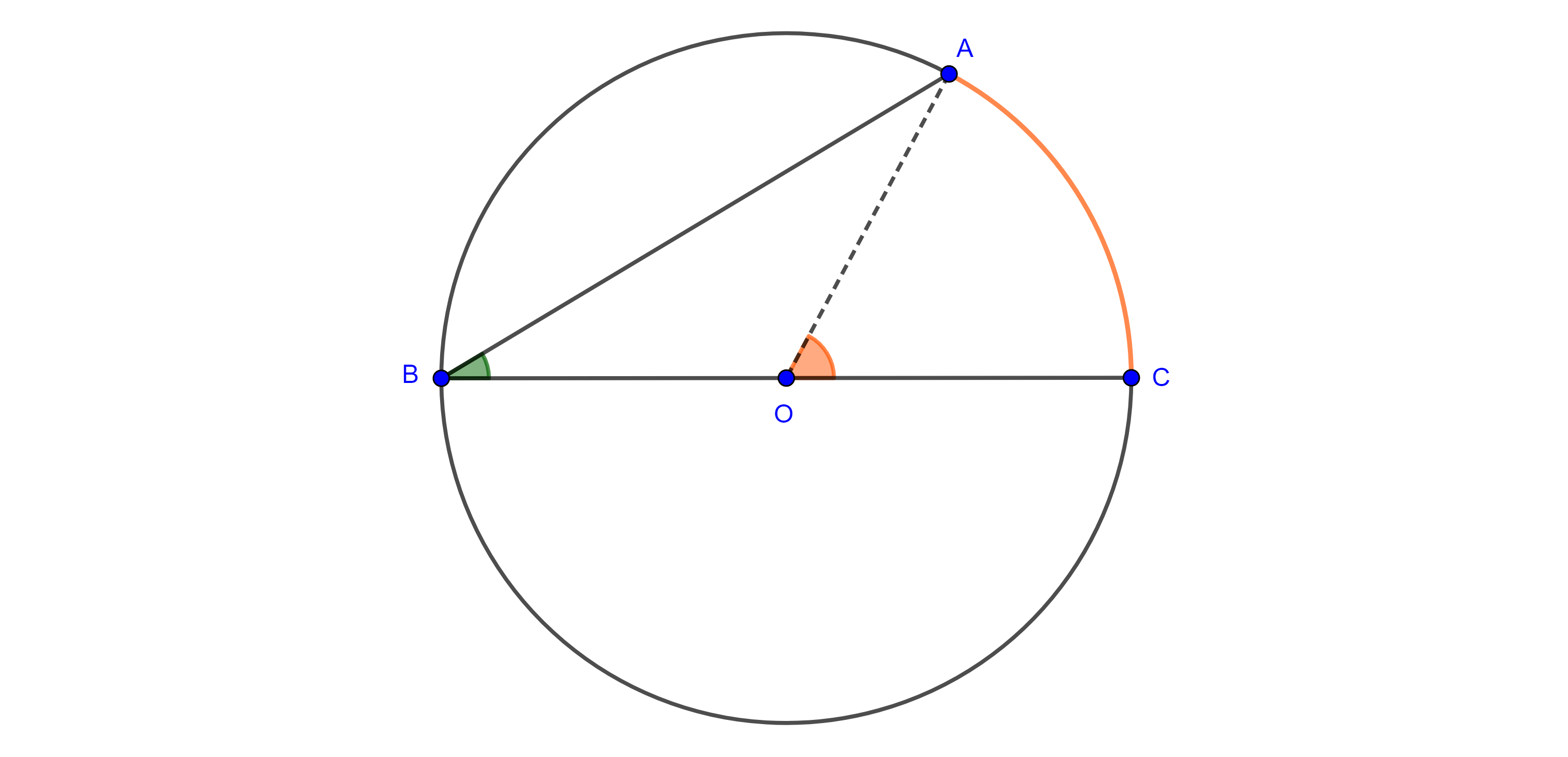
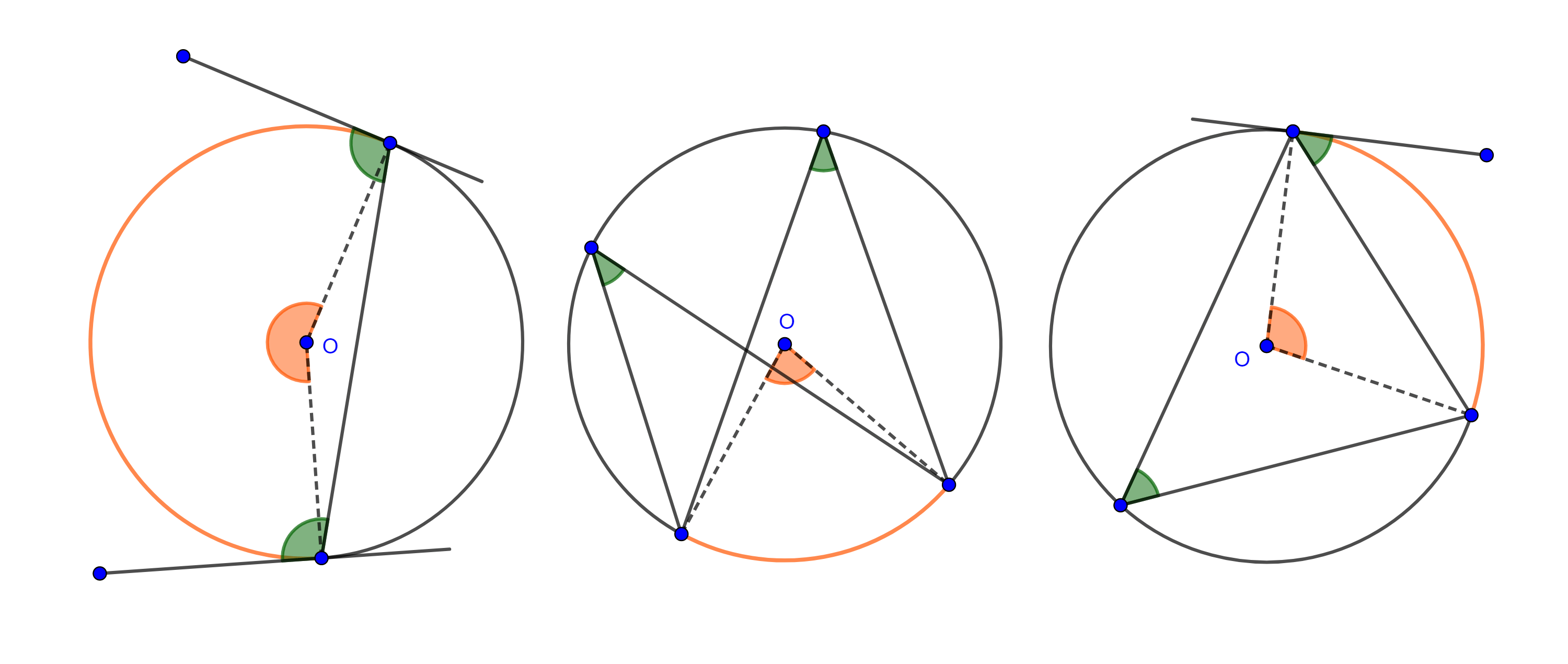
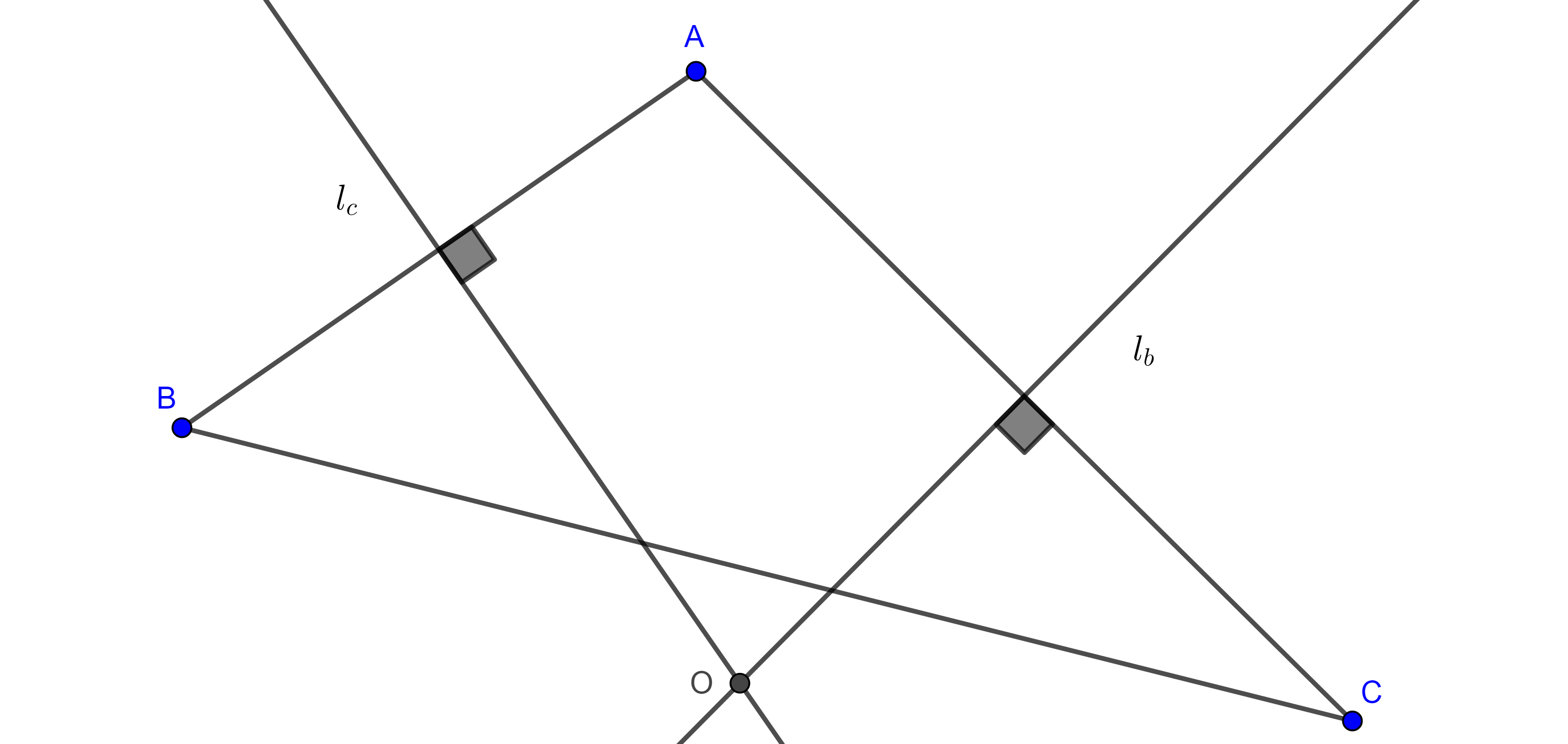
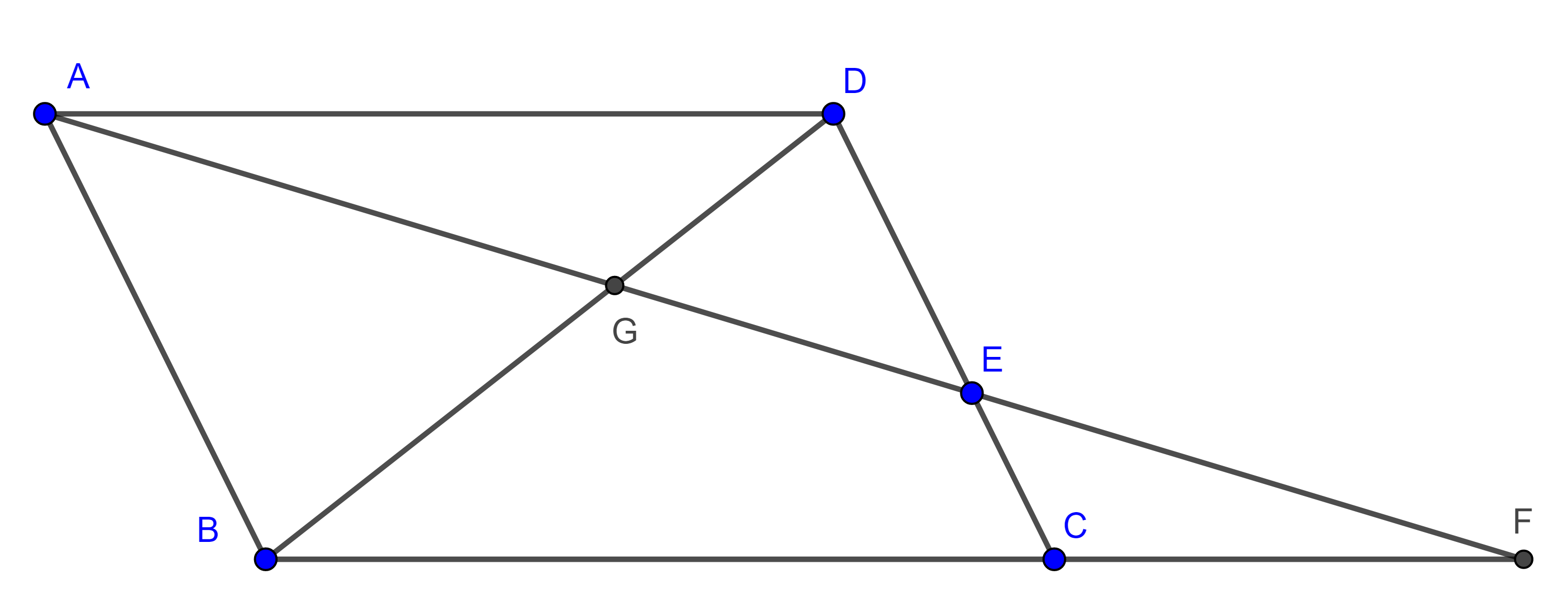
Teorema 1. Dados un segmento $BC$ y un ángulo $\alpha < \pi$ el lugar geométrico de los puntos $A$ que están sobre un mismo lado de la recta $BC$ y tal que el ángulo $\angle BAC = \alpha$, es un arco de circunferencia que pasa por $B$ y $C$.

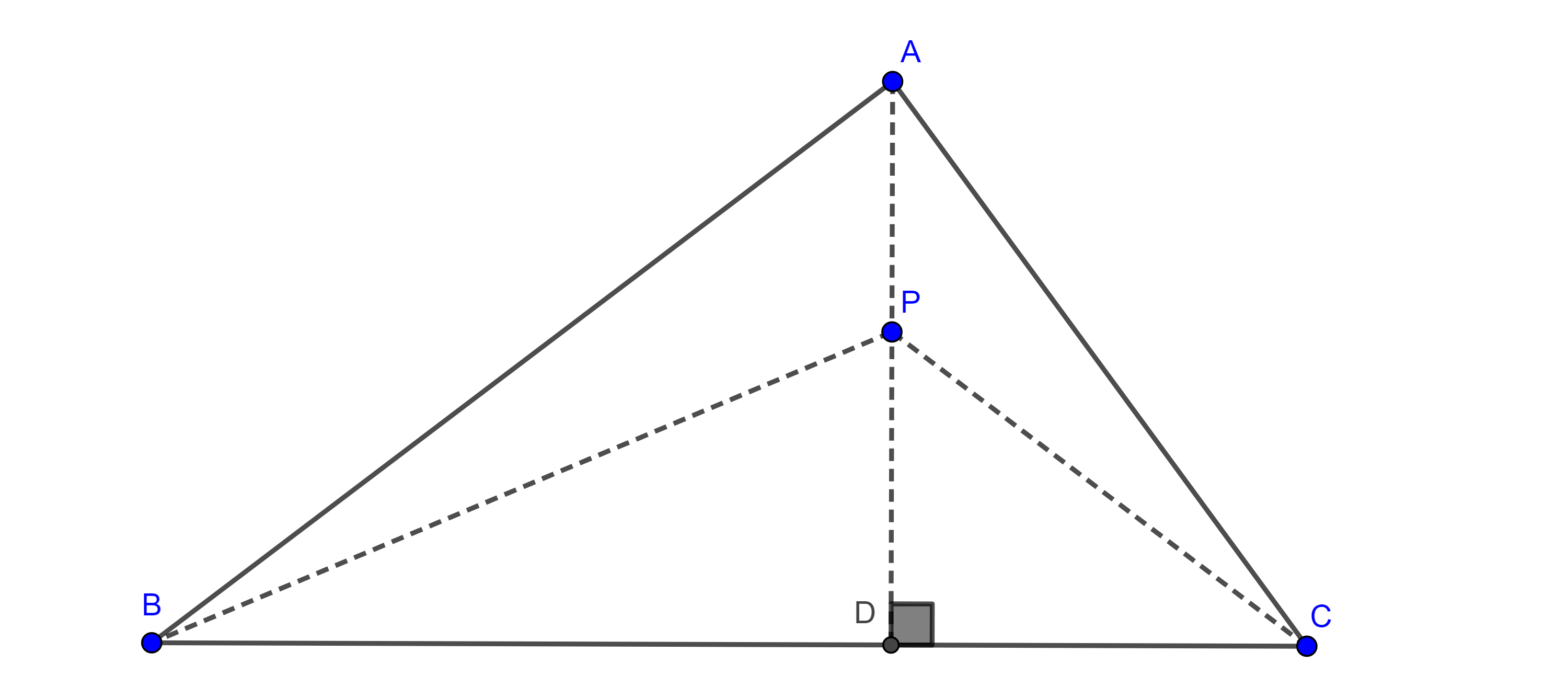
Demostración. Sea $A$ un punto tal que $\angle BAC = \alpha$, consideremos el circuncírculo $\Gamma (O)$ de $\triangle ABC$.

Todos los puntos $A’$ en el arco $\overset{\LARGE{\frown}}{CB}$ cumplen que $\angle BA’C =\alpha$ pues $\angle BAC$ y $\angle BA’C$ abarcan el mismo arco $\overset{\LARGE{\frown}}{BC}$.

Por lo tanto, el arco $\overset{\LARGE{\frown}}{CB}$ es parte del lugar geométrico.

$\blacksquare$

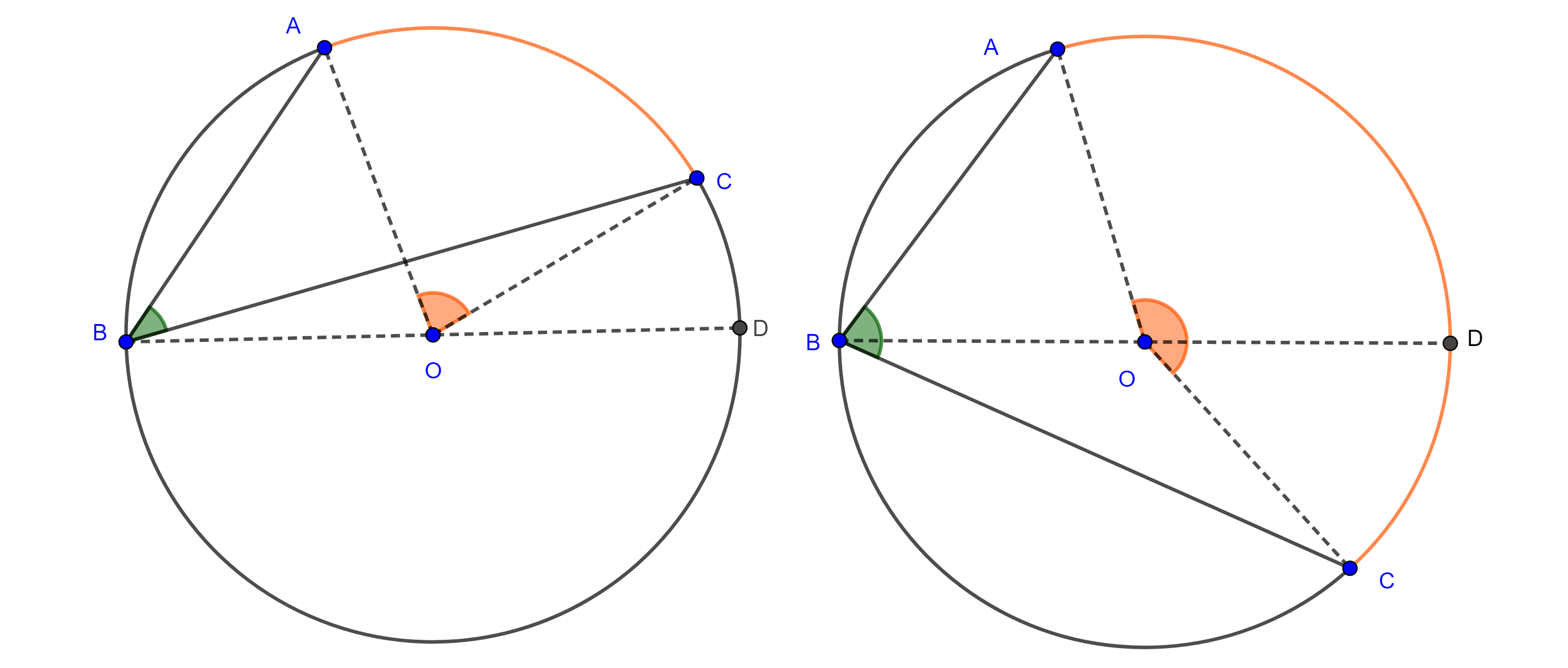
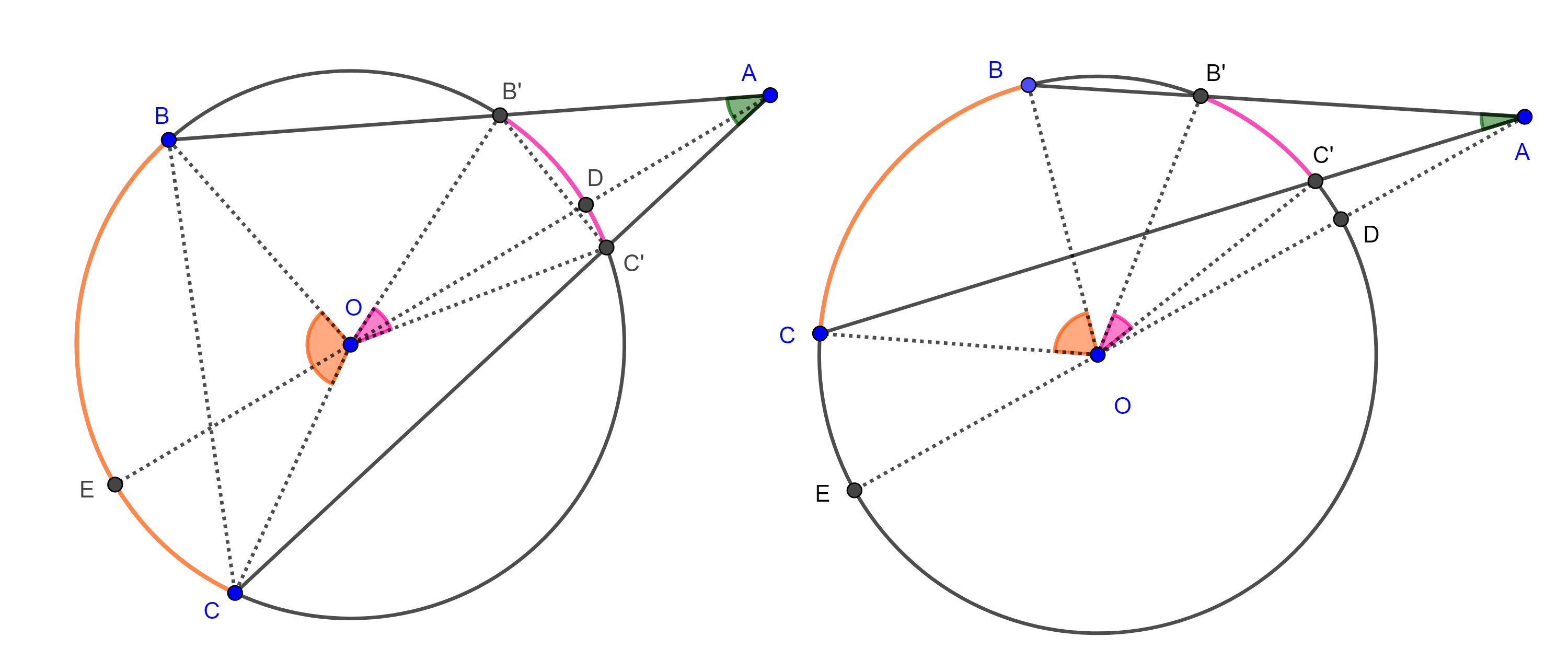
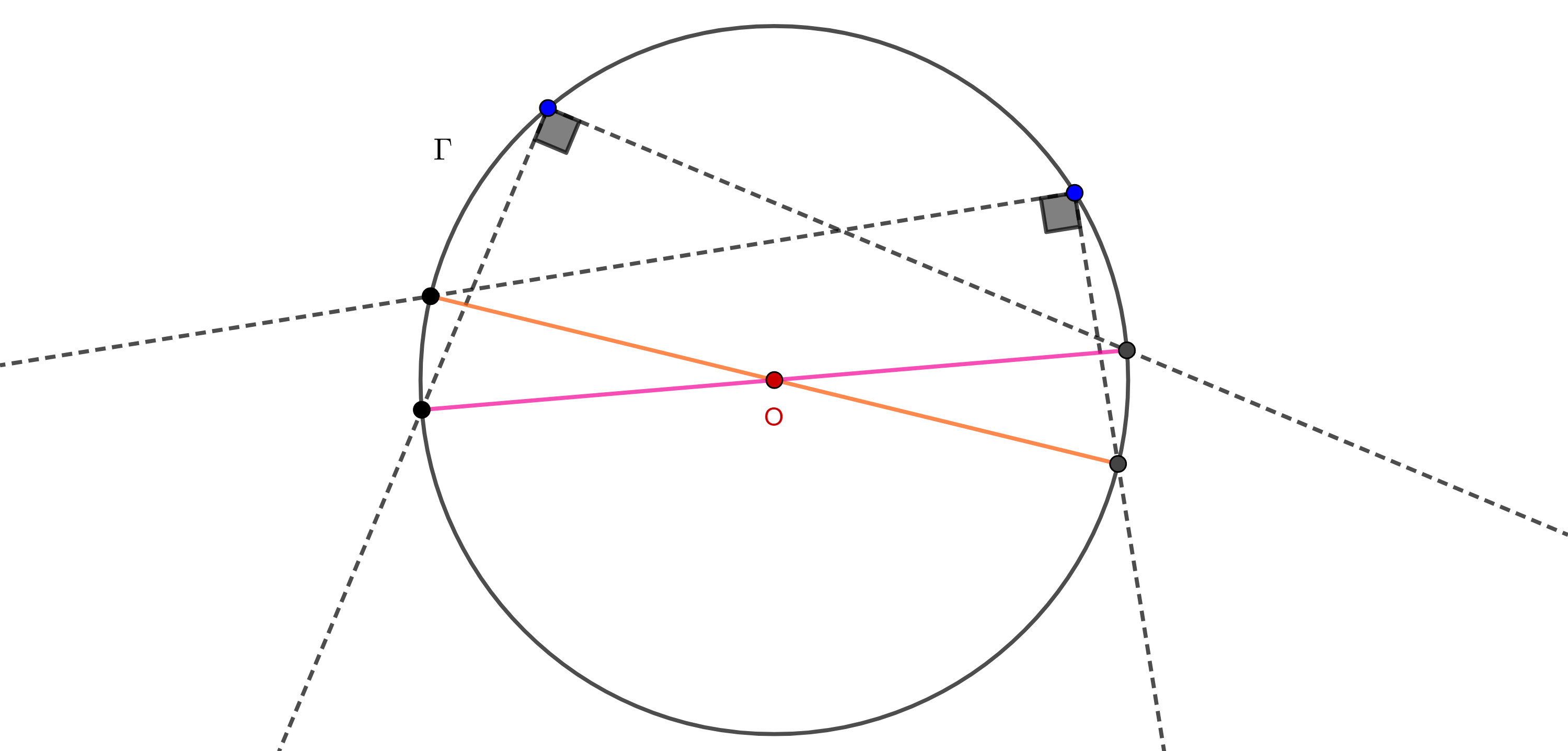
Ahora tomemos $A’$ del mismo lado que $A$ respecto de $BC$ pero $A’ \notin \overset{\LARGE{\frown}}{CB}$ y consideremos $B’ = A’B \cap \overset{\LARGE{\frown}}{CB}$ y $C’ = A’C \cap \overset{\LARGE{\frown}}{CB}$.

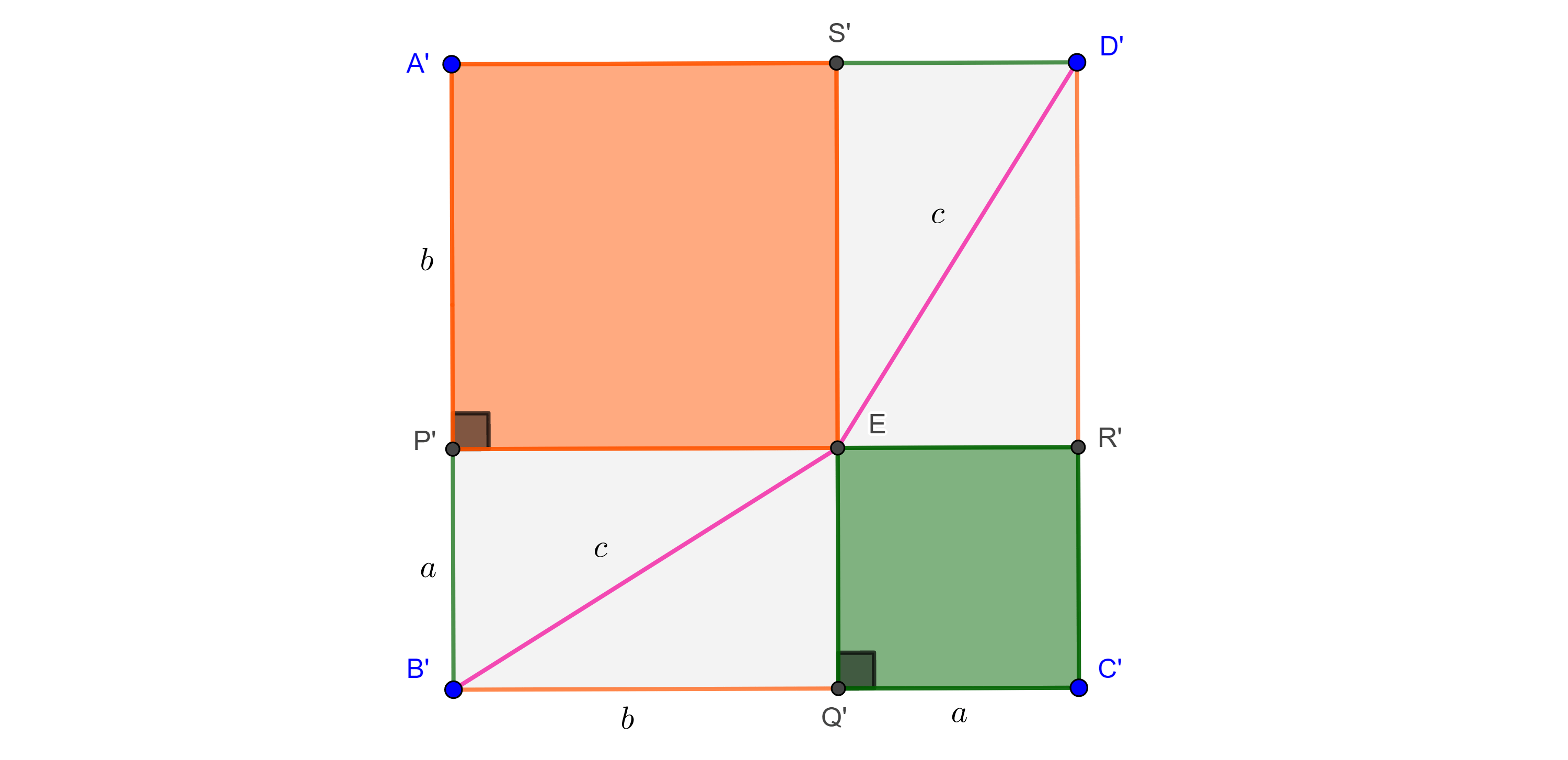
Si $A’$ está dentro del circuncírculo de $\triangle ABC$ (izquierda figura 2), entonces los teoremas de la medida del ángulo interior y el ángulo inscrito nos dicen que
$\angle BA’C = \dfrac{\angle BOC + \angle B’OC’}{2} > \dfrac{\angle BOC}{2} = \angle BAC$.

Por tanto, $A’$ no está en el lugar geométrico.

Si $A’$ esta fuera del circuncírculo de $\triangle ABC$ (derecha figura 2) , entonces la medida del ángulo exterior es
$\angle BA’C = \dfrac{\angle BOC – \angle C’OB’}{2} < \dfrac{\angle BOC}{2} = \angle BAC$.

En consecuencia no existe $A’$ en el lugar geométrico fuera del arco $\overset{\LARGE{\frown}}{CB}$ y así queda demostrado el teorema.

$\blacksquare$

Observación. Si quitamos la condición de que los puntos $A$ estén de un mismo lado respecto de $BC$ entonces obtendremos dos arcos de circunferencia que son simétricos respecto de $BC$.

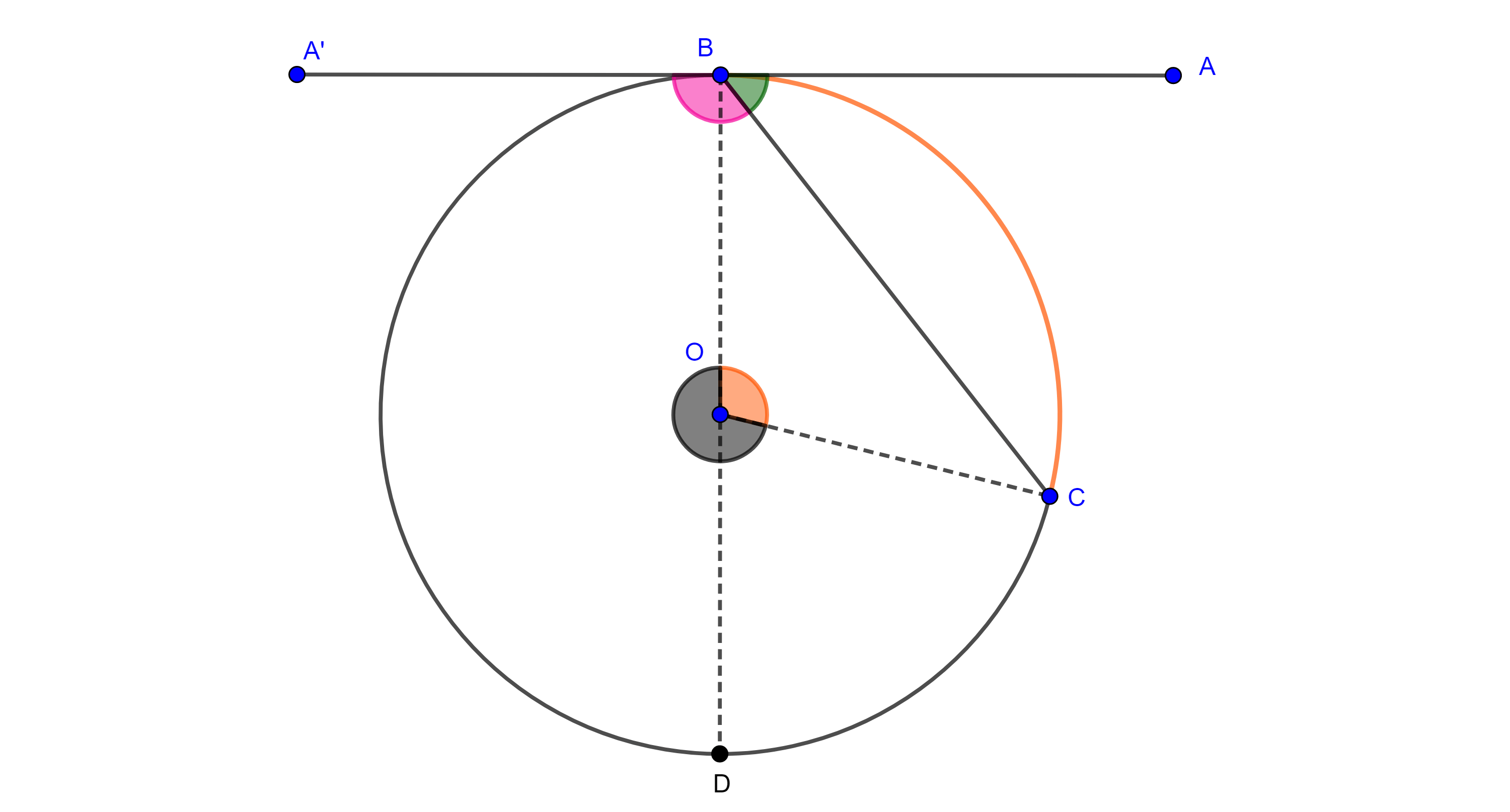
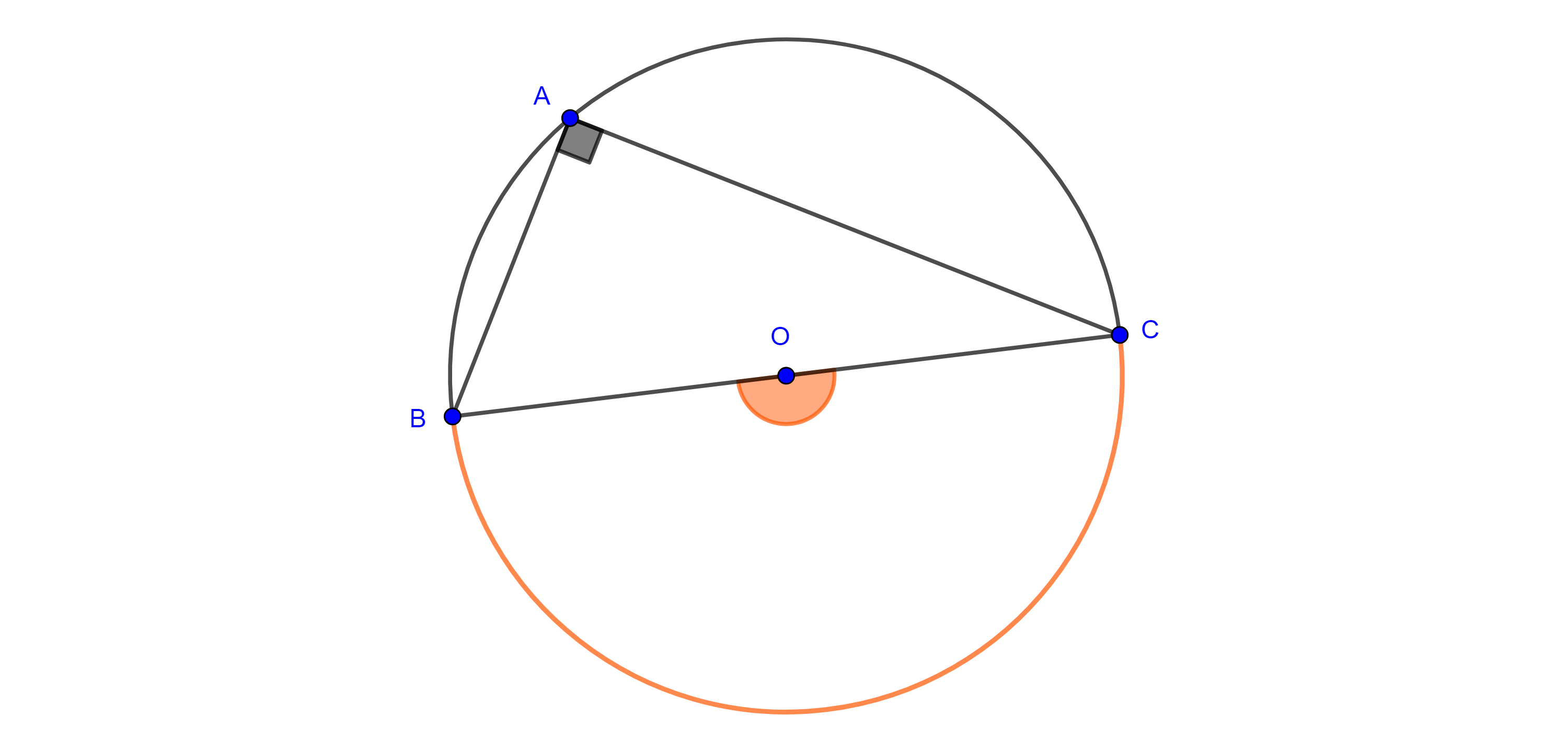
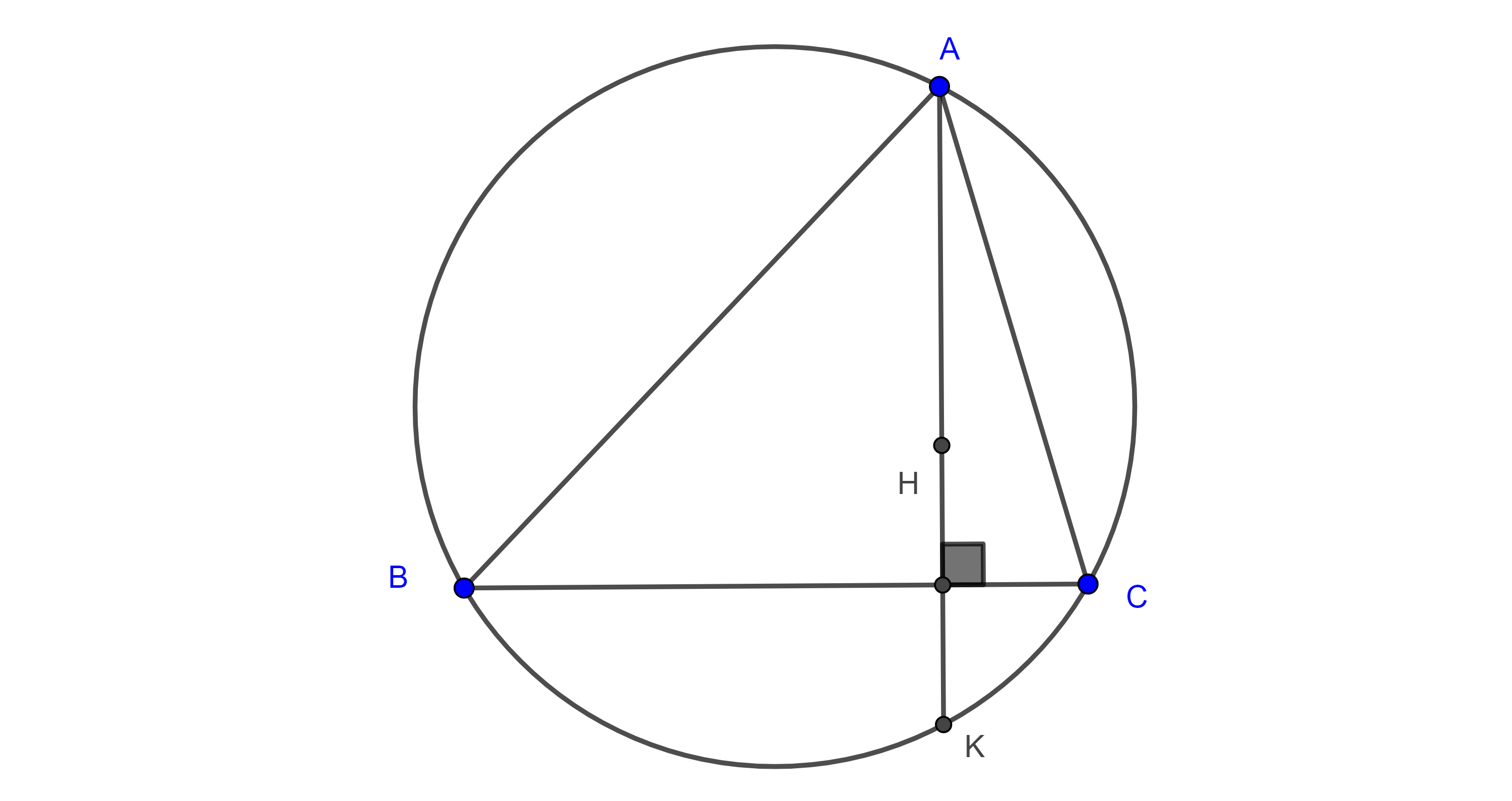
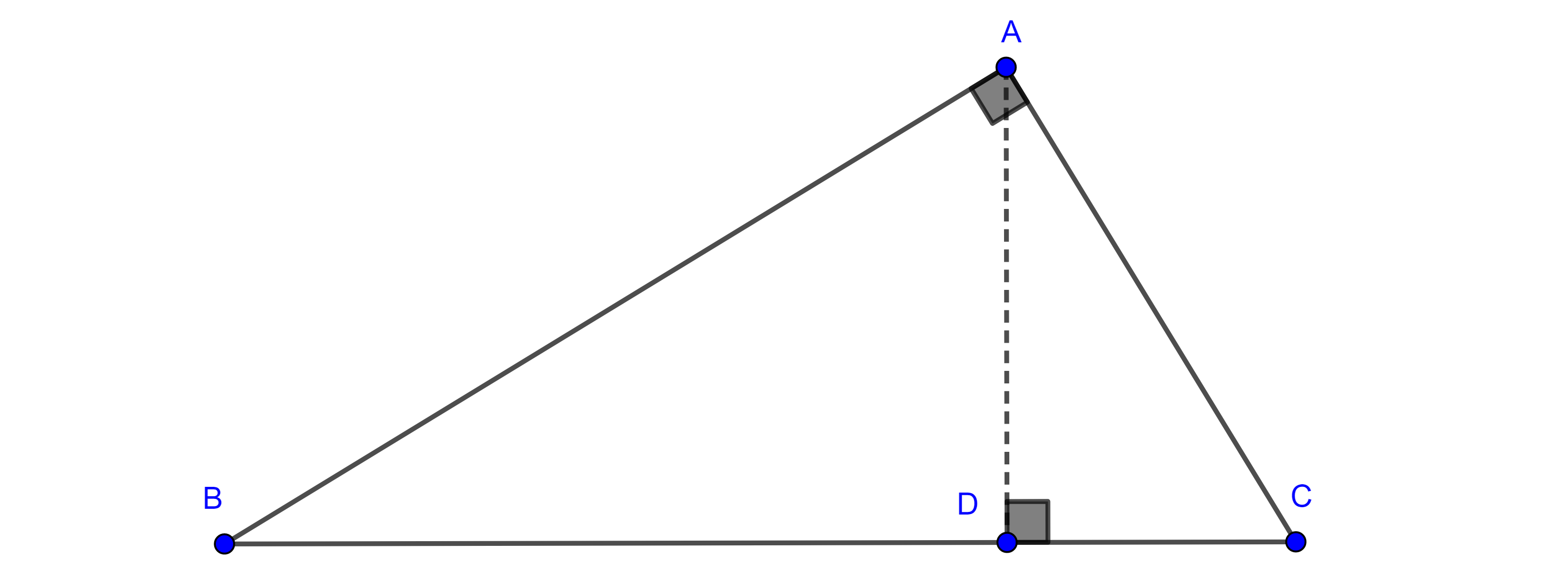
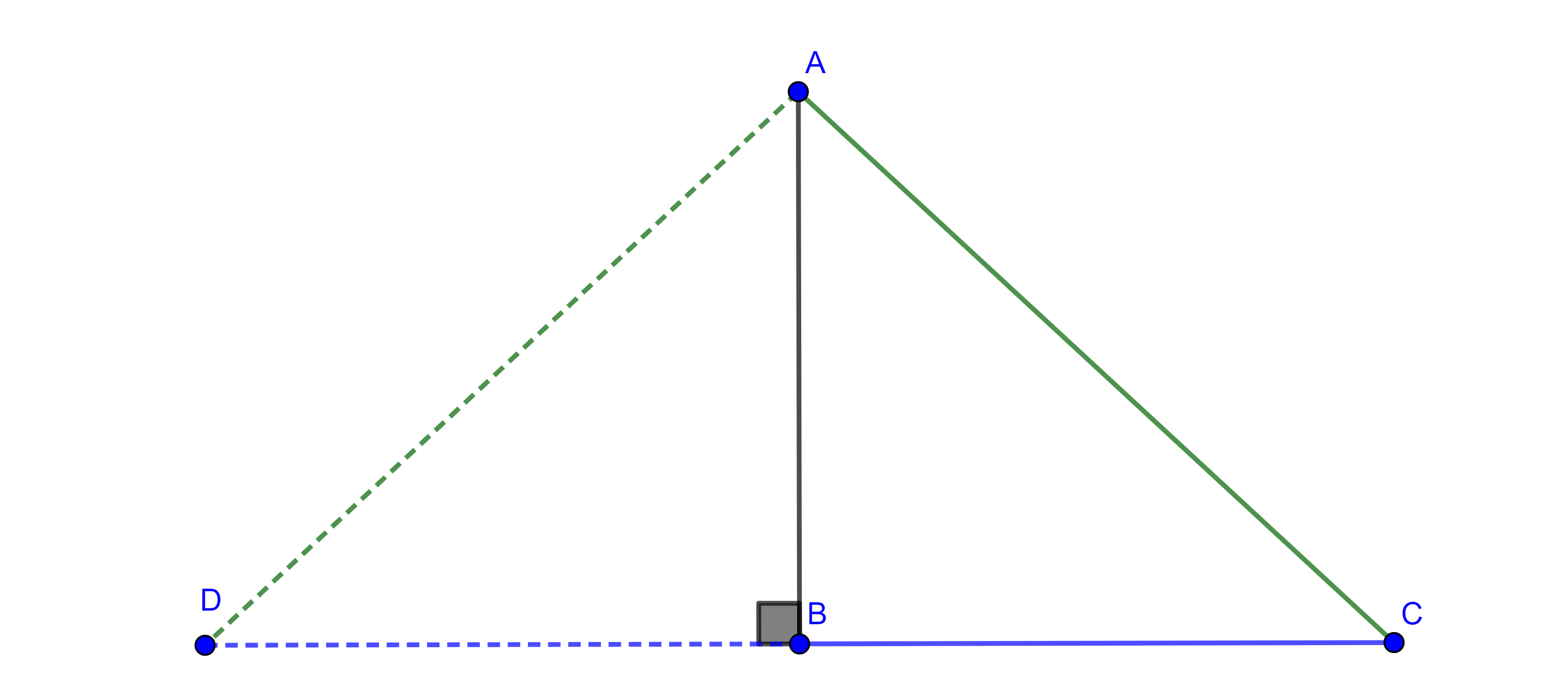
Corolario. Dados un segmento $BC$ el lugar geométrico de los puntos $A$ tal que el ángulo $\angle BAC = \dfrac{\pi}{2}$, es una circunferencia de diámetro $BC$.

Demostración. Por el teorema 1 y la observación, el lugar geométrico son dos arcos de circunferencia simétricos respecto de $BC$, además, por el teorema de Tales, $BC$ es diámetro de cada uno de estos arcos, por tanto los dos arcos forman una misma circunferencia.

$\blacksquare$

Circunferencia de Apolonio

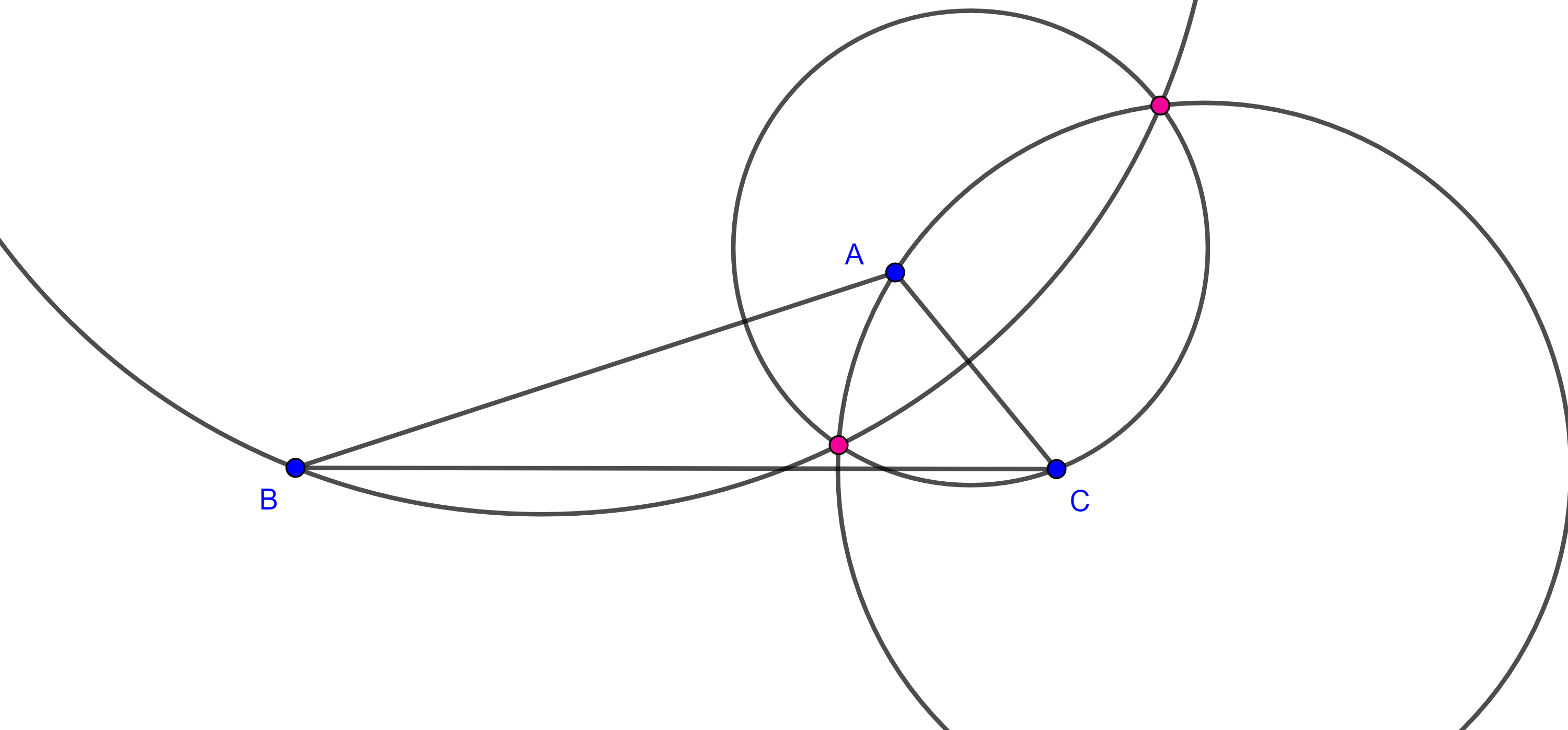
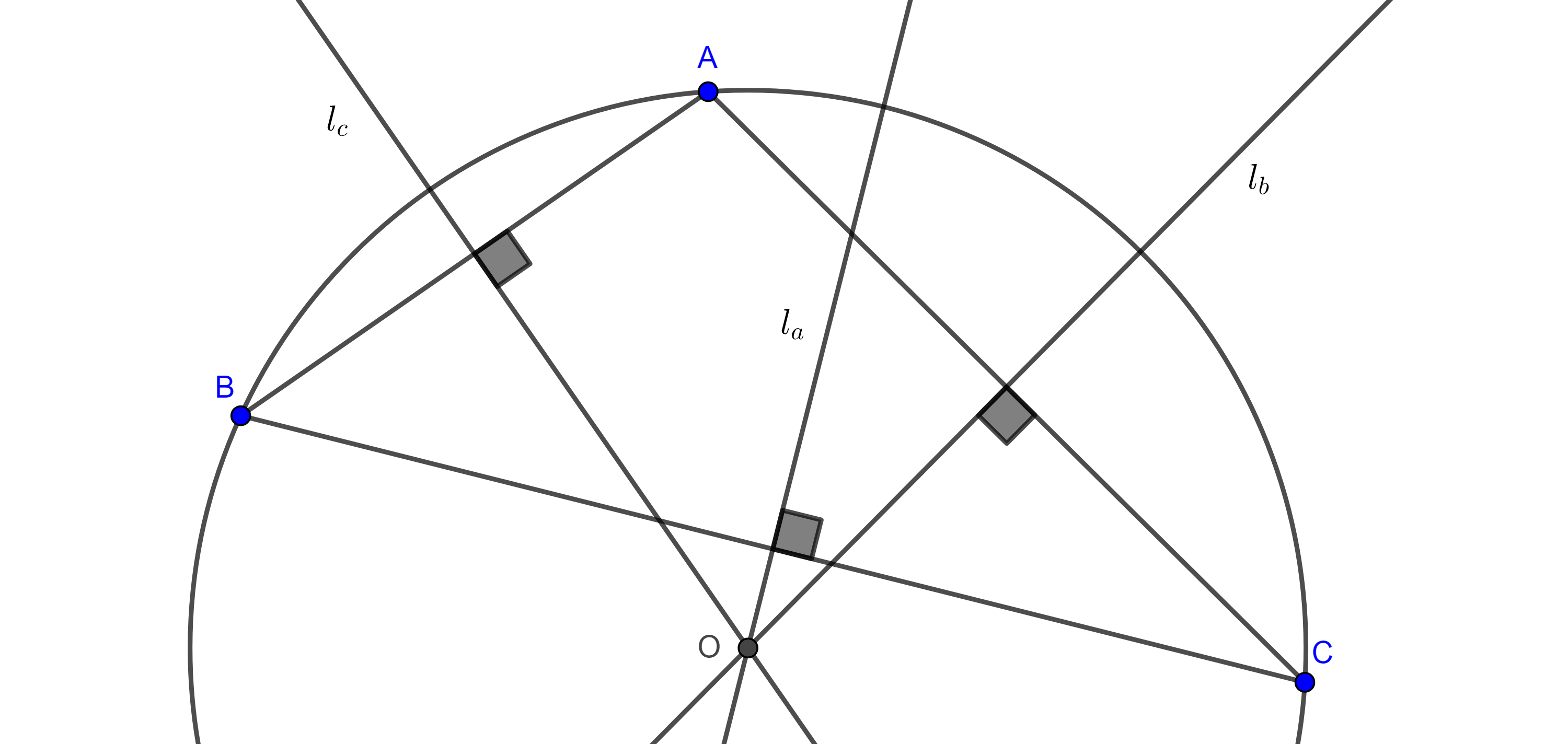
Teorema 2. El lugar geométrico de los puntos $A$ tales que la razón de las distancias a dos puntos fijos $B$ y $C$ es igual a una razón dada $\dfrac{p}{q}$, es una circunferencia llamada circunferencia de Apolonio.

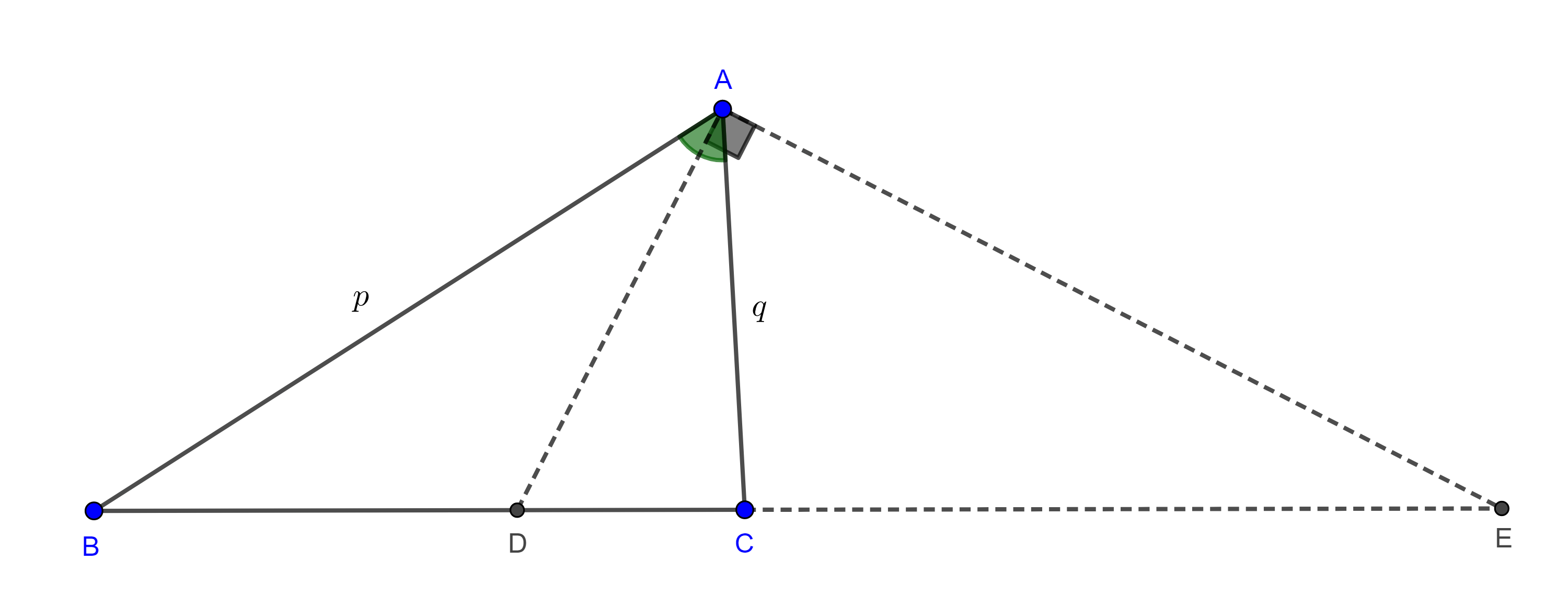
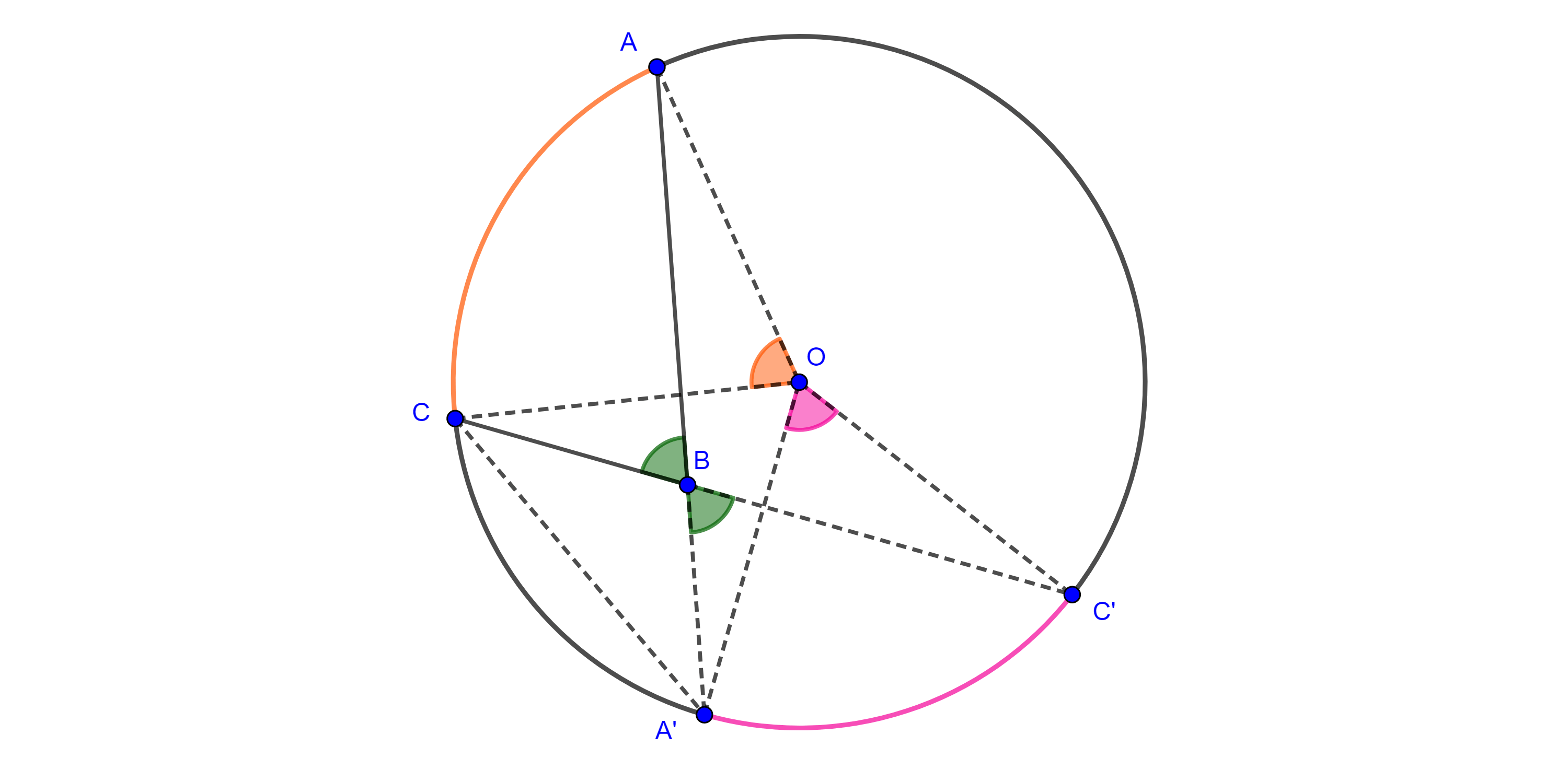
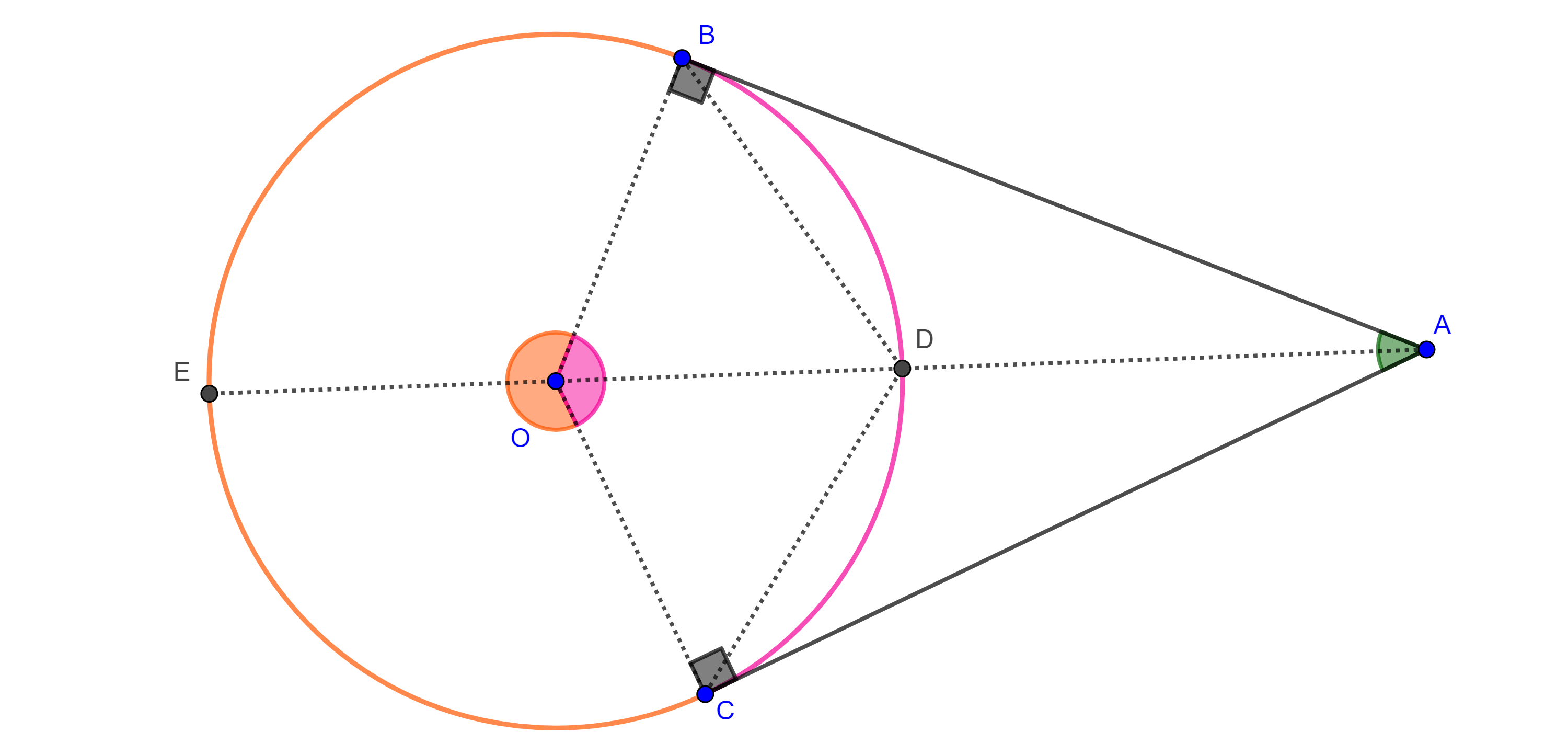
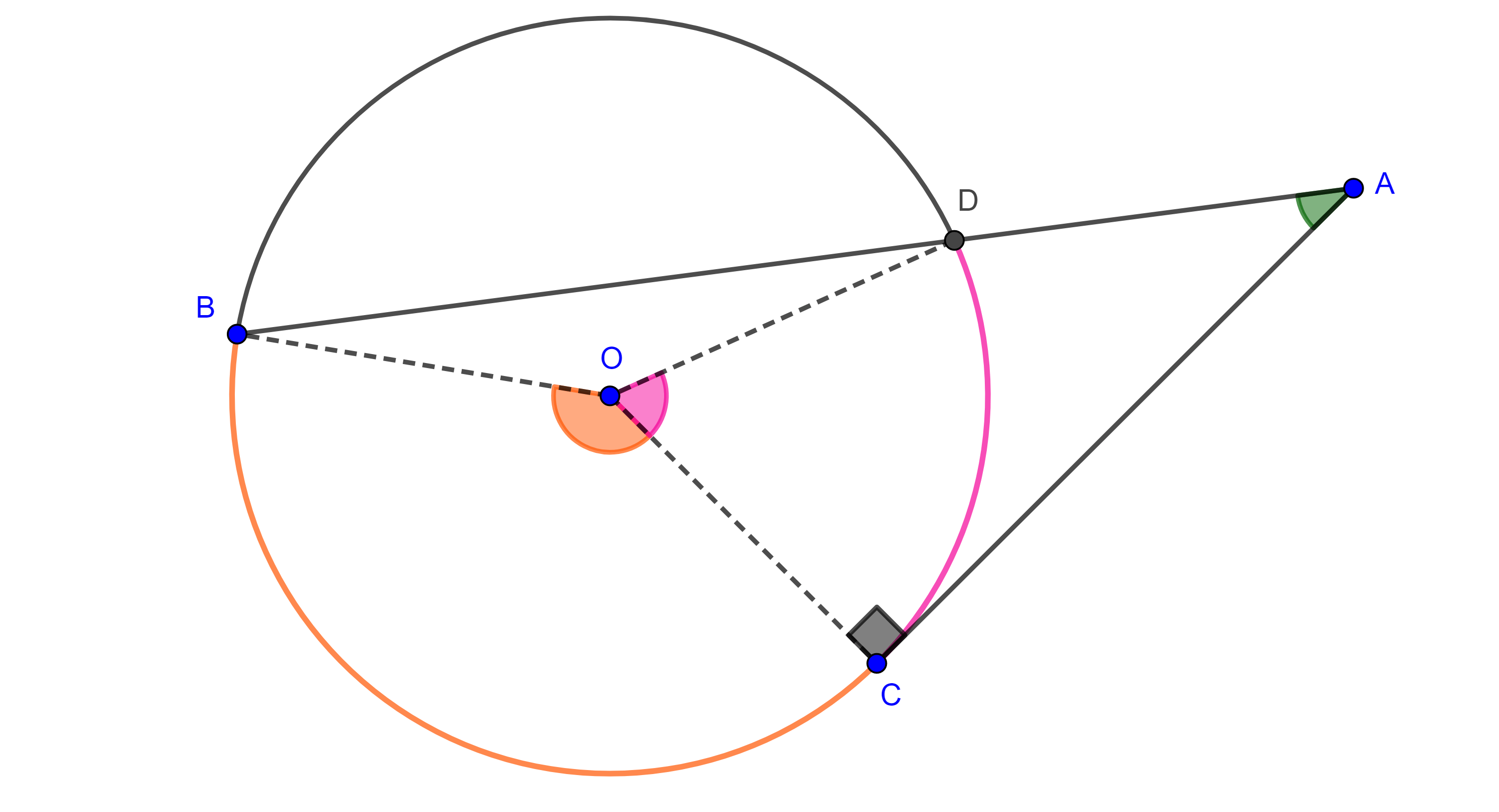
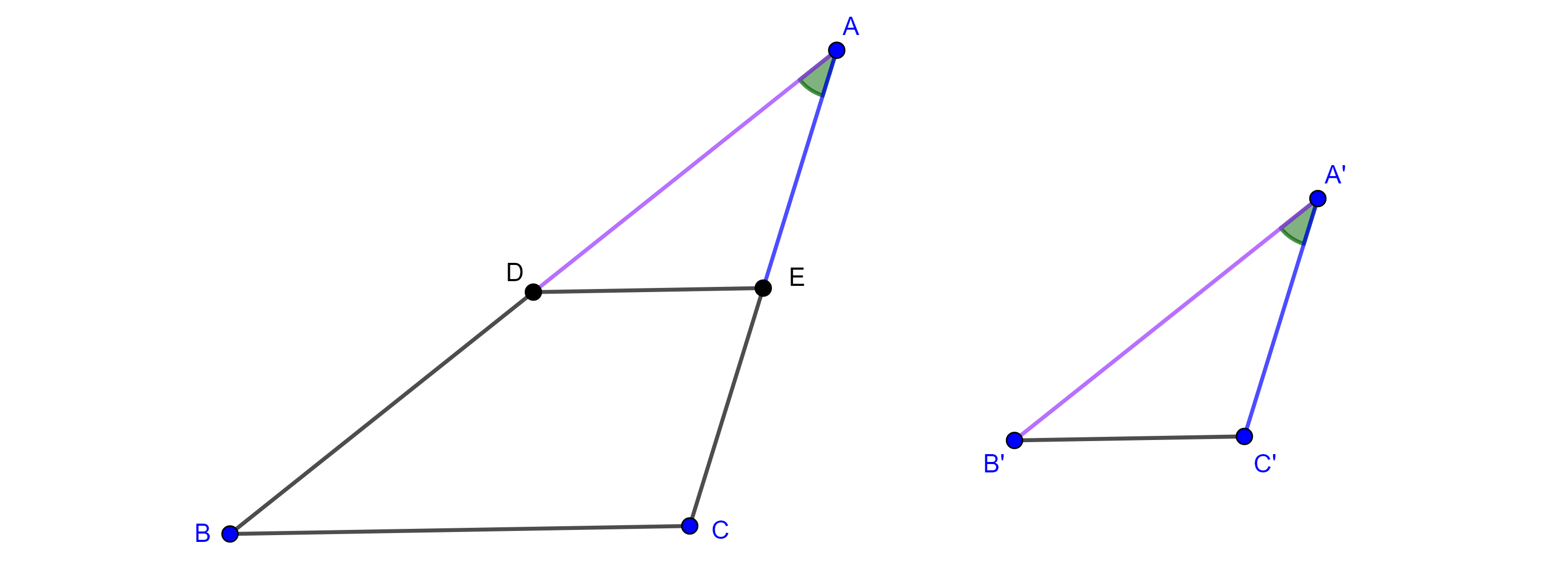
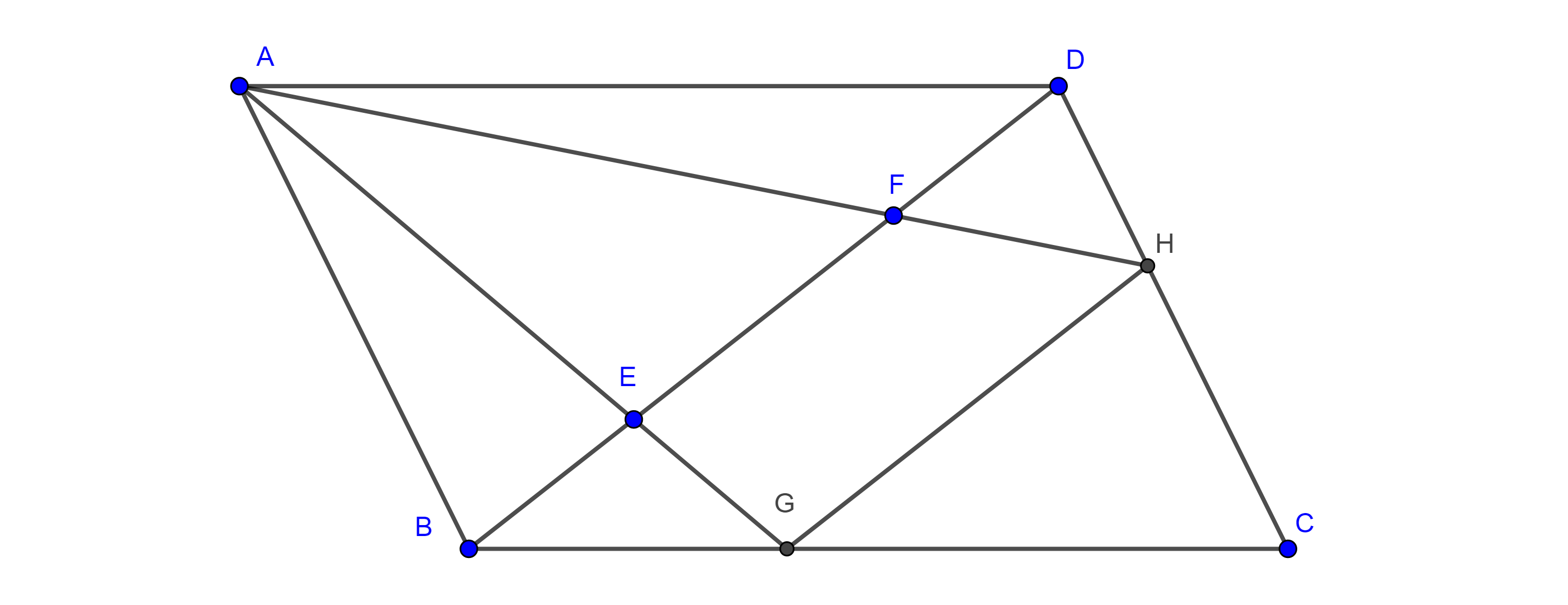
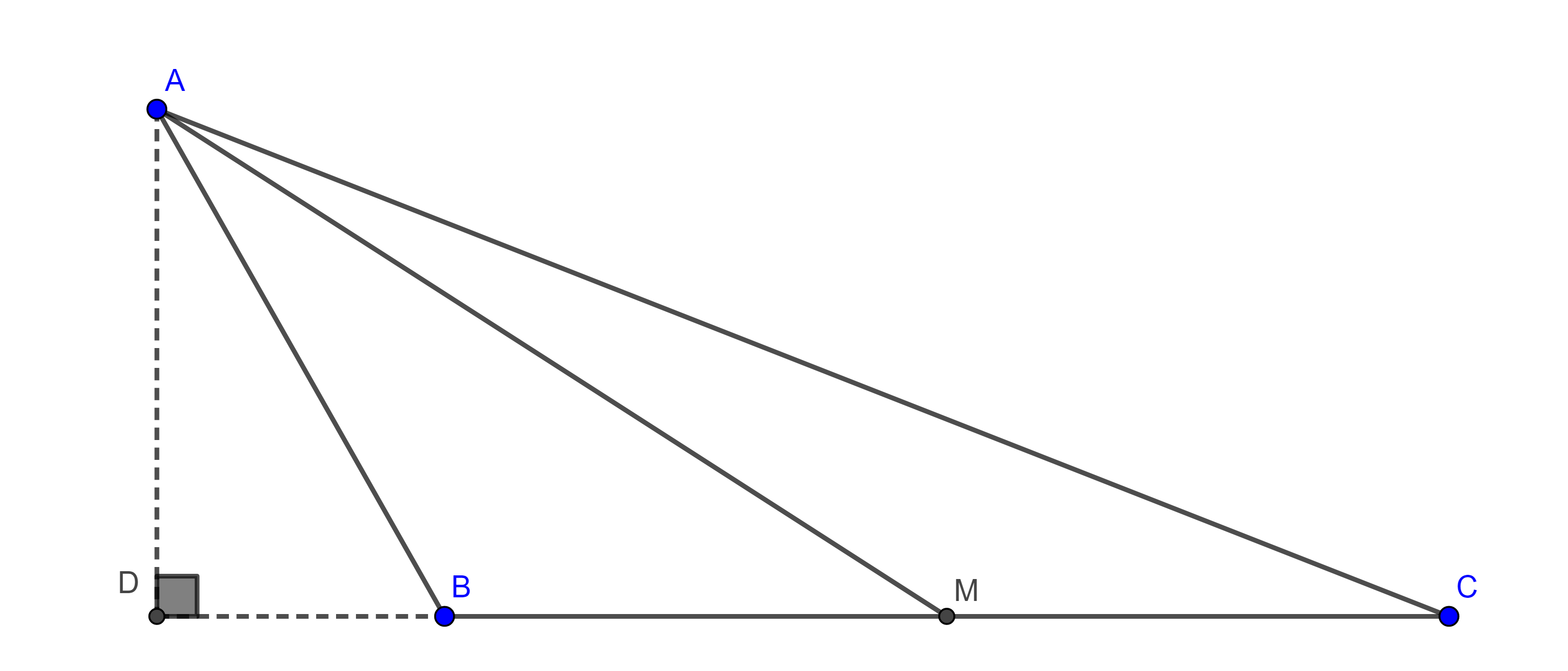
Demostración. Sea $BC = a$, construimos un triángulo de lados $p$, $q$ y $a$, si $p + q < a$ entonces tomamos un múltiplo $mp$ y $mq$ tal que $m(p + q) > a$.

Sea $A$ el vértice construido tal que $AB = p$ y $AC = q$, por el teorema de la bisectriz, las bisectrices interna $AD$ y externa $AE$ de $\angle A$ dividen al segmento $CB$ en la razón dada
$\dfrac{p}{q} = \dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.

De esta manera, hemos encontrado dos putos $D$ y $E$ en la recta $BC$ del lugar geométrico.

Sea $A’$ cualquier punto en el lugar geométrico, entonces $\dfrac{A’B}{A’C} = \dfrac{p}{q} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.

Por el reciproco del teorema de la bisectriz esto implica que las cevianas $AD$ y $AE$ son las bisectrices interna y externa del ángulo $\angle BA’C$.

Como las bisectrices interna y externa de todo ángulo son perpendiculares entre si tenemos que $\angle DA’C = \dfrac{\pi}{2}$.

Por el corolario anterior, $A’ \in \Gamma$, la circunferencia cuyo diámetro es $DE$.

$\blacksquare$

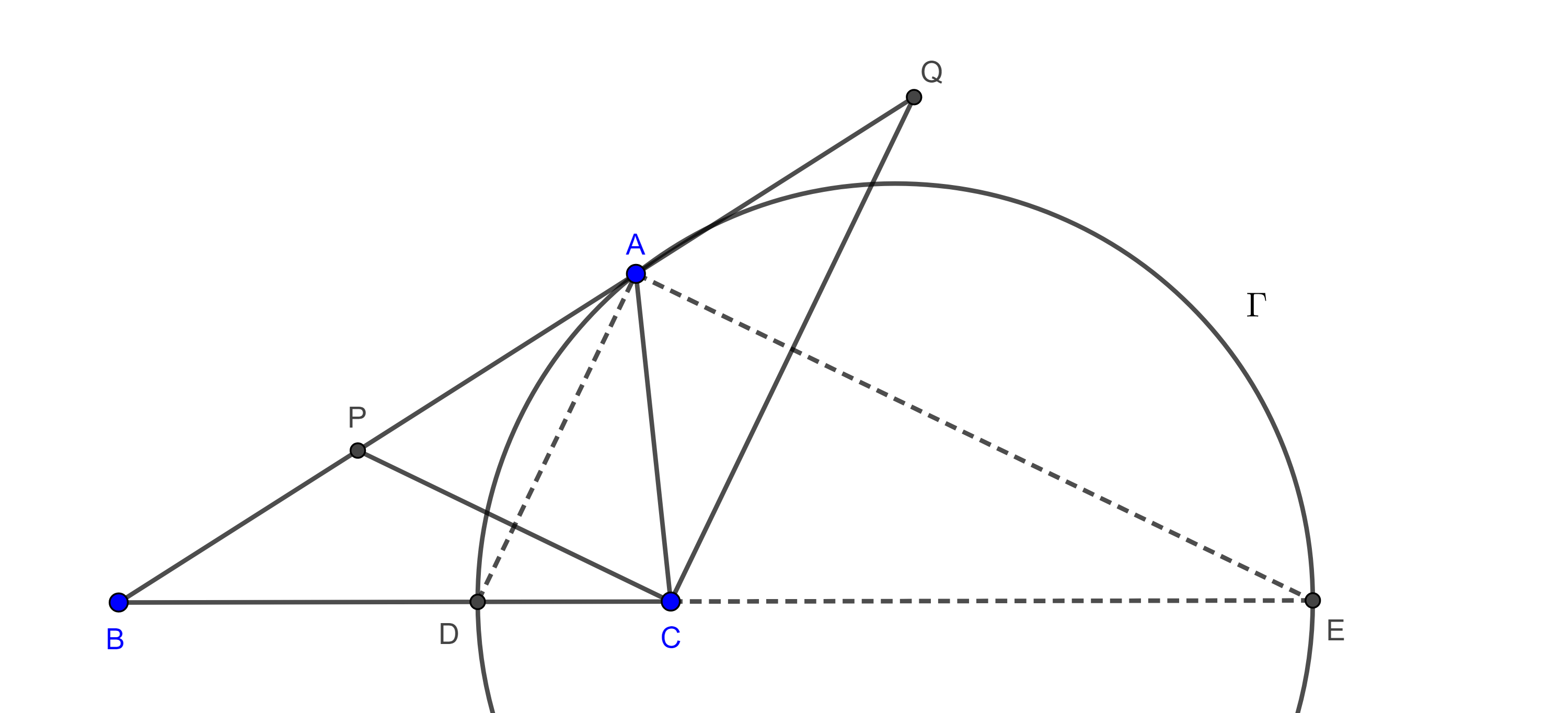
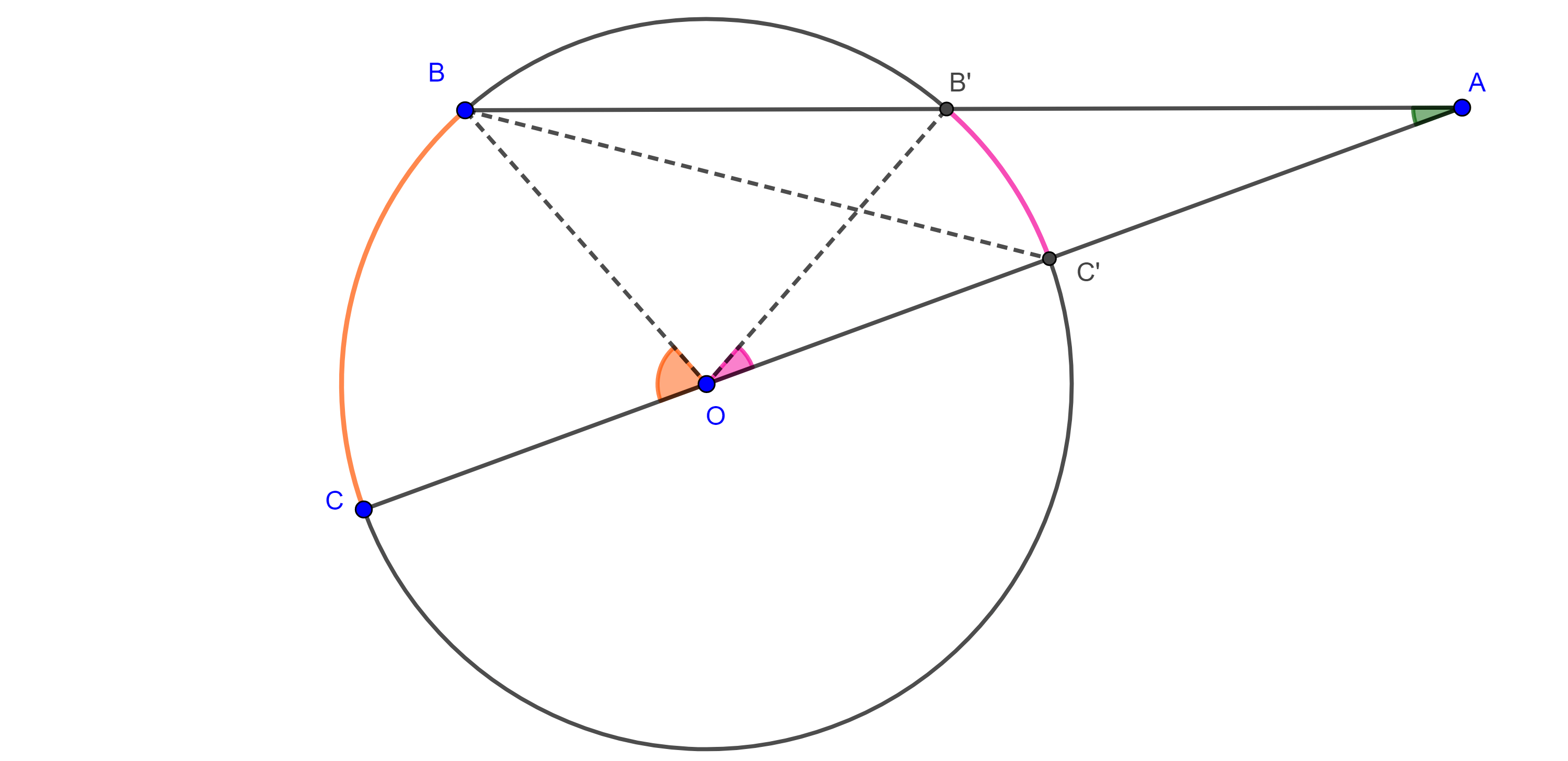
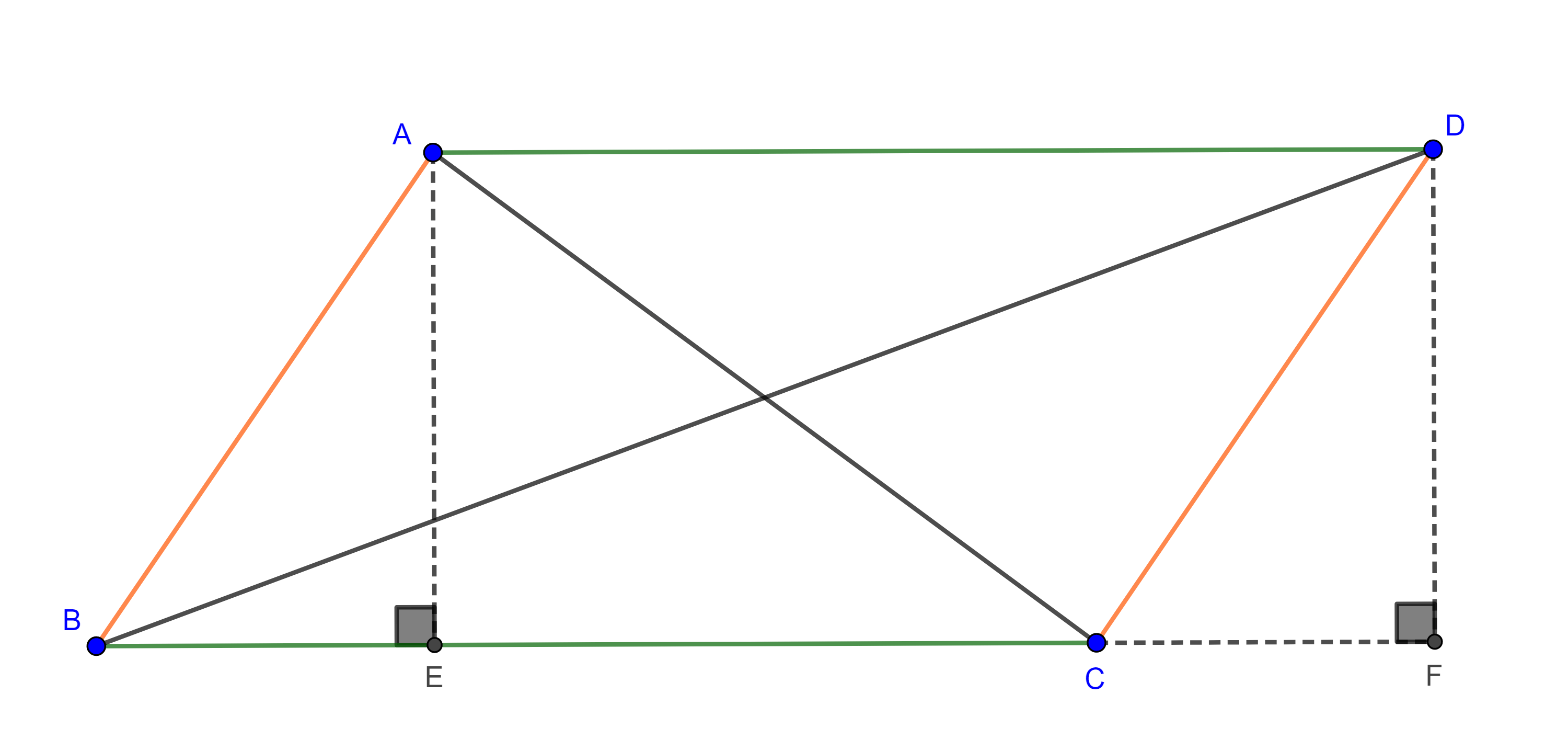
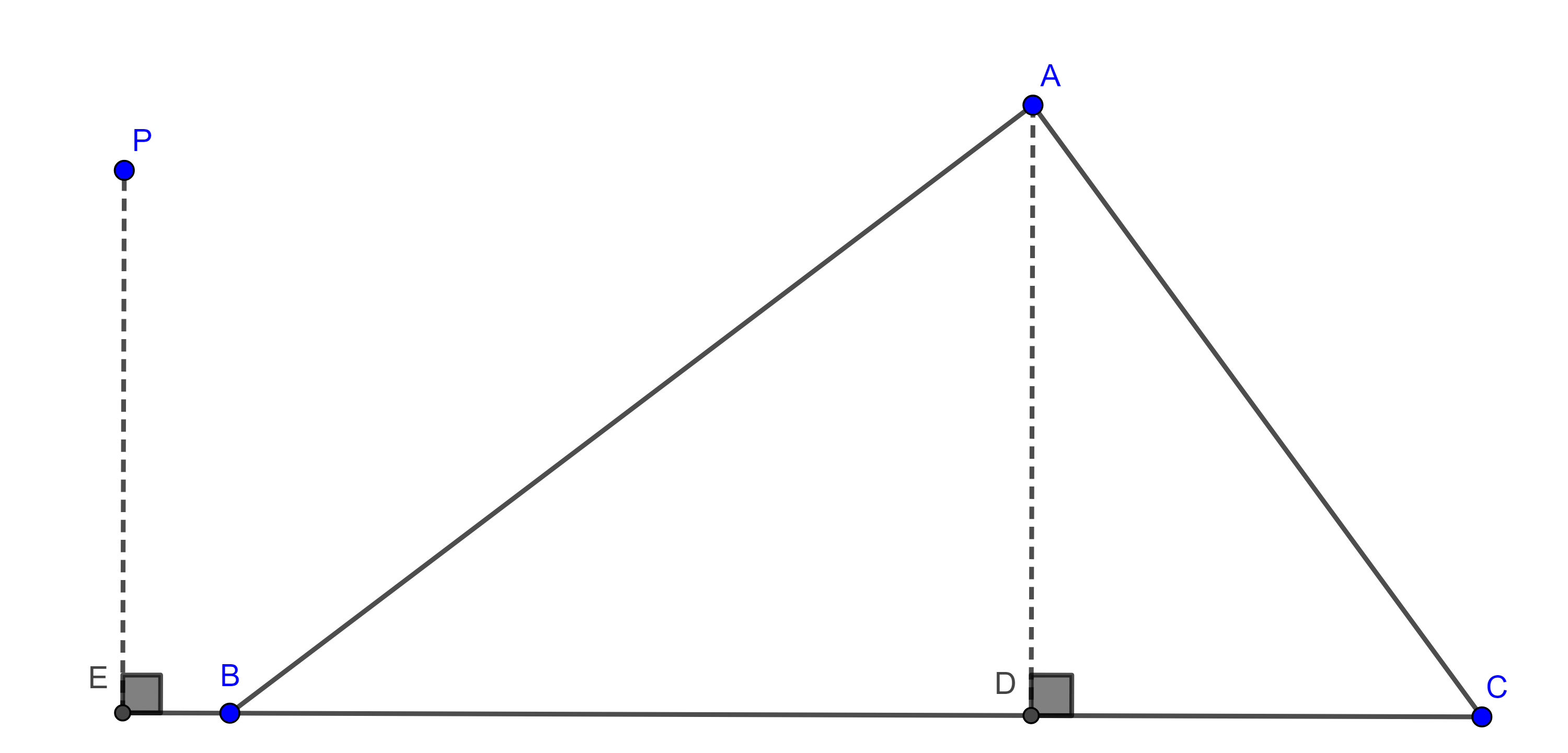
Ahora, sea $A \in \Gamma$, entonces $AD \perp AE$ ya que $DE$ es diámetro.

Por $C$ trazamos las paralelas a $AE$ y $AD$ las cuales intersecan a $AB$ en $P$ y en $Q$ respectivamente, como $AD \perp AE$ entonces $PC \perp CQ$.

Aplicando el teorema de Tales a $\triangle BQC$ y $\triangle BAE$ tenemos
$\begin{equation} \dfrac{AB}{AQ} = \dfrac{BD}{DC} \end{equation}$
$\begin{equation} \dfrac{AB}{AP} = \dfrac{BE}{CE}. \end{equation}$

Por construcción $\dfrac{BD}{DC} = \dfrac{BE}{CE}$
$\Rightarrow \dfrac{AB}{AQ} = \dfrac{AB}{AP} \Rightarrow AP = AQ$.

Es decir, $A$ es el punto medio de la hipotenusa en el triángulo rectángulo $\triangle CPQ$, por tanto, equidista a los tres vértices del triangulo
$\Rightarrow AP = AQ = AC$

Reemplazando en las ecuaciones $(1)$ y $(2)$ obtenemos
$\dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE} = \dfrac{p}{q}$.

Por tanto, $A$ está en el lugar geométrico.

$\blacksquare$

Observación 1. Notemos que, si la razón dada es $1$, el lugar geométrico son los puntos que equidistan a los puntos dados, esto es la mediatriz del segmento que une los puntos dados.

Observación 2. Si $B$, $C$ son los puntos fijos y $\dfrac{p}{q}$ es la razón dada, los puntos $A$ tales que $\dfrac{AB}{AC} = \dfrac{p}{q}$, describen una circunferencia de Apolonio, pero los puntos $A’$ tales que $\dfrac{A’C}{A’B} = \dfrac{p}{q}$ también describen una circunferencia de Apolonio, estos dos lugares no coinciden a menos que $\dfrac{p}{q} = 1$.

En consecuencia, para un segmento dado y una razón dada tenemos dos circunferencias de Apolonio.

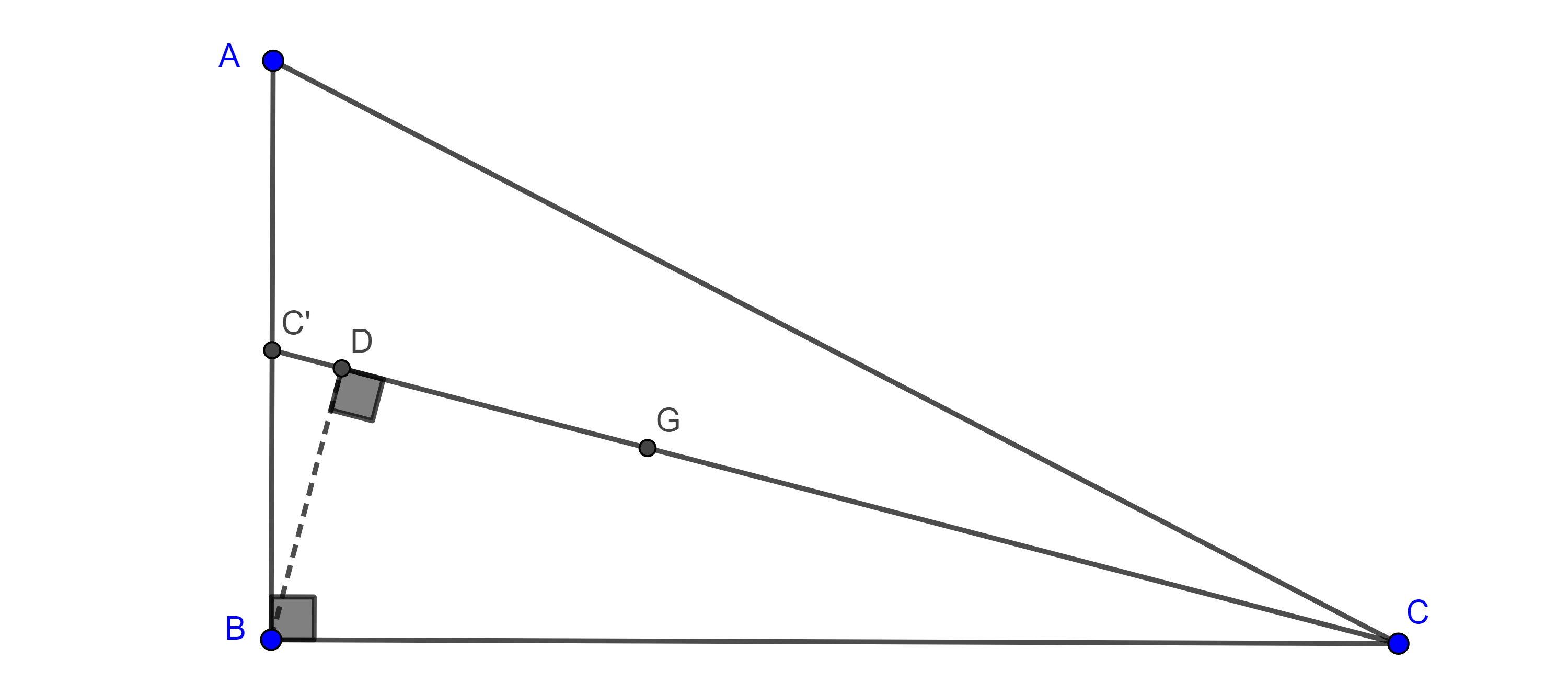
Construcción de un triangulo ($a$, $h_a$, $\dfrac{c}{b}$)

Problema. Construye un triángulo $\triangle ABC$ dados la base, la altura trazada por el vértice opuesto y la razón entre los lados restantes ($BC = a$, $AD = h_a$, $\dfrac{AB}{AC} = \dfrac{c}{b}$).

Solución. Construimos un segmento $BC$ de longitud $a$ y trazamos la circunferencia de Apolonio $\Gamma$ de los puntos $P$ tales que la razón de las distancias a $B$ y a $C$ es la razón dada, $\dfrac{PB}{PC} = \dfrac{c}{b}$.

Luego trazamos una recta $l$ paralela a $BC$ y a una distancia $h_a$. Una de las intersecciones de $l$ con $\Gamma$ es el tercer vértice del triángulo $\triangle ABC$.

Sea $D$ el pie de la perpendicular a $BC$ trazado desde $A$, entonces por construcción $BC = a$, $AD = h_a$ y $\dfrac{AB}{AC} =\dfrac{c}{b}$.

$\blacksquare$

Círculos de Apolonio de un triángulo

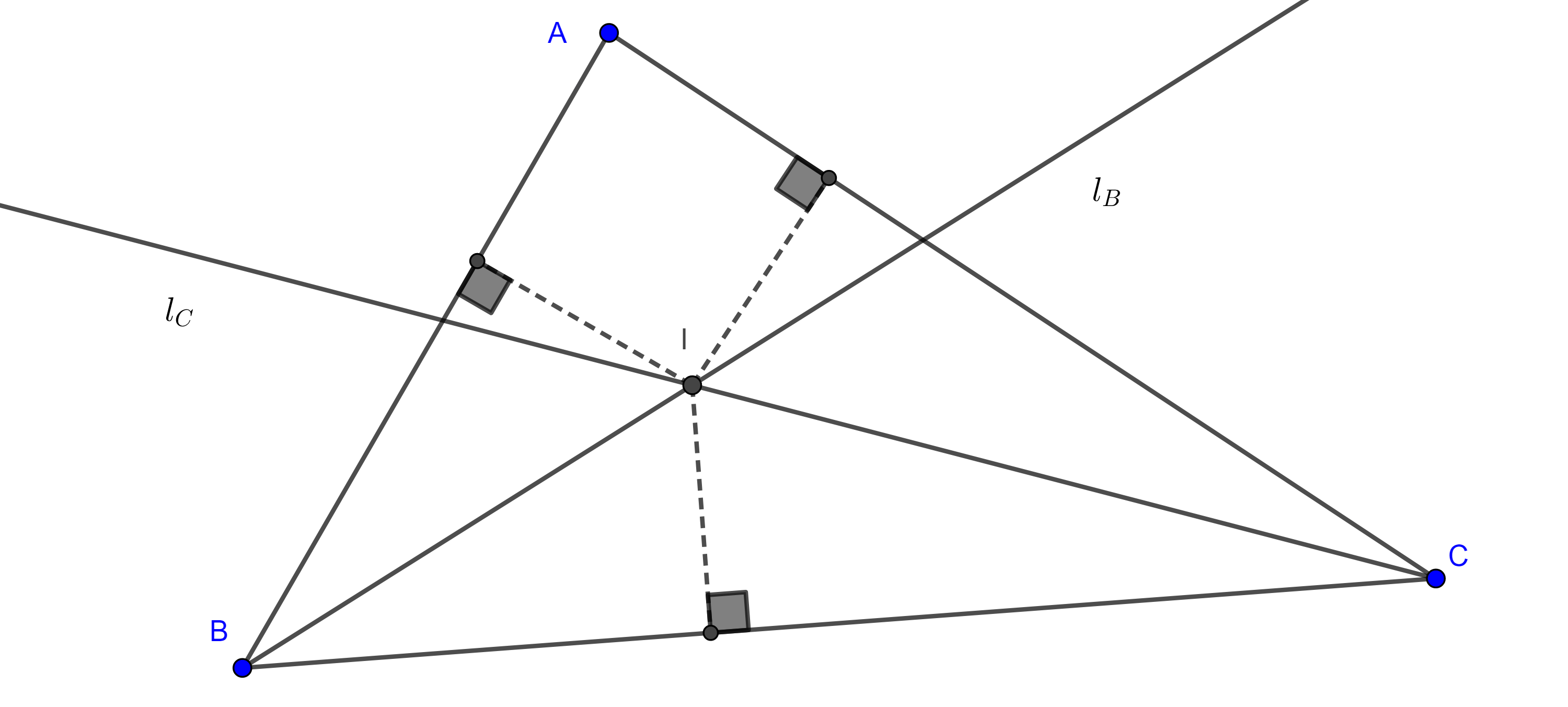
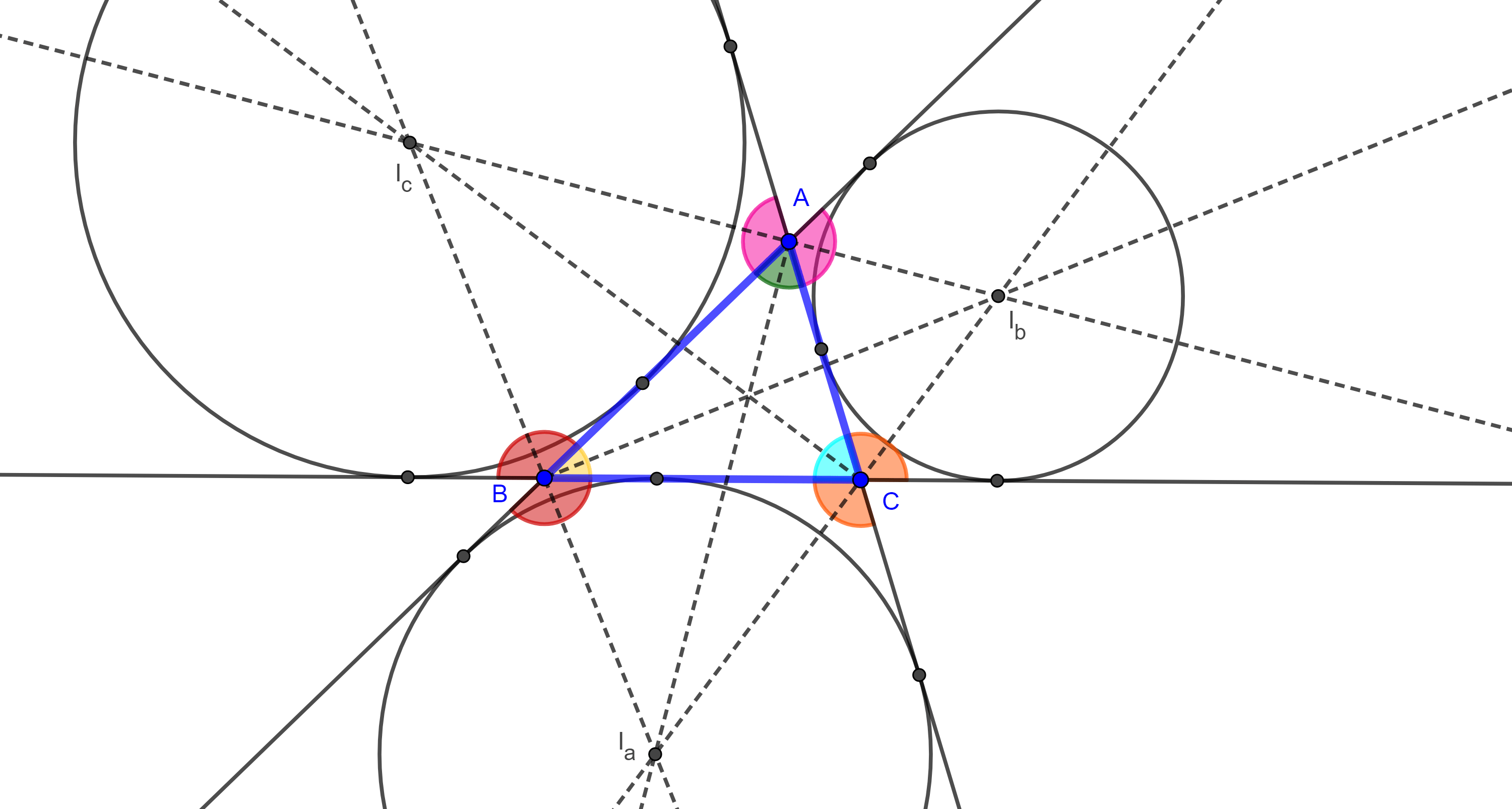
Definición 1. Consideremos un triángulo $\triangle ABC$, el lugar geométrico de los puntos $P$ tales que $\dfrac{PB}{PC} = \dfrac{AB}{AC}$, es la $A$-circunferencia de Apolonio de $\triangle ABC$. De esta manera todo triangulo tiene tres circunferencias de Apolonio asociadas a él, una que pasa por cada vértice.

Definición 2. Decimos que dos circunferencias son ortogonales si se intersecan y los radios trazados desde el punto de intersección son perpendiculares.

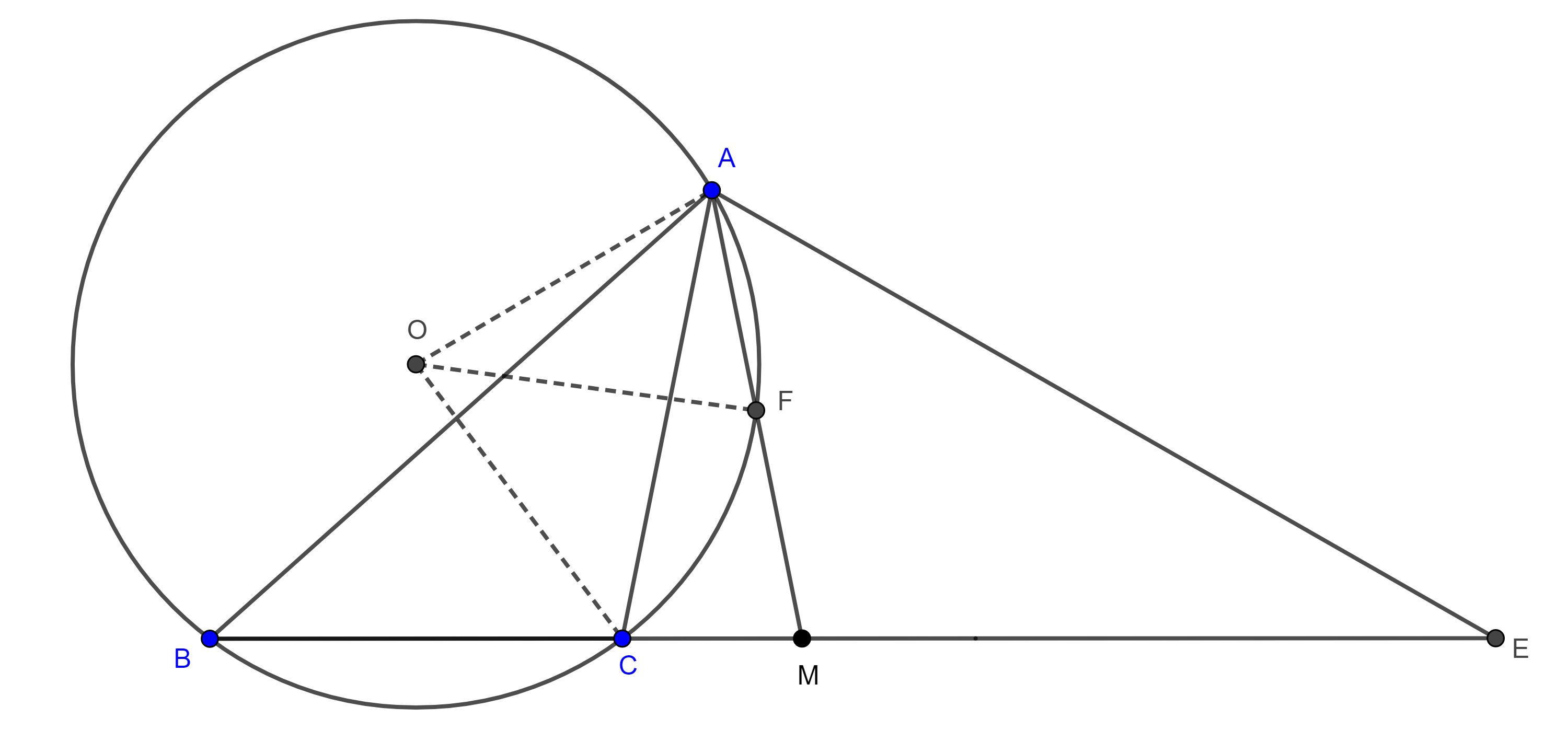
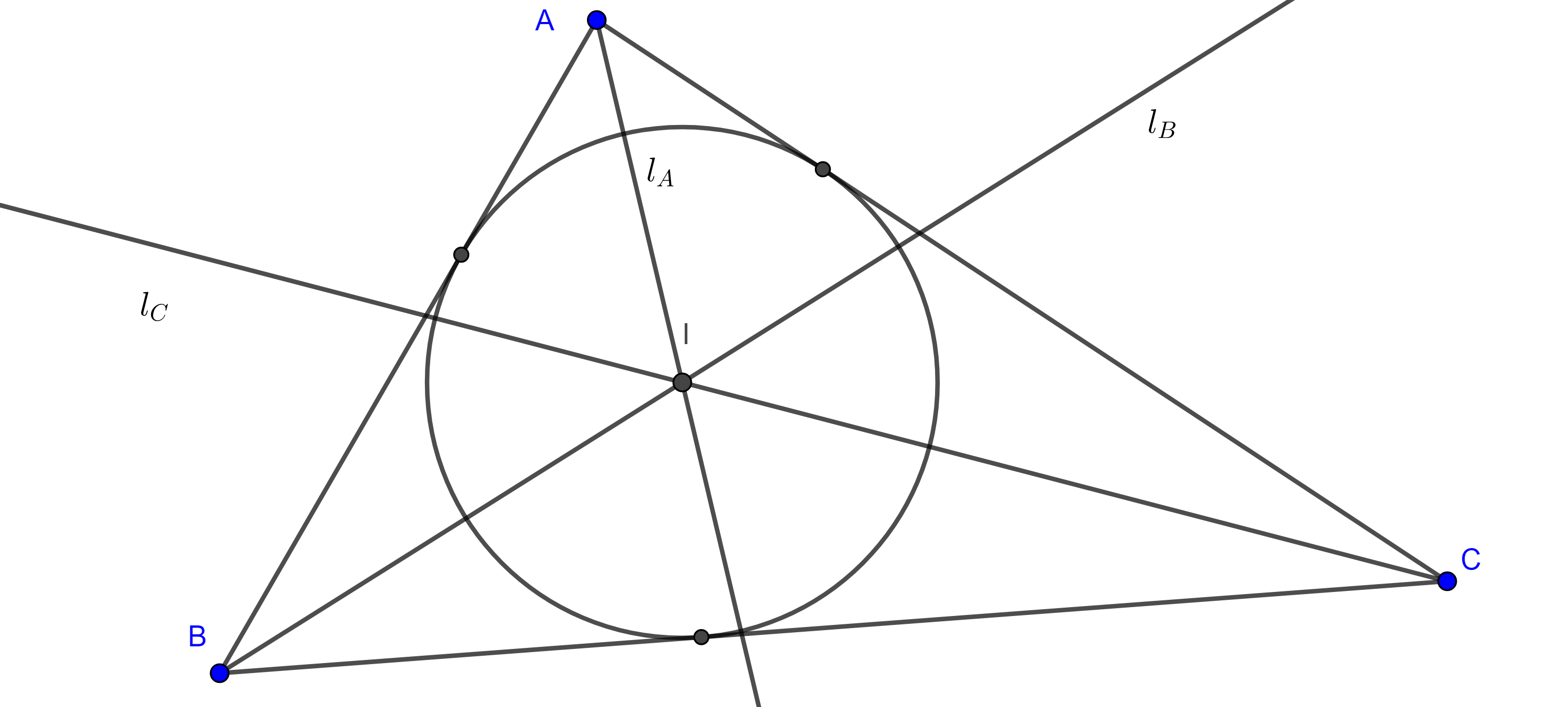
Proposición. Cada circunferencia de Apolonio asociada a un triángulo es ortogonal con el circuncírculo del triángulo.

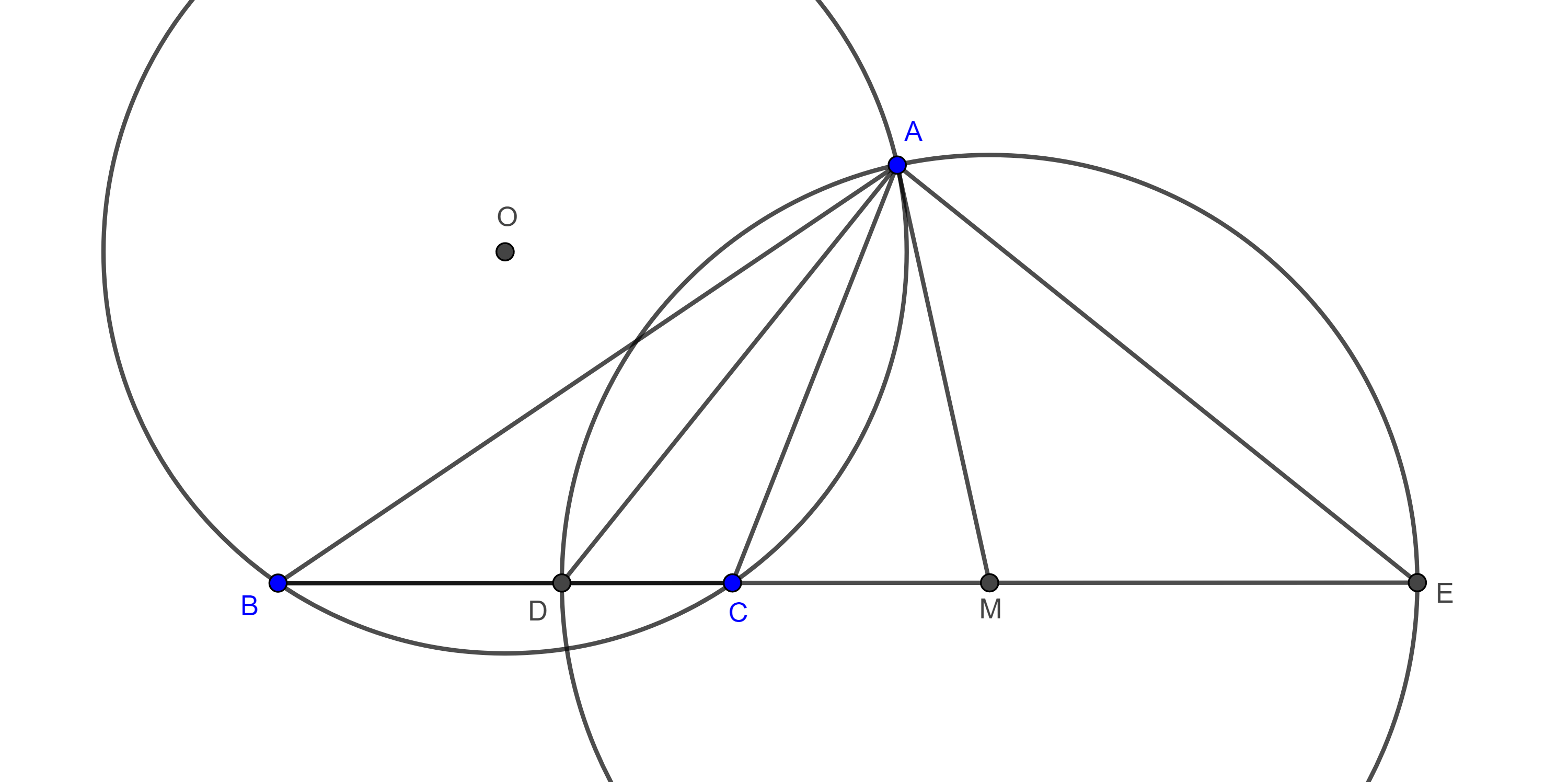
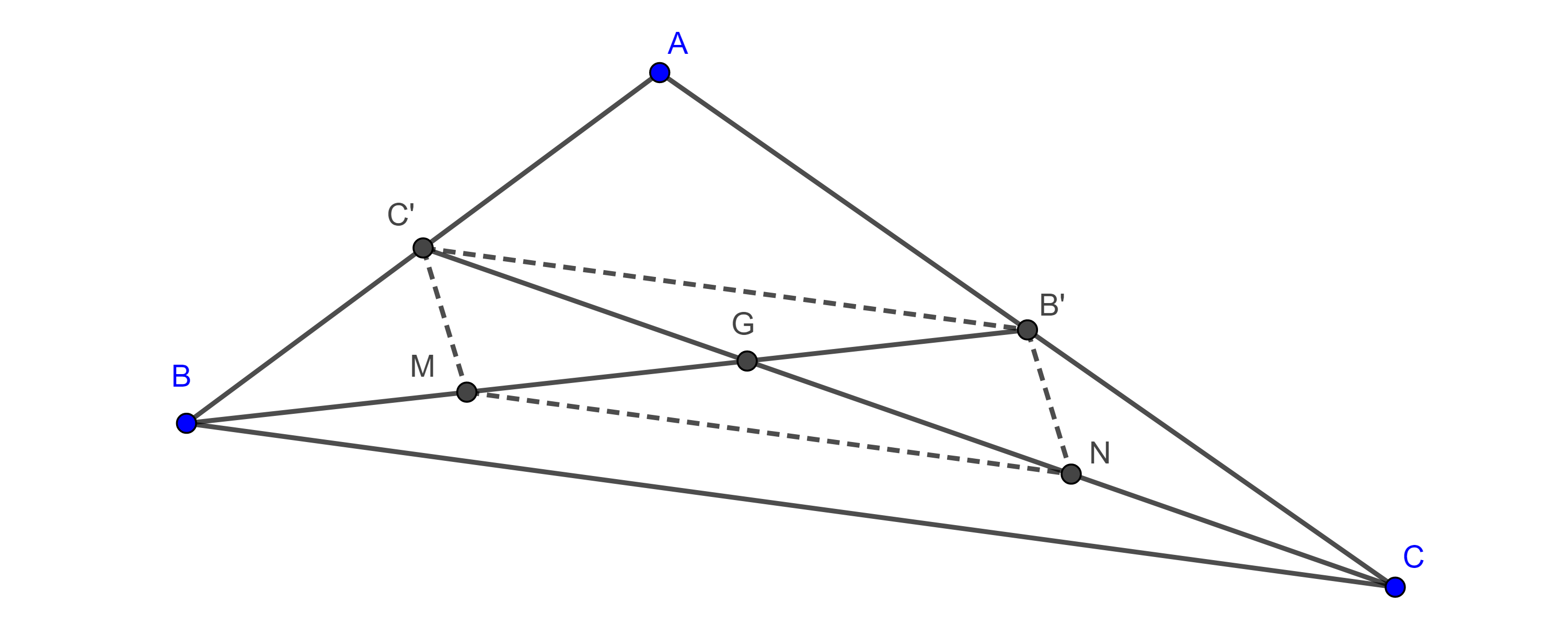
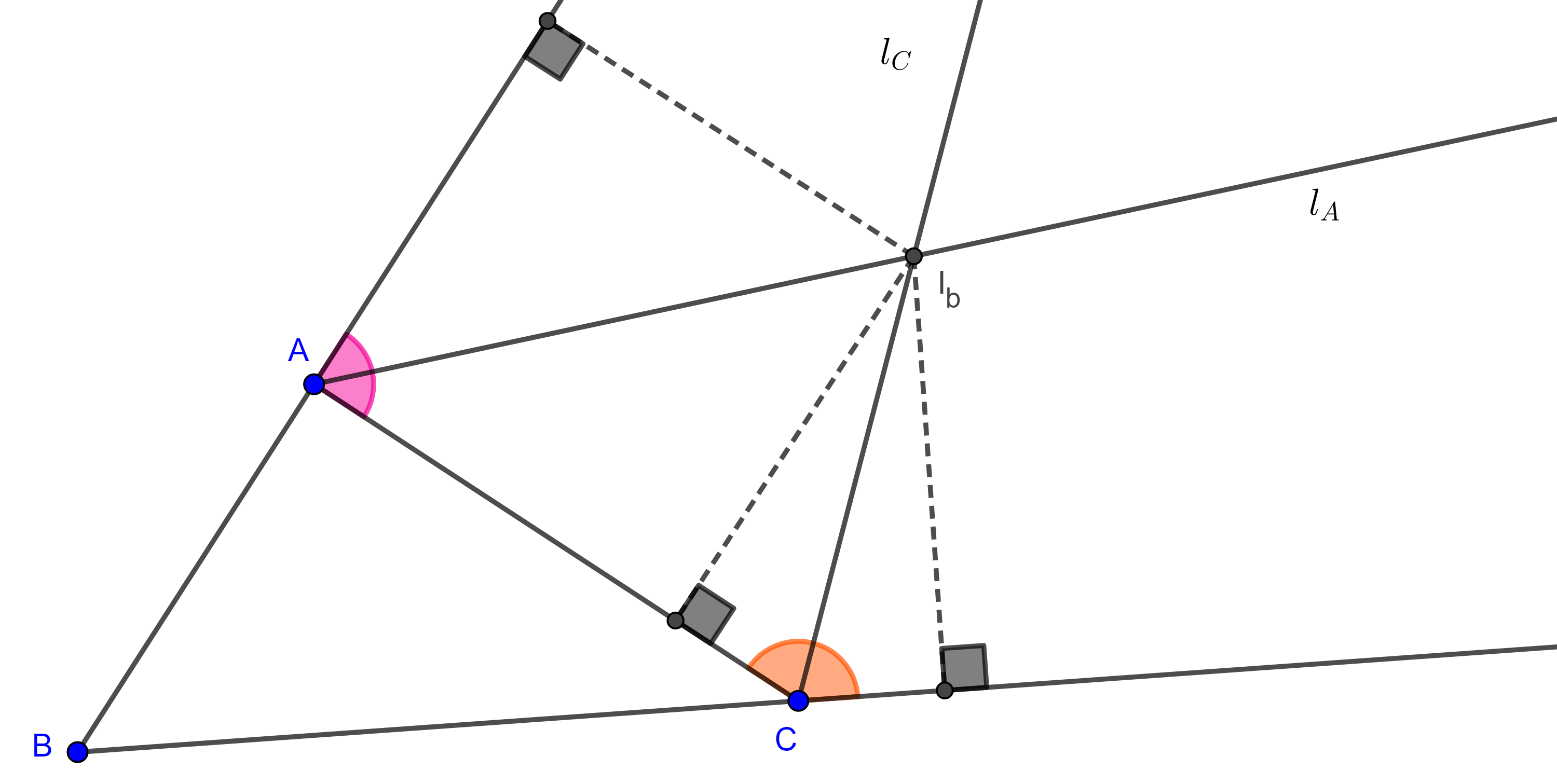
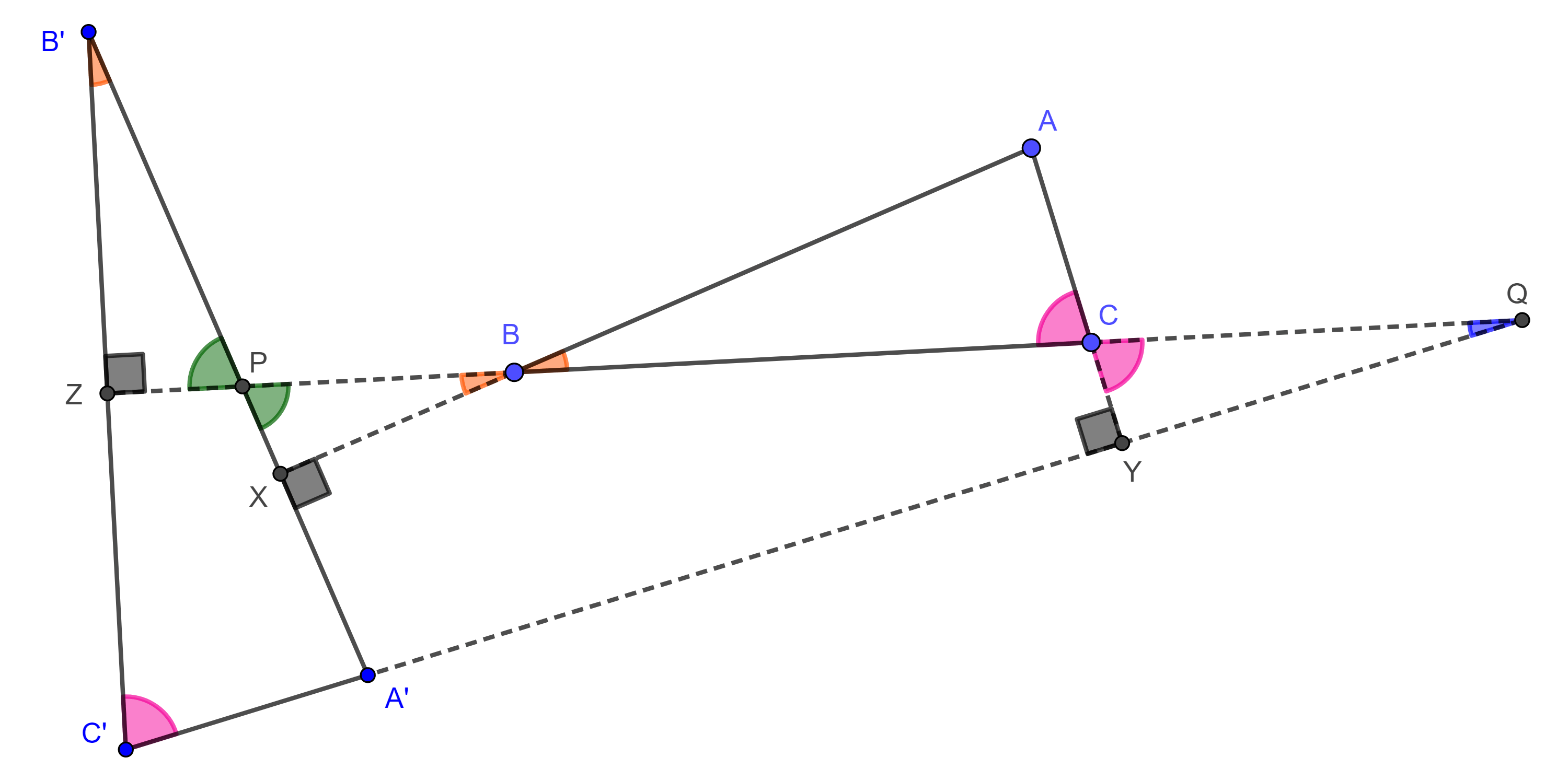
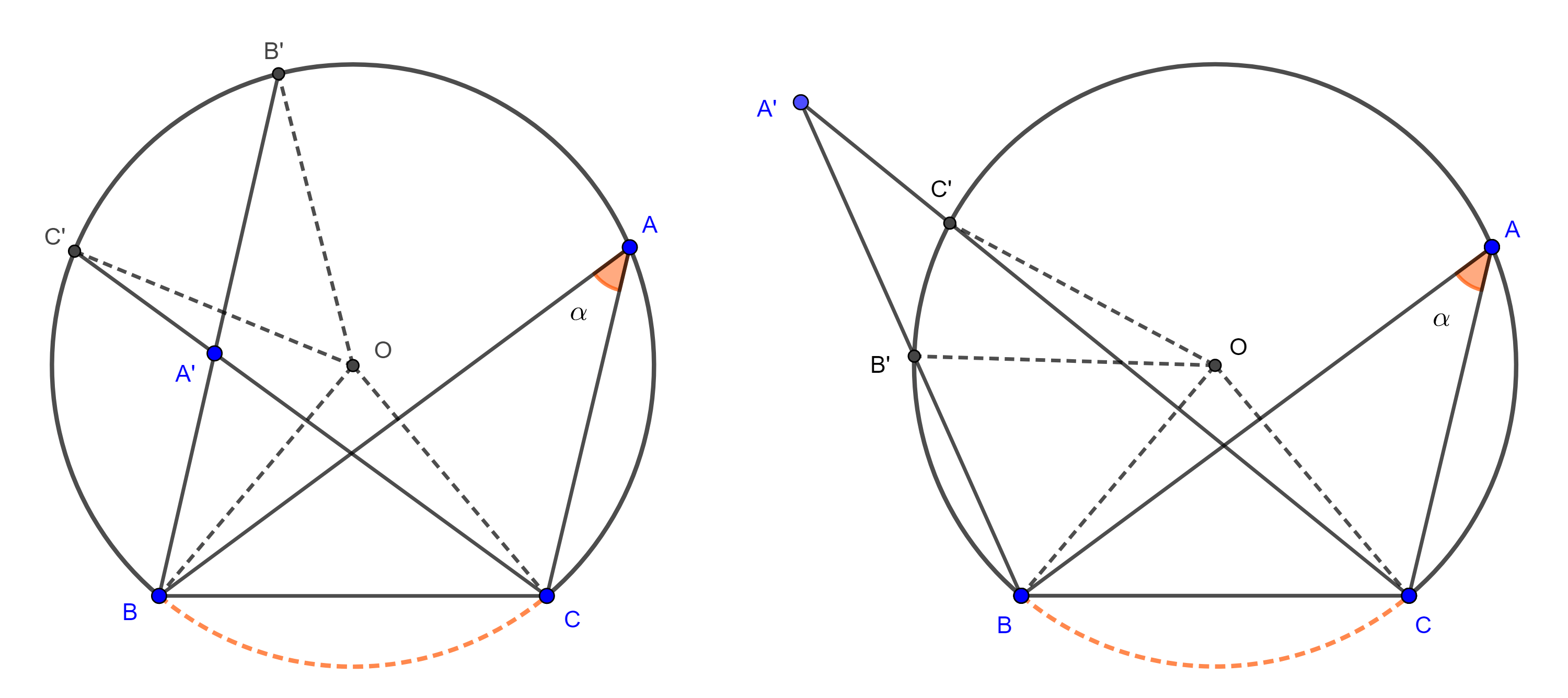
Demostración. Sean $\triangle ABC$, $D$ y $E$ los pies de la bisectriz interior y exterior respectivamente de $\angle A$, consideremos $M$ el punto medio de $DE$.

La circunferencia con centro $M$ y radio $AM$, $(M, AM)$ es la $A$-circunferencia de Apolonio de $\triangle ABC$.

Tenemos lo siguiente
$\dfrac{\pi}{2} = \angle DAE = \angle DAC + \angle CAM + \angle MAE = \dfrac{\angle BAC}{2} + \angle CAM + \dfrac{\angle AMB}{2}$.

$\Rightarrow \pi = \angle BAC + 2\angle CAM + \angle AMB = \angle BAM + \angle AMB + \angle CAM$
$\Rightarrow \angle CBA = \pi – (\angle BAM + \angle AMB)$
$\begin{equation} = \angle CAM. \end{equation}$

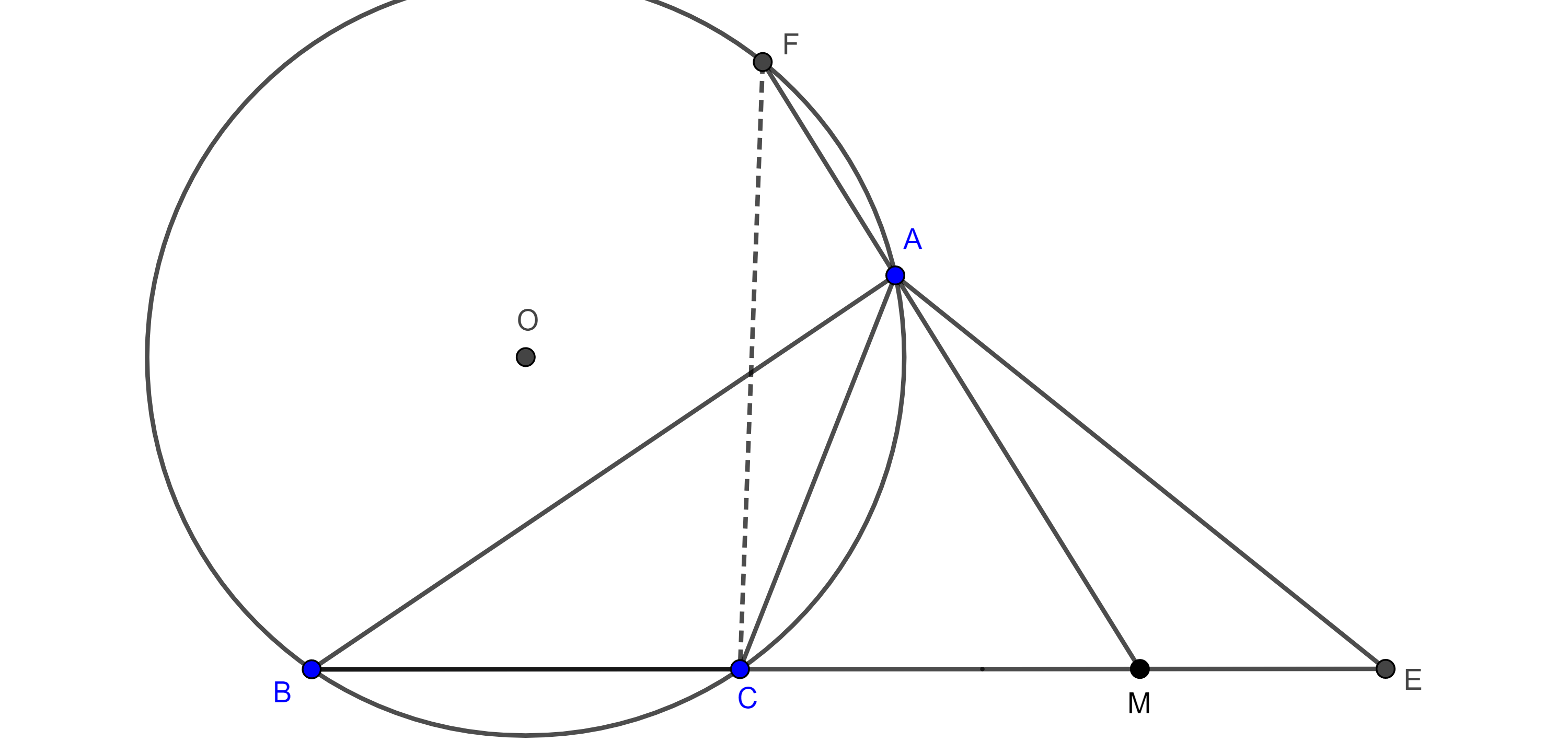
Ahora consideremos el circuncírculo $(O, AO)$ de $\triangle ABC$, y supongamos que $AM$ es secante a $(O, AO)$ en $A$ y $F$, tenemos dos casos:

$F$ esta entre $A$ y $M$,

$\Rightarrow \angle CBA = \dfrac{\angle COA}{2} > \dfrac{\angle COF}{2} = \angle CAF = \angle CAM$.

$A$ esta entre $F$ y $M$,

$\Rightarrow \angle CAM > \angle CFA = \angle CBA$.

Ninguno de los dos casos anteriores es posible, puesto que por la ecuación $(3)$, $\angle CBA = \angle CAM$, por lo tanto, $A$ es tangente a $(O, AO)$ y así $(O, AO)$ y $(M, AM)$ son ortogonales.

La prueba para las otras dos circunferencias de Apolonio de $\triangle ABC$ es análoga.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos un par de métodos generales que nos pueden ayudar a resolver problemas de construcciones geométricas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Dada una circunferencia, muestra que el lugar geométrico de los puntos medios de las cuerdas que pasan por un punto dado es una circunferencia, si el punto esta dentro o en la circunferencia. Analiza el caso cuando el punto se encuentra fuera de la circunferencia.
Dados dos segmentos consecutivos $AB$ y $BC$ sobre una misma recta encuentra el lugar geométrico de los puntos $P$ tales que $\angle APB = \angle BPC$.
Dados tres puntos $A$, $B$, $C$ y un ángulo $\alpha$, construye una circunferencia que pase por $A$ y $B$ y tal que el ángulo entre las tangentes trazadas desde $C$ a la circunferencia sea igual a $\alpha$.

Construye un triangulo, dados:
$i)$ la base, la mediana trazada desde el vértice opuesto y la razón entre los lados restantes,
$ii)$ la base, la bisectriz del ángulo opuesto y la razón entre los lados restantes.
Muestra que las tres circunferencias de Apolonio de un triangulo concurren en dos puntos.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Ángulos en la circunferencia.
Siguiente entrada del curso: Construcciones geométricas.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 11-16.
Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 275-276.
Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 135-137.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 38-39.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Ángulos en la circunferencia

Por Rubén Alexander Ocampo Arellano

4 respuestas

Introducción

Dados un ángulo y una circunferencia nos podemos preguntar si podemos calcular la magnitud del ángulo dado con algún ángulo que tenga como vértice el centro de la circunferencia dada. En esta entrada estudiaremos algunos resultados que nos permitirán establecer dicha relación.

Definición 1. Un ángulo central en una circunferencia es un ángulo formado por dos radios.

Denotamos a una circunferencia con centro en $O$ como $\Gamma (O)$.

Ángulo inscrito

Definición 2. Decimos que un segmento es una cuerda de una circunferencia si sus extremos pertenecen a la circunferencia y el segmento no contiene al centro de la circunferencia, si contiene al centro entonces es un diámetro.

Un ángulo inscrito en una circunferencia es un ángulo formado por dos cuerdas o una cuerda y un diámetro que tienen un extremo en común sobre la circunferencia.

Teorema 1, de la medida del ángulo inscrito. Un ángulo inscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.

Demostración. Sea $\angle CBA$ un ángulo inscrito en $\Gamma (O)$.

Caso 1. $BC$ es diámetro, entonces $\triangle AOB$ es isósceles y por tanto $\angle BAO = \angle CBA$.

Como $\angle COA$ es un ángulo exterior de $\triangle AOB$ entonces es igual a la suma de los ángulos interiores no adyacentes a él,
$\Rightarrow \angle COA = \angle CBA + \angle BAO = 2\angle CBA$
$\Rightarrow \angle CBA = \dfrac{\angle COA}{2}$.

Caso 2. Ambos lados del ángulo son cuerdas, trazamos el diámetro $BO$ y consideramos $D = BO \cap \Gamma (O)$.

Si $AB$ y $BC$ están en un mismo lado respecto de $BD$ (izquierda figura 2), entonces
$\angle CBA = \angle DBA – \angle DBC$ y por el caso 1,
$\Rightarrow \angle CBA = \dfrac{\angle DOA}{2} – \dfrac{\angle DOC}{2} = \dfrac{\angle COA}{2}$.

Si $AB$ y $BC$ están en lados distintos respecto de $BD$ (derecha figura 2), entonces
$\angle CBA = \angle CBD + \angle DBA$ y por el caso 1,
$\Rightarrow \angle CBA = \dfrac{\angle COD}{2} + \dfrac{\angle DOA}{2} = \dfrac{\angle COA}{2}$.

$\blacksquare$

Ángulo semiinscrito

Definición 3. Decimos que una recta es tangente a una circunferencia en un punto si la recta es perpendicular al radio que pasa por el punto.

Definición 4. Decimos que un ángulo es semiinscrito en una circunferencia, si el ángulo está formado por una recta tangente a la circunferencia y una cuerda que tiene como extremo el punto de tangencia.

Teorema 2, de la medida del ángulo semiinscrito. Un ángulo semiinscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.

Demostración. Sea $\angle CBA$ un ángulo inscrito en $\Gamma (O)$, con $AB$ tangente a $\Gamma (O)$ en $B$, consideremos $D = BO \cap \Gamma (O)$.

$\angle DBC$ es inscrito, por el teorema 1, $\angle DBC = \dfrac{\angle DOC}{2}$
$\Rightarrow \angle CBA = \angle DBA – \angle DBC = \dfrac{\pi}{2} – \dfrac{\angle DOC}{2}$
$= \dfrac{\angle DOB}{2} – \dfrac{\angle DOC}{2} = \dfrac{\angle COB}{2}$.

Por otro lado, consideremos $A’ \in AB$ pero del lado opuesto a $A$ respecto de $B$, entonces,
$\angle A’BC = \angle ABD + \angle DBC = \dfrac{\pi}{2} + \dfrac{\angle DOC}{2}$
$= \dfrac{\angle BOD}{2} + \dfrac{\angle DOC}{2} = \dfrac{\angle BOC}{2}$.

$\blacksquare$

Ángulo interior

Definición 5. Si el vértice de un ángulo está en el interior de una circunferencia decimos que el ángulo es interior a la circunferencia.

Teorema 3, de la medida del ángulo interior. Un ángulo interior a una circunferencia es igual a la semisuma del ángulo central que abarca el mismo arco que el ángulo interior y del ángulo central que abarca el mismo arco que el opuesto por el vértice.

Demostración. Sea $\angle ABC$ un ángulo interior a $\Gamma (O)$ con $A$, $C \in \Gamma (O)$, consideremos $A’ = AB \cap \Gamma (O)$ y $C’ = CB \cap \Gamma (O)$.

Como $\angle ABC$ es un ángulo exterior de $\triangle A’BC$ es igual a la suma de los ángulos interiores no adyacentes a él, además $\angle AA’C$ y $\angle A’CC’$ son inscritos y por el teorema 1,
$\Rightarrow \angle ABC = \angle AA’C + \angle A’CC’ = \dfrac{\angle AOC + \angle A’OC’}{2}$.

$\blacksquare$

Ángulo exterior (lados secantes)

Definición 6. Una recta secante a una circunferencia es una recta que la interseca en dos puntos distintos.

Definición 7. Decimos que un ángulo es exterior a una circunferencia si su vértice se encuentra fuera de la circunferencia y los lados que forman el ángulo son tangentes o secantes a la circunferencia.

Teorema 4, de la medida del ángulo exterior. Un ángulo exterior a una circunferencia es igual a la mitad de la diferencia de los ángulos centrales que abarcan arcos cuyos extremos son las intersecciones de cada lado del ángulo con la circunferencia.

Caso 1. Ambos lados del ángulo son secantes a la circunferencia.

Demostración. Sea $\angle BAC$ un ángulo exterior a $\Gamma (O)$.

Supongamos que $B$, $C \in \Gamma (O)$ y consideremos $B’ = AB \cap \Gamma (O)$ y $C’ = AC \cap \Gamma (O)$.

Veamos primero el caso particular en el que $CC’$ es diámetro entonces $\angle BC’C$ es un ángulo exterior de $\triangle AC’B$, por tanto,
$\angle BC’C = \angle A + \angle C’BB’$

Como $\angle BC’C$ y $\angle C’BB’$ son ángulos inscritos, por el teorema 1,
$\Rightarrow \angle A = \angle BC’C – \angle C’BB’ = \dfrac{\angle BOC – \angle C’OB’}{2}$.

Para el caso general sean $D$ y $E$ las intersecciones de $AO$ con $\Gamma (O)$.

Si $B$ y $C$ están en lados distintos respecto de $DE$ (izquierda figura 6), entonces
$\angle A = \angle BAE + \angle EAC$, y por el caso particular,
$\Rightarrow \angle BAE = \dfrac{\angle BOE – \angle DOB’}{2}$ y $\angle EAC = \dfrac{\angle EOC – \angle C’OD}{2}$
$\Rightarrow \angle A = \dfrac{\angle BOE + \angle EOC – (\angle C’OD + \angle DOB’)}{2} = \dfrac{\angle BOC – \angle C’OB’}{2}$.

Si $B$ y $C$ están en el mismo lado respecto de $DE$ (derecha figura 6), entonces
$\angle BAC = \angle BAE – \angle CAE$ y por el caso particular,
$\angle BAE = \dfrac{\angle BOE – \angle DOB’}{2}$ y $\angle CAE = \dfrac{\angle COE – \angle DOC’}{2}$
$\Rightarrow \angle A = \angle BAC = \dfrac{(\angle BOE – \angle COE) – (\angle DOB’ – \angle DOC’)}{2} = \dfrac{\angle BOC – \angle C’OB’}{2}$.

$\blacksquare$

Ángulo exterior (lados tangentes)

Caso 2. Ambos lados del ángulo son tangentes a la circunferencia.

Demostración. Sea $\angle BAC$ un ángulo exterior a $\Gamma (O)$.

Supongamos que $B$, $C \in \Gamma (O)$ y consideremos $D$ y $E$ las intersecciones de $AO$ con $\Gamma (O)$.

Como $\angle BDE$ y $\angle EDC$ son ángulos exteriores de $\triangle ADB$ y $\triangle ADC$ respectivamente, entonces
$\angle BDE = \angle BAD + \angle DBA$ y $\angle EDC = \angle DAC + \angle ACD$
$\Rightarrow \angle A = \angle BAD + \angle DAC = (\angle BDE – \angle DBA) + (\angle EDC – \angle ACD)$
$ = (\angle BDE + \angle EDC) – (\angle ACD + \angle DBA) = \angle BDC – (\angle ACD + \angle DBA)$

$\angle ACD$ y $\angle DBA$ son ángulos semiinscritos y $\angle BDC$ es un ángulo inscrito, por los teoremas 1 y 2 tenemos
$\angle ACD = \dfrac{\angle COD}{2}$, $\angle DBA = \dfrac{\angle DOB}{2}$ y $\angle BDC = \dfrac{\angle BOC}{2}$,
$\Rightarrow \angle A = \dfrac{\angle BOC – (\angle COD + \angle DOB)}{2} = \dfrac{\angle BOC – \angle COB}{2}$.

$\blacksquare$

Caso 3. Un lado del ángulo es tangente a la circunferencia y el otro es secante.

La demostración de este caso queda como ejercicio.

Ejemplos

Proposición 1. Dos ángulos ya sean inscritos o semiinscritos que abarcan el mismo arco de circunferencia son iguales.

Demostración. Por los teoremas 1 y 2, un ángulo inscrito y un ángulo semiinscrito son iguales a la mitad del ángulo central que abarca el mismo arco, si dos ángulos abarcan el mismo arco entonces el ángulo central es el mismo para ambos y por transitividad son iguales.

$\blacksquare$

Teorema 5, de Tales. Sean $A$, $B$ y $C$ puntos distintos en una circunferencia entonces $BC$ es diámetro si y solo si $A$ es un ángulo recto.

Demostración. Sea $\Gamma (O)$ la circunferencia a la que pertenecen $A$, $B$ y $C$, el resultado se sigue del hecho de que el ángulo central que abarca el mismo arco que $\angle A$ es $\angle BOC$ y aplicar el teorema del ángulo inscrito.

$\blacksquare$

Problema. Dado un círculo $\Gamma$ construir su centro.

Solución. Construimos dos ángulos rectos inscritos en la circunferencia, tomando dos puntos distintos como vértice.

Por el teorema de Tales, las intersecciones de los lados de cada ángulo formaran dos diámetros distintos de la circunferencia y su intersección será el centro de la circunferencia.

$\blacksquare$

Proposición 2. Las rectas tangentes trazadas desde un punto exterior a una circunferencia son iguales.

Demostración. Sean $\Gamma (O)$ y $A$ un punto exterior, por $A$ trazamos $AB$ y $AC$ tangentes a $\Gamma (O)$ en $B$ y en $C$ respectivamente (figura 7).

Consideremos los radios $OB$ y $OC$ entonces $OB = OC$, y por definición de tangencia, $OB \perp AB$ y $OC \perp AC$.

Los triángulos rectángulos $\triangle AOB$ y $\triangle AOC$ tienen a $AO$ como lado en común, por criterio de congruencia hipotenusa-cateto $\triangle AOB \cong \triangle AOC$, por tanto, $AB = AC$.

$\blacksquare$

Más adelante…

Apoyándonos de los resultados vistos aquí, en la siguiente entrada daremos una caracterización de arco de circunferencia y veremos la circunferencia de Apolonio.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sean $A$ y $C$ dos puntos fijos en una circunferencia, muestra que para cualesquiera dos puntos $B$ y $D$ en la misma circunferencia se tiene que $\angle ABC = \angle ADC$ o $\angle ABC$ y $\angle CDA$ son suplementarios.
Prueba que una recta es tangente a una circunferencia si y solo si la recta y la circunferencia tienen un solo punto en común.
Demuestra el teorema 4 en el caso en el que el un lado del ángulo exterior es secante a la circunferencia y el otro es tangente, es decir, en la figura 11 muestra que
$\angle BAC = \dfrac{\angle BOC – \angle COD}{2}$.

Dados una circunferencia y un punto fuera de ella, construye las rectas tangentes a la circunferencia dada trazadas desde el punto dado.
Sean $\triangle ABC$, $K$ la intersección de la altura trazada desde $A$ con el circuncírculo de $\triangle ABC$ y $H$ el ortocentro de $\triangle ABC$, muestra que $BC$ biseca a $HK$.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Puntos notables del triángulo.
Siguiente entrada del curso: Circunferencia de Apolonio.
Otros cursos.

Fuentes

Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 133-140.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 34-40.
Wikipedia
Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Puntos notables del triángulo

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos la concurrencia de rectas importantes en el triangulo, a saber, las medianas, mediatrices, bisectrices y alturas. Mencionamos también consecuencias inmediatas de los puntos de concurrencia.

Centroide

Teorema 1. Las medianas de todo triángulo concurren en un punto que las triseca.

Demostración. Sean $\triangle ABC$, $B’$ y $C’$ los puntos medios de $AC$ y $AB$ respectivamente, por el teorema del segmento medio sabemos que $C’B’ = \dfrac{BC}{2}$ y $C’B’ \parallel BC$.

Sea $G$ la intersección de las medianas $BB’$ y $CC’$, en $\triangle GBC$ consideremos $M$ y $N$ los puntos medios de los lados $GB$ y $GC$ respectivamente, entonces
$MN = \dfrac{BC}{2}$ y $MN \parallel BC$.

Por transitividad $C’B’ = MN$ y $C’B’ \parallel MN$, esto implica que $\square C’MNB’$ es un paralelogramo y por lo tanto sus diagonales se bisecan, es decir,
$C’G = GN$ y $MG = GB’$.

Por construcción, $MG = BM$ y $GN = NC$
$\Rightarrow GB’= \dfrac{BB’}{3}$ y $C’G = \dfrac{CC’}{3}$,
esto es, la medianas $BB’$ y $CC’$ se trisecan

Si repetimos el mismo procedimiento pero ahora con las medianas $AA’$ y $BB’$ encontraremos un punto $G’$ en donde las medianas se trisecaran, $G’B’= \dfrac{BB’}{3}$ y $G’A’ = \dfrac{AA’}{3}$.

Como $GB’= \dfrac{BB’}{3} = G’B’$, concluimos que $G’ = G$.

Por lo tanto, las medianas de un triángulo concurren en un punto que las triseca.

$\blacksquare$

Definición 1. Decimos que el punto en que concurren las medianas de un triángulo es el gravicentro, baricentro o centroide del triángulo y lo denotamos con la letra $G$ mayúscula.

Circuncentro

Teorema 2. Las mediatrices de los lados de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, consideremos las mediatrices $l_c$ y $l_b$ de $AB$ y $AC$ respectivamente y $O = l_b \cap l_c$.

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la mediatriz de un segmento si y solo si equidista a los puntos extremos del segmento.

Ya que $O \in l_c$ y $O \in l_b$, entonces $OA = OB$ y $OA = OC$
$\Rightarrow OB = OC$.

Por el resultado mencionado anteriormente $OB = OC$ implica que $O \in l_a$, la mediatriz de $BC$.

Por lo tanto, las mediatrices de un triángulo son concurrentes.

$\blacksquare$

Corolario. Tres puntos distintos y no colineales se encuentran en una única circunferencia.

Demostración. Sea $\triangle ABC$, por el teorema anterior las mediatrices de los segmentos determinados por los vértices del triángulo concurren en un punto $O$ cuya distancia a cada uno de los vértices es la misma $R = OA = OB = OC$.

Por definición de circunferencia, $A$, $B$ y $C$ pertenecen a la circunferencia con centro en $O$ y radio $R$, $A$, $B$, $C \in (O, R) = \Gamma$.

Ahora supongamos que existe $\Gamma’ = (O’, R’)$ tal que $A$, $B$, $C \in \Gamma’$, entonces, por definición, $O’A = O’B = O’C = R’$.

Esto implica que $O’ \in l_a$, $O’ \in l_b$ y $O’ \in l_c$, las mediatices de $BC$, $AC$ y $AB$ respectivamente,
$\Rightarrow O \in l_a \cap l_b \cap l_c$.

Como ya probamos que las mediatrices son concurrentes entonces $O’ = O$ y $R’ = R$, así que $\Gamma$ es única.

$\blacksquare$

Definición 2. Al punto de concurrencia de las mediatrices de los lados de un triángulo le llamamos circuncentro y lo denotamos como $O$.

A la distancia constante de $O$ a los vértices del triángulo le llamamos circunradio denotado con la letra $R$ mayúscula.

A la circunferencia única $(O, R)$ determinada por los vértices del triángulo se le conoce como circuncírculo.

Incentro

Teorema 3. Las bisectrices interiores de todo triángulo son concurrentes.

Demostración. Sean $l_B$ y $l_C$ las bisectrices de los ángulos interiores en $\angle B$ y $\angle C$ respectivamente e $I = l_{B} \cap l_{C}$.

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la bisectriz de un ángulo si y solo si equidista a los lados que forman el ángulo. Recordemos que la distancia de un punto a una recta es la longitud del punto al pie de la perpendicular a la recta trazada desde el punto.

Denotamos la distancia de un punto $P$ a una recta $l$ como $(P, l)$.

Como $I \in l_{b}$ e $I \in l_{c}$, entonces $(I, AB) = (I, BC)$ y $(I, BC) = (I, AC)$,
$\Rightarrow (I, AB) = (I, AC)$.

Por el resultado citado anteriormente, $(I, AB) = (I, AC)$ implica que $I \in l_A$, la bisectriz interior de $\angle A$.

Por tanto, las bisectrices interiores de un triángulo son concurrentes.

$\blacksquare$

Si consideramos los pies de las perpendiculares a los lados del triángulo trazados desde el punto en que concurren las bisectrices, encontramos tres puntos distintos que equidistan a un punto fijo y por el corolario anterior estos determinan una única circunferencia, esto motiva la siguiente definición.

Definición 3. Al punto de concurrencia de las bisectrices interiores de un triángulo se le conoce como incentro del triángulo y lo denotamos con la letra $I$ mayúscula.

A la distancia de $I$ a los lados del triángulo le llamamos inradio y lo denotamos como $r = (I, AB) = (I, BC) = (I, AC)$.

La circunferencia con centro en $I$ y radio $r$, $(I, r)$, se llama incírculo.

Excentros

Teorema 4. En todo triángulo las bisectrices exteriores de dos ángulos y la bisectriz interior del tercer ángulo son concurrentes.

Demostración. Sea $\triangle ABC$, $l_A$ y $l_C$ las bisectrices exteriores de $\angle A$ y $\angle C$ respectivamente e $I_b = l_A \cap l_C$.

De manera análoga al caso de las bisectrices internas tenemos que
como $I_b \in l_A$ e $I_b \in l_C$, entonces $(I_b, AB) = (I_b, AC)$ y $(I_b, AC) = (I_b, BC)$,
$\Rightarrow (I_b, AB) = (I_b, BC)$.

Como $I_b$ está en la región acotada por el ángulo $\angle CBA$ entonces $I \in l_B$, la bisectriz interior de $\angle B$.

Por lo tanto, la bisectriz interna de $\angle B$ y las bisectrices externas de $A$ y $C$ son concurrentes.

De manera análoga probamos que las bisectrices externas de $\angle A$ y $\angle B$ concurren con la bisectriz interna de $\angle C$, y las bisectrices externas de $\angle B$ y $\angle C$ concurren con la bisectriz interna de $\angle A$.

$\blacksquare$

Similarmente a como lo hicimos con el incentro, notamos que, para cada uno de estos tres puntos de concurrencia, existen tres puntos distintos, uno en cada lado del triángulo que equidistan a un punto fijo y por lo tanto determinan una única circunferencia.

Definición 4. A los puntos en que concurren dos bisectrices externas y una bisectriz interna de un triángulo les llamamos excentros del triángulo y los denotamos como $I_a$, $I_b$ e $I_c$ de acuerdo a si se encuentran en la bisectriz interna de $\angle A$, $\angle B$ o $\angle C$ respectivamente y decimos que son opuestos a dichos vértices.

Las distancias de $I_a$, $I_b$ e $I_c$ a los lados del triángulo son los exradios y se les denota como $r_a$, $r_b$ y $r_c$ respectivamente.

A las circunferencias $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ se les conoce como excírculos del triángulo.

Ortocentro

Teorema 5. Las alturas de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, tracemos en cada vértice la paralela al lado opuesto.

Sean $A’$ la intersección de la paralela a $AB$ trazada en $C$ con la paralela a $AC$ trazada en $B$, de manera análoga definimos $B’$ y $C’$.

Por construcción, $\square ABCB’$ es un paralelogramo por lo que $AB’ = BC$, también $\square C’BCA$ es paralelogramo así que $C’A = BC$,
$\Rightarrow AB’ = BC = C’A \Rightarrow A$ es el punto medio de $C’B’$.

De manera similar podemos ver que $B$ es el punto medio de $C’A’$ y $C$ es el punto medio de $A’B’$.

En consecuencia, las alturas del triángulo $\triangle ABC$ son las mediatrices del triángulo $\triangle C’A’B’$ y ya probamos que las mediatrices de los lados de todo triangulo son concurrentes, por lo tanto, las alturas de $\triangle ABC$ son concurrentes.

$\blacksquare$

Definición 5. Al punto en común en que las tres alturas de un triángulo se intersecan le llamamos ortocentro y lo denotamos con la letra $H$ mayúscula.

Más adelante…

En la siguiente entrada demostraremos algunos teoremas que nos permitirán calcular la magnitud de ángulos relativos a una circunferencia.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

¿Qué puntos notables vistos en esta entrada, caen siempre dentro del triangulo y cuales siempre fuera?
Muestra que una recta paralela a un lado de un triangulo a través del centroide divide el área del triangulo en dos partes tal que la razón de esta áreas es $\dfrac{4}{5}$.
Considera un triangulo rectángulo $\triangle ABC$ con $\angle B = \dfrac{\pi}{2}$, sean $CC’$ la mediana por $C$ y $D$ el pie de la perpendicular a $CC’$ trazada desde $B$ (figura 11), calcula la distancia de $D$ al centroide $G$ del triangulo en términos de los catetos.

Un triángulo rectángulo tiene un ángulo interior de $\dfrac{\pi}{3}$, calcula la distancia del vértice donde se intersecan los catetos al incentro $I$ del triángulo en términos de la hipotenusa.
Sea $\triangle ABC$ un triángulo tal que la mediana $AD$ es perpendicular a la mediana $BE$, encuentra $AB$ si $BC = a$ y $AC = b$.

Entradas relacionadas

Ir a Geometría Moderna I
Entrada anterior del curso: Segmentos dirigidos y teorema de Stewart.
Siguiente entrada del curso: Ángulos en la circunferencia.

Fuentes

Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 29-34.
Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-94.
Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Semejanza de triángulos

Por Rubén Alexander Ocampo Arellano

3 respuestas

Introducción

En esta entrada estudiamos otro tipo de relación, la de semejanza de triángulos, la cual es una de las herramientas más útiles en geometría euclidiana.

Definición. Decimos que dos triángulos $\triangle ABC$ y $\triangle A’B’C’$ son semejantes si sus ángulos respectivos son iguales y sus lados respectivos son proporcionales, es decir,

$\angle A = \angle A’$, $\angle B = \angle B’$, $\angle C = \angle C’$ y
$\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{AC}{A’C’}$.

Si dos triángulos son semejantes lo denotamos así $\triangle ABC \sim \triangle A’B’C’$.

Criterio de semejanza ángulo, ángulo, ángulo (AAA o AA)

Teorema 1, criterio de semejanza ángulo, ángulo, ángulo. Si los ángulos correspondientes de dos triángulos son iguales entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\angle A = \angle A’$, $\angle B = \angle B’$, $\angle C = \angle C’$. Por demostrar que los lados correspondientes son proporcionales.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$, como $\angle A = \angle A’$, por el criterio de congruencia LAL, tenemos que los triángulos $\triangle ADE \cong \triangle A’B’C’$.

Por lo tanto, $\angle EDA = \angle C’B’A’$, $\angle AED = \angle A’C’B’$ y $DE = B’C’$.

Dado que $AB$ es transversal a $DE$ y $BC$ y los ángulos correspondientes son iguales, entonces $DE \parallel BC$.

Por el teorema de Tales, $\dfrac{AB}{AD} = \dfrac{AC}{AE} = \dfrac{BC}{DE}$,
$\Rightarrow \dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}$.

Así, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Observación. Como la suma de los ángulos internos de todo triangulo es igual a $\pi$, entonces si conocemos la magnitud de dos ángulos internos conocemos los tres y por lo tanto podemos referirnos a este criterio como AA.

Criterio de semejanza lado, ángulo, lado (LAL)

Teorema 2, criterio de semejanza lado, ángulo, lado. Si dos triángulos tienen dos lados correspondientes proporcionales y el ángulo entre ellos es igual, entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}$ y $\angle A = \angle A’$.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$.

Como $\angle A = \angle A’$ por el criterio de congruencia LAL, $\triangle ADE \cong \triangle A’B’C’$, así $\angle EDA = \angle C’B’A’$ y $\angle AED = \angle A’C’B’$.

Por hipótesis sabemos que $\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}$
$\Rightarrow \dfrac{AB}{AD} = \dfrac{AC}{AE}$.

Esto implica, por el reciproco del teorema de Tales, que $DE \parallel BC$, se sigue que $\angle CBA = \angle EDA$ y $\angle ACB = \angle AED$ por ser ángulos correspondientes.

Por transitividad, $\angle A = \angle A’$, $\angle B = \angle B’$ y $\angle C = \angle C’$

Por criterio de semejanza AAA, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Criterio de semejanza lado, lado, lado (LLL)

Teorema 3, criterio de semejanza lado, lado, lado. Si los lados correspondientes de dos triángulos son proporcionales entonces los triángulos son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ dos triángulos tales que $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{AC}{A’C’}$, por demostrar que $\angle A = \angle A’$, $\angle B = \angle B’$ y $\angle C = \angle C’$.

Sean $D \in AB$ y $E \in AC$ tales que $AD = A’B’$ y $AE = A’C’$ (figura 2).

Como $\angle BAC = \angle DAE$ y $\dfrac{AB}{AD} = \dfrac{AC}{AE}$, por criterio de semejanza LAL, $\triangle ABC \sim \triangle ADE$, y en consecuencia $\dfrac{AB}{AD} = \dfrac{BC}{DE}$.

$AD = A’B’$, por construcción, y $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}$ por hipótesis,
$\Rightarrow \dfrac{BC}{B’C’} = \dfrac{AB}{A’B’} = \dfrac{AB}{AD} = \dfrac{BC}{DE}$
$\Rightarrow B’C’ = DE$.

Por criterio de congruencia LLL, $\triangle A’B’C’ \cong \triangle ADE$.

Por transitividad, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Triángulos con lados perpendiculares

Proposición 1. Dos triángulos cuyos lados correspondientes son perpendiculares son semejantes.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB \perp A’B’$, $BC \perp B’C’$ y $AC \perp A’C’$.

Consideremos $Z$, $P$ y $Q$ las intersecciones de $BC$ con $B’C’$, $A’B’$ y $A’C’$ respectivamente, $X = AB \cap A’B’$ e $Y = AC \cap A’C’$ (figura 3).

$\angle CBA = \angle PBX$, por ser opuestos por el vértice,
como $\triangle BXP$ es rectángulo entonces $\angle PBX$ y $\angle XPB$ son complementarios,
$\Rightarrow \angle CBA$ y $\angle XPB$ son complementarios,
$\angle XPB = \angle B’PZ$, por ser opuestos por el vértice,
$\Rightarrow \angle CBA$ y $\angle B’PZ$ son complementarios.

Como $\triangle B’ZP$ es rectángulo entonces $\angle B’PZ$ y $\angle ZB’P$ son complementarios,
$\Rightarrow \angle CBA = \angle ZB’P$,
$\Rightarrow \angle B’ = \angle B$.

Por otro lado, $\angle ACB = \angle YCQ$, por ser opuestos por el vértice,
como $\triangle CYQ$ es rectángulo entonces $\angle YCQ$ y $\angle CQY$ son complementarios,
$\Rightarrow \angle ACB$ y $\angle CQY$ son complementarios.

Como $\triangle C’ZQ$ es rectángulo entonces $\angle QC’Z$ y $\angle CQY$ son complementarios,
$\Rightarrow \angle ACB = \angle QC’Z$,
$\Rightarrow \angle C = \angle C’$.

Por criterio de semejanza AA, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Proposición 2. Dos triángulos cuyos lados correspondientes son paralelos son semejantes.

Demostración. Podemos construir un triángulo cuyos lados correspondientes sean perpendiculares a los lados de uno de los triángulos, por transitividad sus lados también serán perpendiculares a los lados del segundo triangulo.

Por la proposición anterior los triángulos originales serán semejantes al triangulo construido y por lo tanto serán semejantes entre sí.

$\blacksquare$

Desigualdad entre bisectrices

Proposición 3. En un triángulo entre cualesquiera dos ángulos internos la bisectriz del mayor es menor a la bisectriz del menor de los ángulos.

Demostración. Sea $\triangle ABC$ y supongamos que $\angle B > \angle C$ y sean $D$ y $E$ las intersecciones de las bisectrices de los ángulos $\angle B$ y $\angle C$ respectivamente con los lados opuestos. Debemos mostrar que $BD < CE$.

Sean $F \in AD$ tal que $\angle DBF = \angle ACE = \angle ECB$ y $G$ la intersección de $CE$ con $BF$, por criterio de semejanza AA, $\triangle FBD \sim \triangle FCG$, por lo tanto,

$\begin{equation} \dfrac{BF}{CF} = \dfrac{BD}{CG}. \end{equation}$

Por otro lado, en el triángulo $\triangle BFC$ tenemos que
$\angle CBF = \angle CBD + \angle DBF $
$= \dfrac{\angle B}{2} + \dfrac{\angle C}{2} > \dfrac{\angle C}{2} + \dfrac{\angle C}{2} = \angle C$.

Como al ángulo mayor siempre se opone a el lado mayor, tenemos que $FC > BF$ $\Leftrightarrow$ $1 > \dfrac{BF}{CF} = \dfrac{BD}{CG}$.

Donde la última igualdad se da por la ecuación $(1)$

Por lo tanto, $CE > CG > BD$.

$\blacksquare$

Semejanza en el triángulo rectángulo

Proposición 4. Sean $\triangle ABC$ un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$ y $D$ el pie de la perpendicular a $\overline{BC}$ trazada desde $A$, entonces:
$i)$ $AD^2 = BD \times DC$,
$ii)$ $AB^2 = BC \times BD$,
$iii)$ $AC^2 = BC \times DC$,
$iv)$ $AD \times BC = AB \times AC$.

Demostración. Por criterio de semejanza AA, $\triangle ABC \sim \triangle DBA$ y $\triangle ABC \sim \triangle DAC$,

$i)$ Por la relación de semejanza tenemos
$\dfrac{AD}{AC} =\dfrac{BD}{AB} \Rightarrow AD = \dfrac{BD \times AC}{AB}$,
$\dfrac{AD}{AB} =\dfrac{DC}{AC} \Rightarrow AD = \dfrac{DC \times AB}{AC}$
$\Rightarrow AD^2 = BD \times DC$

$ii)$ Como $\triangle ABC \sim \triangle DBA$, $\dfrac{AB}{BD} =\dfrac{BC}{AB}$
$\Rightarrow AB^2 = BC \times BD$

$iii)$ Como $\triangle ABC \sim \triangle DAC$, $\dfrac{AC}{DC} =\dfrac{BC}{AC}$
$\Rightarrow AC^2 = BC \times DC$

$iv)$ de $ii)$ y $iii)$ tenemos $BC^2 = \dfrac{AB^2 \times AC^2}{BD \times DC}$
y empleando $i)$ obtenemos $AD^2 \times BC^2 = (BD \times DC) \dfrac{AB^2 \times AC^2}{BD \times DC}$
$\Rightarrow AD \times BC = AB \times AC$.

$\blacksquare$

Más adelante…

En la siguiente entrada comenzaremos a distinguir el sentido en el que recorremos un sementó de recta y si la razón en que un punto divide a un segmento es negativa o positiva. Haciendo uso de segmentos dirigidos mostraremos el teorema de Stewart.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra el teorema de Pitágoras usando semejanza de triángulos.
Criterio de semejanza hipotenusa-cateto, muestra que un par de triángulos rectángulos son semejantes si la razón entre sus hipotenusas y la razón entre uno de sus catetos son iguales.
Muestra que si en un triángulo dos bisectrices internas tienen la misma longitud, entonces el triángulo es isósceles.
Sean $\square ABCD$ un paralelogramo,$E \in CD$, $G$ y $F$ las intersecciones de $AE$ con $BD$ y $BC$ respectivamente (figura 6), encuentra $EF$ en términos de $AG$ y $GE$.

Sean $\square ABCD$ un paralelogramo, $E$, $F \in BD$ tales que $BE = DF$, $G = AE \cap BC$ y $H = AF \cap CD$ (figura 7), muestra que $GH \parallel BD$.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Teorema de Tales.
Siguiente entrada del curso: Segmento dirigido y teorema de Stewart.
Otros cursos.

Fuentes

Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 18-24.
Altshiller, N., College Geometry. New York: Dover, 2007, pp 72-73.
Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 6-11.
Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teorema de Pitágoras

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión veremos el teorema de Pitágoras que relaciona la hipotenusa de un triangulo rectángulo con la longitud de sus catetos, esta propiedad permite definir una métrica en el espacio euclidiano, en particular, con esto podemos calcular la longitud de un segmento si conocemos un triángulo rectángulo que tenga como hipotenusa dicho segmento.

Geométricamente el teorema de Pitágoras nos habla sobre el área de cuadrados construidos sobre los lados de un triángulo rectángulo, así que necesitamos presentar un concepto nuevo.

Definición. Definimos el área de un rectángulo como el producto de dos de sus lados adyacentes. De esta manera el área de un cuadrado será su lado al cuadrado.

Como las diagonales de todo rectángulo lo dividen en dos triángulos rectángulos congruentes, de la definición se sigue que el área de un triángulo rectángulo es el semiproducto de sus catetos.

Teorema de Pitágoras

Teorema 1, de Pitágoras. El área de un cuadrado de lado igual a la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de cuadrados de lados igual a los catetos del triángulo rectángulo.

Demostración. Consideremos un triángulo rectángulo de catetos $a$, $b$ e hipotenusa $c$.

Construimos un cuadrado $\square ABCD$ de lados $a + b$, y puntos $P \in AB$, $Q \in BC$, $R \in CD$ y $S \in AD$, tales que $AP = BQ = CR = DS = a$ y $BP = CQ = DR = AS = b$.

Como los ángulos en las esquinas son rectos entonces por criterio LAL
$\begin{equation} \triangle ASP \cong \triangle BPQ \cong \triangle CQR \cong \triangle DRS, \end{equation}$
en particular $PQ = QR = RS = SP$.

Por $(1)$, $\angle CQR$ y $\angle PQB$ son complementarios en consecuencia $\angle RQP = \dfrac{\pi}{2}$.

De manera análoga se ve que
$\angle SRQ = \angle QPS = \angle PSR = \angle RQP = \dfrac{\pi}{2}$.

Por lo tanto, $\square PQRS$ es un cuadrado de lado $c$.

Ahora construimos otro cuadrado $\square A’B’C’D’$ de lados $a + b$, y puntos $P’ \in A’B’$ y $Q’ \in B’C’$ tales que $A’P’ = B’Q’ = b$ y $B’P’ = C’Q’ = a$.

Trazamos una perpendicular a $A’B’$ por $P’$ que interseca a $C’D’$ en $R’$, y una perpendicular a $B’C’$ por $Q’$ que interseca a $A’D’$ en $S’$.

Como $A’B’ \parallel C’D’$ entonces $P’R’ \perp C’D’$, análogamente $Q’S’ \perp A’D’$ y entonces $P’R’ \perp Q’S’$.

Por lo tanto, $\square A’P’ES’$, $\square EQ’C’R’$, $\square P’B’Q’E$ y $\square S’ER’D’$ son rectángulos.

Como los lados opuestos de todo rectángulo son iguales, concluimos que $\square A’P’ES’$ y $\square EQ’C’R’$ son cuadrados de lados $b$ y $a$ respectivamente.

$B’E$ y $ED’$ dividen a $\square P’B’Q’E$ y $\square S’ER’D’$ en cuatro triángulos rectángulos congruentes entre si pues los rectángulos son congruentes.

Pero al mismo tiempo los triángulos en $\square A’B’C’D’$ son congruentes con los triángulos en $\square ABCD$, pues tienen los mismos lados $a$ y $b$, y todos son triángulos rectángulos.

Finalmente, como $\square ABCD$ y $\square A’B’C’D’$ son congruentes entonces sus áreas son iguales y podemos sustraer a cada uno el área de los cuatro triángulos resultando así que el área del cuadrado rosa es igual a la suma de las áreas de los cuadrados verde y naranja.

Por lo tanto, $c^2 = a^2 + b^2$.

$\blacksquare$

Reciproco del Teorema de Pitágoras

Teorema 2. Reciproco del teorema de Pitágoras. Si en un triángulo el cuadrado de uno de sus lados es igual a la suma de los cuadrados de los otros dos lados entonces el triángulo es rectángulo.

Demostración. Sea $\triangle ABC$ un triángulo tal que $AC^2 = AB^2 + BC^2$.

Construimos un punto $D$ del lado opuesto a $C$ respecto de $AB$ tal que $BD = BC$ y $BD \perp AB$.

Por construcción $\triangle ABD$ es rectángulo, por el teorema de Pitágoras, $AD^2 = AB^2 + BD^2$.

Como $BD = BC$ $\Rightarrow BD^2 = BC^2$, por lo tanto, $AD^2 = AB^2 + BC^2 = AC^2$.

Por hipótesis, $AC^2 = AB^2 + BC^2 \Rightarrow AD^2 = AC^2 \Rightarrow AD = AC$.

Por criterio LLL, $\triangle ABC \cong \triangle ADC$, en particular $\angle CBA = \angle ABC = \dfrac{\pi}{2}$.

$\blacksquare$

Caracterización de un ángulo interior

Sea $\triangle ABC$ entonces por los teoremas 1 y 2
$\angle B = \dfrac{\pi}{2} \Leftrightarrow AC^2 = AB^2 + BC^2$.

Ahora consideremos un triángulo $\triangle A’B’C’$ con $A’B’ = AB$ y $B’C’ = BC$ pero $\angle B’ > \dfrac{\pi}{2}$, entonces por la proposición 2 de la entrada desigualdad del triángulo y su reciproco, esto ocurre si y solo si $A’C’ > AC$
$\Leftrightarrow A’C’^2 > AC^2 = AB^2 + BC^2 = A’B’^2 + B’C’^2$

Por otra parte, si tenemos $\triangle A’’B’’C’’$ tal que $A’’B’’ = AB$ y $B’’C’’ = BC$ pero $\angle B’’ < \dfrac{\pi}{2}$, por el resultado antes mencionado, esto ocurre si y solo si $A’’C’’ < AC$
$\Leftrightarrow A’’C’’^2 < AC^2 = AB^2 + BC^2 = A’’B’’^2 + B’’C’’^2$

Resumiendo, tenemos lo siguiente para cualquier triángulo $\triangle ABC$, $\angle B$ es:

recto $\Leftrightarrow AC^2 = AB^2 + BC^2$,
obtuso $\Leftrightarrow AC^2 > AB^2 + BC^2$,
agudo $\Leftrightarrow AC^2 < AB^2 + BC^2$.

Ley del paralelogramo

Teorema 3, ley del paralelogramo. La suma de los cuadrados de los lados de un paralelogramo es igual a la suma de los cuadrados de sus diagonales.

Demostración. Sean $\square ABCD$ un paralelogramo, $E$ y $F$ los pies de las perpendiculares a $BC$ trazadas desde $A$ y $D$ respectivamente.

Recordemos que los lados opuestos de un paralelogramo son iguales, por lo que $AB = CD$ y $AD = BC$, además $\square AEFD$ es un rectángulo y todo rectángulo es paralelogramo, por lo tanto, $AE = DF$ y $EF = AD = BC$, $\Rightarrow BE = CF$.

Aplicando el teorema de Pitágoras a los triángulos $\triangle ABE$, $\triangle DBF$ y $\triangle AEC$ obtenemos:

$\begin{equation} AB^2 = AE^2 + BE^2. \end{equation}$

$DB^2 = DF^2 + BF^2$
$= AE^2 + (BC + CF)^2 = AB^2 – BE^2 + (BC + BE)^2$
$= AB^2 – BE^2 +BC^2 + 2BC \times BE + BE^2$
$\begin{equation} = AB^2 + BC^2 + 2BC \times BE. \end{equation}$

$AC^2 = AE^2 + EC^2$
$= AE^2 + (BC – BE)^2 = AB^2 – BE^2 + BC^2 -2BC \times BE + BE^2$
$\begin{equation} = AB^2 + BC^2 -2BC \times BE. \end{equation}$

Sumamos $(3)$ y $(4)$ para obtener
$AC^2 + BD^2 = 2AB^2 + 2BC^2$.

$\blacksquare$

Teorema de Apolonio

Teorema 4, de Apolonio. En todo triangulo la suma de los cuadrados de dos lados es igual a dos veces el cuadrado de la mitad del tercer lado más dos veces el cuadrado de la mediana que biseca al tercer lado.

Demostración. Sean $\triangle ABC$ y $M$ el punto medio de $BC$. Por demostrar que $AB^2 + AC^2 = 2(BM^2 + AM^2)$.

Sea $D$ el pie de la perpendicular a $BC$ trazada desde $A$, aplicamos el teorema de Pitágoras a los triángulos $\triangle ADM$, $\triangle ADB$ y $\triangle ADC$.

$\begin{equation} AM^2 = AD^2 + DM^2. \end{equation}$

$AB^2 = AD^2 + BD^2$
$= AM^2 – DM^2 + (DM – BM)^2 = AM^2 – DM^2 + DM^2 – 2DM \times BM + BM^2$
$\begin{equation} = AM^2 + BM^2 – 2DM \times BM. \end{equation}$

$AC^2 = AD^2 + DC^2$
$= AM^2 – DM^2 + (DM + MC)^2 = AM^2 – DM^2 +DM^2 + 2DM \times MC + MC^2$
$\begin{equation} = AM^2 + 2DM \times MC + MC^2. \end{equation}$

Como $BM = MC$ sumando $(6)$ y $(7)$ obtenemos
$AB^2 + AC^2 = 2AM^2 + 2MC^2$.

$\blacksquare$

Caracterización de las alturas de un triángulo

Proposición. Sean $BC$ un segmento y $P$ un punto en el plano, considera $D$ el pie de la perpendicular a $BC$ trazada desde $P$, entonces $PB^2 – PC^2 = DB^2 – DC^2$.

Demostración. Los triángulos $\triangle PDB$ y $\triangle PDC$ son rectángulos, por el teorema de Pitágoras tenemos que $PB^2 = PD^2 + DB^2$ y $PC^2 = PD^2 + DC^2$.

Despejando $PD^2$ de ambas ecuaciones e igualando tenemos que $PB^2 – DB^2 = PC^2 – DC^2$
$\Rightarrow PB^2 – PC^2 = DB^2 – DC^2$.

$\blacksquare$

Teorema 5. Sea $\triangle ABC$ un triángulo entonces un punto $P$ está en la altura por $A$ si y solo si $PB^2 – PC^2 = AB^2 – AC^2$.

Demostración. Supongamos que $P$ es un punto en la altura desde $A$ entonces podemos considerar el triángulo $\triangle PBC$.

Por la proposición tenemos que los puntos $P$ y $A$ cumplen que $PB^2 – PC^2 = DB^2 – DC^2$ y $AB^2 – AC^2 = DB^2 – DC^2$ donde $D$ es el pie de la altura.

Por lo tanto $PB^2 – PC^2 = AB^2 – AC^2$.

$\blacksquare$

Ahora supongamos que $P$ es un punto en el plano tal que $PB^2 – PC^2 = AB^2 – AC^2$ por la proposición sabemos que $AB^2 – AC^2 = DB^2 – DC^2$, con $D$ el pie de la altura desde $A$.

Por transitividad se tiene que $PB^2 – PC^2 = DB^2 – DC^2$.

Sea $E$ el pie de la perpendicular a $BC$ trazada desde $P$, nuevamente por la proposición tenemos que $PB^2 – PC^2 = EB^2 – EC^2$ $\Rightarrow DB^2 – DC^2 = EB^2 – EC^2$

Supongamos que $D$ está en el segmento $BC$ y $E$ fuera del segmento y del lado de $B$ (figura 9), otros casos se muestran de manera similar, entonces $EB = ED – BD$ y $EC = ED + DC$.

$\Rightarrow DB^2 – DC^2 = (ED – BD)^2 – (ED + DC)^2$
$= ED^2 – 2ED \times BD + BD^2 – ED^2 – 2ED \times DC – DC^2$
$\Rightarrow 0 = ED \times BD + ED \times DC = ED(BD + DC)$

Como $BD + DC \neq 0 \Rightarrow ED = 0$
$\Rightarrow E = D$

De esto se concluye que $P$ está en la altura trazada desde $A$.

$\blacksquare$

Más adelante…

En la siguiente entada estudiaremos el teorema de Tales también conocido como teorema de la proporcionalidad.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Dado un segmento unitario construye un segmento de longitud $\sqrt{2}$, $\sqrt{3}$, $\sqrt{5}$ …
Si $a$, $b$, $c$, $d$, y $e$ son las longitudes de cinco segmentos tales que con cualesquiera tres de ellos es posible construir un triángulo, muestra que al menos uno de los triángulos es acutángulo.
Sea $P$ un punto en el interior de $\triangle ABC$, considera $D$, $E$ y $F$ las proyecciones de $P$ a los lados $BC$, $AC$ y $AB$ respectivamente, expresa $AE$ en términos de $AF$, $FB$, $BD$, $DC$ y $CE$.
Muestra que en un triángulo con ángulos interiores iguales a $\dfrac{\pi}{2}$, $\dfrac{\pi}{3}$ y $\dfrac{\pi}{6}$, se tiene que el cateto opuesto al ángulo de $\dfrac{\pi}{6}$ es igual a la mitad de la hipotenusa y el cateto opuesto al ángulo de $\dfrac{\pi}{3}$ es igual a $\dfrac{\sqrt{3}}{2}$ veces la hipotenusa.
Si dos de los lados de un triángulo miden $a$ y $b$ y el ángulo entre ellos mide $\dfrac{3\pi}{4}$ encuentra la longitud del segmento medio entre los lados dados.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Paralelogramos.
Siguiente entrada del curso: Teorema de Tales.

Fuentes

Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 22-27, 43-44.
Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 11-14.
Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 39-41.
Wikipedia
Geometría interactiva
Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»