Introducción
Dados un ángulo y una circunferencia nos podemos preguntar si podemos calcular la magnitud del ángulo dado con algún ángulo que tenga como vértice el centro de la circunferencia dada. En esta entrada estudiaremos algunos resultados que nos permitirán establecer dicha relación.
Definición 1. Un ángulo central en una circunferencia es un ángulo formado por dos radios.
Denotamos a una circunferencia con centro en $O$ como $\Gamma (O)$.
Ángulo inscrito
Definición 2. Decimos que un segmento es una cuerda de una circunferencia si sus extremos pertenecen a la circunferencia y el segmento no contiene al centro de la circunferencia, si contiene al centro entonces es un diámetro.
Un ángulo inscrito en una circunferencia es un ángulo formado por dos cuerdas o una cuerda y un diámetro que tienen un extremo en común sobre la circunferencia.
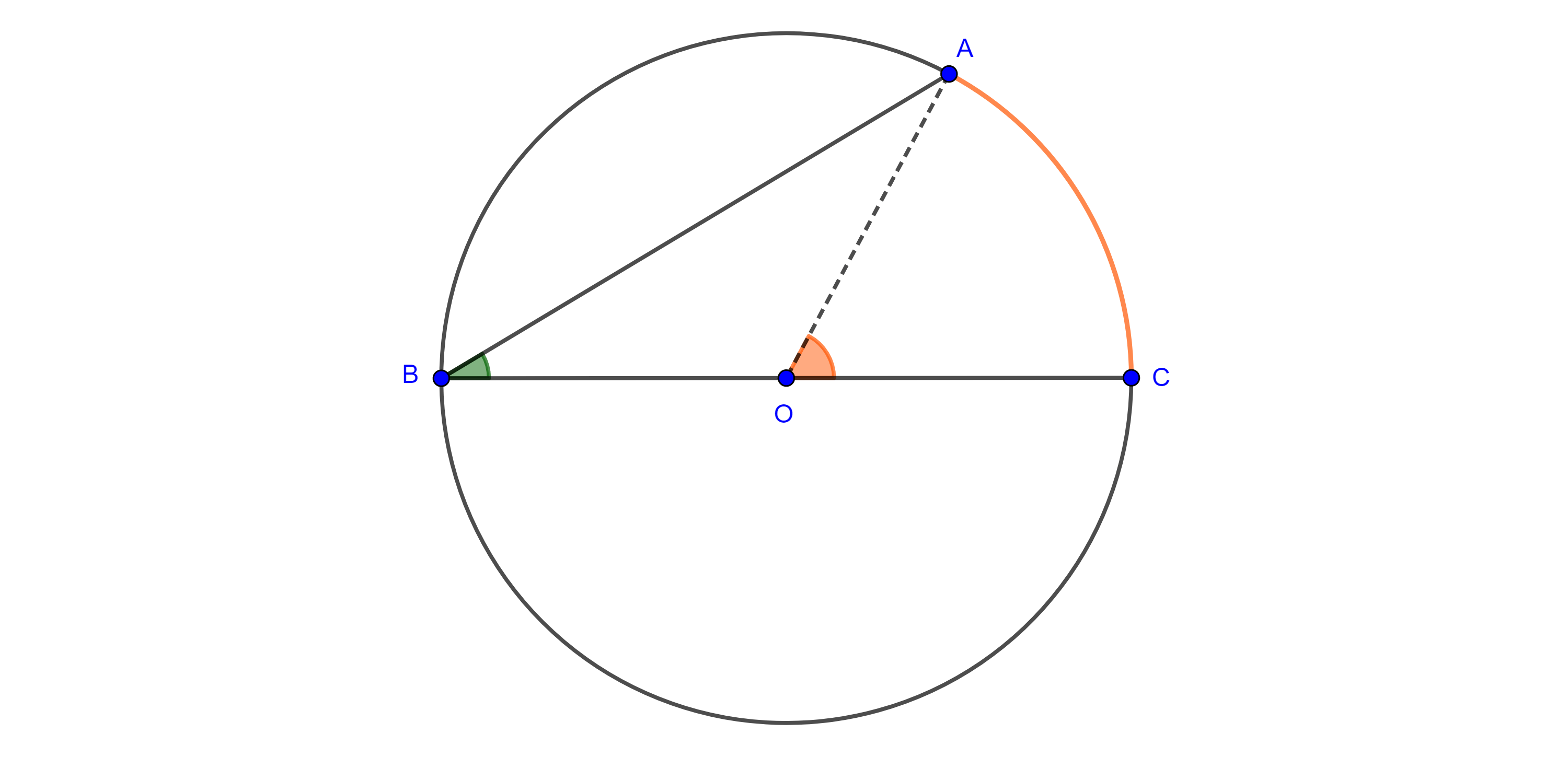
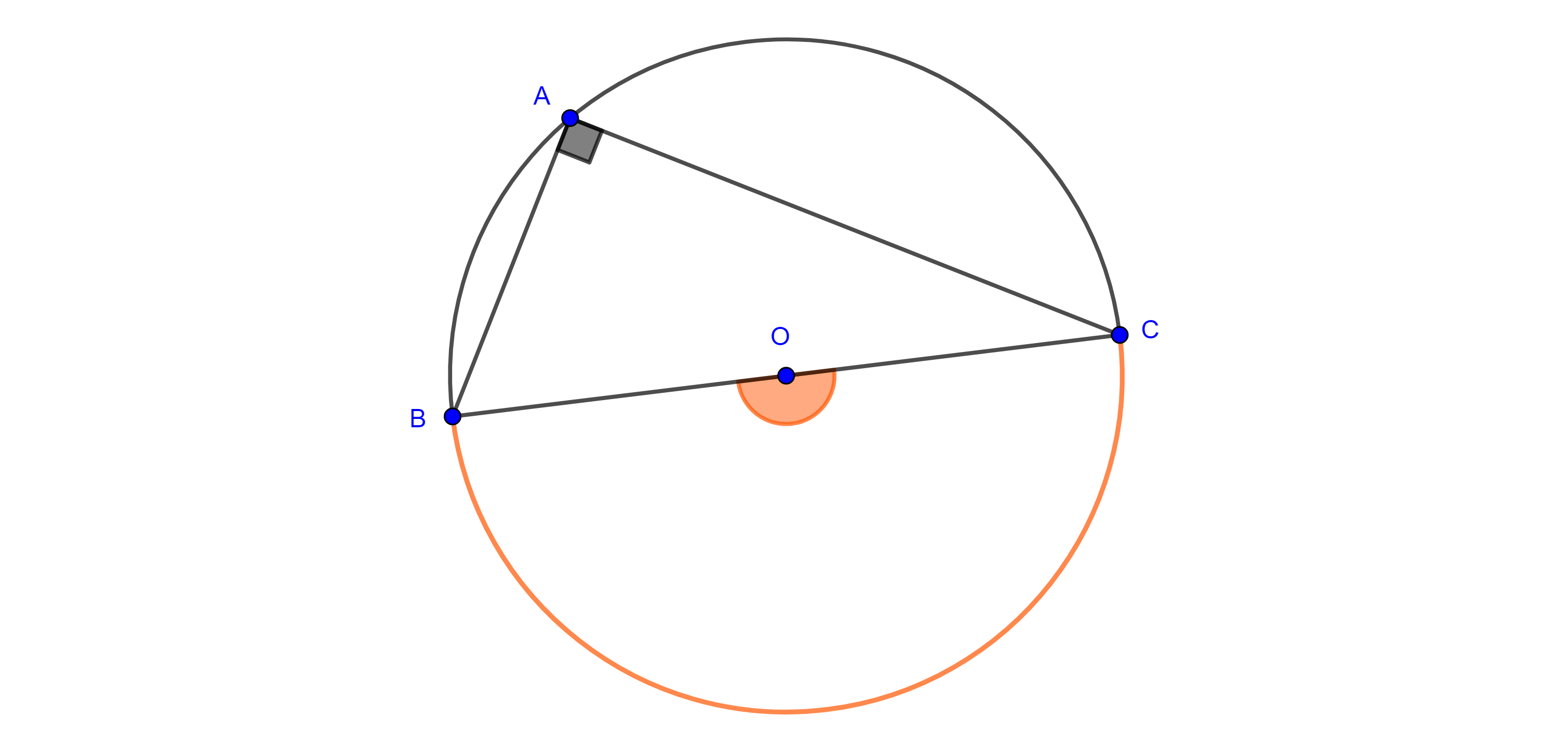
Teorema 1, de la medida del ángulo inscrito. Un ángulo inscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.
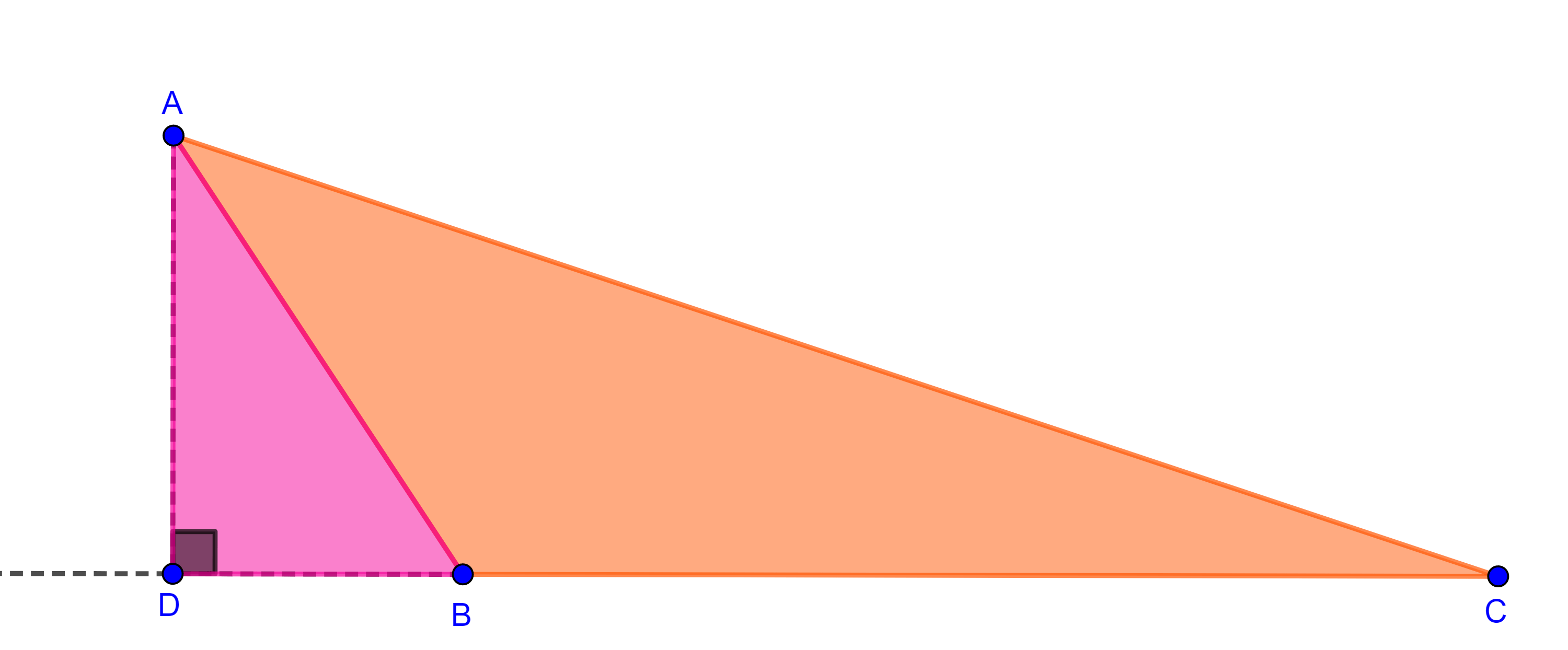
Demostración. Sea $\angle CBA$ un ángulo inscrito en $\Gamma (O)$.
Caso 1. $BC$ es diámetro, entonces $\triangle AOB$ es isósceles y por tanto $\angle BAO = \angle CBA$.
Como $\angle COA$ es un ángulo exterior de $\triangle AOB$ entonces es igual a la suma de los ángulos interiores no adyacentes a él,
$\Rightarrow \angle COA = \angle CBA + \angle BAO = 2\angle CBA$
$\Rightarrow \angle CBA = \dfrac{\angle COA}{2}$.
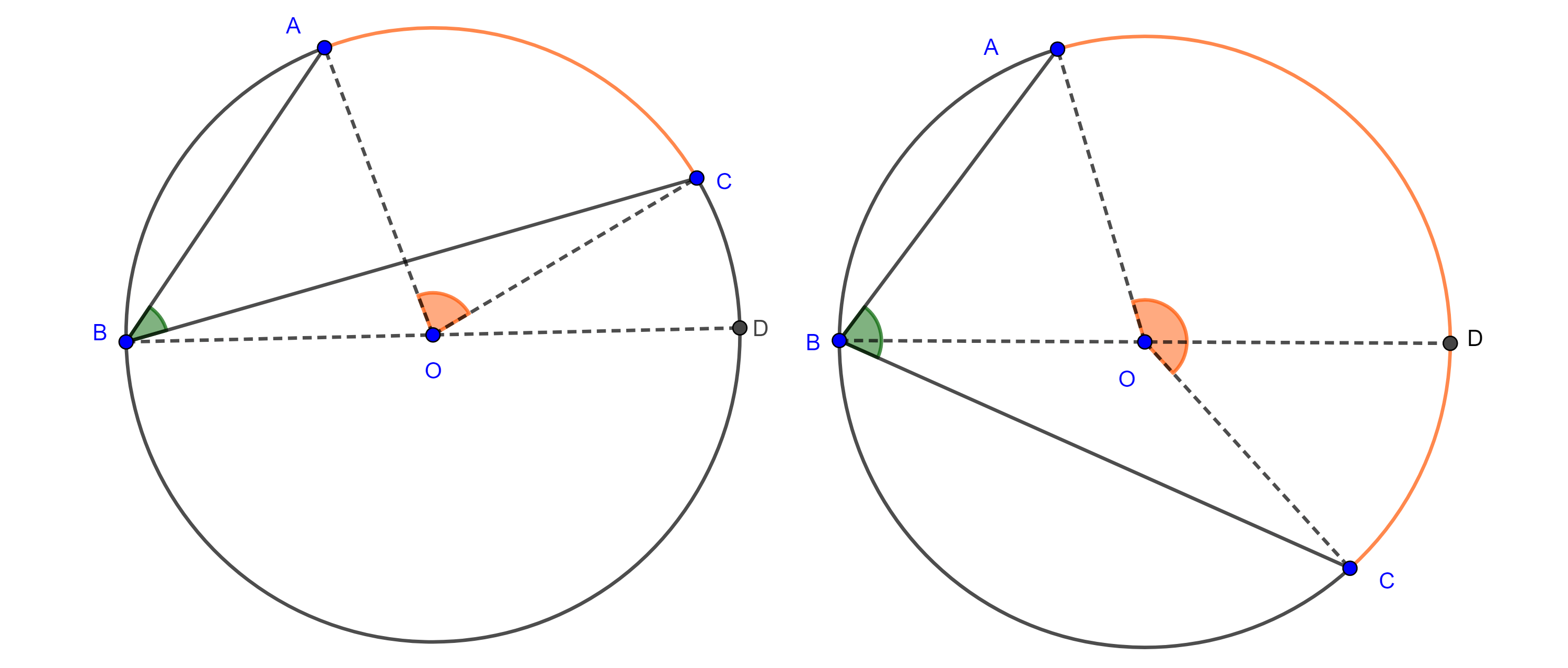
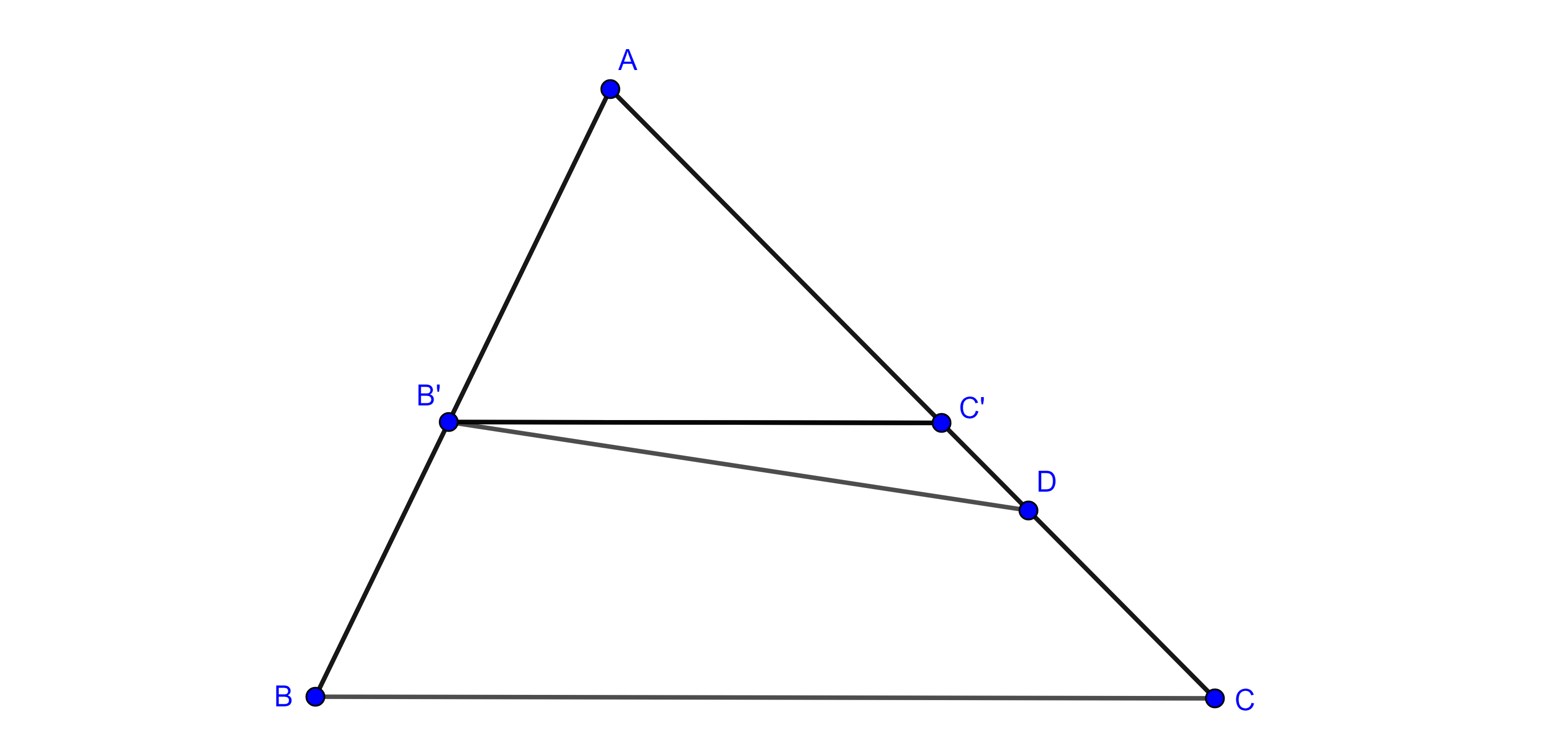
Caso 2. Ambos lados del ángulo son cuerdas, trazamos el diámetro $BO$ y consideramos $D = BO \cap \Gamma (O)$.
Si $AB$ y $BC$ están en un mismo lado respecto de $BD$ (izquierda figura 2), entonces
$\angle CBA = \angle DBA – \angle DBC$ y por el caso 1,
$\Rightarrow \angle CBA = \dfrac{\angle DOA}{2} – \dfrac{\angle DOC}{2} = \dfrac{\angle COA}{2}$.
Si $AB$ y $BC$ están en lados distintos respecto de $BD$ (derecha figura 2), entonces
$\angle CBA = \angle CBD + \angle DBA$ y por el caso 1,
$\Rightarrow \angle CBA = \dfrac{\angle COD}{2} + \dfrac{\angle DOA}{2} = \dfrac{\angle COA}{2}$.
$\blacksquare$
Ángulo semiinscrito
Definición 3. Decimos que una recta es tangente a una circunferencia en un punto si la recta es perpendicular al radio que pasa por el punto.
Definición 4. Decimos que un ángulo es semiinscrito en una circunferencia, si el ángulo está formado por una recta tangente a la circunferencia y una cuerda que tiene como extremo el punto de tangencia.
Teorema 2, de la medida del ángulo semiinscrito. Un ángulo semiinscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.
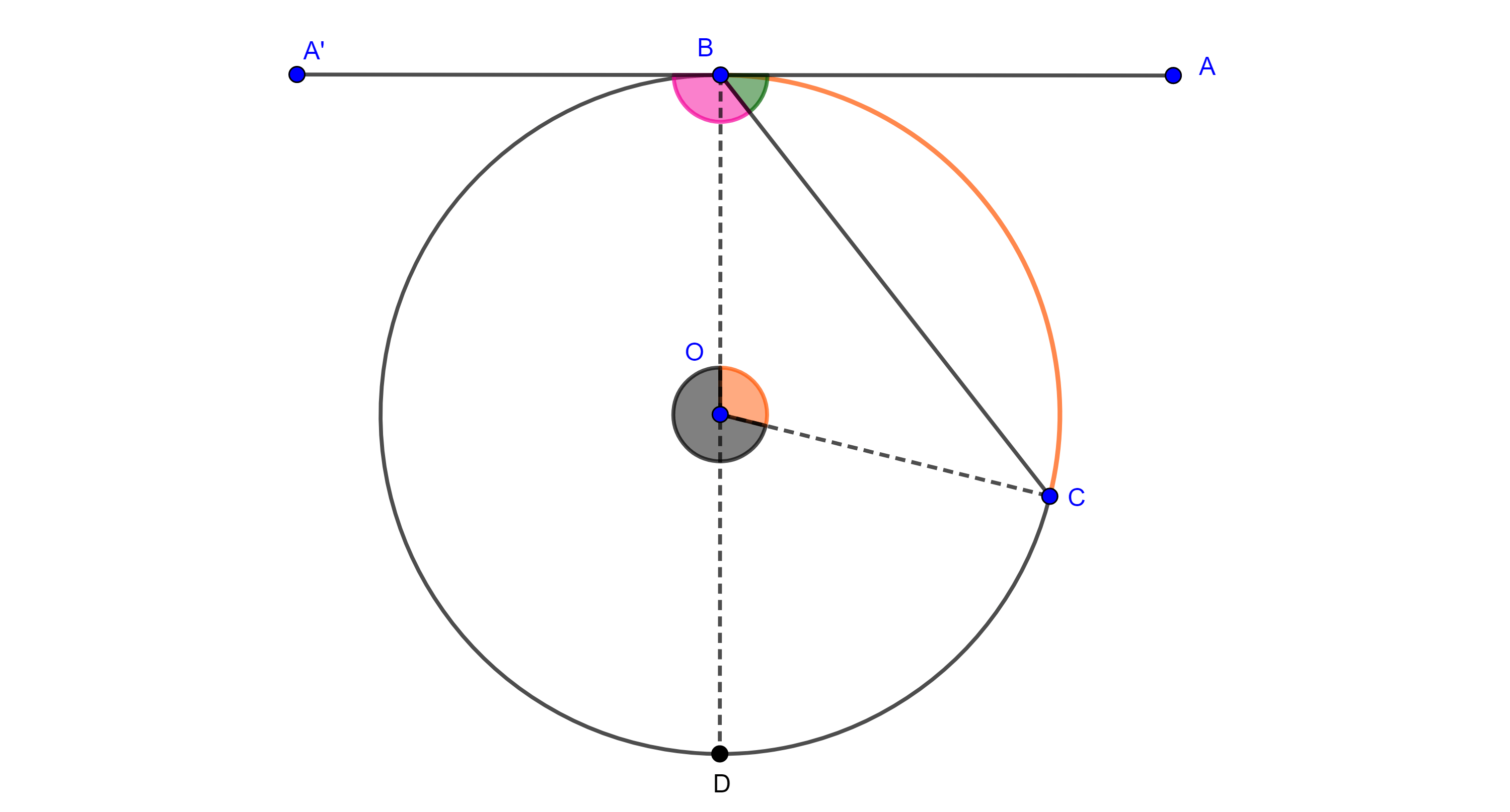
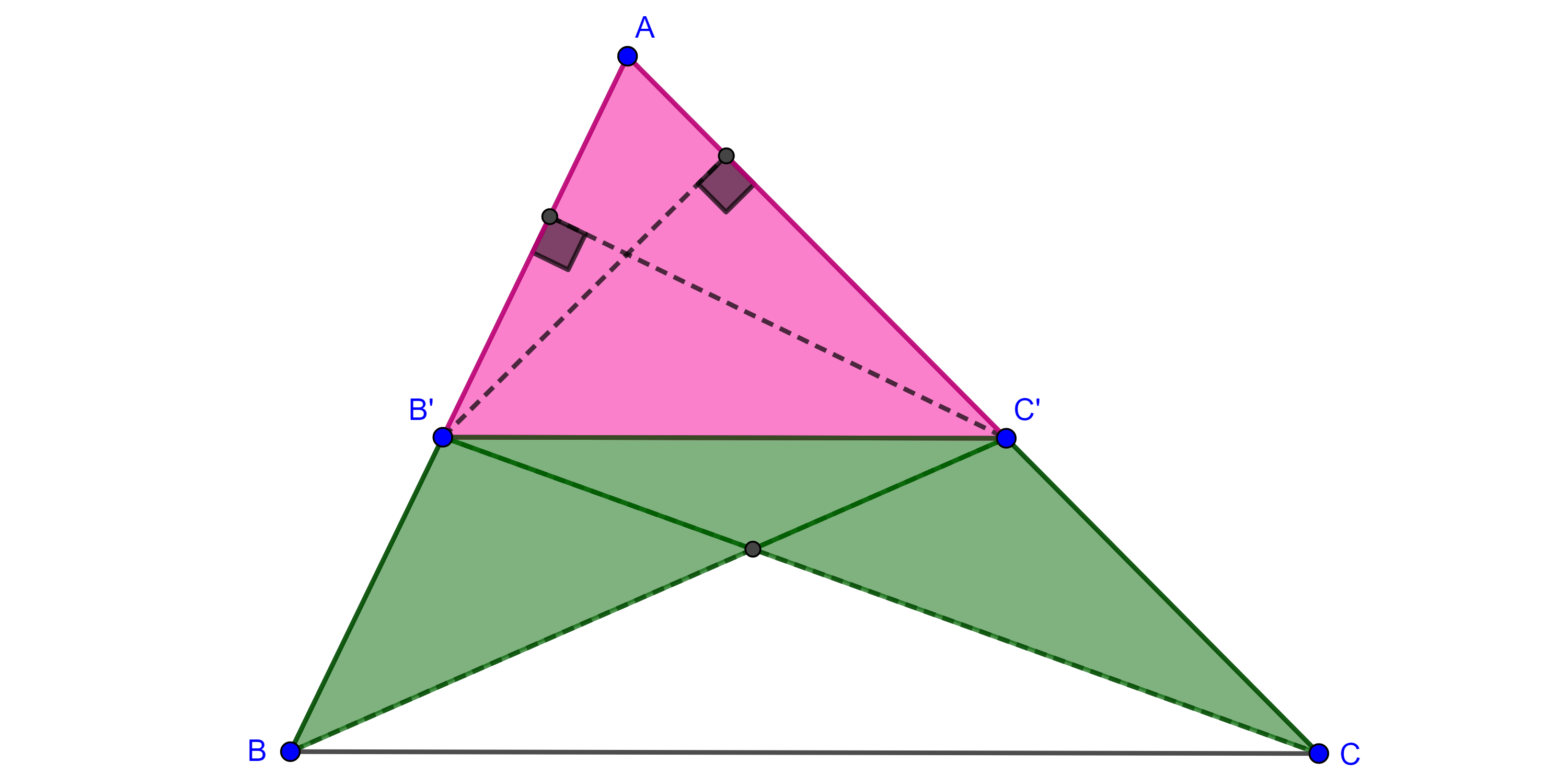
Demostración. Sea $\angle CBA$ un ángulo inscrito en $\Gamma (O)$, con $AB$ tangente a $\Gamma (O)$ en $B$, consideremos $D = BO \cap \Gamma (O)$.
$\angle DBC$ es inscrito, por el teorema 1, $\angle DBC = \dfrac{\angle DOC}{2}$
$\Rightarrow \angle CBA = \angle DBA – \angle DBC = \dfrac{\pi}{2} – \dfrac{\angle DOC}{2}$
$= \dfrac{\angle DOB}{2} – \dfrac{\angle DOC}{2} = \dfrac{\angle COB}{2}$.
Por otro lado, consideremos $A’ \in AB$ pero del lado opuesto a $A$ respecto de $B$, entonces,
$\angle A’BC = \angle ABD + \angle DBC = \dfrac{\pi}{2} + \dfrac{\angle DOC}{2}$
$= \dfrac{\angle BOD}{2} + \dfrac{\angle DOC}{2} = \dfrac{\angle BOC}{2}$.
$\blacksquare$
Ángulo interior
Definición 5. Si el vértice de un ángulo está en el interior de una circunferencia decimos que el ángulo es interior a la circunferencia.
Teorema 3, de la medida del ángulo interior. Un ángulo interior a una circunferencia es igual a la semisuma del ángulo central que abarca el mismo arco que el ángulo interior y del ángulo central que abarca el mismo arco que el opuesto por el vértice.
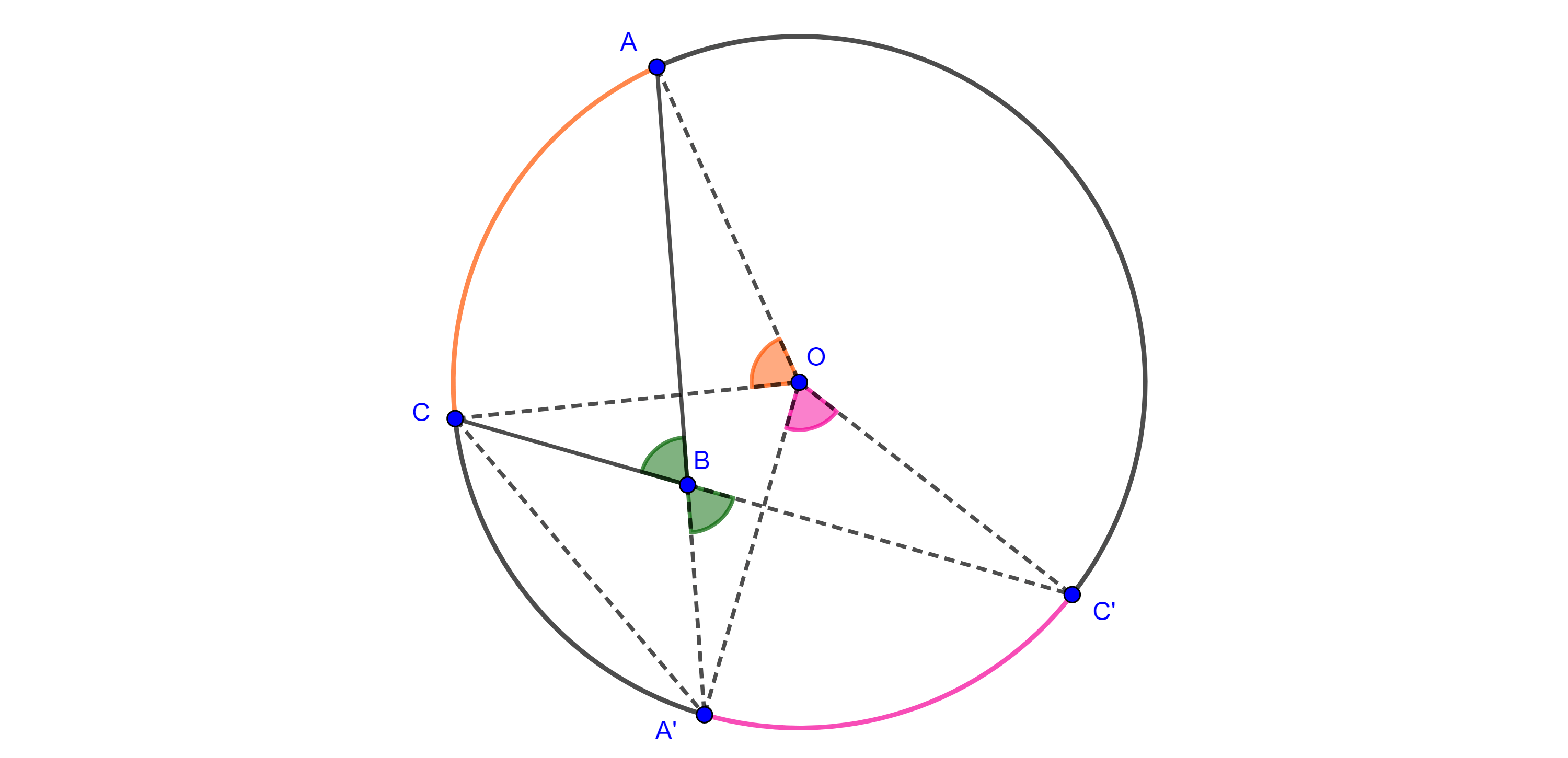
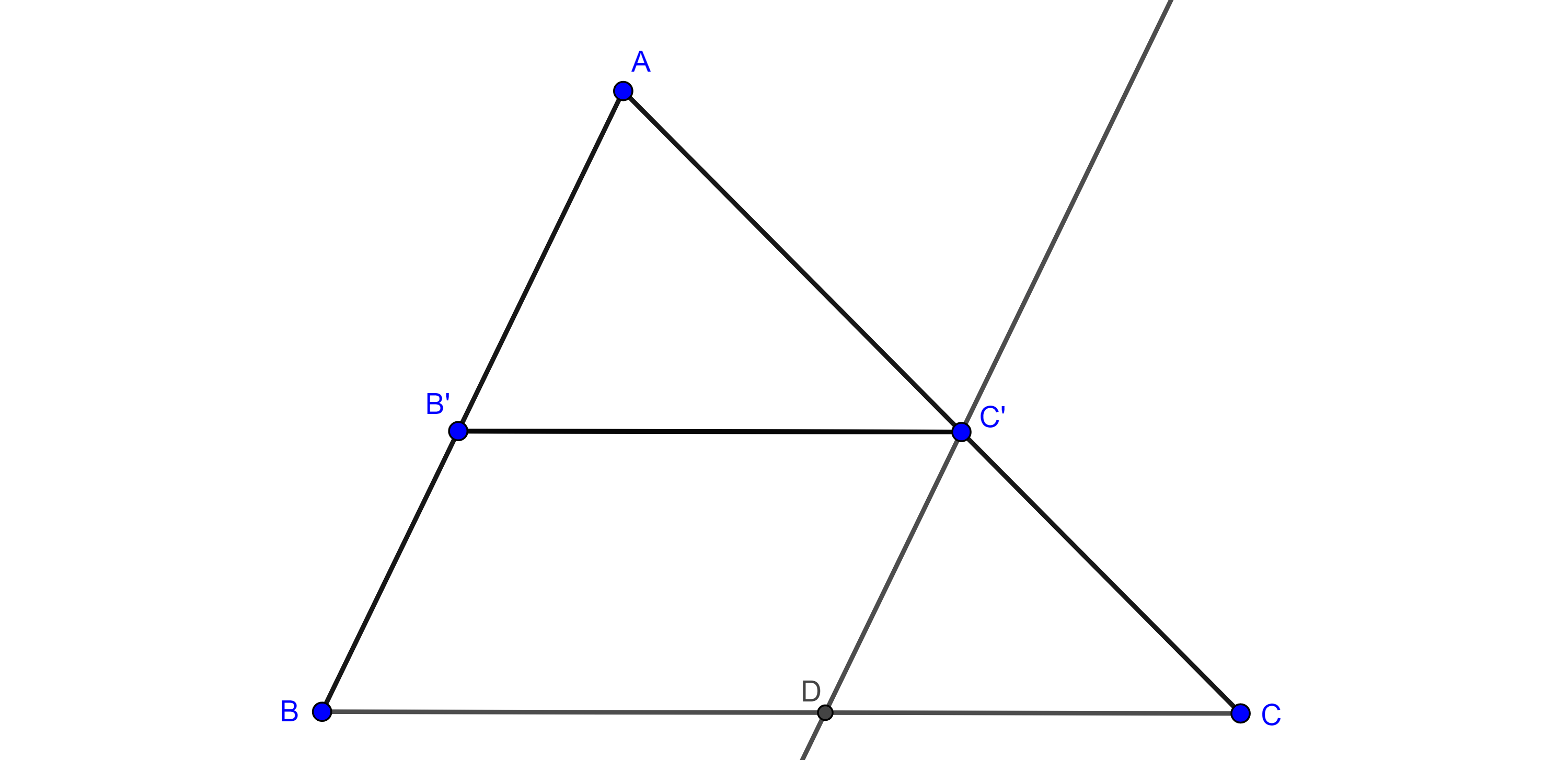
Demostración. Sea $\angle ABC$ un ángulo interior a $\Gamma (O)$ con $A$, $C \in \Gamma (O)$, consideremos $A’ = AB \cap \Gamma (O)$ y $C’ = CB \cap \Gamma (O)$.
Como $\angle ABC$ es un ángulo exterior de $\triangle A’BC$ es igual a la suma de los ángulos interiores no adyacentes a él, además $\angle AA’C$ y $\angle A’CC’$ son inscritos y por el teorema 1,
$\Rightarrow \angle ABC = \angle AA’C + \angle A’CC’ = \dfrac{\angle AOC + \angle A’OC’}{2}$.
$\blacksquare$
Ángulo exterior (lados secantes)
Definición 6. Una recta secante a una circunferencia es una recta que la interseca en dos puntos distintos.
Definición 7. Decimos que un ángulo es exterior a una circunferencia si su vértice se encuentra fuera de la circunferencia y los lados que forman el ángulo son tangentes o secantes a la circunferencia.
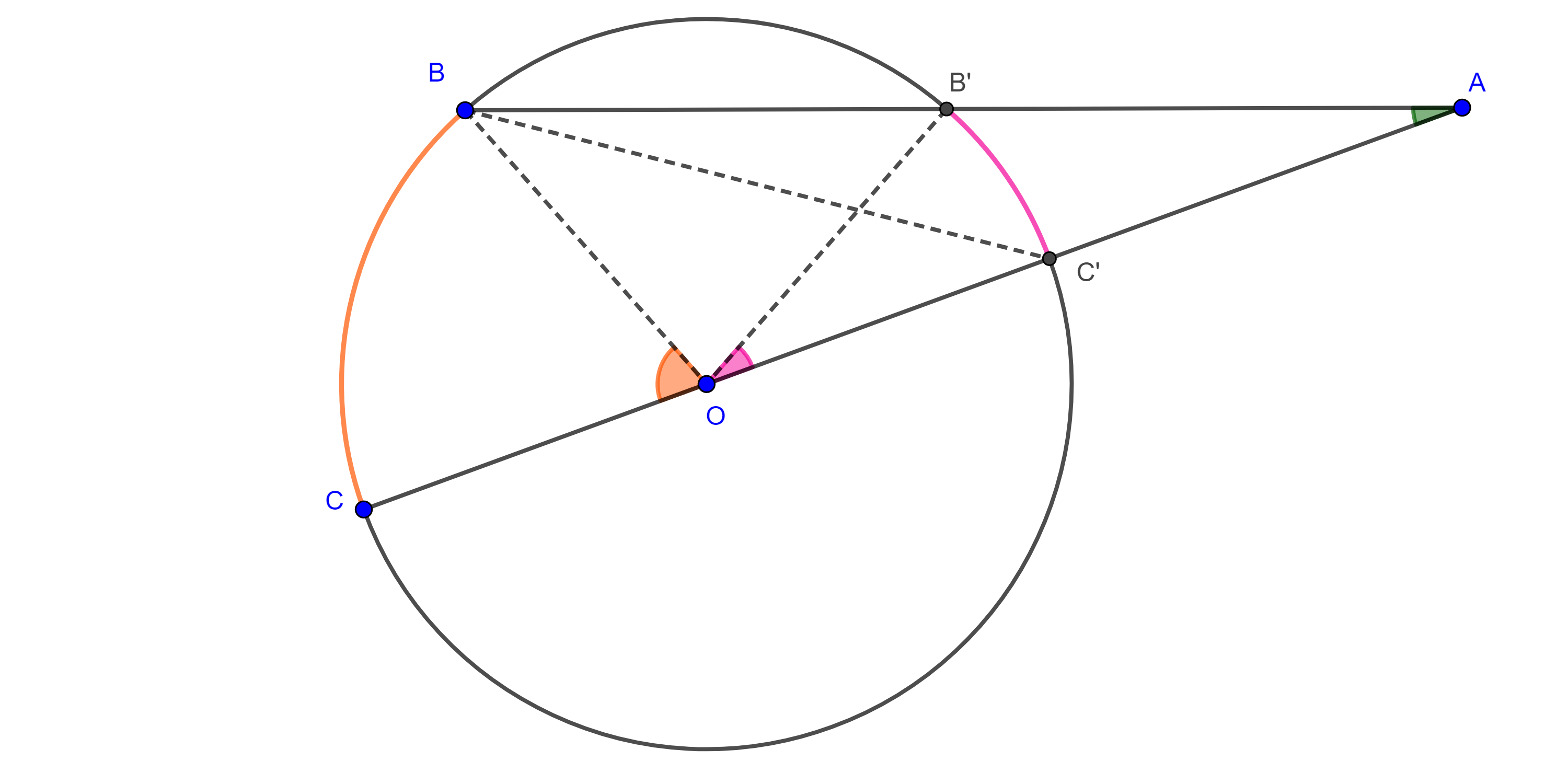
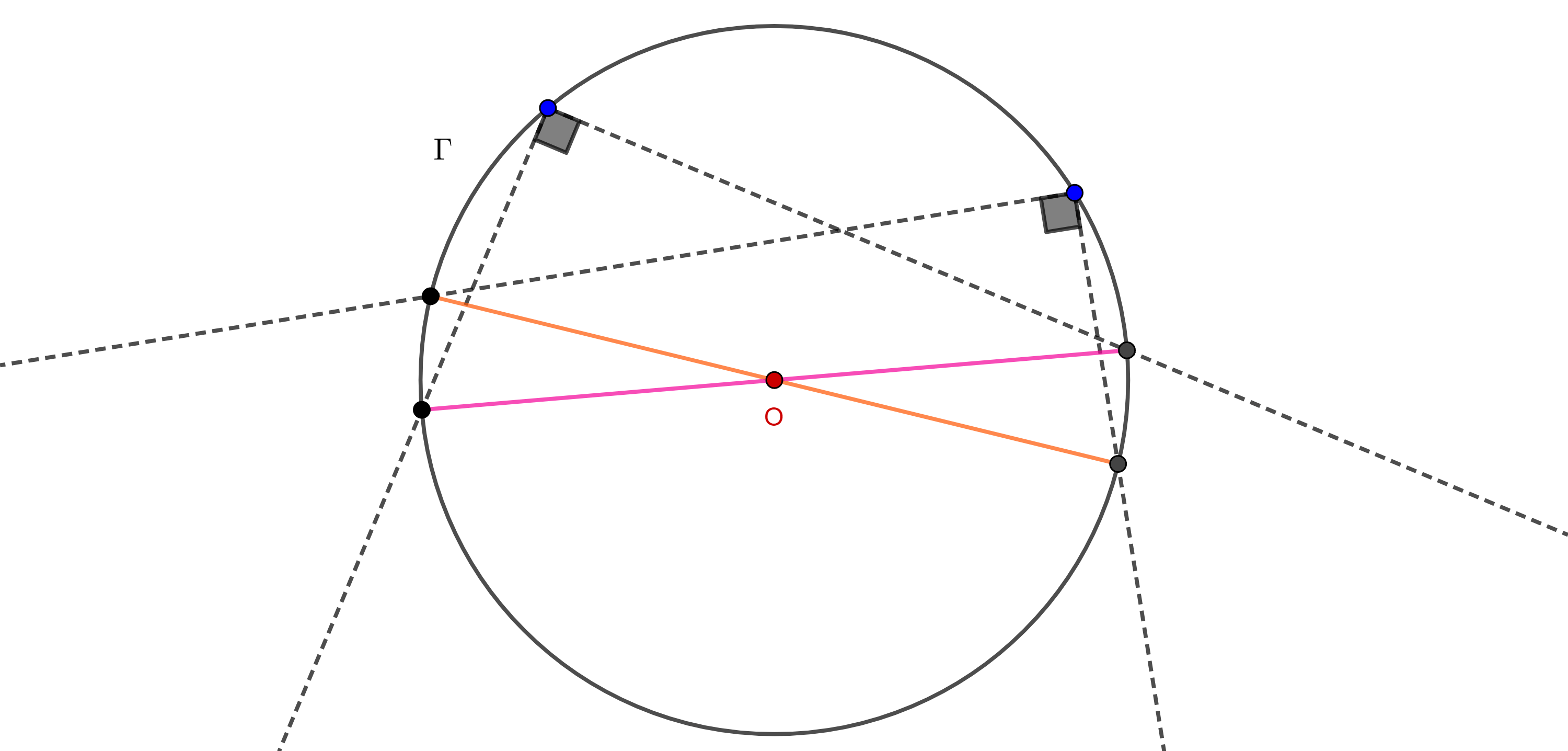
Teorema 4, de la medida del ángulo exterior. Un ángulo exterior a una circunferencia es igual a la mitad de la diferencia de los ángulos centrales que abarcan arcos cuyos extremos son las intersecciones de cada lado del ángulo con la circunferencia.
Caso 1. Ambos lados del ángulo son secantes a la circunferencia.
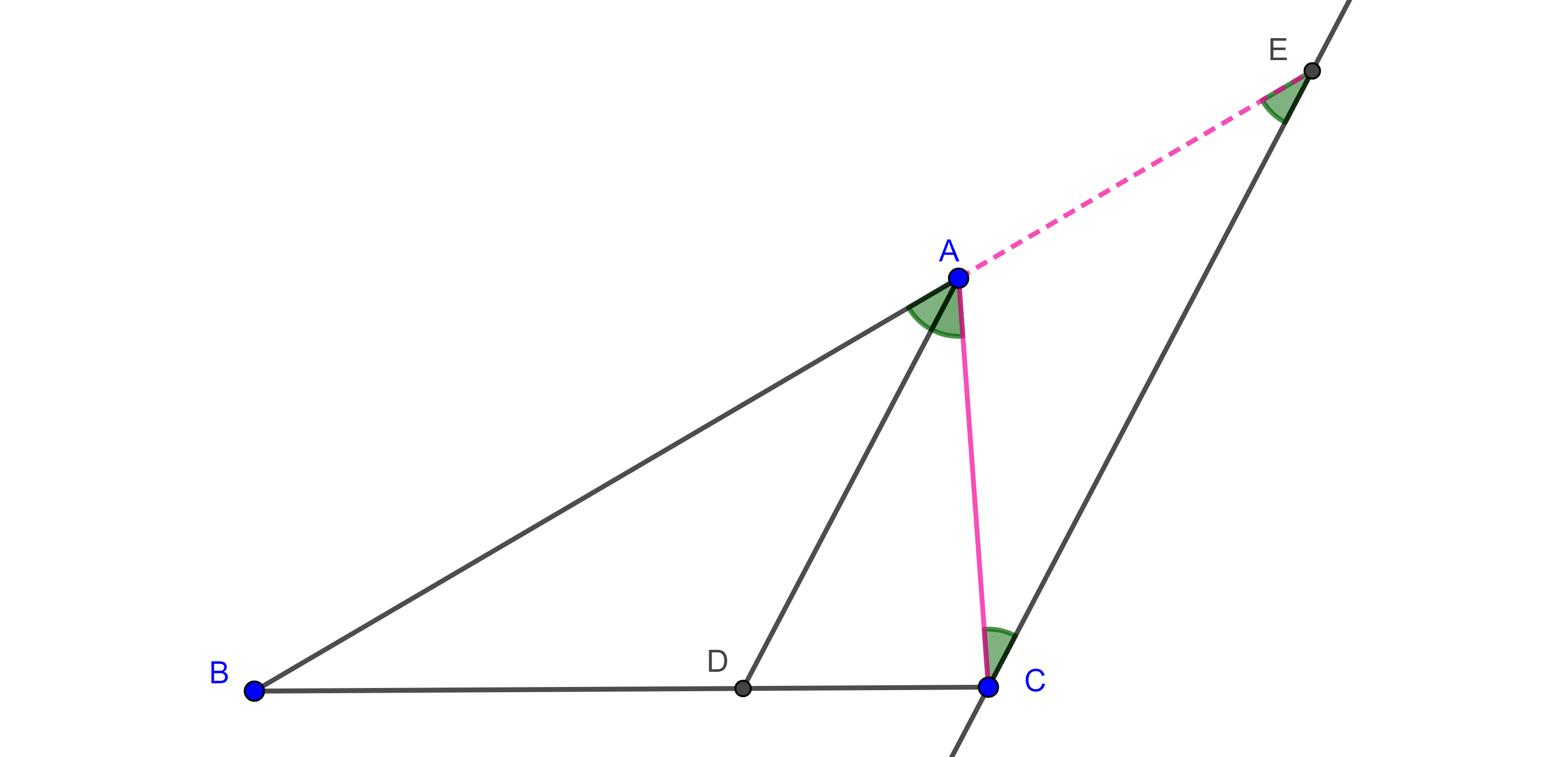
Demostración. Sea $\angle BAC$ un ángulo exterior a $\Gamma (O)$.
Supongamos que $B$, $C \in \Gamma (O)$ y consideremos $B’ = AB \cap \Gamma (O)$ y $C’ = AC \cap \Gamma (O)$.
Veamos primero el caso particular en el que $CC’$ es diámetro entonces $\angle BC’C$ es un ángulo exterior de $\triangle AC’B$, por tanto,
$\angle BC’C = \angle A + \angle C’BB’$
Como $\angle BC’C$ y $\angle C’BB’$ son ángulos inscritos, por el teorema 1,
$\Rightarrow \angle A = \angle BC’C – \angle C’BB’ = \dfrac{\angle BOC – \angle C’OB’}{2}$.
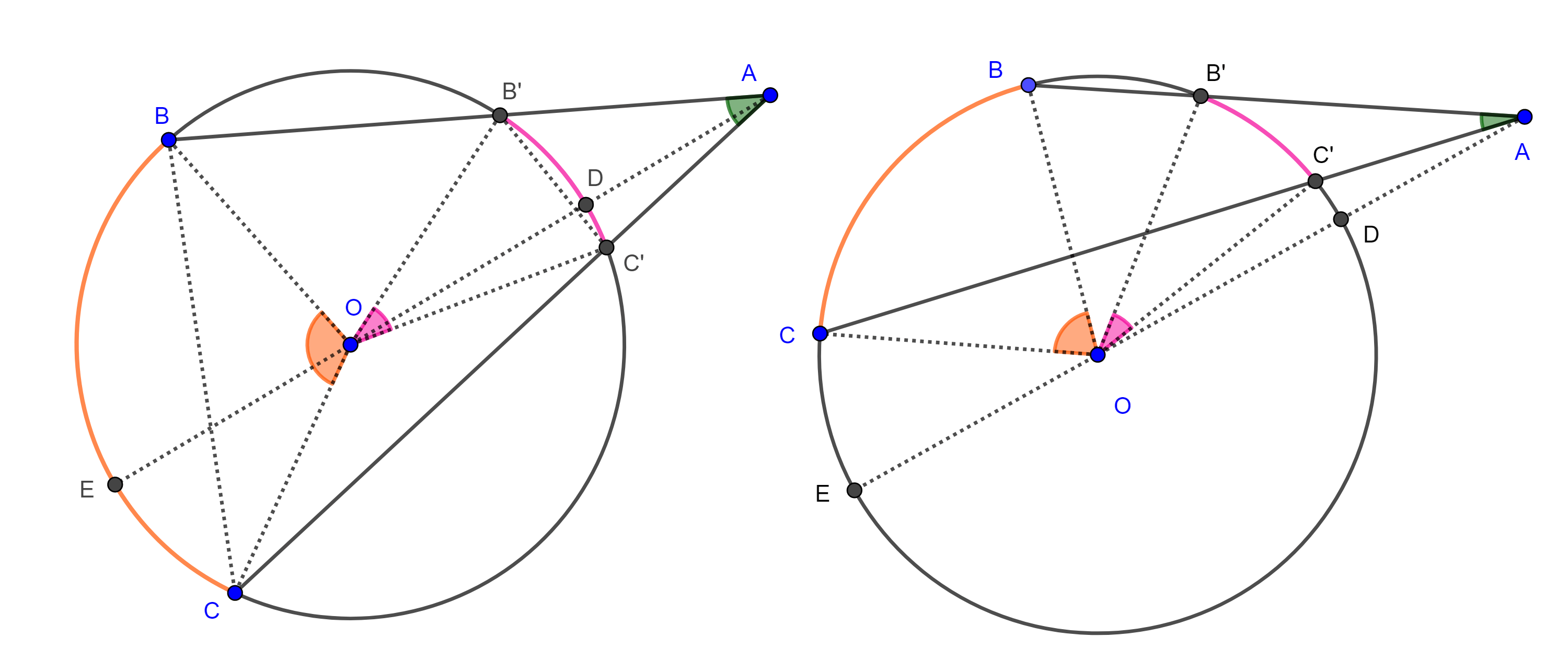
Para el caso general sean $D$ y $E$ las intersecciones de $AO$ con $\Gamma (O)$.
Si $B$ y $C$ están en lados distintos respecto de $DE$ (izquierda figura 6), entonces
$\angle A = \angle BAE + \angle EAC$, y por el caso particular,
$\Rightarrow \angle BAE = \dfrac{\angle BOE – \angle DOB’}{2}$ y $\angle EAC = \dfrac{\angle EOC – \angle C’OD}{2}$
$\Rightarrow \angle A = \dfrac{\angle BOE + \angle EOC – (\angle C’OD + \angle DOB’)}{2} = \dfrac{\angle BOC – \angle C’OB’}{2}$.
Si $B$ y $C$ están en el mismo lado respecto de $DE$ (derecha figura 6), entonces
$\angle BAC = \angle BAE – \angle CAE$ y por el caso particular,
$\angle BAE = \dfrac{\angle BOE – \angle DOB’}{2}$ y $\angle CAE = \dfrac{\angle COE – \angle DOC’}{2}$
$\Rightarrow \angle A = \angle BAC = \dfrac{(\angle BOE – \angle COE) – (\angle DOB’ – \angle DOC’)}{2} = \dfrac{\angle BOC – \angle C’OB’}{2}$.
$\blacksquare$
Ángulo exterior (lados tangentes)
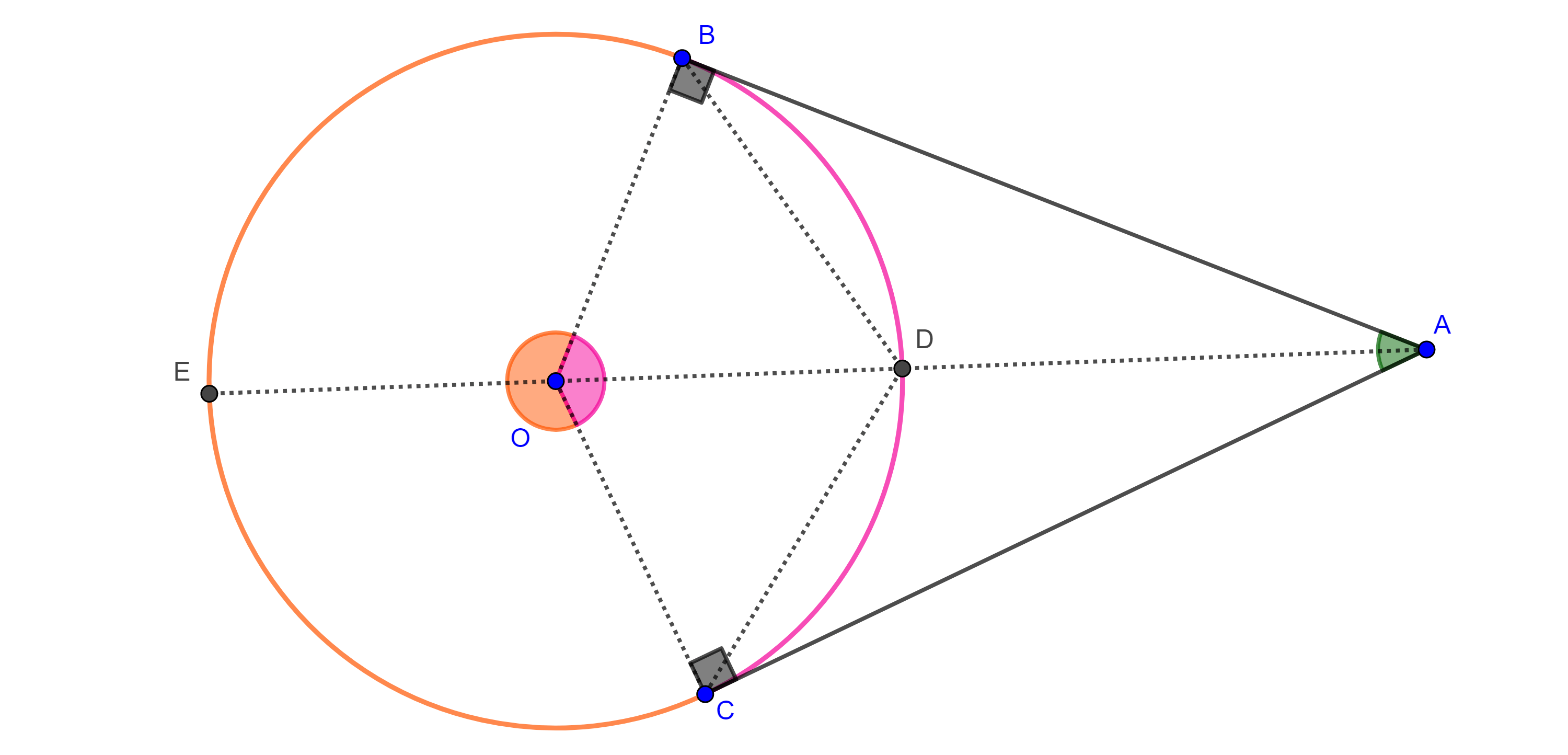
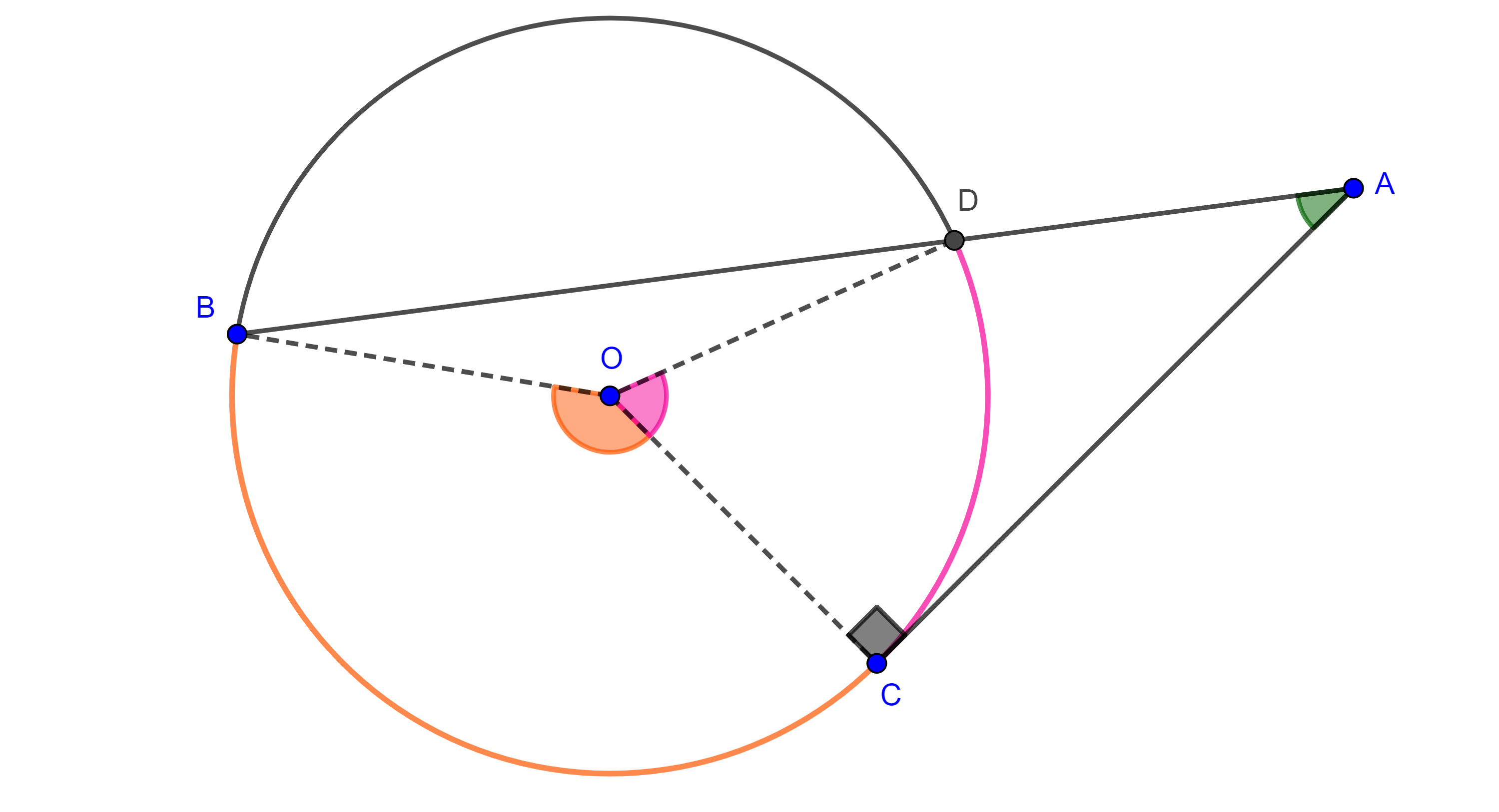
Caso 2. Ambos lados del ángulo son tangentes a la circunferencia.
Demostración. Sea $\angle BAC$ un ángulo exterior a $\Gamma (O)$.
Supongamos que $B$, $C \in \Gamma (O)$ y consideremos $D$ y $E$ las intersecciones de $AO$ con $\Gamma (O)$.
Como $\angle BDE$ y $\angle EDC$ son ángulos exteriores de $\triangle ADB$ y $\triangle ADC$ respectivamente, entonces
$\angle BDE = \angle BAD + \angle DBA$ y $\angle EDC = \angle DAC + \angle ACD$
$\Rightarrow \angle A = \angle BAD + \angle DAC = (\angle BDE – \angle DBA) + (\angle EDC – \angle ACD)$
$ = (\angle BDE + \angle EDC) – (\angle ACD + \angle DBA) = \angle BDC – (\angle ACD + \angle DBA)$
$\angle ACD$ y $\angle DBA$ son ángulos semiinscritos y $\angle BDC$ es un ángulo inscrito, por los teoremas 1 y 2 tenemos
$\angle ACD = \dfrac{\angle COD}{2}$, $\angle DBA = \dfrac{\angle DOB}{2}$ y $\angle BDC = \dfrac{\angle BOC}{2}$,
$\Rightarrow \angle A = \dfrac{\angle BOC – (\angle COD + \angle DOB)}{2} = \dfrac{\angle BOC – \angle COB}{2}$.
$\blacksquare$
Caso 3. Un lado del ángulo es tangente a la circunferencia y el otro es secante.
La demostración de este caso queda como ejercicio.
Ejemplos
Proposición 1. Dos ángulos ya sean inscritos o semiinscritos que abarcan el mismo arco de circunferencia son iguales.
Demostración. Por los teoremas 1 y 2, un ángulo inscrito y un ángulo semiinscrito son iguales a la mitad del ángulo central que abarca el mismo arco, si dos ángulos abarcan el mismo arco entonces el ángulo central es el mismo para ambos y por transitividad son iguales.
$\blacksquare$
Teorema 5, de Tales. Sean $A$, $B$ y $C$ puntos distintos en una circunferencia entonces $BC$ es diámetro si y solo si $A$ es un ángulo recto.
Demostración. Sea $\Gamma (O)$ la circunferencia a la que pertenecen $A$, $B$ y $C$, el resultado se sigue del hecho de que el ángulo central que abarca el mismo arco que $\angle A$ es $\angle BOC$ y aplicar el teorema del ángulo inscrito.
$\blacksquare$
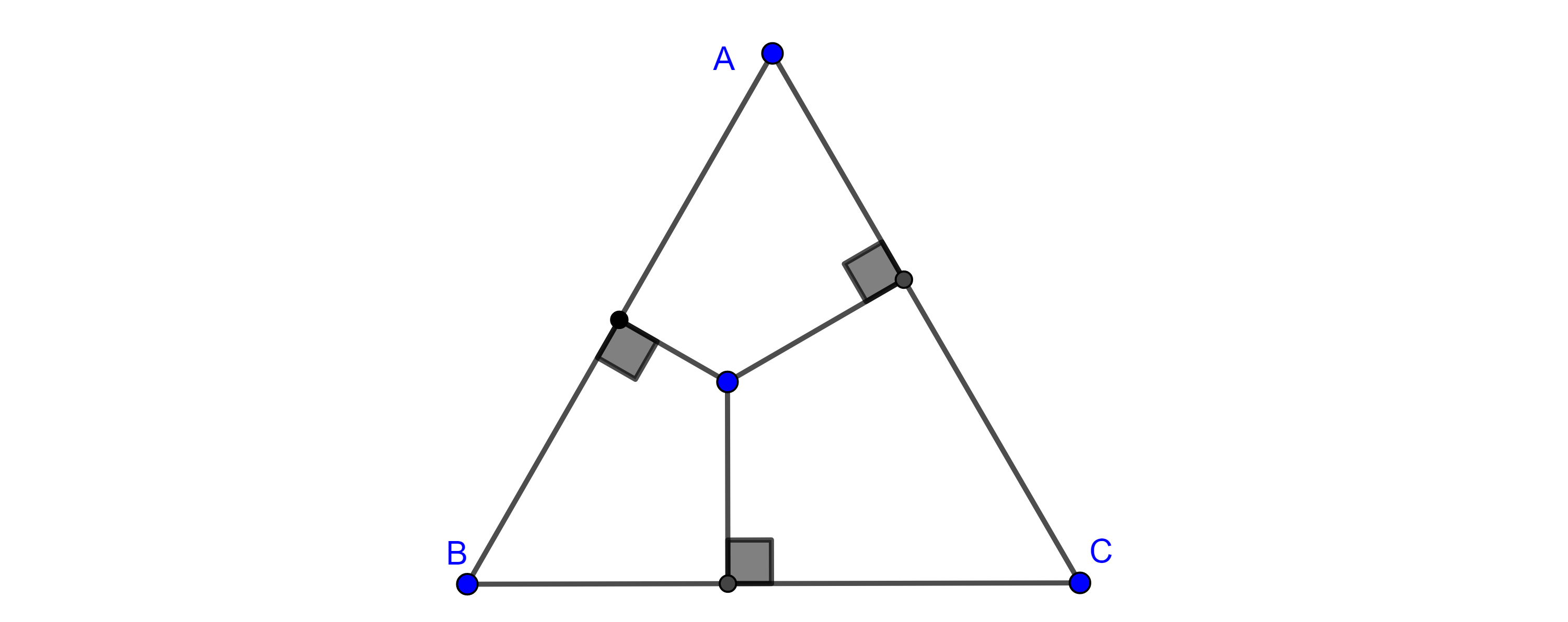
Problema. Dado un círculo $\Gamma$ construir su centro.
Solución. Construimos dos ángulos rectos inscritos en la circunferencia, tomando dos puntos distintos como vértice.
Por el teorema de Tales, las intersecciones de los lados de cada ángulo formaran dos diámetros distintos de la circunferencia y su intersección será el centro de la circunferencia.
$\blacksquare$
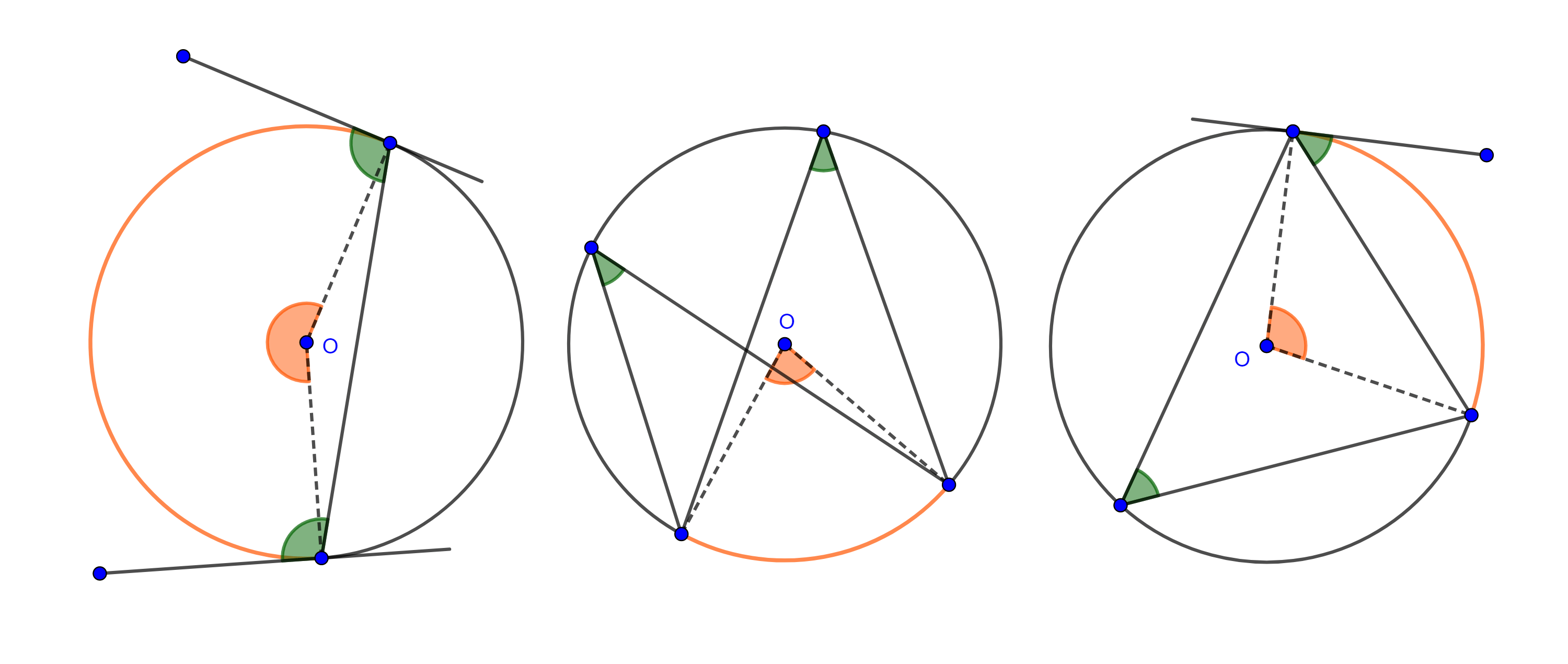
Proposición 2. Las rectas tangentes trazadas desde un punto exterior a una circunferencia son iguales.
Demostración. Sean $\Gamma (O)$ y $A$ un punto exterior, por $A$ trazamos $AB$ y $AC$ tangentes a $\Gamma (O)$ en $B$ y en $C$ respectivamente (figura 7).
Consideremos los radios $OB$ y $OC$ entonces $OB = OC$, y por definición de tangencia, $OB \perp AB$ y $OC \perp AC$.
Los triángulos rectángulos $\triangle AOB$ y $\triangle AOC$ tienen a $AO$ como lado en común, por criterio de congruencia hipotenusa-cateto $\triangle AOB \cong \triangle AOC$, por tanto, $AB = AC$.
$\blacksquare$
Más adelante…
Apoyándonos de los resultados vistos aquí, en la siguiente entrada daremos una caracterización de arco de circunferencia y veremos la circunferencia de Apolonio.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sean $A$ y $C$ dos puntos fijos en una circunferencia, muestra que para cualesquiera dos puntos $B$ y $D$ en la misma circunferencia se tiene que $\angle ABC = \angle ADC$ o $\angle ABC$ y $\angle CDA$ son suplementarios.
- Prueba que una recta es tangente a una circunferencia si y solo si la recta y la circunferencia tienen un solo punto en común.
- Demuestra el teorema 4 en el caso en el que el un lado del ángulo exterior es secante a la circunferencia y el otro es tangente, es decir, en la figura 11 muestra que
$\angle BAC = \dfrac{\angle BOC – \angle COD}{2}$.
- Dados una circunferencia y un punto fuera de ella, construye las rectas tangentes a la circunferencia dada trazadas desde el punto dado.
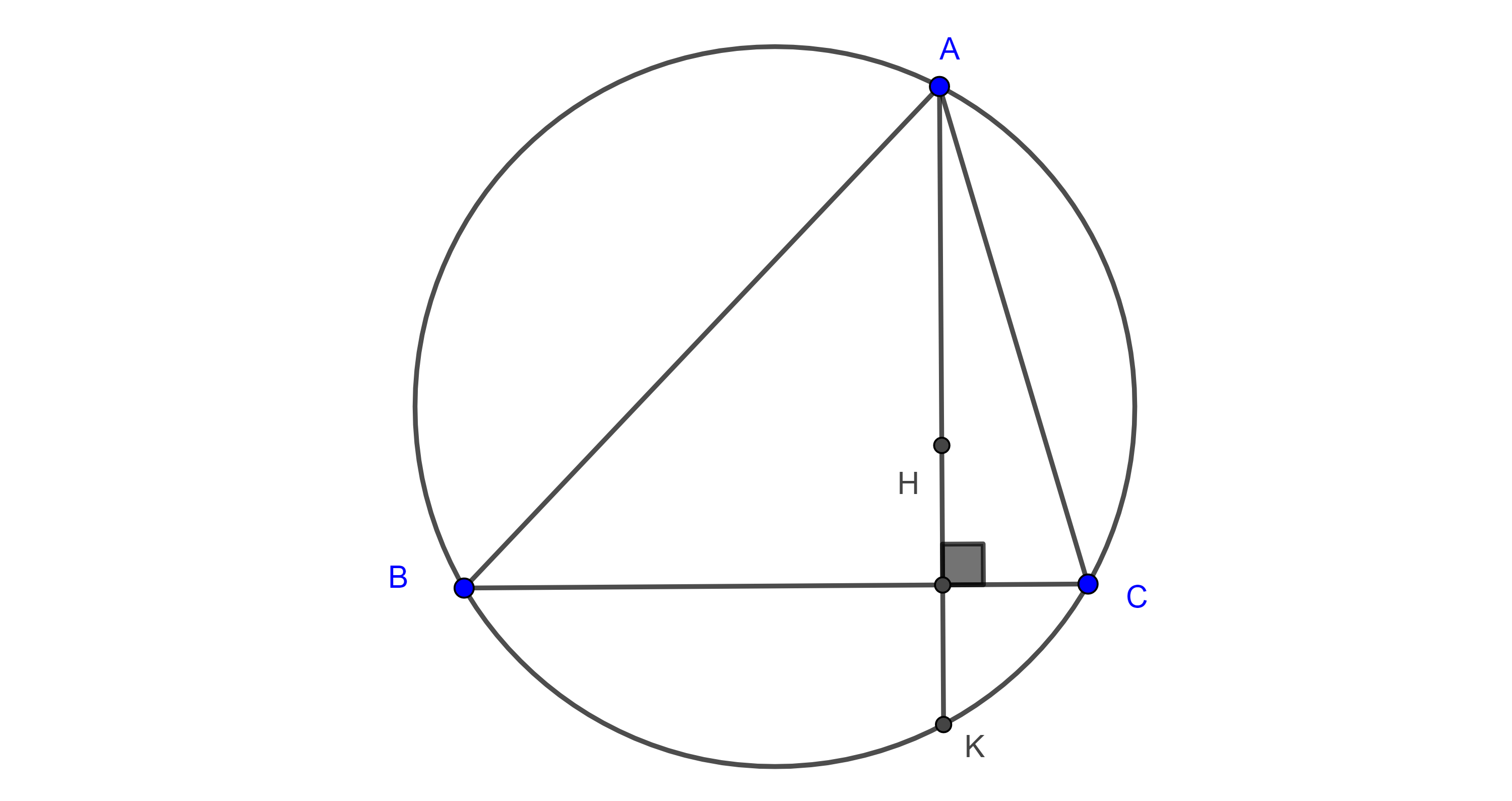
- Sean $\triangle ABC$, $K$ la intersección de la altura trazada desde $A$ con el circuncírculo de $\triangle ABC$ y $H$ el ortocentro de $\triangle ABC$, muestra que $BC$ biseca a $HK$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Puntos notables del triángulo.
- Siguiente entrada del curso: Circunferencia de Apolonio.
- Otros cursos.
Fuentes
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 133-140.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 34-40.
- Wikipedia
- Geometría interactiva
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»