Archivo de la etiqueta: continuidad

Cálculo Diferencial e Integral III: Introducción al teorema de la función inversa

Por Alejandro Antonio Estrada Franco

Introducción

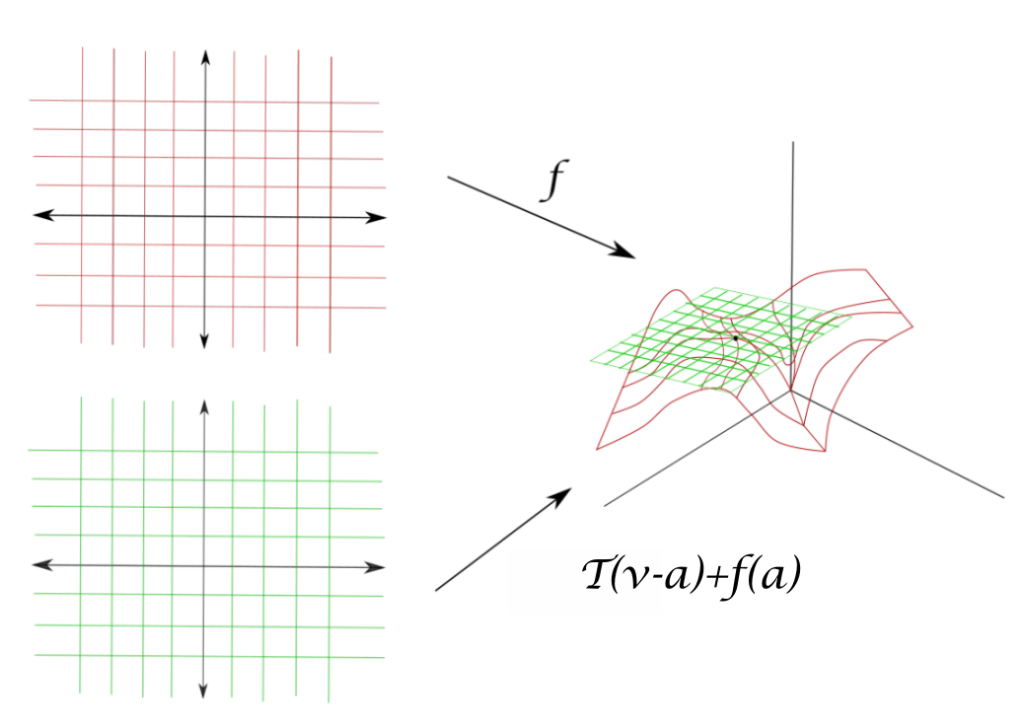
Estamos a punto de entrar a discutir dos de los resultados principales de nuestro curso: el teorema de la función inversa y el teorema de la función implícita. Repasemos un poco qué hemos hecho hasta ahora. En las dos entradas anteriores introdujimos la noción de diferenciabilidad, la cual cuando sucede para una función $f:\mathbb{R}^n\to \mathbb{R}^m$, nos dice que $f$ se parece mucho a una función lineal en un punto dado. Vimos que esta noción implica continuidad y que tiene una regla de la cadena relacionada con el producto de matrices. También, hemos discutido cómo esta noción se relaciona con la existencia de espacios tangentes a gráficas multidimensionales.

Ahora queremos entender todavía mejor a las funciones diferenciables. Hay dos teoremas que nos permiten hacer eso. Uno es el teorema de la función inversa y el otro es el teorema de la función implícita. En esta entrada hablaremos del primero, y en un par de entradas más introduciremos el segundo resultado. El propósito del teorema de la función inversa es dar una condición bajo la cual una función es invertible, por lo menos localmente. De hecho, la mayoría de las veces sólo se puede garantizar la invertibilidad localmente, pues las funciones usualmente no son inyectivas y esto da comportamientos globales más difíciles de manejar.

Enunciar el teorema y entenderlo requiere de cierto esfuerzo. Y demostrarlo todavía más. Por esta razón, en esta entrada nos enfocaremos sólo en dar el teorema y presentar herramientas preliminares que necesitaremos para hacer su demostración.

Enunciado del teorema de la función inversa

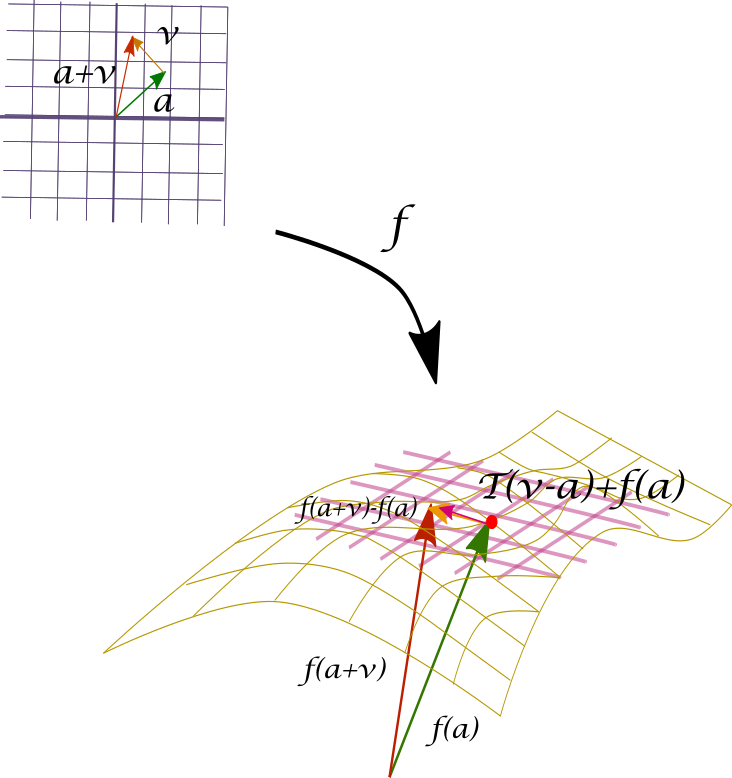
Supongamos que tenemos $f:\mathbb{R}^n\to \mathbb{R}^n$ y que es diferenciable en el punto $\bar{a}$. Entonces, $f$ se parece mucho a una función lineal en $\bar{a}$, más o menos $f(\bar{x})\approx f(\bar{a}) + T_{\bar{a}}(\bar{x}-\bar{a})$. Así, si $T_{\bar{a}}$ es invertible, suena a que «cerquita de $\bar{a}$» la función $f(\bar{x})$ debe de ser invertible. El teorema de la función inversa pone estas ideas de manera formal.

Teorema (de la función inversa). Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el abierto $S$. Si la matriz $Df(\bar{a})$ es invertible, entonces, existe $\delta >0$ tal que:

$B_{\delta}(\bar{a})\subseteq S$ y $f$ es inyectiva en $B_{\delta}(\bar{a})$.
$f^{-1}:f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es continua en $f(B_{\delta}(\bar{a}))$.
$f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}$ es un conjunto abierto.
$f^{-1}$ es de clase $C^{1}$ en $f(B_{\delta}(\bar{a}))$ y además, si $\bar{x}=f(\bar{v})\in f(B_{\delta}(\bar{a}))$, entonces, $Df^{-1}(\bar{x})=Df^{-1}(f(\bar{v}))=(Df(\bar{v}))^{-1}$.

Veamos qué nos dice de manera intuitiva cada una de las conclusiones del teorema.

Tendremos una bola $B_\delta(\bar{a})$ dentro de la cual $f$ será inyectiva, y por lo tanto será biyectiva hacia su imagen. Así, $f$ restringida a esta bola será invertible. Es importante que sea una bola abierta, porque entonces sí tenemos toda una región «gordita» en donde pasa la invertibilidad (piensa que si fuera un cerrado, a lo mejor sólo es el punto $\bar{a}$ y esto no tiene chiste).
La inversa $f^{-1}$ que existirá para $f$ será continua. Esto es lo mínimo que podríamos esperar, aunque de hecho el punto $4$ garantiza algo mucho mejor.
La imagen de $f$ en la bola $B_\delta(\bar{a})$ será un conjunto abierto.
Más aún, se tendrá que $f^{-1}$ será de clase $C^1$ y se podrá dar de manera explícita a su derivada en términos de la derivada de $f$ con una regla muy sencilla: simplemente la matriz que funciona para derivar $f$ le sacamos su inversa como matriz y esa funciona al evaluarla en el punto apropiado.

El teorema de la función inversa es profundo pues tanto su enunciado como su demostración combina ideas de topología, álgebra y cálculo. Por esta razón, para su demostración necesitaremos recopilar varias de las herramientas de álgebra lineal que hemos repasado en la Unidad 2 y la Unidad 5. Así mismo, necesitaremos ideas topológicas de las que hemos visto en la Unidad 3. Con ellas desarrollaremos algunos resultados auxiliares que en la siguiente entrada nos permitirán concluir la demostración.

Un criterio para campos vectoriales $C^1$

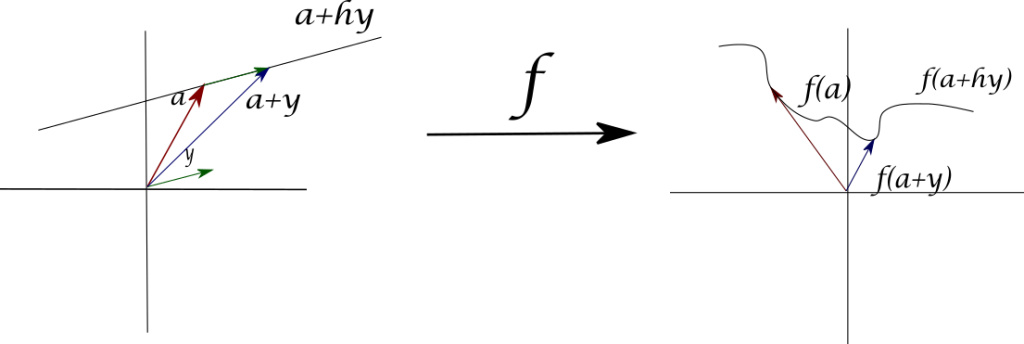
El teorema de la función inversa es para funciones de clase $C^1$. Nos conviene entender esta noción mejor. Cuando una función $f$ es de clase $C^1$, entonces es diferenciable. Pero el regreso no es cierto y hay contraejemplos. ¿Qué le falta a una función diferenciable para ser de clase $C^1$? A grandes rasgos, que las funciones derivadas $T_\bar{a}$ y $T_\bar{b}$ hagan casi lo mismo cuando $\bar{a}$ y $\bar{b}$ son cercanos. En términos de matrices, necesitaremos que la expresión $||(Df(\bar{a})-Df(\bar{b}))(\bar{x})||$ sea pequeña cuando $\bar{a}$ y $\bar{b}$ son cercanos entre sí.

El siguiente teorema será importante en nuestro camino hacia el teorema de la función inversa. Intuitivamente, para lo que lo usaremos es para aproximar una función $f$ localmente, con «cuadritos» que corresponden a los planos tangentes, porque «muy cerquita» estos planos varían muy poco si pedimos que $f$ sea de clase $C^1$. Es decir si $\bar{a}$ y $\bar{b}$ son dos puntos en el dominio de una función diferenciable, y estos están muy cerca uno del otro, sus planos tangentes serán casi el mismo. Esto nos invita a cambiar localmente a una superficie por cuadritos como más adelante se explicará con detalle.

Figura 1. En azul y en rojo dos planos que corresponden a las derivadas $T_{\bar{a}}$ y $T_{\bar{b}}$. Este cambio calculado es distintos puntos cercanos es «suave», esto se expresará con la ecuación $||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\leq \epsilon ||\bar{x}||$ ya con las diferenciales para todo $\bar{x}$.

El teorema concreto que nos interesa demostrar es la siguiente equivalencia para que una función sea de clase $C^1$.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ una función diferenciable en $S$. Se tiene que $f$ es de clase $C^{1}$ en $S$ si y sólo si para todo $\bar{a}\in S$ y para cada $\varepsilon >0$ existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y si $\bar{b}\in B_{\delta}(\bar{a})$ se tiene $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq \varepsilon ||\bar{x}||$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. $\Rightarrow).$ Supongamos que $f$ es de clase $C^1$ en $S$, es decir, todas sus funciones componentes tienen derivadas parciales en $S$ y son continuas. Sea $\varepsilon>0$. Veremos que se puede encontrar una $\delta$ como en el enunciado.

Tomemos $\bar{a}$ y $\bar{b}$ en $S$. Expresamos a $(Df(\bar{b})-Df(\bar{a}))(\bar{x})$ como

\begin{align*}
\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \dots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} x_{1} \\ \vdots \\ x_{n}\end{pmatrix}
\end{align*}

o equivalentemente como

\begin{align*}
\begin{pmatrix} \left( \triangledown f_{1}(\bar{b})-\triangledown f_{1}(\bar{a})\right) \cdot \bar{x} \\ \vdots \\ \left( \triangledown f_{m}(\bar{b})-\triangledown f_{m}(\bar{a})\right) \cdot \bar{x} \end{pmatrix}.
\end{align*}

De tal manera que por Cauchy-Schwarz:

\begin{align*}
||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2&=\sum_{i=1}^m (\left( \triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})\right)\cdot \bar{x})^2\\
&\leq \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2||\bar{x}||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m \sum_{j=1}^{n}\left( \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a})\right) ^{2}
\end{align*}

En este punto se ve la importancia de que las parciales sean continuas. Podemos encontrar una $\delta$ que nos garantice que $B_\delta\subseteq S$ y que si $||\bar{b}-\bar{a}||<\delta$, entonces $$\left| \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a}) \right| < \frac{\varepsilon}{\sqrt{mn}}.$$ En esta situación, podemos seguir acotando $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2$ como sigue:
\begin{align*}
&\leq ||\bar{x}|| \sum_{i=1}^m \sum_{j=1}^{n}\frac{\varepsilon^2}{mn}\\
&=\varepsilon^2||\bar{x}||^2.
\end{align*}

Al sacar raiz cuadrada, obtenemos la desigualdad $$||(Df(\bar{b})-Df(\bar{a}))(x)||\leq \varepsilon||\bar{x}||$$ buscada.

$\Leftarrow).$ Supongamos ahora que para cada $\varepsilon$ existe una $\delta$ como en el enunciado del teorema. Debemos ver que todas las derivadas parciales de todas las componentes son continuas. Podemos aplicar la desigualdad $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq ||\bar{x}||\varepsilon$ tomando como $\bar{x}$ cada vector $\hat{e}_i$ de la base canónica. Esto nos dice que

\[ ||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||< \varepsilon||\hat{e}_i|| =\varepsilon.\]

Por nuestro desarrollo anterior, para cada $i$ tenemos

\begin{align*}
\varepsilon&>||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||\\
&=||\left( \triangledown f_{1}(\bar{b})\cdot \hat{e}_i-\triangledown f_{1}(\bar{a})\cdot \hat{e}_i,\dots ,\triangledown f_{m}(\bar{b})\cdot \hat{e}_i-\triangledown f_{m}(\bar{a})\cdot \hat{e}_i\right)||\\
&=\left| \left|\left( \frac{\partial f_{1}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{i}}(\bar{a}),\dots ,\frac{\partial f_{m}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{i}}(\bar{a})\right) \right| \right|\\
&= \sqrt{\sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right)^{2}}.
\end{align*}

Elevando al cuadrado,

\[ \sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(b)-\frac{\partial f_{j}}{\partial x_{i}}(a)\right)^{2}<\varepsilon ^{2}.\]

Como todos los términos son no negativos, cada uno es menor a $\epsilon^2$. Así, para cada $i,j$ tenemos

\[ \left|\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right|<\varepsilon.\]

Esto es precisamente lo que estábamos buscando: si $\bar{b}$ está lo suficientemente cerca de $\bar{a}$, cada derivada parcial en $\bar{b}$ está cerca de su correspondiente en $\bar{a}$.

$\square$

Invertibilidad de $Df(\bar{a})$ en todo un abierto

En esta sección demostraremos lo siguiente. Si $f:\mathbb{R}^n\to \mathbb{R}^n$ es un campo vectorial diferenciable en $\bar{a}$ y $Df(\bar{a})$ es invertible, entonces $Df(\bar{x})$ será invertible para cualquier $\bar{x}$ alrededor de cierta bola abierta alrededor de $\bar{a}$. Los argumentos en esta ocasión están un poco más relacionados con el álgebra lineal.

Será útil que recuerdes que una transformación lineal $T:\mathbb{R}^n \to \mathbb{R}^n$ es invertible si el único $\bar{x}\in \mathbb{R}^n$ tal que $T(\bar{x})=\bar{0}$ es $\bar{x}=\bar{0}$. El siguiente criterio es otra caracterización de invertibilidad en términos de lo que le hace $T$ a la norma de los vectores.

Teorema. Sea $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una transformación lineal. La transformación $T$ es invertible si y sólo si existe $\varepsilon >0$ tal que $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. $\left. \Rightarrow \right)$ Como $T$ es invertible, para todo $\bar{x}\neq \bar{0}$ sucede que $T(\bar{x})\neq \bar{0}$. En particular, esto sucede para todos los vectores en $S^{n-1}$ (recuerda que es la esfera de radio $1$ y dimensión $n-1$ centrada en $\bar{0}$). Esta esfera es compacta y consiste exactamente de los $\bar{x}\in \mathbb{R}^n$ de norma $1$.

Sabemos que las transformaciones lineales y la función norma son continuas. Por la compacidad de $S^{n-1}$, la expresión $||T(\bar{x})||$ tiene un mínimo digamos $\varepsilon$, que alcanza en $S^{n-1}$. Por el argumento del párrafo anterior, $\varepsilon>0$.

Tomemos ahora cualquier vector $\bar{x}\in \mathbb{R}^n$. Si $\bar{x}=\bar{0}$, entonces $$||T(\bar{0})||=||\bar{0}||=0\geq \varepsilon ||\bar{0}||.$$ Si $\bar{x}\neq \bar{0}$, el vector $\frac{\bar{x}}{||\bar{x}||}$ está en $S^{n-1}$, de modo que $$\left|\left|T\left(\frac{\bar{x}}{||\bar{x}||}\right)\right|\right| \geq \varepsilon.$$ Usando linealidad para sacar el factor $||\bar{x}||$ y despejando obtenemos $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||,$$ como estábamos buscando.

$\left. \Leftarrow \right)$ Este lado es más sencillo. Si existe dicha $\varepsilon >0$, entonces sucede que para $\bar{x}$ en $\mathbb{R}^n$, con $\bar{x}\neq \bar{0}$ tenemos $$||T(\bar{x})||\geq \varepsilon||\bar{x}||>0.$$ Por lo tanto, $T(\bar{x})\neq \bar{0}$ y así $T$ es invertible.

$\square$

Obtengamos una consecuencia del teorema de clasificación de la sección anterior que está muy relacionada con este resultado que acabamos de demostrar.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el conjunto abierto $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces existen $\delta >0$ y $m>0$ tales que $B_{\delta}(\bar{a})\subseteq S$ y $||Df(\bar{b})(\bar{x})||\geq m||\bar{x}||$, para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. Como $Df(\bar{a})$ es invertible, por el teorema que acabamos de demostrar existe $\varepsilon’>0$ tal que $$||Df(\bar{a})(\bar{x})||\geq \varepsilon’||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Por nuestra caracterización de funciones $C^1$, Ahora como $f\in C^{1}$ en $S$ (abierto) para $\varepsilon =\frac{\varepsilon’}{2}>0$, existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y $||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\leq \frac{\varepsilon’}{2}||\bar{x}||$ para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.

Por la desigualdad del triángulo, \[ ||Df(\bar{a})(\bar{x})-Df(\bar{b})(\bar{x})||+||Df(\bar{b})(\bar{x})||\geq ||Df(\bar{a})(\bar{x})||,\]

de donde

\begin{align*}
||Df(\bar{b})(\bar{x})||&\geq ||Df(\bar{a})(\bar{x})||-||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\\
&\geq \varepsilon’||\bar{x}||-\frac{\varepsilon’}{2}||\bar{x}||\\
&= \frac{\varepsilon’}{2} ||\bar{x}||.
\end{align*}

De esta manera, el resultado es cierto para la $\delta$ que dimos y para $m=\frac{\varepsilon’}{2}$.

$\square$

El siguiente corolario es consecuencia inmediata de lo discutido en esta sección y está escrito de acuerdo a la aplicación que haremos más adelante en la demostración del teorema de la función inversa.

Corolario. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una función de clase $C^{1}$ en $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces, existe $\delta > 0$ tal que $B_{\delta}(\bar{a})\subseteq S$ y $Df(\bar{b})$ es invertible para todo $\bar{b}\in B_{\delta}(\bar{a})$.

Queda como tarea moral responder por qué este corolario es consecuencia inmediata del teorema anterior.

Un poco de intuición geométrica

Dejamos esta entrada hasta aquí, la naturaleza densamente teórica de lo que estamos haciendo puede hacer pesadas las exposiciones. Lo que hasta aquí demostramos es que para un campo vectorial $C^1$ si su derivada en $\bar{a}$ es invertible, entonces lo es en toda una vecindad que tiene a $\bar{a}$. Imaginemos al pedacito de superficie $f(B_{\delta}(\bar{a}))$ cubierto con pequeños rectángulos. En cada punto, las imágenes de estos rectángulos están muy cerquita, casi pegados a la superficie. Esto nos garantizaría la invertibilidad de $f$ en esta vecindad.

En la Figura 2 vemos ilustrado esto. El círculo inferior corresponde a la vecindad $B_{\delta}(\bar{a})$ en el dominio de $f$. La función $f$ levanta una porción del plano en la sabana delineada con negro arriba del círculo. En el círculo tenemos al punto $\bar{a}$ en verde agua. Sobre la sábana de arriba tenemos con el mismo color a $f(\bar{a})$. Los puntos negros pequeños dentro de la vecindad alrededor de $\bar{a}$ son alzados por $f$ a puntos negros sobre la sabana. Sobre de cada punto negro en la sabana tenemos un cuadrito rojo que representa al cachito de plano tangente cerca de la imagen de cada punto. La imagen esta llena de estos pequeños cuadritos, todos ellos representan diferenciales invertibles, esto nos permitirá asegurar la invertibilidad de $f$ en al menos una vecindad.

Más adelante…

En la siguiente entrada demostraremos el teorema de la función inversa, inciso por inciso. Es importante que estes familiarizado con los resultados de esta entrada, pues serán parte importante de la demostración.

Tarea moral

¿Qué diría el teorema de la función inversa para campos vectoriales $f:\mathbb{R}^2\to \mathbb{R}^2$? ¿Se puede usar para $$f(r,\theta)=(r\cos(\theta),r\sin(\theta))?$$ Si es así, ¿para qué valores de $r$ y $\theta$? ¿Qué diría en este caso explícitamente?
Explica por qué el corolario que enunciamos en efecto se deduce de manera inmediata de lo discutido en la sección correspondiente.
Revisa todas las desigualdades que usamos en esta entrada. ¿Qué resultado estamos usando? ¿Cuándo se darían estas igualdades?
Demuestra que el determinante de una matriz es una función continua en términos de las entradas de la matriz. Usa esto para demostrar que si $A\in M_n(\mathbb{R})$ es una matriz y $B$ es una matriz muy cercana a $A$, entonces $B$ también es invertible.
Demuestra que si una transformación $T$ es diagonalizable, entonces en el teorema de caracterización de invertibilidad se puede usar como $\epsilon$ al mínimo de la expresión $|\lambda|$ variando sobre todos los eigenvalores $\lambda$ de $T$.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Regla de la cadena para campos vectoriales
Entrada siguiente del curso: Demostración del teorema de la función inversa

Cálculo Diferencial e Integral III: Regla de la cadena para campos vectoriales

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Tenemos ya la definición de diferenciabilidad, y su versión manejable: la matriz jacobiana. Seguiremos construyendo conceptos y herramientas del análisis de los campos vectoriales muy importantes e interesantes. A continuación, enunciaremos una nueva versión de la regla de la cadena, que nos permitirá calcular las diferenciales de composiciones de campos vectoriales entre espacios de dimensión arbitraria. Esta regla tiene numerosas aplicaciones y es sorprendentemente fácil de enunciar en términos de producto de matrices.

Primeras ideas hacia la regla de la cadena

La situación típica de regla de la cadena es considerar dos funciones diferenciables que se puedan componer. A partir de ahí, buscamos ver si la composición también es diferenciable y, en ese caso, intentamos dar la derivada de la composición en términos de las derivadas de las funciones. Veamos qué pasa en campos vectoriales.

Pensemos en $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ y en su composición $h=f\circ g$ definida sobre alguna vecindad $V\subseteq S_g$ de $\bar{a}$ y tal que $g(V)\subseteq S_f$. Pensemos que $g$ es diferenciable en $\bar{a}$ con derivada $G_\bar{a}$ y que $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$.

Exploremos la diferenciabilidad de la composición $h$ en el punto $\bar{a}$. Para ello, tomemos un $\bar{y}\in \mathbb{R}^{l}$ tal que $\bar{a}+\bar{y}\in V$ y consideremos la siguiente expresión:

\begin{align*}
h(\bar{a}+\bar{y})-h(\bar{a})=f(g(\bar{a}+\bar{y}))-f(g(\bar{a})).
\end{align*}

Tomando $\bar{v}=g(\bar{a}+\bar{y})-g(\bar{a})$, tenemos $\bar{b}+\bar{v}=g(\bar{a})+\bar{v}=g(\bar{a}+\bar{y})$. De esta forma,

\begin{align*}
f(g(\bar{a}+\bar{y}))-f(g(\bar{a}))=f(\bar{b}+\bar{v})-f(\bar{b}).
\end{align*}

Por la diferenciabilidad de $g$ en $\bar{a}$, tenemos que podemos escribir

$$\bar{v}=G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}),$$ con $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$.

Usando la diferenciabilidad de $f$ en $\bar{b}$, y la linealidad de su derivada $F_\bar{b}$, tenemos entonces que:

\begin{align*}
f(\bar{b}+\bar{v})-f(\bar{b})&=F_\bar{b}(\bar{v})+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=F_\bar{b}(G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=(F_{b}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||(F_{\bar{b}}\circ E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_{f}(\bar{b};\bar{v}),
\end{align*}

con $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b};\bar{v})=0$.

Concatenando nuestras igualdades, podemos reescribir esto como

\[ h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),\] en donde hemos definido

\[ E_{h}(\bar{a};\bar{y})=(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})+\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b};\bar{v}).\] Si logramos demostrar que $\lim\limits_{\bar{y}\to \bar{0}}E_{h}(\bar{a};\bar{y})=0$, entonces tendremos la diferenciabilidad buscada, así como la derivada que queremos. Dejemos esto en pausa para enunciar y demostrar un lema auxiliar.

Un lema para acotar la norma de la derivada en un punto

Probemos el siguiente resultado.

Lema. Sea $\phi:S\subseteq \mathbb{R}^l\to \mathbb{R}^m$ un campo vectorial diferenciable en un punto $\bar{c}\in S$ y $T_\bar{c}$ su derivada. Entonces, para todo $\bar{v}\in \mathbb{R}^{l}$, se tiene:

$$||T_{\bar{c}}(\bar{v})||\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||.$$

Donde $\phi(\bar{v})=\left( \phi_{1}(\bar{v}),\dots ,\phi_{m}(\bar{v})\right)$

Demostración. Procedemos con desigualdad del triángulo como sigue:

\begin{align*}
||T_{\bar{c}}(\bar{v})||&=\left|\left|\sum_{k=1}^{m}(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_{k}\right|\right|\\
&\leq \sum_{k=1}^{m}||(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_k||\\
&=\sum_{k=1}^{m}|\triangledown \phi_{k}(\bar{c})\cdot \bar{v}|
\end{align*}

y luego usamos la desigualdad de Cauchy-Schwarz en cada sumando para continuar como sigue

\begin{align*}
\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||,
\end{align*}

que es lo que buscábamos.

$\square$

Conclusión del análisis para regla de la cadena

Retomando el análisis para $E_{h}(\bar{a};\bar{y})$, dividamos el límite en los dos sumandos.

Primer sumando:

Como $F_{\bar{b}}$ es lineal, entonces es continua. También, sabemos que $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$. Así,

\begin{align*}
\lim\limits_{\bar{y}\to \bar{0}}(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})&=F_{\bar{b}}\left(\lim\limits_{\bar{y}\to \bar{0}} E_{g}(\bar{a};\bar{y})\right)\\
&=F_\bar{b}(\bar{0})\\
&=0.
\end{align*}

Segundo sumando:

Retomando la definición de $\bar{v}$, aplicando desigualdad del triángulo y el lema que demostramos,

\begin{align*}
||\bar{v}||&=||G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y})||\\
&\leq ||G_{\bar{a}}(\bar{y})||+||\bar{y}||||E_{g}(\bar{a};\bar{y})||\\
&\leq \left(\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||||\bar{y}||\right)+||\bar{y}||||E_{g}(\bar{a};\bar{y})||.
\end{align*}

Dividiendo ambos lados entre $||\bar{y}||$, obtenemos entonces que

$$ \frac{||\bar{v}||}{||\bar{y}||}\leq \sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||+||E_{g}(\bar{a};\bar{y})||. $$

De aquí se ve que conforme $\bar{y}\to \bar{0}$, la expresión $\frac{||\bar{v}||}{||\bar{y}||}$ está acotada superiormente por la constante $A:=\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||.$ Además, si $\bar{y}\to \bar{0}$, entonces $\bar{v}\to \bar{0}$. Así,

\[0\leq \lim\limits_{\bar{y}\to \bar{0}}\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b},\bar{v})\leq A\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})=0 \] pues $\lim\limits_{\bar{y}\to \bar{0}}\bar{v}=\bar{0}$ implica $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})$.

Hemos concluido que $$h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),$$

con $\lim_{\bar{y}\to \bar{0}} E_h(\bar{a};\bar{y})=0$. Esto precisamente es la definición de $h=f\circ g$ es diferenciable en $\bar{a}$, y su derivada en $\bar{a}$ es la transformación lineal dada por la composición de transformaciones lineales $F_\bar{b}\circ G_\bar{a}$.

Recapitulación de la regla de la cadena

Recapitulamos toda la discusión anterior en el siguiente teorema.

Teorema (Regla de la cadena). Sean $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ campos vectoriales. Supongamos que la composición $f\circ g$ está definida en todo un abierto $S\subseteq S_g$. Supongamos que $g$ es diferenciable en un punto $\bar{a}\in S$ con derivada $G_\bar{a}$ y $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$. Entonces, $h$ es diferenciable en $\bar{a}$ con derivada $F_\bar{b}\circ G_\bar{a}$.

Dado que la representación matricial de la composición de dos transformaciones lineales es igual al producto de estas, podemos reescribir esto en términos de las matrices jacobianas como el siguiente producto matricial: $$Dh(\bar{a})=Df(\bar{b})Dg(\bar{a}).$$

Usos de la regla de la cadena

Hagamos algunos ejemplos de uso de regla de la cadena. En el primer ejemplo que veremos a continuación, la función $f$ es un campo escalar.

Ejemplo 1. Tomemos $g:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ campo vectorial, y $f:U\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}$ campo escalar. Consideremos $h=f\circ g$ y supongamos que se satisfacen las hipótesis del teorema de la regla de la cadena. Tenemos: \[ Df(\bar{b})=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix} \] y \[ Dg(\bar{a})=\begin{pmatrix}\frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix} . \]

Por la regla de la cadena tenemos $Dh(\bar{a})=Df(\bar{b})Dg(\bar{a})$ esto implica \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix}\begin{pmatrix} \frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

Así \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}= \begin{pmatrix} \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{1}}(\bar{a}) & \dots & \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

En otras palabras, tenemos las siguientes ecuaciones para calcular cada derivada parcial de $h$: \[ \frac{\partial h}{\partial x_{j}}(\bar{a})=\sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{j}}(\bar{a}).\]

$\triangle$

Ejemplo 2. Sean $\bar{a}=(s,t)$ y $\bar{b}=(x,y)$ puntos en $\mathbb{R}^{2}$. Pensemos que las entradas de $\bar{b}$ están dadas en función de las entradas de $\bar{a}$ mediante las ecuaciones $x=g_{1}(s,t)$ y $y=g_{2}(s,t)$. Pensemos que tenemos un campo escalar $f:\mathbb{R}^2\to \mathbb{R}$, y definimos $h:\mathbb{R}^2\to \mathbb{R}$ mediante $$h(s,t)=f(g_{1}(s,t),g_{2}(s,t)).$$

Por el ejemplo anterior \[ \frac{\partial h}{\partial s}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial s} \] y \[ \frac{\partial h}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}. \] Como tarea moral queda que reflexiones qué significa $\partial x$ cuando aparece en el «numerador» y qué significa cuando aparece en el «denominador».

$\triangle$

Ejemplo 3. Para un campo escalar $f(x,y)$ consideremos un cambio de coordenadas $x=rcos\theta$, $y=rsen\theta$ es decir tomemos la función $\phi (r,\theta)=f(rcos\theta ,rsen\theta )$.

Por el ejemplo anterior tenemos \[ \frac{\partial \phi }{\partial r}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial r} \] y \[ \frac{\partial \phi }{\partial \theta }=\frac{\partial f}{\partial x}\frac{\partial x}{\partial \theta }+\frac{\partial f}{\partial y}\frac{\partial y}{\partial \theta } \] donde, haciendo las derivadas parciales tenemos: \[ \frac{\partial x}{\partial r}=cos\theta ,\hspace{1cm}\frac{\partial y}{\partial r}=sen\theta \] y \[ \frac{\partial x}{\partial \theta }=-rsen\theta,\hspace{1cm}\frac{\partial y}{\partial \theta }=-rcos\theta. \] Finalmente obtenemos: \[ \frac{\partial \phi }{\partial r }=\frac{\partial f }{\partial x }cos\theta +\frac{\partial f }{\partial y }sen\theta \] y \[ \frac{\partial \phi }{\partial \theta }=-\frac{\partial f }{\partial x }rsen\theta +\frac{\partial f }{\partial y }rcos\theta \] que son las derivadas parciales del cambio de coordenadas en el dominio de $f$.

$\triangle$

Mas adelante…

En la siguiente entrada comenzaremos a desarrollar la teoría para los importantes teoremas de la función inversa e implícita si tienes bien estudiada esta sección disfrutaras mucho de las siguientes.

Tarea moral

Considera el campo escalar $F(x,y,z)=x^{2}+y sen(z)$. Imagina que $x,y,z$ están dados por valores $u$ y $v$ mediante las condiciones $x=u+v$, $y=vu$, $z=u$. Calcula $\frac{\partial F}{\partial u}$, $\frac{\partial F}{\partial v}$.
Sea $g(x,y,z)=(xy,x)$, y $f(x,y)=(2x,xy^{2},y)$. Encuentra la matriz jacobiana del campo vectorial $g\circ f$. Encuentra también la matriz jacobiana del campo vectorial $f\circ g$.
En la demostración del lema que dimos, hay un paso que no justificamos: el primero. Convéncete de que es cierto repasando el contenido de la entrada anterior Diferenciabilidad.
Imagina que sabemos que la función $f:\mathbb{R}^n\to \mathbb{R}^n$ es invertible y derivable en $\bar{a}$ con derivada $T_\bar{a}$. Imagina que también sabemos que su inversa $f^{-1}$ es derivable en $\bar{b}=f(\bar{a})$ con derivada $S_\bar{b}$. De acuerdo a la regla de la cadena, ¿Qué podemos decir de $T_\bar{a}\circ S_\bar{b}$? En otras palabras, ¿Cómo son las matrices jacobianas entre sí, en términos de álgebra lineal?
Reflexiona en cómo todas las reglas de la cadena que hemos estudiado hasta ahora son un corolario de la regla de la cadena de esta entrada.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Diferenciabilidad en campos vectoriales
Entrada siguiente del curso: Introducción al teorema de la función inversa

Cálculo Diferencial e Integral III: Diferenciabilidad en campos vectoriales

Por Alejandro Antonio Estrada Franco

3 respuestas

Introducción

Después de haber abordado a modo de repaso las herramientas que usaremos de álgebra lineal, estamos listos para estudiar la diferenciabilidad en funciones más generales. Ya estudiamos la diferenciabilidad en curvas (funciones $f:S\subseteq \mathbb{R}\to \mathbb{R}^m$) y en campos escalares (funciones $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$). Ahora podemos estudiar la diferenciabilidad en campos vectoriales, que recuerda que ahora sí son funciones $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ para cualesquiera $m$ y $n$ enteros positivos.

Intuición de diferenciabilidad en campos vectoriales

Con anterioridad, hemos discutido la intuición geométrica de lo que quiere decir que un campo escalar $f:\mathbb{R}^n\to \mathbb{R}$ sea diferenciable. A grandes rasgos, estamos pidiendo que cerca de un punto $\bar{a}$ la función $f(\bar{a})$ cambie «como una función lineal». Esto quiere decir que la gráfica de la función se parece mucho a un hiperplano en $\mathbb{R}^{n+1}$ cerca del punto $\bar{a}$, tanto que de hecho podemos dar un hiperplano tangente a la gráfica en $\bar{a}$. Bajo suficiente regularidad, esta función lineal estaba dada por las derivadas parciales y estaba muy relacionada con el gradiente $\triangledown f$.

La situación para campos vectoriales es parecida. Si tenemos una función $f:\mathbb{R}^n\to \mathbb{R}^m$, entonces está dada por funciones coordenada que la expresan de la manera $f(\bar{x})=(f_1(\bar{x}),\ldots,f_m(\bar{x}))$ para cada $\bar{x}\in \mathbb{R}^n$. La diferenciabilidad que buscaremos ahora deberá suceder coordenada a coordenada, y por ello lo que pensaremos como derivada tendrá algo así como un gradiente por cada coordenada. Esto nos daría $m$ gradientes, pero una mejor forma de pensar en resumen a la derivada es como una transformación lineal $T:\mathbb{R}^n\to \mathbb{R}^m$ que nos diga con mucha precisión cuándo cambia la funciíon $f$ (cuando esto sea posible).

Para tener clara idea de lo que queremos hacer recordemos el ejemplo de campos escalares, y de aquí construiremos una generalización a campos vectoriales: Observa la Figura $1$. A la izquierda, hemos dibujado dos copias de $\mathbb{R}^n$ (pero que puedes pensar como $\mathbb{R}^2$). A la derecha, hemos dibujado la gráfica de dos funciones. Una es una función cualquiera $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^m$. La otra es una transformación lineal $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^m$ que ha sido trasladada sobre el plano $xy$ y sobre el eje $z$ con la función $G(\bar{v})=T(\bar{v}-\bar{a})+f(\bar{a})$. Estas gráficas son objetos en $\mathbb{R}^n \times \mathbb{R}^m$ (ponemos un punto por cada pareja $(\bar{x},f(\bar{x}))$ con $\bar{x}\in \mathbb{R}^n$).

Como $T$ es lineal, cumple $T(\bar{0})=0$. Al hacer la traslación, obtenemos $G(\bar{a})=T(\bar{0})+f(\bar{a})=f(\bar{a})$. Así, $T$ traslada un subespacio $H$ de dimensión $n$ a un subespacio afín de dimensión $n$ que pasa por $f(\bar{a})$. Lo que buscaremos al pedir que la función $f$ sea diferenciable con derivada $T$ es que la gráfica de $f$ se parezca mucho a este subespacio $H+f(\bar{a})$, tanto que de hecho dicho subespacio lo podremos pensar como tangente a la gráfica en el punto $(\bar{a},f(\bar{a}))$.

Definición de diferenciabilidad para campos vectoriales

¿Cuál es la condición algebraica que pediremos? Será muy similar a lo que pasaba en campos escalares. Lo que queremos es que el cambio $f(\bar{a}+\bar{v})-f(\bar{a})$ se parezca mucho a $T(\bar{v})$ cuando $\bar{v}$ es pequeño. De hecho, tiene que parecerse tanto, tanto, que $f(\bar{a}+\bar{v})-f(\bar{a})$ debe parecerse a $T(\bar{v})$ más rápido de lo que $\bar{v}$ se va a $\bar{0}$. Esto nos lleva a plantear que la condición buscada sea la siguiente:

$$\lim_{\bar{v}\to \bar{0}}\frac{||(f(\bar{a}+\bar{v})-f(\bar{a}))-T(\bar{v})||}{||\bar{v}||}=0.$$ La Figura $2$ tiene un diagrama que ayuda a entender esto un poco mejor. Queremos que la flecha indicada en amarillo acabe muy cerca de $f(\bar{a}+\bar{v})$.

El vector $T(\bar{v}-\bar{a})+f(\bar{a})$ es el vector $T(\bar{v})$ transportado hasta el plano tangente el cual está en color rosa. La idea es que $f(\bar{a}+\bar{v})-f(\bar{a})$, que es el vector señalado con amarillo abajo, se aproxime mucho en el sentido señalado por el límite mencionado en el párrafo de arriba. De esta manera tenemos la mejor aproximación lineal. Esta definición se inspira en el polinomio de Tylor de grado 1 para funciones de una variable real.

Por supuesto, la discusión que hemos tenido sólo aplica para cuando estamos trabajando cerca del punto $\bar{a}$, así que más bien la transformación lineal de la que estamos hablando dependerá del punto $\bar{a}$. Todo esto nos lleva a nuestra primera definición formal de diferenciabilidad.

$$\lim_{\bar{v}\to \bar{0}}\frac{||f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})||}{||\bar{v}||}=0.$$

En este caso, a $T_{\bar{a}}$ le llamamos la derivada de $f$ en el punto $\bar{a}$.

Antes de empezar a demostrar propiedades de esta noción, nos conviene tener una versión alternativa y totalmente equivalente.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Decimos que $f$ es diferenciable en $\bar{a}\in Int(S)$ si existe una transformación lineal $T_{\bar{a}}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ y una función $E:\mathbb{R}^n\times \mathbb{R}^n\to \mathbb{R}^m$ de manera que $$f(\bar{a}+\bar{v})=f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v})$$ con $$\lim_{||\bar{v}||\to 0}E(\bar{a};\bar{v})=0.$$

Esta definición es equivalente a la anterior pues si despejamos tenemos: \[E(\bar{a};\bar{v})=\frac{f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})}{||\bar{v}||},\] de donde se puede verificar que se cumple una definición si y sólo si se cumple la otra. Los detalles quedan como tarea moral.

Ejemplo. Consideremos la función $f(x,y)=(x^2y^2,xy)$ y tomemos el punto $a=(1,1)$. ¿Será $f$ diferenciable en $a$? Afirmamos que sí, que la función lineal $T_a(x,y)=(2x+2y, x+y)$ cumple con la definición de límite que se pide. Veamos esto en la primera versión de la definición. Tendríamos, usando $\bar{v}=(h,k)$, que

\begin{align*}
f((1,1)&+(h,k))-f(1,1)-T_a(h,k)\\
&=((h+1)^2(k+1)^2,(h+1)(k+1))-(1,1)-(2h+2k,h+k)\\
&=(h^2k^2+2h^2k+2hk^2+h^2+k^2+4hk,hk)
\end{align*}

Dividiendo entre $\sqrt{h^2+k^2}$ que es la norma de $v$, y haciendo manipulaciones algebraicas, se obtiene

$$\left(\frac{h^2k^2+2h^2k+2hk^2+h^2+k^2+4hk}{\sqrt{h^2+k^2}},\frac{hk}{\sqrt{h^2+k^2}}\right).$$

Por la desigualdad entre la media cuadrática y la media geométrica, $$\frac{|hk|}{\sqrt{h^2+k^2}}\leq \sqrt{\frac{|hk|}{2}},$$

de modo que cuando $(h,k)\to (0,0)$, la segunda coordenada del vector que nos interesa converge a cero. La primera coordenada también se puede ver que converge a cero: el primero, segundo, tercero y sexto sumandos se acotan de manera similar, pues tienen factores $h$ o $k$ adicionales. El cuarto y quinto sumando se acotan notando que $\frac{h^2+k^2}{\sqrt{h^2+k^2}}=\sqrt{h^2+k^2}$, que también converge a cero con $h$ y $k$. Los detalles quedan de tarea moral.

$\triangle$

Diferenciabilidad implica continuidad

En el caso de las funciones de una variable real teníamos claramente que diferenciabilidad implica continuidad. Como es de esperarse, lo mismo se cumple para campos vectoriales, ya que una función diferenciable es más «suave» que una continua.

Teorema. Supongamos $f:S\subseteq \mathbb{R}^n\to\mathbb{R}^m$ es un campo vectorial diferenciable en un punto $\bar{a}$ de $S$. Entonces $f$ es continuo en $\bar{a}$.

Demostración. Si $f$ es diferenciable en $\bar{a}$ entonces cumple con la ecuación \[f(\bar{a}+\bar{v})=f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v})\] con $E(\bar{a};\bar{v})$ una función tal que $\lim_{\bar{v}\to \bar{0}} E(\bar{a}; \bar{v})=0$ (¿Por qué es válida esta última afirmación?). Por ello:

\begin{align*}
\lim\limits_{\bar{v}\to \bar{0}}f(\bar{a}+\bar{v})&=\lim\limits_{\bar{v}\to \bar{0}}\left( f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v}) \right)\\
&= \lim\limits_{\bar{v}\to \bar{0}}f(\bar{a})+\lim\limits_{\bar{v}\to \bar{0}}T_{\bar{a}}(\bar{v})+\lim\limits_{\bar{v}\to \bar{0}}||\bar{v}||E(\bar{a};\bar{v}).
\end{align*}

El primer sumando no depende de $\bar{v}$, así que es $f(\bar{a})$. El segundo se va a cero pues las transformaciones lineales son continuas. Finalmente, el tercer sumando se va a cero por lo que sabemos de $E(\bar{a},\bar{v})$. Así, $\lim\limits_{\bar{v}\to \bar{0}}f(\bar{a}+\bar{v})=f(\bar{a})$. Por lo tanto $f$ es continua.

$\square$.

Derivadas direccionales y derivadas parciales

Si bien tenemos dos definiciones de diferenciabilidad, aún no tenemos una manera muy práctica de encontrar o describir a la transformación lineal $T_{\bar{a}}$, que es la mejor aproximación lineal. En el ejemplo después de nuestra definición, nos dieron la transformación y funcionó, pero hasta donde hemos platicado, todavía es un misterio cómo obtenerla.

Nos gustaría tener una descripción más explícita pues queremos resolver problemas específicos como encontrar, por ejemplo, la ecuación de un hiperplano tangente. Este problema ya lo habíamos resuelto para campos escalares: si tenemos suficiente regularidad, entonces podemos construir la derivada a través de las derivadas parciales (que a su vez son derivadas direccionales). La teoría que ya desarrollamos prácticamente se puede copiar, considerando que ahora tendremos derivadas en cada función coordenada.

Lo primero que notaremos es que así como para campos escalares, para campos vectoriales también podemos definir la noción de derivadas direccionales. Pensemos en una función $f:S\subseteq \mathbb{R}^{n}\to \mathbb{R}^n$. Tomemos un vector fijo $\bar{a}\in Int=(S)$. Coloquemos una flecha que comience en $\bar{a}$ y tenga dirección dada por otro vector dado $\bar{y}\in \mathbb{R}^{n}$. Si multiplicamos a $\bar{y}$ por un escalar $h$ positivo, esto estira o encoge al vector $\bar{y}$, pero lo deja con la misma dirección. En el ejemplo de la Figura 3, al variar sobre todos los valores de $h$ se genera la recta $\bar{a}+h\bar{y}$. Si a los puntos de esta recta le aplicamos la función $f$, se obtiene un cierto lugar geométrico $$f(\bar{a}+h\bar{y})=(f_1(\bar{a}+h\bar{y}),\ldots,f_m(\bar{a}+h\bar{y})),$$ conforme se varían los valores de $h$. Lo que definiremos como derivada direccional nos permitirá hablar de un espacio afín tangente de dimensión $m$ a este lugar geométrico en el punto $f(\bar{a})$.

A continuación tenemos nuestra definición de derivada direccional para campos vectoriales.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Tomemos $\bar{a}\in Int(S)$, $\bar{y}\in \mathbb{R}^{n}$. Definimos la derivada direccional de $f$ en $\bar{a}$ en la dirección $\bar{y}$ como: \[ f'(\bar{a};\bar{y})=\lim\limits_{h\to 0}\frac{f(\bar{a}+h\bar{y})-f(\bar{a})}{h}, \] siempre y cuando el límite exista.

Notemos que $f'(\bar{a};\bar{y})$ es un vector de $\mathbb{R}^{m}$.

En los campos escalares teníamos derivadas parciales. En este caso también las tenemos y describen a las derivadas direccionales en el mismo sentido que en el caso escalar. Para formalizar las cosas, damos la definición a continuación.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Tomemos $\bar{a}\in Int(S)$, $\bar{y}\in \mathbb{R}^{n}$. Definimos la derivada direccional de $f$ en la coordenada $x_i$ en $a$ como la derivada parcial $f'(\bar{a};\hat{e}_i)$, donde $\hat{e}_i$ es el $i$-ésimo vector de la base canónica, siempre y cuando esta exista.

Como en el caso de los campos escalares, las derivadas direccionales pueden entenderse en términos de las derivadas parciales bajo suficiente regularidad. Tomemos $\hat{e}_1,\ldots,\hat{e}_n$ la base canónica de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$. Pensemos que todas las derivadas parciales de $f$ existen en un punto dado $\bar{a}$ y que son continuas. Expresemos a $\bar{y}$ como $\bar{y}=\alpha_1\hat{e}_1+\alpha_2\hat{e}_2+\ldots+\alpha_n\hat{e}_n$ con $\hat{e}_1,\ldots,\hat{e}_n$ la base canónica de $\mathbb{R}^n$. En esta entrada discutiremos hacia el final que bajo estas condiciones tendremos que $f'(\bar{a};\bar{y})$ existe y de hecho que $$f'(\bar{a};\bar{y})=\sum_{i=1}^n \alpha_i f'(\bar{a};\bar{e}_i).$$

El tener derivadas parciales continuas resultará una hipótesis muy fuerte y de hecho implicará todavía más que la existencia de derivadas direccionales. De hecho, como en el caso de campos escalares, esta hipótesis implicará diferenciabilidad. Antes de discutir esto, veremos en la siguiente sección qué pasa componente a componente.

Si las derivadas parciales no son continuas, no deberíamos esperar que las derivadas direccionales existan: ¡hay muchas posibles direcciones y sólo sabemos que pasa en dos de ellas! Como tarea moral, puedes pensar en un contraejemplo de un campo escalar $f:\mathbb{R}^2\to \mathbb{R}^2$ con derivadas parciales en cierto punto $\bar{a}$, pero sin alguna (o algunas) derivadas direccionales en $\bar{a}$.

Derivadas por componente

Las derivadas direccionales pueden entenderse mediante las derivadas parciales, pero también, como en el caso de las trayectorias, pueden entenderse mediante las derivadas por componente. Para pensar en ello, tomemos $\hat{e}_1,\ldots,\hat{e}_m$ la base canónica de $\mathbb{R}^m$. Tomemos $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ con funciones coordenadas $f(\bar{x})=\left( f_{1}(\bar{x}),\dots ,f_{m}(\bar{x})\right)$. Pensemos que las derivadas direccionales de $f_1,\ldots, f_m$ en $\bar{a}$ en la dirección $\bar{y}$ existen.

Tenemos entonces:

\begin{align*} \lim\limits_{h\to 0}\frac{f(\bar{a}+h\bar{y})-f(\bar{a})}{h} &=\lim\limits_{h\to 0}\frac{\left( f_{1}(\bar{a}+h\bar{y}),\dots ,f_{m}(\bar{a}+h\bar{y})\right) -\left( f_{1}(\bar{a}),\dots ,f_{m}(\bar{a})\right)}{h}\\ &=\lim\limits_{h\to 0}\left( \frac{f_{1}(\bar{a}+h\bar{y})-f_{1}(\bar{a})}{h},\dots ,\frac{f_{m}(\bar{a}+h\bar{y})-f_{m}(\bar{a})}{h}\right)\\ &=\lim\limits_{h\to 0}\sum_{i=1}^{m}\frac{f_{i}(\bar{a}+h\bar{y})-f_{i}(\bar{a})}{h}{\hat{e}_{i}}\\
&=\sum_{i=1}^{m}\lim\limits_{h\to 0}\frac{f_{i}(\bar{a}+h\bar{y})-f_{i}(\bar{a})}{h}{\hat{e}_{i}}\\ &=\sum_{i=1}^{m}f_{i}'(\bar{a};\bar{y}){\hat{e}_{i}}. \end{align*}

En la última igualdad estamos usando la suposición de que las derivadas existen componente a componente. Como mostramos que el límite planteado inicialmente existe, obtenemos entonces que
\begin{equation} \label{eq:porcomponente} f'(\bar{a};\bar{y})=\sum_{i=1}^{m}f_{i}'(\bar{a};\bar{y}){\hat{e}_{i}} .\end{equation}

Lo que tenemos aquí es que la derivada direccional de $f$ en $\bar{a}$ en dirección de $\bar{y}$ es la suma vectorial de cada vector de la base escalado por la derivada direccional del campo escalar $f_{i}$ en $\bar{a}$ con respecto a la dirección de $\bar{y}$.

Diferenciabilidad implica derivadas direccionales

La noción de diferenciabilidad que dimos implica la diferenciabilidad de cada una de las funciones componente $f_i$ de una función $f:\mathbb{R}^n\to \mathbb{R}^m$. Es decir, si el campo vectorial es diferenciable, entonces cada uno de los campos escalares $f_1,\ldots,f_m$ componentes son también diferenciables, pues el límite $$\lim_{\bar{v}\to \bar{0}}\frac{||f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})||}{||\bar{v}||}=0$$ se cumple, y por lo tanto se cumple componente a componente. En el caso de $T_{\bar{a}}$ el $i$-ésimo componente es precisamente hacer el producto interior del $i$-ésimo renglon de la matriz que representa a $T_{\bar{a}}$ con $\bar{v}$, y entonces la derivada $\triangledown f_i(\bar{a})$ del campo escalar $f_i$ está dada precisamente por dicho $i$-ésimo renglón.

A su vez, sabemos que si un campo escalar es diferenciable, entonces existen todas las derivadas parciales. Por lo que hemos platicado en unidades anteriores, si $\bar{y}\in \mathbb{R}^{n}$ se escribe en la base canónica como $\bar{y}=\sum_{j=1}^{n}y_{j}{\hat{e}_{j}}$, al aplicar $\triangledown f_i(\bar{a})$ obtenemos

\begin{align*}
\triangledown f_i(\bar{a})(\bar{y})&=\sum_{j=1}^n y_j\triangledown f_i(\bar{a})(\hat{e}_j)\\
&=\sum_{j=1}^n y_j \frac{\partial f_i}{\partial x_j}(\bar{a}),\\
\end{align*}

lo cual abreviamos como

$$f_i'(\bar{a};\bar{y})=\left(\frac{\partial f_i}{\partial x_1}(\bar{a}), \ldots, \frac{\partial f_i}{\partial x_n}(\bar{a})\right) \cdot \bar{y}.$$

Usando esta igualdad para cada $i$ y sustituyendo la ecuación \eqref{eq:porcomponente} que obtuvimos al analizar componente por componente, obtenemos entonces que

$$f^{\prime}(\bar{a};\bar{y})=\sum_{i=1}^m \left(\left(\frac{\partial f_i}{\partial x_1}(\bar{a}), \ldots, \frac{\partial f_i}{\partial x_n}(\bar{a})\right) \cdot \bar{y}\right)\hat{e}_i.$$

¡Pero esto se puede denotar de manera mucho más compacta mediante un producto matricial! Reflexiona un poco por qué la expresión anterior dice exactamente lo mismo que la siguiente:

$$f'(\bar{a};\bar{y})= \begin{pmatrix} \frac{\partial f_{1}}{\partial y_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial y_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix}.$$

Como tarea moral, tendrás que verificar que en un campo vectorial diferenciable en $\bar{a}$ se debe cumplir que $f'(\bar{a};\bar{y})=T_{\bar{a}}(\bar{y})$. Por lo discutido, debe pasar entonces para cada $y$ que \[ T_{\bar{a}}(\bar{y})=\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix}.\]

Esto precisamente nos está diciendo que si $f$ es diferenciable en $a$, entonces sus derivadas parciales deben existir y se debe cumplir que la forma matricial de $T_{\bar{a}}$ en las bases canónicas de $\mathbb{R}^n$ y $\mathbb{R}^m$ debe ser \begin{equation}\label{eq:jacobiana}\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}.\end{equation}

Matriz jacobiana

Toda la discusión anterior nos lleva a lo siguiente.

Definición. Dado un campo vectorial $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ diferenciable en un punto $\bar{a}\in Int(S)$ con derivada $T_{\bar{a}}$, a la matriz que representa a $T_{\bar{a}}$ en las bases canónicas la denotamos por $Df(\bar{a})$ y le llamamos la matriz jacobiana de $f$ en $\bar{a}$.

Por lo discutido en la sección anterior,

$$Df(\bar{a})=\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}.$$

Escribiremos $Df(\bar{a})(\bar{x})$ para referirnos al producto de la matriz $Df(\bar{a})$ con el vector (columna) $\bar{x}$, que precisamente coincide con $T_{\bar{a}}(\bar{x})$. Así, bajo la hipótesis de diferenciabilidad, hemos recuperado entonces lo que hace $T_{\bar{a}}$ como una multiplicación matricial, donde la matriz tiene como elementos a las derivadas parciales de las funciones coordenada en el punto $\bar{a}$.

Ejemplos de diferenciabilidad en campos vectoriales

Con todo lo discutido hasta ahora, obtenemos un método para obtener la derivada para campos vectoriales, lo que nos permitirá, por ejemplo, encontrar la transformación lineal de forma explícita y encontrar hiperplanos tangentes.

Ejemplo. Consideremos $f(x,y)=(x^{2},xy,y^{2}).$ Calculemos su diferencial en el punto $(1,-1)$. Las funciones coordenada son

\begin{align*}
f_{1}(x,y)&=x^{2}\\
f_{2}(x,y)&=xy\\
f_{3}(x,y)&=y^{2},
\end{align*}

de donde tenemos: \[ \frac{\partial f_{1}}{\partial x}(1,-1)=\left. 2x\right|_{_{(1,-1)}}=2;\hspace{3cm} \frac{\partial f_{1}}{\partial y}(1,-1)=0;\hspace{3cm}\frac{\partial f_{2}}{\partial x}(1,-1)=\left. y\right|_{_{(1,-1)}}=-1;\] \[ \frac{\partial f_{2}}{\partial y}(1,-1)=\left. x\right|_{_{(1,-1)}}=1;\hspace{3cm}\frac{\partial f_{3}}{\partial x}(1,-1)=0;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,-1)=\left. 2y\right|_{_{(1,-1)}}=-2.\] Así \[ Df(1,-1)=\begin{pmatrix} \frac{\partial f_{1}}{\partial x}(1,-1) & \frac{\partial f_{1}}{\partial y}(1,-1) \\ \frac{\partial f_{2}}{\partial x}(1,-1) & \frac{\partial f_{2}}{\partial y}(1,-1) \\ \frac{\partial f_{3}}{\partial x}(1,-1) & \frac{\partial f_{3}}{\partial y}(1,-1) \end{pmatrix}= \begin{pmatrix} 2 & 0 \\ -1 & 1 \\ 0 & -2 \end{pmatrix}.\]

$\triangle$

Ejemplo. Ahora obtengamos el plano tangente a una superficie dada en un punto dado. Sea $\mathcal{S}$ la superficie de $\mathbb{R}^{3}$ descrita por la imagen de la función $f(x,y)=(x,y,xy^{2})$. Vamos a determinar el plano tangente a dicha superficie en el punto $(1,1,1)$. Comencemos calculando $Df(1,1)$. En primer lugar calculemos las parciales: \[ \frac{\partial f_{1}}{\partial x}(1,1)=1;\hspace{3cm}\frac{\partial f_{1}}{\partial y}(1,1)=0;\hspace{3cm}\frac{\partial f_{2}}{\partial x}(1,1)=0 \] \[ \frac{\partial f_{2}}{\partial y}(1,1)=1;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,1)=1;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,1)=2.\]

Por lo tanto \[ Df(1,1)=\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 2 \end{pmatrix}.\]

Esta transformación manda al punto $(x,y)$ del plano $\mathbb{R}^2$ al punto\[ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 2 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x \\ y \\ x+2y \end{pmatrix}.\]

De modo que el plano centrado en el origen es el conjunto $$H=\{(x,y,x+2y)\in \mathbb{R}^{3}|(x,y)\in \mathbb{R}^{2}\}.$$

Pero este plano debemos todavía trasladarlo por el vector $(1,1,1)$ para que pase por el punto $f(1,1)$. Concluimos entonces que el plano tangente buscado es el conjunto

$$\{(x+1,y+1,x+2y+1)\in \mathbb{R}^{3}|(x,y)\in \mathbb{R}^{2}\}.$$

En la Figura 4 tenemos la en rojo la imagen del campo vectorial de este ejemplo y en verde la del plano tangente, el punto negro es el punto $(1,1,1)$.

$\triangle$

¿Y derivadas parciales implica diferenciabilidad?

Cuando un campo vectorial es diferenciable, existen todas las derivadas parciales de todos sus campos escalares coordenados. El regreso no es cierto. Sin embargo, sí se vale bajo una condición adicional de regularidad.

Definición. Diremos que un campo vectorial $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ es de clase $C^1$ (o simplemente es $C^1$) en un punto $\bar{a}\in S$ si todas las derivadas parciales de todas las funciones componentes de $f$ existen y son continuas en $\bar{a}$. Definimos de manera análoga lo que significa que $f$ sea de clase $C^1$ en todo $S$.

Teorema. Si $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ es un campo vectorial, $\bar{a}\in S$ y $f$ es $C^1$ en $\bar{a}$, entonces $f$ es diferenciable y su derivada $T_a$ tiene como forma matricial a la matriz jacobiana \eqref{eq:jacobiana}.

La prueba de este resultado se hace coordenada a coordenada, aplicando en cada una de ellas el teorema de diferenciabilidad y derivadas parciales para campos escalares que demostramos en la entrada del teorema del valor medio para campos escalares.

Más adelante…

En esta entrada introdujimos el concepto de diferenciabilidad, de derivadas parciales, direccionales y por componente. Además, mostramos que cuando una función es diferenciable, entonces su derivada tiene una forma matricial muy sencilla, dada por las derivadas parciales de las componentes. Esto es nuestra primera señal de que las derivadas y las matrices están muy relacionadas entre sí. Lo que veremos en la siguiente entrada es que esta conexión se sigue dando, y de hecho nos permitirá enunciar de manera muy elegante la regla de la cadena para campos vectoriales: ¡será una multiplicación de matrices!

Después de entender mejor la diferenciabilidad, presentaremos y demostraremos teoremas clásicos e importantes de campos vectoriales: el teorema de la función inversa, y el teorema de la función implícita.

Tarea moral

Completa los detalles faltantes del primer ejemplo que dimos de diferenciabilidad.
Calcula la matriz jacobiana de la función $g(x,y,z)=(xz,xy,x^{2}y^{2}z^{2})$. Úsala para encontrar la ecuación del espacio tangente a la gráfica en el punto $g(2,1,0)$.
Halla el campo vectorial cuya imagen es el plano tangente a la superficie dada por la ecuación $F(x,y)=x^{2}y^{2}+1$ en el punto $(1,1)$. Como ayuda al graficar $F$ en $\mathbb{R}^{3}$ nos dibuja la misma superficie que obtenemos de la imagen del campo vectorial $f(x,y)=(x,y,x^{2}y^{2}+1)$ que esta contenida en $\mathbb{R}^{3}$.
Verifica que en efecto las dos definiciones de diferenciabilidad que dimos son equivalentes.
Demuestra que si las parciales de cada componente de un campo vectorial existen, y son continuas, entonces la función es diferenciable. Tendrás que seguir la sugerencia dada en la última sección. Después, justifica la igualdad que dimos que escribe a las derivadas direccionales en términos de las parciales.
Explica a detalle por qué la expresión a la que llegamos para $f^{\prime}(\bar{a};\bar{y})$ en efecto se puede pensar como el producto matricial mencionado.
Encuentra un ejemplo de campo vectorial $f:\mathbb{R}^2\to \mathbb{R}^2$ en donde las derivadas parciales existen en algún punto $\bar{a}$, pero no todas las derivadas direccionales existen.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Formas cuadráticas
Entrada siguiente del curso: Regla de la cadena para campos vectoriales

Cálculo Diferencial e Integral III: Teorema del valor medio para campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Ya hemos definido qué es el gradiente $\nabla f$ de un campo escalar $f$. Hemos visto cómo está relacionado con las derivadas direccionales. Así mismo, mostramos que conocer este gradiente nos permite dar información sobre los máximos y mínimos del campo escalar. En esta entrada mostraremos una propiedad más del gradiente: que nos ayuda a dar una generalización del teorema del valor medio de Cálculo I, pero para campos escalares. Este será un resultado fundamental para demostrar otras propiedades de los campos escalares. Como ejemplo, también damos en esta entrada un criterio suficiente para que un campo escalar sea diferenciable.

Teorema del valor medio para funciones de $\mathbb{R}$ en $\mathbb{R}$

Para facilitar la lectura de este material, recordemos lo que nos dice el teorema del valor medio sencillo, es decir, el de $\mathbb{R}$ en $\mathbb{R}$.

Teorema. Sean $a<b$ reales. Sea $f:[a,b]\to\mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe algún punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

Una vez que uno interpreta el teorema gráficamente, se vuelve muy intuitivo. Considera la siguiente figura.

Intuición geométrica del teorema del valor medio

El término $$\frac{f(b)-f(a)}{b-a}$$ es la pendiente del segmento que une los puntos $(a,f(a))$ y $(b,f(b))$ El término $f'(c)$ va marcando la pendiente de la recta tangente a $f$ en cada punto $c$. En términos geométricos, lo que nos dice este teorema es que para algún valor de $c$, la pendiente de la recta tangente en $c$ es la pendiente del segmento entre los extremos.

Lo que haremos a continuación es dar una generalización apropiada para funciones de $\mathbb{R}^n$ a $\mathbb{R}$.

Teorema del valor medio para funciones de $\mathbb{R}^n$ en $\mathbb{R}$

Para generalizar el teorema del valor medio a funciones de $\mathbb{R}^n$ a $\mathbb{R}$, necesitaremos cambiar un poco las hipótesis. El segmento $[a,b]$ que usábamos ahora será un segmento (multidimensional) que conecte a dos vectores $\bar{x}$ y $\bar{y}$ en $\mathbb{R}^n$. La diferenciabilidad la pediremos en todo un abierto que contenga al segmento. El enunciado apropiado se encuentra a continuación.

Teorema (del valor medio para campos escalares). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar diferenciable. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

En este caso no podemos «pasar dividiendo $\bar{y}-\bar{x}$» pues no tiene sentido dividir entre vectores. Pero en el caso $n=1$ sí se puede, y justo obtenemos de vuelta el teorema del valor medio de $\mathbb{R}$ en $\mathbb{R}$. Uno podría pensar que entonces esta es una manera alternativa de demostrar el teorema para funciones de $\mathbb{R}$ en $\mathbb{R}$. Sin embargo, como veremos a continuación, la demostración de la versión para campos escalares usa la versión para funciones reales.

Demostración. Consideremos la función $\gamma:[0,1] \to \mathbb{R}^{n}$ dada $\gamma (t)=(1-t)\bar{x}+t\bar{y}$. Notemos que $\gamma$ es diferenciable, con $\gamma’ (t)=\bar{y}-\bar{x}$. Además, por hipótesis $f$ es diferenciable en $S$. Así, $f\circ \gamma:[0,1]\to \mathbb{R}$ también es diferenciable, y por regla de la cadena

\begin{align*}
(f\circ \gamma)'(t)&=\nabla f(\gamma(t))\cdot \gamma'(t)\\
&=\nabla f(\gamma(t))\cdot (\bar{y}-\bar{x}).
\end{align*}

¡Pero $f\circ \gamma$ ya es una función de $\mathbb{R}$ en $\mathbb{R}$! Así, podemos aplicarle el teorema del valor medio real (verifica las hipótesis como tarea moral). Al hacer esto, obtenemos que existe una $c\in (0,1)$ tal que
\begin{align*}
(f\circ \gamma)'(c) &= \frac{(f\circ \gamma)(1)-(f\circ \gamma)(0)}{1-0}\\
&=f(\bar{y})-f(\bar{x}).
\end{align*}

Usando la fórmula que obtuvimos por regla de la cadena para $(f\circ \gamma)’$ y la definición de $\gamma$ obtenemos que

$$ \nabla f((1-c)\bar{x}+c\bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}),$$

tal y como buscábamos.

$\square$

En el teorema anterior estamos pidiendo que $f$ sea diferenciable. Sin embargo, basta con que exista la derivada de la composición en el segmento que nos interesa y el resultado también se sigue. Es decir, tenemos la siguiente versión con una hipótesis más débil. La enunciamos pues la usaremos en la siguiente sección.

Teorema (del valor medio para campos escalares, hipótesis debilitada). Sea $S$ un abierto de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Sean $\bar{x}$ y $\bar{y}$ en $S$ tales que el segmento que une a $\bar{x}$ con $\bar{y}$ se queda contenido en $S$ y tales que para toda $c\in[0,1]$ se cumple que la derivada (real) de $f((1-c)\bar{x}+c\bar{y}))$ existe. Entonces, existe $c \in (0,1)$ tal que $$\nabla f((1-c )\bar{x}+c \bar{y})\cdot (\bar{y}-\bar{x})=f(\bar{y})-f(\bar{x}).$$

La demostración es exactamente la misma.

Aplicación del teorema del valor medio

Como primera aplicación del teorema del valor medio para campos escalares mostraremos un criterio de diferenciabilidad muy útil, al que llamaremos el teorema de diferenciabilidad y derivadas parciales.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar. Supongamos que para cierto punto $\bar{a}\in S$ y cierta vecindad $B_r(\bar{a})\subset S$ existen las derivadas parciales $\frac{\partial f}{\partial x_{1}},\dots ,\frac{\partial f}{\partial x_{n}}$ y son continuas en $\bar{a}$. Entonces $f$ es diferenciable en $\bar{a}$.

Demostración. Elijamos un vector $\bar{u}=u_1\hat{e}_1+\dots +u_n\hat{e}_n$ de norma $1$ y tomemos $\bar{v}=\lambda \bar{u}$ con $\lambda$ suficientemente chico como para que $\bar{a}+\bar{v}$ esté en $B_{r}(\bar{a})$. Definamos los siguientes vectores:

\begin{align*}
\bar{v}_0&=\bar{0}\\
\bar{v}_1&=u_1\hat{e}_1\\
\bar{v}_2&=u_1\hat{e}_1+u_2\hat{e}_2\\
&\vdots\\
\bar{v}_n&=u_1\hat{e}_1+u_2\hat{e}_2+\ldots+u_n\hat{e}_n=\bar{u}.
\end{align*}

Con ellos creamos la siguiente suma telescópica para expresar a $f(\bar{a}+\bar{v})-f(\bar{a})$

\begin{align}
f(\bar{a}+\bar{v})-f(\bar{a})&=f(\bar{a}+\lambda \bar{u})-f(\bar{a}) \nonumber\\
&=\sum_{k=1}^{n}[f(\bar{a}+\lambda \bar{v}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1})] \label{eq:telescopica}
\end{align}

Notemos que el $k$-ésimo término de esta suma puede ser escrito como $$f(\bar{a}+\lambda \bar{v}_{k-1}+\lambda u_{k}\hat{e}_{k})-f(\bar{a}+\lambda \bar{v}_{k-1}).$$ Para simplificar, definimos $\bar{b}_{k}=\bar{a}+\lambda \bar{v}_{k-1}$ y reescribiendo el $k$-ésimo término tenemos $$f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k}).$$

Aplicando el teorema del valor medio con hipótesis debilidada para campos escalares a los puntos $\bar{b}_{k}$ y $\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}$ (verifica las hipótesis), tenemos que para cada $k$ existe $\xi_k \in (0,1)$ tal que

\begin{align*}
f(\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})&=\triangledown f((1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k}))\cdot (\lambda u_{k}\hat{e}_{k})\\
&=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}),
\end{align*}

en donde hemos definido $\bar{c}_k:=(1-\xi_k )\bar{b}_{k}+\xi_k (\bar{b}_{k}+\lambda u_{k}\hat{e}_{k})$, que es un punto en el segmento que une a $\bar{b}_k$ con $\bar{b}_k+\lambda u_k\hat{e}_k$.

Tenemos pues que podemos escribir al $k$-ésimo término como:

$$f(\hat{b}_{k}+\lambda u_{k}\hat{e}_{k})-f(\bar{b}_{k})=\lambda u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k}).$$

Notemos además que si $\lambda \to 0$, entonces $\bar{b}_{k}\to \bar{a}$, $\bar{c}_{k} \to a$ y $\bar{v}\to \bar{0}$.

Escribimos entonces la ecuación \eqref{eq:telescopica} como:

\begin{equation}
\label{eq:resumen}
f(\bar{a}+\bar{v})-f(\bar{a})=\lambda \sum_{k=1}^{n}u_k\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})
\end{equation}

En unos momentos usaremos esta expresión. Antes de ello, estudiemos otro de los términos involucrados en la diferenciabilidad. Tenemos que:

\begin{align}
\triangledown f(\bar{a})\cdot \bar{v}&=\triangledown f(\bar{a})\cdot \lambda u \nonumber\\
&=\lambda \triangledown f(\bar{a})\cdot u \nonumber\\
&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a}) \label{eq:ppunto}.
\end{align}

Empecemos entonces a combinar lo visto hasta ahora para entender los términos en la definición de diferenciabilidad. Tenemos juntando \eqref{eq:resumen} y \eqref{eq:ppunto} que

\begin{align*}
f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot v&=\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\lambda \sum_{k=1}^{n}u_{k}\frac{\partial f}{\partial x_{k}}(\bar{a})\\&=\lambda \sum_{k=1}^{n}u_{k}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right].
\end{align*}

Como mencionamos, si $\lambda \to 0$ entonces $\bar{v}\to \bar{0}$. Además, $||\bar{v}||=|\lambda|$. Así:

\[ \lim\limits_{\bar{v}\to \bar{0}} \frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=\lim\limits_{\lambda \to 0} \left|\sum_{k=1}^{n}\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|.\]

Veamos qué más sucede cuando $\lambda \to 0$. Ya notamos que $\bar{c}_k\to \bar{a}$, así que usando la continuidad de las derivadas parciales tenemos:

\[ \lim\limits_{\lambda \to 0}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\lim\limits_{\bar{c}_{k}\to \bar{a}}\frac{\partial f}{\partial x_{k}}(\bar{c}_{k})=\frac{\partial f}{\partial x_{k}}(\bar{a}).\]

Aplicando desigualdad del trángulo en la suma, el límite buscado es menor o igual a

\[ \lim\limits_{\lambda \to 0}\sum_{k=1}^{n}\left|\left[ \frac{\partial f}{\partial x_{k}}(\bar{c}_{k})-\frac{\partial f}{\partial x_{k}}(\bar{a}) \right]u_{k}\right|=0.\]

Y aquí cada sumando se va a $0$. La conclusión final es que

\[ \lim\limits_{\bar{v}\to \bar{0}}\frac{|f(\bar{a}+\bar{v})-f(\bar{a})-\triangledown f(\bar{a})\cdot \bar{v}|}{||\bar{v}||}=0,\]

de modo que $f$ es diferenciable en $\bar{a}$.

$\square$

El regreso del teorema anterior no se vale

El teorema de diferenciabilidad nos dice que si las derivadas parciales existen y son continuas, entonces la función es diferenciable. Sin embargo, el regreso de este teorema no se vale, en el sentido de que existen funciones diferenciables cuyas derivadas parciales no son continuas. En otras palabras, si las derivadas parciales no son continuas, no podemos descartar la diferenciablidad de una función.

A continuación esbozamos un ejemplo que deberás completar como tarea moral.

Ejemplo. Consideremos la función

$$f(x,y)=\begin{cases} (x^2+y^2)\sin\left(\frac{1}{\sqrt{x^2+y^2}}\right) &\text{si $(x,y)\neq (0,0)$}\\ 0 & \text{si $(x,y)=(0,0)$}\end{cases}$$

Se puede demostrar que $f$ es diferenciable en $(0,0)$. De manera intuitiva, la función queda entre las funciones $(x,y)\to x^2+y^2$ y $(x,y)\to -x^2-y^2$. Se puede usar un argumento de acotamiento para mostrar que el plano tangente coincide entonces con el de estas funciones en $(0,0)$ que es el plano $z=0$. Verifica los detalles de tarea moral.

Así mismo, se puede ver que las derivadas parciales en $(0,0)$ existen y que de hecho se satisface $$\frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 0.$$

Finalmente, se puede ver que las derivadas parciales no convergen a $0$. Fuera del $(0,0)$, tenemos por reglas de derivación que

\begin{align*} \frac{\partial f}{\partial x}(x,y) &= 2 x \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{x \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}\\ \frac{\partial f}{\partial y}(x,y) &= 2 y \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{y \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}. \end{align*}

Una manear de ver que estas no son contínuas es aproximándonos por un eje. Por ejemplo, puedes verificar que sobre el eje $x$, conforme $x\to 0$, tenemos que la primera parcial oscila entre $-1$ y $1$.

$\triangle$

Más adelante…

Hemos enunciado y demostrado una versión del teorema del valor medio para campos escalaras. Gracias a ella hemos podido mostrar que si un campo escalar tiene derivadas parciales continuas, entonces es diferenciable. Las aplicaciones del teorema del valor medio para campos escalares van más allá. En la siguiente entrada hablaremos de las derivadas parciales de orden superior. El teorema del valor medio para campos escalares nos permitirá demostrar que bajo ciertas condiciones, en cierto sentido estas derivadas parciales «conmutan».

Tarea moral

¿Qué dice el teorema del valor medio para campos escalares para la función $f(x,y)=\sin(x)\cos(y)$ tomando como extremos los puntos $\left(0,\frac{\pi}{2}\right)$ y $\left(\frac{\pi}{2},0\right)$? Verifica si puedes aplicar las hipótesis.
En la demostración del teorema del valor medio que dimos, verifica que la función $f\circ \gamma$ dada en efecto satisface las hipótesis del teorema del valor medio real.
Supongamos que $f:\mathbb{R}^n\to \mathbb{R}$ es diferenciable en un abierto $S$ que contiene al segmento cuyos extremos son ciertos vectores $\bar{x}$ y $\bar{y}$ de $\mathbb{R}^n$. Supongamos que $f(\bar{x})=f(\bar{y})$. ¿Será cierto siempre que $\nabla f$ se anula en algún vector del segmento que une $x$ con $y$? Ten cuidado, pues hay un producto escalar involucrado. En caso de que no siempre sea cierto, ¿Qué es lo que sí puedes garantizar?
En la demostración del teorema de diferenciabilidad, verifica que se pueden usar las hipótesis del teorema del valor medio para campos escalares con hipótesis debilitada. Necesitarás ver que la derivada real que tiene que existir es justo una parcial de las que suponemos que existen, completa los detalles. Luego, verifica que en efecto la conclusión que obtuvimos es justo la que se obtiene. Observa además que no podemos usar el teorema del valor medio para campos diferenciables con la hipótesis usual pues necesitaríamos saber que $f$ es diferenciable, lo cual es justo lo que queremos mostrar.
Completa el contraejemplo al regreso del teorema de diferenciabilidad. Entre otras cosas, tienes que hacer lo siguiente:
- Verificar que en efecto la función es diferenciable en $(0,0)$. Puedes proceder por definición o acotando como se sugiere.
- Revisar que las parciales en $(0,0)$ en efecto existen y coinciden con lo que sabemos a partir de que el plano tangente en el origen es $(0,0)$.
- Obtener paso a paso la fórmula que dimos para las parciales, usando lo que sabes de regla de la cadena, derivadas en $\mathbb{R}$, etc.
- Verificar que ninguna de las dos derivadas parciales es continua, completando el argumento de que al acercarnos por los ejes tenemos oscilaciones.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Puntos críticos
Entrada siguiente del curso: Derivadas parciales de segundo orden

Cálculo Diferencial e Integral III: Polinomio de Taylor para campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Una intuición que se obtiene de un primer curso de cálculo diferencial e integral es que las funciones que tienen muchas derivadas «se parecen mucho a polinomios», en el sentido de que podemos aproximarlas apropiadamente con este tipo de expresiones. Esta intuición nos las da el teorema del polinomio de Taylor. En muchas aplicaciones, es conveniente estudiar polinomios en vez de funciones en general, así que sería ideal tener una versión de este mismo resultado para cálculo de varias variables. En esta entrada recordaremos un poco del caso unidimensional y luego enunciaremos la teoría correspondiente para el polinomio de Taylor.

Recordatorio de polinomio de Taylor en $\mathbb{R}$

Recordemos qué es lo que dice el teorema del polinomio de Taylor para el caso unidimensional. Esto nos ayudará pues lo usaremos posteriormente para enunciar una versión para varias variables.

Teorema. Sea $f:S\subseteq \mathbb{R}\to \mathbb{R}$ una función y $a\in int(S)$ de tal manera que existen $f^{\prime}(a),\dots ,f^{(k)}(a)$. Sea $$a_{\ell}=\frac{f^{(\ell)}(a)}{\ell!}$$ con $0\leq \ell \leq k$ y definamos a partir de esto $$T_{k,a}(x)=a_{0}+a_{1}(x-a)+\dots +a_{k}(x-a)^k,$$

al que llamamos el polinomio de Taylor de $f$ de grado $k$ alrededor de $a$.

Entonces $$\lim_{x \to a}\frac{f(x)-T_{k,a}(x)}{(x-a)^k}=0.$$

La demostración de este teorema la puedes encontrar en la entrada El Polinomio de Taylor (Parte 1) del curso de Cálculo I. Es recomendable que consultes esta entrada para recordar todo lo referente a este tema en una variable real.

Pidiendo un poco más de regularidad, se puede estudiar el residuo $$R_{k,a}(x):=f(x)-T_{k,a}(x).$$

Por ejemplo, se puede demostrar el siguiente teorema.

Teorema. Sea $f:S\subseteq \mathbb{R}\to\mathbb{R}$. Supongamos que $f^{\prime},\dots ,f^{(k+1)}$ están definidas sobre $[a,x]$. Entonces, se puede expresar el residuo del teorema de Taylor como

\begin{equation}
\label{eq:residuo}
R_{k,a}(x)=\frac{f^{(k+1)}(\xi)}{(k+1)!}(x-a)^{k+1}.
\end{equation}

para algún $\xi\in[a,x]$.

Para la demostración de este teorema y otras expresiones del residuo (por ejemplo, una expresión en términos de integrales), puedes visitar el curso de Cálculo II, en particular la entrada Series de Taylor y de Maclaurin.

Pensemos de momento que $f$ tiene derivadas parciales de todos los órdenes (es decir, que es $C^\infty$). En este caso, $f$ tiene polinomios de Taylor de todos los grados. De entrada, no tendría por qué suceder que $\lim_{k\to \infty} T_{k,a}(x)=f(x)$, y de hecho hay contraejemplos para ello. Pero si además tenemos que se tiene $\lim_{k \to \infty}R_{k,a}(x)=0$, entonces la igualdad anterior sí se cumple. En este caso, verdaderamente $f$ se puede expresar como un polinomio infinito (una serie de potencias) alrededor de $a$ de la siguiente manera:

\begin{equation}\label{eq:taylor-inf}f(x)=\sum_{i=0}^{\infty}\frac{f^{(i)}(a)}{i!}(x-a)^{i}.\end{equation}

Ejemplo. Calculemos en $0$ el polinomio de Taylor de $f(x)=e^x$. Para cada entero positivo $k$ se tiene:

$$\frac{f^{(k)}(0)}{k!}x^{k}=\frac{e^0}{k!}x^{k}=\frac{x^{k}}{k!}.$$

De aquí, por la forma que toma el residuo, existe $\xi\in [0,x]$ para el cual

$$R_{k,0}(x)=\frac{e^\xi}{(k+1)!}x^{k+1}.$$

aquí $e^\xi$ está acotado y el cociente $\frac{x^{k+1}}{(k+1)!}$ se va a cero conforme $k\to \infty$. De este modo, tenemos la igualdad

$$e^x=1+\frac{x}{1}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\dots.$$

$\triangle$

Preliminares para polinomio de Taylor para campos escalares

La manera en la cual generalizaremos el teorema del polinomio de Taylor será a través de evaluar nuestro campo escalar sobre un segmento, muy parecido a como generalizamos el teorema del valor medio. Pongamos la situación en contexto.

Tomemos un abierto $S\subseteq \mathbb{R}^n$ y un campo escalar $f:S\to \mathbb{R}$. Tomemos vectores
\begin{align*}
\bar{a}=(a_1,\ldots,a_n)\\
\bar{v}=(v_1,\ldots,v_n),
\end{align*}

y $t$ en el intervalo $[0,1]$. Supondremos además que para todo dicho $t$ se cumple $\bar{a}+t\bar{v}\in S$.

Podemos recorrer el segmento de $\bar{a}$ a $\bar{a}+\bar{v}$ mediante la trayectoria $\gamma : [0,1] \to \mathbb{R}^{n}$ dada por $\gamma (t)=\bar{a}+t\bar{v}$. Si componemos a esta trayectoria con la función $f$, obtenemos una función $G: [0,1] \to \mathbb{R}$ dada por $$G(t)=(f\circ \gamma )(t)=f(\bar{a}+t\bar{v}).$$

Por la hipótesis de diferenciabilidad de $f$, es una función derivable de una variable real. Por la regla de la cadena su derivada está dada por la siguiente expresión:

\begin{align*}
G^{\prime}(t)&=v_{1}\frac{\partial f}{\partial x_{1}}(\bar{a}+t\bar{v})+\dots +v_n\frac{\partial f}{\partial x_n}(\bar{a}+t\bar{v})
\end{align*}

Vamos a introducir una notación muy usada y útil para el desarrollo que estamos haciendo. Definiremos un operador con la expresión anterior simplemente como

\[ G^{\prime}(t)=(\bar{v}\cdot \triangledown )f(\bar{a}+t\bar{v}).\]

Esta expresión no se sigue de manera tan formal de cosas que hemos hecho antes, pero observa que tiene sentido. En la expresión $\bar{v}\cdot \triangledown$ estamos haciendo algo así como un «producto punto de operadores». En el fondo, este operador manda a cada función diferenciable $f$ a su derivada direccional en la dirección de $\bar{v}$.

Para poder hablar de Taylor, necesitamos derivar iteradamente. Podemos entonces tomar ahora $G’$ y derivarla nuevamente, de donde obtendríamos

\begin{align*}
G^{\prime \prime} (t) &= (\bar{v}\cdot \triangledown) G'(\bar{a}+t\bar{v})\\
&=(\bar{v}\cdot \triangledown)\left((\bar{v}\cdot \triangledown)f(\bar{a}+t\bar{v})\right)\\
&=\left((\bar{v}\cdot \triangledown)(\bar{v}\cdot \triangledown)\right) f(\bar{a}+t\bar{v}).
\end{align*}

Es importante que medites en por qué se da la redistribución de paréntesis que hicimos en la última igualdad. Simplificaremos la expresión $(\bar{v}\cdot \triangledown)(\bar{v}\cdot \triangledown )$ como $(\bar{v}\cdot \triangledown)^2$, y de manera similar definimos $(\bar{v}\cdot \triangledown)^k$ como componer el operador $k$ veces. Continuando como arriba, bajo las hipótesis adecuadas de diferenciabilidad llegamos al siguiente resultado.

Proposición. Sea $k$ un entero positivo y $f:S\subseteq \mathbb{R}^{n}\to \mathbb{R}$ con $S$ abierto y derivadas parciales continuas de orden $1,2,\ldots,k$. Sea $\bar{a}\in S$, y $\bar{v}$ un vector tal que $\bar{a}+t\bar{v}\in S$ para todo $t\in [0,1]$. Entonces:

\begin{equation}\label{eq:iteradas}\left( \frac{d}{dt} \right)^{k}f(\bar{a}+t\bar{v})=(\bar{v}\cdot \triangledown )^{k}f(\bar{a}+t\bar{v}).\end{equation}

Demostración. Queda como tarea moral. Se sugiere hacerlo por inducción.

$\square$

Algo sorprendente y curioso que sucede con las expresiones del estilo $(\bar{v}\cdot \triangle)^k$ es que «se vale el binomio de Newton» para ellas, o en general, cualquier fórmula para elevar a la $k$-ésima potencia. Esto se ve muy claro en el caso de $f:S\subset \mathbb{R}^2\to \mathbb{R}$ y derivadas de orden $2$. Si tenemos $\bar{v}=(v_1,v_2)$, entonces $\bar{v}\cdot \triangledown=v_1\frac{\partial}{\partial x} + v_2\frac{\partial}{\partial y}$. Se puede demostrar, por ejemplo, que si las $k$-ésimas parciales son continuas entonces

\[ \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y}\right)^{k}=\sum_{i
=0}^{k}\binom{k}{i}v_1^iv_2^{k-i}\frac{\partial ^{i}}{\partial x^{i}}\frac{\partial^{k-i}}{\partial y^{k-i}}.\]

Un caso particular sería el de $n=2$ y $k=2$, en el que se obtiene que:

\begin{equation} \label{eq:binomio} \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{2}=v_1^{2}\frac{\partial ^{2}}{\partial x^{2}}+2{v_1}{v_2}\frac{\partial ^{2}}{\partial x\partial y}+v_2^{2}\frac{\partial ^{2}}{\partial y^{2}}.\end{equation}

En la práctica esto nos permitirá encontrar las expresiones que necesitamos para el polinomio de Taylor para campos escalares. Observa que estas expresiones son también las que nos confirman que la expresión que obtendremos será un polinomio en $v_1,v_2$ (en general, en las entradas de $\bar{v}$), pues tras aplicar el operador en $f$ y evaluar en un punto, finalmente \eqref{eq:binomio} quedará escrito para ciertas constantes $A,B,C$ como $$Av_1^2+2Bv_1v_2+Cv_2^2,$$ lo cual en efecto es un polinomio (en este caso de grado $2$ y dos variables).

Polinomio de Taylor para campos escalares

Con la notación que hemos introducido, ahora sí podemos enunciar apropiadamente el polinomio de Taylor. Pensemos en que $f$ es $k+1$ veces diferenciable y que todas esas derivadas son continuas. En la sección anterior vimos que $G=f\circ \gamma$ también sería $k+1$ veces diferenciable y dimos fórmulas para sus derivadas en términos de la notación $\bar{v}\cdot \triangledown$.

Aplicando el teorema de Taylor con la versión de residuo dada en la ecuación \eqref{eq:residuo}, para la función $G$, en los puntos $a=0$, $x=1$, tenemos que existe $\xi\in[0,1]$ tal que se satisface lo siguiente:

\[ G(1)=G(0)+G^{\prime}(0)+\frac{G^{(2)}(0)}{2!}+\dots +\frac{G^{(k)}(0)}{k!}+\frac{G^{(k+1)}(\xi)}{(k+1)!}.\]

Al usar las fórmulas dadas por la ecuación \eqref{eq:iteradas}, obtenemos que

\begin{align*}
G^{(s)}(0)&=(\bar{v}\cdot \triangledown )^{s}f(\bar{a}) & \text{para $s\leq k$}\\
G^{(k+1)}(\xi)&=(\bar{v}\cdot \triangledown )^{k+1}f(\bar{a}+\xi \bar{v}).
\end{align*}

Así, reescribiendo todo en términos de $f$ obtenemos que:

\begin{equation}\label{eq:prepoly}f(\bar{a}+\bar{v})=f(\bar{a})+\frac{(\bar{v}\cdot \triangledown )f(\bar{a})}{1!}+\dots +\frac{(\bar{v}\cdot \triangledown)^{k}f(\bar{a})}{k!}+\frac{(\bar{v}\cdot \triangledown )^{k+1}f(\bar{a}+\tau \bar{v})}{(k+1)!}.\end{equation}

Si de esta expresión quitamos el último término (el correspondiente al residuo) y hacemos la sustitución $\bar{w}=\bar{a}+\bar{v}$, obtenemos la siguiente expresión:

\begin{equation} \label{eq:poltaylor}T_{k,\bar{a}}(\bar{w}):=f(\bar{a})+\frac{((\bar{w}-\bar{a})\cdot \triangledown )f(\bar{a})}{1!}+\dots +\frac{((\bar{w}-\bar{a})\cdot \triangledown)^{k}f(\bar{a})}{k!}\end{equation}

le llamamos el polinomio de Taylor de $f$ de grado $k$ alrededor de $\bar{a}$ y converge a $f(\bar{a})$ conforme $\bar{w}\to \bar{a}$.

Ejemplo de polinomio de Taylor para campos escalares

Ejemplo. Determinemos el polinomio de Taylor de grado 3 de la expresión $f(x,y)=e^{5x+3y}$ alrededor del punto $(0,0)$. Para ello, usaremos la expresión de la fórmula \eqref{eq:prepoly} quitando el residuo y fórmulas tipo «binomio de Newton» como la de la ecuación \eqref{eq:binomio}.

Comencemos con el término de grado $1$. Está dado por el operador

$$\left(v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y}\right)$$

que aplicado a nuestra función es

$$((v_1,v_2)\cdot \triangledown)f(x,y)=5v_1e^{5x+3y}+3v_2e^{5x+3y}.$$

Necesitaremos su evaluación en $(x,y)=(0,0)$, que es $5v_1+3v_2$.

Para pasar al término de segundo grado, necesitamos

\[\left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{2}=v_1^{2}\frac{\partial ^{2}}{\partial x^{2}}+2{v_1}{v_2}\frac{\partial ^{2}}{\partial x\partial y}+v_2^{2}\frac{\partial ^{2}}{\partial y^{2}}.\]

Al aplicar este operador en nuestra $f$, se obtiene:

$$((v_1,v_2)\cdot \triangledown)^2f(x,y)=25v_1^2e^{5x+3y}+30{v_1}{v_2}e^{5x+3y}+9v_2^2 e^{5x+3y}$$

Lo necesitaremos evaluado en $(0,0)$, que es $25v_1^2+30v_1v_2+9v_2^2$.

Finalmente, también requeriremos del término de orden $3$, para el cual es necesario calcular el siguiente operador

\[ \left( v_1\frac{\partial}{\partial x}+v_2\frac{\partial}{\partial y} \right)^{3}=v_1^{3} \frac{\partial}{\partial x^3}+3v_1^{2}{v_2}\frac{\partial}{\partial x^{2}\partial y}+3v_1v_2^{2}\frac{\partial}{\partial x \partial y^2}+v_2^3\frac{\partial}{\partial y^3},\]

y aplicarlo a nuestra $f$ para obtener

$$((v_1,v_2)\cdot \triangledown)^3f(x,y)=125v_1^3e^{5x+3y}+225v_1^2v_2e^{5x+3y}+135v_1v_2^2 e^{5x+3y}+27v_2^3e^{5x+3y}.$$

Una vez más, requerimos la evaluación en $(0,0)$, la cual es $125v_1^3+225v_1^2v_2+135v_1v_2^2+27v_2^3$.

Juntando todo esto, obtenemos que

\begin{align*}
f(v_1,v_2)&=f(0,0)+\frac{((x,y)\cdot \triangledown )f(0,0)}{1!}+\frac{((x,y)\cdot \triangledown )^{2}f(0,0)}{2!}+\frac{((x,y)\cdot \triangledown)^{3}f((0,0))}{3!}\\
&=1+5v_1+3v_2+\frac{25v_1^2+30v_1v_2+9v_2^2}{2}+\frac{125v_1^3+225v_1^2v_2+135v_1v_2^2+27v_2^3}{6}.
\end{align*}

$\square$

Observa que, en efecto, obtenemos un polinomio en dos variables y de grado tres.

Los casos especiales para grado $1$ y grado $2$

Las presentaciones más clásicas del polinomio de Taylor para campos escalares de varias variables son las versiones de primero y segundo grado. Para el polinomio de primer grado, tenemos la siguiente expresión:

$$T_{1,\bar{a}}(\bar{a}+\bar{v})=f(\bar{a})+\sum_{i=1}^{n}(v_i)\frac{\partial f}{\partial x_{i}}(\bar{a}).$$

En el caso de la presentación clásica para la fórmula de segundo orden tenemos

$$\frac{(\bar{v}\cdot \triangledown)^{2}f}{2!}(\bar{a})=\sum_{i=1}^n\sum_{j=1}^nv_{i}v_{j}\frac{\partial ^{2}f}{\partial x_{j}\partial x_{i}}(\bar{a})$$

Donde

$$T_{2,\bar{a}}(\bar{a}+\bar{v})=f(\bar{a})+\sum_{i=1}^{n}v_{i}\frac{\partial f}{\partial x_{i}}(\bar{a})+\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^{n}v_{i}v_{j}\frac{\partial ^{2}f}{\partial x_{j}\partial x_{i}}(\bar{a}).$$

Esta suma tendrá utilidad especial hacia el final del curso, cuando hablemos de optimización. La expresión también puede ponerse en términos de otro objeto matemático que se llama la matriz Hessiana, la cual definiremos más adelante una vez que hayamos hecho un repaso de álgebra lineal, matrices y formas cuadráticas.

Mas adelante…

Con lo que hemos trabajado hasta ahora hemos desarrollado un muy buen entendimiento de las curvas y de los campos escalares, que respectivamente son funciones $f:\mathbb{R}\to \mathbb{R}^m$ y $f:\mathbb{R}^n\to \mathbb{R}$. Sin embargo, nos gustaría ahora poder hablar con mucha mayor generalidad y entender a las funciones del estilo $f:\mathbb{R}^n\to \mathbb{R}^m$. Ya entendimos un poco de cómo son en términos de continuidad, cuando hablamos de la topología de $\mathbb{R}^n$. Sin embargo, para poder hablar de su diferenciabilidad y de otros resultados teóricos será necesario hacer un repaso de algunos conceptos adicionales de álgebra lineal. Por esta razón, en la siguiente unidad hablaremos de temas como transformaciones lineales, matrices, sistemas de ecuaciones, formas lineales y bilineales.

Tarea moral

Encuentra el polinomio de Taylor de primer grado para las siguientes funciones:
- $f(x,y)=e^(x+y)$
- $f(x,y)=e^{sen(x+y)}$
- $f(x,y)=x^2y^2+x+y$
Calcula el polinomio de Taylor de segundo grado para los siguientes campos escalares en el punto dado:
- $f(x,y)=x^2+xy$ en el punto $(1,1)$.
- $f(x,y,z)=xsen(yz)$ alrededor del punto $(\pi ,\pi ,\pi)$.
Demuestra por inducción la fórmula \[\left( \frac{d}{dt} \right)^{k}f(\bar{a}+t\bar{v})=(\bar{v}\cdot \triangledown )^{k}f(\bar{a}+t\bar{v}).\]
Demuestra por inducción \[ \left( x\frac{\partial}{\partial x}+y\frac{\partial}{\partial y}\right)^{k}=\sum_{i=1}^{k}\binom{k}{i}x^{i}y^{k-i}\frac{\partial ^{i}}{\partial x^{i}}\frac{\partial^{k-i}}{\partial y^{k-i}}.\]
En esta entrada sólo discutimos con detalle lo que pasa con el polinomio de Taylor «hasta cierto grado $k$». Sin embargo, no dimos una versión que generalice el polinomio de Taylor para cuando usamos todos los términos posibles (como en la ecuación \eqref{eq:taylor-inf}). Observa que en el recordatorio de una variable real sí pusimos el resultado para la serie de Taylor. Enuncia y demuestra una versión para campos escalares.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Derivadas parciales de orden superior
Entrada siguiente del curso: Matrices