Archivo de la etiqueta: teorema del valor medio

Seminario de Resolución de Problemas: El teorema del valor medio

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Las funciones continuas son bonitas pues tienen la propiedad del valor intermedio y además alcanzan sus valores extremos. Las funciones diferenciables en un intervalo también tienen un par de teoremas que hablan acerca de algo que sucede «dentro del intervalo». Estos son el teorema de Rolle, del cual platicamos en la entrada anterior, y el teorema del valor medio. Ambos nos permiten encontrar en el intervalo un punto en el que la derivada tiene un valor específico.

Teorema de Rolle. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Supongamos que $f(a)=f(b)$. Entonces existe un punto $c\in (a,b)$ tal que $f'(c)=0$.

Teorema del valor medio. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe un punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

En la entrada anterior vimos aplicaciones del teorema de Rolle a resolución de problemas matemáticos. En esta entrada hablaremos brevemente de la intuición geométrica del teorema del valor medio, de algunas de sus consecuencias inmediatas y de cómo usar al teorema y sus consecuencias para resolver problemas concretos.

La intuición geométrica del teorema del valor medio

El teorema del valor medio dice que una función diferenciable en $(a,b)$ y continua en $[a,b]$ cumple que hay un punto $c$ tal que el valor de la derivada en $c$ es igual a la pendiente de la recta que une los puntos del plano $(a,f(a))$ y $(b,f(b))$. En la siguiente figura, se marca en azul el punto $c$ en donde la pendiente de la tangente es lo que queremos, es decir, la pendiente entre los puntos rojos.

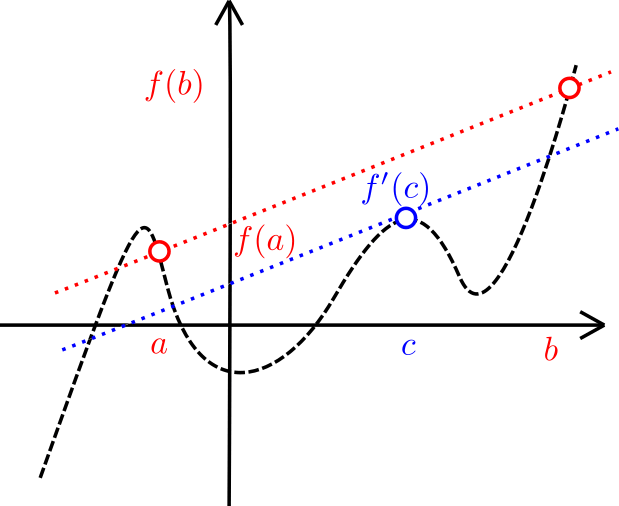
Intuición geométrica del teorema del valor medio
Intuición geométrica del teorema del valor medio

En varios problemas en los que se usa el teorema del valor medio, o bien en los cuales se pide demostrar enunciados parecidos a lo que dice el teorema del valor medio, es conveniente hacer una figura para entender la intuición geométrica del problema.

Consecuencias del teorema del valor medio

Si $f$ y $g$ son funciones continuas en $[a,b]$ y diferenciables en $(a,b)$ entonces se pueden deducir los siguientes resultados a partir del teorema del valor medio. No profundizamos en las demostraciones, y dejamos su verificación como un ejercicio de práctica.

Proposición. Si $f'(x)=0$ para toda $x$ en $(a,b)$, entonces $f$ es constante.

Proposición. Si $f'(x)=g'(x)$ para toda $x$ en $(a,b)$, entonces existe una constante $c$ tal que $f(x)=g(x)+c$ para toda $x$.

Proposición. Si $f'(x)>0$ para toda $x$ en $(a,b)$, entonces $f$ es una función estrictamente creciente. Si $f'(x)<0$ en $(a,b)$, entonces $f$ es una función estrictamente decreciente.

Cuando $f'(x)\geq 0$ y $f'(x)\leq 0$, tenemos resultados análogos que dicen que es no decreciente y no creciente, respectivamente.

Veamos algunas aplicaciones de los resultados anteriores.

Problema. Sean $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ funciones tales que para todo par de reales $x$ y $y$ se cumple que $$|f(x)+g(y)-f(y)-g(x)|\leq (x-y)^2.$$ Demuestra que $f$ y $g$ varían sólo por una constante aditiva.

Sugerencia pre-solución. Identifica cuál de las proposiciones anteriores puedes usar. Hay que tener cuidado con las hipótesis, pues en el enunciado no se habla de la diferenciabilidad de ninguna de las funciones involucradas.

Solución. Podría ser tentador usar la segunda proposición que enunciamos arriba, pero no tenemos hipótesis acerca de la diferenciabilidad de $f$ o de $g$. Sin embargo, vamos a mostrar que sí se puede mostrar que $f-g$ es diferenciable en todo real, y que su derivada es $0$ en todo real. Para ello, definamos $h=f-g$ y notemos que la hipótesis dice que $|h(x)-h(y)|\leq (x-y)^2.$

A partir de aquí, notemos que por la hipótesis, para $x\neq y$, $$\frac{|h(y)-h(x)|}{|y-x|}\leq \frac{(y-x)^2}{|y-x|} = |y-x|,$$ y el límite de esta última expresión conforme $y\to x$ es $0$, de modo que $$\left|\lim_{y\to x} \frac{h(y)-h(x)}{y-x}\right|=\lim_{y\to x} \frac{|h(y)-h(x)|}{|y-x|} = 0.$$ Esto muestra que para cualquier $x$ se tiene que $h$ es diferenciable en $x$ y su derivada es igual $0$ en todo $x$. De este modo, $h$ es una función constante, y por lo tanto existe un $c$ tal que $f(x)=g(x)+c$ para todo $x$.

$\square$

Veamos cómo el teorema del valor medio nos puede ayudar a demostrar desigualdades.

Problema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función dos veces diferenciable tal que $f»(x)\geq 0$ para todo $x$. Demuestra que para todo par de reales $a$ y $b$ con $a<b$ se tiene que $$f\left(\frac{a+b}{2}\right) \leq \frac{f(a)+f(b)}{2}.$$

Sugerencia pre-solución. Haz una figura para convencerte de que el resultado es cierto. En el enunciado del problema, la función está siendo enunciada en tres valores, $a$, $b$ y $\frac{a+b}{2}$. Esto te dará una pista de dónde usar el teorema del valor medio.

Solución. Por el teorema del valor medio, existe un real $r$ en el intervalo $\left(a,\frac{a+b}{2}\right)$ para el cual $$\frac{f\left(\frac{a+b}{2}\right)-f(a)}{\frac{a+b}{2}-a} = f'(r).$$

De manera similar, existe un real $s$ en el intervalo $\left(\frac{a+b}{2},b\right)$ para el cual $$\frac{f(b)-f\left(\frac{a+b}{2}\right)}{b-\frac{a+b}{2}} = f'(s).$$

Como $f»(x)>0$ para todo real $x$, tenemos que $f’$ es una función creciente, y como $r<s$, tenemos entonces que $f'(r)<f'(s)$. De esta forma, $$ \frac{f\left(\frac{a+b}{2}\right)-f(a)}{\frac{a+b}{2}-a}<\frac{f(b)-f\left(\frac{a+b}{2}\right)}{b-\frac{a+b}{2}}.$$ Notemos que el denominador de ambos lados es $\frac{b-a}{2}$. Cancelando los denominadores y reacomodando los términos en esta desigualdad, obtenemos la desigualdad deseada.

$\square$

Problemas resueltos con el teorema del valor medio y otras técnicas

Veamos algunos problemas que combinan el teorema del valor medio con otras técnicas de solución de problemas.

Problema. Sea $f(x)$ una función diferenciable en $(0,1)$ y continua en $[0,1]$ con $f(0)=0$ y $f(1)=1$. Muestra que existen puntos distintos $a,b,c,d$ en el intervalo $[0,1]$ tales que $$\frac{1}{f'(a)}+ \frac{1}{f'(b)} + \frac{1}{f'(c)} + \frac{1}{f'(d)} = 4.$$

Sugerencia pre-solución. Para resolver el problema, hay que combinar el teorema del valor medio con el teorema del valor intermedio. El primer paso del problema es encontrar reales $p<q<r$ tales que $f$ valga en ellos $1/4$, $2/4$ y $3/4$.

Solución. Como $f(0)=0$, $f(1)=1$ y $0<1/4<1$, por el teorema del valor intermedio existe un real $p$ en $(0,1)$ tal que $f(p)=1/4$. De manera similar, existe un real $q$ en $(p,1)$ tal que $f(q)=2/4$ y un real $r$ en $(q,1)$ tal que $f(r)=3/4$.

Aplicando el teorema del valor medio a los intervalos $[0,p]$, $[p,q]$, $[q,r]$ y $[r,1]$ obtenemos reales $a,b,c,d$ respectivamente tales que

\begin{align*}
f'(a)&=\frac{f(p)-f(0)}{p-0}=\frac{1/4}{p}\\
f'(b)&=\frac{f(q)-f(p)}{q-p}=\frac{1/4}{q-p} \\
f'(c)&=\frac{f(r)-f(q)}{r-q}=\frac{1/4}{r-q} \\
f'(d)&=\frac{f(1)-f(r)}{1-r}=\frac{1/4}{1-r}.
\end{align*}

Estos son los valores de $a,b,c,d$ que queremos pues

\begin{align*}
\frac{1}{f'(a)}+ \frac{1}{f'(b)} + \frac{1}{f'(c)} + \frac{1}{f'(d)} &= 4(1-r+r-q+q-p+p)\\
&=4.
\end{align*}

$\square$

Problema. Sean $a$, $b$ y $c$ números distintos. Muestra que la siguiente expresión $$\frac{(x-a)(x-b)}{(c-a)(c-b)}+ \frac{(x-b)(x-c)}{(a-b)(a-c)} + \frac{(x-c)(x-a)}{(b-c)(b-c)}$$ no depende del valor de $x$.

Sugerencia pre-solución. Encuentra la derivada de la expresión. Puedes aprovechar la simetría para hacer menos cuentas.

Solución. Usando la regla del producto, la derivada del primer sumando es
\begin{align*}
\frac{(x-a)+(x-b)}{(c-a)(c-b)}&=\frac{(2x-a-b)(b-a)}{(a-b)(b-c)(c-a)}\\
&=\frac{2x(b-a)+a^2-b^2}{(a-b)(b-c)(c-a)}.
\end{align*}

Por simetría, las derivadas de los otros dos términos tienen el mismo denominador que esta y en el numerador tienen, respectivamente,
\begin{align*}
&2x(c-b)+b^2-c^2\quad \text{y}\\
&2x(a-c)+c^2-a^2,
\end{align*} de modo que al sumar las tres expresiones obtenemos cero. Así, la derivada de la expresión es cero y por lo tanto es constante.

$\square$

Hay otro argumento para resolver el problema anterior, que usa teoría de polinomios. A grandes rasgos, la expresión es un polinomio de grado $2$, que toma tres veces el valor $1$, de modo que debe ser igual al polinomio constante $1$.

Más problemas

Hay más ejemplos de problemas relacionados con el teorema del valor medio en la Sección 6.6 del libro Problem Solving through Problems de Loren Larson.

Seminario de Resolución de Problemas: El teorema de Rolle

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Las funciones continuas son bonitas pues tienen la propiedad del valor intermedio y además alcanzan sus valores extremos. Las funciones diferenciables en un intervalo también tienen un par de teoremas que hablan acerca de algo que sucede «dentro del intervalo». Estos son el teorema de Rolle y el teorema del valor medio. Ambos nos permiten encontrar en el intervalo un punto en el que la derivada tiene un valor específico.

Teorema de Rolle. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Supongamos que $f(a)=f(b)$. Entonces existe un punto $c\in (a,b)$ tal que $f'(c)=0$.

Teorema del valor medio. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe un punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

El teorema del valor medio parece más general. Sin embargo, en cierto sentido, estos dos teoremas son «equivalentes», en el sentido de que uno de ellos nos ayuda a probar al otro de manera fácil, y viceversa.

Ya dimos las demostraciones de ambos teoremas en la entrada anterior, que habla del teorema del valor extremo. En esta entrada nos enfocaremos en ver cómo podemos usar el teorema de Rolle para resolver problemas. En la siguiente veremos algunos ejemplos del uso del teorema del valor medio.

Problemas resueltos con teorema de Rolle

Hay algunos problemas que parece que pueden ser resueltos con el teorema del valor intermedio (el de funciones continuas), pero para los cuales no es sencillo encontrar un intervalo correcto en el cual aplicar el teorema. En estas ocasiones, a veces el teorema de Rolle puede entrar al rescate.

Problema. Muestra que $5x^4-4x+1$ tiene una raíz real entre $0$ y $1$.

Sugerencia pre-solución. Primero, convéncete de que no es sencillo resolver este problema usando el teorema del valor intermedio. Luego, escribe a la función como la derivada de otra y aplica el teorema de Rolle. Funciona trabajar hacia atrás: si $f$ es derivada de una función, ¿quién tendría que ser esta función?

Solución. La idea es expresar a $f(x)=5x^4-4x+1$ como la derivada de una función y aplicar el teorema de Rolle. Para ello, podemos integrar o verificar por inspección que si $g(x)=x^5-2x^2+x$, entonces $g'(x)=f(x)$. Ahora, notemos que $g(0)=g(1)=0$. Por el teorema de Rolle, debe existir un $c$ en $(0,1)$ tal que $f(c)=g'(c)=0$, es decir, esta $c$ es justo una raíz de $f$, como queríamos.

$\square$

En algunas ocasiones hay que aplicar el teorema del valor medio repetidas veces dentro de un mismo problema.

Problema. Demuestra que $f(x)=\frac{x^4}{4}-\frac{3}{2}x^2+bx+c$ puede tener como mucho dos ceros el intervalo $[-1,1]$, sin importar los valores de $b$ y de $c$.

Sugerencia pre-solución. Procede por contradicción, suponiendo que hay más de dos ceros. Aplica el teorema del valor medio dos veces.

Solución. Supongamos que $f$ tiene tres o más ceros en ese intervalo, y que son $r,s,t$, con $-1\leq r < s < t < 1$. Tenemos que $f(r)=f(s)$ y que $f(s)=f(t)$, pues estos tres valores son $0$. Por el teorema de Rolle, tenemos que $f'(x)=x^3-3x+b$ debe tener al menos un cero $p$ en el intervalo $(r,s)$ y al menos un cero $q$ en el intervalo $(s,t)$. Aplicando de nuevo el teorema de Rolle, tenemos que $f»(x)=3x^2-3$ debe tener un cero en el intervalo $(p,q)$. Pero $-1<p<q<1$ y $f»(x)$ sólo tiene como ceros a $1$ y $-1$. Esto es una contradicción.

$\square$

Veamos un ejemplo más, en donde es necesario aplicar el teorema de Rolle varias veces y usar otras propiedades de diferenciabilidad.

Problema. Supongamos que la funciónes $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ son diferenciables y que $f'(x)g(x)\neq f(x)g'(x)$ para todo real $x$. Muestra que si $f(x)=0$ tiene al menos $2020$ soluciones distintas, entonces $g(x)=0$ tiene al menos $1010$ soluciones distintas.

Sugerencia pre-solución. Modifica el problema y generalízalo de la siguiente manera: bajo las hipótesis del problema, se tiene que entre cualesquiera dos ceros de $f$ hay un cero de $g$. Para demostrar esto, procede por contradicción.

Solución. Mostraremos que entre cualesquiera dos ceros de $f$ hay un cero de $g$. Para ello, procedamos por contradicción. Supongamos $a<b$ son ceros de $f$ y que $g$ no tiene ningún cero en el intervalo $[a,b]$.

Consideremos la función $f/g$. Como $g$ no se anula en $[a,b]$, tenemos que $f/g$ es continua en $[a,b]$ y diferenciable en $(a,b)$. Además, $f(a)/g(a)=f(b)/g(b)=0$. Con esto, por el teorema de Rolle tendríamos que la derivada de $f/g$ en algún punto $c$ en $(a,b)$ es cero. Pero esto es una contradicción, pues la derivada en $c$ es $$\frac{f'(c)g(c)-f(c)g'(c)}{g^2(c)},$$ que por hipótesis nunca es $0$. De esta forma, entre cualesquiera dos ceros de $f$ debe haber un cero de $g$.

Para resolver el problema original, consideremos los $2020$ ceros que tiene $f$, digamos $a_1<\ldots<a_{2020}$. En cada uno de los intervalos $[a_{2i-1},a_{2i}]$ para $i=1,\ldots,1010$ debe haber un cero de $g$, y como estos son intervalos disjuntos, estos deben ser ceros distintos. De este modo, tenemos al menos $1010$ ceros de $g$.

$\square$

Más problemas

Hay más problemas en los que se usa el teorema de Rolle en la Sección 6.5 el libro Problem Solving through Problems de Loren Larson.

Seminario de Resolución de Problemas: El teorema del valor extremo

Por Fabian Ferrari

Deja un comentario

Introducción

En una entrada anterior, acerca de funciones continuas, mencionamos dos teoremas fundamentales que estas funciones satisfacen: el teorema del valor intermedio y el teorema del valor extremo. Ya hablamos acerca del teorema del valor intermedio en una entrada anterior. El objetivo de esta entrada es mencionar aplicaciones del teorema del valor extremo.

Como recordatorio, el teorema del valor extremo o teorema de los valores extremos nos dice que si una función $f(x)$ es continua en un intervalo cerrado $[a, b]$, entonces existen valores $c$ y $d$ en $[a, b]$ tales que $f(c) \leq f(x) \leq f(d)$ para toda $x$ en el intervalo $[a, b]$.

En otras palabras, lo que nos dice el teorema es que si una función es continua en un intervalo cerrado, tenemos que la función debe alcanzar un valor máximo y un valor mínimo dentro del intervalo.

Dos teoremas para funciones derivables

Aprovecharemos para mencionar dos teoremas importantes que se ocuparán más adelante. Las demostraciones de dichos teoremas tienen que ver con la aplicación del teorema del valor extremo, estos teoremas son el teorema de Rolle y el teorema del valor medio (no confundir con el teorema del valor intermedio).

Teorema de Rolle. Sean $a<b$ reales y $f:[a,b]\to\mathbb{R}$ una función continua en el intervalo $[a, b]$ y derivable en $(a, b)$. Se tiene que si $f(a)=f(b)$, entonces existe $c$ en $(a, b)$ tal que $f^\prime(c)=0$.

Sugerencia pre-demostración. Por el teorema del valor extremo, la función debe alcanzar un máximo y un mínimo en el intervalo. Divide en casos de acuerdo a dónde están estos valores, si en los extremos o no.

Demostración: Como $f(x)$ es una función continua en $[a, b]$, por el teorema del valor extremo tenemos que $f(x)$ alcanza un valor máximo y un valor mínimo en el intervalo $[a, b]$. Tenemos entonces los siguientes casos.

  • Caso i: Si el valor máximo y mínimo se encuentran en los extremos del intervalo, tenemos que la función $f(x)$ tiene que ser constante dado que $f(a)=f(b)$. y se tiene que $f^\prime(c)=0$ para todo $c$ en $[a, b]$.
  • Caso ii: Si el valor mínimo o máximo no están en los extremos. Sean $c_1$ y $c_2$ en $(a, b)$, los valores en los que la función alcanza su mínimo y máximo respectivamente. Alguno de estos no está en los extremos. Como $f(x)$ es derivable en $(a, b)$, tenemos que también va a ser derivable en alguno de los puntos $c_1$ y $c_2$, teniendo que $f^\prime(c_1)=0$ o $f^\prime(c_2)=0$, así que basta con tomar $c=c_1$ o $c=c_2$.

$\square$

Teorema del valor medio. Sean $a<b$ reales y $f:[a,b]\to\mathbb{R}$ una función continua en $[a, b]$ y diferenciable en $(a, b)$. Entonces existe un número $c$ en $(a, b)$ tal que

$\frac{f(b)-f(a)}{b-a}=f^\prime(c)$.

Demostración: Consideremos la siguiente función auxiliar:

$g(x)=(f(b)-f(a))x-(b-a)f(x)$

Tenemos que $g(x)$ es continua en $[a, b]$ y además es derivable en $(a,b)$. La derivada de $g(x)$ está dada por

$g^\prime(x)=f(b)-f(a)-(b-a)f^\prime(x)$

Como $g(x)$ es continua en $[a, b]$, tenemos que por el teorema del valor extremo, la función alcanza un máximo y un mínimo en el intervalo $[a, b]$. Haciendo las cuentas, $g(a)=g(b)$, de modo que si el máximo y mínimo ocurren en los extremos, entonces $g$ es constante y toda $c\in (a,b)$ satisface $g'(c)=0$

En otro caso, sea $c\in(a, b)$ el valor en donde $g(x)$ alcanza su mínimo o su máximo. Tenemos que $g^\prime(c)=0$.

Así, como $g^\prime(c)=f(b)-f(a)-(b-a)f^\prime(c)$, tenemos que:

$0=f(b)-f(a)-(b-a)f^\prime(c)$

$(b-a)f^\prime(c)=f(b)-f(a)$

$f^\prime(c)=\frac{f(b)-f(a)}{b-a}$

$\square$

Alternativamente, en la función anterior pudimos haber aplicado el teorema de Rolle directamente a la función $g$. En las siguientes entradas veremos aplicaciones de estos resultados a problemas concretos.

Aplicación del teorema del valor extremo a un problema

Problema. Se tiene un circulo de radio $r$, y una tangente $L$ que pasa por un punto $P$ de la circunferencia. De un punto cualquiera $R$ en la circunferencia se traza una paralela a $L$ que corta a la circunferencia en $Q$. Determina el área máxima que puede tener el triángulo $PQR$.

Sugerencia pre-solución. Antes que nada, haz una figura. Usa el teorema del valor extremo para asegurar la existencia del valor máximo. Para ello, necesitarás construir una función continua cuyo valor sea el área buscada. Puedes usar argumentos de simetría para conjeturar cuándo se alcanza el valor máximo.

Solución. Hacemos el siguiente diagrama para entender mejor el problema.

Diagrama del enunciado del problema

Fijémonos que las condiciones de la altura y la base del triángulo $PQR$ se pueden describir mediante la siguiente figura:

Condiciones para la altura y base del triángulo

Notemos que la altura del triángulo está dada por $r+h$, donde $h$ puede variar entre $-r$ y $r$. Este dibujo también nos es de ayuda para determinar el valor de la base. Por el teorema de Pitágoras y sabiendo que la distancia del centro $C$ a los puntos $R$ y $Q$ es igual a $r$, tenemos que la base del triángulo es igual a $2\sqrt{r^2-h^2}$.

Así, el área del triángulo está dada por $(\sqrt{r^2-h^2})(r+h)$, pero como $h$ varía, nos conviene ver el área en función de $h$.

$A(h)=\sqrt{r^2-h^2}(r+h),$

La función $A(h)$ es una función continua en el intervalo $[-r, r]$.

Notemos que cuando $h$ toma los valores de $-r$ y $r$, el valor del área es nulo, es decir que en estos valores alcanza el mínimo, lo cual quiere decir que por el teorema del valor extremo, el valor máximo lo alcanza en algún valor en $(-r, r)$.

Si derivamos la función $A(h)$, tenemos

$A^\prime(h)=\frac{r^2-rh-2h^2}{\sqrt{r^2-h^2}}.$

Como sabemos que hay un máximo en el intervalo $(-r, r)$ y la derivada en este punto máximo debe ser igual a cero, hacemos $A^\prime(h)=0$.

Así,

$\frac{r^2-rh-2h^2}{\sqrt{r^2-h^2}}=0.$

Resolviendo la ecuación tenemos que

$h=\frac{r}{2}.$

Así, el área máxima del triángulo $PQR$ es $$A=\sqrt{r^2-\left(\frac{r}{2}\right)^2}\left(r+\frac{r}{2}\right)=\frac{3\sqrt{3}r^2}{4}.$$

$\square$

Más ejemplos

Se pueden encontrar más problemas de aplicación del teorema del vaalor extremo en la Sección 6.4 del libro Problem Solving through Problems de Loren Larson.