Archivo de la etiqueta: sucesiones convergentes

Cálculo Diferencial e Integral I: Propiedades de las sucesiones convergentes

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En la entrada anterior vimos la definición y algunos ejemplos de sucesiones convergentes y no convergentes. Ahora que ya estamos familiarizados con estos conceptos, revisaremos algunas de las propiedades que tienen las sucesiones convergentes.

Propiedades de las sucesiones convergentes

La siguiente propiedad nos indica que si todos los elementos de una sucesión convergente son no negativos, entonces el límite debe ser no negativo.

Proposición. Sea $\{a_n \}$ una sucesión convergente en $\mathbb{R}$, si $a_n \geq 0$ para todo $n \in \mathbb{N}$, entonces $$\lim_{n \to \infty} a_n \geq 0.$$

Demostración.

Supongamos que $$\lim_{n \to \infty} a_n = L < 0.$$

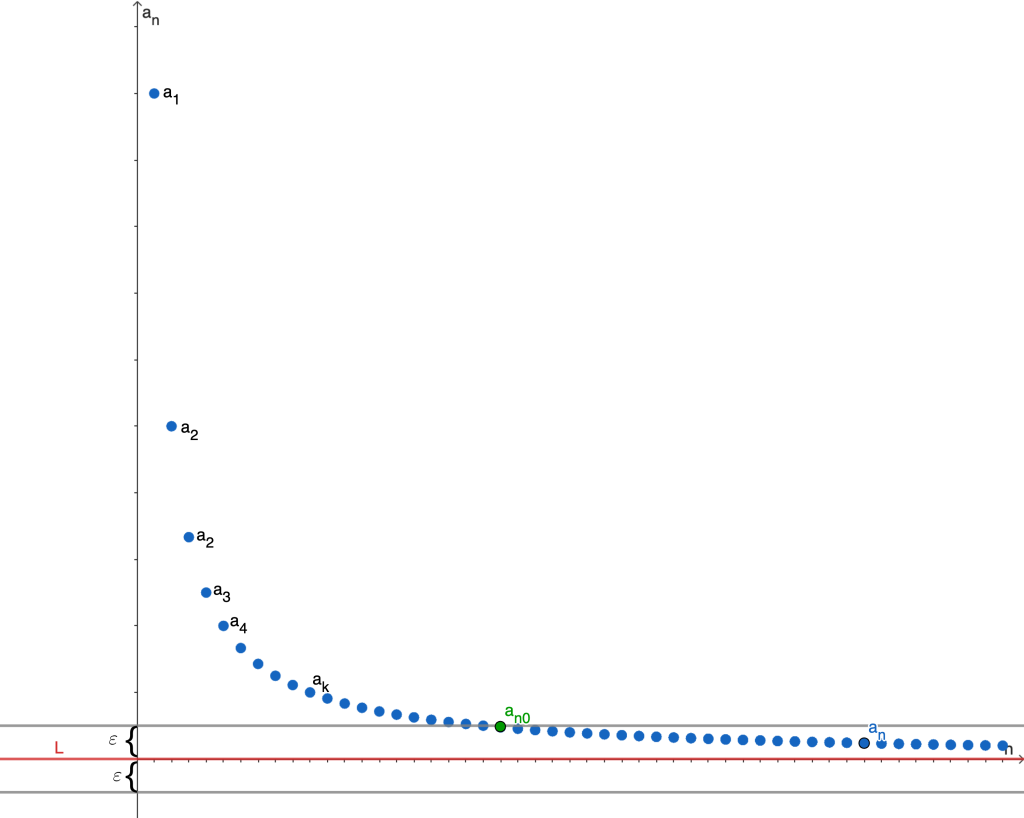
Consideremos $\varepsilon = -L > 0$. Entonces existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se cumple que

\begin{gather*}
& |a_n-L| < \varepsilon. \\
\Leftrightarrow & |a_n-L|< -L. \\
\Leftrightarrow & L < a_n – L < -L. \\
\Leftrightarrow & a_n < 0. \\
\end{gather*}

Lo anterior es una contradicción, dado que $a_n \geq 0$ para todo $n \in \mathbb{N}$. Por tanto, se concluye que $$\lim_{n \to \infty} a_n \geq 0.$$

$\square$

Ejemplo 1. Prueba que $$\lim_{n \to \infty} \frac{1}{2^n} \geq 0.$$

Demostración.

En la entrada anterior, probamos que la sucesión $\{ \frac{1}{2^n} \}$ es decreciente. Además, para todo $n \in \mathbb{N}$, se tiene que $2^n > 1$, por lo que $\frac{1}{2^n} < 1$. De esta forma, la sucesión está acotada. Como es decreciente y acotada, es convergente. También se cumple que $\frac{1}{2^n} > 0$ para todo $n \in \mathbb{N}$, por el teorema anterior, se concluye que $$\lim_{n \to \infty} \frac{1}{2^n} \geq 0.$$

$\square$


Podemos pensar en una especie de «generalización» de la proposición anterior: si tenemos dos sucesiones convergentes $\{a_n\}$, $\{ b_n \}$ y para todo natural se cumple la desigualdad $a_n \leq b_n$, entonces el límite de las sucesiones debe respetar esa misma relación de orden.

Proposición. Sean $\{ a_n \}$ y $\{ b_n \}$ dos sucesiones convergentes en $\mathbb{R}$ tales que $a_n \leq b_n$ para todo $n \in \mathbb{N}$, entonces $$ \lim_{ n \to \infty} a_n \leq \lim_{ n \to \infty} b_n.$$

Demostración.

Definamos la sucesión $c_n = b_n – a_n$. Como $\{ a_n \}$ y $\{ b_n \}$ son convergentes, digamos a $L_1$ y $L_2$, entonces $\{ c_n \}$ es convergente a $L_2-L_1$. Además, sabemos que $a_n \leq b_n$ para todo $n \in \mathbb{N}$, entonces $b_n – a_n \geq 0$ para todo $n \in \mathbb{N}$ y utilizando la proposición anterior tenemos que

$$\lim_{n \to \infty} c_n \geq 0. $$
Es decir, $$ \lim_{n \to \infty} ( b_n – a_n ) \geq 0. $$
$$\therefore \lim_{n \to \infty} b_n \geq \lim_{n \to \infty} a_n.$$

$\square$

Corolario. Sean $\alpha$, $\beta \in \mathbb{R}$ y $\{a_n\}$ una sucesión convergente tal que $\alpha \leq a_n \leq \beta$ para todo $n \in \mathbb{N}$, entonces $$\alpha \leq \lim_{n \to \infty} a_n \leq \beta.$$

Demostración.

Definimos la sucesión constante $\{b_n \} =\{ \beta, \beta, \ldots ,\}$. Por la proposición anterior, se sigue que $\lim\limits_{n \to \infty} a_n \leq \beta.$ De forma análoga, se obtiene que $\alpha \leq \lim\limits_{n \to \infty} a_n.$

Por lo tanto $$\alpha \leq \lim_{n \to \infty} a_n \leq \beta.$$

$\square$

Ahora veremos una propiedad que nos indica que si una sucesión converge a $L$, la sucesión generada tomando el valor absoluto de sus elementos es una sucesión convergente a $|L|$. Para ello, demostraremos antes una propiedad que tiene el valor absoluto.

Proposición. Sean $a$, $b \in \mathbb{R}$. Entonces se cumple que $\lvert |a| – |b| \rvert \leq |a-b|$.

Demostración.

Veamos que
\begin{gather*}
& |a| = |a-b+b| \leq |a-b|+|b|. \\
\Leftrightarrow & |a| – |b| \leq |a-b|. \tag{1}
\end{gather*}

Además, se tiene que
\begin{gather*}
& |b| = |b+a-a| \leq |b-a|+|a|. \\
\Leftrightarrow & |b|-|a| \leq |b-a| = |a-b|. \\
\Leftrightarrow & |a|-|b| \geq – |a-b|. \tag{2}
\end{gather*}

De $(1)$ y $(2)$, se sigue que
$$-|a-b| \leq |a|-|b| \leq |a-b|.$$
$$\therefore ||a|-|b|| \leq |a-b|.$$

$\square$

Proposición. Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$ que converge a $L$. Entonces la sucesión $\{ |a_n| \}$ converge a $|L|$.

Demostración.

Sea $\varepsilon > 0$. Por la proposición anterior, sabemos que $||a_n| – |L|| \leq |a_n – L|$ y como $\{a_n\}$ converge, existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se tiene que $|a_n – L| < \varepsilon$. Entonces

\begin{gather*}
||a_n| – |L|| \leq |a_n – L| < \varepsilon. \\ \\
\therefore ||a_n| – |L||< \varepsilon. \\ \\
\therefore \lim_{n \to \infty} |a_n| = |L|.
\end{gather*}

$\square$

Proposición. Sea $\{ a_n \}$ una sucesión. Si
$$\lim_{n \to \infty} |a_n| = 0, \quad \text{entonces} \quad \lim_{n \to \infty} a_n = 0.$$

Demostración.
Sea $\varepsilon > 0$. Como $$\lim_{n \to \infty} |a_n| = 0.$$
Existe $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se tiene que $||a_n|-0| < \varepsilon.$
Y notemos que
\begin{align*}
||a_n|-0| =& ||a_n|| \\
= & |a_n| \\
= &|a_n-0|.
\end{align*}
\begin{gather*}
\therefore |a_n -0| < \varepsilon. \\ \\
\therefore \lim_{n \to \infty} a_n = 0.
\end{gather*}

$\square$

Proposición. Si $|r|<1$, entonces $$\lim_{n \to \infty} r^n = 0.$$

Demostración.
Si $r = 0$, entonces $r^n = 0$, es decir, la sucesión es una constante lo cual implica que su límite es la misma constante, en este caso $0$.

Supongamos que $r \neq 0$. Como $|r|<1 \Rightarrow \frac{1}{|r|} > 1$. Definamos $b = \frac{1}{|r|}-1$. Notemos que $b > 0 $ y $|r| = \frac{1}{b+1}$. Entonces $|r^n| = (\frac{1}{b+1})^n$, por la desigualdad de Bernoulli tenemos que $(1+ b) ^n \geq 1+ nb $ para todo $n \in \mathbb{N}$. Se sigue que

$$|r^n| = \frac{1}{(1+b) ^n} \leq \frac{1}{1+nb} \leq \frac{1}{nb}.$$

Sea $\varepsilon > 0$ y consideremos $n_0 > \frac{1}{b \varepsilon}$. Se sigue que $\frac{1}{n_0b} < \varepsilon$. De esta forma, si $n \geq n_0$, entonces

\begin{gather*}
|r^n| \leq \frac{1}{nb} \leq \frac{1}{n_0b} < \varepsilon. \\ \\
\therefore |r^n| < \varepsilon. \\ \\
\therefore \lim_{n \to \infty} r^n = 0.
\end{gather*}

$\square$

Proposición. Sea $\{a_n \}$ una sucesión en $\mathbb{R}$ que converge a $L$ y, además, $a_n \geq 0$ para todo $n \in \mathbb{N}$. Entonces la sucesión $\{ \sqrt{a_n} \}$ converge a $\sqrt{L}.$

Demostración.

Sea $\varepsilon > 0$. Dividiremos la demostración en dos casos.

Caso 1: $L > 0$.

Como $L > 0$, se sigue que $\sqrt{a_n} + \sqrt{L} > 0$. Entonces

\begin{align*}
\left\lvert \sqrt{a_n} – \sqrt{L} \right\rvert & = \left\lvert \sqrt{a_n} – \sqrt{L} \cdot \frac{\sqrt{a_n} + \sqrt{L}}{\sqrt{a_n} + \sqrt{L}} \right\rvert \\ \\
& = \left\lvert \frac{a_n-L}{\sqrt{a_n} + \sqrt{L}} \right\rvert \\ \\
& \leq \left\lvert \frac{a_n-L}{\sqrt{L}} \right\rvert \text{, pues $\sqrt{L} + \sqrt{a_n} \geq \sqrt{L}$}.\\ \\
\end{align*}

$$\therefore \left\lvert \sqrt{a_n} – \sqrt{L} \right\rvert \leq \left\lvert \frac{a_n-L}{\sqrt{L}} \right\rvert. \tag{1}$$

Además, como $\{ a_n \}$ converge a $L$, para $\sqrt{L}\varepsilon > 0$ existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$, entonces $|a_n – L| < \sqrt{L}\varepsilon.$ Por $(1)$, se sigue que si $n \geq n_0$, entonces

\begin{align*}
\left\lvert \sqrt{a_n} – \sqrt{L} \right\rvert & \leq \left\lvert \frac{a_n-L}{\sqrt{L}} \right\rvert \\ \\
& = \frac{|a_n-L|}{\sqrt{L}} \\ \\
& < \frac{\sqrt{L}\varepsilon}{\sqrt{L}} \\ \\
& = \varepsilon.
\end{align*}

$$\therefore \lim_{n \to \infty} \sqrt{a_n} = \sqrt{L}.$$

Caso 2: $L = 0$.

Los detalles de la demostración de este caso quedarán como tarea moral.

$\square$

Para finalizar, revisaremos una propiedad muy interesante que nos indica que si dos sucesiones convergentes al mismo límite $L$ «encierran» a una tercera, entonces ésta última también converge y lo hace a $L$. Esta propiedad es conocida como teorema del sándwich.

Teorema. Sean $\{a_n \}$, $\{b_n \}$, $\{c_n \}$ tres sucesiones en $\mathbb{R}$ tales que

$i)$ Para todo $n \in \mathbb{N}$ se tiene que $a_n \leq b_n \leq c_n.$

$ii)$ $\lim\limits_{n \to \infty} a_n = L$ y $\lim\limits_{n \to \infty} c_n = L.$

Entonces $$\lim_{n \to \infty} b_n = L.$$

Demostración.
Sea $\varepsilon >0$. Como $\{a_n \}$ converge a $L$, entonces existe $n_1 \in \mathbb{N}$ tal que si $n \geq n_1$ tal que
\begin{gather*}
& |a_n – L| < \varepsilon. \\
\Leftrightarrow & – \varepsilon < a_n – L < \varepsilon. \\
\Leftrightarrow & L – \varepsilon < a_n < L + \varepsilon.
\end{gather*}

De igual forma, como $\{c_n \}$ converge a $L$, entonces existe $n_2 \in \mathbb{N}$ tal que si $n \geq n_2$ tal que

\begin{gather*}
& |c_n – L| < \varepsilon. \\
\Leftrightarrow & – \varepsilon < c_n – L < \varepsilon. \\
\Leftrightarrow & L – \varepsilon < c_n < L + \varepsilon.
\end{gather*}

Sea $n_0 = max \{ n_1, n_2 \}$. Si $n \geq n_0$, entonces

\begin{gather*}
& L – \varepsilon < a_n \leq b_n \quad \text{ y } \quad b_n \leq c_n < \varepsilon + L.
\end{gather*}

Se sigue que
\begin{gather*}
& L – \varepsilon < b_n < \varepsilon + L. \\ \\
\Leftrightarrow & -\varepsilon < b_n – L < \varepsilon. \\ \\
& \therefore |b_n – L | < \varepsilon. \\ \\
& \therefore \lim_{n \to \infty} b_n = L.
\end{gather*}


$\square$

Ahora veremos un ejemplo donde podemos aplicar el teorema del sándwich.

Ejemplo 2. Determina el límite de la sucesión $\left\lbrace \frac{n}{n^2+1} \right\rbrace$.

Consideremos las sucesiones $\{a_n \} = 0$ y $ \{b_n \} = \frac{1}{n}$. Además, notemos que para todo $n \in \mathbb{N}$, se tiene que $ n^2 \leq n^2+1$, esto implica que $\frac{1}{n^2+1} \leq \frac{1}{n^2}$. De esta forma, se sigue que

$$\{a_n \} = 0 \leq \frac{n}{n^2+1} \leq \frac{n}{n^2} = \frac{1}{n} = \{b_n \}.$$

Y $\{a_n \}$ y $ \{b_n \}$ convergen a $0$ por lo visto en una entrada anterior. Por el teorema del sándwich, podemos concluir que

$$\lim_{n \to \infty} \frac{n}{n^2+1} = 0.$$

Más adelante…

En esta entrada vimos algunas de las propiedades que tienen las sucesiones convergentes. En la siguiente entrada revisaremos propiedades de las sucesiones que divergen a infinito. Una vez que hayamos dominado todas estas propiedades estaremos listos para dar el siguiente paso y llegar a uno de los conceptos frecuentemente usados en cálculo: el límite de una función.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Prueba que si las sucesiones $\{ a_n \}$ y $\{ b_n \}$ están acotadas, entonces $c_n = 5a_n+8b_n$ también está acotada.
  • Sea $\{a_n \}$ una sucesión en $\mathbb{R}$ que converge a $L = 0$ y, además, $a_n \geq 0$ para todo $n \in \mathbb{N}$. Entonces la sucesión $\{ \sqrt{a_n} \}$ converge a $\sqrt{L} = 0.$
  • Demuestra que si $\{ a_n \}$ es una sucesión que converge a $L$, entonces $$\lim_{n \to \infty} \sqrt{(a_n)^2 +12} = \sqrt{L^2 +12}.$$
  • Considera la sucesión $\{ \frac{2n}{3n+1} \}$.
    $i)$ Prueba que $\frac{1}{2} \leq \frac{2n}{3n+1} \leq \frac{2}{3}.$
    $ii)$ Usando el teorema del sándwich, calcula el límite de $a_n = \left( \frac{2n}{3n+1} \right)^n$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Sucesiones convergentes

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Anteriormente se dio la definición de sucesión y revisamos algunos ejemplos. En esta entrada, se definirá la convergencia para una sucesión y se darán varios ejemplos de sucesiones convergentes y no convergentes.

Límite de una sucesión

A continuación daremos la definición de límite de una sucesión:

Definición. Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$. Sea $L \in \mathbb{R}$, decimos que $L$ es el límite de la sucesión $\{a_n\}$ si para todo $ \varepsilon > 0$ existe un número natural $n_0$ tal que para todo $n \geq n_0$ se satisface $ | a_n – L |< \varepsilon$.

Si una sucesión tiene como límite a $L$, también decimos que converge a $L$ y lo denotamos como $$\lim_{n\to \infty} a_n = L.$$

En términos más simples, la definición nos indica que una sucesión es convergente a $L$ si a partir de cierto elemento en la sucesión, $a_{n_0}$, los términos están lo suficientemente cerca, $\varepsilon$, de $L$. Para ilustrar estos elementos, a continuación se presenta la gráfica de la sucesión $\{a_n\} = \{ \frac{1}{n} \}$, y más adelante probaremos que converge a $L = 0$.

Observación. Cada punto de la gráfica está determinado por las coordenadas $(i, a_i)$ con $i \in \mathbb{N}$, pero por simplicidad, se denotan únicamente como $a_i$.

Ejemplos de sucesiones convergentes

Ahora continuaremos con algunos ejemplos de sucesiones convergentes. Es importante recalcar que para demostrar que una sucesión converge a $L$, deberemos especificar las condiciones que $n_0$ debe cumplir tal que para un $\varepsilon > 0$ arbitrario dado, $| a_n – L |< \varepsilon$ para todo $n \geq n_0$.

Ejemplo 1. Sea $k$ un número real y consideremos la sucesión $\{ a_n \} = \{k\}$, entonces $$\lim_{n \to \infty} k = k.$$

Demostración.

Sea $\varepsilon > 0$ (establecemos el valor arbitrario de un épsilon positivo).
Para esta sucesión cualquier valor de $n_0$ sirve, en particular consideremos $n_0 = 1$ (en este caso se puede dar $n_0 $ explícitamente).
Si $n \geq n_0 = 1$, entonces

\begin{gather*}
|a_n-k| = |k-k| = 0 < \varepsilon. \\
\therefore \lim_{n \to \infty} k = k.
\end{gather*}

$\square$


El ejemplo anterior es uno sencillo, sin embargo, como lo podemos ver en los comentarios entre paréntesis, están presentes los pasos relevantes para demostrar la convergencia. En este caso, dado que nuestra sucesión era un valor constante, el valor de $n_0$ que funcionaba era cualquier número natural, pero, en la mayoría de los casos, su valor estará definido en términos de épsilon.

Ejemplo 2. Consideremos la sucesión $\{ \frac{1}{n} \}$, entonces $$\lim_{n \to \infty} \frac{1}{n} = 0.$$

Demostración.

Sea $\varepsilon >0$.

Dado que el valor de $\varepsilon$ es positivo, por la propiedad Arquimediana, existe $n_0 \in \mathbb{N}$ tal que $1 < n_0 \cdot \varepsilon$, es decir, $\frac{1}{n_0} < \varepsilon$. Así, para cualquier $n \geq n_0$ se tiene que $\frac{1}{n} \leq \frac{1}{n_0} < \varepsilon $. De lo anterior se sigue que

$| \frac{1}{n} – 0| = \frac{1}{n} < \varepsilon.$

$\therefore | \frac{1}{n} – 0| < \varepsilon$ para todo $n \geq n_0.$

$$\therefore \lim_{n \to \infty} = 0.$$

$\square$

En este último ejemplo podemos observar cómo se establecen condiciones que $n_0$ debe cumplir en función de $\varepsilon$, así como la relevancia de la propiedad Arquimediana que estará constantemente presente al momento de demostrar convergencia mediante su definición.


Ejemplo 3. Demuestra que

$$\lim_{n \to \infty} \frac{8n-5}{3n} = \frac{8}{3}.$$

Demostración.

Sea $\varepsilon > 0$.
Notemos que

$$\left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert = \left\lvert \frac{8n-5-8n}{3n} \right\rvert = \left\lvert \frac{-5}{3n} \right\rvert = \frac{5}{3n}.$$

\begin{align*}
\therefore \left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert = \frac{5}{3n}. \tag{1}
\end{align*}

Consideremos $n_0 \cdot \varepsilon > \frac{5}{3}$, que sabemos que existe gracias a la propiedad Arquimediana. De esta forma, se tiene que

$$\varepsilon > \frac{5}{3n_0}.$$

Si $n \geq n_0$, entonces tenemos

\begin{align*}
\left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert =& \frac{5}{3n}, \text{ por (1)} \\
\leq & \frac{5}{3n_0}, \text{ pues }n \geq n_0 \\
<& \varepsilon.
\end{align*}

$$\therefore \left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert < \varepsilon.$$

$$\therefore \lim_{n \to \infty} \frac{8n-5}{3n} = \frac{8}{3}.$$

$\square$

Ejemplo 4. $$\lim_{n \to \infty} \left( \sqrt{n+1}-\sqrt{n} \right) = 0.$$

Demostración.

Sea $\varepsilon > 0$. Para simplificar la expresión, multiplicaremos por un uno haciendo uso del conjugado de la expresión anterior.

\begin{align*}
\sqrt{n+1}-\sqrt{n} =& (\sqrt{n+1}-\sqrt{n}) \cdot \frac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}} \\ \\
=& \frac{\sqrt{n+1} ^ 2 – \sqrt{n}^2}{\sqrt{n+1}+\sqrt{n}} \\ \\
=& \frac{n+1 – n}{\sqrt{n-1}+\sqrt{n}} \\ \\
=&\frac{1}{\sqrt{n-1}+\sqrt{n}} \\ \\
\leq & \frac{1}{\sqrt{n}}.
\end{align*}


$$\therefore \sqrt{n-1}-\sqrt{n} \leq \frac{1}{\sqrt{n}}.$$

Consideremos $n_0 > \frac{1}{\varepsilon^2} \Rightarrow \frac{1}{\sqrt{n_0}} < \varepsilon$. Entonces tenemos

\begin{align*}
\left\lvert \sqrt{n-1}-\sqrt{n} – 0 \right\rvert =& \frac{1}{\sqrt{n-1}+\sqrt{n}} \text{, por la observación anterior} \\
\leq & \frac{1}{\sqrt{n}} \\
\leq & \frac{1}{\sqrt{n_0}}, \text{pues } n \geq n_0 \\
< & \varepsilon.
\end{align*}

$\therefore |\sqrt{n-1}-\sqrt{n} – 0| < \varepsilon.$

$$\therefore \lim_{n \to \infty} \left(\sqrt{n+1}-\sqrt{n} \right)= 0.$$

$\square$

Los dos ejemplos de arriba hacen uso de manipulaciones algebraicas que nos permiten simplificar nuestro problema; esta técnica de simplificación de expresiones, cuyo fin es llevarlas a otras más sencillas, es ampliamente usada para demostrar la convergencia de sucesiones.

Ejemplos de sucesiones no convergentes

Después de haber revisado ejemplos de sucesiones convergentes, vale la pena conocer sucesiones que no convergen, es decir, que su límite no existe.

Ejemplo 5. Consideremos la sucesión $\{ a_n \} = \{ (-1)^n \}$. Probaremos que el límite de $\{a_n\}$ no existe.

Demostración.

Procederemos a hacer esta demostración por contradicción. Supongamos que existe $L \in \mathbb{R}$ tal que $$\lim_{n \to \infty} (-1)^n = L.$$

Consideremos $\varepsilon = 1/2 > 0$. Por definición, existe $n_0 \in \mathbb{N}$ tal que si $n\geq n_0$ entonces $|(-1)^n-L| < \frac{1}{2}.$

Como $2n_0 > n_0$ y $2n_0+1>n_0$, entonces
\begin{gather*}
|(-1)^{2n_0}-L| < \frac{1}{2} \Rightarrow |1-L|< \frac{1}{2}. \tag{1} \\
|(-1)^{2n_0+1}-L| < \frac{1}{2} \Rightarrow |-1-L| = |1+L|< \frac{1}{2}. \tag{2}
\end{gather*}

Y notemos que

\begin{align*}
2 = |1+1| =& |1-L+L+1| \\
\leq & |1-L| + |1+L| \\
< & \frac{1}{2} + \frac{1}{2} \text{, por (1) y (2).}
\end{align*}

Lo anterior implica que $2<1$ y esto es una contradicción.
Por tanto, podemos concluir que tal límite no existe.

$\square$

Ahora estudiaremos una nueva definición para un tipo particular de sucesiones que no tienen como límite a un número real $L$.

Definición. Sea $\{a_n\}$ una sucesión en $\mathbb{R}$. Decimos que $\{a_n\}$ diverge a infinito si $\forall M \in \mathbb{R}$ existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ entonces $M < a_n$.

La definición anterior nos indica que una sucesión diverge a infinito si para cualquier número real $M$, existe un término de la sucesión $a_{n_0}$ a partir del cual todos los valores subsecuentes en la sucesión son mayores que $M$. Cuando una sucesión $\{ a_n \}$ diverja a infinito lo denotaremos como $$\lim_{n \to \infty} a_n = \infty.$$

Ejemplo 6. La sucesión $\{a_n\} = \{n\}$ diverge a infinito.

Demostración.

Sea $M \in \mathbb{N}$. Sabemos que $\mathbb{N}$ no está acotado superiormente, entonces existe $n_0 \in \mathbb{N}$ tal que $M< n_0$, de esta forma, si $n \geq n_0$, se tiene que $M<n$.

$\square$

Ejemplo 7. $$\lim_{n \to \infty} n^2 = \infty.$$

Demostración.

Procederemos a hacer la prueba por contradicción. Supongamos que para todo $n\in \mathbb{N}$ se tiene que $n^2 \leq M$ para algún $M \in \mathbb{R}$. Se sigue que

$\sqrt{n^2} \leq \sqrt{M}.$

Es decir,

$n \leq \sqrt{M}.$

Lo cual es una contradicción pues sabemos que el conjunto de los números naturales no está acotado superiormente.

$\therefore \{ n^2 \}$ diverge a infinito.

$\square$

Más adelante…

Se han revisado las definiciones de convergencia y divergencia a infinito, hemos visto diversos ejemplos de ambas definiciones. En las siguientes entradas se revisarán criterios para la convergencia de sucesiones, así como sus propiedades y teoremas con lo cual podremos determinar si una sucesión es convergente o no de manera más rápida.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Prueba que el límite de una sucesión convergente $\{ a_n \}$ es único.
    Sugerencia:
    1. Proceder por contradicción y asumir que existen dos números reales distintos $L$ y $L’$ tales que
    $$\lim_{n \to \infty} a_n = L \quad \text{y} \quad \lim_{n \to \infty} a_n = L’.$$
    2. Utilizar la definición de límite de una sucesión empleando el siguiente valor de épsilon: $$\varepsilon = \frac{|L-L’|}{2}.$$
    $\varepsilon > 0$, ¿por qué?
  • Demuestra lo siguiente:
    a) $$\lim_{n \to \infty} \frac{(-1)^n}{n} = 0.$$
    b) $$\lim_{n \to \infty} \sqrt{n} = \infty.$$
    c) $$\lim_{n \to \infty} \sqrt{12+ \frac{1}{n}} = \sqrt{12}.$$
  • Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$ y sea $L \in \mathbb{R}$. Prueba que $$\lim_{n \to \infty} a_n = L \Leftrightarrow \lim_{n \to \infty} a_n – L = 0.$$
  • Una sucesión también puede ser divergente a $-\infty$. Propón una definición análoga a la de divergencia a infinito y prueba que $$\lim_{n \to \infty} – \sqrt{n} = – \infty.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»