Archivo de la etiqueta: series

Cálculo Diferencial e Integral II: Criterio de la integral

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos dos criterios de convergencia para las series, el criterio de la raíz y el criterio de la razón. En esta sección veremos el criterio de la integral enunciado el siguiente teorema.

Criterio de la integral

Teo: (Criterio de la integral)

Sea $f$ una función continua, positiva y decreciente en $[1, \infty)$ y sea $\left \{ a_{n} \right \}$ una sucesión tal que $a_{n} = f(n)$ entonces:

$$\sum_{n=\infty}^{\infty}a_{n} \space converge \space \Leftrightarrow \int_{1}^{\infty}f(x)dx \space converge$$

Demostración:

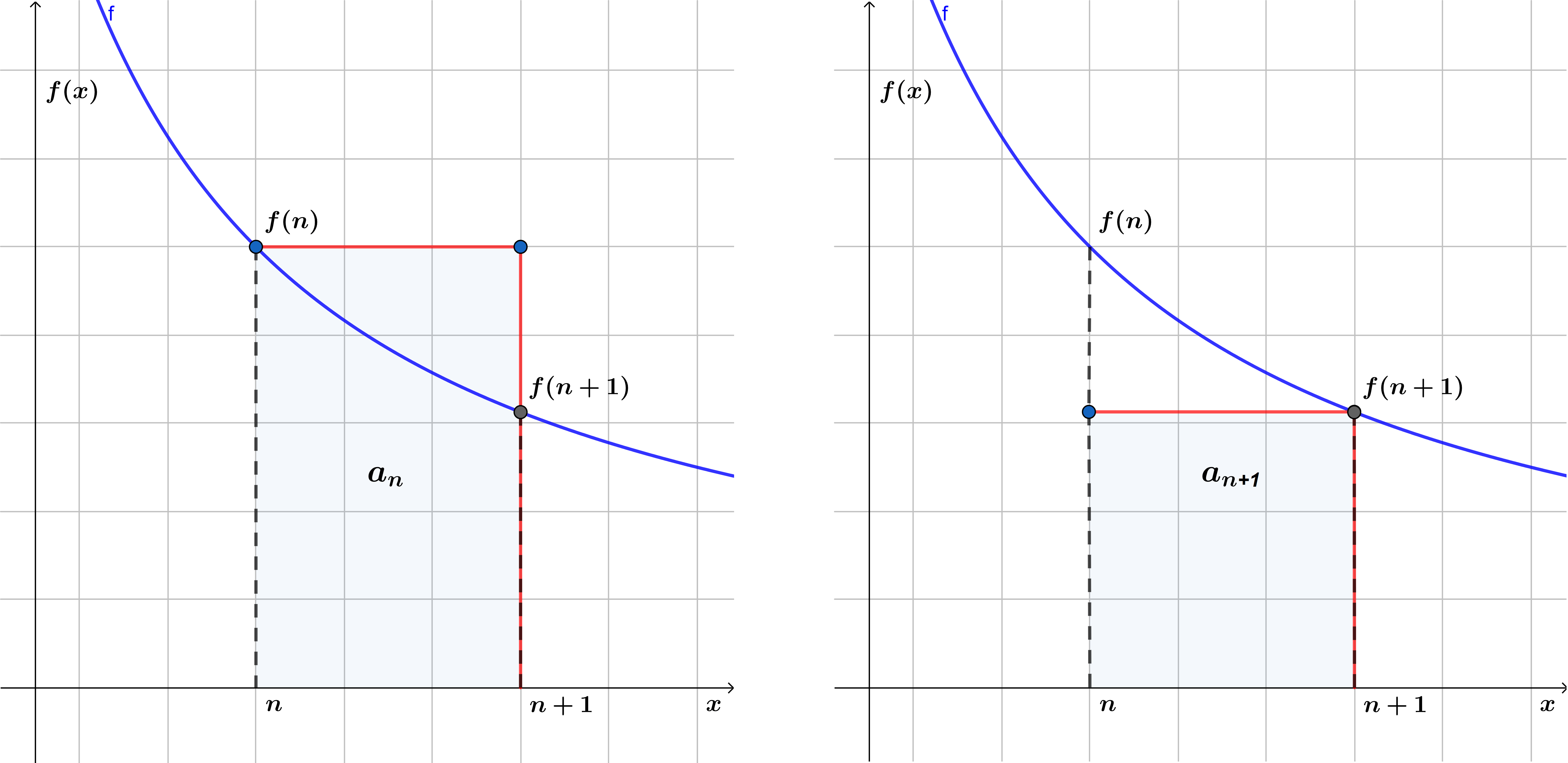
Figura 1: Función decreciente en el intervalo $[1,\infty]$ (curva azul), área del valor n-esimo de la sucesión $a_{n}$ con altura $f(n)$ (figura de la izquierda), área del valor n-esimo de la sucesión $a_{n+1}$ con altura $f(n+1)$ (figura de la derecha).

$\Rightarrow \lrcorner$

Supongamos que $\sum_{i=1}^{n}a_{n}$ converge.

De la figura $(1)$ vemos que el área del rectángulo con altura $f(n)$ (figura de la izquierda) es mayor que el área bajo la curva entre $n$ y $n+1$, en donde se interpretan a estos rectángulos como el área del valor n-esimo de la sucesión $a_{n}$.

Matemáticamente, podemos interpretar lo anterior como:

$$\Rightarrow a_{n} \geq\int_{n}^{n+1}f(x)dx$$

Si hacemos lo anterior para $n$ rectángulos, se tiene que:

$$\Rightarrow \sum_{i=1}^{n}a_{i} \geq \sum_{i=1}^{n}\int_{n}^{n+1}f(x)$$

$$\Rightarrow \sum_{i=1}^{n}a_{i} \geq \int_{1}^{2}f(x)d+\int_{2}^{3}f(x)+…+\int_{n}^{n+1}f(x)dx$$

$$\Rightarrow \sum_{i=1}^{n}a_{i}\geq \int_{1}^{n+1}f(x)dx$$

$$\Rightarrow \lim_{n \to \infty } \sum_{i=1}^{n}a_{i}\geq \lim_{n \to \infty}\int_{1}^{n+1}f(x)dx$$

$$\Rightarrow \sum_{i=1}^{\infty}a_{n}\geq \int_{1}^{\infty} f(x)dx$$

Como $\sum_{i=1}^{\infty}a_{n}$ converge, por el criterio de comparación:

$$\Rightarrow \int_{1}^{\infty} f(x)dx \space \space converge$$

$\Leftarrow \lrcorner$

Supongamos que $ \int_{1}^{\infty}f(x)dx \space converge $.

De la figura $(1)$ vemos que el área del rectángulo con altura $f(n+1)$ (figura de la derecha) es menor que el área bajo la curva entre $n$ y $n+1$, vemos en este caso que la sucesión correspondiente es $a_{n+1}$.

$$\Rightarrow a_{n+1}\leq \int_{n}^{n+1}f(x)dx$$

$$\Rightarrow \sum_{i=1}^{n+1}a_{i}\leq \int_{1}^{2}f(x)dx+\int_{2}^{3}f(x)+…+\int_{n}^{n+1}f(x)dx$$

$$\Rightarrow \sum_{i=1}^{n+1}a_{i}\leq \int_{1}^{n+1}f(x)dx$$

$$\Rightarrow \lim_{n \to \infty}\sum_{i=1}^{n+1}a_{i}\leq \lim_{n \to \infty}\int_{1}^{n+1}f(x)dx$$ $$\Rightarrow \sum_{i=1}^{\infty}a_{n}\leq \int_{1}^{\infty}f(x)dx$$

Como $\int_{1}^{\infty}f(x)dx$ converge, por el criterio de comparación

$$ \Rightarrow \sum_{i=1}^{\infty}a_{n} \space \space converge$$

$\square$

Veamos unos ejemplos:

Ejemplos

Diga si las siguientes series convergen o divergen.

  • $$\sum_{n=1}^{\infty}\frac{1}{n}$$

Tomemos $f(x)=\frac{1}{x}$, sabemos que la función es continua en el intervalo $[1, \infty)$ y es decreciente, además de que sabemos que es continua, por lo que podemos utilizar el criterio de la integral como sigue:

$$\int_{1}^{\infty}\frac{1}{x}dx=\lim_{x \to \infty}\int_{1}^{x}\frac{1}{t}dt=\lim_{x \to \infty}\left [ ln(t) \right ]\bigg|_{1}^{x}=\lim_{x \to \infty}(ln(x)-ln(1))=\lim_{n \to \infty}ln(x)=\infty$$

$$\therefore \int_{1}^{\infty}\frac{1}{x}dx \space diverge$$

$$\therefore \sum_{n=1}^{\infty}\frac{1}{n} \space diverge$$

  • $$\sum_{i=1}^{\infty}\frac{n}{n^{2}+1}$$

Tomamos $f(x)=\frac{x}{x^{2}+1}$

Claramente, $f$ es continua en $\mathbb{R} \Rightarrow f$ es continua en $[1, \infty)$, vemos que:

$$x^{2}+1>0 \space \forall \space x \space \epsilon \space \mathbb{R} \space y \space x>0 \Rightarrow x \space \epsilon \space [1,\infty)$$

$$\therefore \frac{x}{x^{2}+1}>0$$

Veamos si $f(x)$ es decreciente, para ello derivamos:

$$f'(x)=\frac{x^{2}+1-2x^{2}}{(x^{2}+1)^{2}}=\frac{-x^{2}+1}{(x^{2}+1)^{2}}$$

Vemos que $(x^{2}+1)^{2}>0$ y si $x \space \epsilon \space [1,\infty)$, entonces $x^{2}+1>0$, pero tenemos un signo negativo en $f'(x)$:

$\therefore f$ es decreciente en $[1,\infty)$.

Por lo que podemos utilizar el criterio de la integral como sigue:

$$\Rightarrow \int_{1}^{\infty}\frac{x}{x^{2}+1}dx=\lim_{n \to \infty}\int_{1}^{t}\frac{t}{t^{2}+1}dt=\lim_{n \to \infty}\left [ \frac{1}{2}ln(t^{2}+1) \right ]\bigg|_{1}^{x}=\lim_{n \to \infty}[\frac{1}{2}ln(x^{2}+1)-\frac{1}{2}ln(2)]=\infty$$

$$\therefore \sum_{n=1}^{\infty}\frac{n}{n^{2}+1} \space diverge \space a \space \infty$$

  • $$\sum_{n=1}^{\infty}\frac{1}{n^{2}+1}$$

Sea $f(x)=\frac{1}{x^{2}+1}$ Claramente $f$ es continua, positiva y decreciente en $[1, \infty)$, por lo que podemos aplicar el teorema:

$$\int_{1}^{\infty}\frac{1}{x^{2}+1}dx=\lim_{n \to \infty}\int_{1}^{x}\frac{1}{t^{2}+1}dt=\lim_{n \to \infty}\left [ \arctan(t) \right ]\bigg{|}_{1}^{x}=\lim_{n \to \infty}(\arctan(x)-\arctan(1))=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}$$

$$\therefore \int_{1}^{\infty}\frac{1}{x^{2}+1} \space converge$$

$$\therefore \sum_{n=1}^{\infty}\frac{1}{n^{2}+1} \space converge$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Diga si la siguientes series convergen o divergen.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $$\sum_{n=1}^{\infty} \arctan(n)$$
  2. $$\sum_{n=1}^{\infty} \frac{ln(n)}{n}$$
  3. $$\sum_{n=1}^{\infty} \frac{1}{n^{3}}$$
  4. $$\sum_{n=1}^{\infty} \frac{e^{\frac{1}{n}}}{n^{2}}$$
  5. $$\sum_{n=1}^{\infty} \frac{2^{n}}{3^{n}}$$

Más adelante…

En esta sección vimos el criterio de la integral en el cual se toma como función $f(x)$ a la sucesión $\left \{ a_{n} \right \}$ de la serie, esta función tiene que ser continua, decreciente y positiva en el intervalo $[1,\infty)$ para utilizar este criterio de la integral y observar la convergencia o divergencia de la serie, en la siguiente sección veremos otras series especiales llamadas p-series.

Entradas relacionadas

Cálculo Diferencial e Integral II: Criterio de la razón y el criterio de la raíz

Por Miguel Ángel Rodríguez García

2 respuestas

Introducción

En la sección anterior vimos dos criterios de convergencia: el criterio de comparación y el criterio de comparación del límite, en esta sección veremos el criterio de la prueba del cociente o de la razón, y el criterio de la raíz, comencemos enunciando el teorema del criterio de la razón.

Criterio de la razón

Teorema. (Prueba de la razón o del cociente)

Sea $\left \{a_{n} \right \}$ una sucesión positiva y supón que:

$$\lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}=r$$

Entonces $\sum_{n=1}^{\infty}a_{n}$ converge si $r<1$, diverge si $r>1$ y si $r=1$ no es concluyente.

Demostración:

Observemos que:

$$a_{n}>0 \space \space \forall \space n \space \epsilon \space \mathbb{N} \Rightarrow \frac{a_{n+1}}{a_{n}}>0 \space \forall \space n \space \epsilon \space \mathbb{N} \Rightarrow \lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}=r \geq 0$$

Para demostrar este teorema, dividamos por los casos siguientes:

  • Caso $1)$: Si $0\leq r < 1$, entonces:

$$\lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}=r$$

Podemos escoger un número $S$ tal que $r < S < 1 \space \Rightarrow \exists \space k \space \epsilon \space \mathbb{N}$

Tal que:

$$\forall \space n \space \geq k \space \Rightarrow \bigg{|}\frac{a_{n+1}}{a_{n}} \bigg{|}<S \space \Rightarrow a_{n+1} <S a_{n}$$

En particular:

$$a_{k+1}<S a_{k} \space \space y \space \space a_{k+2}<S a_{k+1}<S(S a_{k})=S^{2} a_{k}$$

Por tanto:

$$a_{k+2}<S^{2} a_{k} \Rightarrow a_{k+3}<S a_{k+2 }<S^{3} a_{k}$$

Continuando de esta manera hasta $n$, se tiene que:

$$a_{n}=a_{k+m}<S^{m} a_{k}$$

Por otro lado, como $S<1$, entonces la siguiente serie:

$$\sum_{m=1}^{\infty}S^{m} \space \space con \space m \geq 1$$

Es una serie geométrica, por tanto:

$\Rightarrow \sum_{m=1}^{\infty}S^{m}$ converge $\Rightarrow \sum_{m=1}^{\infty}S^{m}a_{k}$ converge

$\Rightarrow \sum_{m=1}^{\infty}a_{k+m}$ converge.

Por el criterio de comparación, así $\sum_{n=k+1}^{\infty}a_{n}$ converge,

$$\therefore \sum_{n}^{\infty}a_{n} \space converge$$

  • Caso $2)$: Si $r>1$

Vemos que:

$$\lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}=r$$

Podemos escoger un número $S$ tal que $r >S > 1 \space \Rightarrow \exists \space k \space \epsilon \space \mathbb{N}$

Tal que:

$$\forall n\geq k \space \space \bigg{|} \frac{a_{n+1}}{a_{n}} \bigg{|}>S \Rightarrow \forall \space n \geq k \space \Rightarrow a_{n+1}>S a_{n}$$

Se tiene que para:

$$a_{k+1}>S a_{k}$$

$$a_{k+2}>S a_{k+1}>S(S a_{k})=S^{2} a_{k}$$

$$a_{k+3}>S a_{k+2}>S(S^{2} a_{k})=S^{3} a_{k}$$

Continuando de esta manera, $\forall \space n\geq k$, entonces:

$$a_{k+n}>S^{n} a_{k}$$

$\sum_{n=1}^{\infty}S^{n}$ es una serie geométrica con $|S|>1$

$\Rightarrow \sum_{n=1}^{\infty}S^{n}$ diverge $\Rightarrow \sum_{n=1}^{\infty}S^{n}a_{k}$ diverge $\Rightarrow \sum_{n=1}^{\infty}a_{k+n}$ diverge

$\Rightarrow \sum_{n=k+1}^{\infty}a_{n}$ diverge

$$\therefore \sum_{n=1}^{\infty}a_{n} \space diverge$$

$\square$

  • Caso $3)$: Para este caso solo hay que dar un ejemplo, veamos:

Tomemos siguientes las series:

$$\sum_{i=1}^{\infty}\frac{1}{n^{2}} \space \space y \space \space \sum_{i=1}^{\infty}1$$

Es fácil ver que la segunda serie diverge cuando $n \to \infty$, para la primera serie, tenemos que:

$$\lim_{n \to \infty} \frac{a_{n+1}}{a_{n}}=\lim_{n \to \infty} \frac{\frac{1}{(n+1)^2}}{\frac{1}{n^2}}=\lim_{n \to \infty} \frac{n^2}{(n+1)^2}=\lim_{x \to \infty} \frac{1}{(1+\frac{1}{n^2})^2}=1$$

Lo cual sabemos que esta serie converge.

Por lo que para $r=1$ no hay conclusión de la convergencia de la serie.

$\square$

Veamos un ejemplo.

Ejemplo

Diga si la siguiente serie converge o diverge.

$$\sum_{n=1}^{\infty}\frac{1}{n!}$$

Usamos el criterio de la razón, tomamos el límite de la sucesión como:

$$\lim_{n \to \infty}\frac{a_{n+1}}{a_{n}}=\lim_{n \to \infty}\frac{\frac{1}{(n+1)!}}{\frac{1}{n!}}=\lim_{n \to \infty}\frac{n!}{(n+1)!}=\lim_{n \to \infty}\frac{n!}{(n+1)n!}=\lim_{n \to \infty}\frac{1}{n+1}=0<1$$

Por tanto, por el criterio de la razón:

$$\therefore \sum_{n=1}^{\infty}\frac{1}{n!} \space converge$$

Ahora veamos el criterio de la raíz.

Criterio de la raíz

Teorema. (Criterio de la raíz)

Sea $\left \{ a_{n}\right \}$ una sucesión con $a_{n}\geq 0 \space \space \forall \space n \space \epsilon \space \mathbb{N}$ tal que:

$$\lim_{n \to \infty}\sqrt[n]{a_{n}}=L$$

Entonces $\sum_{n=1}^{\infty}a_{n}$ converge si $L<1$ y diverge si $L>1$.

Demostración:

Divimos esta demostración por casos:

  • $1): L<1$

Supongamos que $L<1$, observamos que $L \geq0$, tomamos $r$ tal que $L<r<1$, por definición del limite:

$$\exists \space k \space \epsilon \space \mathbb{N}$$

Tal que:

$$\forall \space n\geq k \Rightarrow \space \sqrt[n]{a_{n}}<r$$

$$\Rightarrow a_{n}<r^{n}$$

Pero:

$\sum_{n=k}^{\infty }r^{n}$ converge ya que $r<1$ y es una serie geométrica, por el criterio de comparación.

$$\Rightarrow \sum_{n=k}^{\infty }a_{n} \space converge$$

$$\therefore \sum_{n=1}^{\infty }a_{n} \space converge$$

  • $2): L>1$

Ahora, supongamos que $L>1$, toma $r$ tal que $1<r<L$, por definición del límite:

$$\exists \space k \space \epsilon \space \mathbb{N}$$

Tal que:

$$\forall \space n\geq k \Rightarrow \space \sqrt[n]{a_{n}}>r$$

$$\Rightarrow a_{n}>r^{n}$$

Pero $1<r$, por consiguiente por el criterio de las series geométricas:

$$\Rightarrow \sum_{n=k}^{\infty }r^{n} \space diverge \space \Rightarrow \sum_{n=r}^{\infty }a_{n} \space diverge$$

Por el criterio de comparación:

$$\therefore \sum_{n=1}^{\infty }a_{n} \space diverge$$

$\square$

Veamos un ejemplo.

Ejemplo

Diga si la siguiente serie converge o diverge.

  • $$\sum_{n=1}^{\infty }\frac{(1+\frac{1}{n})^{2n}}{e^{n}}$$

Apliquemos el criterio de la raíz, tomamos el límite de la sucesión como:

$$\lim_{n \to \infty}\sqrt[n]{a_{n}}=\lim_{n \to \infty }\sqrt[n]{\frac{(1+\frac{1}{n})^{2n}}{e^{n}}}=\lim_{n \to \infty }\frac{(1+\frac{1}{n})^{2n}}{e^{n}}=\frac{1}{e}<1$$

Por tanto, por el criterio de la raíz:

$$\therefore \sum_{n=1}^{\infty }\frac{(1+\frac{1}{n})^{2n}}{e^{n}} \space converge$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Diga si la siguientes series convergen o divergen.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $$\sum_{n=1}^{\infty}\frac{9^{n}}{2^{n+1}n}$$
  2. $$\sum_{n=1}^{\infty }(\frac{1}{n^{2}}-\frac{1}{n^{10}})^{n}$$
  3. $$\sum_{n=1}^{\infty}\frac{(2n)!}{n!n!}$$
  4. $$\sum_{n=1}^{\infty}\left ( \frac{1}{1+n} \right )^{n}$$
  5. $$\sum_{n=1}^{\infty}\left ( \frac{2n+3}{3n+2} \right )^{n}$$

Más adelante…

En esta sección vimos otros dos criterios más de convergencia que son el criterio de la razón en el cual el valor del límite de la división entre la sucesión $a_{n+1}$ y $a_{n}$ nos dice si la serie es convergente o divergente, y el criterio de la raíz que dependiente del valor se toma del límite de la raíz n-esima de la sucesión nos dice si la sucesión es convergente o divergente. En la siguiente sección veremos otro criterio de convergencia, que es el criterio de la integral.

Entradas relacionadas

Cálculo Diferencial e Integral II: Criterio de comparación y comparación del limite

Por Miguel Ángel Rodríguez García

2 respuestas

Introducción

En la sección anterior vimos dos criterios de convergencia para las series, el criterio de la divergencia y el criterio de acotación, en esta sección veremos otros dos criterios de convergencia para las series que son los criterios de comparación y el criterio del límite.

Criterio de comparación

Teorema. (Criterio de comparación)

Sea $\left \{ a_{n} \right \}$ y $\left \{ b_{n} \right \}$ tal que $0 \leq a_{n} \leq b_{n}$ $\forall \space n \space \epsilon \space \mathbb{N}$ y supón que $\sum_{n=1}^{\infty }b_{n}$ converge, entonces $\sum_{n=1}^{\infty }a_{n}$ converge.

Mientras que si $\sum_{n=1}^{\infty }a_{n}$ diverge, entonces $\sum_{n=1}^{\infty }b_{n}$ diverge.

Demostración:

Sea $0\leq a_{n}\leq b_{n}$ y supón que $\sum_{n=1}^{\infty }b_{n}$ converge.

Sea $\left \{ S_{n} \right \}$ la sucesión de sumas parciales de $\left \{ b_{n} \right \}$, y sea $\left \{ t_{n} \right \}$ las sumas parciales de $\left \{ a_{n} \right \}$.

Por demostrar que $\left \{ t_{n} \right \}$ esta acotada.

Observemos que $\sum_{n=1}^{\infty }b_{n}$ converge, entonces $\left \{ S_{n} \right \}$ esta acotada por el criterio de acotación, por lo que, $\exists \space M \space \epsilon \space \mathbb{R}$ tal que $|S_{n}| \space \leq M \space \forall \space n \space \epsilon \space \mathbb{N}$.

Pero $a_{i}\leq b_{i} \space \forall \space i \space\epsilon \space \mathbb{N}$.

$$\Rightarrow a_{1}+a_{2}+….+a_{n}\leq b_{1}+b_{2}+….+b_{m}$$

$$\Rightarrow t_{n} \leq S_{n}\leq M$$

$$\Rightarrow t_{n}\leq M \space \space \forall \space n \space \epsilon \space \mathbb{N} $$

Por lo cual $t_{n}$ está acotado, nuevamente, por el criterio de acotación como $t_{n}$ está acotado, entonces $a_{n}$ también lo está.

$\therefore \left \{ t_{n} \right \}$ esta acotado $\Rightarrow \sum_{n=1}^{\infty }a_{n}$ converge.

Ahora la demostración de sí $\sum_{n=1}^{\infty }a_{n}$ diverge entonces $\sum_{n=1}^{\infty }b_{n}$ diverge, lo podemos demostrar por contradicción:

Por hipótesis $\sum_{n=1}^{\infty }a_{n}$ diverge, pero supongamos que $\sum_{n=1}^{\infty }b_{n}$ converge, entonces por lo que acabamos de ver, $\sum_{n=1}^{\infty }a_{n}$ converge, lo cual con lleva a una contradicción, ya que $\sum_{n=1}^{\infty }a_{n}$ diverge.

$\therefore \sum_{n=1}^{\infty }b_{n}$ diverge.

$\square$

Los que nos dice este teorema es que podemos acotar una serie $ \left \{ a_{n} \right \} $ por otra serie $\left \{ b_{n} \right \}$ y conocer su convergencia o divergencia, para posteriormente, saber la convergencia o divergencia de la serie $ \left \{ a_{n} \right \} $.

Veamos un ejemplo.

Ejemplo

Diga si la siguiente serie converge o diverge.

  • $$\sum_{n=1}^{\infty} \sqrt[n]{n}$$

Sabemos que para $n >2: \space \space \sqrt[n]{n}<\sqrt{n} \space n \space \epsilon \space \mathbb{N}$

Pero sabemos que $\sum_{n=1}^{\infty} \sqrt{n}$ diverge, por el criterio de comparación, entonces se tiene que $\sqrt[n]{n}$ diverge.

$$\therefore \sum_{n=1}^{\infty} \sqrt[n]{n} \space \space diverge$$

Ahora veamos el criterio de comparación del límite.

Criterio de comparación del límite

Teorema. (Comparación del límite)

Sea $a_{n}>0$ y $b_{n}>0$ tal que:

$$\lim_{n\to \infty }\frac{a_{n}}{b_{n}}=C>0.$$

$\Rightarrow \sum_{n=1}^{\infty}a_{n}$ converge $\Leftrightarrow \sum_{n=1}^{\infty}b_{n}$ converge.

En otras palabras:

$\Rightarrow \sum_{n=1}^{\infty}a_{n}$ diverge $\Leftrightarrow \sum_{n=1}^{\infty}b_{n}$ diverge.

Demostración:

$\Leftarrow \lrcorner$

Supón que $\sum_{n=1}^{\infty}b_{n}$ converge, tratemos de acotar $a_{n}$ por algo convergente.

Tomemos $\varepsilon = C$.

Como $\lim_{n \to \infty}\frac{a_{n}}{b_{n}}=C$, por definición del limite se tiene que:

$\exists \space k \space\epsilon \space \mathbb{N}$ tal que si $n\geq k$ entonces:

$$\bigg{|}\frac{a_{n}}{b_{n}}-C \bigg{|}<\epsilon =C$$

$$\Rightarrow -C<\frac{a_{n}}{b_{n}}-C<C$$

$$\Rightarrow 0<\frac{a_{n}}{b_{n}} < 2C$$

$$\Rightarrow a_{n}<2 \space C \space b_{n}$$

Pero por hipótesis tenemos que:

$\sum_{n=1}^{\infty}b_{n}$ converge $\Rightarrow \sum_{n=1}^{\infty}2b_{n}$ converge $\Rightarrow \sum_{n=1}^{\infty}2Cb_{n}$ converge.

ya que, por la propiedades de las series:

$$ \sum_{n=1}^{\infty}2Cb_{n}=2C\sum_{n=1}^{\infty}b_{n} \space \space y \space \space \sum_{n=1}^{\infty}b_{n} \space \space converge $$

$$\therefore \space Por \space el \space criterio \space de \space comparación \space \space \sum_{n=1}^{\infty}a_{n} \space \space converge.$$

Ahora demostremos el de ida:

$\Rightarrow \lrcorner$

Supón que $\sum_{n=1}^{\infty}a_{n}$ converge, consideremos $\lim_{n \to \infty} \frac{b_{n}}{a_{n}}=\frac{1}{C}$, como:

$$C>0 \Rightarrow \frac{1}{C}>0$$

Tomemos $\epsilon =\frac{1}{C}$. Por definición del límite $\exists \space N \space \epsilon \space \mathbb{N}$ tal que:

$$\forall \space n \geq N \Rightarrow \bigg{|}\frac{b_{n}}{a_{n}}-\frac{1}{C}\bigg{|}< \epsilon =\frac{1}{C}$$

$$\Rightarrow -\frac{1}{C}<\frac{b_{n}}{a_{n}}-\frac{1}{C}<\frac{1}{C}$$

$$\Rightarrow 0<\frac{b_{n}}{a_{n}}< \frac{2}{C}$$

$\Rightarrow b_{n}<\frac{2}{C}a_{n}$ por lo que acotamos $b_{n}$, así:

$\sum_{n=1}^{\infty}a_{n}$ converge $\Rightarrow \sum_{n=1}^{\infty}2a_{n}$ converge $\Rightarrow \sum_{n=1}^{\infty} \frac{2}{C}a_{n}$ converge.

$$\therefore \space Por \space el \space criterio \space de \space comparación \space \space \sum_{n=1}^{\infty}b_{n} \space \space converge.$$

La demostración para el caso cuando divergen es muy similar a la demostración anterior, solo cambiamos la desigualdad en la definición del límite y aplicamos nuevamente el criterio de comparación.

$\square$

Ejemplo

Diga si la siguiente serie converge o diverge.

  • $$\sum_{n=1}^{\infty} \frac{1}{a\sqrt{n}+b}$$

Donde $a$ y $b$ son constantes y $ a\neq 0 $.

Sea $\left \{ b_{n} \right \}=\frac{1}{a\sqrt{n}+b}$, tomemos a la sucesión $\left \{ a_{n} \right \}=\frac{1}{\sqrt{n}}$ entonces tomando el límite tenemos que:

$$ \lim_{n \to \infty}\frac{a_{n}}{b_{n}} =\lim_{n \to \infty}\frac{\frac{1}{\sqrt{n}}}{\frac{1}{a\sqrt{n}+b}}=\lim_{n \to \infty}\frac{a\sqrt{n}+b}{\sqrt{n}} \Rightarrow \lim_{n \to \infty}(a+\frac{b}{\sqrt{n}})= a$$

Con $a\neq 0$

Pero como $\sum_{n=1}^{\infty}\frac{1}{\sqrt{n}}$ diverge, por el criterio de comparación del límite:

$$\Rightarrow \sum_{n=1}^{\infty} \frac{1}{a\sqrt{n}+b} \space diverge $$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Diga si la siguientes series convergen o divergen.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $$\sum_{n=1}^{\infty}\frac{ln(n)}{n}$$
  2. $$\sum_{n=1}^{\infty}\frac{1}{2^{n}-1}$$
  3. $$\sum_{n=1}^{\infty}\frac{5}{5n-1}$$
  4. $$\sum_{n=1}^{\infty}\frac{2n^{2}+3n}{\sqrt{5+n^{5}}}$$
  5. $$\sum_{n=1}^{\infty}\frac{1}{2^{n}-1}$$

Más adelante…

En esta sección vimos dos criterios más de convergencia, el criterio de comparación, el cual se acota una sucesión con otra sucesión para estudiar si diverge o no converge la sucesión que está acotando, lo cual nos dice la convergencia o divergencia de la sucesión que está acotada; y el criterio de comparación del límite que nos dice que si la división entre dos sucesiones positivas, da como resultado una constante entonces las sucesiones convergen o divergen. En la siguiente sección veremos el criterio de la raíz y el criterio de la razón.

Entradas relacionadas

Cálculo Diferencial e Integral II: Criterio de la divergencia y de acotación

Por Miguel Ángel Rodríguez García

3 respuestas

En la sección anterior vimos unas series especiales llamadas series geométricas, donde, dependiendo del valor de $r$ la serie converge o diverge, además, vimos algunas propiedades de las series, lo cual usaremos en adelante. En esta sección veremos algunos teoremas sobre los criterios de divergencia o convergencia de series. Comencemos con anunciando el teorema del criterio de Cauchy.

Criterios de convergencia

Teorema. (Criterio de Cauchy)

La sucesión $\left \{a_{n} \right \}$ es sumable (convergente) si y solo si $\forall \space m, \space n \space \epsilon \space \mathbb{N}$

$$\lim_{m, n \to \infty}(a_{m+1}+a_{m+2}+….+a_{n})=0$$

Para $n>m \geq N$

Demostración:

Utilizando el criterio de Cauchy para sucesiones, como $\left \{a_{n} \right \}$ es sumable $\Leftrightarrow \lim_{n \to \infty} S_{n}$ converge $\Leftrightarrow \forall \space \epsilon >0, \space \exists \space N \space \epsilon \space \mathbb{N}$ tal que si $m, \space n \geq N \Rightarrow |S_{n}-S_{m}|<\varepsilon$

$$\Leftrightarrow |(a_{1}+a_{2}+….+a_{n})-(a_{1}+a_{2}+….+a_{m})|<\varepsilon$$

Como $n>m$, entonces:

$$ =|(a_{1}+a_{2}+….+a_{m}+a_{m+1}+….+a_{n})-(a_{1}+a_{2}+….+a_{m})|\Leftrightarrow |a_{m+1}+….+a_{n}|<\varepsilon$$

$\forall \space n>m$

En particular:

$$\Leftrightarrow |a_{m+1}+….+a_{n}-0|<\varepsilon \Leftrightarrow \lim_{m, n \to \infty}(a_{m+1}+….+a_{n})=0$$

Por tanto, la serie $a_{n}$ es convergente.

$\square$

Teorema. Si la serie $\sum_{n=1}^{\infty}a_{n}$ es convergente, entonces $\lim_{n \to \infty}a_{n}=0$.

Demostración:

Puesto que la serie $\sum_{n=1}^{\infty}a_{n}$ es convergente, la sucesión $\left \{ a_{n} \right \}$ es convergente $\Rightarrow \lim_{n \to \infty}S_{n}$ converge a un numero $L$.

$$\Rightarrow \lim_{n \to \infty}S_{n+1}=L$$

Pero: $$\lim_{n \to \infty}a_{n+1}=\lim_{n \to \infty}\left [ (a_{1}+a_{2}+….+a_{n+1})-(a_{1}+a_{2}+….+a_{n}) \right ]=\lim_{n \to \infty}(S_{n+1}-S_{n})$$

$$\lim_{n \to \infty}(S_{n+1})-\lim_{n \to \infty}(S_{n})=L-L=0$$

$$\therefore \lim_{n \to \infty}a_{n+1}=0$$

Como $a_{n+1}$ converge, entonces también lo hace $a_{n}$.

$$\therefore \lim_{n \to \infty}a_{n} =0$$

$\square$

Nota: En general, el inverso de este teorema no es valido, si $lim_{n \to \infty}a_{n}=0$ no se puede concluir que $\sum_{n=1}^{\infty}a_{n}$ es convergente.

Criterio de la divergencia

Teorema. (La prueba o criterio de la divergencia):

Si $\lim_{n \to \infty}a_{n}$ no existe o si $\lim_{n \to \infty}a_{n}\neq 0$ entonces la serie $\sum_{n=1}^{\infty}a_{n}$ diverge.

La demostración se infiere del teorema anterior porque si la serie no es divergente, entonces es convergente y, por tanto, $\lim_{n \to \infty}a_{n}= 0$.

$\square$

Veamos unos ejemplos.

Ejemplos

  • $$\sum_{n=1}^{\infty }\frac{n}{4n+1}$$

Tomando el límite, obtenemos lo siguiente:

$$\lim_{n\rightarrow \infty }\frac{1}{4+\frac{1}{n}}=\frac{1}{4}\neq 0$$

Por el criterio de la divergencia:

$$\sum_{n=1}^{\infty}\frac{n}{4n+1} \space diverge$$

  • $$\sum_{n=1}^{\infty} \frac{n!}{2n!+1}$$

Tomamos el límite y multiplicamos por el factor $\frac{\frac{1}{n!}}{\frac{1}{n!}}$, por lo que se tiene que:

$$\lim_{n \to \infty} \frac{n!}{2n!+1}=\lim_{n \to \infty } \frac{\frac{n!}{n!}}{2\frac{n!}{n!}+\frac{1}{n!}}=\lim_{n \to \infty} \frac{1}{2+\frac{1}{n!}}=\frac{1}{2}\neq 0$$

$$\therefore \sum_{i=1}^{\infty}\frac{n!}{2n!+1} \space diverge$$

Existe otro criterio de convergencia llamado el criterio de acotación

Series con términos no negativos

Teorema. (Criterio de acotación)

Una sucesión no negativa $\left \{ a_{n} \right \}$ es sumable, $\Leftrightarrow$ sus sumas parciales $\left \{S_{n} \right \}$ está acotada.

Demostración:

$\Rightarrow \lrcorner $

Si $\left \{ a_{n} \right \}$ es sumable $\Leftrightarrow \lim_{n \to \infty } S_{n}=L$ converge por el teorema visto anteriormente.

Habiamos visto en cálculo 1 que si, converge $S_{n}$ $\Rightarrow S_{n}$ esta acotada.

$\Leftarrow \lrcorner$

Supongamos que $\left \{ S_{n} \right \}$ está acotado, observemos que:

$$S_{n+1}=S_{n}+a_{n+1} \geq S_{n}$$

Ya que:

$$a_{n+1}\geq 0$$

$$\Rightarrow S_{n} \leq S_{n+1} \space\forall \space n \space \epsilon \space \mathbb{N}$$

$\therefore S_{n}$ es creciente y además, está acotado por hipótesis, por cálculo I, si una sucesión es creciente y acotada, entonces se tiene que:

$\Rightarrow \left \{ S_{n} \right \}$ es convergente $\Rightarrow \left \{ a_{n} \right \}$ es sumable.

$\square$

Teorema. Sea $k \space \epsilon \space \mathbb{N}$ fijo. La serie$\sum_{n=k}^{\infty}a_{n}$ converge$\space \Leftrightarrow\sum_{n=0}^{\infty } a_{n}$ converge.

Demostración:

Como la serie converge por hipótesis, entonces:

$$\sum_{n=k}^{\infty }a_{n} \Leftrightarrow \lim_{n \to \infty }(a_{k}+a_{k+1}+…+a_{n}) \Leftrightarrow$$

$$a_{0}+a_{1}+…+a_{k-1}+\lim_{k \to \infty }(a_{k}+a_{k+1}+…+a_{n}) \Leftrightarrow$$

$$\lim_{n \to \infty }(a_{0}+a_{1}+…+a_{k}+a_{k+1}+…a_{n}) \space \space converge$$

$$\Leftrightarrow \sum_{n=0}^{\infty }a_{n} \space \space converge$$

$\square$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Diga si la siguientes series convergen o divergen.

  1. $$\sum_{i=1}^{\infty}\frac{1}{\sqrt{n}}$$
  2. $$\sum_{i=1}^{\infty}\frac{n^{2}}{5n^{2}+4}$$
  3. $$\sum_{i=1}^{\infty} \frac{-n}{2n+5}$$
  4. $$\sum_{n=0}^{\infty}e^{-2n}$$
  5. $$\sum_{n=1}^{\infty}ln\left ( \frac{1}{n} \right )$$

Más adelante…

En esta sección vimos dos teoremas importantes de criterios de convergencia, el criterio de la divergencia, en el cual nos dice que si el límite de la sucesión es diferente de cero o no existe, entonces la serie diverge, y el criterio de acotación que nos dice la reciprocidad entre una sucesión convergente y la acotación de sus sumas parciales. En la siguiente sección veremos otros dos criterios de acotación, el criterio de comparación y comparación del límite.

Entradas relacionadas

Cálculo Diferencial e Integral II: Definición de series y series infinitas

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En esta entrada veremos la definición de series y sumas parciales para conocer lo básico en este nuevo tema que con llevará a teoremas que nos dirán si una serie es divergente o convergente.

Cabe recalcar que para este tema se debe tener noción de sucesiones que se estudió en Cálculo Diferencial e Integral I. Comenzamos estudiando las sumas parciales que se definen como sigue.

Sumas parciales

Definición. Sea $\left \{ a_{n} \right \}$ una sucesión, definimos la nueva sucesión $S_{n}$ «la sucesión de la sumas parciales de $\left \{ a_{n} \right \}$» como:

$$S_{n}=a_{1}+a_{2}+….+a_{n}$$

Esta serie se denota comúnmente como:

$$S_{n}= a_{1}+a_{2}+….+a_{n} =\sum_{i=1}^{n}a_{i}$$

Donde $a_{i}$ es el término general de la sucesión y se va sumando desde el valor inferior $i=1$ hasta el valor $i=n$.

Veamos unos ejemplos:

  • Sea $\left \{ a_{n} \right \}$ una sucesión dada por $a_{n}=\frac{1}{n}$

En este caso tenemos que $a_{1}=\frac{1}{1}$, $a_{2}=\frac{1}{2}$ y $a_{3}=\frac{1}{3}$ entonces tenemos que la sucesión de sumas parciales hasta $n=3$ es:

$$S_{1}=\sum_{i=1}^{1}a_{i}=a_{1}=1, \space$$

$$S_{2}=\sum_{i=1}^{2}a_{i}=a_{1}+a_{2}=1+\frac{1}{2}=\frac{3}{2}, \space$$

$$S_{3}=\sum_{i=1}^{3}a_{i}=a_{1}+a_{2}+a_{3}=1+\frac{1}{2}+\frac{1}{3}=\frac{11}{6}$$

  • Sea $\left \{ a_{n} \right \}$ una sucesión dada por $a_{n}=(-1)^{n}$

Tenemos que las sumas parciales hasta $n=4$ son:

$$S_{1}=-1, \space$$

$$S_{2}=S_{1}+a_{2}=-1+1=0, \space$$

$$S_{3}=S_{2}+a_{3}=-1$$

$$S_{4}=S_{3}+a_{4}=0$$

A este tipo de series se les conoce como series oscilantes, ya que como vemos, las sumas parciales van oscilando sobre algunos valores.

  • Sea $a_{n}=\left ( \frac{1}{2} \right )^{n}$

Tenemos que:

$$S_{1}=\frac{1}{2},$$

$$S_{2}=S_{1}+a_{2}=\frac{1}{2}+\frac{1}{4}=\frac{3}{4},$$

$$S_{3}=S_{2}+a_{3}=\frac{7}{8}$$

$$S_{4}=S_{3}+a_{4}=\frac{15}{16}$$

Se puede afirmar que las sumas parciales de esta sucesión tienden al valor siguiente:

Afirmación: $$\sum_{i=1}^{n} \left ( \frac{1}{2} \right )^{n} = S_{n}=\frac{2^{n}-1}{2^{n}}=1-\left ( \frac{1}{2} \right )^{n} \tag{1}$$

Demostración:

Esta afirmación se demuestra por inducción, por lo que recordamos que demostrar por inducción consta de tres pasos siguientes:

$1)$ para $n=1$ tenemos que:

$$ \sum_{i=1}^{1} \left ( \frac{1}{2} \right )^{1} =S_{1}=\frac{2^{1}-1}{2^{1}}=1-\left ( \frac{1}{2} \right )^{1}=\frac{1}{2}$$

Por lo que para $n=1$ cumple.

$2)$ Supongamos valido para $n=k$ entonces:

$$ \sum_{i=1}^{k} \left ( \frac{1}{2} \right )^{k}=\frac{2^{k}-1}{2^{k}}=1-\left ( \frac{1}{2} \right )^{k}$$

$3)$ Demostremos para $n=k+1$, por lo que:

$$ \sum_{i=1}^{k+1} \left ( \frac{1}{2} \right )^{k+1} =S_{k+1}=S_{k}+a_{k+1}=\frac{2^{k}-1}{2^k}+\left ( \frac{1}{2} \right )^{k+1}=\frac{2^{k}-1}{2^{k}}+\frac{1}{2^{k+1}}$$

Multiplicamos por $\frac{2}{2}$ en la fracción de la izquierda, por lo que se tiene que:

$$ 1-\left ( \frac{1}{2} \right )^{k+1} =\frac{2\left ( 2^{k}-1 \right )}{2^{k+1}}+\frac{1}{2^{k+1}}=\frac{2^{k+1}-2}{2^{k+1}}+\frac{1}{2^{k+1}}=\frac{2^{k+1}-2+1}{2^{k+1}}=\frac{2^{k+1}-1}{2^{k+1}}$$

$$\therefore \space \forall \space n \space \epsilon \space \mathbb{N} \space \space \space \space \space \space \sum_{i=1}^{n} \left ( \frac{1}{2} \right )^{n} =S_{n}=\frac{2^{n}-1}{2^{n}}= 1-\left ( \frac{1}{2} \right )^{n} $$

$\square$

Ya que hemos estudiado un poco las sumas parciales, veamos cuando una serie converge o diverge.

Series

Definición. Si la sucesión de sumas parciales $S_{n}$ de la sucesión $a_{n}$, converge a un número $L$ con $L \space \epsilon \space \mathbb{R}$, entonces:

$$\sum_{i=1}^{n}a_{n}=L$$

Es decir, la serie $a_{n}$ converge al valor $L$.

En caso contrario, si $S_{n}$ no converge, entonces la serie $\sum_{i=1}^{n}a_{n}$ diverge.

La anterior definición es para series que no son infinitas, a las series infinitas las definimos como sigue:

Definición. Se dice que la sucesión $\left \{ a_{n} \right \}$ es sumable (o convergente) si la sucesión de sumas parciales $S_{n}$ converge, para $\lim_{n \to \infty} S_{n}$, es decir:

$$\lim_{n \to \infty} S_{n}=L$$

Donde $L$ es un número. La notación anterior se puede denotar de la siguiente manera:

$$\lim_{n \to \infty} S_{n}=\lim_{n \to \infty}\left ( a_{1}+a_{2}+….+a_{n} \right )=\lim_{n \to \infty}\sum_{i=1}^{n}a_{i}=\sum_{i=1}^{\infty}a_{i} \tag{2}$$

$\sum_{i=1}^{\infty}a_{i}$ recibe el nombre de suma infinita de $a_{n}$ ó la serie infinita de $a_{n}$.

  • Si $S_{n}$ converge se dice que la serie converge.
  • Si $S_{n}$ diverge se dice que la serie diverge.

Veamos unos ejemplos.

Ejemplos

  • Sea la serie $\sum_{i=1}^{\infty }a_{i}$ con $a_{i}=\frac{1}{2^{i}}$, diga si esta serie converge o diverge.

De la definición $(2)$ tenemos que:

$$\sum_{i=1}^{\infty}a_{i}=\lim_{n \to \infty}\sum_{i=1}^{n}\frac{1}{2^{i}}=\lim_{n \to \infty}S_{n}$$

Por la afirmación de la relación $(1)$, tenemos que:

$$\lim_{n \to \infty}S_{n}=\lim_{n \to \infty}\left ( \frac{2^{n}-1}{2^n} \right )=\lim_{n \to \infty}(1-\frac{1}{2^{n}})=1$$

ya que:

$$\lim_{n \to \infty}\frac{1}{2^{n}}=0$$

$$\therefore \sum_{i=1}^{\infty }\frac{1}{2^{i}}=\frac{1}{2}+\frac{1}{4}+….+\frac{1}{2^{i}}=1$$

Por tanto, la serie converge a un valor y ese valor es $1$.

  • Sea la serie $\sum_{i=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1})$, diga si esta serie converge o diverge.

Vemos que:

$$a_{n}=\left ( \frac{1}{n}-\frac{1}{n+1} \right )$$

Así :

$$S_{1}=1-\frac{1}{2}=\frac{1}{2}$$

$$S_{2}=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{2})=\frac{2}{3}$$

$$S_{3}=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})=1-\frac{1}{4}$$

Vemos que sigue una secuencia, por lo que podemos afirmar lo siguiente:

Afirmación: $$\sum_{i=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1})=S_{n}=1-\frac{1}{n+1} \tag{3}$$

La demostración se le dejará como tarea moral, recuerde que este tipo de demostraciones se usa comúnmente la demostración por inducción.

Entonces de la afirmación $(3)$ tenemos que:

$$\sum_{i=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1})=\lim_{n \to \infty}S_{n}=\lim_{n \to \infty}(1-\frac{1}{n+1})=1$$

ya que:

$$\lim_{n \to \infty}(\frac{1}{n+1})=0$$

$$\therefore \sum_{i=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1})=1$$

Por lo tanto, la serie converge.

  • Sea la serie $\sum_{i=1}^{\infty }(-1)^{n}$, diga si esta serie converge o diverge.

Entonces tenemos que $a_{n}=(-1)^{n}$, vemos que:

$$S_{1}=-1,$$

$$S_{2}=0,$$

$$S_{3}=-1$$

$$S_{4}=0$$

Vemos que esta serie está oscilando, por lo que esta serie está dada como:

$$S_{n}=\left\{ \begin{array}{lcc}
             -1 & si \space n \space es \space impar   \\
             \\ 0 & si \space n \space es \space par \\
             \end{array}
   \right.$$

Por lo que:

$$\sum_{i=1}^{\infty }(-1)^{n}=\lim_{n \to \infty }S_{n} \to diverge$$

No existe el límite, porque vemos que la serie oscila entre los valores $-1$ y $0$.

A este tipo de series se les conoce como series oscilantes.

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Diga si las siguientes series convergen o divergen:

  1. $$\sum_{i=1}^{5} 1$$
  2. $$\sum_{i=1}^{\infty} \frac{1}{n}$$
  3. $$\sum_{i=1}^{\infty}\left ( \frac{1}{2} \right )^{n}$$
  4. $$\sum_{i=1}^{\infty}\frac{2}{4n^{2}-1}$$ Hint: Utilice fracciones parciales y demuestre por inducción que $\sum_{i=1}^{\infty}\frac{2}{4n^{2}-1}=\frac{1}{2n-1}-\frac{1}{2n+1}=1-\frac{1}{2n+1}$.
  5. Demuestre por inducción que: $\sum_{i=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1})=1-\frac{1}{n+1}$

Más adelante…

En esta sección vimos la definición y notación de series y series infinitas viendo algunos ejemplos para entender las sumas parciales de estas series y determinando la convergencia y divergencia de algunas series, en la siguiente sección veremos unas series particulares que se llaman series geométricas.

Entradas relacionadas