Introducción
En esta entrada abordaremos el concepto de serie de potencias, la cual es un tipo particular de serie de números complejos y/o serie de funciones de números complejos, por lo que los resultados de las dos entradas anteriores nos serán de gran utilidad para caracterizar a dichas series.
En general, las series de potencias resultan de gran interés puesto que nos permiten aproximar y definir funciones, en particular a las funciones complejas elementales como lo haremos en las siguientes entradas. Nuestro objetivo en esta entrada es establecer algunos resultados elementales para determinar cuándo y en qué conjuntos estas series convergen.
Definición 29.1. (Serie de Potencias.)
Sean $z_0 \in\mathbb{C}$ y $\{c_n\}_{n\geq 0} \subset \mathbb{C}$ una sucesión de números complejos. Una serie de la forma: \begin{equation*}
\displaystyle \sum_{n=0}^\infty c_n \left(z-z_0\right)^n, \tag{29.1}
\end{equation*} para cada $z\in\mathbb{C}$, es llamada serie de potencias centrada en $z_0$ y los números $c_n\in\mathbb{C}$ son llamados los coeficientes de la serie.
Observación 29.1.
Recordemos que hemos hecho antes la convención $(z-z_0)^0 = 1$ para todo $z-z_0\in\mathbb{C}$.
Considerando lo anterior, podemos pensar a una serie de potencias como una serie de números complejos o como una serie de funciones, por lo que, en cualquiera de los dos casos podemos hablar de los conceptos de convergencia, convergencia absoluta, convergencia puntual y convergencia uniforme establecidos en las entradas anteriores.
Si consideramos a una serie de potencias, dada en (29.1), como una serie de funciones, entonces dicha serie está definida por la sucesión de funciones:
\begin{equation*}
f_0(z) = c_0, \quad f_n(z) = c_n\left(z-z_0\right)^n, \forall n\geq 1.
\end{equation*}
Bajo esta idea, es claro que cada serie de potencias define a una función compleja, de variable $z$, cuyo dominio natural consistirá de todos los $z\in\mathbb{C}$ para los cuales la serie de funciones (29.1) converge. Por tanto, en caso de ser necesario podemos elegir distintos dominios para dicha función, correspondientes con subconjuntos del dominio natural dado por la convergencia de la serie.
Observación 29.2.
Notemos que la serie dada por (29.1) siempre converge en el centro, es decir, si $z=z_0$ entonces para $n \geq 1$ todos los términos de la serie se anulan, mientras que para $n=0$ se obtiene la constante $c_0 \in \mathbb{C}$, por lo que la serie de potencias converge.
Por otra parte, para $z\neq z_0$ la serie de potencias puede converger o diverger, como veremos más adelante.
Si planteamos el cambio de variable:
\begin{equation*}
\zeta = z – z_0, \tag{29.2}
\end{equation*} es claro que $\zeta = 0$ si y solo si $z = z_0$ y $\zeta \neq 0$ si y solo si $z \neq z_0$, entonces la serie de potencias dada en (29.1) toma la forma:
\begin{equation*}
\displaystyle \sum_{n=0}^\infty c_n \zeta^n, \quad \forall \zeta \in\mathbb{C}, \tag{29.3}
\end{equation*} de donde (29.3) converge si $\zeta = 0$, mientras que para $\zeta \neq 0$ la serie puede converger o diverger.
El cambio de variable dado en (29.2) puede simplificar un poco las cuentas, por lo que trabajaremos indistintamente con una serie de potencias de la forma (29.1) ó (29.3), simplemente considerando $z=\zeta$ y a la serie centrada en el origen, es decir, $z_0 = 0$. Para recuperar el caso general bastará con realizar el cambio de variable (29.2).
Ejemplo 29.1.
Veamos que para una serie de potencias, de la forma (29.1) ó (29.3), se cumple alguna de las siguientes condiciones.
- La serie converge para todo $z\in\mathbb{C}$ ó $\zeta\in\mathbb{C}$.
- La serie converge solo para $z=z_0$ ó $\zeta = 0$.
- La serie converge solo para los $z$ ó $\zeta$ en alguna región del plano complejo $\mathbb{C}$.
Solución. Por ahora, para verificar la afirmación basta con dar un ejemplo para cada caso. Más adelante, corolario 29.1, probaremos esta afirmación.
Veamos que cada condición se cumple sin importar si la serie de potencias es de la forma (29.1) ó (29.3).
- Consideremos a las series de potencias: \begin{equation*} \displaystyle \sum_{n=0}^\infty \frac{(z-1+i)^n}{(n!)^2} \quad \text{y} \quad \displaystyle \sum_{n=0}^\infty \frac{\zeta^n}{n!}. \end{equation*} Para la primera serie tenemos que $z_0 = 1-i$. Es claro que para $z=z_0$ la serie de potencias converge. Supongamos que $z\neq z_0$, entonces: \begin{align*} \lambda = \lim_{n\to \infty} \dfrac{\left|\dfrac{(z-1+i)^{n+1}}{\left[(n+1)!\right]^2}\right|}{\left|\dfrac{(z-1+i)^{n}}{(n!)^2}\right|} & = \lim_{n\to \infty} \left|\dfrac{(z-1+i)^{n+1}(n!)^2}{(z-1+i)^{n}\left[(n+1)!\right]^2} \right|\\ & = \lim_{n\to \infty} \dfrac{\left|z-1+i\right|(n!)^2}{(n+1)^2(n!)^2}\\ & = \lim_{n\to \infty} \dfrac{\left|z-1+i\right|}{(n+1)^2} = 0. \end{align*} Entonces, por el criterio del cociente de D’Alembert, proposición 27.5, para todo $z\neq z_0$ la serie converge absolutamente. Por lo tanto, para todo $z\in\mathbb{C}$ la primera serie de potencias converge.
Por otra parte, para la segunda serie de potencias, por el ejemplo 27.8, sabemos que la serie es absolutamente convergente para todo $\zeta\in\mathbb{C}$, por lo que la segunda serie de potencias también converge para todo $\zeta\in\mathbb{C}$. - Consideremos a las series de potencias: \begin{equation*} \displaystyle \sum_{n=1}^\infty \frac{n^n (z-i)^n}{n} \quad \text{y} \quad \displaystyle \sum_{n=0}^\infty n! \zeta^n. \end{equation*} Para la primera serie tenemos que $z_0 = i$, $c_0 = 0$ y $c_n = \dfrac{n^n}{n}$ para $n\geq 1$. Es claro que para $z=z_0$ la serie de potencias converge. Supongamos que $z\neq z_0$, entonces: \begin{equation*} \lambda = \lim_{n\to \infty} \left|\frac{n^n (z-i)^n}{n}\right|^{1/n} = \lim_{n\to \infty} \frac{n \left|z-i\right|}{n^{1/n}} = \infty, \end{equation*} ya que $\lim\limits_{n\to\infty} n = \infty$ y $\lim\limits_{n\to\infty} n^{1/n} = 1$.
Entonces, por el criterio de la raíz, proposición 27.6, tenemos que la serie diverge para toda $z\neq z_0$. Por lo tanto, la primera serie de potencias converge solo para $z=z_0$.
Por otra parte, para la segunda serie de potencias es claro que la serie converge si $\zeta=0$. Mientras que para $\zeta \neq 0$ tenemos que: \begin{equation*} \lim_{n \to \infty} n! \zeta^n = \infty, \end{equation*} desde que $\lim\limits_{n\to\infty} n! = \infty$ y $|\zeta^n| \geq r >0$ para toda $n\in\mathbb{N}$, es decir, la sucesión $\{\zeta^n\}_{n\geq 0}$, con $\zeta\neq 0$, está separada de cero, proposición 8.2(5).
Por lo tanto, la segunda serie solo converge para $\zeta = 0$. - Consideremos a las series de potencias: \begin{equation*} \displaystyle \sum_{n=0}^\infty (-2)^n \frac{(z+2)^n}{n+1} \quad \text{y} \quad \displaystyle \sum_{n=0}^\infty \zeta^n. \end{equation*}Para la primera serie tenemos que $z_0 = -2$. Es claro que para $z=z_0$ la serie de potencias converge. Si $z\neq z_0$, tenemos: \begin{align*} \lambda = \lim_{n\to \infty} \dfrac{\left|(-2)^{n+1} \dfrac{(z+2)^{n+1}}{n+2}\right|}{\left|(-2)^n \dfrac{(z+2)^n}{n+1}\right|} & = \lim_{n\to \infty} \left|-2\right| \left|\dfrac{(n+1)(z+2)^{n+1}}{(n+2)(z+2)^{n}}\right|\\ & = \lim_{n\to \infty} \left(2\right) \left|z+2\right| \frac{n+1}{n+2}\\ & = 2 \left|z+2\right|. \end{align*}Entonces, por el criterio del cociente de D’Alembert, proposición 27.5, tenemos que la serie converge si $\lambda = 2 \left|z+2\right| < 1$, es decir, para todo $z\in\mathbb{C}$ tal que $\left|z+2\right| < 1/2$, mientras que la serie diverge si $\left|z+2\right| > 1/2$.
Por último, para la segunda serie de potencias, por el ejemplo 27.3 sabemos que la serie geométrica es convergente para todo $\zeta\in\mathbb{C}$ tal que $\left|\zeta\right|<1$ y divergente si $\left|\zeta\right|\geq 1$.
Observación 29.3.
Al trabajar con una serie de potencias, ya sea de la forma (29.1) ó (29.3), debemos ser cuidadosos al identificar los coeficientes de la serie, puesto que no siempre están dados de forma explícita y esto puede llegar a causar errores al manipular a las series de potencias y/o al deducir algo relacionado con su convergencia.
Una vez que estemos seguros de que los coeficientes de la serie corresponden con la regla explícita dada en la serie, podemos trabajar con dicha regla para obtener los coeficientes.
Ejemplo 29.2.
Identifiquemos los coeficientes de las siguientes series de potencias.
a) $\displaystyle \sum_{n=0}^\infty \frac{(-1)^n}{2^n} z^{2n}$.
b) $\displaystyle \sum_{n=1}^\infty \frac{z^n}{n}$.
c) $\displaystyle \sum_{n=1}^\infty \frac{(-1)^n z^{n-1}}{n(n+1)}$.
Solución. Es claro que las tres series están centradas en $z_0 = 0$. Procedemos a escribir a las series de potencias de acuerdo con la definición 29.1.
a) Tenemos que:
\begin{equation*}
\sum_{n=0}^\infty \frac{(-1)^n}{2^n} z^{2n} = \sum_{k=0}^\infty c_k z^{k},
\end{equation*} de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{(-1)^{n}}{2^n}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = 2n,\\
\\ 0, & \text{en otro caso.}\\
\end{array}
\right.
\end{equation*}
Por lo que:
\begin{equation*}
c_0 = 1, \quad c_1 = 0,\quad c_2 = -\frac{1}{2}, \quad c_3 = 0, \quad \ldots, \quad c_{2n} = \dfrac{(-1)^{n}}{2^n}, \quad c_{2n+1} = 0,
\end{equation*}
es decir:
\begin{equation*}
c_k = \left\{ \begin{array}{lcc}
\dfrac{(-1)^{n}}{2^n}, & \text{si} & k = 2n,\\
\\ 0, & \text{si} & k = 2n+1,\\
\end{array}
\right. \quad \text{con} \,\, n\in\mathbb{N}.
\end{equation*}
b) Tenemos que:
\begin{equation*}
\sum_{n=1}^\infty \frac{z^n}{n} = \sum_{k=0}^\infty c_k z^{k},
\end{equation*} de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{1}{n}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n,\\
\\ 0, & \text{en otro caso.}\\
\end{array}
\right.
\end{equation*}
Por lo que:
\begin{equation*}
c_0 = 0, \quad c_1 = 1,\quad c_2 = \frac{1}{2}, \quad c_3 = \frac{1}{3}, \quad \ldots, \quad c_{n} = \dfrac{1}{n},
\end{equation*}es decir:
\begin{equation*}
c_k = \left\{ \begin{array}{lcc}
\dfrac{1}{k}, & \text{si} & k \geq 1,\\
\\ 0, & \text{si} & k = 0.\\
\end{array}
\right.
\end{equation*}
c) Tenemos que:
\begin{equation*}
\sum_{n=1}^\infty \frac{(-1)^n z^{n-1}}{n(n+1)} = \sum_{k=0}^\infty c_k z^{k},
\end{equation*}de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{(-1)^{n}}{n(n+1)}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n-1,\\
\\ 0, & \text{en otro caso.}\\
\end{array}
\right.
\end{equation*}
Por lo que:
\begin{equation*}
c_0 = \dfrac{(-1)^{1}}{1(1+1)} = -\frac{1}{2}, \quad c_1 = \dfrac{(-1)^{2}}{2(2+1)} = \frac{1}{6},\quad c_2 = \dfrac{(-1)^{3}}{3(3+1)} = -\frac{1}{12}, \quad \ldots,
\end{equation*} es decir:
\begin{equation*}
c_k = \dfrac{(-1)^{k+1}}{(k+1)(k+2)}, \quad k\in\mathbb{N}.
\end{equation*}
Nuestra primera tarea es determinar bajo qué condiciones una serie de potencias converge, pues como vimos en el ejemplo 29.1, existen series de potencias que convergen en todo $\mathbb{C}$, en un sólo punto o en alguna región del plano complejo. Es claro que un ejemplo no es una prueba de este hecho, por lo que procedemos a verificarlo de manera formal.
Proposición 29.1. (Lema de Abel.)
Si la serie de potencias $\displaystyle \sum_{n=0}^\infty c_n z^n$ converge para algún $z=z_0 \neq 0$, entonces la serie converge absolutamente para todo $z\in\mathbb{C}$ tal que $|z| < |z_0|$.
Más aún, si la serie diverge para algún $z=z_1 \neq 0$, entonces la serie diverge para todo $z\in\mathbb{C}$ tal que $|z_1| < |z|$.
Demostración. Dadas las hipótesis, procedemos a verificar la primera parte de la proposición.
Si la serie $\displaystyle \sum_{n=0}^\infty c_n z_0^n$ converge, con $z_0 \neq 0$, entonces, por el corolario 27.1, se cumple que:
\begin{equation*}
\lim_{n\to\infty} c_n z_0^n = 0,
\end{equation*}
es decir, la sucesión $\{c_n z_0^n\}_{n\geq 0}$ converge a 0, por lo que, proposición 8.1, es una sucesión acotada. Entonces, existe $M>0$ tal que:
\begin{equation*}
|c_n| \, |z_0|^n = |c_n z_0^n| \leq M, \quad \forall n\in\mathbb{N}.
\end{equation*}
Como $z_0\neq 0$, tenemos que:
\begin{equation*}
|c_n| \leq \frac{M}{|z_0|^n}, \quad \forall n\in\mathbb{N},
\end{equation*}
de donde:
\begin{equation*}
|c_n z^n | \leq M \left|\frac{z}{z_0}\right|^n, \quad \forall n\in\mathbb{N}.
\end{equation*}
Si $|z|<|z_0|$, entonces la serie geométrica $\displaystyle \sum_{n=0}^\infty M \left|\frac{z}{z_0}\right|^n$ es convergente, por lo que, se sigue del criterio de comparación, proposición 27.4, que la serie $\displaystyle \sum_{n=0}^\infty c_n z^n$ es absolutamente convergente.
Por último, para la segunda parte procedemos por reducción al absurdo. Supongamos que $\displaystyle \sum_{n=0}^\infty c_n z_1^n$ diverge. Si $|z_1| < |z|$ y la serie $\displaystyle \sum_{n=0}^\infty c_n z^n$ converge, entonces de la primera parte se sigue que $\displaystyle \sum_{n=0}^\infty c_n z_1^n$ converge, lo cual claramente es una contradicción. Por lo tanto $\displaystyle \sum_{n=0}^\infty c_n z^n$ diverge si $|z|>|z_1|$.
$\blacksquare$
El lema de Abel es de suma importancia para poder establecer el siguiente resultado, el cual será un parteaguas para los resultados de esta entrada.
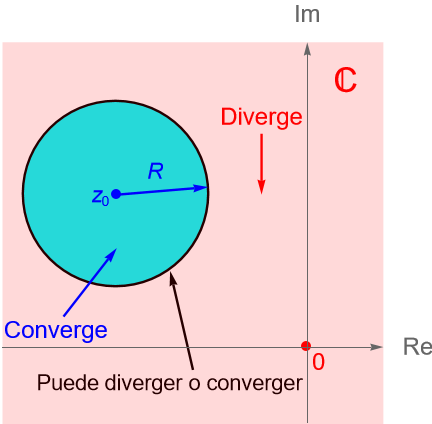
Proposición 29.2. (Radio de convergencia.)
Sea $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ una serie de potencias, entonces existe un número $R\in[0,\infty]$ tal que:
- la serie es absolutamente convergente si $|z-z_0| < R$;
- la serie converge absoluta y uniformemente en todo disco cerrado $\overline{B}(z_0, r)$, con $r$ fijo tal que $r<R$;
- si $|z-z_0| > R$ la serie diverge.
Demostración. Sea $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ una serie de potencias, definimos:
\begin{equation*}
S:= \left\{\rho \in [0, \infty) : \sum_{n=0}^\infty c_n \rho^n \,\, \text{converge}\right\}.
\end{equation*}
Notemos que $S \neq \emptyset$ desde que $0\in S$.
Afirmamos que el número $R$ que cumple lo anterior está dado por $ R:= \sup S$.
- De acuerdo con el enunciado de la proposición, debe ser claro que podemos tener dos casos extremos: si $R = 0$ ó si $R = \infty$, los cuales están dados por la definición de $R$ como sigue.
Si $S$ no es acotado superiormente, adoptamos la convención $R = \infty$. Veamos que en tal caso, la serie $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ converge absoluta y uniformemente en $\overline{B}(z_0, r)$, para cualquier $r\geq 0$.
Si elegimos a $\rho\in S$ tal que $|z-z_0| \leq r <\rho$, entonces la serie $\displaystyle \sum_{n=0}^\infty c_n \rho^n$ es convergente y de la proposición 27.4(1) tenemos que la serie $\displaystyle \sum_{n=0}^\infty c_n r^n$ es absolutamente convergente. Dado que: \begin{equation*}|c_n(z-z_0)^n| \leq |c_n r^n| = |c_n| r^n, \quad \forall n\in\mathbb{N}, \end{equation*} entonces del criterio $M$ de Weierstrass, proposición 28.3, se sigue que la serie $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ converge absoluta y uniformemente en $\overline{B}(z_0, r)$. Como $r$ es arbitario, entonces tenemos el caso $R=\infty$.
Supongamos que $S$ es acotado superiormente. Si $R=0$, entonces la serie solo converge si $z=z_0$, por lo que, lema de Abel, la serie converge absolutamente solo en el centro.
Si $R>0$ y $|z-z_0|<R$, entonces, por la definición de $R$, existe $r\in S$ tal que: \begin{equation*}|z-z_0| < r \leq R. \end{equation*}Dado que $r\in S$, entones la serie $\displaystyle \sum_{n=0}^\infty c_n r^n$ es convergente. Notemos que la serie $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ converge para $z = r+z_0$, por lo que, lema de Abel, la serie converge absolutamente para $|z-z_0| < r \leq R$, lo cual completa el caso $|z-z_0| < R$. - Sea $z \in \overline{B}(z_0, r)$, con $r$ fijo tal que $r<R$, entonces, por la definición de $R$, podemos elegir $\rho \in S$ tal que $r<\rho \leq R$. Como la serie $\displaystyle \sum_{n=0}^\infty c_n \rho^n$ converge, entonces, proposición 27.4(1), la serie $\displaystyle \sum_{n=0}^\infty |c_n| r^n$ converge, por lo que, criterio $M$ de Weierstrass, la serie $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ es absoluta y uniformemente convergente en $\overline{B}(z_0, r)$.
- Supongamos que $|z-z_0| > R$, entonces, por la definición de $R$, existe $r\not\in S$ tal que: \begin{equation*} R \leq r < |z-z_0|. \end{equation*} Como la serie $\displaystyle \sum_{n=0}^\infty c_n r^n$ diverge, entonces la serie $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ diverge para $z=z_0+r$, por lo que, por lema de Abel, la serie diverge para todo $z\in\mathbb{C}$ tal que $R \leq r < |z-z_0|$.
$\blacksquare$
Definición 29.2. (Radio de convergencia.)
Se llama radio de convergencia de la serie de potencias $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ al número $R$ dado en la proposición 29.2.
Al conjunto $B(z_0, R) = \{z\in\mathbb{C} : |z-z_0| < R\}$ se le llama su disco de convergencia asociado, figura 108. En algunos textos suele hablarse del círculo de convergencia de la serie, el cual se asocia al conjunto $\overline{B}(z_0, R) = \{z\in\mathbb{C} : |z-z_0| \leq R\}$, ya que geométricamente corresponde con el interior y la frontera de una circunferencia de radio $R$ centrada en $z_0$.
Observación 29.4.
Notemos que la proposición no nos dice nada sobre la convergencia o divergencia de la serie para el caso en que $R=|z-z_0|$. Como veremos en la proposición 29.3, no podemos afirmar nada sobre tal caso.
La proposición 29.2 nos da la prueba de la afirmación hecha en el ejemplo 29.1.
Corolario 29.1.
Sea $\displaystyle \sum_{n=0}^\infty c_n\left(z-z_0\right)^n$ una serie de potencias y sea $R$ su radio de convergencia. Entonces:
- Si $R=\infty$, la serie converge absolutamente para todo $z\in\mathbb{C}$.
- Si $R=0$, la serie converge solo para $z=z_0$.
- Si $0<R<\infty$, la serie converge solo para los $z\in\mathbb{C}$ tales que $|z-z_0|<R$ y diverge para $|z-z_0|>R$.
Demostración. Es inmediato de la proposición 29.2.
Ejemplo 29.3.
Analicemos la siguiente serie y determinemos su radio de convergencia.
\begin{equation*}
\sum_{n=0}^\infty \frac{(-1)^n}{2^n} z^{2n} = 1 – \frac{z^2}{2} + \frac{z^4}{2^2} – \frac{z^6}{2^3} + \ldots .
\end{equation*}
Solución. Por el ejemplo 29.2 sabemos que se trata de una serie de potencias con centro en $z_0 = 0$ y coeficientes:
\begin{equation*}
c_k = \left\{ \begin{array}{lcc}
\dfrac{(-1)^{n}}{2^n}, & \text{si} & k = 2n,\\
\\ 0, & \text{si} & k = 2n+1,\\
\end{array}
\right. \quad \text{con} \,\, n\in\mathbb{N}.
\end{equation*}
Notemos que si hacemos $w = \dfrac{-z^2}{2}$ entonces:
\begin{equation*}
\sum_{n=0}^\infty \frac{(-1)^n}{2^n} z^{2n} = \sum_{n=0}^\infty \left(\frac{-z^2}{2}\right)^n = \sum_{n=0}^\infty w^n.
\end{equation*}
Entonces, tenemos una serie geométrica convergente si $|w|<1$, es decir, si $|z^2| < 2$. En tal caso la serie converge a:
\begin{equation*}
\frac{1}{1-w} = \frac{2}{2-z^2}.
\end{equation*}
Para esta serie es claro que su radio de convergencia es $R = \sqrt{2}$.
En general, obtener el radio de convergencia de una serie de potencias no es una tarea fácil, el ejemplo anterior resultó sencillo pues conocemos bien a la serie geométrica, pero en general las series de potencias pueden resultar más complejas. Por ello, procedemos a establecer una serie de resultados que nos permitan determinar el radio de convergencia de una serie de potencias a través de la sucesión de números complejos $\{c_n\}_{n\geq 0}$, correspondiente con los coeficientes de la serie.
Primeramente, recordemos los siguientes conceptos y resultados estudiados y probados en nuestros cursos de Cálculo y/o Análisis.
Definición 29.3.
Sea $\{a_n\}_{n\geq0}\subset\mathbb{R}$ una sucesión de números reales acotada. Se define:
\begin{align*}
l_{0} = \sup \{ a_n : n\geq 0\} & = \sup \{a_0 , a_1,\ldots, a_n ,\ldots\},\\
l_{1} = \sup \{ a_n : n\geq 1\} &= \sup \{a_1 , a_2,\ldots, a_n ,\ldots\},\\
l_{2} = \sup \{ a_n : n\geq 2\} &= \sup \{a_2 , a_3,\ldots, a_n ,\ldots\},\\
& \,\,\, \vdots\\
l_{k} = \sup \{ a_n : n\geq k\} &= \sup \{ a_k , a_{k+1},\ldots, a_n ,\ldots\}.
\end{align*}
Es claro que:
\begin{equation*}
\{ a_n : n\geq k+1\} \subset \{ a_n : n\geq k\}, \quad \forall k\in\mathbb{N},
\end{equation*}
por lo que:
\begin{equation*}
l_{k+1} = \sup \{ a_n : n\geq k+1\} \leq l_{k} = \sup \{ a_n : n\geq k\},
\end{equation*}
es decir, la sucesión $\{ l_{k}\}_{k\geq0}$ es decreciente.
Dado que $\{a_n\}_{n\geq0}$ es acotada, entonces existe $M>0$ tal que $|a_n| \leq M$ para todo $n\in\mathbb{N}$, es decir:
\begin{equation*}
– M \leq a_n \leq M, \quad \forall n\in\mathbb{N},
\end{equation*}
de donde:
\begin{equation*}
– M \leq l_k \leq M, \quad \forall k\in\mathbb{N},
\end{equation*} es decir, la sucesión $\{ l_{k}\}_{k\geq0}$ también es acotada.
Por lo tanto, se sigue del teorema de la convergencia monótona para sucesiones, teorema 27.1, que la sucesión $\{ l_{k}\}_{k\geq0}$ converge.
Si la sucesión $\{a_n\}_{n\geq0}$ no es acotada superiormente, tenemos que $l_k = \infty$ para todo $k\in\mathbb{N}$, en tal caso se define:
\begin{equation*}
\lim_{k \to \infty} l_k = \infty. \tag{29.4}
\end{equation*}
Análogamente, se define a la sucesión:
\begin{equation*}
m_k = \inf \{a_n : n\geq k\}, \quad k\in\mathbb{N}.
\end{equation*}
Claramente $m_k \leq m_{k+1}$ para todo $k\in\mathbb{N}$ y $\{m_k\}_{k\geq 0}$ es acotada, entonces, teorema 27.1, la sucesión $\{m_k\}_{k\geq 0}$ converge.
Si la sucesión $\{a_n\}_{n\geq0}$ no es acotada inferiormente, tenemos que $m_k = -\infty$ para todo $k\in\mathbb{N}$, en tal caso se define:
\begin{equation*}
\lim_{k \to \infty} m_k = -\infty. \tag{29.5}
\end{equation*}
Definición 29.4. (Límite superior e inferior de una sucesión.)
Sea $\{a_n\}_{n\geq0}\subset\mathbb{R}$ una sucesión de números reales arbitraria. Considerando a las sucesiones $\{l_k\}_{k\geq 0}$ y $\{m_k\}_{k\geq 0}$, dadas como en la definición 29.3, se define el límite inferior y superior de $\{a_n\}_{n\geq0}$, respectivamente, como:
\begin{align*}
\lim_{k\to\infty} m_k & = \lim_{k\to\infty} \inf\{a_n : n\geq k\},\\
\lim_{k\to\infty} l_k & = \lim_{k\to\infty} \sup\{a_n : n\geq k\},
\end{align*}
a los cuales se denota, respectivamente, como:
\begin{align*}
\liminf_{n\to\infty} a_n = \lim_{k\to\infty} m_k,\\
\limsup_{n\to\infty} a_n = \lim_{k\to\infty} l_k.
\end{align*}
Observación 29.5.
Dado que una sucesión monótona (acotada) siempre tiene límite, entonces si permitimos que se cumplan (29.4) y (29.5), es claro que $ \lim\limits_{k\to\infty} m_k$ y $\lim\limits_{k\to\infty} l_k$ siempre existen y por tanto los límites inferior y superior de una sucesión arbitraria de números reales $\{a_n\}_{n\geq0}$ siempre existen.
Más aún, de acuerdo con las definiciones 29.3 y 29.4 es claro que se cumple:
\begin{align*}
m_0 &\leq m_1 \leq \cdots \leq m_k \leq \cdots,\\
\cdots &\leq l_k \leq \cdots \leq l_1 \leq l_0,
\end{align*} y $m_i \leq l_j$, por lo que:
\begin{equation*}
\liminf_{n\to\infty} a_n \leq \limsup_{n\to\infty} a_n.
\end{equation*}
Observación 29.6.
Dada una sucesión arbitraria de números reales $\{a_n\}_{n\geq0}$, de acuerdo con la definición 7.7 de la entrada 7, tenemos que $\liminf\limits_{n\to\infty} a_n$ y $\limsup\limits_{n\to\infty} a_n$ corresponden, respectivamente, con el menor y mayor punto de acumulación del conjunto $\{a_n : n\in\mathbb{N}\}$.
Es importante notar que $\liminf\limits_{n\to\infty} a_n$ y $\limsup\limits_{n\to\infty} a_n$ no son necesariamente, el valor más pequeño o más grande, respectivamente, del conjunto $\{a_n : n\in\mathbb{N}\}$.
Ejemplo 29.4.
a) Para la sucesión $\{(-1)^n\}_{n\geq 0} = \{1, -1, 1, -1, \ldots\}$ tenemos que:
\begin{equation*}
\sup\{(-1)^n : n\geq k\} = 1 \quad \text{e} \quad \inf\{(-1)^n : n\geq k\} = -1 \quad \forall k\in\mathbb{N},
\end{equation*}
por lo que:
\begin{equation*}
\liminf_{n\to\infty} (-1)^n = -1 \quad \text{y} \quad \limsup_{n\to\infty} (-1)^n = 1.
\end{equation*}
b) Para la sucesión $\{(-1)^n n\}_{n\geq 0} = \{0, -1, 2, -3, \ldots\}$ tenemos que:
\begin{equation*}
\sup\{(-1)^n n : n\geq k\} = \infty \quad \text{e} \quad \inf\{(-1)^n n : n\geq k\} = -\infty \quad \forall k\in\mathbb{N},
\end{equation*}
por lo que:
\begin{equation*}
\liminf_{n\to\infty} (-1)^n n = -\infty \quad \text{y} \quad \limsup_{n\to\infty} (-1)^n n = \infty.
\end{equation*}
c) Para la sucesión $\left\{\dfrac{1}{n}\right\}_{n\geq 1} = \left\{1, \dfrac{1}{2}, \dfrac{1}{3}, \ldots\right\}$ tenemos que:
\begin{equation*}
\sup\left\{\frac{1}{n} : n\geq k\right\} = \frac{1}{k} \quad \text{e} \quad \inf\left\{\frac{1}{n} : n\geq k\right\} = 0, \quad \forall k\in\mathbb{N},
\end{equation*}por lo que:\begin{equation*}
\liminf_{n\to\infty} \dfrac{1}{n} = 0 = \limsup_{n\to\infty} \dfrac{1}{n},
\end{equation*}
aún cuando cada término de la sucesión es más mayor que $0$.
Teorema 29.1.
Una sucesión de números reales $\{a_n\}_{n\geq 0} \subset\mathbb{R}$ converge si y solo si $ \liminf\limits_{n\to\infty} a_n$ y $ \limsup\limits_{n\to\infty} a_n$, existen, son finitos y son iguales. En tal caso:
\begin{equation*}
\liminf\limits_{n\to\infty} a_n = \limsup\limits_{n\to\infty} a_n = \lim\limits_{n\to\infty} a_n.
\end{equation*}
Teorema 29.2.
Una sucesión $\{a_n\}_{n\geq 0} \subset\mathbb{R}$ converge a $L\in\mathbb{R}$ si y solo si toda subsucesión de $\{a_n\}_{n\geq 0}$ converge a $L$.
Lema 29.1.
Una sucesión $\{a_n\}_{n\geq 0} \subset\mathbb{R}$ converge a $L\in\mathbb{R}$ si y solo si las subsucesiones $\{a_{2n}\}_{n\geq 0}$ y $\{a_{2n+1}\}_{n\geq 0}$ convergen ambas a $L$.
Demostración. Dadas las hipótesis.
$\Rightarrow)$ Si $\lim\limits_{n\to\infty} a_n = L$, entonces, por el teorema 29.2, ambas subsucesiones $\{a_{2n}\}_{n\geq 0}$ y $\{a_{2n+1}\}_{n\geq 0}$ convergen a $L$.
$(\Leftarrow$ Supongamos que ambas subsucesiones $\{a_{2n}\}_{n\geq 0}$ y $\{a_{2n+1}\}_{n\geq 0}$ convergen a $L$. Sea $\varepsilon>0$, entonces existen $N_1, N_2\in\mathbb{N}$ tales que:
\begin{align*}
\left|a_{2n} – L \right| & <\varepsilon, \quad \text{para todo} \,\,\, n\geq N_1,\\
\left|a_{2n+1} – L \right| & < \varepsilon, \quad \text{para todo} \,\,\, n\geq N_2.
\end{align*}
Sea $N=\max\{2N_1, 2N_2 +1 \}$. Para $n \geq N $, tenemos que $n \geq 2N_1$ y $n \geq 2N_2+1$.
Si $n = 2k$, para algún $k\in\mathbb{N}$, y $n \geq N$, entonces $k \geq N_1$, por lo que:
\begin{equation*}
|a_n – L| = |a_{2k} – L| < \varepsilon.
\end{equation*}
Análogamente, si $n = 2k+1$, para algún $k\in\mathbb{N}$, y $n \geq N$, entonces $k \geq N_2$, por lo que:
\begin{equation*}
|a_{n} – L| = |a_{2k+1} – L| < \varepsilon.
\end{equation*}
De ambos casos concluimos que, dado $\varepsilon>0$ existe $N\in\mathbb{N}$, tal que si $n\geq N$, entonces $ |a_{n} – L| < \varepsilon$.
$\blacksquare$
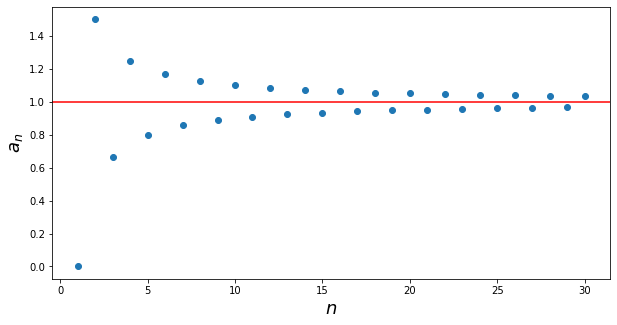
Ejemplo 29.5.
a) Para la sucesión $\left\{a_n\right\}_{n\geq 1}$, con $a_n = \dfrac{(-1)^n +n}{n}$, tenemos que:
\begin{equation*}
a_{2n} = \dfrac{(-1)^{2n} +2n}{2n} = 1 + \frac{1}{2n} \quad \Longrightarrow \quad \lim_{n\to\infty} a_{2n} = 1,
\end{equation*}
\begin{equation*}
a_{2n+1} = \dfrac{(-1)^{2n+1} +(2n+1)}{2n+1} = 1 – \frac{1}{2n+1} \quad \Longrightarrow \quad \lim_{n\to\infty} a_{2n+1} = 1,
\end{equation*}
por lo que, del lema 29.1 y el teorema 29.1 se sigue que:
\begin{equation*}
\lim_{n\to\infty} a_{n} = 1 = \limsup_{n\to\infty} a_{n} = \liminf_{n\to\infty} a_{n}.
\end{equation*}
Consideremos a la sucesión $\{b_n\}_{n\geq 1}$ dada por:
\begin{equation*}
b_n = \left\{ \begin{array}{lcc}
\dfrac{n}{n+1} & \text{si} & n=2k, \\
\\ \dfrac{1}{n+1} & \text{si} & n=2k+1,
\end{array}
\right. \quad k\in\mathbb{N}^{+}.
\end{equation*}
Tenemos que:
\begin{equation*}
\{b_n\}_{n\geq 1} = \left\{\frac{1}{2}, \frac{2}{3}, \frac{1}{4}, \frac{4}{5}, \frac{1}{6}, \ldots\right\}.
\end{equation*}
Notemos que para dicha sucesión, los puntos $1$ y $0$ son de acumulación del conjunto $\{b_n : n\in\mathbb{N}^{+}\}$, proposición 8.6, ya que existen las subsucesiones $\left\{b_{2k}\right\}_{k\geq 1}$ y $\left\{b_{2k+1}\right\}_{k\geq 1}$ de la sucesión original tales que $1\neq b_{2k}$ y $0\neq b_{2k+1}$ para todo $k\in\mathbb{N}^{+}$ y se cumple que:
\begin{equation*}
b_{2k} = \dfrac{2k}{2k+1} \quad \Longrightarrow \quad \lim_{k\to\infty} b_{2k} = 1,
\end{equation*}
\begin{equation*}
b_{2k+1} = \dfrac{1}{2k+1} \quad \Longrightarrow \quad \lim_{k\to\infty} b_{2k+1} = 0.
\end{equation*}
Más aún, es claro que la sucesión está acotada superiormente e inferiormente por $1$ y $0$, respectivamente, por lo que:
\begin{equation*}
\limsup_{n\to\infty} b_n = 1 \quad \text{y} \quad \liminf_{n\to\infty} b_n = 0.
\end{equation*}
De acuerdo con el teorema 29.1, tenemos que la sucesión no converge ya que estos límites son distintos.
Teorema 29.3.
Sea $\{a_n\}_{n\geq 1} \subset\mathbb{R}$ una sucesión de números reales positivos, entonces:
\begin{equation*}
\liminf_{n\to \infty} \frac{a_{n+1}}{a_{n}} \leq \liminf_{n\to \infty} a_{n}^{1/n} \leq \limsup_{n\to \infty} a_{n}^{1/n} \leq \limsup_{n\to \infty} \frac{a_{n+1}}{a_{n}}. \tag{29.6}
\end{equation*}
Corolario 29.2.
Si $\{a_n\}_{n\geq 1} \subset\mathbb{R}$ es una sucesión de números reales positivos tales que $\lim_{n\to \infty} \dfrac{a_{n+1}}{a_{n}}$ existe, entonces las cuatro cantidades dadas en (29.6) son iguales, por lo que:
\begin{equation*}
\lim_{n\to \infty} \frac{a_{n+1}}{a_{n}} = \lim_{n\to \infty} a_{n}^{1/n}.
\end{equation*}
Observación 29.7.
Puede suceder que la sucesión $\left\{\sqrt[n]{a_{n}}\right\}_{n\geq 1}$ sea convergente, pero que la sucesión $\left\{\dfrac{a_{n+1}}{a_n}\right\}_{n\geq 1}$ sea divergente.
Ejemplo 29.6.
Sea $\{a_n\}_{n\geq 1}$ dada por:
\begin{equation*}
a_{2n} = a_{2n-1} = \frac{1}{2^n}, \quad n\in\mathbb{N}^+,
\end{equation*}
es decir:
\begin{equation*}
\{a_n\}_{n\geq 1} = \left\{ \frac{1}{2}, \frac{1}{2}, \frac{1}{4}, \frac{1}{4}, \frac{1}{8}, \frac{1}{8}, \ldots , \frac{1}{2^n}, \frac{1}{2^n}, \ldots\right\}.
\end{equation*}
Tenemos que:
\begin{equation*}
\sqrt[2n]{a_{2n}} = \left(\frac{1}{2^n}\right)^{1/2n} = \frac{1}{\sqrt{2}} \quad \Longrightarrow \quad \lim_{n\to\infty} \sqrt[2n]{a_{2n}} = \frac{1}{\sqrt{2}},
\end{equation*}
\begin{equation*}
\sqrt[2n-1]{a_{2n-1}} = \left(\frac{1}{2^n}\right)^{\frac{1}{2n-1}} = \frac{1}{2^{\frac{n}{2n-1}}} \quad \Longrightarrow \quad \lim_{n\to\infty} \sqrt[2n-1]{a_{2n-1}} = \frac{1}{\sqrt{2}}.
\end{equation*}
Entonces, por el lema 29.1, tenemos que:
\begin{equation*}
\lim_{n\to\infty} a_n = \frac{1}{\sqrt{2}},
\end{equation*} es decir, la sucesión $\left\{\sqrt[n]{a_{n}}\right\}_{n\geq 1}$ converge.
Por otra parte, notemos que:
\begin{equation*}
\frac{a_{2n}}{a_{2n-1}} =\dfrac{\dfrac{1}{2^n}}{\dfrac{1}{2^n}} = 1 \quad \Longrightarrow \quad \lim_{n\to\infty} \frac{a_{2n}}{a_{2n-1}} = 1,
\end{equation*}
\begin{equation*}
\frac{a_{2n+1}}{a_{2n}} =\dfrac{\dfrac{1}{2^{n+1}}}{\dfrac{1}{2^n}} = \frac{1}{2} \quad \Longrightarrow \quad \lim_{n\to\infty} \frac{a_{2n+1}}{a_{2n}} = \frac{1}{2},
\end{equation*} por lo tanto, del lema 29.1 se sigue que $\left\{\dfrac{a_{n+1}}{a_n}\right\}_{n\geq 1}$ no converge.
Puede consultarse la prueba de estos resultados en alguno de los siguientes textos:
- Elementary Analysis: The Theory of Calculus de Kenneth A. Ross.
- An Introduction to Analysis de William R. Wade.
Una vez recordados estos resultados, procedemos a establecer el resultado esperado para poder determinar el radio de convergencia a través de la sucesión de números complejos dada por los coeficientes de una serie de potencias.
Proposición 29.3. (Fórmula de Cauchy-Hadamard para el radio de convergencia.)
Sea $\displaystyle \sum_{n=0}^\infty c_n\left(z-z_0\right)^n$ una serie de potencias y sea $\lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|}$. Definimos a $R\in[0,\infty]$ como el radio de convergencia de la serie dado por $R = 1/\lambda$, con la definición de $R = 0$ si $\lambda=\infty$ y $R = \infty$ si $\lambda=0$. Entonces:
- Si $R=\infty$, la serie converge absolutamente para todo $z\in \mathbb{C}$.
- Si $R=0$, la serie solo converge para $z=z_0$.
- Si $0<r<R<\infty$ entonces la serie es absolutamente convergente para $|z-z_0|< R$ y uniformemente convergente en $\overline{B}(z_0, r)$. La serie diverge si $|z-z_0|> R$ y no podemos afirmar nada para $|z-z_0|=R$.
Demostración. Dadas las hipótesis.
- Si $R=\infty$, entonces tenemos que $\lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|} = 0$. Notemos que para todo $z\in \mathbb{C}$ se cumple: \begin{equation*} \limsup\limits_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} = |z-z_0| \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|} = |z-z_0| \lambda = 0. \end{equation*} Dado que la sucesión $\left\{\sqrt[n]{|c_n(z-z_0)^n|}\right\}_{n\geq1}$ es una sucesión de números reales no negativos, entonces: \begin{equation*} 0\leq \liminf\limits_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} \leq \limsup\limits_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} = 0, \end{equation*} es decir: \begin{equation*} \liminf\limits_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} = 0. \end{equation*} Considerando lo anterior, por el teorema teorema 29.1, tenemos que: \begin{equation*} \lim_{n\to\infty} \sqrt[n]{|c_n(z-z_0)^n|} = 0 < 1, \end{equation*} por lo que, se sigue del criterio de la raíz, proposición 27.6, que la serie $\displaystyle \sum_{n=0}^\infty c_n\left(z-z_0\right)^n$ es absolutamente convergente para todo $z\in\mathbb{C}$.
- Si $R=0$, entonces tenemos que $\lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|} = \infty$. Es claro que para $z = z_0$ la serie converge: \begin{equation*} \sum_{n=0}^\infty c_n(z-z_0)^n = \sum_{n=0}^\infty c_n(z_0-z_0)^n = c_0. \end{equation*} Veamos que la serie no puede converger en ningún otro punto. Procedamos por contradicción, supongamos que la serie converge para $z=a\neq z_0$, entonces, corolario 27.1, se cumple que: \begin{equation*} \lim_{n\to\infty} c_n(a-z_0)^n = 0, \end{equation*} lo cual es equivalente, considerando el ejercicio 6 de la entrada 8, a que: \begin{equation*} \lim_{n\to\infty} \sqrt[n]{|c_n|}|a-z_0| = 0, \end{equation*} es decir, para todo $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*} \sqrt[n]{|c_n|}|a-z_0| = |\sqrt[n]{|c_n|}|a-z_0|| <\varepsilon, \end{equation*} por lo que: \begin{equation*} \sqrt[n]{|c_n|} < \frac{\varepsilon}{|a-z_0|}, \quad \forall n \geq N, \end{equation*} de donde, teorema 29.1:\begin{equation*} \lim_{n \to \infty} \sqrt[n]{|c_n|} = \limsup_{n \to \infty } \sqrt[n]{|c_n|}= \lambda < \infty, \end{equation*} lo cual contradice nuestro supuesto de que $\lambda = \infty$. Por lo que, la serie solo converge para $z=z_0$.
- Supongamos que $|z-z_0|< R$. De acuerdo con la definición 29.3: \begin{equation*} \lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|} = \lim_{k\to\infty} \sup\left\{\sqrt[n]{|c_n|} : n\geq k\right\}, \end{equation*} por lo que, de la definición del límite tenemos que para todo $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $k\geq N$, entonces:\begin{equation*} \left| \sup\left\{\sqrt[n]{|c_n|} : n\geq k\right\} – \lambda\right| <\varepsilon \quad \Longleftrightarrow \quad – \varepsilon + \lambda < \sup\left\{\sqrt[n]{|c_n|} : n\geq k\right\} <\varepsilon + \lambda, \end{equation*} de donde: \begin{equation*} -\varepsilon + \lambda < \sqrt[n]{|c_n|} < \varepsilon + \lambda, \quad \forall n\geq N. \end{equation*} Sea $\rho = \dfrac{|z-z_0| + R}{2}>0$, entonces $|z-z_0| < \rho < R$. Tenemos que: \begin{equation*} 0< \rho < R = \dfrac{1}{\lambda} \quad \Longrightarrow \quad \lambda < \frac{1}{\rho}, \end{equation*} por lo que, para $\varepsilon = \dfrac{1}{\rho} – \lambda >0$ existe $N\in\mathbb{N}$ tal que:
\begin{equation*} \sqrt[n]{|c_n|} < \frac{1}{\rho} – \lambda + \lambda, \quad \forall n\geq N, \end{equation*} es decir: \begin{equation*}|c_n| < \frac{1}{\rho^n}, \quad \forall n\geq N. \end{equation*} De lo anterior se sigue que: \begin{equation*}|c_n(z-z_0)^n| = |c_n| |z-z_0|^n < \left(\frac{|z-z_0|}{\rho}\right)^n, \quad \forall n\geq N. \end{equation*} Dado que $|z-z_0| < \rho$, entonces la serie geométrica: \begin{equation*} \sum_{n=0}^\infty \left(\frac{|z-z_0|}{\rho}\right)^n, \end{equation*} es convergente. Por tanto, del criterio de comparación, proposición 27.4, se sigue que la serie: \begin{equation*} \sum_{n=0}^\infty c_n(z-z_0)^n, \end{equation*} es absolutamente convergente para todo $z\in\mathbb{C}$ tal que $|z-z_0|< R$.
Supongamos que $0<r<R$. Sea $\rho = \dfrac{r+R}{2}>0$, entonces $r< \rho < R =\dfrac{1}{\lambda}$, por lo que $\lambda < \dfrac{1}{\rho}$. Entonces, para $\varepsilon = \dfrac{1}{\rho} – \lambda >0$ existe $N\in\mathbb{N}$ tal que:\begin{equation*}|c_n| < \frac{1}{\rho^n}, \quad \forall n\geq N. \end{equation*} Como $r < \rho$, tenemos que la serie geométrica es convergente:\begin{equation*} \sum_{n=0}^\infty \left(\frac{r}{\rho}\right)^n. \end{equation*} Si $|z-z_0| \leq r$, de lo anterior se sigue que:\begin{equation*}|c_n(z-z_0)^n| = |c_n| |z-z_0|^n \leq \left(\frac{r}{\rho}\right)^n, \quad \forall n\geq N, \end{equation*} por lo que, se sigue del criterio $M$ de Weierstrass, proposición 28.3, que la serie: \begin{equation*} \sum_{n=0}^\infty c_n(z-z_0)^n, \end{equation*} es absoluta y uniformemente convergente en $\overline{B}(z_0, r)$, para $0<r<R$.
Supongamos ahora que $|z-z_0|> R$. Sea $r=\dfrac{|z-z_0|+ R}{2}>0$ tal que $R< r < |z-z_0|$, de donde $\dfrac{1}{r}<\dfrac{1}{R} = \lambda$. Entonces, para $\varepsilon=\lambda – \dfrac{1}{r} >0$ existe $N\in\mathbb{N}$ tal que:\begin{equation*}\frac{1}{r} = -\varepsilon + \lambda < \sqrt[n]{|c_n|}, \quad \forall n\geq N, \end{equation*} de donde: \begin{equation*} \left(\frac{|z-z_0|}{r}\right)^n < |c_n| |z-z_0|^n = |c_n (z-z_0)^n|, \quad \forall n\geq N. \end{equation*} Como $0 < r < |z-z_0|$, entonces la serie geométrica:\begin{equation*} \sum_{n=0}^\infty \left(\frac{|z-z_0|}{r}\right)^n, \end{equation*} es divergente. Por el criterio de comparación, proposición 27.4, concluimos que la serie de potencias diverge.
Por último, consideremos a la serie de potencias: \begin{equation*}\sum_{n=1}^\infty \frac{z^n}{n}.\end{equation*} Es claro que dicha serie está centrada en $z_0 = 0$ y del ejemplo 29.2(b) tenemos que:\begin{equation*}c_n = \left\{ \begin{array}{lcc}\dfrac{1}{n}, & \text{si} & n \geq 1,\\ \\ 0, & \text{si} & n = 0.\\ \end{array} \right. \end{equation*} Dado que: \begin{equation*} \sup\left\{\sqrt[n]{|c_n|} : n\geq k\right\} = \left(\frac{1}{k}\right)^{1/k}, \quad \forall k \geq 1, \end{equation*} entonces:\begin{equation*} \lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|} = \lim\limits_{k\to\infty} \left(\frac{1}{k}\right)^{1/k} = 1.\end{equation*} Notemos que, para $z=1$ tenemos que $|z-z_0| = 1 = R = \dfrac{1}{\lambda}$ y en ese caso tenemos a la serie armónica: \begin{equation*} \sum_{n=1}^\infty \frac{1}{n}, \end{equation*} la cual diverge.
Mientras que, para $z=-1$ tenemos que $|z-z_0| = 1 = R = \dfrac{1}{\lambda}$ y la serie es convergente:\begin{equation*}\sum_{n=1}^\infty \frac{(-1)^n}{n}. \end{equation*} Por lo tanto, no podemos afirmar nada para el caso $|z-z_0|=R$.
$\blacksquare$
Considernado lo anterior, podemos dar de manera equivalente la siguiente:
Definición 29.5. (Radio de convergencia.)
Sea $\displaystyle \sum_{n=0}^\infty c_n\left(z-z_0\right)^n$ una serie de potencias y sea $\lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|c_n|}$. Entonces definimos a $R \in[0,\infty]$ como el radio de convergencia de la serie de potencias, dado por:
- $R = \infty$ si $\lambda = 0$.
- $R = 0$ si $\lambda = \infty$.
- $R = 1/\lambda$ si $0< \lambda < \infty$.
Definición 29.6. (Dominio de convergencia.)
Sea $\displaystyle \sum_{n=0}^\infty c_n\left(z-z_0\right)^n$ una serie de potencias. El conjunto de valores de $z\in\mathbb{C}$ para los cuales la serie de potencias converge es llamado su dominio de convergencia.
Ejemplo 29.7.
Determinemos el radio de convergencia de las siguientes series de potencias y veamos dónde la convergencia es uniforme.
a) $\displaystyle \sum_{n=0}^\infty c_n z^n = 1 + 4z + 5^2 z^2 + 4^3 z^3 + 5^4 z^4 + 4^5 z^5 + \cdots$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{(z-1+i)^n}{(2-i)^n}$.
c) $\displaystyle \sum_{n=1}^\infty z^{n^2}$.
Solución.
a) Tenemos que:
\begin{equation*}
c_0 = 1, \quad c_n = \left\{ \begin{array}{lcc}
5^n, & \text{si} & n = 2k,\\
\\ 4^n, & \text{si} & n = 2k+1,\\
\end{array}
\right. \quad \text{con} \,\, k\in\mathbb{N}^+,
\end{equation*}
por lo que:
\begin{equation*}
\sup\{|c_n|^{1/n} : n\geq k\} = 5, \quad \forall k\geq 1.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \limsup_{n\to\infty} |c_n|^{1/n} = \lim_{k\to\infty} \sup\{|c_n|^{1/n} : n\geq k\} = 5, \quad \Longrightarrow \quad R = \frac{1}{\lambda} = \frac{1}{5}.
\end{equation*}
De la proposición 29.3 se sigue que la serie converge uniformemente en todo disco cerrado $\overline{B}(0,r)$, con $r < R$.
b) Tenemos que:
\begin{equation*}
z_0 = 1-i, \quad c_0 = 1 \quad \text{y} \quad c_n = \frac{1}{(2-i)^n}, \quad \forall n\in\mathbb{N}^+,
\end{equation*}
por lo que:
\begin{equation*}
\sup\{|c_n|^{1/n} : n\geq k\} = \left(\frac{1}{|2-i|^{k}}\right)^{1/k} = \frac{1}{|2-i|} = \frac{1}{\sqrt{5}}, \quad \forall k \geq 1.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \limsup_{n\to\infty} |c_n|^{1/n} = \lim_{k\to\infty} \sup\{|c_n|^{1/n} : n\geq k\} = \frac{1}{\sqrt{5}}, \quad \Longrightarrow \quad R = \frac{1}{\lambda} = \sqrt{5}.
\end{equation*}
De la proposición 29.3 se sigue que la serie converge uniformemente en todo disco cerrado $\overline{B}(1-i,r)$, con $r < \sqrt{5}$.
c) Tenemos que:
\begin{equation*}
\sum_{n=0}^\infty z^{n^2} = \sum_{k=0}^\infty c_k z^{k},
\end{equation*}
de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
1, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n^2,\\
\\ 0, & \text{en otro caso,}\\
\end{array}
\right.
\end{equation*}
es decir:
\begin{equation*}
c_0 = 1, \quad c_1 = 1, \quad c_2 =0, \quad c_3 = 0, \quad c_4 = 1, \quad \ldots .
\end{equation*}
Considerando lo anterior es claro que la serie tiene un número infinitos de coeficientes que son $0$. Sin embargo, notemos que:
\begin{equation*}
\sup\{|c_n|^{1/n} : n\geq k\} = |1|^{1/k} = 1, \quad \forall k \geq 1.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \limsup_{n\to\infty} |c_n|^{1/n} = \lim_{k\to\infty} \sup\{|c_n|^{1/n} : n\geq k\} = 1, \quad \Longrightarrow \quad R = \frac{1}{\lambda} = 1.
\end{equation*}
De la proposición 29.3 se sigue que la serie converge uniformemente en todo disco cerrado $\overline{B}(0,r)$, con $r < 1$.
Corolario 29.3. (Determinación del radio de convergencia de una serie de potencias.)
El radio de convergencia $R\in[0,\infty]$, de una serie de potencias $\displaystyle\sum_{n=0}^\infty c_n\left(z-z_0\right)^{n}$ puede determinarse por alguno de los siguientes métodos.
- Criterio de D’Alembert del radio de convergencia. Si $\lambda = \lim\limits_{n\to\infty} \dfrac{|c_{n+1}|}{|c_n|}$ existe o es infinito, entonces:\begin{equation*} R = \frac{1}{\lambda}.\end{equation*}
- Criterio de la raiz de Cauchy. Si $\lambda = \lim\limits_{n\to\infty} |c_n|^{1/n}$ existe o es infinito, entonces:\begin{equation*} R = \frac{1}{\lambda}. \end{equation*}
En ambos casos consideramos la definición natural de $R=0$ si $\lambda =\infty$ y $R=\infty$ si $\lambda =0$.
Demostración. Los dos casos son una consecuencia de la proposición 29.3, de los teoremas 29.1 y 29.3 y del corolario 29.1, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Observación 29.8.
Es posible dar una formulación de los criterios de convergencia de D’Alembert y de la raíz, proposiciones 27.5 y 27.6 respectivamente, en términos del límite superior, es decir, considerando:
\begin{align*}
\lambda = \limsup\limits_{n\to\infty} \frac{|z_{n+1}|}{|z_{n}|},\\
\lambda = \limsup\limits_{n\to\infty} \sqrt[n]{|z_n|},
\end{align*} respectivamente, en cada caso. Esta formulación de dichos criterios es de gran utilidad cuando los límites $\lim\limits_{n\to\infty}\dfrac{|z_{n+1}|}{|z_{n}|}$, $\lim\limits_{n\to\infty}\sqrt[n]{|z_{n}|}$ no existen.
Ejemplo 29.8.
Veamos que la serie:
\begin{equation*}
\sum_{n=1}^\infty z_n, \quad \text{con} \,\,\, z_n = \frac{1}{2^n}\left[1+(-1)^n\right] + \frac{1}{3^n}\left[1-(-1)^n\right],
\end{equation*} converge.
Solución. Tenemos que:
\begin{equation*}
z_{2n} = \frac{2}{2^{2n}} \quad \text{y} \quad z_{2n+1} = \frac{2}{3^{2n+1}}.
\end{equation*}
Entonces, el límite $\lim\limits_{n\to\infty} \dfrac{|z_{n+1}|}{|z_{n}|} = \lim\limits_{n\to\infty} \dfrac{z_{n+1}}{z_{n}}$ no existe, lema 29.1, ya que las subsucesiones:
\begin{equation*}
\frac{z_{2n+2}}{z_{2n}} = \frac{z_{2n+2}}{z_{2n+1}} \frac{z_{2n+1}}{z_{2n}} \quad \text{y} \quad \frac{z_{2n+3}}{z_{2n+1}} = \frac{z_{2n+3}}{z_{2n+2}} \frac{z_{2n+2}}{z_{2n+1}},
\end{equation*}
tienen diferentes límites:
\begin{align*}
\lim_{n\to\infty} \dfrac{z_{2n+2}}{z_{2n}} = \lim_{n\to\infty} \dfrac{2(2^{-2(n+1)})}{2(2^{-2n})} = \dfrac{1}{4},\\
\lim_{n\to\infty} \frac{z_{2n+3}}{z_{2n+1}} = \lim_{n\to\infty} \frac{2(3^{-(2n+3)})}{2(3^{-(2n+1)})} = \frac{1}{9}.
\end{align*}
Sin embargo, notemos que:
\begin{equation*}
\limsup_{n\to \infty} \frac{|z_{n+1}|}{|z_{n}|} = \limsup_{n\to \infty} \frac{z_{n+1}}{z_{n}} = \frac{1}{4} < 1,
\end{equation*}
por lo que, de acuerdo con el criterio de D’Alembert, la serie converge.
Ejemplo 29.9.
Determinemos el radio de convergencia de las siguientes series de potencias.
a) $\displaystyle \sum_{n=1}^\infty \left(1+\dfrac{1}{n}\right)^{n^2} z^n$.
b) $\displaystyle \sum_{n=1}^\infty \dfrac{(n+1) z^n}{(n+2)(n+3)}$.
c) $\displaystyle \sum_{n=1}^\infty \left(a+ib\right)^{n} z^n$, con $a,b\in\mathbb{R}$ no ambos cero.
d) $\displaystyle \sum_{n=1}^\infty \left(\dfrac{n+2}{3n+1}\right)^{n} (z-4)^n$.
Solución. Para las cuatro series utilizaremos el corolario 29.3.
a) Tenemos que:
\begin{equation*}
\sum_{n=1}^\infty \left(1+\dfrac{1}{n}\right)^{n^2} z^n = \sum_{k=0}^\infty c_k z^{k},
\end{equation*}
de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\left(1+\dfrac{1}{n}\right)^{n^2}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n,\\
\\ 0, & \text{en otro caso,}\\
\end{array}
\right.
\end{equation*}
es decir:
\begin{equation*}
c_0 = 0 \quad \text{y} \quad c_n = \left(1+\dfrac{1}{n}\right)^{n^2}, \quad \forall n\geq 1.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \lim_{n\to\infty} |c_n|^{1/n} = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n = e, \quad \Longrightarrow \quad R = \frac{1}{\lambda} = \frac{1}{e}.
\end{equation*}
b) Tenemos que:
\begin{equation*}
c_n = \dfrac{n+1}{(n+2)(n+3)}, \quad \forall n\in\mathbb{N},
\end{equation*}
por lo que:
\begin{equation*}
c_{n+1} = \dfrac{n+2}{(n+3)(n+4)}.
\end{equation*}
Entonces:
\begin{align*}
\lambda = \lim_{n\to\infty} \frac{|c_{n+1}|}{|c_n|}
& = \lim_{n\to\infty} \frac{(n+2)^2(n+3)}{(n+1)(n+3)(n+4)}\\
& = \lim_{n\to\infty} \frac{n^2+4n+4}{n^2+5n+4}\\
& = 1,
\end{align*} de donde $R = 1/\lambda = 1$.
c) Tenemos que:
\begin{equation*}
c_n = \left(a+ib\right)^{n} \quad \forall n\in\mathbb{N},
\end{equation*} con $a,b\in\mathbb{R}$ no ambos cero, por lo que:
\begin{equation*}
c_{n+1} = \left(a+ib\right)^{n+1}.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \lim_{n\to\infty} \frac{|c_{n+1}|}{|c_n|} = \lim_{n\to\infty} \left| \frac{\left(a+ib\right)^{n+1}}{\left(a+ib\right)^{n}}\right| = \lim_{n\to\infty} |a+ib| = \sqrt{a^2 + b^2},
\end{equation*} de donde $R = 1/\lambda$.
d) Tenemos que:
\begin{equation*}
z_0 = 4, \quad c_0 = 1 \quad \text{y} \quad c_n = \left(\dfrac{n+2}{3n+1}\right)^{n} \quad \forall n\in\mathbb{N}^+.
\end{equation*}
Entonces:
\begin{equation*}
\lambda = \lim_{n\to\infty} \sqrt[n]{|c_n|} = \lim_{n\to\infty} \left(\left| \dfrac{n+2}{3n+1}\right|^n\right)^{1/n} = \lim_{n\to\infty} \dfrac{n+2}{3n+1} = \dfrac{1}{3},
\end{equation*} de donde $R = 1/\lambda = 3$.
Ejemplo 29.10.
Determinemos el dominio de convergencia de la siguiente serie de potencias e identifiquemos gráficamente a dicho conjunto en el plano complejo.
\begin{equation*}
\displaystyle\sum_{n=1}^\infty \frac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)}{n!}\left(\dfrac{1-z}{z}\right)^{n}.
\end{equation*}
Solución. Sea $w = \dfrac{1-z}{z}$, entonces:
\begin{equation*}
\sum_{n=1}^\infty \frac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)}{n!} w^{n} = \sum_{k=0}^\infty c_k w^k,
\end{equation*}
de donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)}{n!}, & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k = n,\\
\\ 0, & \text{en otro caso,}\\
\end{array}
\right.
\end{equation*}
es decir:
\begin{equation*}
c_0 = 0 \quad \text{y} \quad c_n = \dfrac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)}{n!} \quad \forall n\geq 1.
\end{equation*}
Tenemos que:
\begin{equation*}
c_{n+1} = \dfrac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)(2n+1)}{(n+1)!},
\end{equation*}
por lo que:
\begin{align*}
\lambda = \lim_{n\to\infty} \frac{|c_{n+1}|}{|c_n|} & = \lim_{n\to\infty} \left|\dfrac{\dfrac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)(2n+1)}{(n+1)!}}{\dfrac{1\cdot3\cdot5 \cdot \ldots \cdot (2n-1)}{n!}}\right|\\
& = \lim_{n\to\infty} \left|\dfrac{(2n+1)n!}{(n+1)!}\right|\\
& = \lim_{n\to\infty} \dfrac{2n+1}{n+1}\\
& = 2,
\end{align*} de donde $R = 1/\lambda = 1/2$.
Entonces, el dominio de convergencia de la serie está dado por la condición $|w|<1/2$, es decir:
\begin{align*}
\left|\frac{1-z}{z}\right| < \frac{1}{2} \quad & \Longrightarrow \quad 2 |1-z|< |z|,\\
& \Longrightarrow \quad 4 |1-z|^2< |z|^2,\\
& \Longrightarrow \quad 4 (1-z)\overline{(1-z)}< z \overline{z},\\
& \Longrightarrow \quad 4 -4\overline{z} – 4z + 3z \overline{z}< 0,\\
& \Longrightarrow \quad z \overline{z} -\frac{4}{3}\overline{z} – \frac{4}{3}z + \frac{4}{3}< 0 \tag{29.7}.
\end{align*}
De acuerdo con los resultados de la entrada 6, sabemos que la ecuación general de una circunfernecia en el plano complejo $\mathbb{C}$ es:
\begin{equation*}
z \overline{z} +a \overline{z} + \overline{a} z + b = 0,
\end{equation*} cuyo centro es el punto $-a$ y $r = \sqrt{|a|^2-b}$ su radio.
De (29.7) tenemos:
\begin{equation*}
z \overline{z} + \left(-\frac{4}{3}\right)\overline{z} + \left(-\frac{4}{3}\right) z + \frac{4}{3} = 0,
\end{equation*}
de donde:
\begin{equation*}
-a = \frac{4}{3}, \quad b= \frac{4}{3} \quad \text{y} \quad r = \sqrt{|a|^2-b} = \sqrt{\frac{4}{9}} = \frac{2}{3}.
\end{equation*}
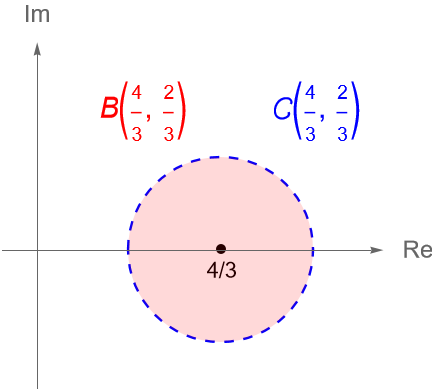
Por lo que, la expresión en (29.7) corresponde con el interior de la circunferencia $C\left(\dfrac{4}{3}, \dfrac{2}{3}\right)$, es decir, el disco abierto $B\left(\dfrac{4}{3}, \dfrac{2}{3}\right)$ es el dominio de convergencia de la serie de potencias, figura 109.
Tarea moral
- Muestra que el radio de convergencia de la serie de potencias: \begin{equation*} \sum_{n=0}^\infty \frac{(-1)^n}{n} z^{n(n+1)},\end{equation*} es 1 y analiza la convergencia para $z=1$, $z=-1$ y $z=i$.
Hint: Observa que el $(n+1)$-ésimo coeficiente de la serie no es $\dfrac{(-1)^n}{n}$. Procede como en el ejemplo 29.1. - Determina el dominio de convergencia de las siguientes series de potencias y gráficalo.
a) $\displaystyle \sum_{n=0}^\infty \left[\dfrac{(iz-1)}{3+4i}\right]^n$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{(z+2)^{n-1}}{(n+1)^3 4^n}$. - Muestra que el radio de convergencia de las siguientes series de potencias es infinito.
a) $\displaystyle \sum_{n=0}^\infty \dfrac{z^n}{n!}$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{(-1)^n z^{2n}}{(2n)!}$.
c) $\displaystyle \sum_{n=0}^\infty \dfrac{(-1)^n z^{2n+1}}{(2n+1)!}$. - Considera las tres series del ejemplo 29.2 y obtén su radio de convergencia, ¿en qué conjuntos la convergencia es uniforme?
- Prueba el corolario 29.3.
- Sean $\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ y $\displaystyle \sum_{n=0}^\infty d_n (z-z_0)^n$ dos series de potencias con radio de convergencia $R_1$ y $R_2$, respectivamente.
a) ¿Cuál es el radio de convergencia de la serie $\displaystyle \sum_{n=0}^\infty (c_n+d_n)(z-z_0)^n$?
b) ¿Cuál es el radio de convergencia de la serie $\displaystyle \sum_{n=0}^\infty (c_n \cdot d_n)(z-z_0)^n$? - Obtén el radio de convergencia de las siguientes series de potencias:
a) $\displaystyle \sum_{n=1}^\infty \dfrac{z^n}{n}$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{z^{4n}}{4n+1}$.
c) $\displaystyle \sum_{n=0}^\infty n^2\left(\dfrac{z^{2}+1}{1+i}\right)^n$.
d) $\displaystyle \sum_{n=0}^\infty \left(\dfrac{2i}{x+i+1}\right)^n$.
e) $\dfrac{1}{2} z + \dfrac{1 \cdot 3}{2\cdot5} z^2 + \dfrac{1 \cdot 3 \cdot 5}{2\cdot 5 \cdot 8} z^3 + \cdots$
f) $\displaystyle \sum_{n=1}^\infty (\operatorname{ln}(n))^n z^n$. - Si $\displaystyle \sum_{n=0}^\infty c_n z^n$ tiene radio de convergencia $R$, determina el radio de convergencia de las siguientes series de potencias:
a) $\displaystyle \sum_{n=0}^\infty c_n z^{2n}$.
b) $\displaystyle \sum_{n=0}^\infty c_n^2 z^{n}$.
c) $\displaystyle \sum_{n=0}^\infty n^d c_n z^{n}$, para cualquier $d\in\mathbb{N}^+$.
d) $\displaystyle \sum_{n=0}^\infty (-1)^n c_n z^{n}$.
Más adelante…
En esta entrada definimos de manera formal el concepto de serie de potencias y establecimos una serie de resultados relacionados con su convergencia. En particular, vimos que a través del concepto del radio de convergencia de una serie de potencias es posible establecer su dominio de convergencia, que geométricamente corresponde con discos abiertos, a los cuales comúnmente se les llama círculos de convergencia.
En la siguiente entrada estudiaremos algunas propiedades importantes de las series de potencias como la continuidad y analicidad de las mismas, propiedades que nos serán de utilidad en el estudio de las funciones complejas, pues como veremos, toda función compleja que es analítica en un dominio $D\subset\mathbb{C}$ puede tener un desarrollo en series de potencias en todo disco abierto completamente contenido en $D$.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Sucesiones y series de funciones.
- Siguiente entrada del curso: Series de potencias y funciones.