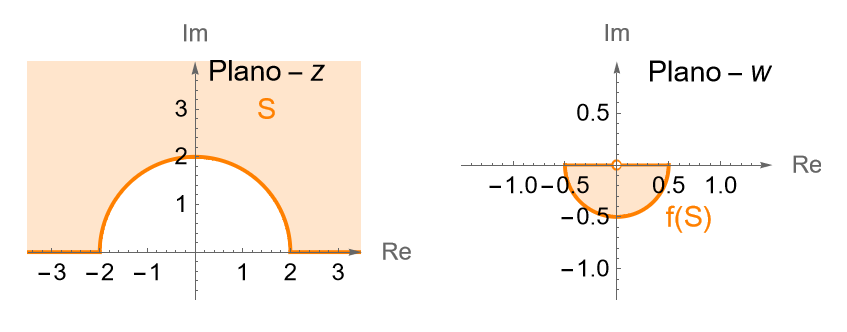Archivo de la etiqueta: rotaciones

Variable Compleja I: Funciones complejas como transformaciones. Técnicas de graficación

Por Pedro Rivera Herrera

Introducción

Sabemos que la gráfica de una función de $\mathbb{R}^2$ a $\mathbb{R}^2$ es un subconjunto de $\mathbb{R}^4$, por lo que si quisiéramos visualizar la gráfica de una función compleja de variable compleja, como hacíamos usualmente con funciones cuyas gráficas tenían lugar en $\mathbb{R}^2$ o en $\mathbb{R}^3$, nos será imposible.

Al trabajar en Cálculo con integrales dobles era de nuestro interés saber cómo se transformaban ciertas regiones $A\subset\mathbb{R}^2$ del plano, bajo ciertas transformaciones $T:\mathbb{R}^2 \to \mathbb{R}^2$ para poder entender de manera geométrica lo que sucedía al aplicar un cambio de variable con nuestras regiones de integración.

Una primera alternativa para poder estudiar la geometría de las funciones complejas, es analizar su comportamiento gráfico siguiendo esta idea de las transformaciones entre planos. Por lo que, resultará conveniente considerar a las funciones complejas como transformaciones del plano complejo, es decir, para darnos una idea de lo que hacen estas funciones las veremos como mapeos o transformaciones de un subconjunto de $\mathbb{C}$ en un plano $z$, que toman valores en un plano $w$. Si escribimos a $z=x+iy\in\mathbb{C}$ y a $w=u+iv\in\mathbb{C}$, tendremos al plano $z$ asociado con los ejes $x$ y $y$, mientras que para el plano $w$ se tienen los ejes $u$ y $v$, los cuales, en ambos casos, corresponden con los ejes real e imaginario, respectivamente.

Observación 26.1.
Debemos tener presente que esta alternativa no es la única forma para dar una interpretación del comportamiento geométrico de una función compleja, ya que también puede representarse a las funciones complejas mediante:

las gráficas de su parte real e imaginaria,
las gráficas del módulo complejo de la función,
superficies de Riemann.

Se puede consultar un poco sobre estás técnicas en las siguientes ligas:

Sin embargo, para los fines del curso bastará con esta alternativa de pensar a las funciones como transformaciones del plano en el plano.

Para plantear lo anterior consideremos la siguiente:

Definición 26.1.
Sea $S\subset\mathbb{C}$, se define a la imagen de $S$ bajo una función $f$, denotada por $f(S)$, como el conjunto:
\begin{equation*}
f(S) = \left\{ w\in\mathbb{C} \,:\, w = f(z),\, z\in S\right\}.
\end{equation*}

Analicemos los siguientes ejemplos para comprender mejor esta idea de las transformaciones complejas.

Ejemplo 26.1.
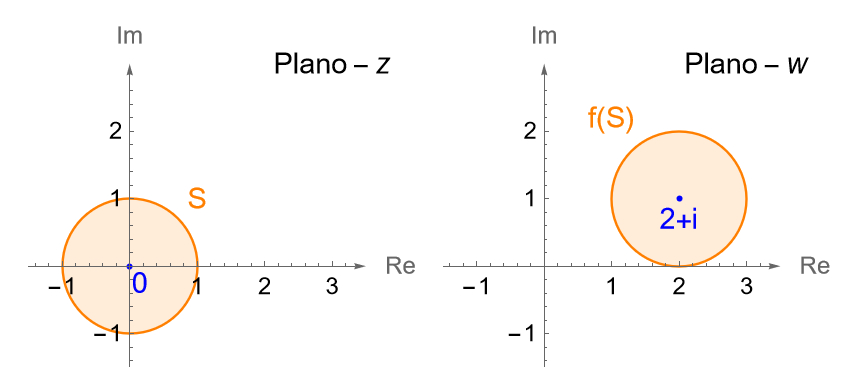
Sea $S$ el disco unitario, es decir $S=\overline{B}(0,1)$. Determinemos la imagen de $S$ bajo la transformación $f(z) = z+2+i$.

Solución. Notemos que para cada $z\in S$ el valor de $w=f(z)$ está dado por la suma de $2+i$ al valor de $z$. Considerando a $z=x+iy$, tenemos que:
\begin{equation*}
w = f(z) = (x+2) + i(y+1),
\end{equation*}
por lo que la función $f$ transforma los puntos $(x,y)$ en los puntos $(u,v)$, donde $u=x+2$ y $v=y+1$. Es claro que $f$ simplemente traslada a cada elemento del disco unitario $S$ dos unidades a la derecha y una unidad hacia arriba, figura 98, es decir:
\begin{align*}
f(S) & = \{ w\in\mathbb{C} \,:\, |\,w-(2+i)\,|\leq 1 \}\\
& = \overline{B}(2+i,1).
\end{align*}

Figura 98: Gráfica del conjunto $S$ en el plano $z$ y del conjunto $f(S)$ en el plano $w$.

Esta transformación de la forma $f(z)=z+b$, con $b\in\mathbb{C}$ constante, nos determina una traslación. Consideremos ahora transformaciones de la forma $f(z) = az$, con $a\in\mathbb{C}\setminus\{0\}$. Veamos que dichas transformaciones nos determinan rotaciones y homotecias en el plano complejo.

Observación 26.2.
Recordemos que al multiplicar a los números complejos $a=\rho\operatorname{cis}(\alpha)\neq 0$ y $z = r \operatorname{cis}(\theta)$ tenemos:
\begin{equation*}
az = r\rho \operatorname{cis}(\alpha + \theta) = r \rho e^{i(\alpha + \theta)},
\end{equation*} de donde es claro que la transformación $f(z) = az$ nos devuelve una homotecia desde que al módulo de $z$ se le multiplica por una constante $\rho>0$. Por otra parte, notemos que tenemos una rotación del número complejo $z$ desde que a su argumento $\theta$ se le suma el argumento $\alpha$. Además, dado que el producto de números complejos es conmutativo, es claro que la homotecia y rotación que se le aplica a cada número complejo $z$ se puede realizar en cualquier orden. Notemos que tenemos los siguientes casos:

Si $a = \rho >0$, entonces tenemos que la transformación $f(z) = az$ es simplemente una homotecia por un factor $a$.
Si $\rho = 1$, entonces tenemos que la transformación $f(z) = az = e^{i\alpha} z$ es simplemente una rotación por un ángulo $\alpha$.
Si $\rho>0$, entonces tenemos que la transformación $f(z) = az = \rho e^{i\alpha} z$ es una homotecia por un factor $\rho$ seguida de una rotación por un ángulo $\alpha$.

Ejemplo 26.2.
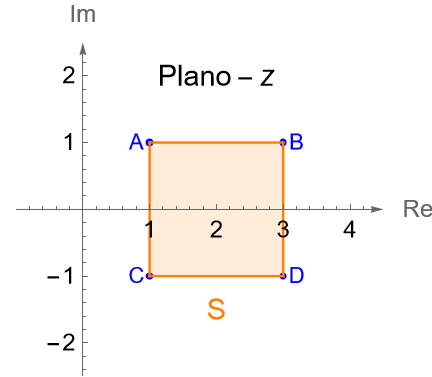
Sea $S$ el cuadrado cerrado con centro en el punto $z=2$, cuyos lados son paralelos a los ejes real e imaginario y tienen una longitud $2$, figura 99.

a) ¿Cuál es la imagen de $S$ bajo la transformación $f(z)=3z$?
b) ¿Cuál es la imagen de $S$ bajo la transformación $f(z)=2iz$?

Figura 99: Gráfica del conjunto $S$ en el plano $z$.Gráfica del conjunto $S$ en el plano $z$.

Solución.

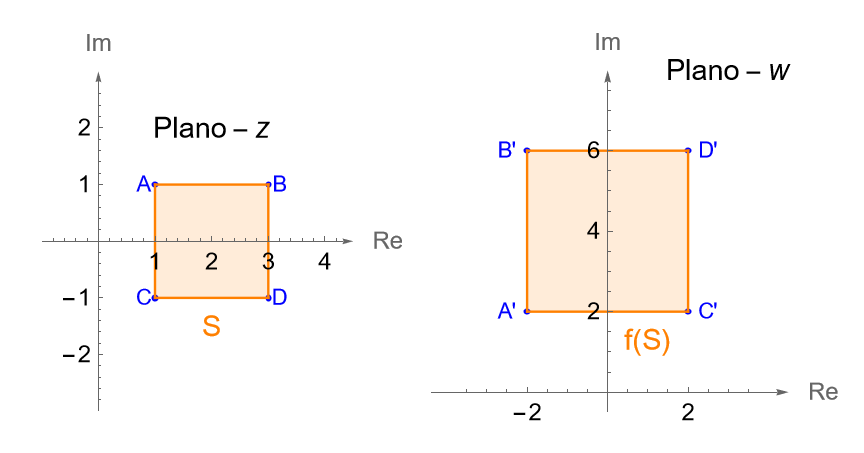
a) De acuerdo con la observación 26.2 tenemos que $a=3>0$ es una constante, por lo que la transformación $f(z)=3z$ corresponde con una homotecia, ya que bajo $f$ la distancia de cada número complejo $w=f(z)$, medida desde el origen, será tres veces la distancia de cada $z\in S$, medida desde el origen, es decir, el módulo de cada número complejo $z\in S$ será triplicado, mientras que su argumento permanecerá sin cambios. Entonces la imagen de $S$ bajo la transformación $f$, es decir, $f(S)$ será otro cuadrado cuyos vértices corresponden con las imágenes de los vértices del cuadrado $S$, figura 100.

Entonces $f(S)$ en el plano $w$ es el cuadrado cerrado con centro en el punto $w=6$ cuyos lados son paralelos a los ejes real e imaginario y tienen longitud 6.

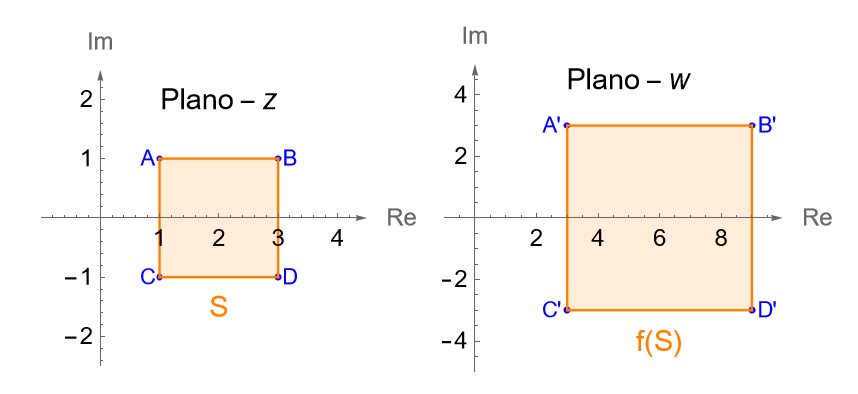
Figura 100: Gráfica del conjunto $S$ en el plano $z$ y del conjunto $f(S)$ en el plano $w$.

b) Considerando la observación 26.2, tenemos que $a=2i$ es un número complejo cuyo módulo es $r=2$ y su argumento principal es $\alpha = \frac{\pi}{2}$, por lo que la transformación $f(z)=2iz$ corresponde con una homotecia por un factor $r=2$ seguida de una rotación por un ángulo $\alpha=\frac{\pi}{2}$, en sentido contrario a las manecillas del reloj. Entonces, bajo $f$ a cada punto $z\in S$ se le duplicará su módulo y se le sumará $\frac{\pi}{2}$ a su argumento, entonces $f(S)$ será nuevamente un cuadrado cerrado para el cual la distancia del origen a cada $w=f(z)$ será dos veces la distancia del origen a cada $z\in S$ y sus vértices serán las imágenes de los vértices del cuadrado $S$ bajo $f$, figura 101.

Tenemos que el centro del cuadrado $S$ es $z=2$, mientras que sus vértices son $A=1+i$, $B=3+i$, $C=1-i$ y $D=3-i$, por lo que el centro y los vértices del nuevo cuadrado cerrado son:
\begin{align*}
f(2) = 2(2)\operatorname{cis}\left(\frac{\pi}{2} + 0\right) = 4i,\\
f(A) = 2\sqrt{2}\operatorname{cis}\left(\frac{\pi}{2} + \frac{\pi}{4}\right) = -2+2i,\\
f(B) = 2\sqrt{10}\operatorname{cis}\left(\frac{\pi}{2} + \operatorname{arc tan}\left(\frac{1}{3}\right)\right) = -2+6i,\\
f(C) = 2\sqrt{2}\operatorname{cis}\left(\frac{\pi}{2} – \frac{\pi}{4}\right) = 2+2i,\\
f(D) = 2\sqrt{10}\operatorname{cis}\left(\frac{\pi}{2} + \operatorname{arc tan}\left(\frac{-1}{3}\right)\right) = 2+6i.
\end{align*}

Entonces $f(S)$ en el plano $w$ es el cuadrado cerrado con centro en el punto $w=4i$ cuyos lados son paralelos a los ejes real e imaginario y tienen longitud 4.

Figura 101: Gráfica del conjunto $S$ en el plano $z$ y del conjunto $f(S)$ en el plano $w$.

Es posible visualizar las transformaciones de los ejemplos 26.1 y 26.2 en el siguiente applet de GeoGebra https://www.geogebra.org/m/pasmamyw.

Observación 26.3.
En conjunto, los ejemplos 26.1 y 26.2 corresponden con transformaciones del tipo $f(z) = az + b$, donde $a,b\in\mathbb{C}$ son dos constantes, y $a\neq 0$ para no trabajar con transformaciones constantes, es decir, transformaciones afines lineales, definición 25.1.

Más aún, de acuerdo con dichos ejemplos, debe ser claro que las transformaciones afines lineales mapean regiones del plano a regiones geométricamente similares. En el caso en que $a=1$ y $b=0$, entonces tenemos a la transformación identidad $\mathbb{I}_\mathbb{C}(z)=z$.

Una pregunta interesante es ¿qué sucede con las transformaciones que no son lineales?, es decir ¿en qué se transforman los subconjuntos de $\mathbb{\mathbb{C}}$ bajo una transformación no lineal? Para responder a esta pregunta analicemos los siguientes ejemplos.

Ejemplo 26.3.
Determinemos la imagen de los siguientes conjuntos bajo la transformación inversión, $f(z) = \dfrac{1}{z}$, con $z\neq 0$, $w=f(z)\neq 0$.

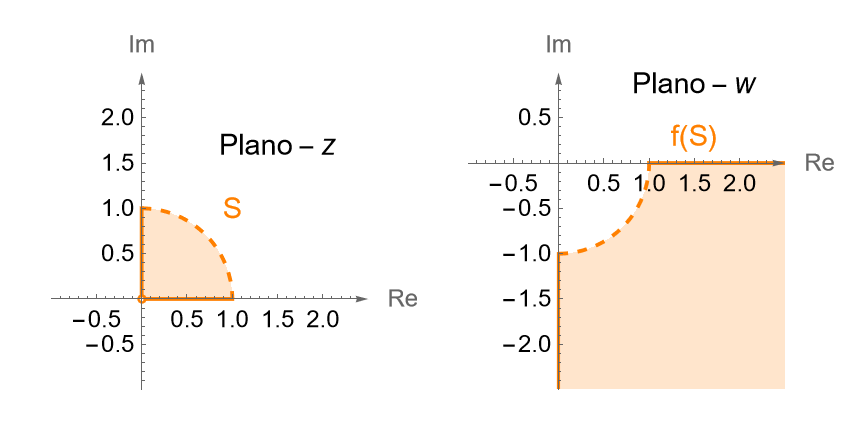
a) $S = \left\{z\in\mathbb{C} \,:\, 0<|\,z\,|<1, 0\leq \operatorname{arg} z \leq \dfrac{\pi}{2}\right\}.$
b) $S = \left\{z\in\mathbb{C} \,:\, 2\leq |\,z\,|, 0\leq \operatorname{arg} z \leq \pi\right\}.$

Solución. De acuerdo con el corolario 4.1 (fórmula de De Moivre), para $z = r\operatorname{cis}(\theta)\neq 0$, con $r=|\,z\,|$ y $\theta = \operatorname{arg} z$, tenemos que:
\begin{equation*}
f(z) = \frac{1}{z} = r^{-1}\operatorname{cis}(\theta) = \frac{1}{r}\left[\operatorname{cos}(-\theta) + i\,\operatorname{sen}(-\theta) \right].
\end{equation*}

Entonces, para cada $z\neq 0$, se tiene que el módulo de $f(z)$ es el recíproco del módulo de $z$, mientras que el argumento de $f(z)$ será el negativo del argumento de $z$.

a) Notemos que si $z\in S$, entonces $z$ cae en el primer cuadrante dentro de la circunferencia unitaria, incluyendo a los ejes real e imaginario, pero sin considerar a $z=0$, figura 102, ya que:

Si $0<|z|<1$, entonces $z$ cae dentro del disco unitario perforado, es decir $z\in B^*(0,1)$.
Si $0\leq \theta \leq \dfrac{\pi}{2}$, entonces tenemos a los $z$ en el primer cuadrante.

Por lo que bajo $f$, los $z\in S$ serán mapeados, en el plano $w$, fuera del disco unitario y en el cuarto cuadrante, incluyendo a los ejes real e imaginario, pero a partir de los $w$ tales que $|w|>1$, ya que $|\,f(z)\,| = \dfrac{1}{|\,z\,|} > 1$ y $-\frac{\pi}{2}\leq -\theta \leq 0$. Entonces:
\begin{equation*}
f(S) = \left\{ w\in\mathbb{C} \, : \, 1<|\,w\,|, -\frac{\pi}{2}\leq \operatorname{arg} w \leq 0 \right\}.
\end{equation*}

b) Notemos que si $z\in S$, entonces $z$ cae en el primer y segundo cuadrante fuera del disco de radio 2 con centro en el origen, incluyendo a la circunferencia de radio $2$ y a los ejes real e imaginario, figura 103, ya que:

Si $|z|\geq 2$, entonces $z$ cae sobre la circunferencia de radio $2$ y fuera de la misma.
Si $0\leq \theta \leq \pi$, entonces tenemos a los $z$ en el primer y segundo cuadrante.

Como el módulo de $z$ crece de $2$ a infinito, entonces bajo $f$ el módulo de $w=f(z)$ decrece de $\dfrac{1}{2}$ a $0$, pero sin llegar a valer $0$, ya que $|\,f(z)\,| = \dfrac{1}{|\,z\,|} \leq \dfrac{1}{2}$ y $|\,f(z)\,| >0$ para $z\neq 0$. Por otra parte, como $-\pi \leq – \theta \leq 0$, entonces bajo $f$ los $z$ serán mapeados, en el plano w, en el tercer y cuarto cuadrante en el disco cerrado con centro en el origen y radio $\dfrac{1}{2}$, por lo que:
\begin{equation*}
f(S) = \left\{ w\in\mathbb{C} \, : \, 0<|\,w\,| \leq \frac{1}{2}, -\pi\leq \operatorname{arg} w \leq 0 \right\}.
\end{equation*}

Figura 102: Gráfica del conjunto $S$ en el plano $z$ y del conjunto $f(S)$ en el plano $w$.

Figura 103: Gráfica del conjunto $S$ en el plano $z$ y del conjunto $f(S)$ en el plano $w$.

Ejemplo 26.4.
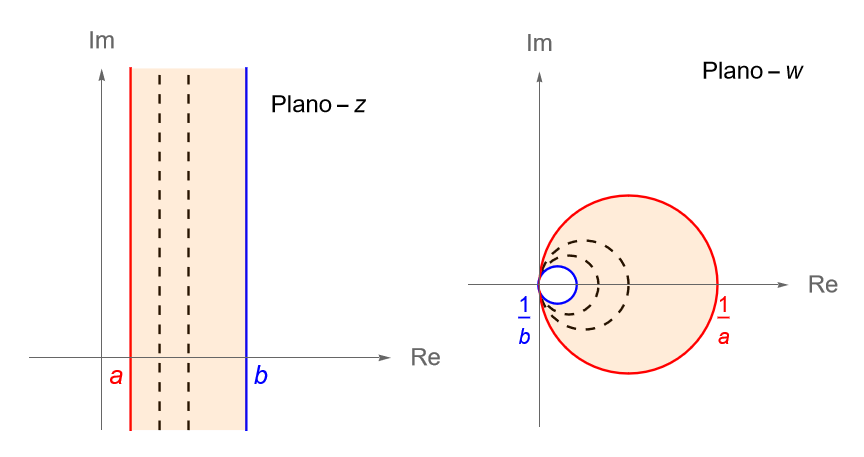
Sean $a,b\in\mathbb{R}$ tales que $0<a<b$. Veamos cuál es la imagen de los siguientes conjuntos bajo la transformación inversión, $T(z)=\dfrac{1}{z}$.
a) La recta vertical $x = x_0 > 0$ en el plano $z$, es decir $S = \left\{z=x+iy\in\mathbb{C} \,:\, x=x_0>0, y\in\mathbb{R}\right\}$.
b) La franja vertical $S = \left\{z=x+iy\in\mathbb{C} \,:\, a\leq x \leq b, y\in\mathbb{R}\right\}$, en el plano $z$.
\end{itemize}

Solución.

a) De acuerdo con la observación 25.8 como la recta vertical $x=x_0>0$ no pasa por el origen, entonces la imagen de $S$ bajo $T$ será una circunferencia que pase por el origen en el plano $w$.

Sea $z=x+iy \in S$, entonces tenemos $x = x_0 > 0$ y $y\in\mathbb{R}$. La imagen de $z$ bajo $T$ esta dada por:
\begin{equation*}
w = u+iv = \frac{1}{z}.
\end{equation*}

De acuerdo con (25.7), proposición 25.6, tenemos que:
\begin{equation*}
u=\frac{x_0}{x_0^2+y^2}, \quad v = -\frac{y}{x_0^2+y^2},
\end{equation*}de donde:
\begin{equation*}
u^2 +v^2 = \frac{x_0^2 +y^2}{\left(x_0^2+y^2\right)^2} = \frac{1}{x_0^2+y^2} = \frac{u}{x_0},
\end{equation*}por lo que:
\begin{align*}
&u^2 -\frac{u}{x_0} + v^2 = 0,\\
& \Longleftrightarrow u^2 -\frac{u}{x_0} + \left(-\frac{1}{2x_0}\right)^2 + v^2 = \left(-\frac{1}{2x_0}\right)^2,\\
& \Longleftrightarrow \left( u -\frac{1}{2x_0}\right)^2 + v^2 = \left(\frac{1}{2x_0}\right)^2, \tag{26.1}
\end{align*}la cual corresponde con la ecuación de una circunferencia con centro en el punto $w_0 = \dfrac{1}{2x_0} + i0$ y radio $r=\dfrac{1}{2x_0}$, en el plano $w$. Además, notemos que mientras el punto $z=0$ no cae en la recta $S$, el punto $w=0$ sí pertenece a $T(S)$.

b) Considerando el inciso anterior y la observación 25.8, si $0<a<x_0<b$, entonces la recta vertical $x=x_0$ recorre la franja vertical $S$ en el plano $z$, por lo que la imagen de cada recta vertical $x=x_0$ bajo la transformación inversión corresponderá con una circunferencia dada por (26.1), en el plano $w$. De acuerdo con la figura 104 tenemos que $T(S)$ es la región anular acotada por fuera por la circunferencia centrada en $\left(\dfrac{1}{2a}, 0\right)$ de radio $\dfrac{1}{2a}$ y por dentro por la circunferencia centrada en $\left(\dfrac{1}{2b}, 0\right)$ de radio $\dfrac{1}{2b}$.

Figura 104: Gráfica de la franja vertical $S$ bajo la transformación inversión.

Ejemplo 26.5.
Determinemos la imagen de la recta vertical $x=k$, donde $k\in\mathbb{C}$ es una constante, bajo la transformación $f(z)=z^2$.

Solución. Sean $z=x+iy\in\mathbb{C}$ y $w=u+iv = f(z)$, entonces:
\begin{equation*}
u(x,y)=x^2-y^2, \quad v(x,y)=2xy.
\end{equation*}

Dado que $x=k$, entonces los puntos sobre dicha recta vertical son de la forma:
\begin{equation*}
z=k+iy, \quad y\in\mathbb{R},
\end{equation*}por lo que, la imagen de dicha recta, bajo $f$, es:
\begin{equation*}
u=k^2-y^2, \quad v=2ky, \quad y\in\mathbb{R} \tag{26.2}.
\end{equation*}

Si $k=0$, entonces la imagen de la recta vertical $x=0$, correspondiente con el eje imaginario, está dada por:
\begin{equation*}
u=-y^2, \quad v=0, \quad y\in\mathbb{R}.
\end{equation*}

Es decir, la imagen del eje imaginario, bajo la función $f(z)=z^2$, corresponde con el semieje real negativo.

Por otra parte, si $k\neq 0$, entonces de (26.2) tenemos que:
\begin{equation*}
y = \frac{v}{2k} \quad \Longrightarrow \quad u = k^2 – \frac{v^2}{4k^2}, \quad \Longrightarrow \quad v^2 = -4k^2(u – k^2), \quad v\in\mathbb{R}.
\end{equation*}

Por lo que, para $k\neq0$, la imagen de la recta $x=k$ corresponde con la familia de parábolas con eje paralelo al eje real $u$, con vértice en el punto $\left(k^2,0\right)$, las cuales abren hacia la izquierda y cuya intersección con el eje imaginario $v$ son los puntos $\left(0, \pm 2k^2\right)$. Dado que la imagen de las rectas $x=k$ y $x=-k$ es la misma, entonces ambas rectas, bajo $f$, son mapeadas en la parábola $v^2 = -4k^2(u – k^2)$.

Podemos visualizar lo anterior en el siguiente applet de GeoGebra https://www.geogebra.org/m/y75hxksq.

Observación 26.4.
De manera general, se puede hacer un análisis para la transformación $f(z)=z^n$, con $n>2$. Si consideramos a $z\neq 0$ tal que $z=re^{i\theta}$ y $w=\rho e^{i\phi}$, entonces:
\begin{equation*}
w=f(z) \quad \rho e^{i\phi} = r^n e^{in\theta}.
\end{equation*}

No es difícil verificar que dicha transformación mapea la región:
\begin{equation*}
\left\{z=re^{i\theta}\in\mathbb{C}\setminus\{0\} : r\geq 0, \, 0\leq \theta \leq \frac{\pi}{n}\right\},
\end{equation*}en el semiplano superior del plano $w$.

Ejemplo 26.6.
Consideremos a la región rectangular:
\begin{equation*}
S=\left\{z=x+iy\in\mathbb{C} : -1\leq x\leq 1, 0\leq y\leq \pi\right\}
\end{equation*}y determinemos su imagen bajo la transformación $f(z) = e^z$.

Solución. Fijemos a $x_0\in[-1,1]$ y consideremos al segmento de la recta vertical $x=x_0$ que está completamente contenido en $S$. Los puntos de dicho segmento son de la forma $z=x_0+iy$, con $0\leq y \leq \pi$. Para dichos puntos, por la proposición 20.2, tenemos que:
\begin{equation*}
w = f(z) = e^{x_0+iy} = e^{x_0} e^{iy} = e^{x_0}\left[\operatorname{cos}(y) + i \operatorname{sen}(y)\right], \quad 0\leq y \leq \pi,
\end{equation*}de donde se sigue que los puntos $w=e^{x_0}\operatorname{cis}(y)$ tienen módulo $e^{x_0}$ y argumento principal $y$.

Notemos que los puntos $w=f(z)$ están sobre la circunferencia de radio $e^{x_0}$ y centro en el origen. Más aún, como $y\in[0,\pi]$, entonces dichos puntos trazan la semicircunferencia ubicada en el semiplano superior del plano $w$.

Dado que $x_0\in[-1,1]$, entonces $e^{-1}<e^1$, por lo que, los segmentos de las rectas verticales $x=x_0$, contenidos en $S$, corresponden con circunferencias de radio creciente y en conjunto forman la región anular delimitada por las semicircunferencias de radio $e^{-1}$ y $e^1$, respectivamente, amabas centradas en el origen.

De manera análoga, podemos verificar que bajo la transformación $f(z)=e^z$, la región rectangular:
\begin{equation*}
\left\{z=x+iy\in\mathbb{C} : -1\leq x\leq 1, -\pi\leq y\leq 0\right\},
\end{equation*}es mapeada en la región anular delimitada por las mismas semicircunferencias de radio $e^{-1}$ y $e^1$, con centro en el origen, ubicada en el semiplano inferior del plano $w$.

En general, si consideramos a la región fundamental de la exponencial, figura 78 entrada 20, es decir, la banda infinita:
\begin{equation*}
\left\{z=x+iy\in\mathbb{C} : -\infty <x<\infty, -\pi< y < \pi\right\},
\end{equation*}entonces, dicho conjunto es mapeado bajo la transformación $f(z)=e^z$ en el conjunto:
\begin{equation*}
\mathbb{C}\setminus{L_{-\pi}} = \left\{z\in\mathbb{C} : |z|>0, -\pi< \operatorname{Arg}(z) < \pi\right\},
\end{equation*}ya que $\lim\limits_{x\to-\infty} e^x =0$ y $\lim\limits_{x\to\infty} e^x = \infty$.

Podemos visualizar lo anterior en el siguiente applet de GeoGebra https://www.geogebra.org/m/qqyhwmgv.

Ejemplo 26.7.
Sean $0<a<b$ y $0\leq \theta_1 <\theta_2 \leq \pi$. Determinemos la imagen de la región circular:
\begin{equation*}
S = \left\{z\in\mathbb{C} : a \leq |z| \leq b,\,\, \theta_1 \leq \operatorname{Arg}(z) \leq \theta_2\right\},
\end{equation*}bajo la transformación $\operatorname{Log}(z)$.

Solución. Notemos que la región $S$ está delimitada por las semirrectas que parten del origen y se forman por los ángulos $0\leq\theta_1$, $\theta_2\leq\pi$ y por los arcos de circunferencia de radio $a$ y $b$ con centro en el origen, como se puede ver en el siguiente applet de GeoGebra https://www.geogebra.org/m/qjzxhefv.

Consideremos a una semirrecta $L$ que parte del origen y está determinada por un ángulo $\theta$ tal que $\theta_1 \leq \theta \leq \theta_2$. Sea $z\in L \cap S$, entonces:
\begin{align*}
\operatorname{Log}(z) & = \operatorname{ln}|z| +i \operatorname{Arg}(z)\\
& = \operatorname{ln}|\,z\,| +i \theta.
\end{align*}

Dado que $0<a\leq |\,z\,| \leq b$, tenemos que $\operatorname{ln}(a) \leq \operatorname{ln}|\,z\,| \leq \operatorname{ln}(b)$, por lo que los puntos $w=\operatorname{Log}(z)$ describen el segmento de la recta horizontal:
\begin{equation*}
w=u+iv, \quad \operatorname{ln}(a) \leq u \leq \operatorname{ln}(b), \quad v=\theta.
\end{equation*}

Como $v\in[\theta_1, \theta_2]$, entonces el segmento de la semirrecta $L$, que está completamente contenido en $S$, cubre a $S$ conforme $v$ varía, por lo que bajo $f$ dicho segmento cubre a la región rectangular en el plano $w$ determinada por los vértices $\left(\operatorname{ln}(a), \theta_1\right)$, $\left(\operatorname{ln}(b), \theta_1\right)$, $\left(\operatorname{ln}(b), \theta_2\right)$ y $\left(\operatorname{ln}(a), \theta_2\right)$.

Observación 26.5.
De acuerdo con los ejemplos 26.6 y 26.7, geométricamente debe ser claro que las funciones $\operatorname{Log}(z)$ y $e^z$ biyectan una región anular en una región rectangular y viceversa. Además, la frontera de la región anular es mapeada en la frontera de la región rectangular y viceversa.

Cerraremos esta entrada con el siguiente ejemplo correspondiente con la transformación trigonométrica $\operatorname{sen}(z)$. Por simplicidad consideraremos solo una parte de una banda infinita, pues para la parte restante el planteamiento es el mismo, sin embargo no deja de ser de suma importancia pues en conjunto nos permiten concluir que la función compleja $\operatorname{sen}(z)$ tiene como imagen a todo el plano complejo $\mathbb{C}$.

Ejemplo 26.8.
Determinemos la imagen de la semibanda infinita:
\begin{equation*}
S = \left\{z=x+iy\in\mathbb{C} : -\frac{\pi}{2}\leq x\leq \frac{\pi}{2},\, y\geq 0\right\},
\end{equation*}bajo la transformación $f(z)=\operatorname{sen}(z)$.

Solución. De manera análoga a los ejemplos anteriores, procedemos a cubrir la región del dominio de $f$ con alguna curva simple que bajo $f$ nos permita cubrir la imagen de $S$ y así determinar dicho conjunto.

Sea $0\leq y_0 <\infty$ fijo. Consideramos el segmento de recta horizontal contenido en $S$ dado por:
\begin{equation*}
y=y_0, \quad -\frac{\pi}{2}\leq x\leq \frac{\pi}{2}.
\end{equation*}

Sea $z=x+iy_0$ un punto sobre dicho segmento de recta, entonces, bajo $f$, por la proposición 22.1(10) tenemos que:
\begin{align*}
w=u+iv & = \operatorname{sen}(x+iy_0)\\
& = \operatorname{sen}(x) \operatorname{cosh}(y_0) + i \operatorname{cos}(x) \operatorname{senh}(y_0),
\end{align*}de donde:
\begin{equation*}
u(x,y) = \operatorname{sen}(x) \operatorname{cosh}(y_0) \quad \text{y} \quad v(x,y) = \operatorname{cos}(x) \operatorname{senh}(y_0).
\end{equation*}

Si $y_0=0$, tenemos que $\operatorname{cosh}(0)=1$ y $\operatorname{senh}(0)=0$, por lo que $v=0$ y $u=\operatorname{sen}(x)$, entonces la imagen del intervalo $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, bajo $f(z)=\operatorname{sen}(z)$, es el intervalo $[-1,1]$.

Supongamos ahora que $y_0>0$. Tenemos que $\operatorname{cosh}(y_0)>0$ y $\operatorname{senh}(y_0)>0$, por lo que:
\begin{equation*}
\operatorname{sen}(x) = \frac{u}{\operatorname{cosh}(y_0)} \quad \text{y} \quad \operatorname{cos}(x) = \frac{v}{\operatorname{senh}(y_0)} \tag{26.3}.
\end{equation*}

Para $x\in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ tenemos que $\operatorname{cos}(x)\leq 0$, por lo que $v\geq 0$.

Elevando al cuadrado ambas igualdades en (26.3) y sumándolas tenemos que:
\begin{equation*}
1 = \operatorname{sen}^2(x) + \operatorname{cos}^2(x) = \left(\frac{u}{\operatorname{cosh}(y_0)}\right)^2 + \left(\frac{v}{\operatorname{senh}(y_0)}\right)^2. \tag{26.4}
\end{equation*}

De acuerdo con (26.4), como $x\in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, entonces los puntos $w=u+iv$ trazan la semielipse superior:
\begin{equation*}
\left(\frac{u}{\operatorname{cosh}(y_0)}\right)^2 + \left(\frac{v}{\operatorname{senh}(y_0)}\right)^2 = 1, \quad v\geq 0.
\end{equation*}

Los puntos de intersección de dicha semielipse con el eje real $u$ son $\left(\pm\operatorname{cosh}(y_0), 0\right)$, mientras que el punto intersección con el eje imaginario $v$ es $\left(0,\operatorname{senh}(y_0)\right)$.

Dado que:
\begin{align*}
\lim\limits_{y_0\to\infty} \operatorname{senh}(y_0) = \infty, &\quad \lim\limits_{y_0\to\infty} \operatorname{cosh}(y_0) = \infty,\\
\lim\limits_{y_0\to 0 } \operatorname{senh}(y_0) =0, &\quad \lim\limits_{y_0\to 0} \operatorname{cosh}(y_0) = 1,
\end{align*}y $y_0\in(0,\infty)$, entonces la imagen de las semielipses se encuentra en el semiplano superior $v\geq 0$, del plano $w$, incluyendo el eje real $u$.

Se puede verificar fácilmente, ejercicio 5, que la frontera de $S$ es mapeada en la frontera de $f(S)$, correspondiente con el eje real $u$.

Podemos visualizar lo anterior en el siguiente applet de GeoGebra https://www.geogebra.org/m/byzgzgzb.

Tarea moral

Determina la imagen $f(S)$ bajo la transformación lineal dada.
a) $f(z) = 4z$ y $S=\left\{ z\in\mathbb{C} : |z|<1 \right\}$.
b) $f(z) = iz+i$ y $S=\left\{ z\in\mathbb{C} : \operatorname{Re}(z)>0 \right\}$.
c) $f(z) = -z+2i$ y $S=\left\{ z\in\mathbb{C} : \operatorname{Re}(z)>0, \operatorname{Im}(z)>0 \right\}$.
d) $f(z) = iz+2$ y $S=\left\{ z\in\mathbb{C} : |z|\leq 2, 0\leq \operatorname{Arg}(z)\leq \dfrac{\pi}{2} \right\}$.
Sea $f(z)=\dfrac{1}{z}$ la transformación inversión. Para cada conjunto $S$ determina su imagen $f(S)$.
a) $S=\left\{ z\in\mathbb{C} : 0<|z|\leq 1 \right\}$.
b) $S=\left\{ z\in\mathbb{C} : |z|\geq 1 \right\}$.
c) $S=\left\{ z\in\mathbb{C} : 0<|z|\leq 3, \dfrac{\pi}{3}\leq \operatorname{Arg}(z)\leq \dfrac{2\pi}{3} \right\}$.
d) $S=\left\{ z\in\mathbb{C} : z\neq 0, 0 \leq \operatorname{Arg}(z)\leq \dfrac{\pi}{2} \right\}$.
Encuentra la imagen de $S=\left\{ z\in\mathbb{C} : |z|<1 \right\}$ bajo $f(z)=z+\overline{z}$.
Sea $f(z) = z^2$. Determina la imagen $f(S)$ de cada conjunto $S$.
a) $S$ es el cuadrado con vértices $(0,0), (1,0), (1,1)$ y $(0,1)$.
b) $S=\left\{ z\in\mathbb{C} : 0\leq \operatorname{Im}(z) \leq 1 \right\}$.
c) $S=\left\{ z\in\mathbb{C} : \operatorname{Re}(z)>0, \operatorname{Im}(z)>0 \right\}$.
d) $S=\left\{ z\in\mathbb{C} : -2 \leq \operatorname{Re}(z) \leq 0 \right\}$.
Sea $f(z) = \operatorname{sen}(z)$.
a) Muestra que bajo $f$ la semirrecta $x=\dfrac{\pi}{2}$, $y\geq 0$ es mapeada en la semirrecta $u\geq 1$, $v = 0$.
b) Muestra que bajo $f$ la semirrecta $x=-\dfrac{\pi}{2}$, $y\geq 0$ es mapeada en la semirrecta $u\leq -1$, $v = 0$.
c) Concluye que la frontera del conjunto $S$ en el ejemplo 26.8 es mapeada en la drontera del conjunto $f(S)$.
d) Sabemos que la elipse:
\begin{equation*}
\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1,
\end{equation*}con $0<b<a$, tiene focos en los puntos $\left(\pm \sqrt{a^2 – b^2}, 0\right)$. Muestra que todas las elipses del ejemplo 26.8 tienen los mismos focos en los puntos $(\pm 1,0)$.
Sea $S$ la semibanda horizontal:
\begin{equation*}
\left\{z=x+iy\in\mathbb{C} : x\geq 0, -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \right\}.
\end{equation*}Determina la imagen de $S$ bajo la función $f(z)=\operatorname{senh}(z)$.

Hint: Expresa a $\operatorname{senh}(z)$ en términos de $\operatorname{sen}(z)$.
Sea $w=\rho e^{i\phi}$. Muestra que la transformación $w=\dfrac{i}{z}$ mapea la hipérbola $x^2-y^2=1$ en la lemniscata $\rho^2 = 2 \operatorname{cos}(2\phi)$.
Determina una transformación que rote a la elipse $x^2+xy+y^2=2$, en el sentido de las manecillas del reloj, tal que su ecuación se reduzca a su forma canónica. Obtén la longitud de su semieje mayor y menor.

Hint: Supón que la transformación es de la forma $w=\rho e^{i\phi}$. Determina un ángulo $\alpha$ tal que el coeficiente de $uv$ en la imagen de la curva es cero.

Más adelante…

En esta entrada hemos abordado, a manera de ejemplos, el estudio de las funciones complejas como transformaciones del plano complejo, esto con el objetivo de dar una interpretación geométrica del comportamiento de las funciones complejas, ya que como mencionamos antes, visualizar la gráfica de tales funciones resulta imposible. Debe ser claro que la propuesta de esta entrada es solo una de las distintas alternativas conocidas para el estudio de la parte gráfica de una función compleja, sin embargo hay otras alternativas que pueden ser de utilidad para la comprensión del comportamiento geométrico de estas funciones, por lo que se recomienda consultar estas otras propuestas.

Con esta entrada finalizamos la segunda unidad del curso. En la siguiente entrada es la primera de la tercera unidad del curso, correspondiente con el tema de series de números complejos, en la cual estudiaremos algunos de los conceptos básicos así como algunas de las propiedades más importantes de estos objetos matemáticos, mediante los cuales probaremos una serie de resultados que serán de utilidad para caracterizar a las funciones complejas a través de dichos objetos.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Transformaciones lineales y transformaciones de Möbius.
Siguiente entrada del curso: Preliminares de series de números complejos.

Geometría Analítica I: Encontrar el centro y los ejes de una cónica

Por Paola Lizeth Rojas Salazar

Deja un comentario

Introducción

En esta entrada, continuaremos con el estudio de las cónicas, pero en esta ocasión, vamos a encontrar su centro y ejes, a partir de dos grupos de isometrías que ya son familiares para nosotros, las rotaciones y traslaciones y usando otro tema que ya ha sido estudiado con anterioridad, la equivalencia de polinomios y reducción de términos lineales y cuadráticos.

Encontrando el centro de las traslaciones

Para cualquier vector $h \in \mathbb R^2$, consideremos la traslación $g(x)=x+h$ y veamos cómo se escribe el polinomio $P \circ g$ con $P(x)=x*Ax+k*x+f$:

\begin{equation}\left(P\circ g\right)(x)= P(x+h)=(x+h)*A(x+h)+k*(x+h)+f\end{equation}

Factorizando y desarrollando un poco la expresión anterior, obtenemos:

\begin{equation}\left(P\circ g\right)(x)=x*Ax+x*Ah+h*Ax+k*x+(h*Ah+k*h+f)\end{equation}

Donde $h*Ah+k*h+f=P(h)$

Lo que nos lleva, finalmente, a:

\begin{equation}\left(P\circ g\right)(x)=x*Ax+x*Ah+h*Ax+k*x+P(h)\end{equation}

La pregunta ahora es, ¿hay una forma de encontrar el centro de la traslación g a partir de esta expresión? Lo que, por muy extraño que parezca, es cierto, pero, ¿cómo?

Enunciemos unos lemas que nos ayudarán a encontrar la respuesta a la pregunta anterior.

Lema 4.4: Dadas $A$ y $B$ dos matrices que se puedan multiplicar, se cumple que $(AB)^T=B^TA^T$

Lema 4.5: Si tenemos una matriz simétrica $A$ (recordemos que una matriz $A$ es simétrica si $A=A^T$), entonces, para todo par de vectores $x,y$ en $\mathbb R$, se cumple que $x*Ay=Ax*y$

Demostración

Sean $x,y$ vectores, recordemos que $x=x^T$ y que $y=y^T$, por esto y el lema anterior, tenemos que:

\begin{equation}x*Ay=x^TAy=\left(x^TAy\right)^T=\left(Ay\right)^T\left(x^T\right)^T=y^TA^Tx=y*Ax=Ax*y\end{equation}

Ahora sí podemos encontrar el centro de la traslación considerando:

\begin{equation}\left(P\circ g\right)(x)=x*Ax+x*Ah+h*Ax+k*x+P(h)\end{equation}

Ya que, considerando el lema anterior, podemos simplificar $\left(P\circ g\right)(x)$ de la siguiente manera:

\begin{equation}\left(P\circ g\right)(x)=x*Ax+x*Ah+h*Ax+k*x+P(h)=2(Ah*x)+k*x+P(h)\end{equation}

Y, finalmente:

\begin{equation}\left(P\circ g\right)(x)=(2Ah+k)*x+P(h)\end{equation}

Donde $(2Ah+k)*x$ es la parte lineal de esta composición por lo que, si podemos encontrar una $h \in \mathbb R^2$ que cumpla que $2Ah+k=0$, entonces habremos encontrado una traslación que no contenga la parte lineal del polinomio. Si esta $h$ existe, es el centro de la traslación (en el caso de este capítulo, estaremos hablando de traslaciones de cónicas).

Lo anterior lo podemos resumir en el siguiente lema:

Lema 4.6: Sea $P(x)=x*Ax+k*x+f$ un polinomio cuadrático (es decir que $A=A^T$) tal que $det(A)\neq 0$. Si definimos $c:=-\frac{A^{-1}}{k}$, $c$ es el centro de la curva asociada al polinomio $P$, $C(P)$ donde:

\begin{equation}P(x+c)=x*Ax+P(c)\end{equation}

Como buena conclusión de este apartado, observa que las traslaciones afectan la parte lineal de los polinomios cuadráticos.

Encontrando los ejes de las rotaciones

Ahora considera la rotación $g(x)=Bx$ con $B$ en el general lineal de $\mathbb R^2$, es decir, $B \in Gl(2)$ y $P$ el polinomio cuadrático general. Entonces:

\begin{equation}(P\circ g)(x) = P(Bx)=(Bx)*A(Bx)+k(Bx)+f\end{equation}

Si desarrollamos y simplificamos esta expresión, obtenemos:

\begin{equation}(P\circ g)(x) = x*(B^TAB)x+(B^Tk)*x+f\end{equation}

La pregunta en este caso es, ¿existe una forma de encontrar los ejes de la rotación a partir de esta expresión? La respuesta es sí.

A diferencia de las traslaciones, en las que se afectaba la parte lineal, para las rotaciones nos vamos a enfocar en la parte cuadrática. Debemos encontrar una manera de simplificar la expresión $B^TAB$.

Considera a $B$ como matriz ortogonal $(B \in O(2))$, esto implica que $B^TAB=B^{-1}AB$ que es la matriz que expresa la función $A$ en la base de las columnas de $B$.

Finalmente, toma a $u,v$ columnas de $B$ que forman una base ortonormal y que $A$ alarga estas columnas en factores $\lambda, \mu$, es decir, que $Au=\lambda u$ y $Av=\mu v$. Entonces, las siguientes igualdades se cumplen:

\begin{equation}A=\begin{pmatrix} \lambda & 0 \\
0 & \mu\end{pmatrix}\end{equation}

\begin{equation}B^TAB=\begin{pmatrix} u,&v \end{pmatrix}^T*A\begin{pmatrix} u,&v \end{pmatrix}=\begin{pmatrix} u^TAu & u^TAv\\ v^TAu & v^TAv\end{pmatrix}\end{equation}

Si desarrollamos esta última igualdad, obtenemos:

\begin{equation}B^TAB=\begin{pmatrix} \lambda & 0 \\
0 & \mu\end{pmatrix}\end{equation}

Si encontramos una matriz B que cumpla $(3)$, podemos eliminar el término mixto del polinomio $P$ y acercarnos a los polinomios canónicos.

Tarea moral

Demuestra el Lema 4.4.
Demuestra que, para $A,B,C$ matrices que se pueden multiplicar, se tiene que: $\left(ABC\right)^T=C^TB^TA^T$
Encuentra el centro, si es que tienen, de las curvas asociadas a los siguientes polinomios:
- $xy-3x-2y-2$,
- $x^2+2y^2-6x+4y+3$
- $9x^2-4xy+6y^2-58x+24y+59$

Más adelante…

Continuaremos con el estudio de la equivalencia y reducción de polinomios, con valores y vectores propios.

Geometría Analítica I: Rotaciones y traslaciones

Por Paola Lizeth Rojas Salazar

Deja un comentario

Introducción

En este apartado, vamos a continuar con el estudio de las isometrías que se empezaron a analizar en la unidad anterior, las rotaciones y traslaciones.

Encontrando un punto fijo

Recuerda que ya definimos la rotación de un ángulo $\theta$ con centro en $c$ ($\rho_{\theta,c}$), en función de la traslación de $c$ al origen $\tau_c$ y la rotación de $\theta$ en el origen $\rho_\theta$, como: $\rho_{\theta,c}=\tau_c\circ \rho_\theta \circ \tau_{-c}$. Usando matrices, esta expresión se convierte en:

\begin{equation}\rho_{\theta,c}(x)= R_\theta (x-c)+c=R_\theta x+(c-R_\theta c)\end{equation}

Observa que esta expresión es de la forma $Ax+b$ con $b$ constante, por lo que $\rho_{\theta,c} \in Iso^+ (2).

Por otro lado, si el problema se invierte y ahora queremos ver que una función $f(x)=Ax+b \in Iso^+ (2)$ es la rotación de una función en algún centro, debemos encontrar un punto fijo $c$ para el que $f(c)=c$. Es decir:

\begin{equation}c=Ac+b\end{equation}

\begin{equation}c-Ac=b\end{equation}

Esto quiere decir, que debemos encontrar una solución a la ecuación $x-Ax=b$, que se puede reescribir como:

\begin{equation}(I-A)x=b\end{equation}

Por lo que has visto en los capítulos anteriores, esperamos que, al ver esta expresión, hayas recordado que este sistema tiene solución única si y solo si su determinante es distinto de cero, donde su determinante es:

\begin{equation}det(I-R_\theta)=det\begin{pmatrix} 1-\cos(\theta) & \sin(\theta) \\
-\sin(\theta) & 1-\cos(\theta)\end{pmatrix}\end{equation}

Donde puedes comprobar que $det(I-R_\theta)=2(1-\cos(\theta))$.

Lo anterior implica que, si $\theta\neq 0$, entonces $det(I-R_\theta)\neq 0)$, lo que resulta en una solución única para el sistema resultante que es $A=R_\theta$ el punto fijo que estábamos buscando. Finalmente, podemos concluir que $f$ es una rotación.

Centro de rotación para composición de rotaciones

Lo anterior implica el siguiente corolario:

Corolario A: La composición de rotaciones es una nueva rotación.

La nueva pregunta que surge es, ¿cuál es el centro de rotación de la composición de rotaciones? Las siguientes líneas, las dedicaremos a encontrar este nuevo centro de rotación.

Considera $\rho_{\alpha,a}$ y $\rho_{\beta,b}$ las rotaciones de ángulos $\alpha$ y $beta$ y centros en $a$ y $b$ respectivamente. La composición de estas dos rotaciones tiene un ángulo $\alpha + \beta$, pero su centro depende del orden de composición.

Para encontrar el centro de rotación, de forma geométrica, para $\rho_{\beta,b} \circ \rho_{\alpha,a}$, se trazan las líneas que van de $a$ a $b$, después, midiendo los ángulos a partir de esta recta, la línea que pasa por $a$ con ángulo $-\frac{\alpha}{2}$ y la que pasa por $b$ con ángulo $\frac{\beta}{2}$. La intersección de las últimas dos líneas es el nuevo centro de rotación $c$.

Observa que, para la composición $\rho_{\alpha,a} \circ \rho_{\beta,b}$, su nuevo centro de rotación es el reflejado de $c$ respecto de la línea que pasa por $a$ y $b$.

Tarea moral

Verifica que, efectivamente, se cumple que $det(I-R_\theta)=2(1-\cos(\theta))$.
Demuestra el Corolario A.
Como veremos más delante, las homotecias, son transformaciones de la forma $f(x)=kx+b$ donde $k\neq 0$ se conoce como el factor de expansión. Demuestra que las homotecias con $k\neq 1$ tienen un punto fijo (este punto fijo se llama centro de expansión).

Más adelante…

En la siguiente entrada de esta unidad, hablaremos sobre otro tipo de isometrías que ya estudiamos en la unidad anterior, las reflexiones.

Álgebra Lineal II: El teorema de clasificación de transformaciones ortogonales

Por Ayax Calderón

8 respuestas

Introducción

En la entrada anterior definimos las transformaciones ortogonales y probamos algunas de sus propiedades relacionadas con el producto interior, norma y la transformación adjunta. Vimos también que el conjunto de todas las transformaciones ortogonales de un espacio euclideano $V$ forma un grupo $O(V)$ bajo composición.

En esta entrada queremos entender mucho mejor dicho grupo. El resultado principal que probaremos nos dirá exactamente cómo son todas las posibles transformaciones ortogonales en un espacio euclideano (que podemos pensar que es $\mathbb{R}^n$). Para llegar a este punto, comenzaremos con algunos resultados auxiliares y luego con un lema que nos ayudará a entender a las transformaciones ortogonales en dimensión $2$. Aprovecharemos este lema para probar el resultado para cualquier dimensión.

El lema de los subespacios estables

Lo primero que veremos es que las transformaciones ortogonales preservan completamente los subespacios estables, así como sus espacios ortogonales. Este es el resultado que nos permitirá un poco más adelante trabajar inductivamente.

Lema. Sean $V$ un espacio euclidiano, $T\in O(V)$ y $W$ un subespacio de $V$ estable bajo $T$.

Se tiene que $T(W)=W$ y $T(W^\bot)=W^\bot$.
Se tiene que $T|_W\in O(W)$ y $T|_{W^\bot}\in W^\bot$.

Demostración. 1. Como $T(W)\subseteq W$ y $T|_W$ es inyectiva (pues $T$ es inyectiva en $V$), se sigue que $T|_W:W\to W$ es suprayectiva y por lo tanto $T(W)=W$. Veamos ahora que $W^\bot$ también es estable bajo $T$. Tomemos $x\in W^\bot$ y $y\in W$. Queremos demostrar que $T(x)\in W^\bot$, es decir, que $\langle T(x),y \rangle=0$. Como $T$ es ortogonal, entonces $T^*=T^{-1}$ y por lo tanto
$$\langle T(x),y \rangle=\langle x,T^{-1}(y) \rangle.$$

Como $T|_W:W\to W$ es biyectiva, se tiene que $W$ es estable bajo $T^{-1}$. Entonces $T^{-1}(y)\in W$, y como $x\in W^\bot$, entonces $\langle x,T^{-1}(y) \rangle=0$. Por lo tanto $\langle T(x),y \rangle=0$. Esto muestra que $W^\bot$ es estable bajo $T$ y por la primer parte de este inciso, llegamos a $T(W^\bot)=W^\bot$.

2. Para todo $x\in W$ se tiene que
$$||T|_W(x)||=||T(x)||=||x||,$$
lo que significa que $T|_W\in O(W)$. De manera análoga se tiene que $T_{W^\bot}\in O(W^\bot)$.

$\square$

El lema de la invarianza de una recta o un plano

Para poder aplicar el lema de la sección anterior, tendremos que poder encontrar subespacios estables. El siguiente lema nos dice que siempre podemos encontrar subespacios estables en espacios euclideanos.

Lema. Sea $V$ un espacio euclidiano y $T$ una transformación lineal sobre $V$. Entonces existe una recta (subespacio de dimensión $1$) o un plano (subespacio de dimensión $2$) en $V$ estable bajo $T$.

Demostración. El polinomio mínimo de $T$ es un polinomio $\mu_T(x)$ con coeficientes reales. Si tiene una raíz real, se sigue que $T$ tiene un eigenvalor y por consiguiente, la recta generada por un eigenvector es estable bajo $T$.

Ahora supongamos que $\mu_T(x)$ no tiene raíces reales. Sea $z$ una raíz compeja de $\mu_T(x)$, que existe por el teorema fundamental del álgebra. Como $\mu_T(x)$ tiene coeficientes reales, entonces $\overline{z}$ también es raíz de $\mu_T(x)$.Por lo tanto, $Q(x)=(x-z)(x-\overline{z})$ divide a $\mu_T(x)$.

Es imposible que $Q(T)$ sea una matriz invertible, pues de serlo, tendríamos que $\frac{\mu_T}{Q}(x)$ sería un polinomio de grado más chico que $\mu_T(x)$ y anularía a $T$. Esto nos dice que existe $x\in V$ distinto de $0$ tal que $Q(T)(x)=0$. Si $Q(x)=x^2+ax+b$, esto se traduce a $T^2(x)+aT(x)+bx=0$. De aquí, se tiene que $x$ y $T(x)$ generan un plano estable bajo $T$.

$\square$

Las transformaciones ortogonales en dimensión $2$

Los lemas de las secciones anteriores nos permitirán ir partiendo a un espacio euclideano $T$ en «cachitos estables» ya sea de dimensión $1$ o de dimensión $2$. En los de dimensión $1$ ya sabemos cómo debe verse una matriz que represente a $T$: simplemente corresponden a eigenvectores y entonces consistirán en reescalamientos (que deben de ser por factor $1$ ó $-1$ para tener ortogonalidad). Pero, ¿cómo se verá matricialmente la transformación $T$ en subespacios estables de dimensión $2$ que no se puedan descomponer más? Esto es lo que nos responde el siguiente lema.

Lema. Sea $V$ un espacio euclidiano de dimensión $2$ y $T\in O(V)$ sin eigenvalores reales. Entonces existe una base ortonormal de $V$ tal que la matriz asociada a $T$ en dicha base es de la forma
$$R_\theta=\begin{pmatrix}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta\end{pmatrix}.$$

Demostración. Sea $\beta=\{e_1,e_2\}$ una base ortonormal de $V$ y escribimos $T(e_1)=ae_1+be_2$ para algunos números reales $a,b$. Como
$$a^2+b^2=||T(e_1)||^2=||e_1||^2=1,$$ entonces podemos encontrar un número real $\theta$ tal que $(a,b)=(\cos\theta,\sin\theta)$.

Para que $\langle T(e_1), T(e_2)\rangle = 0$, necesitamos que exista un $c$ tal que $T(e_2)=c(-\sin\theta e_1+\cos \theta e_2)$. Finalmente, ya que $$||T(e_2)||=||e_2||=1, $$ debemos tener $|c|=1$ y así $c\in \{-1,1\}$.

El caso $c=-1$ podemos descartarlo pues la matriz que representa a $T$ en la base $\beta$ sería
$$\begin{pmatrix}
\cos \theta & \sin \theta\\
\sin \theta & -\cos\theta\end{pmatrix},$$
cuyo polinomio caracterísitco es $x^2-1$ y por lo tanto tiene a $1$ como eigenvalor, lo cual no entra en nuestras hipótesis. Así, $c=1$ y por lo tanto la matriz que representa a $T$ en la base $\beta$ es
$$\begin{pmatrix}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta\end{pmatrix},$$

como queríamos.

$\square$

El teorema de clasificación

Con lo visto hasta ahora, ya estamos listos para demostrar el teorema fundamental de clasificación de transformaciones lineales ortogonales de un espacio euclidiano.

Teorema (clasificación de ortogonales). Sea $V$ un espacio euclidiano y $T\in O(V)$. Entonces podemos encontrar una base ortonormal $\beta$ de $V$ tal que la matriz asociada a $T$ con respecto a la base $\beta$ es de la forma
\begin{equation}\label{forma}
A=\begin{pmatrix}
I_p & 0 & 0 & \dots & 0\\
0 & -I_q & 0 & \dots & 0\\
0 & 0 & R_{\theta_1} & \dots & 0\\
\vdots & \vdots & \vdots &\ddots & \vdots\\
0 & 0 & 0 &\dots & R_{\theta_k}
\end{pmatrix},\end{equation}
donde $\theta_1,\dots, \theta_k$ son números reales y
$$R_\theta=\begin{pmatrix}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta
\end{pmatrix}.$$

Demostración. Procederemos por inducción sobre $\dim V$. Si $\dim V=1$, entonces ya terminamos, pues se tendría que $T=\pm id$ (esto quedó de tarea moral en la entrada anterior).

Supongamos que el resultado se satisface para todos los espacios euclideanos de dimensión a lo más $n-1$. Tomemos $V$ un espacio euclideano de dimensión $n$ y $T$ una transformación ortogonal de $V$. Por el lema de la invarianza de una recta o un plano, o bien $V$ tiene una recta estable bajo $T$, o bien un plano estable bajo $T$.

El caso en que $T$ tiene una recta estable bajo $T$ corresponde a que $T$ tiene un eigenvalor real $t$ con eigenvector, digamos, $e_1$. Entonces $$|t|||e_1||=||te_1||=||T(e_1)||=||e_1||,$$
por lo cual $t\in\{-1,1\}$. Sea $W$ la recta generada por $e_1$.

Tenemos que $V=W\oplus W^\bot$. Por el lema de subespacios estables, $T(W)=W$ y $T|_{W^\bot}$ es ortogonal de $W^\bot$. Por hipótesis inductiva, $W^\bot$ tiene una base ortonormal $\{e_2,\dots , e_n\}$ tal que la matriz asociada a dicha base y restringida a $W^\bot$ es de la forma \eqref{forma}. Añadiendo el vector $\frac{e_1}{||e_1||}$ se añade un $1$ o $-1$ en la diagonal, así que, posiblemente permutando la base ortonormal resultante $\{\frac{e_1}{||e_1||},e_2,\dots ,e_n\}$ de $V$ obtenemos una base ortonormal tal que la matriz asociada a $T$ con respecto a esta base es de la forma \eqref{forma}.

Ahora supongamos que $T$ no tiene valores propios reales, es decir, que estamos en el caso de tener un plano estable bajo $T$. Como $T$ es ortogonal, el espacio $W^\bot$ también es estable bajo $T$, y las restricciones de $T$ a $W$ y $W^\bot$ son transformaciones otogonales sobre estos espacios. Por hipótesis inductiva, $W^\bot$ tiene una base ortonormal $\{e_3,\dots,e_n\}$ tal que la matriz asociada a $T|_{W^\bot}$ con respecto a esta base es una matriz diagonal de bloques de la forma $R_{\theta_i}$. Por el lema de transformaciones ortogonales en dimensión $2$, el subespacio $W$ tiene una base ortonormla $\{e_1,e_2\}$ tal que la matriz asociada a $T|_W$ con respecto a esta base es de la forma $R_\theta$. Como $V=W\oplus W^\bot$, entonces la matriz asociada a $T$ con respecto a la base $\{e_1,\dots, e_n\}$ es de la forma \eqref{forma}, con lo cual concluimos con la prueba deseada.

$\square$

También podemos enunciar el teorema anterior en términos de matrices:

Corolario. Sea $A\in M_n(\mathbb{R})$ una matriz ortogonal. Entonces existen enteros $p,q,k$ que satisfacen $p+q+2k=n$, una matriz ortogonal $P\in M_n(\mathbb{R})$ y números reales $\theta_1,\dots , \theta_n$ tales que
$$A=P^{-1}\begin{pmatrix}
I_p & 0 & 0 & \dots & 0\\
0 & -I_q & 0 & \dots & 0\\
0 & 0 & R_{\theta_1} & \dots & 0\\
\vdots & \vdots & \vdots &\ddots & \vdots\\
0 & 0 & 0 &\dots & R_{\theta_k}
\end{pmatrix}P.$$

Observación. El determinante de la matriz
$$\begin{pmatrix}
I_p & 0 & 0 & \dots & 0\\
0 & -I_q & 0 & \dots & 0\\
0 & 0 & R_{\theta_1} & \dots & 0\\
\vdots & \vdots & \vdots &\ddots & \vdots\\
0 & 0 & 0 &\dots & R_{\theta_k}
\end{pmatrix}$$
es $(-1)^q\in\{1,-1\}$ (estamos usando $\det R_{\theta_i}=1$ para $1\leq i\leq k$). Se sigue que $$\det T\in\{-1,1\}$$ para cualquier $T\in O(V)$.

Más adelante…

Por lo platicado en esta entrada, ya podemos decir cómo es cualquier transformación ortogonal, y no es tan complicado: simplemente en alguna base apropiada, se rota en pares de coordenadas, o bien se refleja en coordenadas, o bien no se hace nada en alguna coordenada (o una combinación de estas cosas). Todo esto intuitivamente deja fijas las normas y el teorema de clasificación nos dice que si se fijan normas entonces debe ser así. Por ello, podemos pensar a las transformaciones ortonormales como «sencillas» o por lo menos «entendibles».

Aprovecharemos esto en el siguiente tema, pues enunciaremos el teorema espectral real, que nos dice que las transformaciones simétricas se entienden muy bien a partir de las ortogonales y de las diagonales. Así, las transformaciones simétricas también serán «entendibles». Finalmente, con el teorema de descomposición polar llevaremos este entendimiento a todas, todas las matrices.

Tarea moral

Verifica que, en efecto, las matrices $R_\theta$ de la entrada tienen determinante igual a $1$.
Sea $V$ un espacio euclidiano y $T:V\to V$ una transformación lineal. Demuestra que $T$ es ortogonal si y sólo si $||T(x)||=||x||$ para los vectores $x$ de norma $1$.
Encuentra la matriz de rotación de ángulo $\frac{\pi}{3}$ alrededor de la recta generada por el vector $(1,1,1)$.
Describe todas las matrices en $M_3(\mathbb{R})$ que son simultaneamente ortogonales y diagonales.
Describe todas las matrices en $M_3(\mathbb{R})$ que sean simultáneamente ortogonales y triangulares superiores.

Entradas relacionadas

Ir a Álgebra Lineal II
Entrada anterior del curso: Isometrías reales, transformaciones ortogonales y sus propiedades
Siguiente entrada del curso: El teorema espectral real

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: rotaciones

Variable Compleja I: Funciones complejas como transformaciones. Técnicas de graficación

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Geometría Analítica I: Encontrar el centro y los ejes de una cónica

Introducción

Encontrando el centro de las traslaciones

Encontrando los ejes de las rotaciones

Tarea moral

Más adelante…

Geometría Analítica I: Rotaciones y traslaciones

Introducción

Encontrando un punto fijo

Centro de rotación para composición de rotaciones

Tarea moral

Más adelante…

Álgebra Lineal II: El teorema de clasificación de transformaciones ortogonales

Introducción

El lema de los subespacios estables

El lema de la invarianza de una recta o un plano

Las transformaciones ortogonales en dimensión $2$

El teorema de clasificación

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos