Introducción

En esta ocasión presentamos el teorema de Menelao, una herramienta muy útil que nos da condiciones necesarias y suficientes para que tres puntos, cada uno sobre los lados de un triángulo, sean colineales.

Teorema de Menelao

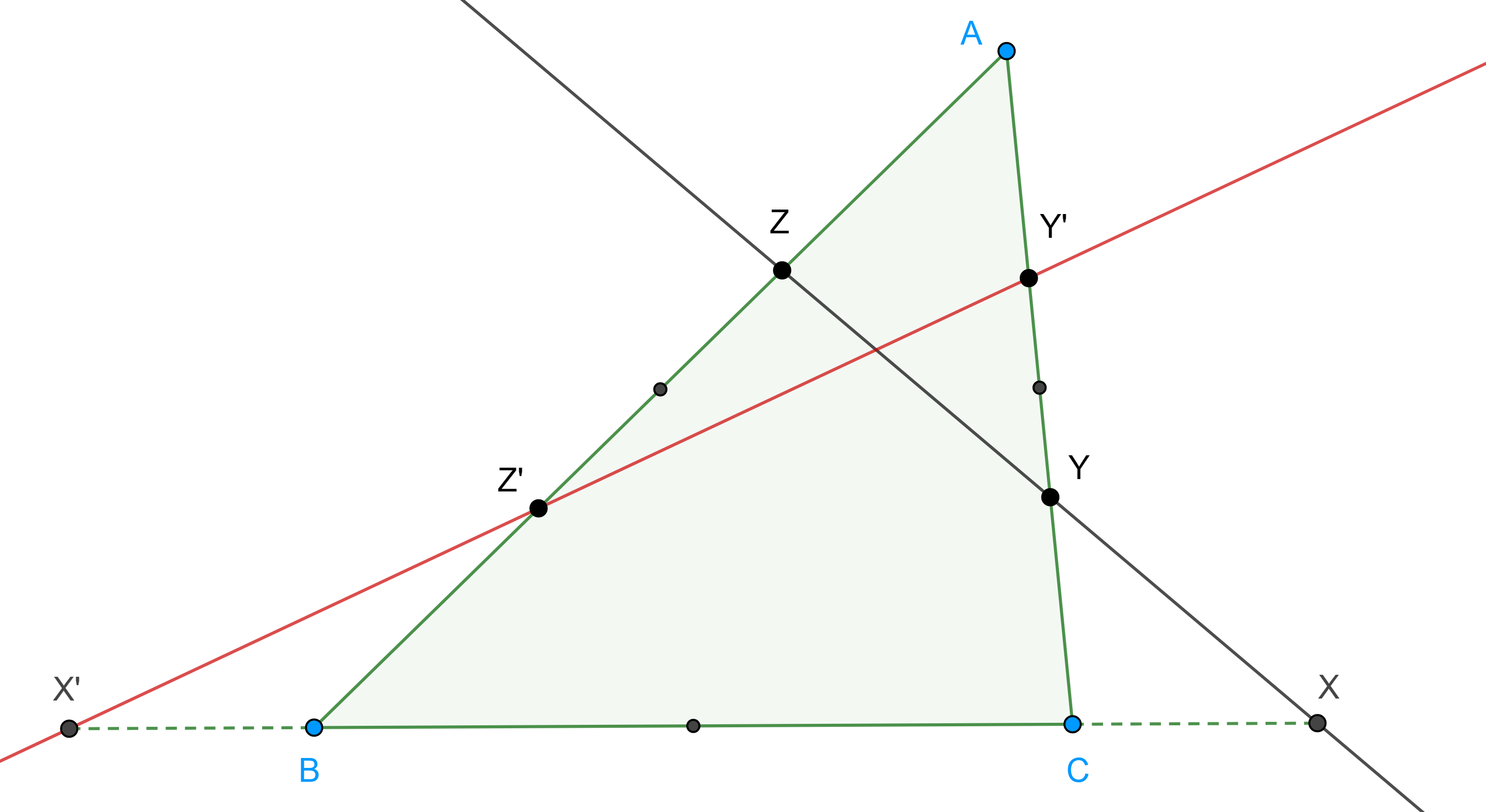
Teorema 1, de Menelao. Sean $\triangle ABC$ y $X$, $Y$, $Z$ puntos en los lados $BC$, $CA$ y $AB$ respectivamente, tal que uno o los tres puntos se encuentran en la extensión de los lados de $\triangle ABC$, entonces $X$, $Y$ y $Z$ son colineales si y solo si
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = – 1$.

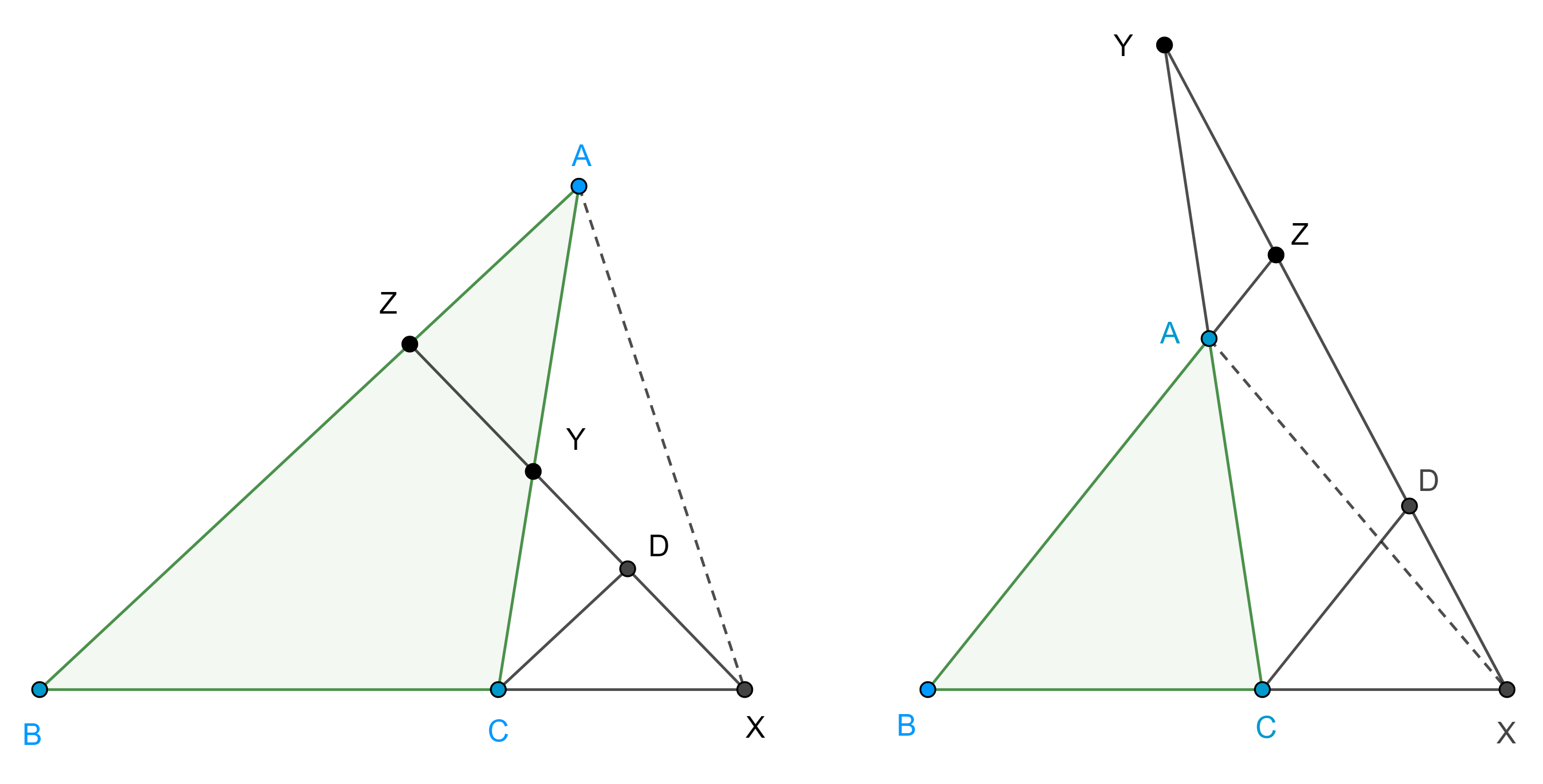
Demostración. Supongamos que $X$, $Y$ y $Z$ son colineales, sea $D \in XYZ$ tal que $CD \parallel AB$ entonces $\triangle XZB \sim \triangle XDC$ y $\triangle YAZ \sim \triangle YCD$, esto es

$\dfrac{DC}{ZB} = \dfrac{XC}{XB} \Leftrightarrow DC = \dfrac{ZB \times XC}{XB}$,

$\dfrac{DC}{ZA} = \dfrac{YC}{YA} \Leftrightarrow DC = \dfrac{ZA \times YC}{YA}$.

Por lo tanto,
$ \dfrac{ZA}{YA} \dfrac{YC}{ZB} \dfrac{XB}{XC} = 1 \Leftrightarrow \dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = – 1$.

La última ecuación se obtiene al considerar segmentos dirigidos.

$\blacksquare$

Conversamente, ahora supongamos sin pérdida de generalidad que $Z$ e $Y$ se encuentran en $AB$ y $CA$ respectivamente y $X$ en la extensión de $BC$ (izquierda figura 1), el caso en que los tres puntos están en las extensiones de los lados es análogo, y supongamos que
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = – 1$.

Sea $X’ = YZ \cap BC$, entonces por la implicación que ya probamos tenemos que
$\dfrac{AZ}{ZB} \dfrac{BX’}{X’C} \dfrac{CY}{YA} = – 1$.

Esto, junto con nuestra hipótesis nos dice que $\dfrac{BX’}{X’C} = \dfrac{BX}{XC}$, es decir $BC$ es dividido exteriormente por $X$ y $X’$ en la misma razón.

Por lo tanto, $X = X’$, entonces $X$, $Y$ y $Z$ son colineales.

$\blacksquare$

Forma trigonométrica del teorema de Menelao

Lema de la razón. Considera $\triangle ABC$ y sea $X$ un punto en $BC$ o su extensión, entonces
$\begin{equation} \dfrac{BX}{XC} = \dfrac{AB}{CA} \dfrac{\sin \angle BAX}{\sin \angle CAX}. \end{equation}$.

Demostración. Aplicamos la ley de los senos a los triángulos $\triangle BAX$ y $\triangle XAC$ (figura 1),
$\begin{equation} \dfrac{BX}{\sin \angle BAX} = \dfrac{AB}{\sin \angle AXB}, \end{equation}$

$\begin{equation} \dfrac{CX}{\sin \angle CAX} = \dfrac{AC}{\sin \angle AXC}. \end{equation}$

Notemos que $\sin \angle AXB = \sin \angle AXC$, pues si $X$ está en la extensión de $BC$ entonces $\angle AXB = \angle AXC$ o si $X$ está en el segmento $BC$ entonces $\angle AXB$ y $\angle AXC$ son suplementarios.

Por lo tanto, haciendo el cociente de $(2)$ entre $(3)$ obtenemos $(1)$.

$\blacksquare$

Forma trigonométrica del teorema de Menelao. Sea $\triangle ABC$ y $X$, $Y$, $Z$ puntos en los lados $BC$, $CA$ y $AB$ respectivamente, tal que uno o los tres puntos se encuentran en la extensión de los lados de $\triangle ABC$, entonces $X$, $Y$ y $Z$ son colineales si y solo si

$\dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBY}{\sin \angle YBA} \dfrac{\sin \angle ACZ}{\sin \angle ZCB} = – 1$.

Demostración. Aplicamos el lema de la razón a $X$, $Y$ y $Z$, entonces:
$-1 = \dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA}$

$= (\dfrac{CA}{BC} \dfrac{\sin \angle ACZ}{\sin \angle ZCB}) (\dfrac{AB}{CA} \dfrac{\sin \angle BAX}{\sin \angle XAC}) (\dfrac{BC}{AB} \dfrac{\sin \angle CBY}{\sin \angle YBA})$

$= \dfrac{\sin \angle BAX}{\sin \angle XAC} \dfrac{\sin \angle CBY}{\sin \angle YAC} \dfrac{\sin \angle ACZ}{\sin \angle ZCB}$.

En consecuencia, por el teorema de Menelao la igualdad es cierta si y solo si $X$, $Y$ y $Z$ son colineales.

$\blacksquare$

Bisectrices

Proposición 1.
$i)$ Dos bisectrices internas y la bisectriz externa del tercer ángulo de un triángulo intersecan a los lados opuestos del triángulo en tres puntos colineales,
$ii)$ las tres bisectrices externas de un triángulo intersecan a los lados opuestos del triángulo en tres puntos colineales.

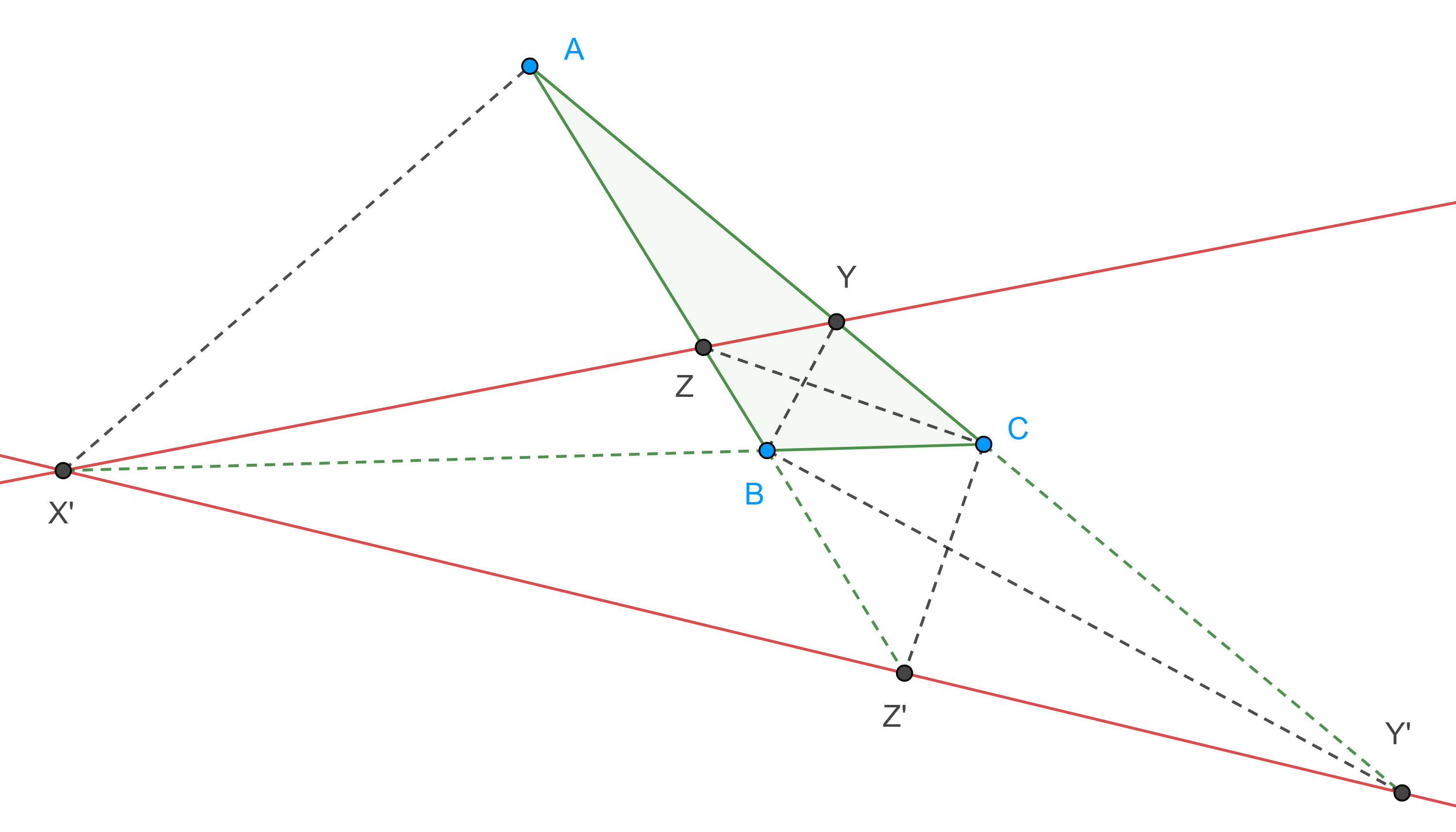
Demostración. Sean $\triangle ABC$, $X’$, la intersección de la bisectriz externa de $\angle A$ con $BC$, $Y$ y $Z$ las intersecciones de las bisectrices internas de $\angle B$ y $\angle C$ con $CA$ y $AB$ respectivamente.

Por el teorema de la bisectriz tenemos las siguientes igualdades
$\dfrac{BX’}{X’C} = \dfrac{AB}{AC}$,
$\dfrac{CY}{YA} = \dfrac{BC}{BA}$,
$\dfrac{AZ}{ZB} = \dfrac{CA}{CB}$.

Considerando segmentos dirigidos,
$\dfrac{AZ}{ZB} \dfrac{BX’}{X’C} \dfrac{CY}{YA} = \dfrac{CA}{CB} \dfrac{AB}{AC} \dfrac{BC}{BA} = -1$.

Por lo tanto, $X’$, $Y$ y $Z$ son colineales.

Análogamente, si $Y’$ y $Z’$ son las intersecciones de las bisectrices externas de $\angle B$ y $\angle C$ con $CA$ y $AB$ respectivamente, entonces por el teorema de la bisectriz
$\dfrac{CY’}{Y’A} = \dfrac{BC}{BA}$,
$\dfrac{AZ’}{Z’B} = \dfrac{CA}{CB}$.

Por lo tanto
$\dfrac{AZ’}{Z’B} \dfrac{BX’}{X’C} \dfrac{CY’}{Y’A} = \dfrac{CA}{CB} \dfrac{AB}{AC} \dfrac{BC}{BA} = -1$.

Por lo tanto, por el teorema de Menelao, $X’$, $Y’$ y $Z’$ son colineales.

$\blacksquare$

Recta de Lemoine y recta de Gergonne

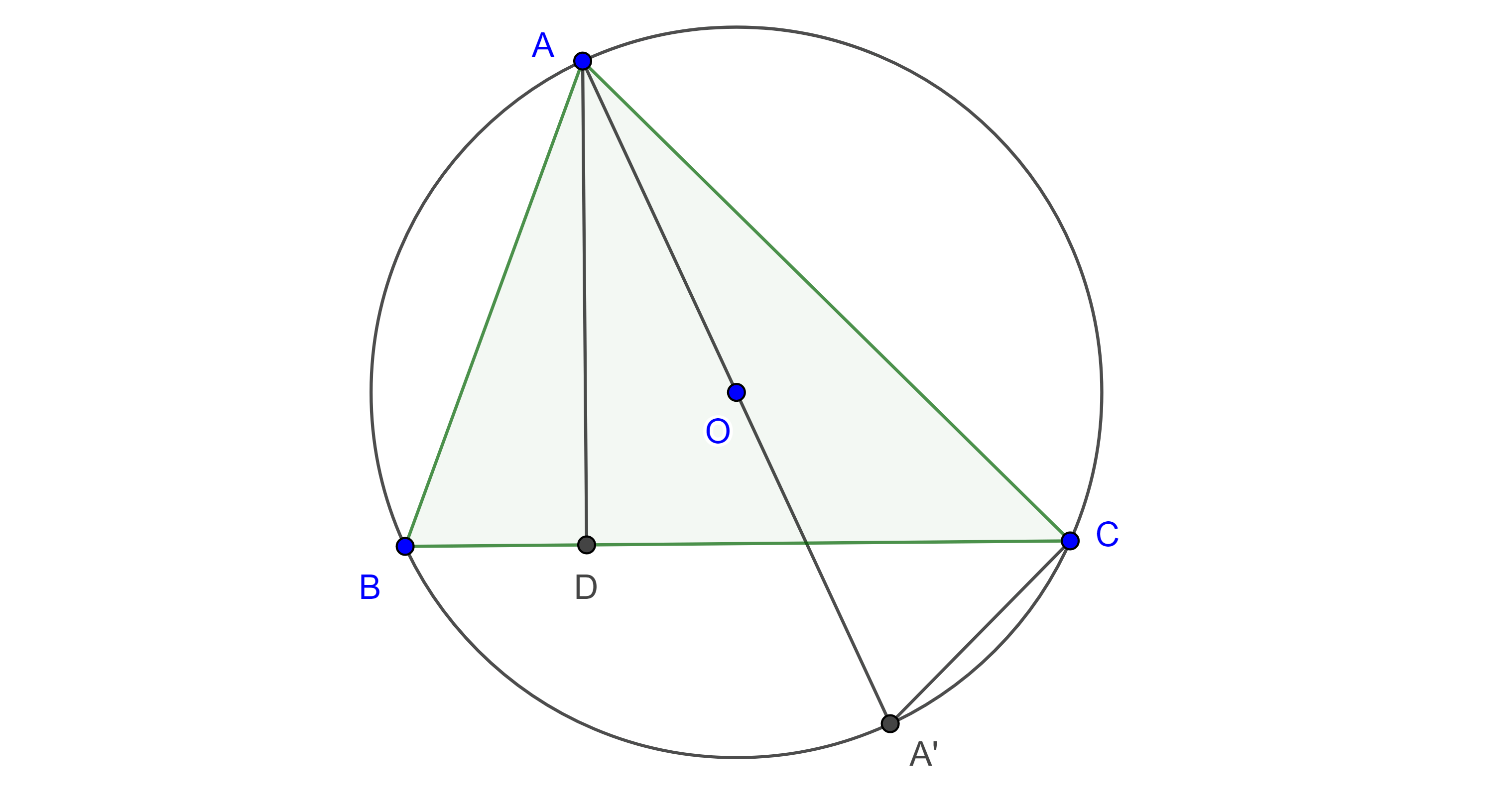
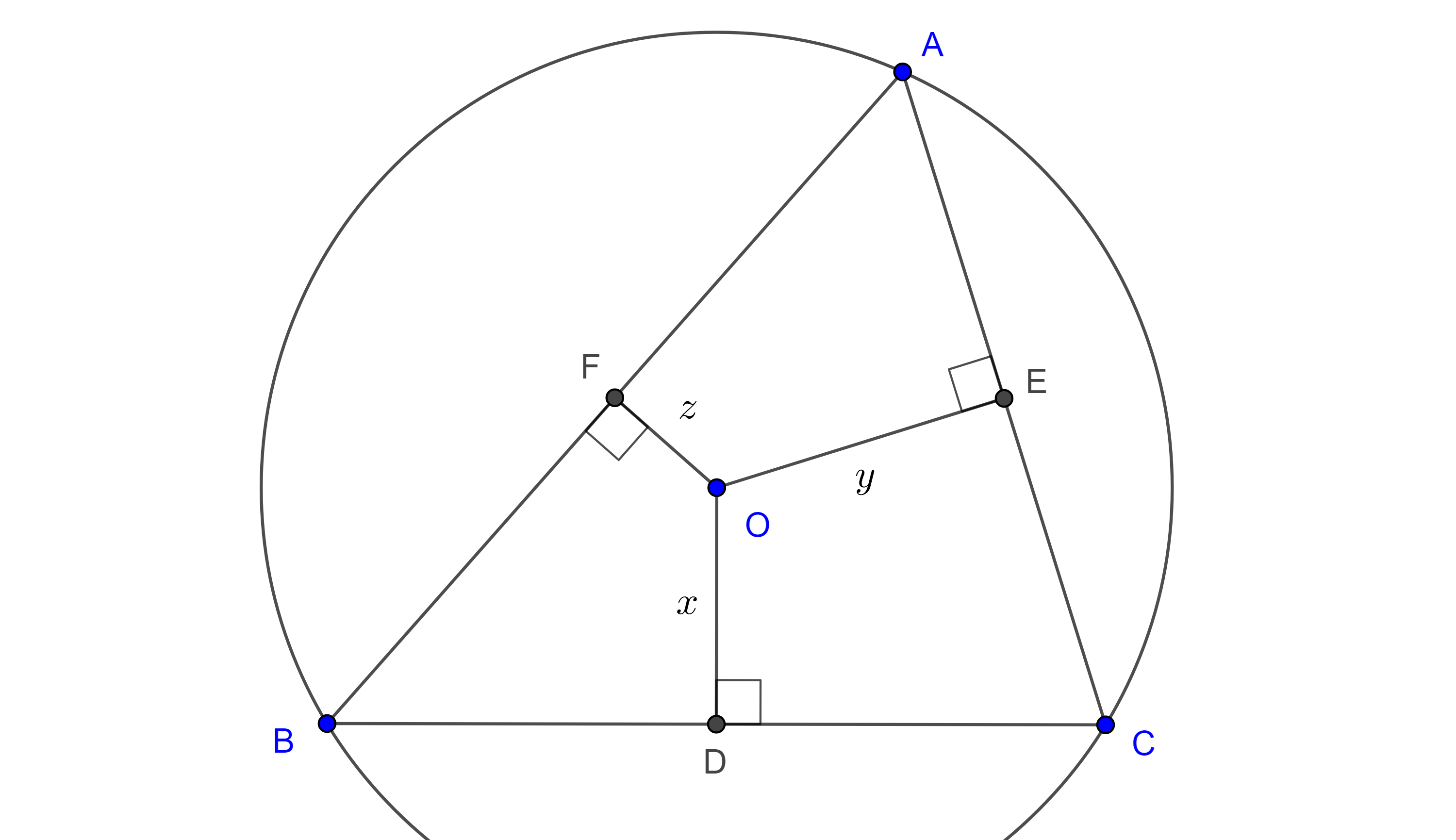
Teorema 2. Las rectas tangentes al circuncírculo de un triángulo a través de sus vértices intersecan a los lados opuestos del triángulo en tres puntos colineales.

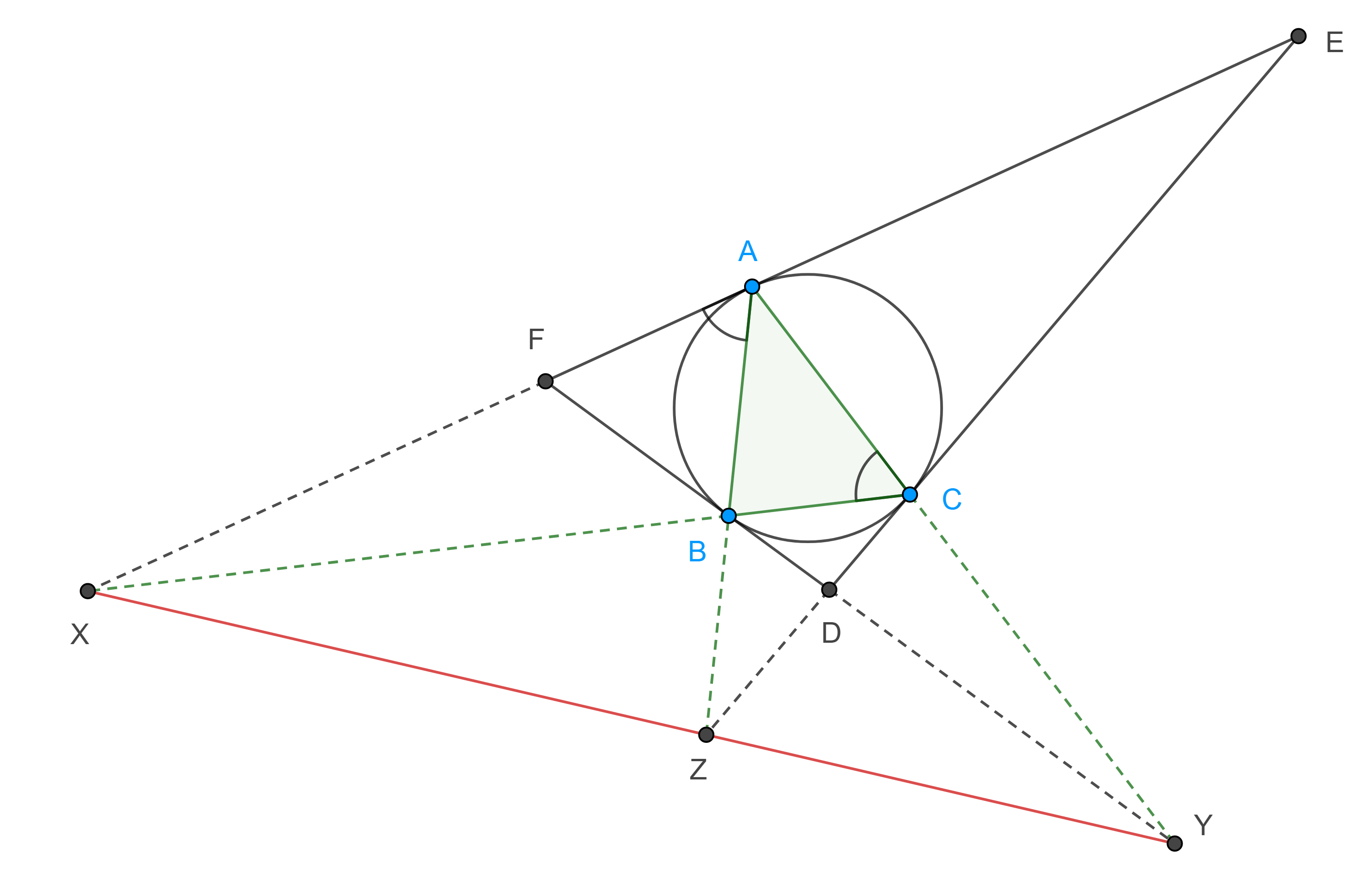
Demostración. Sean $\triangle ABC$ y $\triangle DEF$ su triángulo tangencial, sean $X = EF \cap BC$, $Y = DF \cap CA$ y $Z = DE \cap AB$.

Como el ángulo semiinscrito $\angle XAB$ abarca el mismo arco que el ángulo inscrito $\angle ACB$ entonces son iguales, por criterio de semejanza AA, $\triangle AXB \sim \triangle CXA$, por lo tanto,
$\dfrac{AX}{CX} = \dfrac{AB}{CA}$ $\Leftrightarrow \dfrac{AX^2}{CX^2} = \dfrac{AB^2}{CA^2}$.

Por otro lado, la potencia de $X$ respecto al circuncírculo de $\triangle ABC $ es
$AX^2 = XB \times XC$.

Por lo tanto,
$\begin{equation} \dfrac{XB}{XC} = \dfrac{AB^2}{CA^2}. \end{equation}$

Igualmente podemos encontrar,
$\dfrac{YC}{YA} = \dfrac{BC^2}{BA^2}$ y $\dfrac{ZB}{ZA} = \dfrac{CB^2}{CA^2}$.

Por lo tanto,
$\dfrac{XB}{XC} \dfrac{YC}{YA} \dfrac{ZA}{ZB} = \dfrac{AB^2}{CA^2} \dfrac{BC^2}{BA^2} \dfrac{CA^2}{CB^2} = 1$.

Considerando segmentos dirigidos tenemos
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = – 1$.

Como resultado, por el teorema de Menelao, $X$, $Y$ y $Z$ son colineales.

A la recta $XYZ$ se le conoce como recta de Lemoine de $\triangle ABC$.

$\blacksquare$

Observación 1. Notemos que $X$, $Y$ y $Z$ son los centros de las circunferencias de Apolonio de $\triangle ABC$.

Observación 2. También hemos mostrado que la tangente al circuncírculo de un triangulo por uno de sus vértices divide al lado opuesto al vértice, en la razón de los cuadrados de los lados que concurren en el vértice, ecuación $(4)$.

Corolario. Los lados del triángulo cuyos vértices son los puntos de tangencia del incírculo de un triángulo dado con sus lados, intersecan a los lados opuestos del triángulo dado en tres puntos colineales.

Demostración. Notemos que en el teorema anterior si el triángulo dado es $\triangle DEF$, entonces su incírculo es el circuncírculo de $\triangle ABC$.

Por lo tanto, se tiene el resultado.

A la recta $XYZ$ se le conoce como recta de Gergonne de $\triangle DEF$.

$\blacksquare$

Teorema de Monge

Teorema 3. Las tangentes externas comunes a tres circunferencias, tales que ninguna esta completamente contenida en las otras dos, se intersecan dos a dos en tres puntos colineales.

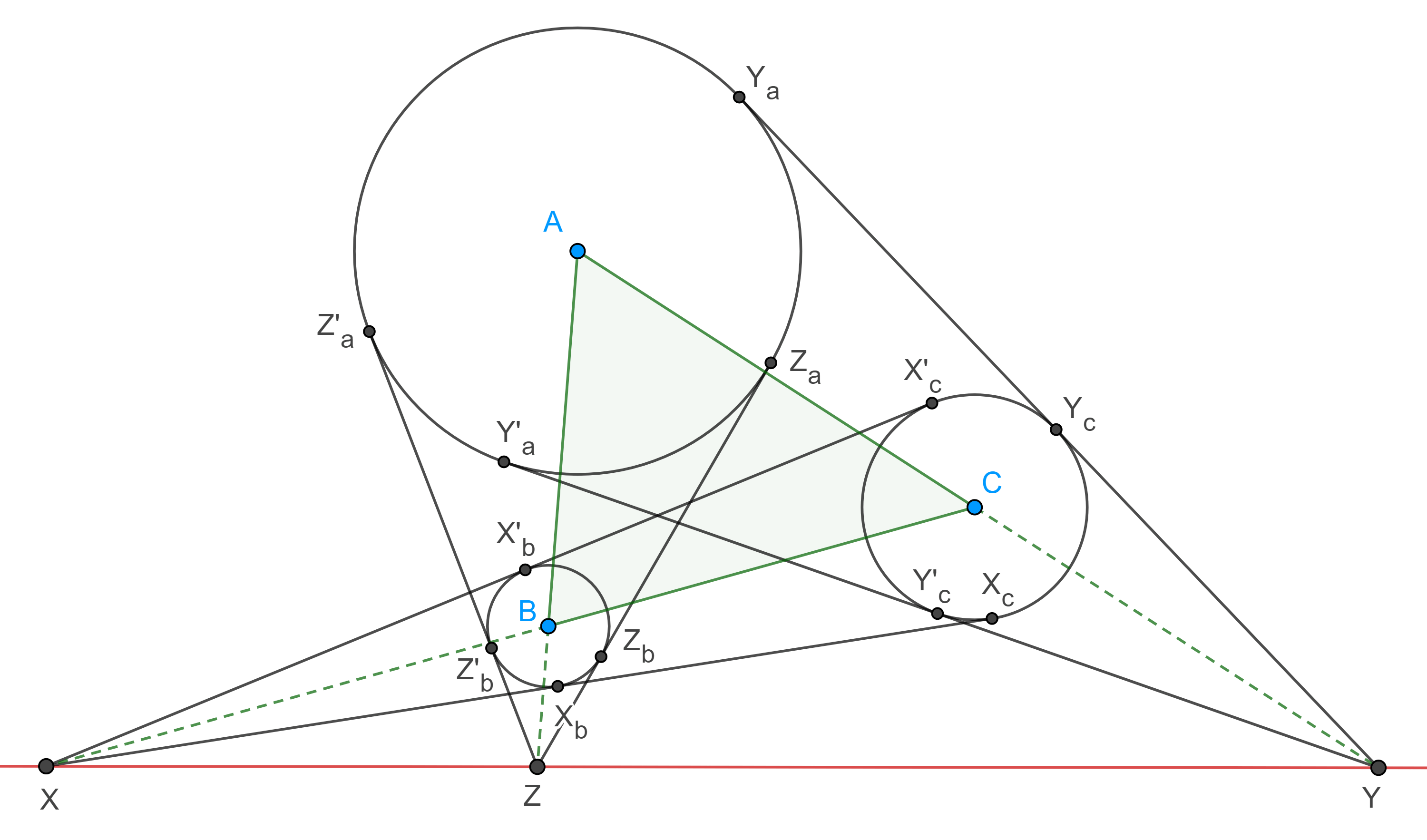
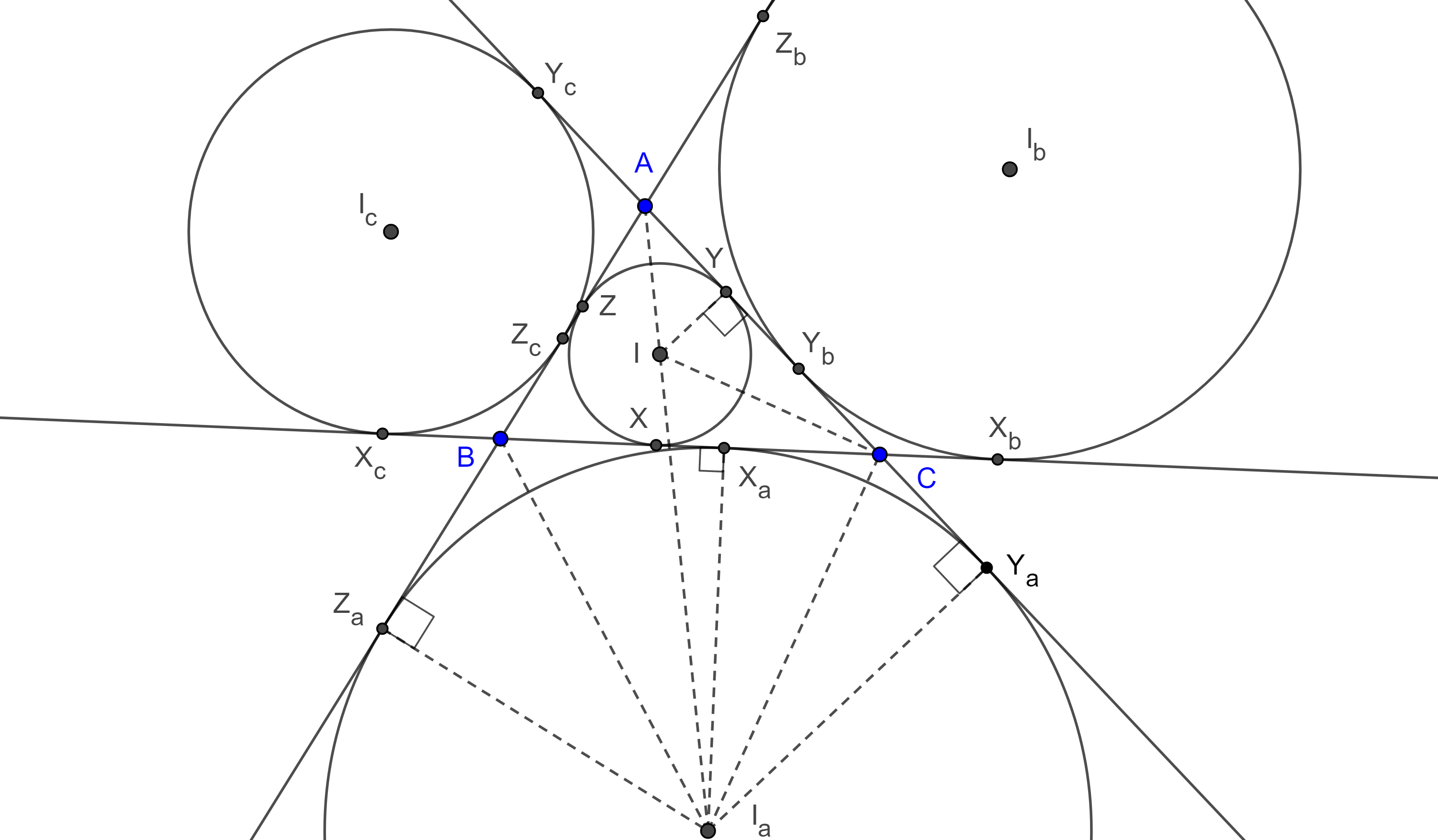
Demostración. Sean $\Gamma(A)$, $\Gamma(B)$ y $\Gamma(C)$, tres circunferencias que cumplen las hipótesis. Sean $X = X_bX_c \cap X’_bX’_c$, $Y = Y_aY_c \cap Y’_aY’_c$ y $Z = Z_aZ_b \cap Z’_aZ’_b$, las intersecciones de las tangentes comunes a $\Gamma(B)$, $\Gamma(C)$; $\Gamma(A)$, $\Gamma(C)$  y $\Gamma(A)$, $\Gamma(B)$ respectivamente (figura 4).

Recordemos que la intersección de dos tangentes externas comunes a dos circunferencias es un centro de homotecia entre dichas circunferencias.

Entonces $X$ es un centro de homotecia para $\Gamma(B)$ y $\Gamma(C)$, por lo tanto
$\dfrac{XB}{XC} = \dfrac{BX_b}{CX_c}$.

Igualmente vemos que
$\dfrac{YC}{YA} = \dfrac{CY_c}{AY_a}$ y $\dfrac{ZB}{ZA} = \dfrac{BZ_b}{AZ_a}$.

Tomando en cuenta que $AZ_a = AY_a$, $BZ_b = BX_b$ y $CX_c = CY_c$, tenemos
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = \dfrac{- AZ_a}{BZ_b} \dfrac{- BX_b}{CX_c} \dfrac{- CY_c}{AY_a} = – 1$.

Por lo tanto, por el teorema de Menelao $X$, $Y$ y $Z$ son colineales.

$\blacksquare$

Puntos isotómicos

Proposición 2. Los puntos isotómicos de tres puntos colineales son colineales.

Demostración. Recordemos que dos puntos en uno de los lados de un triángulo son isotómicos si equidistan al punto medio de ese lado.

Sean $\triangle ABC$ y $X$, $Y$, $Z$ en los lados $BC$, $CA$ y $AB$ respectivamente tal que $XYZ$ es una recta, consideremos $X’$, $Y’$ y $Z’$ sus correspondientes puntos isotómicos.

Entonces
$\dfrac{AZ’}{Z’B} \dfrac{BX’}{X’C} \dfrac{CY’}{Y’A} = \dfrac{ZB}{AZ} \dfrac{XC}{BX} \dfrac{YA}{CY} = (\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA})^-1 = – 1$.

Por lo tanto, por el teorema de Menelao $X’$, $Y’$ y $Z’$ son colineales.

$\blacksquare$

Proposición 3. Si sobre los lados de $\triangle ABC$ tenemos pares de puntos isotómicos $X$, $X’ \in BC$, $Y$, $Y’ \in CA$ y $Z$, $Z’ \in AB$ entonces las áreas de los triángulos $\triangle XYZ$ y $\triangle X’Y’Z’$ coinciden.

Demostración. Sean $U = ZY \cap BC$ y $U’ = Z’Y’ \cap BC$, consideremos $D$ y $F$ las proyecciones de $X$ y $C$ en $ZU$, entonces $\triangle XDU \sim \triangle CEU$.

Entonces,
$\dfrac{(\triangle XYZ)}{(\triangle CYZ)} = \dfrac{XD}{CE} = \dfrac{XU}{CU}$.

Igualmente vemos que, $\dfrac{(\triangle X’Y’Z’)}{(\triangle BY’Z’)} = \dfrac{X’U’}{BU’}$.

Por la proposición anterior, el punto isotómico de $U$ debe ser colineal con $Y’$ y $Z’$, por lo tanto, $U$ y $U’$ son isotómicos $\Rightarrow CU = U’B$ y $XU = U’X’$.

Por lo tanto $\dfrac{(\triangle XYZ)}{( \triangle CYZ)} = \dfrac{(\triangle X’Y’Z’)}{( \triangle BY’Z’)}$.

Pero $(\triangle CYZ) = (\triangle AY’Z) = (\triangle BY’Z’)$.

Por lo tanto, $\triangle XYZ$ y $\triangle X’Y’Z’$ tienen la misma área.

$\blacksquare$

Más adelante…

Con la ayuda del teorema de Menelao, en la próxima entrada definiremos y estableceremos algunos resultados sobre triángulos en perspectiva. También mostraremos el teorema de Pascal.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Prueba que si una recta que pasa por el centroide $G$ de un triangulo $\triangle ABC$ interseca a $AB$ y $AC$ en $Z$ e $Y$ respectivamente, entonces $AZ \times YC + AY \times ZB = AZ \times AY$.
2. Una recta interseca los lados de un cuadrilátero $\square ABCD$, $BC$, $CD$, $DA$ y $AB$ en $X$, $Y$, $Z$ y $W$ respectivamente, muestra que $\dfrac{BX}{XC} \dfrac{CY}{YD} \dfrac{DZ}{ZA} \dfrac{AW}{WB} = 1$.
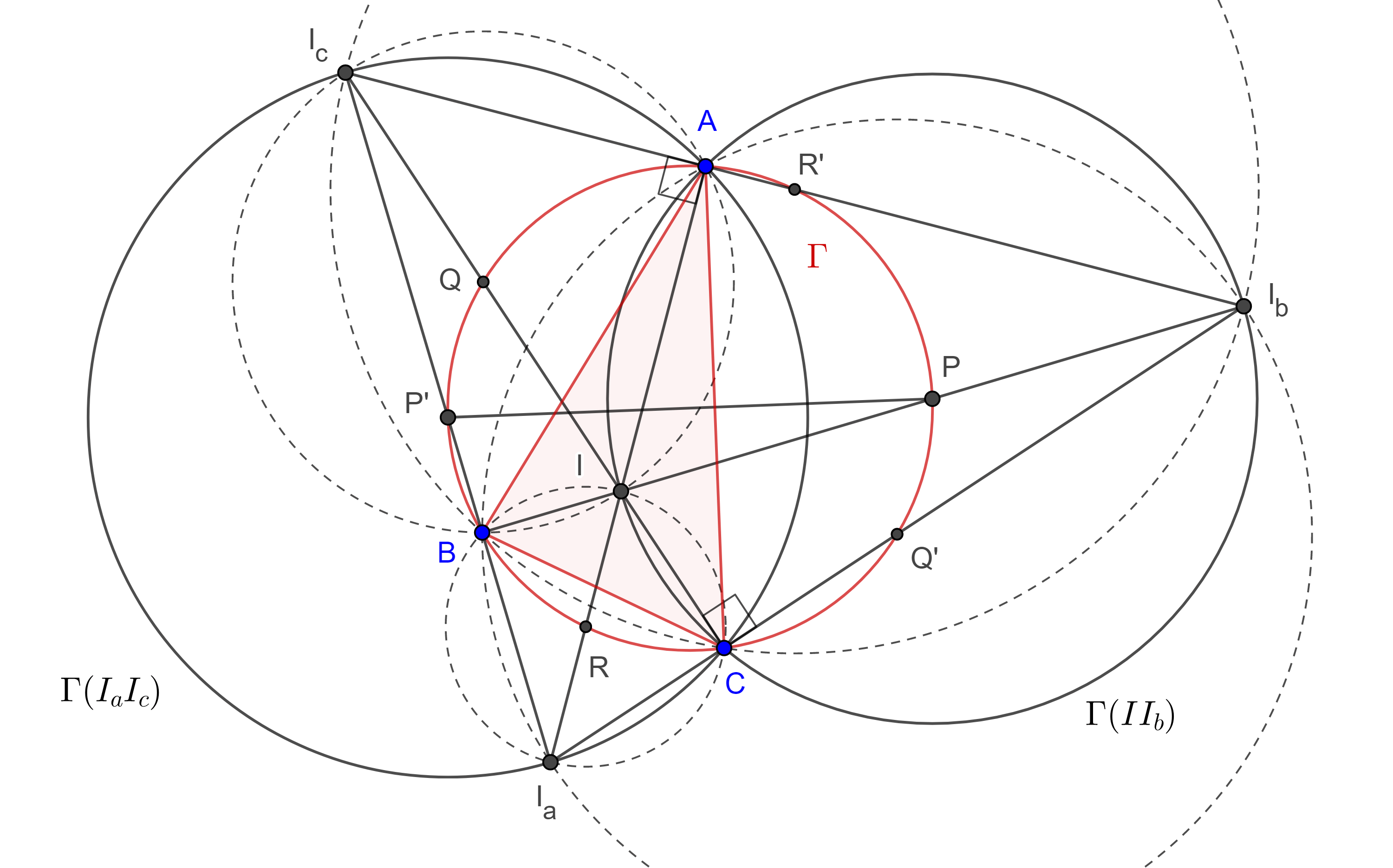
3. Una circunferencia cuyo centro es equidistante a los vértices $B$ y $C$ de un triángulo $\triangle ABC$ interseca a $AB$ en $P$ y $P’$ y a $AC$ en $Q’$ y $Q$, las rectas $PQ$ y $P’Q’$ intersecan a $BC$ en $X$ y $X’$ respectivamente, muestra que:
   $i)$ $BX \times BX’ = CX \times CX’$,
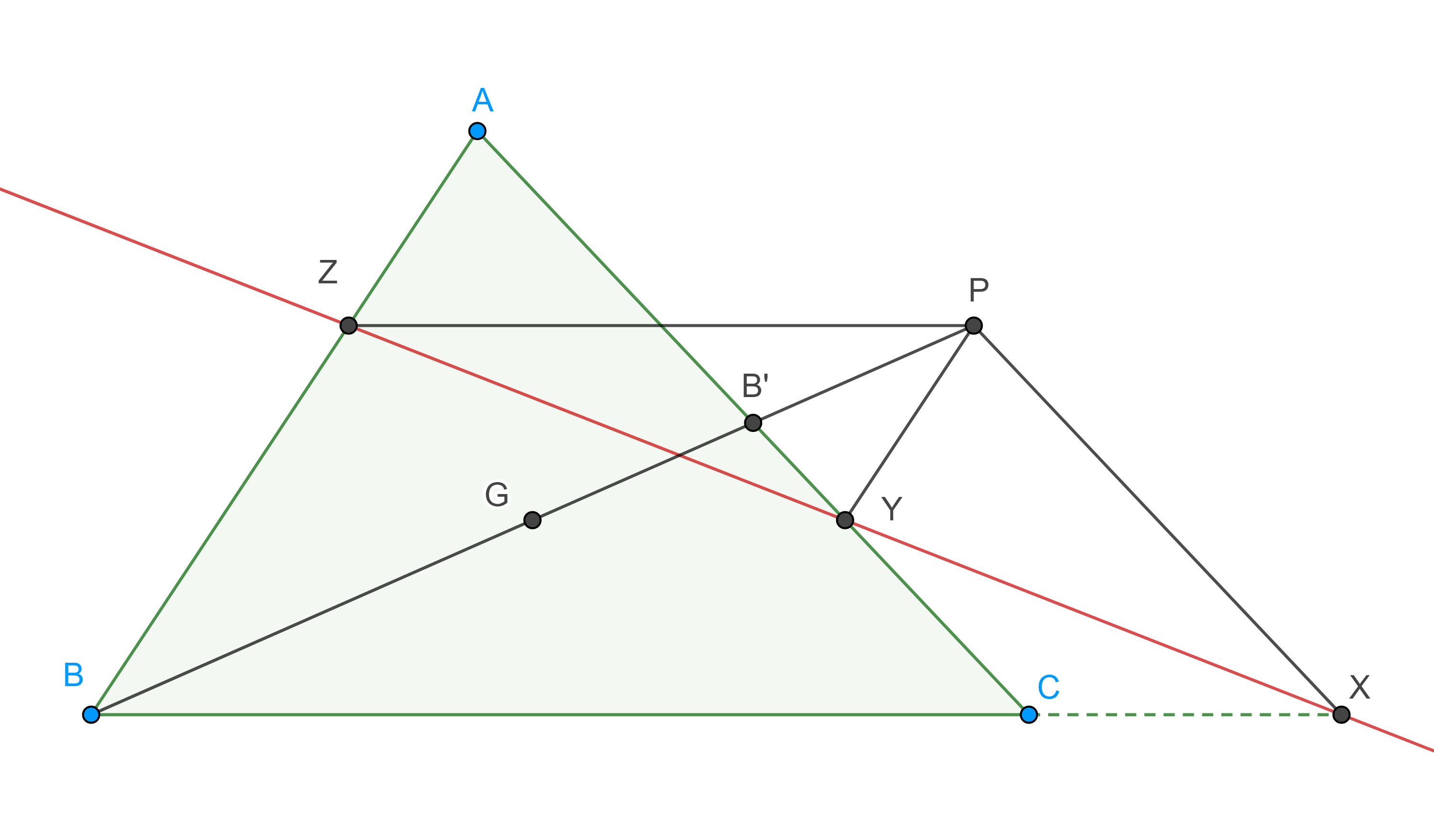
   $ii)$ $X$ y $X’$ son puntos isotómicos.
4. Sean $\triangle ABC$ y $B’$ el punto medio de $CA$, considera $G$ el centroide de $\triangle ABC$, sea $P$ tal que $B’$ es el punto medio de $GP$, la paralela a $AC$ por $P$ interseca a $BC$ en $X$, la paralela a $AB$ por $P$ corta a $AC$ en $Y$, la paralela a $BC$ por $P$ interseca a $AB$ en $Z$ (figura 7), muestra que $X$, $Y$ y $Z$ son colineales.

5. Demuestra que las mediatrices de las bisectrices de los ángulos internos de un triángulo, intersecan a los lados opuestos a los ángulos desde donde se trazo la bisectriz, en tres puntos colineales. Considera el segmento de bisectriz formado por el vértice y el punto de intersección con el lado opuesto.
6. Considera $XYZ$ y $X’Y’Z’$ dos rectas transversales a los lados de un triángulo $\triangle ABC$, tales que $X$, $X’ \in BC$, $Y$, $Y’ \in CA$ y $Z$, $Z’ \in AB$, sean $D = Z’Y \cap BC$, $E = X’Z \cap CA$ y $F = Y’X \cap AB$, prueba que $D$, $E$ y $F$ son colineales.
7. Demuestra el teorema de la recta de Simson usando el teorema de Menelao.
8. Dadas tres circunferencias tales que dos a dos sus interiores son ajenos, muestra que las tangentes comunes externas de dos de ellas se intersecan en un punto colineal con las intersecciones de las tangentes comunes internas de esas dos circunferencias con la tercera.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Puntos de Fermat y triángulos de Napoleón.
• Siguiente entrada del curso: Triángulos en perspectiva.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 153-158.
• Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 57-68.
• Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 36-42.
• Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 85-88.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»