Archivo de la etiqueta: criterio LAL

Geometría Moderna I: Semejanza de triángulos

Por Rubén Alexander Ocampo Arellano

Introducción

En esta entrada estudiamos otro tipo de relación, la de semejanza de triángulos, la cual es una de las herramientas más útiles en geometría euclidiana.

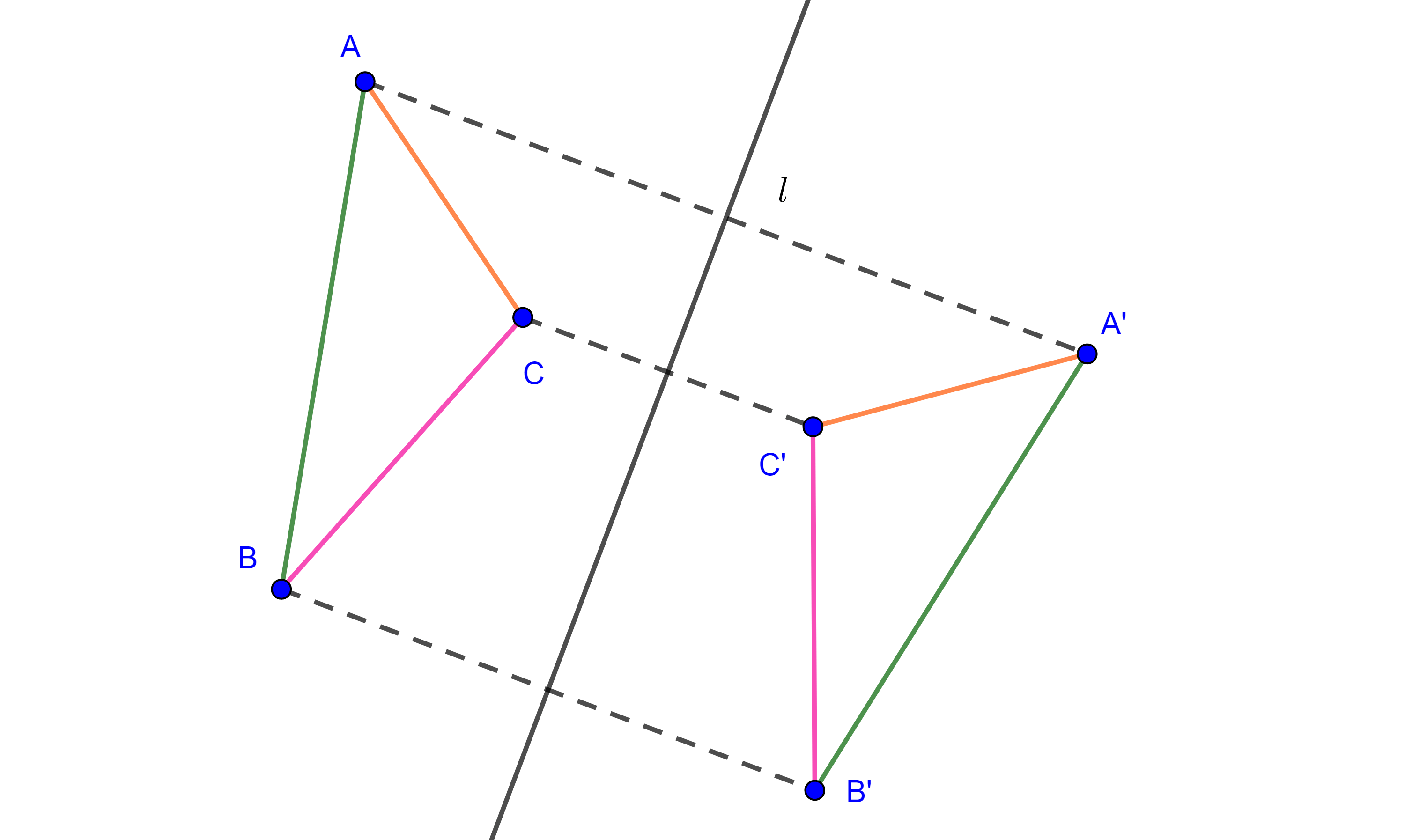
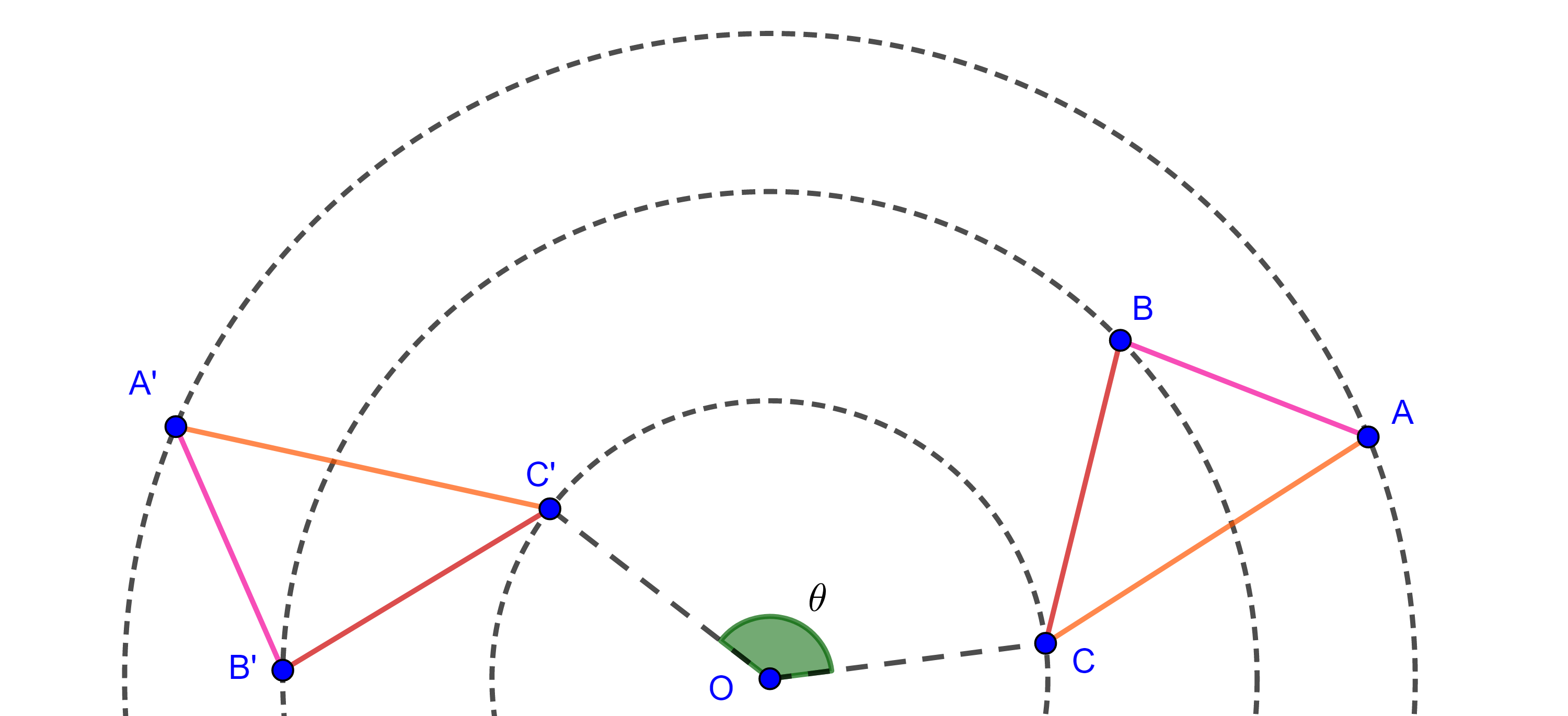
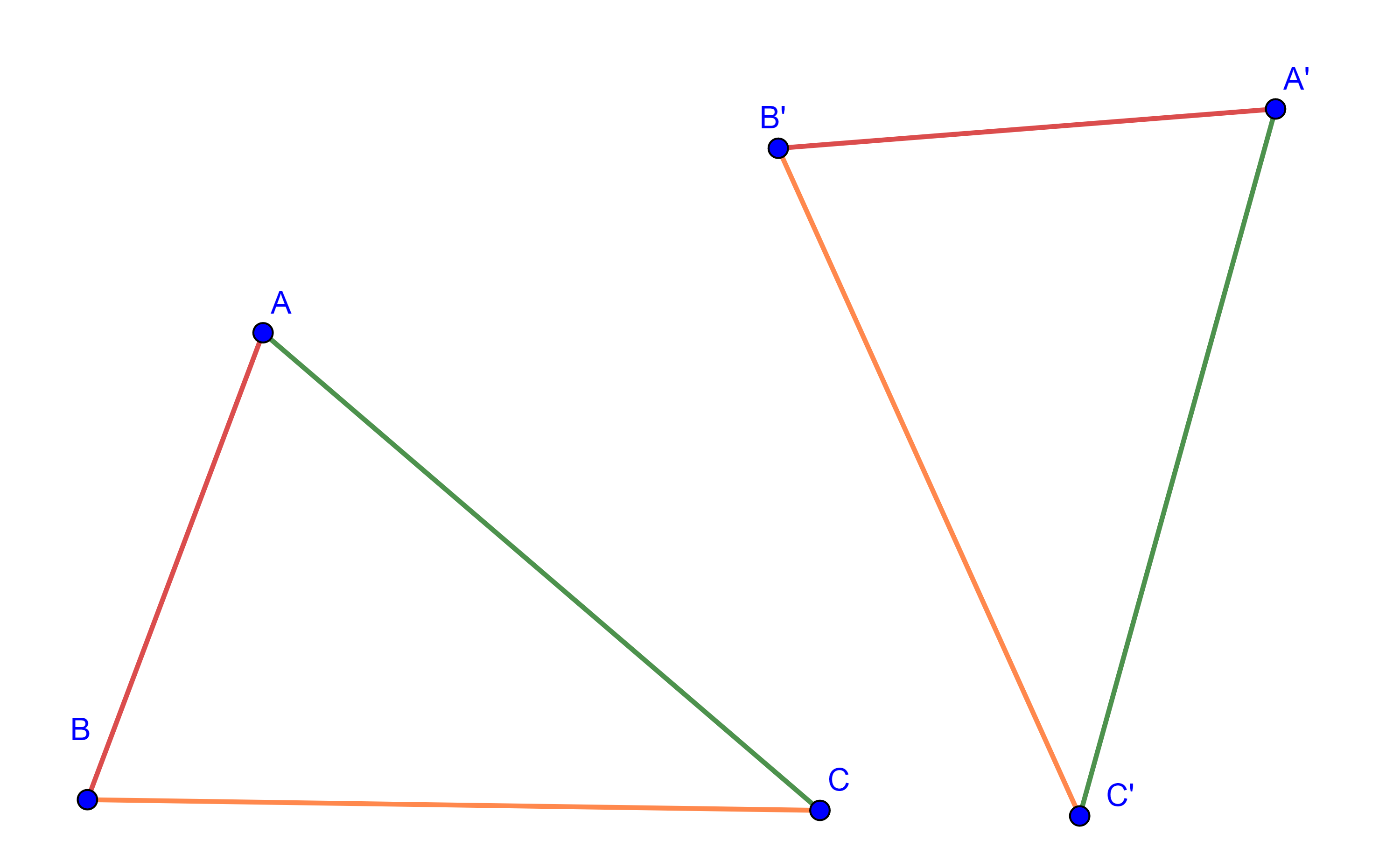
Definición. Decimos que dos triángulos $△ A B C$ y $△ A^{'} B^{'} C^{'}$ son semejantes si sus ángulos respectivos son iguales y sus lados respectivos son proporcionales, es decir,

$∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ , $∠ C = ∠ C^{'}$ y
$\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{A C}{A^{'} C^{'}}$ .

Si dos triángulos son semejantes lo denotamos así $△ A B C \sim △ A^{'} B^{'} C^{'}$ .

Criterio de semejanza ángulo, ángulo, ángulo (AAA o AA)

Teorema 1, criterio de semejanza ángulo, ángulo, ángulo. Si los ángulos correspondientes de dos triángulos son iguales entonces los triángulos son semejantes.

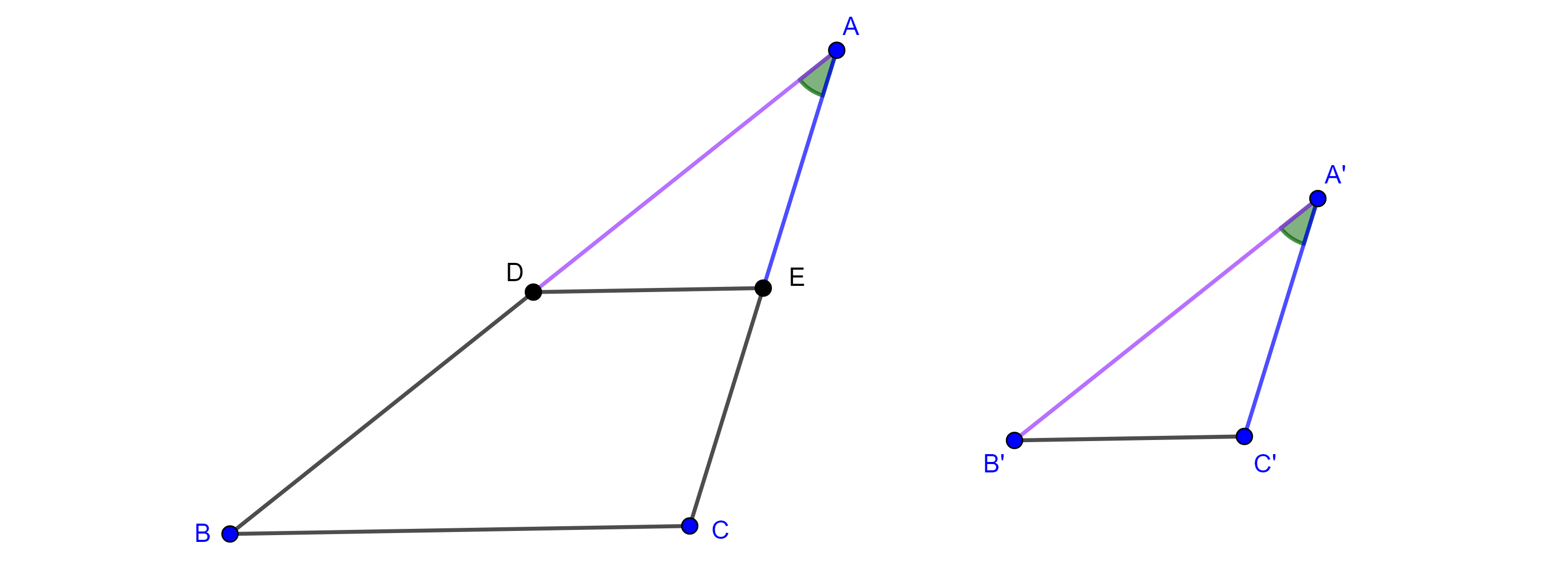
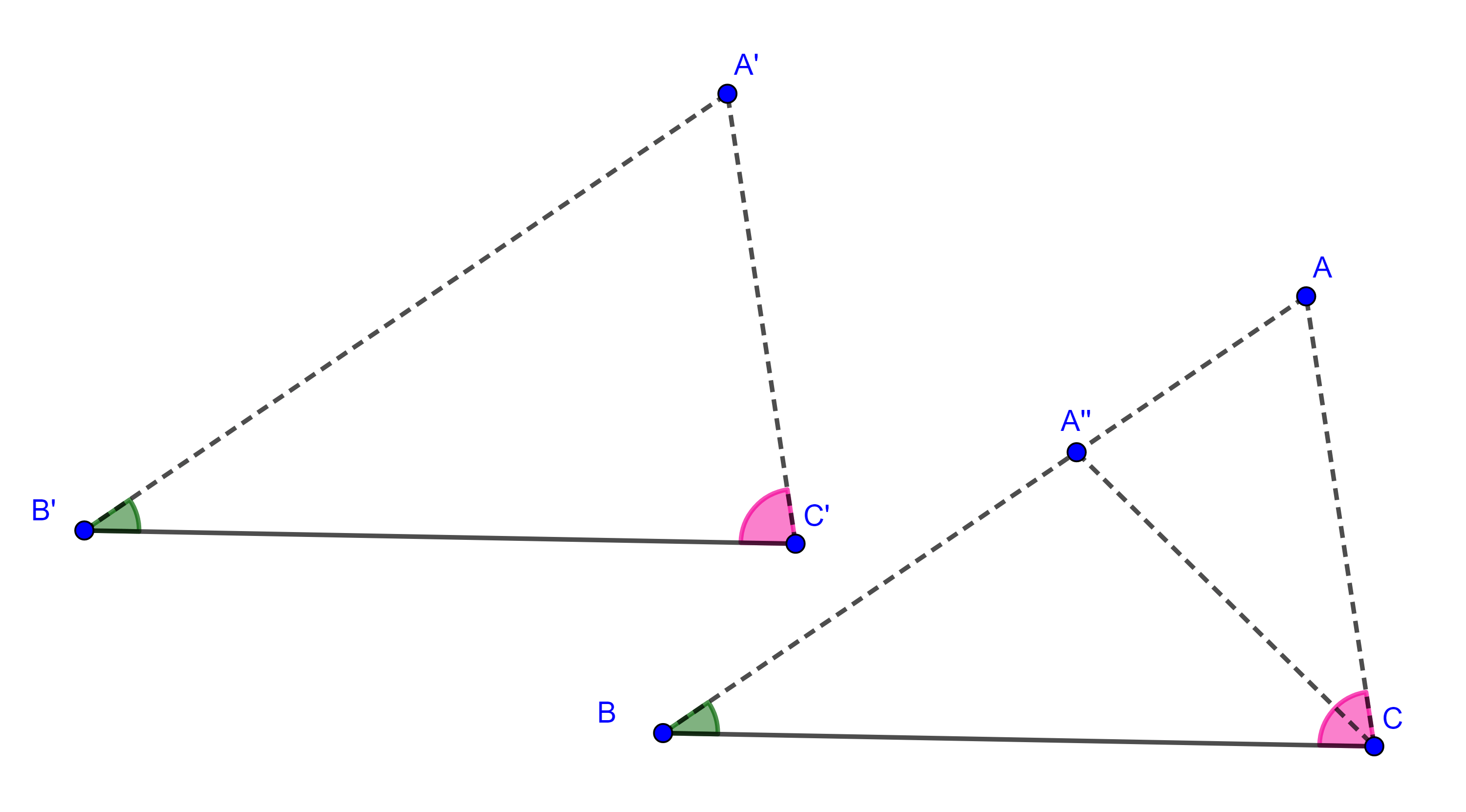
Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ dos triángulos tales que $∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ , $∠ C = ∠ C^{'}$ . Por demostrar que los lados correspondientes son proporcionales.

Sean $D \in A B$ y $E \in A C$ tales que $A D = A^{'} B^{'}$ y $A E = A^{'} C^{'}$ , como $∠ A = ∠ A^{'}$ , por el criterio de congruencia LAL, tenemos que los triángulos $△ A D E ≅ △ A^{'} B^{'} C^{'}$ .

Por lo tanto, $∠ E D A = ∠ C^{'} B^{'} A^{'}$ , $∠ A E D = ∠ A^{'} C^{'} B^{'}$ y $D E = B^{'} C^{'}$ .

Dado que $A B$ es transversal a $D E$ y $B C$ y los ángulos correspondientes son iguales, entonces $D E ∥ B C$ .

Por el teorema de Tales, $\frac{A B}{A D} = \frac{A C}{A E} = \frac{B C}{D E}$ ,
$\Rightarrow \frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$ .

Así, $△ A B C \sim △ A^{'} B^{'} C^{'}$ .

Observación. Como la suma de los ángulos internos de todo triangulo es igual a $π$ , entonces si conocemos la magnitud de dos ángulos internos conocemos los tres y por lo tanto podemos referirnos a este criterio como AA.

Criterio de semejanza lado, ángulo, lado (LAL)

Teorema 2, criterio de semejanza lado, ángulo, lado. Si dos triángulos tienen dos lados correspondientes proporcionales y el ángulo entre ellos es igual, entonces los triángulos son semejantes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ dos triángulos tales que $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}}$ y $∠ A = ∠ A^{'}$ .

Sean $D \in A B$ y $E \in A C$ tales que $A D = A^{'} B^{'}$ y $A E = A^{'} C^{'}$ .

Como $∠ A = ∠ A^{'}$ por el criterio de congruencia LAL, $△ A D E ≅ △ A^{'} B^{'} C^{'}$ , así $∠ E D A = ∠ C^{'} B^{'} A^{'}$ y $∠ A E D = ∠ A^{'} C^{'} B^{'}$ .

Por hipótesis sabemos que $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}}$
$\Rightarrow \frac{A B}{A D} = \frac{A C}{A E}$ .

Esto implica, por el reciproco del teorema de Tales, que $D E ∥ B C$ , se sigue que $∠ C B A = ∠ E D A$ y $∠ A C B = ∠ A E D$ por ser ángulos correspondientes.

Por transitividad, $∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ y $∠ C = ∠ C^{'}$

Por criterio de semejanza AAA, $△ A B C \sim △ A^{'} B^{'} C^{'}$ .

Criterio de semejanza lado, lado, lado (LLL)

Teorema 3, criterio de semejanza lado, lado, lado. Si los lados correspondientes de dos triángulos son proporcionales entonces los triángulos son semejantes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ dos triángulos tales que $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{A C}{A^{'} C^{'}}$ , por demostrar que $∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ y $∠ C = ∠ C^{'}$ .

Sean $D \in A B$ y $E \in A C$ tales que $A D = A^{'} B^{'}$ y $A E = A^{'} C^{'}$ (figura 2).

Como $∠ B A C = ∠ D A E$ y $\frac{A B}{A D} = \frac{A C}{A E}$ , por criterio de semejanza LAL, $△ A B C \sim △ A D E$ , y en consecuencia $\frac{A B}{A D} = \frac{B C}{D E}$ .

$A D = A^{'} B^{'}$ , por construcción, y $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}}$ por hipótesis,
$\Rightarrow \frac{B C}{B^{'} C^{'}} = \frac{A B}{A^{'} B^{'}} = \frac{A B}{A D} = \frac{B C}{D E}$
$\Rightarrow B^{'} C^{'} = D E$ .

Por criterio de congruencia LLL, $△ A^{'} B^{'} C^{'} ≅ △ A D E$ .

Por transitividad, $△ A B C \sim △ A^{'} B^{'} C^{'}$ .

Triángulos con lados perpendiculares

Proposición 1. Dos triángulos cuyos lados correspondientes son perpendiculares son semejantes.

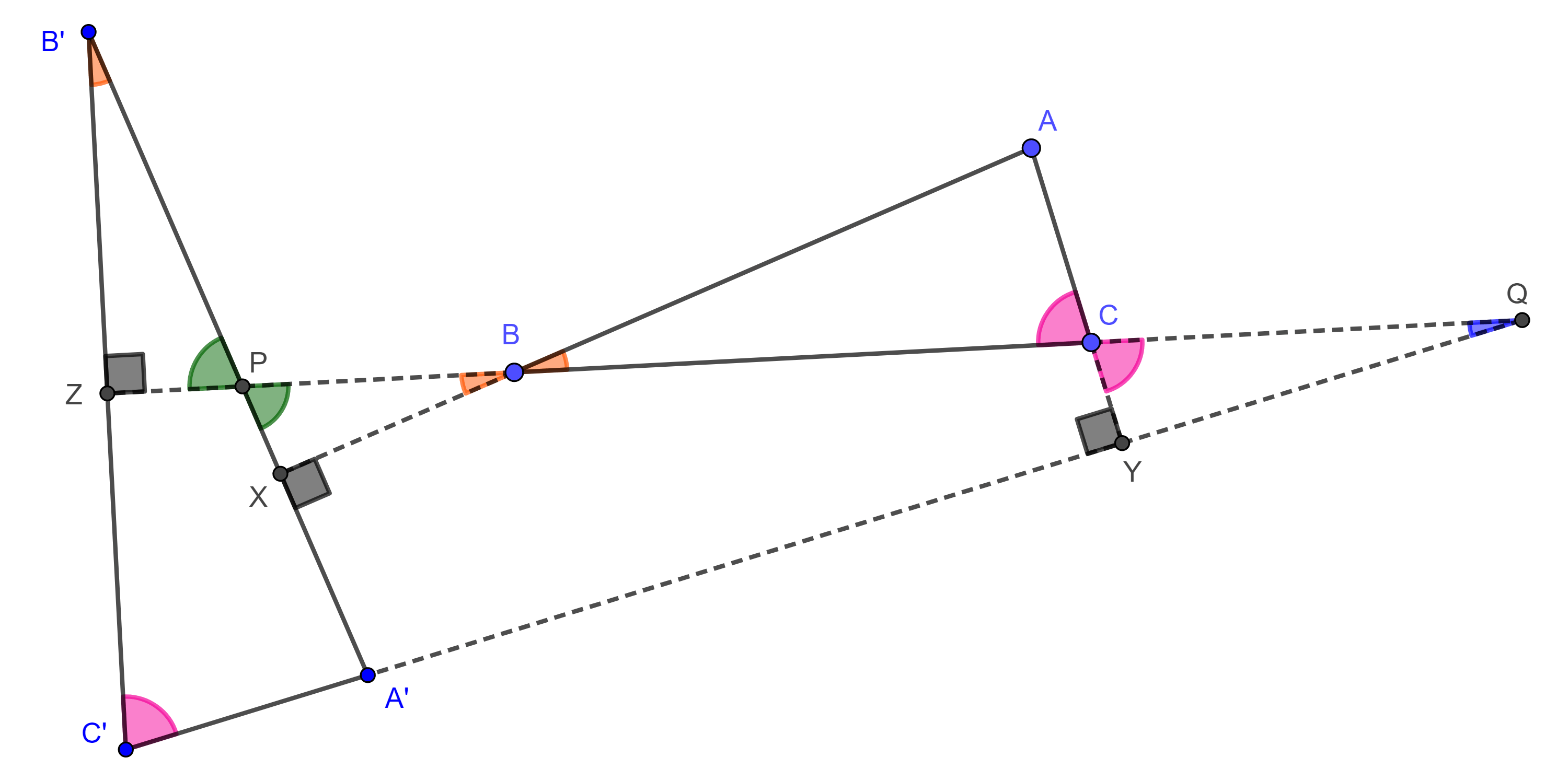
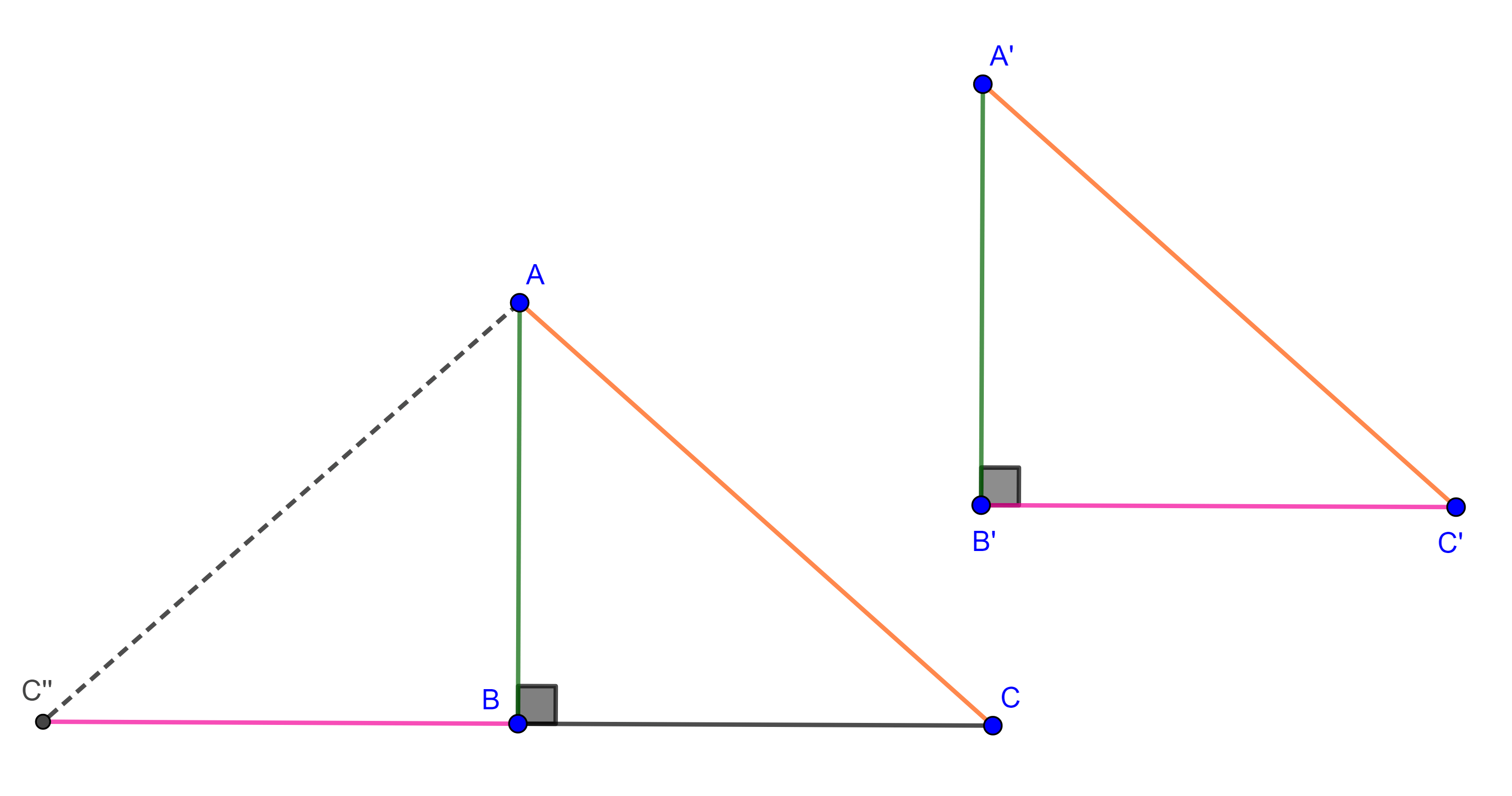
Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ tales que $A B ⊥ A^{'} B^{'}$ , $B C ⊥ B^{'} C^{'}$ y $A C ⊥ A^{'} C^{'}$ .

Consideremos $Z$ , $P$ y $Q$ las intersecciones de $B C$ con $B^{'} C^{'}$ , $A^{'} B^{'}$ y $A^{'} C^{'}$ respectivamente, $X = A B \cap A^{'} B^{'}$ e $Y = A C \cap A^{'} C^{'}$ (figura 3).

$∠ C B A = ∠ P B X$ , por ser opuestos por el vértice,
como $△ B X P$ es rectángulo entonces $∠ P B X$ y $∠ X P B$ son complementarios,
$\Rightarrow ∠ C B A$ y $∠ X P B$ son complementarios,
$∠ X P B = ∠ B^{'} P Z$ , por ser opuestos por el vértice,
$\Rightarrow ∠ C B A$ y $∠ B^{'} P Z$ son complementarios.

Como $△ B^{'} Z P$ es rectángulo entonces $∠ B^{'} P Z$ y $∠ Z B^{'} P$ son complementarios,
$\Rightarrow ∠ C B A = ∠ Z B^{'} P$ ,
$\Rightarrow ∠ B^{'} = ∠ B$ .

Por otro lado, $∠ A C B = ∠ Y C Q$ , por ser opuestos por el vértice,
como $△ C Y Q$ es rectángulo entonces $∠ Y C Q$ y $∠ C Q Y$ son complementarios,
$\Rightarrow ∠ A C B$ y $∠ C Q Y$ son complementarios.

Como $△ C^{'} Z Q$ es rectángulo entonces $∠ Q C^{'} Z$ y $∠ C Q Y$ son complementarios,
$\Rightarrow ∠ A C B = ∠ Q C^{'} Z$ ,
$\Rightarrow ∠ C = ∠ C^{'}$ .

Por criterio de semejanza AA, $△ A B C \sim △ A^{'} B^{'} C^{'}$ .

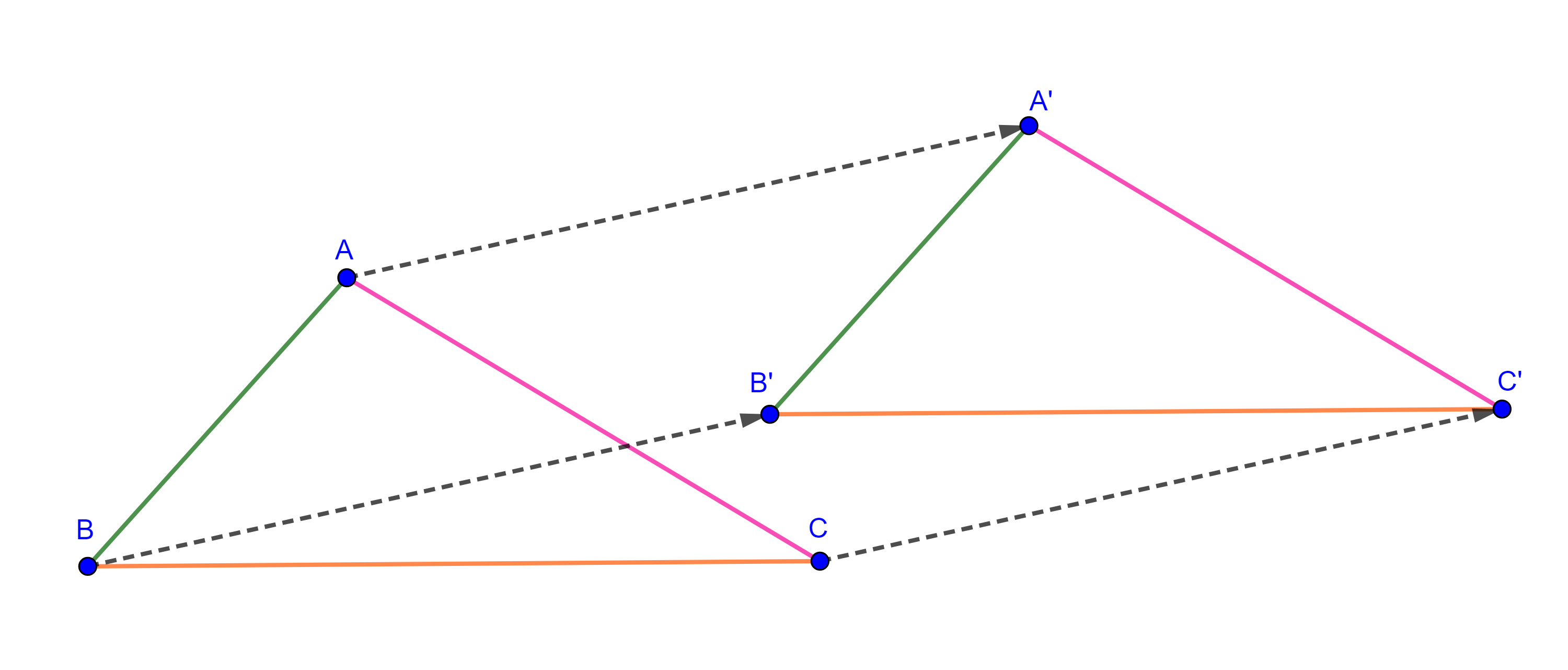
Proposición 2. Dos triángulos cuyos lados correspondientes son paralelos son semejantes.

Demostración. Podemos construir un triángulo cuyos lados correspondientes sean perpendiculares a los lados de uno de los triángulos, por transitividad sus lados también serán perpendiculares a los lados del segundo triangulo.

Por la proposición anterior los triángulos originales serán semejantes al triangulo construido y por lo tanto serán semejantes entre sí.

Desigualdad entre bisectrices

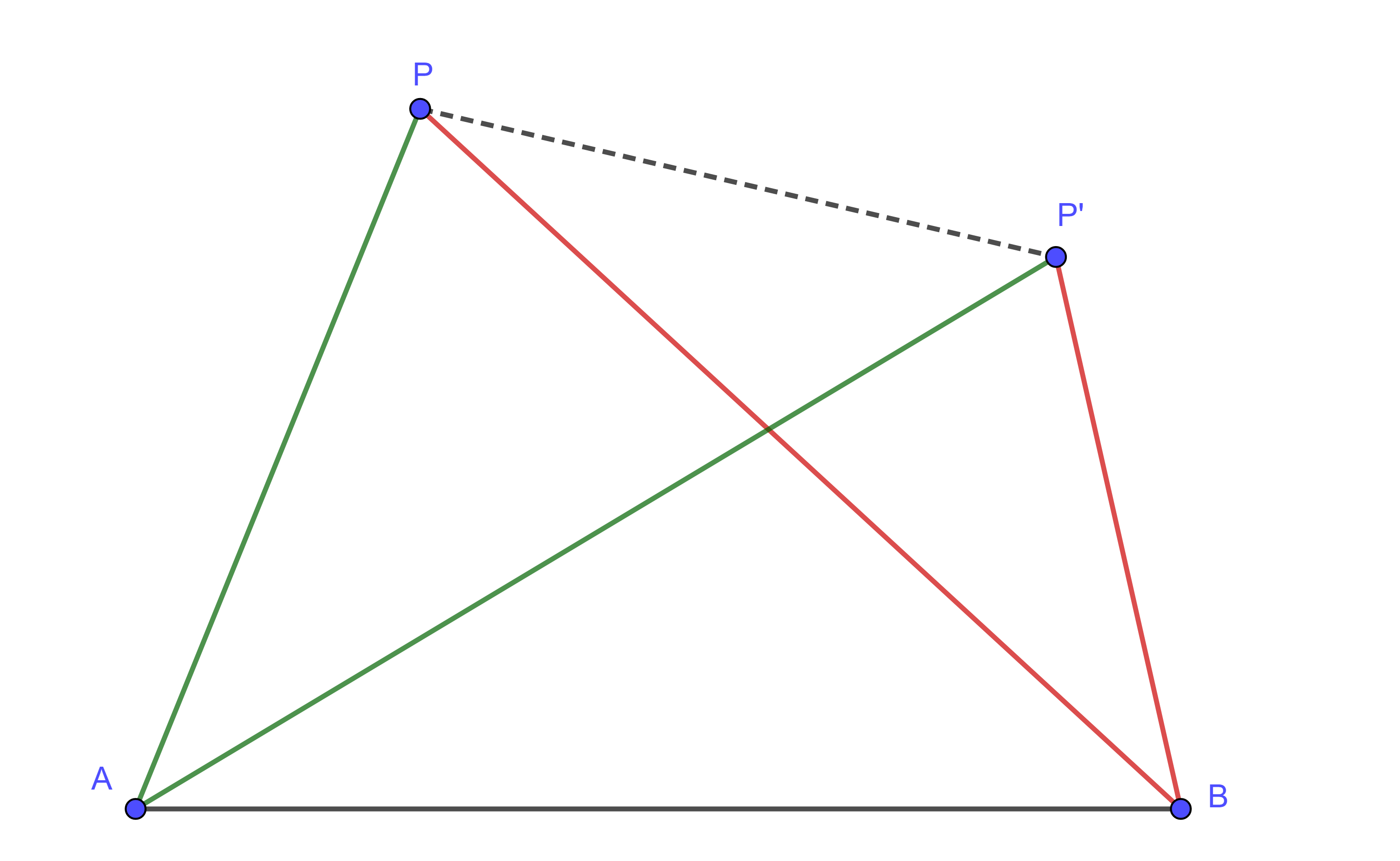
Proposición 3. En un triángulo entre cualesquiera dos ángulos internos la bisectriz del mayor es menor a la bisectriz del menor de los ángulos.

Demostración. Sea $△ A B C$ y supongamos que $∠ B > ∠ C$ y sean $D$ y $E$ las intersecciones de las bisectrices de los ángulos $∠ B$ y $∠ C$ respectivamente con los lados opuestos. Debemos mostrar que $B D < C E$ .

Sean $F \in A D$ tal que $∠ D B F = ∠ A C E = ∠ E C B$ y $G$ la intersección de $C E$ con $B F$ , por criterio de semejanza AA, $△ F B D \sim △ F C G$ , por lo tanto,

$\begin{matrix} (1) & \frac{B F}{C F} = \frac{B D}{C G} . \end{matrix}$

Por otro lado, en el triángulo $△ B F C$ tenemos que
$∠ C B F = ∠ C B D + ∠ D B F$
$= \frac{∠ B}{2} + \frac{∠ C}{2} > \frac{∠ C}{2} + \frac{∠ C}{2} = ∠ C$ .

Como al ángulo mayor siempre se opone a el lado mayor, tenemos que $F C > B F$ $\Leftrightarrow$ $1 > \frac{B F}{C F} = \frac{B D}{C G}$ .

Donde la última igualdad se da por la ecuación $(1)$

Por lo tanto, $C E > C G > B D$ .

Semejanza en el triángulo rectángulo

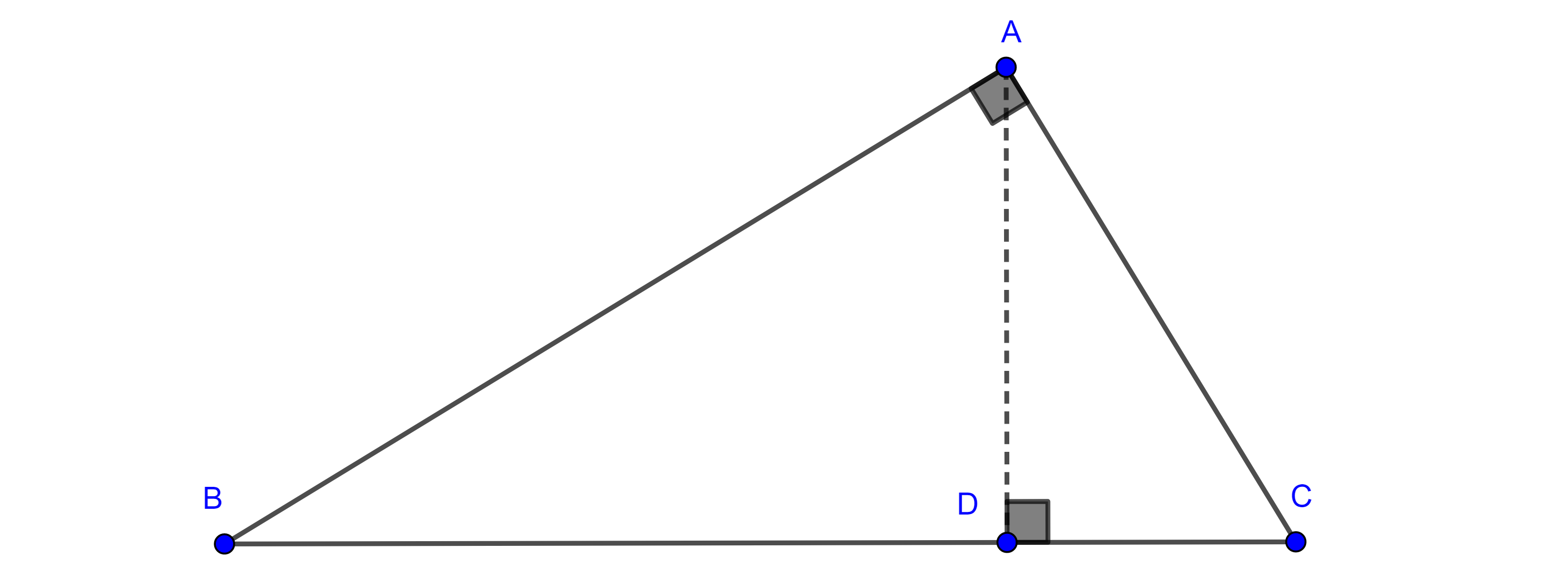
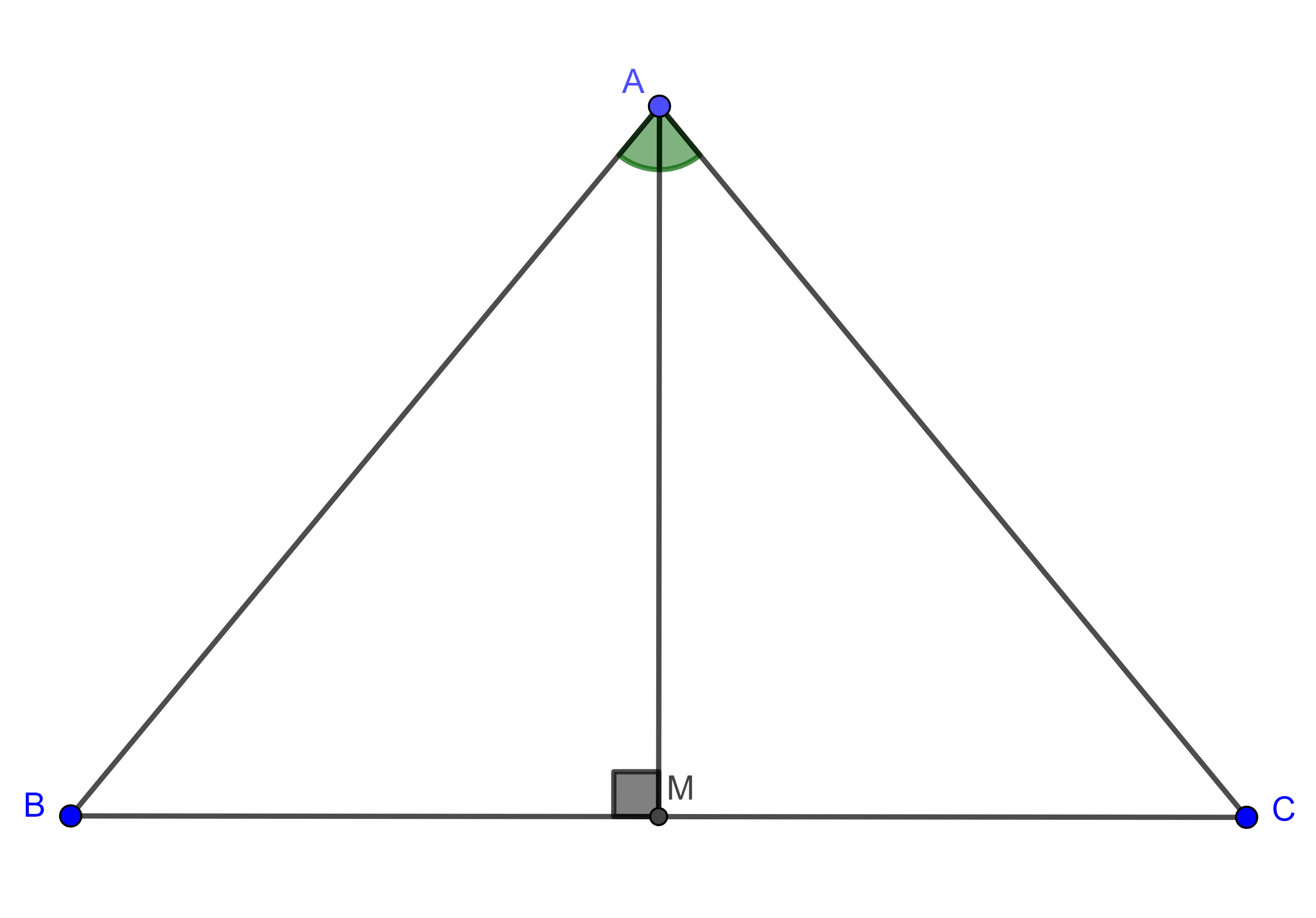
Proposición 4. Sean $△ A B C$ un triángulo rectángulo con $∠ A = \frac{π}{2}$ y $D$ el pie de la perpendicular a $\overset{―}{B C}$ trazada desde $A$ , entonces:
$i)$ $A D^{2} = B D \times D C$ ,
$i i)$ $A B^{2} = B C \times B D$ ,
$i i i)$ $A C^{2} = B C \times D C$ ,
$i v)$ $A D \times B C = A B \times A C$ .

Demostración. Por criterio de semejanza AA, $△ A B C \sim △ D B A$ y $△ A B C \sim △ D A C$ ,

$i)$ Por la relación de semejanza tenemos
$\frac{A D}{A C} = \frac{B D}{A B} \Rightarrow A D = \frac{B D \times A C}{A B}$ ,
$\frac{A D}{A B} = \frac{D C}{A C} \Rightarrow A D = \frac{D C \times A B}{A C}$
$\Rightarrow A D^{2} = B D \times D C$

$i i)$ Como $△ A B C \sim △ D B A$ , $\frac{A B}{B D} = \frac{B C}{A B}$
$\Rightarrow A B^{2} = B C \times B D$

$i i i)$ Como $△ A B C \sim △ D A C$ , $\frac{A C}{D C} = \frac{B C}{A C}$
$\Rightarrow A C^{2} = B C \times D C$

$i v)$ de $i i)$ y $i i i)$ tenemos $B C^{2} = \frac{A B^{2} \times A C^{2}}{B D \times D C}$
y empleando $i)$ obtenemos $A D^{2} \times B C^{2} = (B D \times D C) \frac{A B^{2} \times A C^{2}}{B D \times D C}$
$\Rightarrow A D \times B C = A B \times A C$ .

Más adelante…

En la siguiente entrada comenzaremos a distinguir el sentido en el que recorremos un sementó de recta y si la razón en que un punto divide a un segmento es negativa o positiva. Haciendo uso de segmentos dirigidos mostraremos el teorema de Stewart.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra el teorema de Pitágoras usando semejanza de triángulos.
Criterio de semejanza hipotenusa-cateto, muestra que un par de triángulos rectángulos son semejantes si la razón entre sus hipotenusas y la razón entre uno de sus catetos son iguales.
Muestra que si en un triángulo dos bisectrices internas tienen la misma longitud, entonces el triángulo es isósceles.
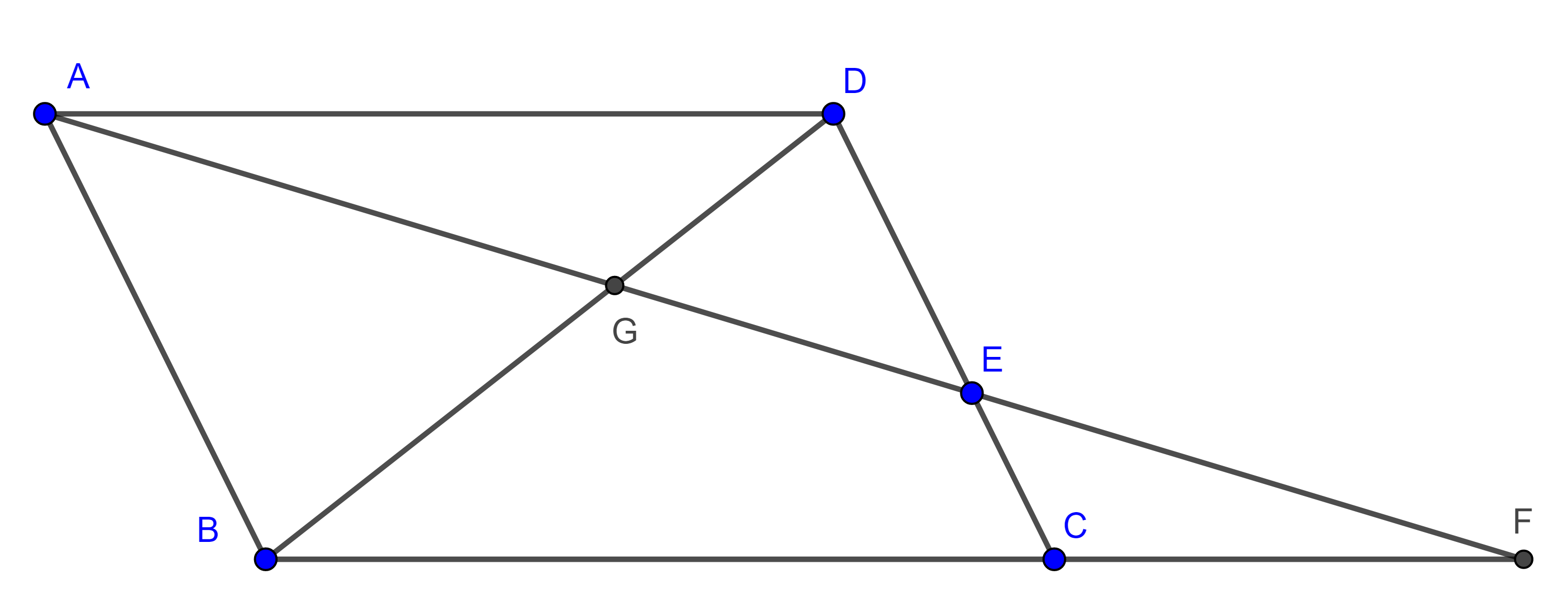
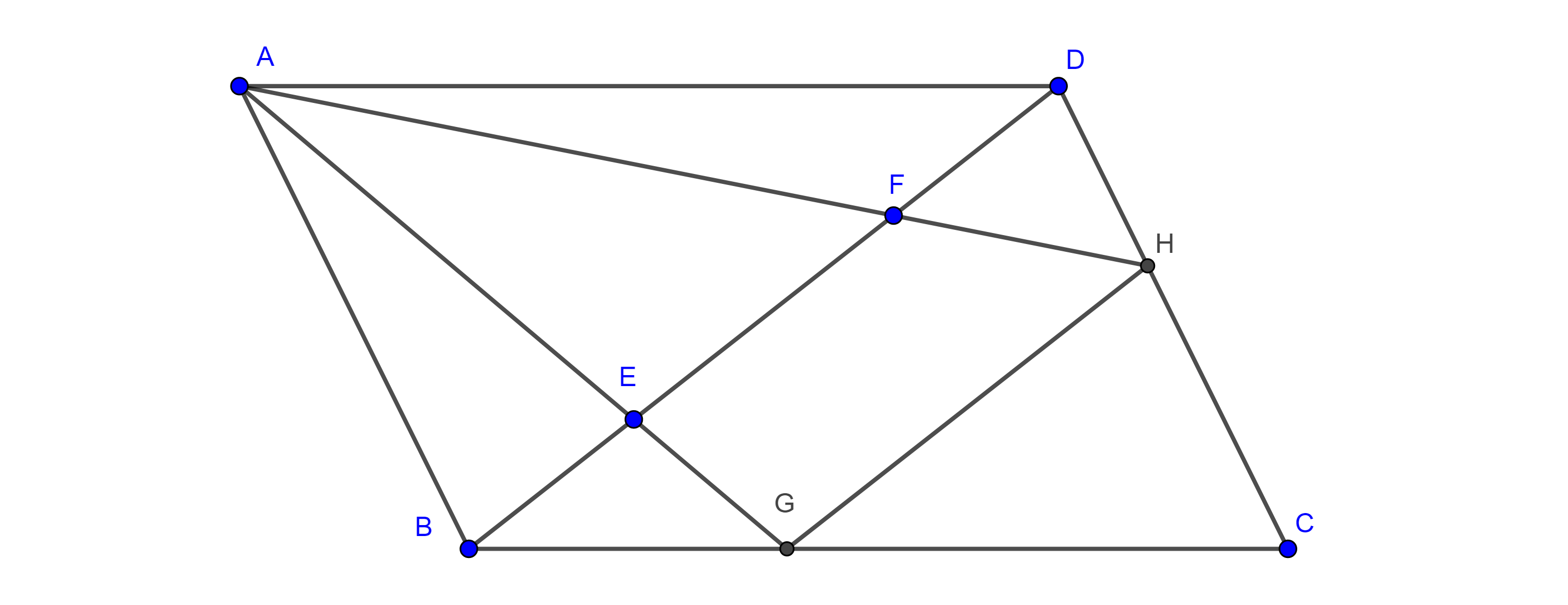
Sean $A B C D$ un paralelogramo, $E \in C D$ , $G$ y $F$ las intersecciones de $A E$ con $B D$ y $B C$ respectivamente (figura 6), encuentra $E F$ en términos de $A G$ y $G E$ .

Sean $A B C D$ un paralelogramo, $E$ , $F \in B D$ tales que $B E = D F$ , $G = A E \cap B C$ y $H = A F \cap C D$ (figura 7), muestra que $G H ∥ B D$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Teorema de Tales.
Siguiente entrada del curso: Segmento dirigido y teorema de Stewart.
Otros cursos.

Fuentes

Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 18-24.
Altshiller, N., College Geometry. New York: Dover, 2007, pp 72-73.
Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 6-11.
Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Congruencia de triángulos

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

En esta entrada estudiaremos los criterios de congruencia para triángulos, los cuales estaremos usando a lo largo del curso, nos apoyaremos en las transformaciones rígidas las cuales presentamos a continuación.

Definición 1. Decimos que dos triángulos distintos $△ A B C$ y $△ A^{'} B^{'} C^{'}$ son congruentes y lo denotamos como $△ A B C ≅ △ A^{'} B^{'} C^{'}$ , si los lados y los ángulos correspondientes son iguales, esto es,

$∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ , $∠ C = ∠ C^{'}$ y
$A B = A^{'} B^{'}$ , $B C = B^{'} C^{'}$ , $A C = A^{'} C^{'}$ .

Definición 2. Una transformación rígida es una función del plano en sí mismo, o un subconjunto de él, donde la preimagen y la imagen son congruentes.

Una reflexión en una recta es una transformación rígida que manda a todo punto en la preimagen con su punto simétrico respecto a la recta.

Una traslación es una transformación rígida que mueve a todos los puntos en la preimagen una distancia constante en una dirección especifica.

Una rotación es una transformación rígida donde todos los puntos en la preimagen giran alrededor de un punto fijo en un ángulo constante.

Criterio lado, ángulo, lado (LAL)

Teorema 1, de congruencia lado, ángulo, lado. Si en un triángulo dos de sus lados y el ángulo interior que estos forman, son iguales a dos lados y el ángulo interior comprendido entre ellos de un segundo triángulo entonces los triángulos son congruentes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ tales que $A B = A^{'} B^{'}$ , $A C = A^{'} C^{'}$ y $∠ A = ∠ A^{'}$ , debemos mostrar que $B C = B^{'} C^{'}$ , $∠ B = ∠ B^{'}$ y $∠ C = ∠ C^{'}$ .

La idea es superponer los ángulos $∠ B A C$ y $∠ B^{'} A^{'} C^{'}$ de la siguiente manera, hacemos una composición de transformaciones rígidas para que $A$ y $A^{'}$ coincidan y los segmentos $A B$ y $A^{'} B^{'}$ se superpongan.

Entonces como $A B = A^{'} B^{'}$ los puntos $B$ y $B^{'}$ coincidirán, ahora como $∠ B A C = ∠ B^{'} A^{'} C^{'}$ los segmentos $A C$ y $A^{'} C^{'}$ quedaran sobrepuestos, si no es así entonces hacemos una reflexión a través de $A B$ para que esto suceda.

Como $A C$ y $A^{'} C^{'}$ tienen la misma longitud sucederá que $C$ y $C^{'}$ coincidirán, de esta manera los segmentos $B C$ y $B^{'} C^{'}$ coincidirán pero también los pares de ángulos ( $∠ C B A$ , $∠ C^{'} B^{'} A^{'}$ ) y ( $∠ A C B$ , $∠ A^{'} C^{'} B^{'}$ ) coincidirán.

Por lo tanto, por la noción común numero 4 (cosas que coinciden una con otra son iguales entre sí), tendrán la misma magnitud,
$B C = B^{'} C^{'}$ , $∠ C B A = ∠ C^{'} B^{'} A^{'}$ , $∠ A C B = ∠ A^{'} C^{'} B^{'}$ .

Como resultado, $△ A B C ≅ △ A^{'} B^{'} C^{'}$ .

Notemos que el procedimiento de “superponer” las figuras no se menciona en los axiomas de Euclides ni en las nociones comunes, así que este es un ejemplo de que los postulados de Euclides son incompletos como lo mencionábamos en la entrada anterior.

En el siguiente interactivo se ilustra un caso particular de como con una traslación y una rotación podemos superponer dos triángulos.

Criterio lado, lado, lado (LLL)

Definición 3. La mediatriz de un segmento es la recta perpendicular al segmento y que pasa por su punto medio, es decir, lo biseca.

La bisectriz de un ángulo es la recta que pasa por el vértice del ángulo y lo divide en dos ángulos iguales. Notemos que en un triángulo hay tres bisectrices internas y tres bisectrices externas.

Decimos que un vértice y un lado de un triángulo son opuestos si el lado no contiene al vértice. La altura de un triángulo, es el segmento que une uno de sus vértices con el pie de la perpendicular al lado opuesto.

La mediana de un triángulo es el segmento que une un vértice con el punto medio del lado opuesto.

Proposición. Los ángulos internos de un triángulo isósceles, que no son aquel comprendido entre los lados iguales, son iguales entre sí, además, la bisectriz del ángulo interior formado por los lados iguales, la altura trazada por ese vértice, la mediana y mediatriz del lado opuesto coinciden.

Demostración. Sea $△ A B C$ un triángulo isósceles con $A B = A C$ y tracemos la bisectriz de $∠ A$ , sea $M$ el punto en donde la bisectriz corta al lado opuesto.

Los triángulos $△ A M B$ y $△ A M C$ tienen dos lados iguales, $A B = A C$ por hipótesis y $A M$ es un lado en común, además $∠ B A M = ∠ M A C$ por ser $A M$ bisectriz, por criterio LAL los triángulos son congruentes.

Por lo tanto, $B M = C M$ , $∠ A M B = ∠ C M A$ y $∠ B = ∠ C$
esta última igualdad es la primera de las afirmaciones que se quería mostrar.

Por otro lado, como $B M = C M$ , entonces $M$ es punto medio de $B C$ por lo que $A M$ es mediana.

Ahora, como $∠ A M B + ∠ C M A = π$ y $∠ A M B = ∠ C M A$ , entonces $A M$ es perpendicular a $B C$ y así $A M$ es mediatriz y altura.

Lema. Dado un segmento $A B$ y un punto $P$ no colineal con $A$ y $B$ , no existe otro punto $P^{'}$ diferente de $P$ y en el mismo semiplano que $P$ respecto de $A B$ , tal que $A P = A P^{'}$ y $B P = B P^{'}$ .

Demostración. Por reducción al absurdo, supongamos que existe $P^{'} \neq P$ talque $A P = A P^{'}$ y $B P = B P^{'}$ , entonces consideremos los triángulos isósceles, $△ P A P$ ´ y $△ P B P^{'}$ .

Por la proposición anterior $∠ A P P^{'} = ∠ P P^{'} A$ y $∠ B P P^{'} = ∠ P P^{'} B$ .

Pero $∠ A P P^{'} = ∠ A P B + ∠ B P P^{'} = ∠ A P B + ∠ P P^{'} B$ ,
$\Rightarrow A P P^{'} > P P^{'} B$ .

Por otro lado, $∠ P P^{'} B = ∠ P P^{'} A + ∠ A P^{'} B$ ,
$\Rightarrow P P^{'} B > P P^{'} A$ .

De las últimas dos desigualdades concluimos que $A P P^{'} > P P^{'} A$ , lo cual es una contradicción al axioma de tricotomía pues vimos que $A P P^{'} = P P^{'} A$ .

Por lo tanto, no existe $P^{'}$ distinto de $P$ tal que $A P = A P^{'}$ y $B P = B P^{'}$ .

Teorema 2, de congruencia lado, lado, lado. Si los lados de un triángulo son iguales a los lados de otro triángulo, entonces los triángulos son congruentes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ tales que $A B = A^{'} B^{'}$ , $B C = B^{'} C^{'}$ y $A C = A^{'} C^{'}$ , veamos que los ángulos respectivos tienen la misma magnitud.

Hagamos la composición de transformaciones rígidas necesaria para para hacer coincidir los puntos $B$ y $B^{'}$ de manera que los segmentos $B C$ y $B ´ C^{'}$ se sobrepongan.

Como $B C = B^{'} C^{'}$ entonces $C$ y $C^{'}$ coincidirán.

Ahora realizamos otra composición de transformaciones rígidas para que $A$ y $A^{'}$ se encuentren en el mismo semiplano respecto de $B C$ y $B^{'} C^{'}$ , que ahora son el mismo segmento.

Por el lema anterior, como $A B = A^{'} B^{'}$ y $A C = A^{'} C^{'}$ , no es posible que $A \neq A^{'}$ , por lo tanto, coinciden, como $△ A B C$ y $△ A ´ B ´ C ´$ coinciden, por la noción común número 4, todas sus magnitudes son iguales, por lo que $∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ y $∠ C = ∠ C^{'}$ .

Problema. Dado un ángulo construir su bisectriz.

Solución. Sea $∠ A B C$ el ángulo dado, trazamos una circunferencia de radio arbitrario pero positivo que corta a $A B$ en $D$ y a $B C$ en $E$ .

Ahora construimos un triángulo equilátero sobre $D E$ , como lo hicimos en la primera entrada, cuyo tercer vértice será $F$ .

Veamos que $B F$ es la bisectriz de $∠ A B C$ . Tenemos que $B D = B E$ , pues son radios de una misma circunferencia, $D F = E F$ , ya que $△ D E F$ es equilátero por construcción, por LLL $△ B D F ≅ △ B E F$ , en consecuencia $∠ D B F = ∠ F B E$ , por lo tanto, $B F$ es bisectriz de $∠ A B C$ .

Criterio ángulo, lado, ángulo (ALA)

Teorema 3, de congruencia ángulo, lado, ángulo. Si dos ángulos y el lado comprendido entre ellos de un triángulo son iguales a dos ángulos y el lado comprendido entre ellos de otro triangulo, entonces los triángulos son congruentes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ tales que $∠ B = ∠ B^{'}$ , $∠ C = ∠ C^{'}$ y $B C = B^{'} C^{'}$ .

Como la suma de los ángulos internos de todo triangulo es $π$ entonces
$∠ A + ∠ B + ∠ C = π = ∠ A^{'} + ∠ B^{'} + ∠ C^{'}$
$\Rightarrow A = A^{'}$ .

Si cualquier otro par de lados correspondientes fuese igual entonces por LAL, los triángulos serian congruentes. Supongamos lo contrario para llegar a una contradicción, es decir, que $A C \neq A^{'} C^{'}$ y $A B \neq A^{'} B^{'}$ .

Sin pérdida de generalidad supongamos que $A C > A^{'} C^{'}$ .

Construimos sobre $A C$ un punto $A^{″}$ tal que $A^{″} B = A^{'} B^{'}$ , entonces $△ A^{″} B C ≅ △ A^{'} B^{'} C^{'}$ por LAL, por lo que $∠ A^{″} C B = ∠ A^{'} C^{'} B^{'}$ .

Por hipótesis, $∠ A C B = ∠ A^{'} C^{'} B^{'}$ así que $∠ A C B = ∠ A^{″} C B$ , pero $∠ A C B > ∠ A^{″} C B$ , lo que es una contradicción.

Por lo tanto, $A C = A^{'} C^{'}$ y por LAL, $△ A B C ≅ △ A^{'} B^{'} C^{'}$ .

Criterio hipotenusa, cateto

Definición 4. En un triángulo rectángulo a los lados que forman el ángulo recto le llamamos catetos y al lado opuesto al ángulo recto le llamamos hipotenusa.

Teorema 4. De congruencia hipotenusa, cateto. Si la hipotenusa y un cateo de un triángulo rectángulo son iguales a la hipotenusa y un cateto de otro triángulo rectángulo, entonces los triángulos son congruentes.

Demostración. Sean $△ A B C$ y $△ A^{'} B^{'} C^{'}$ tales que $∠ B = ∠ B^{'} = \frac{π}{2}$ , $A B = A^{'} B^{'}$ y $A C = A^{'} C^{'}$ .

Sobre la recta determinada por $B$ y $C$ construimos un punto $C^{″}$ del lado opuesto a $C$ respecto a $B$ , tal que $B C^{″} = B^{'} C^{'}$ .

Entonces por LAL, $△ A B C^{″} ≅ △ A^{'} B^{'} C^{'}$ , por lo tanto, $A C^{″} = A^{'} C^{'}$ , por hipótesis $A C = A^{'} C^{'}$ , así que $A C = A C^{″}$ .

Como $△ C^{″} A C$ es isósceles y por construcción $A B$ es la altura trazada desde $A$ , por la proposición, $A B$ coincide con la mediatriz de $C^{″} C$ , por lo que $B C^{″} = B C$ , pero $B C^{″} = B^{'} C^{'}$ por construcción, por lo tanto, $B C = B^{'} C^{'}$ , finalmente por LLL, $△ A B C ≅ △ A^{'} B^{'} C^{'}$ .

Más adelante…

En la siguiente entrada estudiaremos la desigualdad del triangulo y su reciproco, presentaremos el concepto de lugar geométrico y mostraremos un par de ejemplos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas paralelas, el resultado es una traslación.
Muestra que si se hacen dos reflexiones sucesivas con respecto a dos rectas concurrentes, se obtiene una rotación con respecto al punto de intersección entre las rectas.
$i)$ Muestra que si un triangulo tiene dos ángulos iguales, entonces los lados opuestos a estos ángulos también son iguales.
$i i)$ Muestra que los ángulos internos de un triángulo equilátero son iguales.
Si dos rectas distintas se intersecan forman 4 ángulos, prueba que las bisectrices de ángulos opuestos por el vértice son la misma y que las bisectrices de ángulos adyacentes son perpendiculares.
Dado un segmento, construye su mediatriz.
Demuestra sin usar el quinto postulado (lo que implica que los ángulos interiores de todo triangulo suman dos ángulos rectos), que todo ángulo exterior de un triángulo es mayor que cualquiera de los ángulos interiores no adyacentes a el.
Muestra con un ejemplo que el criterio LLA en general no se cumple, es decir, cuando dos triángulos diferentes tienen dos lados y un ángulo correspondientes iguales, pero el ángulo no es el que forman los lados correspondientes iguales.

Entradas relacionadas

Ir a Geometría Moderna I
Entrada anterior del curso: Postulados de Euclides.
Siguiente entrada del curso: Desigualdad del triángulo y lugar geométrico.

Fuentes

Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 10-16.
Math Bits Notebook
Geometría interactiva
Geometry Help
Math Open Reference
Math is Fun

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: criterio LAL

Geometría Moderna I: Semejanza de triángulos

Introducción

Criterio de semejanza ángulo, ángulo, ángulo (AAA o AA)

Criterio de semejanza lado, ángulo, lado (LAL)

Criterio de semejanza lado, lado, lado (LLL)

Triángulos con lados perpendiculares

Desigualdad entre bisectrices

Semejanza en el triángulo rectángulo

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Congruencia de triángulos

Introducción

Criterio lado, ángulo, lado (LAL)

Criterio lado, lado, lado (LLL)

Criterio ángulo, lado, ángulo (ALA)

Criterio hipotenusa, cateto

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos