Archivo de la etiqueta: convergencia uniforme

Variable Compleja I: Teoremas de Weierstrass

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En la entrada anterior establecimos una versión general del Teorema Integral de Cauchy, la cual nos es de mucha utilidad al resolver problemas relacionados con el cálculo de integrales.

En esta entrada veremos algunos resultados importantes que relacionan a las series de funciones y los conceptos de integral y derivada de las mismas, en particular probaremos bajo qué condiciones es posible integrar y derivar término a término a este tipo de series. Más aún, veremos que toda serie de potencias define a una función analítica en su disco de convergencia.

Proposición 39.1.(Weierstrass sobre integración término a término.)
Sean $D\subset\mathbb{C}$ un dominio, $\gamma$ un contorno en $D$ y $\{f_n:D\to\mathbb{C}\}_{n\geq 0}$ una sucesión de funciones continuas que converge uniformemente a una función $f:D \to \mathbb{C}$ en $D$. Entonces:
\begin{equation*}
\lim_{n\to\infty} \int_{\gamma} f_n(z) dz = \int_{\gamma} f(z) dz = \int_{\gamma} \lim_{n\to\infty} f_n(z) dz.
\end{equation*}

En particular:
\begin{equation*}
\sum_{n=0}^{\infty} \int_{\gamma} f_n(z) dz = \int_{\gamma} \sum_{n=0}^{\infty} f_n(z) dz.
\end{equation*}

Demostración. Dadas las hipótesis, por la proposición 28.1 tenemos que $f$ es una función continua en $D$, por lo que $\int_\gamma f(z) dz$ existe.

Por la definición de convergencia uniforme, dado $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$, se cumple que:
\begin{equation*}
|f_n(z) – f(z)|<\frac{\varepsilon}{1+\ell(\gamma)}, \quad \forall z\in D.
\end{equation*}

Entonces, si $n\geq N$, por las proposiciones 34.2(1) y 34.3(5), tenemos que:
\begin{align*}
\left|\int_{\gamma} f_n(z) dz – \int_{\gamma} f(z) dz\right| & = \left|\int_{\gamma} \left[f_n(z)-f(z)\right] dz\right|\\
& \leq \int_{\gamma} \left|f(z)-f_n(z)\right| \, |dz|\\
& < \frac{\varepsilon}{1+\ell(\gamma)} \ell(\gamma)\\
& < \varepsilon.
\end{align*}

Como $\varepsilon>0$ es arbitrario, entonces:
\begin{equation*}
\lim_{n\to\infty} \int_{\gamma} f_n(z) dz = \int_{\gamma} f(z) dz = \int_{\gamma} \lim_{n\to\infty} f_n(z) dz.
\end{equation*}

La última parte se sigue de aplicar la primera parte del resultado a la sucesión de sumas parciales de la serie, por lo que los detalles se dejan como ejercicio al lector.

$\blacksquare$

Definición 39.1. (Convergencia uniformemente compacta.)
Una sucesión de funciones $\{f_n\}_{n\geq 0}$ definidas en un conjunto abierto $U\subset\mathbb{C}$ se dice que converge uniformemente en compactos o que converge compactamente en $U$ si para cada subconjunto compacto $K\subset U$ la sucesión de restricciones $\{f_n:K\to\mathbb{C}\}_{n\geq 0}$ converge uniformemente a la restricción $f:K\to\mathbb{C}$.

Lema 39.1.
Sea $\{f_n\}_{n\geq 0}$ una sucesión de funciones definidas en un conjunto abierto $U\subset\mathbb{C}$. La sucesión converge compactamente en $U$ si y solo si converge uniformemente en cada disco cerrado contenido en $U$.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Teorema 39.1. (Weierstrass sobre la convergencia analítica.)
Sea $\{f_n\}_{n\geq 0}$ una sucesión de funciones analíticas definidas en un dominio $D\subset\mathbb{C}$ y $f:D \to \mathbb{C}$ una función. Si $f_n \to f$ uniformemente en todo subconjunto compacto de $D$, entonces $f$ es analítica en $D$. Más aún, para cada $k\in\mathbb{N}$ se cumple que $f_n^{(k)} \to f^{(k)}$ uniformemente en cada subconjunto compacto de $D$.

Demostración. Dadas las hipótesis, sea $\gamma$ un contorno cerrado en $D$. Como cada función $f_n$ es analítica en $D$, en particular es continua en $D$, proposición 16.1, y dado que $f_n \to f$ uniformemente en todo subconjunto compacto de $D$, por la proposición 28.1 tenemos que $f$ es continua en todo subconjunto compacto de $D$, entonces de la proposición 10.12 se sigue que $f$ es continua en $D$.

Por el teorema de la curva de Jordan, teorema 36.1, sabemos que los puntos en $\gamma$ y su interior forman un conjunto cerrado y acotado $S$, es decir, compacto, proposición 10.7.

Entonces, por la definición de convergencia uniforme, dado $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$, se cumple que:
\begin{equation*}
|f_n(z) – f(z)|<\varepsilon, \quad \forall z\in \gamma.
\end{equation*}

Como para todo $n\geq 0$ la función $f_n$ es analítica en $D$, entonces, por la proposición 34.3(5), el teorema de integral de Cauchy y la desigualdad del triángulo, tenemos que:
\begin{align*}
\left|\int_{\gamma} f(z) dz\right| & = \left|\int_{\gamma} \left[f(z)-f_n(z) + f_n(z)\right] dz\right|\\
& \leq \left|\int_{\gamma} \left[f(z)-f_n(z) \right] dz\right| + \left|\int_{\gamma} f_n(z) dz\right|\\
& = \left|\int_{\gamma} \left[f(z)-f_n(z) \right] dz\right|\\
& \leq \int_{\gamma} \left|f(z)-f_n(z)\right| \, |dz|\\
& < \varepsilon \cdot \ell(\gamma).
\end{align*}

Como $\varepsilon>0$ es arbitrario, entonces:
\begin{equation*}
\left|\int_{\gamma} f(z) dz\right| = 0 \quad \Longrightarrow \quad \int_{\gamma} f(z) dz = 0,
\end{equation*}y dado que $\gamma$ es un contorno cerrado arbitrario en $D$, el resultado se cumple para todo contorno cerrado $\gamma$ en $D$. Entonces, por el teorema de Morera tenemos que $f$ es una función analítica en $D$.

De acuerdo con el lema 39.1, solo basta con verificar el resultado para discos cerrados contenidos en $D$. Sean $z_0\in D$ fijo, $r>0$ tal que $\overline{B}(z_0,r) \subset D$ y parametrizamos a la frontera del disco cerrado como $\gamma_r = \partial \overline{B}(z_0,r)$, orientada positivamente. Por la definición de convergencia uniforme, dado $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$, se cumple que:
\begin{equation*}
|f_n(z) – f(z)| < \frac{\varepsilon r^{k}}{k! 2^{k+1}}, \quad \forall z\in \overline{B}(z_0,r), \tag{39.1}
\end{equation*}donde $r>0$ y $k\in\mathbb{N}^{+}$.

Para $k\in\mathbb{N}^+$ fijo, por la fórmula integral de Cauchy para las derivadas de orden superior, proposición, tenemos que:
\begin{equation*}
f^{(k)}(z) = \frac{k!}{2\pi i} \int_{\gamma_r} \frac{f(\zeta)}{(\zeta – z)^{k+1}} d\zeta, \quad \forall z\in B(z_0,r). \tag{39.2}
\end{equation*}

Análogamente, para cada función $f_n$ tenemos que:
\begin{equation*}
f_n^{(k)}(z) = \frac{k!}{2\pi i} \int_{\gamma_r} \frac{f(\zeta)}{(\zeta – z)^{k+1}} d\zeta, \quad \forall z\in B(z_0,r). \tag{39.3}
\end{equation*}

Notemos que para $z\in \overline{B}(z_0,r/2) \subset \overline{B}(z_0,r)$ se tiene por la proposición 3.3 que:
\begin{equation*}
\frac{r}{2} \leq |\zeta – z_0| – |z_0 -z| \leq |\zeta -z| \quad \Longrightarrow \quad \frac{1}{|\zeta -z|} \leq \frac{2}{r} \tag{39.4}.
\end{equation*}

Es claro que:
\begin{equation*}
\ell(\gamma_r) = \int_{\gamma_r} |d\zeta| =2 \pi r.
\end{equation*}

Entonces, si $n\geq N$ y $z\in \overline{B}(z_0,r/2)$, por las proposiciones 34.2(1), 34.3(5) y por (39.1), (39.2), (39.3) y (39.4), se tiene que:
\begin{align*}
\left|f_n^{(k)}(z) – f^{(k)}(z)\right| & = \left|
\frac{k!}{2\pi i} \int_{\gamma_r} \frac{f_n(\zeta)}{(\zeta – z)^{k+1}} d\zeta – \frac{k!}{2\pi i} \int_{\gamma_r} \frac{f(\zeta)}{(\zeta – z)^{k+1}} d\zeta \right|\\
& = \frac{k!}{2\pi} \left|\int_{\gamma_r} \frac{f_n(\zeta) – f(\zeta)}{(\zeta – z)^{k+1}} d\zeta \right|\\
& \leq \frac{k!}{2\pi} \int_{\gamma_r}\left| \frac{f_n(\zeta) – f(\zeta)}{(\zeta – z)^{k+1}} \right| \, |d\zeta| \\
& = \frac{k!}{2\pi} \int_{\gamma_r} \frac{\left|f_n(\zeta) – f(\zeta)\right|}{\left|\zeta – z\right|^{k+1}} \, |d\zeta| \\
& \leq \frac{k!}{2\pi} \frac{2^{k+1}}{r^{k+1}} \frac{\varepsilon r^{k}}{k! 2^{k+1}} \int_{\gamma_r} |d\zeta|\\
& = \varepsilon,
\end{align*}como $z\in \overline{B}(z_0,r/2)$ y $r>0$ son arbitrarios, entonces $f_n^{(k)} \to f^{(k)}$ uniformemente en cualquier disco cerrado contenido en $D$, por lo que del lema 39.1 se sigue el resultado.

$\blacksquare$

Corolario 39.1.
Sean $z_0\in\mathbb{C}$ fijo y $f:B(z_0, R) \to \mathbb{C}$ una función dada por la serie de potencias:
\begin{equation*}
f(z) = \displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n,
\end{equation*}con radio de convergencia $R>0$. Entonces $f$ es analítica en $B(z_0, R)$.

Demostración. Dadas las hipótesis, por la proposición 29.2 tenemos que la serie de potencias converge uniformemente a $f$ en todo subdisco cerrado $\overline{B}(z_0,r)$, con $r<R$, por lo que, del teorema 39.1 se sigue que $f$ es analítica en $B(z_0, R)$.

$\blacksquare$

Teorema 39.2. (Weierstrass sobre derivación término a término.)
Sea $\{f_n\}_{n\geq 0}$ una sucesión de funciones analíticas definidas en un dominio $D\subset\mathbb{C}$ y sea $f(z) = \displaystyle \sum_{n=0}^\infty f_n(z)$. Si la serie converge uniformemente a $f$ en cada disco cerrado contenido en $D$, definición 28.6, entonces $f$ es analítica en $D$ y puede derivarse término a término, es decir:
\begin{equation*}
f^{(k)}(z) = \displaystyle \sum_{n=0}^\infty f_n^{(k)}(z), \quad \forall z\in D,
\end{equation*}para todo $k\in\mathbb{N}^+$.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Observación 39.1.
Notemos que los resultados anteriores no suponen la convergencia uniforme en todo el dominio $D$, es decir, la convergencia uniforme es únicamente en los subconjuntos compactos de $D$ o equivalentemente, lema 39.1, en los subdiscos cerrados en $D$.

Ejemplo 39.1.
Sea $D = \{z\in\mathbb{C} : |z|<1\}$. Consideremos a la serie:
\begin{equation*}
f(z) = \sum_{n=1}^\infty \frac{z^n}{n}, \quad \forall \, z\in D.
\end{equation*}

No es difícil verificar que dicha serie converge puntualmente en $D$ y uniformemente en los discos cerrados $\overline{B}(0,r)$, para $0\leq r <1$, ejercicio 1. Por lo que converge uniformemente en todos los discos cerrados en $A$, entonces por los teoremas 39.1 y 39.2 concluimos que $f$ es analítica en $D$ y que su derivada $f'(z) = \displaystyle \sum_{n=1} z^{n-1}$ también converge en $D$. Sin embargo, se tiene convergencia puntual y no uniforme en $D$.

Ejemplo 39.2. (Derivación término a término.)
Consideremos a la serie geométrica $\displaystyle\sum_{n=0}^\infty z^n$. De acuerdo con el ejemplo 28.8 sabemos que dicha serie converge uniformemente en todo disco cerrado $\overline{B}(0,r)$, con $0<r<1$, en tal caso:
\begin{equation*}
\displaystyle\sum_{n=0}^\infty z^n = \dfrac{1}{1-z}. \tag{39.5}
\end{equation*}

Es claro que la función $f_n(z) = z^n$ es entera para todo $n\in\mathbb{N}$, en particular es analítica en $\overline{B}(0,r)$. Por lo que, podemos utilizar el teorema 39.2 para derivar a la serie geométrica término a término.

Derivando el lado derecho de la igualdad (39.5) tenemos:
\begin{equation*}
\frac{d}{dz} \frac{1}{1-z} = \frac{1}{(1-z)^2}.
\end{equation*}

Por otra parte, derivando el lado izquierdo de la igualdad (39.5), por el teorema tenemos que:
\begin{align*}
\frac{d}{dz} \left(\displaystyle\sum_{n=0}^\infty z^n \right) & = \displaystyle\sum_{n=0}^\infty \frac{d}{dz} z^n\\
& = 1 + 2z + 3z^2 + 4z^3 + \cdots\\
& = \displaystyle\sum_{n=0}^\infty (n+1) z^n.
\end{align*}

Entonces:
\begin{equation*}
\displaystyle\sum_{n=0}^\infty (n+1) z^n = \frac{1}{(1-z)^2}, \quad \text{si} \,\, |z| \leq r <1.
\end{equation*}

Notemos que este mismo resultado se obtuvo en el ejemplo 27.13 de la entrada 27, sin embargo, es claro que mediante el teorema de derivación término a término fue más sencillo deducirlo.

Ejemplo 39.3. (Integración término a término.)
Continuemos trabajando con la serie geométrica $\displaystyle\sum_{n=0}^\infty z^n$. Dado que dicha serie converge uniformemente en todo disco cerrado $\overline{B}(0,r)\subset B(0, 1)$ y para todo $n\in\mathbb{N}$ la función $f_n(z) = z^n$ es entera, entonces podemos considerar a dicha serie para utilizar el la proposición 39.1 para integrar término a término.

Sea $\gamma$ el segmento de recta que une a $0$ y $\zeta$ de modo que $\gamma \subset B(0,1)$, es decir, $\gamma$ es el segmento de recta $[0,\zeta]$, tal que $|\zeta|<1$. Entonces:
\begin{align*}
\int_{[0, \zeta]} \frac{1}{1-z} dz & = \sum_{n=0}^\infty \int_{[0, \zeta]} z^n \, dz \\
& = \int_{[0, \zeta]} 1 \, dz + \int_{[0, \zeta]} z \, dz + \int_{[0, \zeta]} z^2 \, dz + \cdots
\end{align*}

Notemos que el integrando del lado izquierdo de la igualdad, es decir, la función $\dfrac{1}{1-z}$, salvo una constante, corresponde con la derivada de alguna de las ramas de la función multivaluada $\operatorname{log}(1-z)$.

Dado que la rama principal $\operatorname{Log}(1-z)$ es analítica en $\mathbb{C}\setminus[1, \infty)$, ejercicio 10 de la entrada 21, entonces en particular es analítica en el disco abierto $B(0, 1)$, por lo que, al tener la condición $|z|<1$, elegimos a dicha rama.

Por otra parte, por el corolario 21.1 sabemos que para la rama principal del logaritmo se cumple que $-\operatorname{Log}(w) = \operatorname{Log}(w^{-1})$ si $w$ no está en el corte de rama de dicha función. Para nuestro caso, como $|z|<1$, entonces los valores de $z$ que consideramos no están en el corte de rama de la función $\operatorname{Log}(1-z)$, por lo que se cumple:
\begin{equation*}
-\operatorname{Log}(1-z) = \operatorname{Log}\left(\frac{1}{1-z}\right).
\end{equation*}

Considerando el TFC, proposición 35.1, tenemos que:
\begin{align*}
\int_{[0, \zeta]} \frac{1}{1-z} dz = \int_{0}^{\zeta} \frac{1}{1-z} dz & = -\operatorname{Log}(1-z)\Big|_{0}^{\zeta}\\
& = \operatorname{Log}\left(\frac{1}{1-\zeta}\right)\Bigg|_{0}^{\zeta}\\
& = \operatorname{Log}\left(\frac{1}{1-\zeta}\right) – \operatorname{Log}\left(\frac{1}{1-0}\right)\\
& = \operatorname{Log}\left(\frac{1}{1-\zeta}\right).
\end{align*}

Por otra parte, para el lado derecho de la igualdad, por el TFC, proposición 35.1, es claro que:
\begin{align*}
\sum_{n=0}^\infty \int_{[0, \zeta]} z^n \, dz & = \int_{[0, \zeta]} 1 \, dz + \int_{[0, \zeta]} z \, dz + \int_{[0, \zeta]} z^2 \, dz + \cdots\\
& = \int_{0}^{\zeta} 1 \, dz + \int_{0}^{\zeta} z \, dz + \int_{0}^{\zeta} z^2 \, dz + \cdots\\
& = \zeta + \frac{\zeta^2}{2} + \frac{\zeta^3}{3} + \cdots\\
& = \sum_{n=1}^\infty \frac{\zeta^n}{n}.
\end{align*}

Entonces:
\begin{equation*}
\operatorname{Log}\left(\frac{1}{1-z}\right) = \sum_{n=0}^\infty \frac{z^{n+1}}{n+1}, \quad \text{si} \,\, |z|\leq r <1.
\end{equation*}

Notemos que habíamos llegado al mismo resultado en el ejercicio 5 de la entrada 30, sin embargo, utilizando el teorema de integración término a término el procedimiento fue más sencillo.

Tarea moral

  1. Sea $D = \{z\in\mathbb{C} : |z|<1\}$. Considera a la serie:
    \begin{equation*}
    f(z) = \sum_{n=1}^\infty \frac{z^n}{n}, \quad \forall \, z\in D.
    \end{equation*}Muestra que dicha serie converge puntualemente en $D$ y uniformemente en todo disco cerrado $\overline{B}(0,r)$, para $0\leq r <1$.
  2. Completa la demostración de la proposición 39.1.
  3. Demuestra el lema 39.1.
  4. Prueba el teorema 39.2.
  5. Muestra que si $|z|<1$, entonces:
    \begin{equation*}
    \operatorname{Log}(1+z) = \displaystyle \sum_{n=0}^\infty (-1)^n \dfrac{z^{n+1}}{n+1}.
    \end{equation*}Hint: Considera el contorno $\gamma$ dado por el segmento de recta $[0, \zeta]$ con $|\zeta|<1$ y utiliza la proposición 39.1.
  6. Muestra que la sucesión de funciones $\{f_n\}_{n\geq 1}$, dada por:
    \begin{equation*}
    f_n(z)=\frac{z^{n+1}}{n(n+1)}, \quad \forall n\in\mathbb{N}^+,
    \end{equation*}converge uniformemente en el disco abierto $B(0,1)$, pero que la sucesión de derivadas:
    \begin{equation*}
    f_n^{(2)}(z)=z^{n-1}, \quad \forall n\in\mathbb{N}^+,
    \end{equation*}no converge uniformemente en dicho disco.
  7. $D\subset\mathbb{C}$ un dominio, $f:D \to \mathbb{C}$ una función y $\{f_n\}_{n\geq 0}$ una sucesión de funciones continuas definidas en $D$, tales que:
    \begin{equation*}
    \int_{\gamma} f_n(z) dz =0, \quad \forall n\in\mathbb{N},
    \end{equation*}para todo contorno cerrado $\gamma$ en $D$. Si $f_n \to f$ converge uniformemente en $D$, muestra que $f$ es analítica en $D$.
  8. Sean $D\subset\mathbb{C}$ un dominio, $f:D \to \mathbb{C}$ una función y $\{f_n\}_{n\geq 0}$ una sucesión de funciones continuas definidas en $D$, tales, que $f_n \to f$ converge uniformemente en $D$, entonces:
    \begin{equation*}
    \int_{\gamma} f(z) |dz| = \lim_{n\to\infty} \int_{\gamma} f_n(z) |dz|,
    \end{equation*}para todo contorno $\gamma$ en $D$.

Más adelante…

En esta entrada hemos establecido algunos resultados importantes sobre las series de funciones y los conceptos de convergencia uniforme, integración y diferenciación, en particular vimos bajo qué condiciones posible integrar o derivar término a término este tipo de funciones.

En la siguiente entrada definiremos dos tipos de funciones complejas muy particulares, las funciones conjugadas armónicas y las funciones conformes, las cuales están relacionadas con algunos de los conceptos de esta entrada y que nos serán de utilidad para construir funciones analíticas. Dichas funciones nos permitirán caracterizar aún más la geometría de las funciones complejas.

Entradas relacionadas

Variable Compleja I: Sucesiones y series de funciones

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En la entrada 8 definimos el concepto de sucesión de números complejos y obtuvimos algunos resultados sobre dichos objetos matemáticos. Como vimos, muchas de las definiciones y resultados son similares a los que ya conocíamos sobre sucesiones de números reales con los que ya estábamos familiarizados.

Por otra parte, en la entrada anterior definimos el concepto de serie de números complejos y vimos que para determinar su comportamiento, así como muchas de sus propiedades, requerimos de los resultados de sucesiones de números complejos.

En ésta entrada definiremos el concepto de sucesiones de funciones y series de funciones, desde el enfoque complejo. Al igual que con las sucesiones numéricas, intuimos que para las sucesiones de funciones debe haber una noción de convergencia. Sin embargo, veremos que para el caso de sucesiones de funciones, podemos tener distintos tipos de convergencia, por lo que requeriremos ser muy meticulosos al trabajar con ellas.

Definición 28.1. (Sucesión de funciones.)
Sea $S\subset\mathbb{C}$. Consideremos al conjunto de todas las funciones $f:S \to \mathbb{C}$, es decir, $\mathcal{F}(S)$. Una sucesión de funciones en $S$ es una función $F:\mathbb{N} \to \mathcal{F}$, que a cada $n\in\mathbb{N}$ asigna una función $f\in\mathcal{F}(S)$, es decir, $F(n) = f_n(z)$, lo cual denotamos como $\left\{f_n\right\}_{n\geq 0}$.

Procedemos a definir el primer tipo de convergencia para una sucesión de funciones, el cual es en esencia el más elemental.

Definición 28.2. (Convergencia puntual de una sucesión de funciones.)
Sean $S\subset\mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$. Diremos que la sucesión $\left\{f_n\right\}_{n\geq 0}$ converge puntualmente en $S$ a una función $f: S\to \mathbb{C}$ si: \begin{equation*} \lim_{n\to\infty} f_n(z) = f(z), \end{equation*} para todo $z\in S$. Es decir, si para todo $\varepsilon>0$ y todo $z\in S$ existe $N\in\mathbb{N}$, que depende de $\varepsilon$ y de $z$, tal que si $n \geq N$, entonces:
\begin{equation*}
\left|f_n(z) – f(z)\right| < \varepsilon.
\end{equation*} A la función $f$ que satisface lo anterior la llamaremos el límite puntual de $\left\{f_n\right\}_{n\geq 0}$.

Observación 28.1.
La convergencia puntual es simplemente la convergencia de la sucesión de números complejos $\left\{f_n(z)\right\}_{n\geq 0}$ al número complejo $f(z)$, para cada $z\in S$

Definición 28.3. (Convergencia uniforme de una sucesión de funciones.)
Sean $S\subset\mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$. Diremos que la sucesión $\left\{f_n\right\}_{n\geq 0}$ converge uniformemente en $S$ a una función $f: S\to \mathbb{C}$ si para todo $\varepsilon>0$ existe $N\in\mathbb{N}$, que depende únicamente de $\varepsilon$, tal que si $n \geq N$, entonces:
\begin{equation*}
\left|f_n(z) – f(z)\right| < \varepsilon,
\end{equation*} para todo $z\in S$.

A la función $f$ que satisface lo anterior la llamaremos el límite uniforme de $\left\{f_n\right\}_{n\geq 0}$.

Observación 28.2.
Una vez especificado el tipo de convergencia, utilizaremos la notación $f_n \to f$ para denotar la convergencia de una sucesión de funciones $\left\{f_n\right\}_{n\geq 0}$ a una función $f$.

Ejemplo 28.1.
Sea $f_n : B(0,1) \to \mathbb{C}$ dada por $f_n(z) = z^n$, con $n\in\mathbb{N}^+$. Consideremos a la función $f: B(0,1) \to \mathbb{C}$ dada por $f(z) = 0$. Veamos que la sucesión de funciones $\left\{f_n\right\}_{n\geq 1}$ cumple lo siguiente.

a) $f_n \to f$ puntualmente en $B(0,1)$.
b) $f_n \not \to f$ uniformemente en $B(0,1)$.
c) $f_n \to f$ uniformemente en $\overline{B}(0,r)$, con $0<r<1$.

Solución.
a) Si $z\in B(0,1)$, entonces $|z|<1$. Es claro que para $z =0$ el resultado es inmediato, por lo que supondremos que $0<|z|<1$. Notemos que bajo esta condición se cumple que $\operatorname{ln}|z| < 0$.

Sea $\varepsilon>0$ y $0<|z|<1$. Elegimos $N\in \mathbb{N}^+$ tal que $N > \dfrac{\operatorname{ln}(\varepsilon)}{\operatorname{ln}|z|}$, entonces para todo $n\geq N$ tenemos que:
\begin{equation*}
|f_n(z) -f(z)| = |z^n – 0| = |z|^n \leq |z|^N < \varepsilon,
\end{equation*} es decir, $f_n \to f$ puntualmente en $B(0,1)$.

b) Procedemos por contradicción. Supongamos que $f_n \to f$ uniformemente en $B(0,1)$.

Sea $\varepsilon = \dfrac{1}{3} > 0$, entonces existe $N\in\mathbb{N}^+$ tal que $|z^N| < \varepsilon$, para todo $z\in B(0,1)$.

Notemos que $z = 2^{-1/N} \in B(0,1)$, pero:
\begin{equation*}
|z^N| = \left|\left(\frac{1}{2^{1/N}}\right)^N\right| = \frac{1}{2} > \frac{1}{3}.
\end{equation*}

Por lo que $f_n \not \to f$ uniformemente en $B(0,1)$.

c) Sea $0<r<1$. En tal caso sabemos que $\lim\limits_{n\to\infty} r^n = 0$.

Sea $\varepsilon>0$. De acuerdo con lo anterior tenemos que existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces $|r^n – 0| = r^n < \varepsilon$.

Sea $z\in\overline{B}(0,r)$, entonces:
\begin{equation*}
|f_n(z) -f(z)| = |z^n – 0| = |z|^n \leq r^n < \varepsilon,
\end{equation*} por lo que $f_n \to f$ uniformemente en $\overline{B}(0,r)$, con $0<r<1$.

Ejemplo 28.2.
Para cada $n\in\mathbb{N}$ definimos a la función $f_n : \mathbb{C} \to \mathbb{C}$ como:
\begin{equation*}
f_n(z) = \frac{z+in}{n+1}.
\end{equation*}

Veamos que la sucesión converge puntualmente a la función constante $f(z) = i$, pero que la sucesión no converge uniformemente a $f$.

Solución. Notemos que para cualquier $z\in\mathbb{C}$ se cumple que:
\begin{equation*}
\lim_{n\to\infty} f_n(z) = \lim_{n\to\infty} \frac{z+in}{n+1} = \lim_{n\to\infty} \frac{\dfrac{z}{n} + i}{1 + \dfrac{1}{n}} = i,
\end{equation*} de donde se sigue la sucesión $\left\{f_n\right\}_{n\geq 0}$ converge puntualmente en $\mathbb{C}$ a la función constante $f(z) = i$.

Notemos que para todo $n\in\mathbb{N}$ se cumple que:
\begin{equation*}
f_n(-in) = \frac{-in+in}{n+1} = 0, \quad f(-in) = i,
\end{equation*} por lo que:
\begin{equation*}
f_n(-in) – f(-in) = -i, \quad \forall n\in\mathbb{N}.
\end{equation*}

Entonces, no existe $n\in\mathbb{N}$ tal que $| f_n(z) – f(z)| < 1$ para todo $z\in\mathbb{C}$, por lo que la sucesión $\left\{f_n\right\}_{n\geq 0}$ no converge uniformemente a $f(z)=i$ en $\mathbb{C}$.

Observación 28.3.
Notemos que existe una sutil diferencia entre las definiciones de convergencia puntual y convergencia uniforme. Si $f_n \to f$ puntualmente en $S$, dado $\varepsilon>0$, para cada $z\in S$ existe un $N_{z} \in \mathbb{N}$ tal que si $n\geq N_z$, entonces $\left|f_n(z) – f(z)\right| < \varepsilon$. Lo anterior nos dice que es posible que el valor de $N_z$ sea diferente para cada valor de $z$.

Por otra parte, si $f_n \to f$ uniformemente, entonces el valor de $N\in\mathbb{N}$ se puede elegir de forma que sea el mismo para todo $z\in S$. Esta condición es mucho más fuerte que la primera, por lo que la convergencia uniforme implica la convergencia puntual, pero el recíproco no es cierto.

Entonces, la diferencia clave entre ambos tipos de convergencia radica en dónde consideramos la expresión «para todo $z\in S$» en las definiciones. Para la convergencia uniforme requerimos que la diferencia entre $f_n(z)$ y $f(z)$ sea arbitrariamente pequeña de forma simultánea para todo $z\in S$.

Observación 28.4.
Si definimos $M_n = \operatorname{max}\left\{\left|f_n(z) – f(z)\right| : z \in S\right\}$, entonces una definición equivalente para la convergencia uniforme es:
\begin{equation*}
f_n \to f \,\,\, \text{uniformemente en S}\quad \Longleftrightarrow \quad \lim_{n\to\infty} M_n = 0.
\end{equation*}

En caso de que no se alcance el máximo, basta con tomar $M_n = \operatorname{sup}\left\{\left|f_n(z) – f(z)\right| : z \in S\right\}$.

Ejemplo 28.3.
Sean $x\in[0, 1]$, $n\in\mathbb{N}^+$ y $f(x) = 0$. Consideremos a la sucesión de funciones reales $\{f_n\}_{n\geq 1}$, dada por:
\begin{equation*}
f_n(x) = \frac{2nx}{1+n^2 x^2}.
\end{equation*}

Veamos que:
a) $f_n \to f$ puntualmente en $[0,1]$.
b) $f_n \not \to f$ uniformemente en $[0,1]$.

Solución. Primeramente, podemos visualizar el comportamiento de la sucesión $\{f_n\}_{n\geq 1}$ en el siguiente applet de GeoGebra https://www.geogebra.org/m/shs5mw8b.

a) Es claro que si $x=0$, entonces para todo $n\in\mathbb{N}^+$ se cumple que $f_n(0) = 0$ y en tal caso $f_n \to f$ puntualmente.

Supongamos que $x \neq 0$, entonces $x \in (0,1]$ y en tal caso:
\begin{equation*}
\lim_{n \to \infty} f_n(x) = \lim_{n \to \infty} \frac{2nx}{1+n^2 x^2} = \lim_{n \to \infty} \frac{1}{n} \left(\dfrac{2x}{\frac{1}{n^2}+ x^2}\right) = 0.
\end{equation*}

Por lo que, para toda $x \in [0,1]$, $f_n \to f$ puntualmente.

Entonces, para cada $x\in[0,1]$, la sucesión de números complejos $\{f_n(x)\}_{n\geq 1}$ converge a $0$, como se puede visualizar en el applet mencionado previamente.

b) Dado que para cada $n\in\mathbb{N}^+$ la función $f_n : [0, 1] \to \mathbb{R}$ es continua y $[0, 1] \subset \mathbb{R}$ es un conjunto compacto, entonces, proposición 10.10, la función $f_n$ alcanza sus valores mínimo y máximo (absolutos) en $[0, 1]$. Sea:\begin{align*}
M_n &= \underset{x \in[0,1]}{\max} \left| f_n(x) – f(x) \right|\\
& = \underset{x \in[0,1]}{\max} \left| \frac{2nx}{1+n^2 x^2} \right|\\
& = \underset{x \in[0,1]}{\max} \dfrac{2nx}{1+n^2 x^2}\\
& = \underset{x \in[0,1]}{\max} f_n(x).
\end{align*}

Es claro que para $x = 0$, la función $f_n$ alcanza su mínimo absoluto, por lo que consideremos a $x\in(0,1]$.

Procedemos a obtener el máximo absoluto de la función $f_n$. Derivando tenemos:
\begin{equation*}
f_n'(x) = \dfrac{2n(1-n^2 x^2)}{(1+n^2 x^2)^2}.
\end{equation*}Entonces, para $x\in(0, 1]$, tenemos que:
\begin{equation*}
f_n'(x) = 0 \quad \Longleftrightarrow \quad 1 – n^2 x^2 = 0 \quad \Longleftrightarrow \quad x = \frac{1}{n}.
\end{equation*}Notemos que:
\begin{equation*}
f_n\left(\frac{1}{n}\right) = \dfrac{2n\left(\frac{1}{n}\right)}{1+n^2\left(\frac{1}{n}\right)^2} = \frac{2}{2} = 1,
\end{equation*} \begin{equation*}
f_n\left(1\right) = \dfrac{2n\left(1\right)}{1+n^2\left(1\right)^2} = \frac{2n}{1+n^2} \leq 1,
\end{equation*} donde esta última desigualdad se sigue del hecho de que $(n-1)^2\geq 0$ para todo $n\in\mathbb{N}^+$, por lo que, en $x=\dfrac{1}{n}$ la función alcanza su máximo absoluto.

Entonces:
\begin{equation*}
M_n = \underset{x \in[0,1]}{\max} f_n(x) = 1,
\end{equation*}de donde:
\begin{equation*}
\lim_{n\to\infty} M_n = 1 \neq 0,
\end{equation*} por lo que, observación 28.4, $f_n \not \to f$ uniformemente en $[0,1]$.

Ahora procedemos a probar un resultado que nos permite garantizar la continuidad de la función límite de una sucesión convergente de funciones continuas, bajo la convergencia uniforme. Cabe mencionar que este resultado es válido en general para dos espacios métricos $(X, d_X)$ y $(Y, d_Y)$ que cumplan las condiciones dadas.

En este punto, es importante que enfaticemos en que dada una sucesión de funciones, podemos hablar de su convergencia puntual y/o uniforme, por lo que, antes de probar el resultado mencionado, consideremos el siguiente ejemplo, el cual nos deja ver una de las principales diferencias entre la convergencia puntual y la convergencia uniforme.

Ejemplo 28.4.
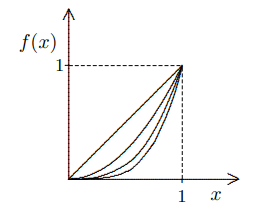
Consideremos a la sucesión de funciones reales $f_n:[0,1] \to \mathbb{R}$ dada por $f_n(x) = x^n$, con $n\in\mathbb{N}^+$. Claramente, para cada $n\in\mathbb{N}^+$ la función $f_n$ es continua en el intervalo $[0,1]$.

Sin embargo, el límite puntual de la sucesión $\left\{f_n\right\}_{n\geq 1}$, es decir, la función:
\begin{equation*}
f(x)= \lim_{n\to\infty} f_n(x) = \left\{ \begin{array}{lcc}
0 & \text{si} & 0 \leq x < 1, \\
\\ 1 & \text{si} & x=1, \end{array}
\right.
\end{equation*} no es continua en $[0,1]$, por lo que la convergencia puntual de la sucesión de funciones continuas $\left\{f_n\right\}_{n\geq 1}$ no garantiza la continuidad de la función $f$ en el intervalo real $[0,1]$.

El ejemplo anterior nos deja ver que, en general, la función límite de una sucesión de funciones continuas que converge puntualmente, puede no ser continua. Pero, ¿qué sucede si la convergencia de la sucesión de funciones continuas es uniforme?

Proposición 28.1.
Sean $S\subset \mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones continuas en $S$. Supongamos que la sucesión $\left\{f_n\right\}_{n\geq 0}$ converge uniformemente a una función $f:S\to\mathbb{C}$, entonces $f$ es continua.

Demostración. Dadas las hipótesis, tomemos al punto $a \in S$ fijo y sea $\varepsilon>0$.

Como la sucesión converge uniformemente a $f$, existe $N(\varepsilon)\in\mathbb{N}$ tal que si $n\geq N$, entonces:
\begin{equation*}
\left|f_n(z) – f(z) \right| < \frac{\varepsilon}{3}, \quad \forall z\in S.
\end{equation*}

Por otra parte, para cada $n\in\mathbb{N}$ tenemos que la función $f_n$ es continua en $S$, en particular es continua en $a$, por lo que para el $\varepsilon>0$ dado, existe $\delta>0$ tal que si $z\in S$ y $|z-a|<\delta$, entonces:
\begin{equation*}
\left|f_n(z) – f_n(a) \right| < \frac{\varepsilon}{3}.
\end{equation*}

Entonces, para todo $z\in S$ tal que $|z-a|<\delta$, se cumple que:
\begin{align*}
\left|f(z) – f(a) \right| & \leq \left|f_n(z) – f(z) \right| + \left|f_n(z) – f_n(a) \right| + \left|f_n(a) – f(a) \right|\\
& < \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon.
\end{align*}Por lo que, $f$ es continua en $a\in S$.

$\blacksquare$

Observación 28.5.
La proposición 28.1 suele utilizarse para determinar cuándo una sucesión de funciones no converge uniformemente, es decir, considerando la contrapuesta se deduce que si una sucesión de funciones continuas converge puntualmente a una función discontinua, entonces la convergencia no es uniforme. Sin embargo, no se cumple el recíproco, ya que puede suceder que el límite puntual de una sucesión de funciones sea una función continua y que dicha sucesión no converga uniformemente.

Ejemplo 28.5.
De acuerdo con el ejemplo 28.3, sabemos que la función límite puntual de la sucesión de funciones continuas $f_n(x) = \dfrac{2nx}{1+n^2 x^2}$, con $x\in[0, 1]$ y $n\in\mathbb{N}^+$, es la función continua $f(x) = 0$. Sin embargo, la sucesión $\left\{f_n\right\}_{n\geq 1}$ no converge uniformemente a $f$ en el intervalo real $[0, 1]$.

Ejemplo 28.6.
Por el ejemplo 28.4, tenemos que la función límite (puntual) de la sucesión de funciones continuas $\left\{f_n\right\}_{n\geq 1}$, dada por $f_n(x) = x^n$ con $x\in[0, 1]$, es una función discontinua, por lo que, la convergencia de la sucesión no puede ser uniforme.

Observación 28.6.
Recordemos que en Matemáticas muchos problemas difíciles se simplifican al saber bajo qué condiciones es posible el intercambio de límites, por lo que, la proposición 28.1 es de gran ayuda en este hecho.

Dada una sucesión de funciones $\left\{f_n\right\}_{n\geq 0}$ en $S\subset\mathbb{C}$ que converge uniformemente en $S$ se cumple que:
\begin{equation*}
\lim_{z\to z_0} \lim_{n\to\infty} f_n(z) = \lim_{n\to\infty} \lim_{z\to z_0} f_n(z) = \lim_{n\to\infty} f_n(z_0),
\end{equation*} para todo $z_0\in S$ que es un punto de acumulación de $S$.

Definición 28.4. (Sucesión de funciones uniformemente de Cauchy.)
Sea $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S\subset\mathbb{C}$. Diremos que $\left\{f_n\right\}_{n\geq 0}$ es uniformemente de Cauchy en $S$ si para todo $\varepsilon>0$ existe $N(\varepsilon)\in\mathbb{N}$ tal que si $m, n\geq N$, con $n>m$, entonces:
\begin{equation*}
|f_n(z) – f_m(z)| < \varepsilon, \quad \forall z\in S.
\end{equation*}

Proposición 28.2. (Criterio de Cauchy para convergencia uniforme.)
Sea $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S\subset\mathbb{C}$. Entonces, $\left\{f_n\right\}_{n\geq 0}$ converge uniformemente en $S$ si y solo si es una sucesión uniformemente de Cauchy en $S$.

Demostración. Dadas las hipótesis.

$\Longrightarrow)$

Sea $\varepsilon>0$. Supongamos que $\left\{f_n\right\}_{n\geq 0}$ converge uniformemente en $S$ a una función $f:S\to\mathbb{C}$, por lo que existe $N(\varepsilon)\in\mathbb{N}$ tal que si $n\geq N$ entonces:
\begin{equation*}
|f_n(z) – f(z)| < \frac{\varepsilon}{2}, \quad \forall z\in S.
\end{equation*}

De la desigualdad del triángulo, para $z\in S$ y $n>m \geq N$, se sigue que:
\begin{equation*}
|f_n(z) – f_m(z)| \leq |f_n(z) – f(z)| + |f(z) – f_m(z)| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.
\end{equation*}

Por lo que $\left\{f_n\right\}_{n\geq 0}$ es uniformemente de Cauchy en $S$.

$(\Longleftarrow$

Supongamos que $\left\{f_n\right\}_{n\geq 0}$ es uniformemente de Cauchy en $S$.

Notemos que para cada $z\in S$, tenemos que la sucesión de números complejos $\left\{f_n(z)\right\}_{n\geq 0}$ es de Cauchy, por lo que es una sucesión convergente, entonces existe $f: S\to \mathbb{C}$ dada por:
\begin{equation*}
f(z) = \lim_{n\to\infty} f_n(z), \quad \forall z\in S,
\end{equation*} es decir, $f_n \to f$ puntualmente en $S$.

Sea $\varepsilon>0$. Por hipótesis sabemos que existe $N\in\mathbb{N}$ tal que si $m,n \geq N$, con $n>m$, entonces:
\begin{equation*}
|f_n(z) – f_m(z)| < \frac{\varepsilon}{2}, \quad \forall z\in S.
\end{equation*}

Si fijamos $m\in\mathbb{N}$, con $m\geq N$, y $z\in S$, entonces:
\begin{equation*}
|f(z) – f_m(z)| = \lim_{n\to \infty} |f_n(z) – f_m(z)| \leq \frac{\varepsilon}{2} <\varepsilon.
\end{equation*}

Como $m\geq N$ era arbitrario, entonces:
\begin{equation*}
|f(z) – f_m(z)| < \varepsilon.
\end{equation*}

Por lo que $f_n \to f$ uniformemente en $S$.

$\blacksquare$

Definición 28.5. (Sucesión de sumas parciales de una sucesión de funciones.)
Sean $S\subset\mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$. Para cada $k\in\mathbb{N}$ definimos a la función $s_k : S \to \mathbb{C}$ como:
\begin{equation*}
s_n(z) = \sum_{k=0}^n f_k(z).
\end{equation*}

A las funciones $s_n$ las llamaremos las sumas parciales de la sucesión de funciones $\left\{f_n\right\}_{n\geq 0}$ y a la sucesión de sumas parciales la denotamos como $\left\{s_n\right\}_{n\geq 0}$.

Definición 28.6. (Convergencia puntual y convergencia uniforme de una serie de funciones.)
Sean $S\subset\mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$. Diremos que la serie de funciones $\displaystyle \sum_{n=0}^\infty f_n$ converge puntualmente en $S$ si la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ converge puntualmente en $S$ a una función $s: S\to \mathbb{C}$.

Por otra parte, si la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ converge uniformemente en $S$ a una función $s: S\to \mathbb{C}$, diremos que la serie de funciones $\displaystyle\sum_{n=0}^\infty f_n$ converge uniformemente en $S$.

En cualquiera de ambos casos, una vez especificado el tipo de convergencia, denotaremos la convergencia de la serie de funciones a la función $s$ como:
\begin{equation*}
s(z) = \sum_{n=0}^\infty f_n(z),
\end{equation*}

y a la función $s$ la llamaremos la función suma de la serie.

De acuerdo con la definición anterior y considerando el corolario 27.1, no es difícil probar el siguiente:

Corolario 28.1.
Sea $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S\subset \mathbb{C}$. Si la serie $\displaystyle\sum_{n=0}^\infty f_n$ converge puntualmente en $S$, entonces la sucesión $\left\{f_n\right\}_{n\geq 0}$ converge puntualmente a $0$ en $S$.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Observación 28.7.
Considerando la observación 28.3 y la definición 28.6, debe ser claro que la convergencia uniforme de una serie de funciones implica la convergencia puntual de la misma.

Definición 28.7. (Serie de funciones absolutamente convergente.)
Sea $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S\subset\mathbb{C}$. Diremos que la serie de funciones $\displaystyle \sum_{n=0}^\infty f_n$ es absolutamente convergente en $S$ si la serie $\displaystyle \sum_{n=0}^\infty |f_n|$ es puntualmente convergente en $S$.

Observación 28.8.
Al igual que con las series de números complejos, una serie de funciones absolutamente convergente es puntualmente convergente.

Como lo hicimos con las sucesiones de funciones, podemos preguntarnos qué pasa en el caso de tener una serie infinita de funciones continuas que es convergente, ¿su función límite será continua? Para responder esta pregunta debemos recordar que al hablar de una serie de funciones convergente podemos tener la convergencia puntual y/o la convergencia uniforme de la sucesión de sumas parciales. Es claro que en el caso de una suma finita de funciones continuas, la función suma también será continua. Sin embargo, de acuerdo con la proposición 28.1, inferimos que la continuidad de la función límite de una serie convergente de funciones continuas se dará siempre que la convergencia sea uniforme.

Corolario 28.2.
Sean $S\subset \mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones continuas en $S$. Si la serie $\displaystyle\sum_{n=0}^\infty f_n$ converge uniformemente en $S$ a la función $s:S\to\mathbb{C}$, entonces $s$ es continua.

Demostración. Se sigue de la proposición 28.1, por lo que los detalles de la prueba se dejan como ejercicio al lector.

$\blacksquare$

Ejemplo 28.7.
Veamos que la serie:
\begin{equation*}
\displaystyle \sum_{n=1}^{\infty} 2^n \operatorname{sen}\left(\frac{1}{3^n z}\right),
\end{equation*} es absolutamente convergente en $\mathbb{C}\setminus\{0\}$, pero que la serie no converge uniformemente en $\mathbb{C}$.

Solución. Primeramente, notemos que para cada $z\neq 0$ la sucesión de funciones $\left\{f_n\right\}_{n\geq 1}$, dada por:
\begin{equation*}
f_n(z) = 2^n \operatorname{sen}\left(\frac{1}{3^n z}\right),
\end{equation*} define una sucesión de números complejos, es decir, $\left\{f_n(z)\right\}_{n\geq 1}$. Por lo que, para $z\neq 0$ podemos verificar que la serie es absolutamente convergente utilizando el criterio del cociente de D’Alembert.

De acuerdo con el ejemplo 22.5 sabemos que:
\begin{equation*}
\lim_{w\to 0} \frac{\operatorname{sen}(w)}{w} = 1,
\end{equation*}

y del ejercicio 3 de la entrada 14 se sigue que:
\begin{equation*}
\lim_{w\to 0} \left|\frac{\operatorname{sen}(w)}{w}\right| = \lim_{n\to\infty} \left|\dfrac{\operatorname{sen}\left(\dfrac{1}{3^{n+1} z}\right)}{\dfrac{1}{3^{n+1} z}}\right| = 1, \quad z\neq 0.
\end{equation*}

Sea $z\neq 0$, entonces:
\begin{align*}
\lim_{n\to\infty} \frac{\left|f_{n+1}(z)\right|}{\left|f_{n}(z)\right|} & = \lim_{n\to\infty} \left|\dfrac{2^{n+1} \operatorname{sen}\left(\dfrac{1}{3^{n+1} z}\right)}{2^n \operatorname{sen}\left(\dfrac{1}{3^n z}\right)}\right|\\
& = \lim_{n\to\infty} 2 \left|\dfrac{\dfrac{\operatorname{sen}\left(\dfrac{1}{3^{n+1} z}\right)}{\dfrac{1}{3^{n+1} z}}}{\dfrac{\operatorname{sen}\left(\dfrac{1}{3^{n} z}\right)}{\dfrac{1}{3^{n} z}}}\right| \left|\dfrac{\dfrac{1}{3^{n+1} z}}{\dfrac{1}{3^n z}}\right|\\
& = \lim_{w\to 0 } \frac{2}{3} \left| \dfrac{\dfrac{\operatorname{sen}(w)}{w}}{\dfrac{\operatorname{sen}(3w)}{3w}} \right|\\
&= \frac{2}{3} < 1.
\end{align*}

Entonces, para todo $z\neq 0$ la serie $ \displaystyle \sum_{n=1}^{\infty} 2^n \operatorname{sen}\left(\frac{1}{3^n z}\right)$ es absolutamente convergente y por tanto la serie converge puntualmente en $\mathbb{C}\setminus\{0\}$.

Por otra parte, es claro que las funciones de la sucesión $\left\{f_n\right\}_{n\geq 1}$ son continuas para todo $z\neq 0$. Sin embargo, para $z = 0$ dichas funciones no están definidas y como $\lim\limits_{z \to 0} f_n(z)$ no existe, entonces la función límite puntual $s(z) = \displaystyle \sum_{n=1}^{\infty} 2^n \operatorname{sen}\left(\frac{1}{3^n z}\right)$ no es continua en $z=0$, por lo que, corolario 28.2, la serie no converge uniformemente en $\mathbb{C}$.

Proposición 28.3. (Criterio $M$ de Weierstrass.)
Sean $S\subset \mathbb{C}$ y $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$. Si para cada $n\in\mathbb{N}$ existe $M_n\geq 0$ tal que $\left|f_n(z)\right| \leq M_n$ para todo $z\in S$ y la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge, entonces la serie de funciones $\displaystyle\sum_{n=0}^\infty f_n$ converge absolutamente y uniformemente en $S$.

Demostración. Dadas las hipótesis, tenemos que para todo $z\in S$ se cumple que:
\begin{equation*}
|f_n(z)| \leq M_n, \quad \forall n\in\mathbb{N}.
\end{equation*}

Dado que la serie $\displaystyle\sum_{n=0}^\infty M_n$ es convergente, se sigue del criterio de comparación, proposición 27.4, que la serie $\displaystyle\sum_{n=0}^\infty f_n$ es absolutamente convergente. Más aún, de la convergencia absoluta de la serie se sigue que la serie $\displaystyle\sum_{n=0}^\infty f_n$ converge, proposición 27.3, para todo $z\in S$.

Definimos a la función $f:S\to\mathbb{C}$ como:
\begin{equation*}
f(z) = \lim_{n\to\infty} \sum_{k=0}^n f_k(z) = \sum_{n=0}^\infty f_n(z), \quad \forall z\in S.
\end{equation*}

Sea $\left\{s_n\right\}_{n\geq 0}$ la sucesión de sumas parciales de la serie. Veamos que dicha sucesión de funciones converge uniformemente a $f$ en $S$.

Sea $\varepsilon>0$. Por el criterio de Cauchy, proposición 27.1, tenemos que existe $N(\varepsilon)\in\mathbb{N}$ tal que si $n, m\geq N$, con $n>m$, entonces:
\begin{equation*}
\sum_{k=m+1}^n M_k = \left|\sum_{k=m+1}^n M_k\right| < \varepsilon.
\end{equation*}

Por la desigualdad del triángulo, para todo $n,m\geq N$, con $n>m$ y todo $z\in S$, se tiene que:
\begin{align*}
|s_n(z) – s_m(z)| = \left|\sum_{k=0}^n f_k(z) – \sum_{k=0}^m f_k(z) \right|
& = \left|\sum_{k=m+1}^n f_k(z) \right|\\
& \leq \sum_{k=m+1}^n \left| f_k(z) \right|\\
& \leq \sum_{k=m+1}^n M_k < \varepsilon.
\end{align*}

Entonces, la sucesión de funciones $\left\{s_n\right\}_{n\geq 0}$ es uniformemente de Cauchy en $S$, por lo que, proposición 28.2, converge uniformemente a $f$ en $S$.

$\blacksquare$

Ejemplo 28.8.
Veamos que la serie geométrica $\displaystyle\sum_{n=0}^\infty z^n$ converge uniformemente a la función $s(z) =\dfrac{1}{1-z}$ en todo subdisco cerrado $\overline{B}(0,r)$, con $0<r<1$, del disco abierto $B(0,1)$, pero que la convergencia en $B(0,1)$ es solo puntual y no uniforme.

Solución. De acuerdo con el ejemplo 27.3, sabemos que la serie geométrica $\displaystyle\sum\displaystyle_{n=0}^\infty z^n$ converge a $\dfrac{1}{1-z}$ si $|z|<1$.

Sean $z \in \overline{B}(0,r)$, con $0< r < 1$, y $f_n(z) = z^n$ para todo $n\in\mathbb{N}$.

Notemos que:
\begin{equation*}
|f_n(z)| = |z^n| = |z|^n \leq r^n = M_n, \quad z \in \overline{B}(0,r).
\end{equation*}

Es claro que la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge para $0 < r < 1$. Por lo que, de acuerdo con el criterio $M$ de Weierstrass, la serie $\displaystyle\sum_{n=0}^\infty z^n$ converge uniformemente a la función $f(z) =\dfrac{1}{1-z}$ en todo disco cerrado $\overline{B}(0,r) \subset B(0,1)$ si $|z| \leq r < 1$.

Por otra parte, sabemos que la $n$-ésima suma parcial de la serie geométrica es:
\begin{equation*}
s_n(z) = \frac{1 – z^{n+1}}{1-z},
\end{equation*}

de donde:
\begin{equation*}
f(z) = \lim_{n \to \infty} s_n(z) = \frac{1}{1-z}, \quad \forall z \in B(0,1),
\end{equation*}

es decir que la convergencia es puntual en el disco abierto $B(0,1)$.

Por último, notemos que si $z=x\in\mathbb{R}$, con $0<x<1$, entonces:
\begin{equation*}
|f(z) – s_n(z)| = \left|\frac{1}{1-x} – \frac{1 – x^{n+1}}{1-x}\right| = \frac{\left|x^{n+1}\right|}{\left|1-x\right|} = \frac{x^{n+1}}{1-x}.
\end{equation*}

Claramente $|f(z) – s_n(z)| \to \infty$ si $x\to 1^{-}$. Entonces, no existe $n\in\mathbb{N}$ tal que:
\begin{equation*}
|f(z) – s_n(z)| = \frac{x^{n+1}}{1-x} <\varepsilon, \quad \forall x\in (0,1).
\end{equation*}

Por lo que la convergencia no es uniforme en $B(0,1)$.

Ejemplo 28.9.
Consideremos las siguientes series de funciones:
a) $\displaystyle\sum_{n=0}^\infty \dfrac{z^n+6i}{2^n +1}$, para $z\in B(0,1)$.
b) Función zeta de Riemann: \begin{equation*} \zeta(z) = \displaystyle \sum_{n=1}^\infty n^{-z}, \end{equation*} donde consideramos la rama principal de $n^{-z}$, para $z \in S_\sigma = \left\{z\in\mathbb{C} : \operatorname{Re}(z) \geq \sigma\right\}$, con $\sigma>1$.

Veamos que ambas series son uniformemente y absolutamente convergentes en el dominio dado.

Solución.
a) Primeramente recordemos que si $z\in B(0,1)$, entonces $|z|<1$.

Por la desigualdad del triángulo, para todo $n\in\mathbb{N}$ tenemos que:
\begin{equation*}
\left| \frac{z^n+6i}{2^n +1} \right| = \frac{\left|z^n+6i\right|}{2^n +1} \leq \frac{|z|^n + 6}{2^n + 1} \leq \frac{7}{2^n}.
\end{equation*}

Sea $M_n = 7/2^n$, entonces $M_n>0$ para todo $n\in\mathbb{N}$. Más aún, dado que $\left|1/2\right| < 1$, entonces la serie geométrica $\displaystyle\sum_{n=0}^\infty \, \dfrac{1}{2^n}$ es convergente y por la proposición 27.2 tenemos que:
\begin{equation*}
\displaystyle\sum_{n=0}^\infty \dfrac{7}{2^n} = 7 \, \, \displaystyle\sum_{n=0}^\infty \dfrac{1}{2^n}= 7 \left(\frac{1}{1-\dfrac{1}{2}}\right) = 14,
\end{equation*} entonces la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge, por lo que, de acuerdo con el criterio $M$ de Weierstrass, la serie $\displaystyle\sum_{n=0}^\infty \dfrac{z^n+6i}{2^n +1}$ es absoluta y uniformemente convergente en $B(0,1)$.

Por último, notemos que para cada $n\in\mathbb{N}$, la función $f_n(z) = \dfrac{z^n+6i}{2^n +1}$ es una función polinomial, por lo que es continua en todo $\mathbb{C}$, en particular en el disco $B(0,1)$. Entonces, por el corolario 28.2, concluimos que la función $s: B(0,1) \to \mathbb{C}$ a la que converge la serie, es una función continua.

b) Considerando la rama principal de la función multivaluada $n^{-z}$, definición 21.6, para cada $n\in\mathbb{N}^+$ tenemos la función:
\begin{equation*}
f_n(z) = n^{-z} = e^{-z \operatorname{Log}(n)}.
\end{equation*}

Si $z = x+iy \in S_\sigma$, entonces $x\geq \sigma > 1$ y por la proposición 20.2 tenemos que:
\begin{align*}
\left|f_n(z)\right| = \left|n^{-z}\right| & = \left| e^{-(x+iy) \operatorname{Log}(n)}\right|\\
& = \left| e^{-x\operatorname{Log}(n)} e^{-iy\operatorname{Log}(n)}\right|\\
& = \left| e^{-x\operatorname{Log}(n)} \right| \left|e^{-iy\operatorname{Log}(n)}\right|\\
& = e^{-x \operatorname{Log}(n)}\\
& \leq e^{-\sigma \operatorname{Log}(n)}\\
& = n^{-\sigma}.
\end{align*}

Para cada $n\geq 1$ sea $M_n = n^{-\sigma}$, con $\sigma >1$.

Considerando el criterio de convergencia de las series reales $p$, es decir, las series de la forma:
\begin{equation*}
\sum_{n=1}^{\infty} n^{-p}
\end{equation*}

visto en nuestros cursos de Cálculo, sabemos que estas series son convergentes si y solo si $p>1$. Entonces, dado que $\sigma>1$, es claro que la serie:
\begin{equation*}
\sum_{n=1}^{\infty} M_n = \sum_{n=1}^{\infty} n^{-\sigma},
\end{equation*}

es convergente, por lo que, de acuerdo con el cirterio $M$ de Weierstrass, la función zeta de Riemann, $\zeta(z) = \displaystyle \sum_{n=1}^\infty n^{-z}$, es absoluta y uniformemente convergente en $S_\sigma$, con $\sigma>1$.

Ejemplo 28.10.
Veamos que las siguientes series de funciones son uniformemente y absolutamente convergentes en todo disco cerrado $\overline{B}(0, R)$, con $R>0$.
a)$\displaystyle\sum_{n=0}^\infty \dfrac{z^n}{n!}$.
b) $\displaystyle\sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{(2n+1)!}$.
c) $\displaystyle \sum_{n=0}^\infty \frac{(-1)^n z^{2n}}{(2n)!}$.

Solución. Sea $z\in \overline{B}(0, R)$, con $R>0$, entonces $|z|\leq R$. El procedimiento es completamente análogo en los tres casos, por lo que los detalles de los últimos dos incisos se dejan como ejercicio al lector.

a) Para cada $n\in\mathbb{N}$ definimos:
\begin{equation*}
f_n(z) = \frac{z^n}{n!}.
\end{equation*}

Notemos que:
\begin{equation*}
\left|f_n(z)\right| = \left|\frac{z^n}{n!}\right| = \frac{\left|z\right|^n}{n!} \leq \frac{R^n}{n!}.
\end{equation*}

Para cada $n\in\mathbb{N}$ sea $M_n = \dfrac{R^n}{n!}$. Dado que $R>0$, es claro que $M_n > 0$ para todo $n\geq 0$.

Tenemos que:
\begin{equation*}
\lim_{n\to\infty} \frac{M_{n+1}}{M_n} = \lim_{n\to\infty} \dfrac{\dfrac{R^{n+1}}{(n+1)!}}{\dfrac{R^n}{n!}} = \lim_{n\to\infty} \frac{R}{n+1} = 0 < 1,
\end{equation*} entonces, por el criterio del cociente de D’Alembert, proposición 27.5, la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge.

Por lo tanto, de acuerdo con el criterio $M$ de Weierstrass, concluimos que la serie:
\begin{equation*}
\displaystyle\sum_{n=0}^\infty f_n(z) = \displaystyle\sum_{n=0}^\infty \dfrac{z^n}{n!},
\end{equation*} es absoluta y uniformemente convergente en todo disco cerrado $\overline{B}(0,R)$, con $R>0$.

b) Para cada $n\in\mathbb{N}$ definimos:
\begin{equation*}
f_n(z) = \frac{(-1)^n z^{2n+1}}{(2n+1)!} \quad \text{y} \quad M_n(z) = \frac{R^{2n+1}}{(2n+1)!}.
\end{equation*}

Por el criterio del cociente de D’Alembert, proposición 27.5, la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge.

Notemos que para todo $n\in \mathbb{N}$ y todo $z\in \overline{B}(0,R)$, con $R>0$, se cumple que $|f_n(z)| \leq M_n$, entonces por el criterio $M$ de Weierstrass se tiene que la serie $\displaystyle\sum_{n=0}^\infty \frac{(-1)^n z^{2n+1}}{(2n+1)!}$ es absoluta y uniformemente convergente en todo disco cerrado $\overline{B}(0,R)$.

c) Para cada $n\in\mathbb{N}$ sea:
\begin{equation*}
f_n(z) = \frac{(-1)^n z^{2n}}{(2n)!} \quad \text{y} \quad M_n(z) = \frac{R^{2n}}{(2n)!}.
\end{equation*}

Del criterio de D’Alembert, proposición 27.5, se sigue que la serie $\displaystyle\sum_{n=0}^\infty M_n$ converge.

Como para todo $n\in \mathbb{N}$ y todo $z\in \overline{B}(0,R)$, con $R>0$, se cumple que $|f_n(z)| \leq M_n$, entonces por el criterio $M$ de Weierstrass se tiene que la serie $\displaystyle \sum_{n=0}^\infty \frac{(-1)^n z^{2n}}{(2n)!}$ es absoluta y uniformemente convergente en todo disco cerrado $\overline{B}(0,R)$.

Ejemplo 28.11.
Determinemos el conjunto $S \subset \mathbb{C}$ dónde la serie $\displaystyle \sum_{n=1}^\infty \dfrac{\operatorname{cos(nz)}}{n^3}$ es absoluta y uniformemente convergente.

Solución. Para cada $n\in\mathbb{N}^+$ definimos:
\begin{equation*}
f_n(z) = \frac{\operatorname{cos}(nz)}{n^3} = \frac{e^{i(nz)} + e^{-i(nz)}}{2n^3}.
\end{equation*}

Sea $z=x+iy\in\mathbb{C}$. De acuerdo con la proposición 20.2 tenemos que:
\begin{align*}
\left|f_n(z)\right| & = \left|\frac{e^{i(nz)} + e^{-i(nz)}}{2n^3}\right|\\
& \leq \frac{1}{2n^3}\left(\left|e^{in(x+iy)}\right| + \left|e^{-in(x+iy)}\right|\right)\\
& = \frac{1}{2n^3}\left(\left|e^{inx}\right| \left|e^{-ny}\right| + \left|e^{-inx}\right| \left|e^{ny}\right|\right)\\
& = \frac{1}{2n^3}\left(e^{-ny} + e^{ny}\right)\\
& =: M_n.
\end{align*}

De acuerdo con la proposición 27.2, sabemos que:
\begin{align*}
\sum_{n=1}^\infty M_n & = \sum_{n=1}^\infty \frac{e^{-ny} + e^{ny}}{2n^3}\\
& = \sum_{n=1}^\infty \frac{e^{-ny}}{2n^3} + \sum_{n=1}^\infty \frac{e^{ny}}{2n^3},
\end{align*} si y solo si las series del lado derecho de la igualdad son convergentes.

Analicemos a las series:
\begin{equation*}
\sum_{n=1}^\infty \frac{e^{-ny}}{2n^3} \quad \text{y} \quad \sum_{n=1}^\infty \frac{e^{ny}}{2n^3}.
\end{equation*}

Para $z=x+iy \in\mathbb{C}$ tenemos que $y>0$, $y<0$ ó $y=0$.

Si $y>0$, entonces $\lim\limits_{n\to\infty} \dfrac{e^{ny}}{2n^3} \neq 0$. Por lo que, la serie $\displaystyle \sum_{n=1}^\infty \frac{e^{ny}}{2n^3}$ diverge para $y>0$.

Análogamente, si $y<0$, entonces $\lim\limits_{n\to\infty} \dfrac{e^{-ny}}{2n^3} \neq 0$. Por lo que, la serie $\displaystyle \sum_{n=1}^\infty \frac{e^{-ny}}{2n^3}$ diverge para $y<0$.

Por último, si $y=0$, entonces ambas series convergen por el criterio de convergencia de las series $p$, con $p=3>1$. En tal caso:
\begin{equation*}
\sum_{n=1}^\infty M_n = \sum_{n=1}^\infty \frac{e^{-ny} + e^{ny}}{2n^3} = \sum_{n=1}^\infty \frac{2}{2n^3} = \sum_{n=1}^\infty \frac{1}{n^3},
\end{equation*} la cual es una serie convergente.

Es claro que para $y=0$ tenemos que $z=x\in\mathbb{C}$, entonces el conjunto $S\subset\mathbb{C}$ de convergencia de la serie es $S =\mathbb{R}$, es decir, la recta real.

Para $z = x \in \mathbb{R}$, tenemos que:
\begin{equation*}
\left|f_n(z)\right| = \left|\frac{\operatorname{cos}(nx)}{n^3}\right| \leq M_n, \quad \forall n\in\mathbb{N}^+.
\end{equation*}

Entonces, por el criterio $M$ de Weierstrass, concluimos que la serie $\displaystyle \sum_{n=1}^\infty \dfrac{\operatorname{cos(nz)}}{n^3}$ es absolutamente y uniformemente convergente en $\mathbb{R}$.

Tarea moral

  1. Prueba la observación 28.4. Sean $S\subset \mathbb{C}$, $\left\{f_n\right\}_{n\geq 0}$ una sucesión de funciones en $S$ y $f: S\to\mathbb{C}$ una función. Supón que para todo $n\in\mathbb{N}$ existe: \begin{equation*} M_n = \operatorname{sup}\left\{\left|f_n(z) – f(z)\right| : z \in S\right\}. \end{equation*} Prueba que $f_n \to f$ uniformemente si y solo si $\lim\limits_{n\to\infty} M_n = 0$.
  2. Considera las siguientes sucesiones de funciones. Para cada una (i) determina si la sucesión converge puntualmente, en caso afirmativo obtén su función límite, (ii) analiza si la función converge uniformemente en el dominio $S \subset \mathbb{C}$ dado y (iii) si la convergencia uniforme no se da en $S$ determina algún subconjunto cerrado y acotado de $S$ donde se de la convergencia uniforme.
    a) $f_n(z) = \dfrac{\operatorname{sen}(nz)}{n^2}$, para $S = \left\{z\in\mathbb{C} : |z| \leq 1\right\}$.
    b) $f_n(z) = \dfrac{z^2+nz+1}{n^2 z + 1}$, para $S = \left\{z\in\mathbb{C} : 2 < |z|\right\}$.
    c) $f_n(z) = \dfrac{1}{(z+n+1)^2}$, para $S = \left\{z\in\mathbb{C} : \operatorname{Re}(z) > 0\right\}$.
    d) $f_n(z) = \dfrac{z^n+z}{n+1}$, para $S = \left\{z\in\mathbb{C} : |z| \leq 1\right\}$.
  3. Utiliza el criterio $M$ de Weierstrass para mostrar que las siguientes series convergen uniformemente en la región dada.
    a) $\displaystyle\sum_{n=1}^\infty \operatorname{Re}\left(\dfrac{(z + i)^n}{3^n}\right)$ en $B(0,1)$.
    b) $\displaystyle\sum_{n=1}^\infty \dfrac{1+z^n}{2^n – z}$ en $B(0,1)$.
    c) $\displaystyle\sum_{n=0}^\infty \dfrac{1}{(5-z)^n}$ para $|z|\leq \dfrac{7}{2}$.
    d) $\displaystyle\sum_{n=0}^\infty \dfrac{(z+1-3i)^n}{4^n}$ para $|z-3i|\leq \dfrac{1}{2}$.
  4. Considera la sucesión de funciones dada por: \begin{equation*} f_n(z)= \left\{ \begin{array}{lcc} n|z| & \text{si} & |z| \leq \dfrac{1}{n}, \\ \\ 1 & \text{si} & \dfrac{1}{n} \leq |z| \leq 1. \end{array} \right. \end{equation*} ¿La sucesión de funciones $\left\{f_n\right\}_{n\geq 1}$ converge puntualmente en el disco cerrado $\overline{B}(0,1)$?

    Hint: Analiza la continuidad de la función límite puntual en $\overline{B}(0,1)$ y considera la proposición 28.1.
  5. La $n$-ésima suma parcial de una serie de funciones está dada por la función $s_n(z) = \dfrac{z^n}{n}$ para $|z|\leq 1$. Considerando la $n$-ésima suma parcial construye la serie. ¿Dicha serie converge uniformemente en el disco cerrado $\overline{B}(0,1)$?
  6. Muestra que las siguientes series son absolutamente y uniformemente convergentes en el dominio dado.
    a) $\displaystyle\sum_{n=1}^\infty \dfrac{z^{2n}}{1- z^{2n}}$ en todo disco cerrado $\overline{B}(0,r)$, con $0<r<1$.
    b) $\displaystyle\sum_{n=1}^\infty \dfrac{z^n}{n\sqrt{n+1}}$ en $\overline{B}(0,1)$.
    c) $\displaystyle\sum_{n=1}^\infty \dfrac{1}{n^2+z^2}$ para $1<|z|<2$.
    d) $\displaystyle\sum_{n=1}^\infty \dfrac{e^{inz}}{n^2}$ en $S = \{z\in\mathbb{C} : \operatorname{Im}(z) > 0\}$.
  7. Demuestra los corolarios 28.1 y 28.2.
  8. Muestra que la serie:\begin{equation*} \sum_{n=1}^\infty \frac{z^{n-1}}{(1-z^n)(1-z^{n+1})},\end{equation*} converge a $\dfrac{1}{(1-z)^2}$ si $|z|<1$ y a $\dfrac{1}{z(1-z)^2}$ si $|z|>1$. Prueba que la convergencia es uniforme para $|z|\leq r<1$ en el primer caso y para $|z|\geq \rho>1$ en el segundo caso.

    Hint: Multiplica y divide cada término de la serie por $1-z$ y utiliza una descomposición por fracciones parciales para obtener una suma telescópica.

Más adelante…

En esta entrada hemos abordado las definiciones de sucesión y serie de funciones complejas, que como vimos resultaron idénticas a las que teníamos para el caso real. Además, probamos una serie de resultados, con los que ya estábamos familiarizados para la versión real, que extienden las propiedades de convergencia uniforme y puntual para el caso complejo, a través de los cuales podemos estudiar la convergencia de las sucesiones y series de funciones complejas.

En particular, vimos que al igual que en el caso real, el criterio $M$ de Weierstrass resulta de gran utilidad para el estudio de la convergencia uniforme de una serie.

Por otra parte, vimos que podemos garantizar la continuidad del límite uniforme de una sucesión de funciones continuas, así como la continuidad de la función suma de una serie de funciones continuas que converge uniformemente, lo cual resulta de gran interés pues nos permite el intercambio formal de los límites que definen la continuidad y la convergencia, observación 28.6.

En la siguiente entrada veremos el concepto de series de potencias para el caso complejo y probaremos una serie de resultados importantes que nos permitirán caracterizar propiedades de estas series como la continuidad y analicidad. Aunque podemos pensar a una serie de potencias como una serie de funciones complejas o como una serie de números complejos con una forma muy particular, veremos que el estudio de este tipo de series es de gran interés y utilidad pues nos permitirán escribir a las funciones complejas, en particular a las funciones elementales, como una serie de números complejos y así aprovechar las propiedades de convergencia de la serie.

Entradas relacionadas

Ecuaciones Diferenciales I: Teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden

Por Omar González Franco

Deja un comentario

El gran arquitecto parece ser un matemático; a aquellos que no saben matemáticas
les resulta realmente difícil sentir la profunda belleza de la naturaleza.
– Richard Feynman

Introducción

¡Hemos llegado al final de la unidad 3 del curso!.

Concluiremos presentando el teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden en el caso general.

En la primera entrada de esta unidad enunciamos el teorema de existencia y unicidad en el caso general, en esta entrada retomaremos dicho teorema con la diferencia de que lo adaptaremos a la notación vectorial que ya conocemos ya que esto tiene una enorme ventaja al momento de hacer la demostración.

La demostración de este teorema, al igual que el teorema de Picard – Lindelöf, requiere de una extensa teoría preliminar. En este caso no demostraremos dicha teoría preliminar, sólo la justificaremos ya que una enorme ventaja que tenemos es que mucho de los que vimos en la primer unidad se puede extender a los sistemas de ecuaciones diferenciales, así que lo que haremos será desarrollar esta extensión generalizando los resultados para así demostrar el teorema.

Se recomienda, si lo crees necesario, revisar las tres últimas entradas de la primera unidad para recordar la teoría previa a la demostración del teorema de Picard – Lindelöf, así como la demostración misma.

Comencemos por construir el enunciado del teorema.

Teorema de existencia y unicidad para sistemas de ecuaciones diferenciales

Como vimos en la primer entrada de esta unidad, un sistema de ecuaciones diferenciales de primer orden en su forma general es de la forma

\begin{align*}
y_{1}^{\prime}(t) & = F_{1}(t, y_{1}, y_{2}, \cdots, y_{n}) \\
y_{2}^{\prime}(t) & = F_{2}(t, y_{1}, y_{2}, \cdots, y_{n}) \\
& \vdots \\
y_{n}^{\prime}(t) &= F_{n}(t, y_{1}, y_{2}, \cdots, y_{n}) \label{1} \tag{1}
\end{align*}

Donde las $F_{i}$, $i = 1, 2, 3, \cdots, n$ son funciones con valores reales que dependen de las $n + 1$ variables en un intervalo $\delta$. Sabemos que

$$\mathbf{Y}(t) = \begin{pmatrix}
y_{1}(t) \\ y_{2}(t) \\ \vdots \\ y_{n}(t)
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{Y}^{\prime}(t) = \begin{pmatrix}
y^{\prime}_{1}(t) \\ y^{\prime}_{2}(t) \\ \vdots \\ y^{\prime}_{n}(t)
\end{pmatrix} \label{2} \tag{2}$$

Con ayuda de estos vectores podemos definir el vector

$$\mathbf{F}(t, \mathbf{Y}(t)) = \begin{pmatrix}
F_{1}(t, y_{1}, y_{2}, \cdots, y_{n}) \\ F_{2}(t, y_{1}, y_{2}, \cdots, y_{n}) \\ \vdots \\ F_{n}(t, y_{1}, y_{2}, \cdots, y_{n})
\end{pmatrix} \label{3} \tag{3}$$

De manera que el sistema de ecuaciones diferenciales (\ref{1}) se puede escribir en forma vectorial como

$$\mathbf{Y}^{\prime}(t) = \mathbf{F}(t, \mathbf{Y}(t)) \label{4} \tag{4}$$

Si el sistema de ecuaciones diferenciales (\ref{4}) esta sujeto a valores iniciales

$$\mathbf{Y}(t_{0}) = \begin{pmatrix}
y_{1}(t_{0}) \\ y_{2}(t_{0}) \\ \vdots \\ y_{n}(t_{0})
\end{pmatrix} = \begin{pmatrix}
b_{1} \\ b_{2} \\ \vdots \\ b_{n}
\end{pmatrix} = \mathbf{Y}_{0} \label{5} \tag{5}$$

con $b_{i}$, $i = 1, 2, \cdots, n$ constantes, entonces tenemos un problema de valores iniciales (PVI).

Definamos, por otro lado, una región $U$ como el producto cartesiano

$$\delta \times \delta_{1} \times \delta_{2} \times \delta_{3} \times \cdots \times \delta_{n} = U \in \mathbb{R}^{n + 1} \label{6} \tag{6}$$

en donde

$$t_{0} \in \delta, \hspace{0.5cm} b_{1} \in \delta_{1}, \hspace{0.5cm} b_{2} \in \delta_{2}, \hspace{0.5cm} \cdots, \hspace{0.5cm} b_{n} \in \delta_{n}$$

de tal forma que $(t_{0}, b_{1}, b_{2}, \cdots, b_{n}) \in U$, es decir, $\mathbf{Y}(t_{0}) = \mathbf{Y}_{0} \in U$.

Con estos resultados, el teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden se puede enunciar de la siguiente forma.

Este es el teorema que demostraremos.

Ecuación integral equivalente a un PVI

Como lo hicimos con el teorema de Picard – Lindelöf, es posible mostrar que el problema de valores iniciales (\ref{7}) es equivalente a una ecuación integral. El siguiente teorema establece este resultado.

La demostración es bastante similar a la que realizamos para el caso de ecuaciones diferenciales de primer orden. Intenta hacer la demostración. A continuación presentaremos una justificación que te puede ser de ayuda en tu demostración formal.

Justificación: Consideremos el sistema

$$\mathbf{Y}^{\prime}(t) = \mathbf{F}(t, \mathbf{Y}(t))$$

Integremos de $t_{0}$ a $t$.

$$\int_{t_{0}}^{t} \mathbf{Y}^{\prime}(s) ds = \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s)) ds \label{9} \tag{9}$$

Apliquemos el teorema fundamental del cálculo.

$$\mathbf{Y}(t) -\mathbf{Y}(t_{0}) = \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s))ds \label{10} \tag{10}$$

Como $\mathbf{Y}(t_{0}) = \mathbf{Y}_{0}$, del resultado anterior se obtiene la ecuación integral (\ref{8})

$$\mathbf{Y}(t) = \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s))ds$$

$\square$

Este es nuestro primer resultado generalizado. Lo siguiente que haremos será generalizar las iteraciones (o iterantes) de Picard.

Iterantes de Picard

En su forma desglosada las iterantes de Picard se pueden escribir como

\begin{align*}
\mathbf{Y}_{0}(t) &= \mathbf{Y}_{0} \\
\mathbf{Y}_{1}(t) &= \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{0}(s))ds \\
\mathbf{Y}_{2}(t) &= \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{1}(s)) ds \\
\mathbf{Y}_{3}(t) &= \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{2}(s)) ds \\
\vdots \\
\mathbf{Y}_{n}(t) &= \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{n -1}(s))ds \label{12} \tag{12}
\end{align*}

Lo interesante de las iterantes de Picard es que, cumpliendo ciertas hipótesis, éstas convergen a la solución del PVI (\ref{7}). El siguiente teorema nos ayudará a mostrar este hecho.

La demostración para el caso de ecuaciones de primer orden la hicimos como parte de la demostración del teorema de Picard – Lindelöf. Intenta generalizar dicha demostración.

Consideremos cierto este teorema, notemos lo siguiente.

Sea $\{ \mathbf{Y}_{n}(t) \}$ una sucesión de iteraciones de Picard que convergen uniformemente a una función $\mathbf{Y}(t)$ en el intervalo $\delta$ y sea $\mathbf{F}(t, \mathbf{Y}(t))$ una función continua en $U \subseteq \mathbb{R}^{n + 1}$, tal que $\forall$ $t \in \delta$ y $\forall$ $n \in \mathbb{N}$, $(t,\mathbf{Y}_{n}(t)) \in U$, entonces

\begin{align*}
\mathbf{Y}(t) &= \lim_{n \to \infty} \mathbf{Y}_{n}(t) \\
&= \lim_{n \to \infty } \left( \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{n -1}(s)) ds \right ) \\
&= \mathbf{Y}_{0} + \int_{t_{0}}^{t} \lim_{n \to \infty} \mathbf{F}(s, \mathbf{Y}_{n -1}(s)) ds
\end{align*}

Usando (\ref{13}) se obtiene la ecuación integral (\ref{8}).

$$\mathbf{Y}(t) = \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s)) ds$$

Con este resultado mostramos que si se satisfacen las hipótesis del teorema anterior, entonces la función a la que convergen las iteraciones de Picard satisface la ecuación integral (\ref{8}), lo que es equivalente a que dicha función sea solución del PVI (\ref{7}).

Ahora bien, para que las iterantes de Picard converjan a la solución del PVI (\ref{7}) deben satisfacer las hipótesis del teorema anterior por lo que es necesario que exista un dominio $U$ en el que $(t,\mathbf{Y}_{n}(t)) \in U$ y en el que la sucesión de iteraciones $\{ \mathbf{Y}_{n}(t) \}$ converja. Debemos encontrar este dominio, para hacerlo generalicemos algunos resultados más.

Funciones Lipschitzianas

Un primer resultado que usaremos es el siguiente.

En este teorema podemos describir a la región $R$ como

$$R = \{ (t, \mathbf{Y}(t)) \in \mathbb{R}^{n + 1} : |t -t_{0}| \leq a, \left\|\mathbf{Y}(t) -\mathbf{Y}_{0} \right\| \leq b \} \label{16} \tag{16}$$

En esta región garantizamos que las iterantes de Picard están todas contenidas.

Un resultado más que necesitaremos tiene que ver con que $\mathbf{F}(t, \mathbf{Y}(t))$ sea una función lipschitziana respecto a la segunda variable. Recordando la definición que dimos para el caso de ecuaciones de primer orden, podemos definir una función lipschitziana como sigue.

Un resultado sumamente útil para determinar si una función es lipschitziana es el siguiente.

Intenta generalizar la demostración.

Una herramienta más que necesitamos generalizar es el criterio mayorante de Weierstrass.

Finalmente, recordemos el lema de Gronwall.

Este resultado no requiere de generalización, lo usaremos de esta forma.

Todo lo anterior corresponde a la teoría preliminar que debemos conocer para lograr demostrar el teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden. Lo visto corresponde a una generalización de la teoría preliminar al teorema de Picard – Lindelöf, por lo que las demostraciones a los resultados de esta entrada serán prácticamente una generalización de las demostraciones vistas para el caso de ecuaciones de primer orden. De tarea moral intenta demostrar todos estos resultados para lograr convencerte del siguiente resultado.

Demostración del teorema de existencia y unicidad para sistemas de ecuaciones diferenciales de primer orden

Demostración: Comenzaremos por mostrar la existencia de la solución.

Consideremos las hipótesis del teorema y las dos primeras iteraciones de Picard $\mathbf{Y}_{1}(t)$ y $\mathbf{Y}_{0}(t)$, sabemos que ambas son continuas en el intervalo $I$ definido en (\ref{14}), entonces existe $M > 0$, tal que

$$\left\| \mathbf{Y}_{1}(t) -\mathbf{Y}_{0}(t) \right\| \leq M \label{19} \tag{19}$$

Queremos demostrar que la norma de la diferencia entre iterantes de Picard esta acotada, es decir, que $\forall$ $n \in \mathbb{N}$ y $\forall$ $t \in \mathbf{I}$,

$$\left\| \mathbf{Y}_{n}(t) -\mathbf{Y}_{n -1}(t) \right\| \leq M \left ( \dfrac{(L |t -t_{0}|)^{n -1}}{(n -1)!} \right) \label{20} \tag{20}$$

La prueba la haremos por inducción. El caso $n = 1$ ya lo vimos en (\ref{19}). Supongamos que es cierto para $n = k$.

$$\left\| \mathbf{Y}_{k}(t) -\mathbf{Y}_{k -1}(t) \right\| \leq M \dfrac{(L |t -t_{0}|)^{k -1}}{(k -1)!} \label{21} \tag{21}$$

Esta es nuestra hipótesis de inducción. Queremos probar que

$$\left\| \mathbf{Y}_{k + 1}(t) -\mathbf{Y}_{k}(t) \right\| \leq M \dfrac{(L |t -t_{0}|)^{k}}{k!} \label{22} \tag{22}$$

Usando la forma de la iteraciones de Picard (\ref{12}), notemos lo siguiente.

\begin{align*}
\left\| \mathbf{Y}_{k + 1}(t) -\mathbf{Y}_{k}(t) \right\| &= \left\| \left( \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{k}(t)) ds \right) -\left( \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{k -1}(s)) ds \right) \right\| \\
&= \left\| \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}_{k}(t)) -\mathbf{F}(s, \mathbf{Y}_{k -1}(s)) ds \right\| \\
&\leq \int_{t_{0}}^{t} \left\| \mathbf{F}(s, \mathbf{Y}_{k}(s)) -\mathbf{F}(s, \mathbf{Y}_{k -1}(s)) \right\| ds
\end{align*}

Como $\mathbf{F}$ es lipschitziana con respecto de la segunda variable, entonces se satisface (\ref{17}), de manera que

$$ \int_{t_{0}}^{t} \left\| \mathbf{F}(s, \mathbf{Y}_{k}(s)) -\mathbf{F}(s, \mathbf{Y}_{k -1}(s)) \right\| ds \leq \int_{t_{0}}^{t} L \left\| \mathbf{Y}_{k}(s) -\mathbf{Y}_{k -1}(s) \right\| ds \label{23} \tag{23}$$

Así,

\begin{align*}
\left\| \mathbf{Y}_{k + 1}(t) -\mathbf{Y}_{k}(t) \right\| &\leq \int_{t_{0}}^{t} L \left\| \mathbf{Y}_{k}(s) -\mathbf{Y}_{k -1}(s) \right\| ds \\
&= L \int_{t_{0}}^{t} \left\| \mathbf{Y}_{k}(s) -\mathbf{Y}_{k -1}(s) \right\| ds
\end{align*}

Usemos la hipótesis de inducción (\ref{21}).

\begin{align*}
\left\| \mathbf{Y}_{k + 1}(t) -\mathbf{Y}_{k}(t) \right\| &\leq L \int_{t_{0}}^{t} M \dfrac{(L |s -t_{0}|)^{k -1}}{(k -1)!} ds \\
&= \dfrac{ML^{k}}{(k -1)!} \int_{t_{0}}^{t} |s -t_{0}|^{k -1} ds \\
&= \dfrac{ML^{k}}{(k -1)!} \dfrac{|t -t_{0}|^{k}}{k} \\
&= M \dfrac{(L |t -t_{0}|)^{k}}{k!}
\end{align*}

Esto es,

$$ \left\| \mathbf{Y}_{k + 1}(t) -\mathbf{Y}_{k}(t) \right\| \leq M \dfrac{(L |t -t_{0}|)^{k}}{k!}$$

Hemos obtenido (\ref{22}) que es lo que queríamos probar.

Como $|t -t_{0}| \leq h$, observemos que

$$M \dfrac{(L |t -t_{0}|)^{k}}{k!} \leq M \dfrac{(Lh)^{k}}{k!} \label{24} \tag{24}$$

y sabemos que

$$\sum_{k = 0}^{\infty} M \dfrac{(Lh)^{k}}{k!} = Me^{Lh} \label{25} \tag{25}$$

Como $M$, $L$ y $h$ son valores fijos, entonces $Me^{Lh}$ es una valor fijo lo que muestra que la serie

$$\sum_{k = 0}^{\infty} M \dfrac{(Lh)^{k}}{k!} < \infty \label{26} \tag{26}$$

Es decir, la serie es convergente. Consideremos la sucesión de diferencias de iterantes de Picard consecutivas $\{ \mathbf{Y}_{n}(t) -\mathbf{Y}_{n -1}(t) \}$, $n \in \mathbb{N}$. De los resultados anteriores sabemos que

$$\left\| \mathbf{Y}_{k}(t) -\mathbf{Y}_{k -1}(t) \right\| \leq M \dfrac{(Lh)^{k -1}}{(k -1)!} \label{27} \tag{27}$$

y como $\forall$ $t \in I$,

$$\sum_{k = 1}^{\infty} M \dfrac{(Lh)^{k -1}}{(k -1)!} = M e^{Lh}$$

entonces, por el criterio mayorante de Weierstrass, se tiene que

$$\sum_{k = 1}^{\infty}(\mathbf{Y}_{k}(t) -\mathbf{Y}_{k -1}(t)) < \infty \label{28} \tag{28}$$

es decir, converge uniformemente en $I$ a una función, digamos $\hat{\mathbf{Y}}(t)$. Así

$$\mathbf{Y}_{0} + \sum_{k = 1}^{\infty}(\mathbf{Y}_{k}(t) -\mathbf{Y}_{k -1}(t)) < \infty \label{29} \tag{29}$$

también converge uniformemente en $I$ a una función, digamos $\mathbf{Y}(t)$. La sucesión de sumas parciales converge uniformemente en $I$. Para $k = 1$ en (\ref{29}) se tiene la suma parcial $S_{1}$ como

$$S_{1} = \mathbf{Y}_{0} + [\mathbf{Y}_{1}(t) -\mathbf{Y}_{0}(t)] = \mathbf{Y}_{1}(t) \label{30} \tag{30}$$

Ya que $ \mathbf{Y}_{0}(t) = \mathbf{Y}_{0}$. Para $S_{2}$, se tiene

$$S_{2} = \mathbf{Y}_{0} + [\mathbf{Y}_{1}(t) -\mathbf{Y}_{0}(t)] + [\mathbf{Y}_{2}(t) -\mathbf{Y}_{1}(t)] = \mathbf{Y}_{2}(t) \label{31} \tag{31}$$

Así sucesivamente obtendremos que

$$S_{n} = \mathbf{Y}_{n}(t) \label{32} \tag{32}$$

Por lo tanto, la sucesión de iteraciones de Picard converge uniformemente en $I$ a una función $\mathbf{Y}(t)$, esto significa que $\mathbf{Y}(t)$ es solución de la ecuación integral

$$\mathbf{Y}(t) = \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s)) ds$$

y por lo tanto, $\mathbf{Y}(t)$ es solución del problema de condición inicial.

Con esto queda demostrada la existencia de la solución del PVI. Concluyamos con la demostración de la unicidad.

Sea $\mathbf{Y}(t)$ la solución del PVI (\ref{7}) y supongamos que existe otra función $\mathbf{Z}(t)$ que también es solución del PVI, entonces

$$\mathbf{Y}(t) = \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s)) ds$$

y

$$\mathbf{Z}(t) = \mathbf{Y}_{0} + \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Z}(s)) ds \label{33} \tag{33}$$

Notemos lo siguiente.

\begin{align*}
\left\| \mathbf{Y}(t) -\mathbf{Z}(t) \right\| &= \left\| \int_{t_{0}}^{t} \mathbf{F}(s, \mathbf{Y}(s)) -\mathbf{F}(s, \mathbf{Z}(s)) ds \right\|\\
&\leq \int_{t_{0}}^{t} \left\| \mathbf{F}(s, \mathbf{Y}(s)) -\mathbf{F}(s, \mathbf{Z}(s)) \right\| ds \\
&\leq L \int_{t_{0}}^{t} \left\| \mathbf{Y}(s) -\mathbf{Z}(s) \right\|ds
\end{align*}

En donde se ha aplicado nuevamente la propiedad de $\mathbf{F}$ de ser lipschitziana con respecto de la segunda variable.

Definamos la función escalar

$$g(t) = \left\| \mathbf{Y}(t) -\mathbf{Z}(t) \right\|$$

Entonces el resultado anterior se puede escribir como

$$g(t) \leq L \int_{t_{0}}^{t} g(s) ds \label{34} \tag{34}$$

Notemos que esta expresión se parece a la desigualdad (\ref{18}) del lema de Gronwall con $\alpha = 0$ y $\beta = L$. Usando este lema, se obtiene

$$0 < g(t) = \left\| \mathbf{Y}(t) -\mathbf{Z}(t) \right\| \leq 0 e^{L(t -t_{0})} = 0 \label{35} \tag{35}$$

De donde necesariamente debe ocurrir que

$$\left\| \mathbf{Y}(t) -\mathbf{Z}(t) \right\| = 0 \label{36} \tag{36}$$

Por lo tanto, ambas funciones tienen que ser iguales.

$$\mathbf{Y}(t) = \mathbf{Z}(t) \label{37} \tag{37}$$

Y es así como queda demostrada la unicidad de la solución. Y, por lo tanto, queda demostrado el teorema.

$\square$

Con esto concluimos la tercera unidad del curso.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Demostrar formalmente los teoremas vistos en la teoría preliminar de esta entrada.
    Puedes guiarte de las demostraciones hechas en la primera unidad generalizando los resultados.

Más adelante…

Hemos concluido con la unidad 3 del curso.

La siguiente y última unidad del curso será un complemento de esta unidad 3, ya que hemos estudiado a los sistemas de ecuaciones diferenciales de primer orden desde una perspectiva analítica y es posible construir toda una teoría geométrica y cualitativa de estos mismos sistemas.

En la siguiente unidad estudiaremos la teoría cualitativa de las ecuaciones diferenciales.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I: Teorema de Existencia y Unicidad – Iterantes de Picard y Convergencia

Por Omar González Franco

Deja un comentario

No te preocupes por tus dificultades en matemáticas.
Te puedo asegurar que las mías son aún mayores.
– Albert Einstein

Introducción

En la entrada anterior iniciamos con el desarrollo de una teoría preliminar para demostrar el teorema de existencia y unicidad de Picard – Lindelöf. Hasta ahora hemos visto que un problema de valor inicial, en el caso de ecuaciones diferenciales ordinarias de primer orden, se puede escribir de forma equivalente como una ecuación integral. Aprendimos lo que es una función lipschitziana respecto de la segunda variable, demostramos algunos resultados importantes al respecto y concluimos con la demostración del lema de Gronwall.

Continuando con esta teoría preliminar, en esta entrada definiremos las iterantes de Picard, pero antes de ello es importante hacer un breve recordatorio sobre series y sucesiones de funciones.

También enunciaremos el teorema de Picard – Lindelöf para el caso local y resolveremos un ejercicio en el que apliquemos este resultado.

Recordemos el teorema de Picard – Lindelöf para que lo tengamos presente.

Bien, comencemos con el repaso de series y sucesiones de funciones.

Series y sucesiones de funciones

En cursos anteriores ya se han estudiado series y sucesiones de funciones. Aquí presentaremos, a manera de repaso, el concepto de convergencia puntual, convergencia uniforme y convergencia absoluta, además del criterio mayorante de Weierstrass.

Recordemos que una sucesión $\{f_{n}\}$ de funciones de $D$ a $\mathbb{R}$ converge en un punto $x \in D$ cuando la sucesión de números reales $\{f_{n}(x)\}$ es convergente. Cuando esto ocurre en todos los puntos de un conjunto no vacío $I \subset D$ se dice que $\{f_{n}\}$ converge puntualmente en $I$. En tal caso podemos definir una función $f: I \rightarrow \mathbb{R}$ escribiendo

$$f(x) = \lim_{n \to \infty} f_{n}(x) \label{3} \tag{3}$$

para todo $x \in I$, y decimos que $f$ es el límite puntual de $\{f_{n}\}$ en $I$.

Por otro lado, se dice que la sucesión $\{f_{n}(x)\}$ converge uniformemente a la función $f(x)$ en $I$ si

$$\lim_{n \to \infty} \left( \sup_{x \in I} |f_{n}(x) -f(x)|\right) = 0 \label{4} \tag{4}$$

En la práctica las ecuaciones (\ref{3}) y (\ref{4}) nos serán de mucha utilidad, sin embargo es conveniente tener presente las definiciones formales de convergencia puntual y convergencia uniforme para sucesiones de funciones.

El concepto de convergencia uniforme es un concepto más fuerte que el de convergencia puntual. En el caso de convergencia puntual $N$ puede depender de $\varepsilon$ y de $x$, mientras que en la convergencia uniforme sólo puede depender de $\varepsilon$. Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, realicemos un ejemplo para mostrar esto.

Ejemplo: Mostrar que la sucesión $f_{n}: [0, 1] \rightarrow \mathbb{R}$ definida por $f_{n}(x) = x^{n}$ converge puntualmente pero no uniformemente.

Solución: Para $x \in [0, 1)$ la sucesión $f_{n}(x) = x^{n}$ converge puntualmente a $f(x) = 0$ ya que

$$|f_{n}(x) -f(x)|=|x^{n} -0| = |x^{n}| = x^{n}$$

y

$$\lim_{n \to \infty} x^{n} = 0$$

esto para $x \in [0, 1)$, pero cuando $x = 1$ ocurre que $f_{n}(1) = 1^{n} = 1$, es decir, converge puntualmente a $f(x) = 1$ y así

$$|f_{n}(x) -f(x)|=|x^{n} -1| = |1 -1| = 0$$

Geométricamente podemos observar que, en efecto, todas las gráficas convergen a $f(x) = 0$ para $x \in [0, 1)$ y sólo cuando $x = 1$ es cuando la sucesión converge a $f(x) = 1$.

Gráficas de $f_{n}(x) = x^{n}$ para distintas $n$´s.

Sin embargo, la sucesión $f_{n}(x) = x^{n}$ no converge uniformemente, es sencillo darse cuenta que no existe $N \in \mathbb{N}$ para cumplir con (\ref{5}). Por muy pequeña que tomemos a $\varepsilon$ siempre va a haber alguna $n$ para $x \in [0, 1]$ que haga que

$$|f_{n}(x) -f(x)|> \varepsilon$$

Dicho de otra forma,

$$\lim_{n \to \infty} \left( \sup_{x \in I} |f_{n}(x) -f(x)|\right) \neq 0$$

$\square$

Será necesario extender el concepto de convergencia uniforme al caso de series de funciones.

Un resultado importante que utilizaremos más adelante es el criterio de comparación directa. No lo demostraremos.

Para decir que la serie $\sum_{n = 1}^{\infty} a_{n}$ converge es común usar la notación

$$\sum_{n = 1}^{\infty} a_{n} < \infty \label{8} \tag{8}$$

Ahora definamos lo que significa que una serie sea absolutamente convergente.

La convergencia absoluta implica convergencia, pero la afirmación recíproca no es verdadera.

Una propiedad que nos será de mucha utilidad es la siguiente.

$$ \left| \sum_{n=1}^{\infty }a_{n} \right| \leq \sum_{n = 1}^{\infty}|a_{n}| \label{9} \tag{9}$$

Una herramienta más que nos será útil a la hora de demostrar el teorema de Picard – Lindelöf es el criterio mayorante de Weierstrass o mejor conocido como prueba M de Weierstrass. Este criterio nos permite comprobar la convergencia uniforme de una serie infinita cuyos términos son al mismo tiempo funciones de variable real o compleja.

Demostración: Por hipótesis sabemos que para cada $x$ en $D$

$$\left| \sum_{n = 1}^{\infty} f_{n}(x) \right| \leq \sum_{n = 1}^{\infty}|f_{n}(x)| \leq \sum_{n = 1}^{\infty }M_{n} < \infty \label{10} \tag{10}$$

es decir, la serie $\sum_{n = 1}^{\infty} M_{n}$ converge y como $|f_{n}(x)| \leq M_{n}$ y usando el criterio de comparación directa, entonces $\sum_{n = 1}^{\infty}| f_{n}(x)|$ converge, en consecuencia $\sum_{n = 1}^{\infty}f_{n}(x)$ converge absolutamente, esto significa que existe una función $f$ límite puntual de la serie de funciones tal que

$$f(x) = \sum_{n = 1}^{\infty}f_{n}(x)$$

o bien,

$$|f(x)| = \left| \sum_{n = 1}^{\infty}f_{n}(x) \right| \label{11} \tag{11}$$

Como queremos demostrar la convergencia uniforme tomemos $N \in \mathbb{N}$, tal que para $n > N$ la serie sea convergente. Vemos que podemos escribir lo siguiente.

$$\left|f(x) -\sum_{n = 1}^{N}f_{n}(x) \right| = \left |\sum_{n = N + 1}^{\infty}f_{n}(x) \right| \label{12} \tag{12}$$

sabemos que

$$\left|\sum_{n = N + 1}^{\infty}f_{n}(x) \right | \leq \sum_{n = N + 1}^{\infty} |f_{n}(x)| \label{13} \tag{13}$$

y por hipótesis

$$\sum_{n = N + 1}^{\infty}|f_{n}(x)| \leq \sum_{n = N + 1}^{\infty}M_{n} \label{14} \tag{14}$$

De los resultados (\ref{13}) y (\ref{14}) obtenemos

$$\left| \sum_{n = N + 1}^{\infty}f_{n}(x)\right| \leq \sum_{n = N + 1}^{\infty}M_{n} \label{15} \tag{15}$$

Al ser $\sum_{n = 1}^{\infty }M_{n}$ convergente, el número

$$\varepsilon = \sum_{n = N + 1}^{\infty }M_{n}$$

puede hacerse tan pequeño como se quiera eligiendo $N$ suficiente grande, así

$$\left| \sum_{n = N + 1}^{\infty}f_{n}(x) \right | < \varepsilon \label{16} \tag{16}$$

Por lo tanto, de acuerdo a (\ref{7}), la serie $\sum_{n = 1}^{\infty}f_{n}(x)$ converge uniformemente.

$\square$

Con esto concluimos nuestro repaso sobre series y sucesiones de funciones. Teniendo presente estos resultados definamos las iterantes de Picard.

Iterantes de Picard

El matemático francés Charles Émile Picard (1856 – 1941) desarrolló un método iterativo para obtener una solución de una ecuación diferencial de primer orden. A este método iterativo se le conoce como iterantes de Picard.

Las iterantes de Picard de manera desglosada tienen la siguiente forma:

\begin{align*}
y_{0}(x) &= y_{0} \\
y_{1}(x) &= y_{0} + \int_{x_{0}}^{x}f(t,y_{0}(t)) dt \\
y_{2}(x) &= y_{0} + \int_{x_{0}}^{x}f(t,y_{1}(t)) dt \\
y_{3}(x) &= y_{0} + \int_{x_{0}}^{x}f(t,y_{2}(t))dt \\
\vdots \\
y_{n}(x) &= y_{0} + \int_{x_{0}}^{x} f(t, y_{n -1}(t)) dt
\end{align*}

Las iterantes de Picard siempre convergen, en el intervalo adecuado, a la solución del PVI (\ref{1}), esto lo verificaremos al momento de demostrar el teorema de Picard – Lindelöf, pero considerando que es cierto se puede deducir un resultado interesante, para ello consideremos el siguiente teorema.

La demostración de este resultado también será parte de la demostración del teorema de Picard – Lindelöf, así que por el momento consideremos que es cierto y observemos lo siguiente.

Si las iterantes de Picard satisfacen las hipótesis del teorema anterior y suponiendo que $f(x,y)$ es una función continua en $U$ que contiene a los puntos $(x, y_{n}(x))$, $\forall x \in [a, b]$, $\forall n \in \mathbb{N},$ entonces se tiene lo siguiente.

\begin{align*}
y(x) &= \lim_{n \to \infty } y_{n + 1}(x) \\
&= \lim_{n \to \infty} \left[y_{0} + \int_{x_{0}}^{x} f(t, y_{n}(t)) dt \right] \\
&= y_{0} + \int_{x_{0}}^{x} \lim_{n \to \infty} f(t, y_{n}(t)) dt \\
&= y_{0} + \int_{x_{0}}^{x} f(t, y(t)) dt
\end{align*}

es decir,

$$ y(x) = y_{0} + \int_{x_{0}}^{x} f(t, y(t)) dt \label{19} \tag{19}$$

Este resultado corresponde a la ecuación integral equivalente al problema de valor inicial. Con este método notamos que si las iterantes de Picard convergen a la solución del PVI, entonces $y(x)$ verifica la ecuación integral, tal como lo demostramos en la entrada anterior.

Por otro lado, al definir las iterantes de Picard hemos considerado un conjunto de la forma

$$R = \{ (x, y) \in \mathbb{R}^{2} \mid |x -x_{0}| \leq a, |y -y_{0}| \leq b, \hspace{0.2cm} a, b \in \mathbb{R} \}$$

La forma de este conjunto evita tener problemas para definir las iterantes. En general un conjunto de la forma $U = \delta \times \mathbb{R}$, $\delta = [a, b]$, $a, b \in \mathbb{R}$ conocidos como bandas verticales permite, no solamente que estén bien definidas, sino que además todas las iterantes estén definidas en el intervalo $\delta$.

Realicemos un ejemplo en el que apliquemos las iterantes de Picard para obtener la solución particular de un problema de valor inicial.

Ejemplo: Usando las iterantes de Picard, resolver el siguiente problema de valor inicial.

$$\dfrac{dy}{dx} = y; \hspace{1cm} y(0) = 1$$

Solución: En este caso tenemos la función, $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ definida por

$$f(x, y(x)) = y(x)$$

Es claro que es una función continua en $\mathbb{R}^{2}$. Por tanto, la ecuación integral equivalente al PVI para este caso es

$$y(x) = y_{0} + \int_{x_{0}}^{x} f(t, y(t)) dt = 1 + \int_{0}^{x} y(t)dt$$

La iterante inicial es la función constante $y_{0}(x) = 1$. Comencemos a calcular el resto de las iterantes de Picard de acuerdo a la relación iterativa (\ref{17}).

\begin{align*}
y_{1}(x) &= 1 + \int_{0}^{x} y_{0}(t) dt = 1 + \int_{0}^{x} 1dt = 1 + x \\
y_{2}(x) &= 1 + \int_{0}^{x} y_{1}(t) dt = 1 + \int_{0}^{x} (1 + t) dt = 1 + x + \dfrac{x^{2}}{2!} \\
y_{3}(x) &= 1 + \int_{0}^{x} y_{2}(t) dt = 1 + \int_{0}^{x} \left(1 + t + \dfrac{t^{2}}{2}\right) dt = 1 + x + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} \\
\vdots
\end{align*}

La afirmación que hacemos es que para $n$ se obtiene

$$y_{n}(x) = 1 + \int_{0}^{x} y_{n -1}(t) dt = 1 + \dfrac{x}{1!} + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} + \cdots + \dfrac{x^{n}}{n!} \label{20} \tag{20}$$

Ya lo hemos probado para $n = 1$, supongamos que la afirmación (\ref{20}) es verdadera y probemos para $n + 1$.

\begin{align*}
y_{n + 1}(x) &= 1 + \int_{0}^{x} y_{n}(t)dt \\
&= 1 + \int_{0}^{x} \left(1 + \dfrac{t}{1!} + \dfrac{t^{2}}{2!} + \cdots + \dfrac{t^{n}}{n!} \right) dt \\
&= 1 + x + \dfrac{x^{2}}{2 \cdot 1!} + \dfrac{x^{3}}{3 \cdot 2!} + \cdots + \dfrac{x^{n + 1}}{(n + 1) \cdot n!} \\
&= 1 + \dfrac{x}{1!} + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} + \cdots + \dfrac{x^{n + 1}}{(n + 1)!}
\end{align*}

Esto es,

$$y_{n + 1}(x) = 1 + \dfrac{x}{1!} + \dfrac{x^{2}}{2!} + \dfrac{x^{3}}{3!} + \cdots + \dfrac{x^{n + 1}}{(n + 1)!}$$

Con esto hemos probado por inducción que las iterantes de Picard corresponden a la serie

$$y_{n}(x) = \sum_{k = 0}^{n} \dfrac{x^{k}}{k!}$$

Para obtener la solución al PVI debemos ver a qué converge esta serie, para ello tomemos el limite $n \rightarrow \infty$ observando que para cada $x \in \mathbb{R}$ existe el límite.

\begin{align*}
y(x) = \lim_{n \to \infty} y_{n}(x) = \lim_{n \to \infty} \sum_{k = 0}^{n} \dfrac{x^{k}}{k!} = \sum_{k = 0}^{\infty}\dfrac{x^{k}}{k!} = e^{x}
\end{align*}

Por lo tanto, la solución del problema de valor inicial

$$\dfrac{dy}{dx} = y; \hspace{1cm} y(0) = 1$$

es

$$y(x) = e^{x}$$

Sólo para verificar el resultado apliquemos el método de separación de variables para resolver el PVI.

\begin{align*}
\dfrac{dy}{dx} &= y \\
\dfrac{1}{y}\dfrac{dy}{dx} &= 1 \\
\int{\dfrac{dy}{y}} &= \int{dx} \\
\ln y &= x + c \\
y &= Ce^{x}
\end{align*}

La solución general de la ecuación diferencial $\dfrac{dy}{dx} = y$ es $y(x) = Ce^{x}$.

Apliquemos la condición inicial $y(0) = 1$.

$$y(0) = Ce^{0} = C = 1$$

En efecto, la solución al PVI es $y(x) = e^{x}$, tal como lo obtuvimos con las iterantes de Picard.

Para garantizar que las iterantes de Picard convergen a la solución del PVI se deben satisfacer las condiciones del teorema de existencia y unicidad, pero las hemos pasado por alto ya que el propósito de este ejercicio es ver cómo calcular las iterantes de Picard, sin embargo cabe mencionar que este PVI si las cumple por lo que la solución obtenida si es única. Más adelante veremos un ejemplo en el que si verificaremos que se cumple el teorema de existencia y unicidad.

$\square$

Con esto concluimos con la teoría preliminar que necesitamos conocer para demostrar el teorema de existencia y unicidad de Picard – Lindelöf. Sin embargo, es necesario hacer algunas aclaraciones.

Anteriormente mencionamos que existe un resultado global y uno local y esto es porque existen dos situaciones. En el teorema de Picard – Lindelöf hemos considerado como hipótesis un conjunto de la forma $U = \delta \times \mathbb{R}$ con $\delta = [a, b]$, $a, b \in \mathbb{R}$ y $f: U \rightarrow \mathbb{R}$ continua en $U$, además de que $f$ sea lipschitziana respecto de la segunda variable en $U$, estas condiciones son suficientes para tener un resultado global en el que siempre tendremos una solución única del problema de valor inicial definida en $\delta$, sin embargo es posible y más común que el conjunto $U$ no sea una banda vertical o siéndolo que $f$ no sea lipschitziana respecto de la segunda variable en $U$ o ambas a la vez. En esta segunda situación, bajo determinadas hipótesis, tendremos un teorema de existencia y unicidad local.

A continuación presentamos el teorema de existencia y unicidad local, este teorema no lo demostraremos pero gran parte de lo que veremos en la demostración del resultado global puede ser adaptado a las condiciones de este teorema.

Teorema de existencia y unicidad local

Es usual encontrarnos con ecuaciones diferenciales donde no se cumplan las tres condiciones del teorema global, sin embargo es posible que se cumplan en un pequeño conjunto $R \subset \mathbb{R}^{2}$ que contenga el punto $(x_{0}, y_{0})$ del PVI, de ahí la localidad del teorema. El conjunto compacto y convexo que más se parece a una banda vertical es el producto cartesiano de dos intervalos compactos en $\mathbb{R}$, es decir, un rectángulo con lados paralelos a los ejes de coordenadas. Un conjunto apropiado sería un rectángulo centrado en el punto $(x_{0}, y_{0})$.

$$R = \{(x, y) \in \mathbb{R}^{2} \mid |x- x_{0}| < a, |y -y_{0}| < b, \hspace{0.2cm} a, b \in \mathbb{R} \} \label{21} \tag{21}$$

El teorema de existencia y unicidad local establece lo siguiente.

En este curso nos enfocamos en el resultado global porque es un resultado general, sin embargo el resultado local nos permite hallar una región cerca del punto $(x_{0}, y_{0})$ donde un problema de valor inicial puede cumplir con las hipótesis del teorema para garantizar la existencia y unicidad de una solución, de esta forma es que, en la práctica, el resultado local puede ser un resultado más útil.

La demostración a detalle de este teorema se puede encontrar en la sección de videos de este mismo curso.

Para concluir esta entrada realicemos un ejemplo de un problema de valor inicial en el que apliquemos el teorema local para garantizar la existencia y unicidad de la solución y resolvamos el PVI aplicando las iterantes de Picard.

Aplicación del teorema de existencia y unicidad

  • Verificar las hipótesis del teorema local para el siguiente problema de valor inicial.

$$\dfrac{dy}{dx} = 2x(y -1); \hspace{1cm} y(0) = 2 \label{23} \tag{23}$$

  • Resolver este problema usando las iterantes de Picard.
  • Hallar el intervalo de solución $\delta$.

Solución: El primer ejercicio consiste en verificar que el PVI satisface las hipótesis del teorema local.

En este caso la función $f$ está dada por

$$f(x, y) = 2x(y -1)$$

la cual está definida en todo $\mathbb{R}^{2}$. Buscamos la solución particular que pasa por el punto $(x_{0}, y_{0}) = (0, 2)$ y como la función es continua en $\mathbb{R}^{2}$, en particular lo es en todo rectángulo de la forma

$$R = \{(x, y) \in \mathbb{R}^{2} \mid |x| \leq a, |y -2| \leq b \}, \hspace{1cm} (a > 0, b > 0) \label{24} \tag{24}$$

Con esto hemos verificado las dos primeras hipótesis del teorema local, veamos ahora si la función es lipschitziana.

Para todo $(x, y_{1}), (x, y_{2})$ puntos de $R$, se tiene

\begin{align*}
|f(x, y_{1}) -f(x, y_{2})| &= |2x(y_{1} -1) -2x(y_{2} -1)| \\
&= 2|x||y_{1} -y_{2}| \\
&= 2|x||(y_{1} -2) + (2 -y_{2})| \\
&\leq 2|x|(|y_{1} -2| + |2 -y_{2}|) \\
\end{align*}

Como $|x| \leq a$ y $|y -2| \leq b$, en particular

$$|y_{1} -2| + |2 -y_{2}| \leq b + b = 2b$$

entonces podemos acotar el último resultado de la siguiente manera.

$$2|x|(|y_{1} -2| + |2 -y_{2}|) \leq 2(a)(2b) = 4ab$$

Si definimos la constante de Lipschitz $L = 4ab$, obtenemos finalmente que

$$|f(x, y_{1}) -f(x, y_{2})| \leq L = 4ab \label{25} \tag{25}$$

probando así que $f$ es Lipschitziana en $U$.

Con esto hemos verificado que se cumplen las hipótesis del teorema local de Picard, por lo tanto podemos concluir que existe una única solución $y = y(x)$ al problema de valor inicial dado. Ahora resolvamos el PVI usando las iterantes de Picard.

Recordemos que las iterantes de Picard $y_{n}(x)$ asociadas al problema de valor inicial son

$$y_{0}(x) = y_{0}, \hspace{1cm} y_{n}(x) = y_{0} + \int_{x_{0}}^{x} f(t, y_{n -1}(t)) dt$$

Ya sabemos que $y_{0} = 2$ y $x_{0} = 0$ y recordemos que la función $f$ es $f(x, y) = 2x(y-1)$, así para $n = 1$, tenemos

$$y_{1}(x) = 2 + \int_{0}^{x} f(t, 2) dt = 2 + \int_{0}^{x} 2t(2 -1) dt = 2 + x^{2}$$

$$\Rightarrow y_{1}(x) = 2 + x^{2}$$

Para $n = 2$, tenemos

$$y_{2}(x) = 2 + \int_{0}^{x} f(t, 2 + t^{2}) dt = 2 + \int_{0}^{x} 2t(1 + t^{2})dt = 2 +x^{2} + \dfrac{x^{4}}{2}$$

$$\Rightarrow y_{2}(x) = 2 +x^{2} + \dfrac{x^{4}}{2}$$

Para $n = 3$, se tiene

$$y_{3}(x) = 2 + \int_{0}^{x} f \left( t, 2 + t^{2} + \dfrac{t^{4}}{2} \right) dt = 2 + \int_{0}^{x} 2t \left( 1 + t^{2} + \dfrac{t^{4}}{2} \right) dt$$

$$\Rightarrow y_{3}(x) = 2 + x^{2} + \dfrac{x^{4}}{2} + \dfrac{x^{6}}{3!}$$

Uno más, para $n = 4$, tenemos

$$y_{4}(x) = 2 + \int_{0}^{x} f \left( t, 2 + t^{2} + \dfrac{t^{4}}{2} + \dfrac{t^{6}}{3!} \right) dt = 2 + \int_{0}^{x} 2t \left( 1 + t^{2} + \dfrac{t^{4}}{2} + \dfrac{t^{6}}{3!} \right) dt$$

$$\Rightarrow y_{4}(x) = 2 + x^{2} + \dfrac{x^{4}}{2} + \dfrac{x^{6}}{3!} + \dfrac{x^{8}}{4!}$$

Estas iteraciones sugieren la siguiente serie.

$$y_{n}(x) = 1 + 1 + x^{2} + \dfrac{x^{4}}{2!} + \dfrac{x^{6}}{3!} + \dfrac{x^{8}}{4!} + \cdots +\dfrac{x^{2n}}{n!}$$

Esta fórmula es cierta para $n = 1,2,3, 4$ y si es cierta para $n$, entonces podemos sustituirla en la formula general de las iterantes de Picard mostrando que es cierta para $n+1$.

\begin{align*}
y_{n + 1}(x) &= 2 + \int_{0}^{x} f(t, y_{n}(t))dt \\
&= 2 + \int_{0}^{x} 2t\left( 1 + t^{2} + \dfrac{t^{4}}{2} + \dfrac{t^{6}}{3!} + \dfrac{t^{8}}{4!} + \cdots + \dfrac{t^{2n}}{n!}\right) dt \\
&= 2 + x^{2} + \dfrac{x^{4}}{2} + \dfrac{x^{6}}{3!} + \dfrac{x^{8}}{4!} + \dfrac{x^{10}}{5!} + \cdots + \dfrac{x^{2(n + 1)}}{(n + 1)!}
\end{align*}

Por lo tanto,

$$y_{n}(x) = 1 + \sum_{k = 0}^{n}\dfrac{x^{2k}}{k!} \label{26} \tag{26}$$

Como el PVI cumple con las hipótesis del teorema de existencia y unicidad entonces el límite $n \rightarrow \infty$ de las iterantes de Picard será la solución al problema de valor inicial. Apliquemos el límite a la serie (\ref{26}).

\begin{align*}
y(x) &= \lim_{n \to \infty} y_{n}(x) \\
&= \lim_{n \to \infty} \left( 1 + \sum_{k = 0}^{n} \dfrac{(x^{2})^{k}}{k!} \right) \\
&= 1 + \lim_{n \to \infty} \left( \sum_{k = 0}^{n} \dfrac{(x^{2})^{k}}{k!} \right) \\
&= 1 +\sum_{k = 0}^{\infty} \dfrac{(x^{2})^{k}}{k!} \\
&= 1 + e^{x^{2}}
\end{align*}

Por lo tanto, la solución al PVI (\ref{23}) es

$$y(x) = 1 + e^{x^{2}} \label{27} \tag{27}$$

Inmediatamente se puede verificar que $y(0)=2$ y que para todo $x \in \mathbb{R}$

$$\dfrac{dy}{dx} = 2xe^{x^{2}} = 2x \left(e^{x^{2}} \right) = 2x (y -1)$$

lo cual implica que la solución es válida en $\delta = (-\infty, \infty)$.

Sólo para verificar el resultado resolvamos rápidamente este PVI aplicando el método de separación de variables.

\begin{align*}
\dfrac{dy}{dx} &= 2x(y -1) \\
\dfrac{1}{y -1} \dfrac{dy}{dx} &= 2x \\
\int {\dfrac{dy}{y -1}} &= \int {2x dx} \\
\ln{(y -1)} &= x^{2} + c \\
y -1 &= e^{x^{2} + c} \\
y &= 1 + Ce^{x^{2}}
\end{align*}

La solución general a la ecuación diferencial

$$\dfrac{dy}{dx} = 2x(y -1)$$

es

$$y(x) = 1 + Ce^{x^{2}}$$

Apliquemos la condición inicial $y(0) = 2$.

$$y(0) = 1 + Ce^{0} = 1 + C = 2$$

De donde $C = 2 -1 = 1$. Con este resultado concluimos que la solución particular es

$$y(x) = 1 + e^{x^{2}}$$

tal como lo obtuvimos con las iterantes de Picard.

$\square$

Ya sea el resultado global o el local, este teorema garantiza completamente la existencia y unicidad de la solución particular a un problema de valor inicial para el caso de una ecuación diferencial de primer orden.

En los métodos de resolución presentados a lo largo de esta unidad hemos pasado por alto las condiciones del teorema de Picard – Lindelöf y hemos tratado de justificar nuestros resultados con los teoremas de existencia y unicidad presentados para el caso de una ED de primer orden y para el caso de una ED de primer orden lineal, se hizo esto debido a la complejidad de la demostración del teorema de Picard – Lindelöf, pero ahora ya contamos con todo lo necesario para demostrarlo y así darle una completa justificación a lo que hemos hecho a lo largo de esta primer unidad.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Sea la sucesión de funciones $\{f_{n}\}$ donde, para cada $n \in \mathbb{N}$, $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$ es la función dada por $$f_{n}(x) = \dfrac{x^{2n}}{1 + x^{2n}}$$ $\forall x\in \mathbb{R}$. Estudiar la convergencia puntual y uniforme de $\{f_{n}(x)\}$.
  1. Sea la sucesión de funciones $\{f_{n}\}$ donde, para cada $n \in \mathbb{N}$, $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$ es la función dada por $$f_{n}(x) = \dfrac{x}{1 + nx^{2}}$$ $\forall x\in \mathbb{R}$. Estudiar la convergencia puntual y uniforme de $\{f_{n}(x)\}$.
  1. Resolver el siguiente problema de valor inicial usando las iterantes de Picard. $$\dfrac{dy}{dx} = x + y; \hspace{1cm} y(0) = 2$$ Verificar el resultado resolviendo el PVI usando algún método visto anteriormente.
  1. Resolver el siguiente problema de valor inicial usando las iterantes de Picard. $$\dfrac{dy}{dx} = 2(y + 1); \hspace{1cm} y(0) = 0$$ Verificar el resultado resolviendo la ecuación usando algún método visto anteriormente.

Más adelante…

Con esta entrada concluimos con la teoría preliminar necesaria para poder demostrar el resultado global del teorema de existencia y unicidad de Picard – Lindelöf. Hemos hecho un breve repaso sobre convergencia de series y sucesiones de funciones, definimos las iterantes de Picard y presentamos el resultado local del teorema de existencia y unicidad.

Usando lo visto en esta y la anterior entrada concluiremos la primera unidad del curso demostrando el resultado global del teorema de existencia y unicidad de Picard – Lindelöf.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»