Introducción
En la segunda unidad estudiamos a las funciones complejas en general y definimos a algunas de las funciones complejas más elementales. Es importante recordar que a través de las componentes real e imaginaria, es decir, las funciones reales $u(x,y)$ y $v(x,y)$ de una función compleja $f(z)=u(x,y) + iv(x,y)$, vimos que es posible caracterizar la analicidad de $f$ considerando a las ecuaciones de C-R. Por otra parte, en la entrada 36, de esta unidad, vimos que una función analítica en un dominio $D\subset\mathbb{C}$ tiene derivadas de todos los órdenes.
En esta entrada veremos que las propiedades de diferenciabilidad de las componentes real e imaginaria de una función compleja, nos permitirán caracterizar aún más a las funciones analíticas, en particular nos centraremos en las funciones complejas dadas por un par de funciones reales $u(x,y)$ y $v(x,y)$ de clase $C^2$, es decir, tales que todas sus segundas derivadas parciales existen y son continuas, definición 17.2, las cuales resultarán ser analíticas. Por lo que, a través de este tipo de funciones reales nos será posible construir funciones analíticas y estudiar algunas de sus propiedades geométricas.
Es importante enfatizar en el hecho de que una función analítica en un dominio es de clase $C^\infty$, corolario 36.3, por lo que sus componentes real e imaginaria son también de clase $C^\infty$ en el dominio de definición de $f$.
Definición 40.1. (Funciones conjugadas.)
Sean $D\subset\mathbb{C}$ un dominio y $f:D\to\mathbb{C}$ una función. Si $f(z)=u(x,y) + iv(x,y)$ es analítica en $D$ se dice que las funciones reales $u(x,y)$ y $v(x,y)$ son funciones conjugadas.
Proposición 40.1.
Sea $f(z) = u(x,y)+iv(x,y)$ una función analítica en un dominio $D\subset\mathbb{C}$. Entonces las funciones reales $u(x,y)$ y $v(x,y)$ satisfacen la ecuación de Laplace, es decir:
\begin{equation*}
\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0.
\end{equation*}
\begin{equation*}
\nabla^2 v = \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = 0.
\end{equation*}
Demostración. Supongamos que $f(z) = u(x,y)+iv(x,y)$ es una función analítica en algún dominio $D\subset\mathbb{C}$. Por el corolario 17.1 sabemos que las funciones reales $u(x,y)$ y $v(x,y)$ satisfacen las ecuaciones de C-R en todo punto del dominio $D$, es decir:
\begin{equation*}
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial u}{\partial y} = – \frac{\partial v}{\partial x},\quad \forall z=x+iy\in D.
\end{equation*}
Dado que $f$ es analítica en $D$, entonces por el corolario 36.3 tenemos que existen las derivadas de todos los órdenes de $f$ en $D$ y por tanto las funciones reales $u(x,y)$ y $v(x,y)$ son de clase $C^{k}(D)$, en particular son de clase $C^2(D)$, por lo que existen y son continuas todas las derivadas parciales de segundo orden de dichas funciones. Entonces, por el teorema 38.1 tenemos que para $z=x+iy\in D$ se cumple:
\begin{equation*}
\frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 v}{\partial y \partial x} = \frac{\partial^2 v}{\partial x \partial y} = – \frac{\partial^2 u}{\partial y^2},
\end{equation*}de donde:
\begin{equation*}
\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0.
\end{equation*}
Análogamente, para $z=x+iy\in D$ tenemos que:
\begin{equation*}
\frac{\partial^2 v}{\partial y^2} = \frac{\partial^2 u}{\partial x \partial y} = \frac{\partial^2 u}{\partial y \partial x} = – \frac{\partial^2 v}{\partial x^2},
\end{equation*}de donde:
\begin{equation*}
\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = 0.
\end{equation*}
$\blacksquare$
Definición 40.2. (Funciones armónicas.)
Sean $U\subset\mathbb{R}^2$ un conjunto abierto y $u: U \to \mathbb{R}$ una función de clase $C^2(U)$. Se dice que $u(x,y)$ es armónica si para todo $(x,y)\in U$ se cumple la ecuación de Laplace:
\begin{equation*}
\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0. \tag{40.1}
\end{equation*}
En particular, si $f(z) = u(x,y) + iv(x,y)$ es analítica en un dominio $D\subset\mathbb{C}$, entonces, por la proposición 40.1, tenemos que $u(x,y)$ y $v(x,y)$ son armónicas en $D$. En tal caso, las funciones $u$ y $v$ son llamadas funciones armónicas conjugadas.
Proposición 40.2.
Si las funciones armónicas conjugadas $u(x,y)$ y $v(x,y)$ satisfacen las ecuaciones de C-R, entonces la función $f(z) = u(x,y)+iv(x,y)$ es una función analítica.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Definición 40.3.
Si $u(x,y)$ y $v(x,y)$ son dos funciones armónicas en algún dominio $D\subset\mathbb{C}$ y dichas funciones reales satisfacen las ecuaciones de C-R en $D$, es decir, la función $f(z) = u(x,y)+iv(x,y)$ es analítica $D$, entonces se dice que $v$ es una función armónica conjugada de $u$.
Corolario 40.1.
Una función $f(z) = u(x,y)+iv(x,y)$ es analítica en un dominio $D$ si y solo si $v(x,y)$ es una función armónica conjugada de $u(x,y)$.
Demostración. Se sigue de las proposiciones 40.1 y 40.2, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Teorema 40.1.
Sea $D\subset\mathbb{C}$ un dominio. Entonces cada función real $u:D\to\mathbb{R}$, que es armónica en $D$, tiene una armónica conjugada en $D$ si y solo si $D$ es simplemente conexo.
Demostración. Sea $D\subset\mathbb{C}$ un dominio.
$(\Longleftarrow$ Supongamos que $D$ es simplemente conexo. Procedemos a construir una función armónica conjugada de $u$, la cual por hipótesis es armónica en $D$.
Sea $g:D\to\mathbb{C}$ dada por:
\begin{equation*}
g(z) = \frac{\partial u(x,y)}{\partial x} – i\frac{\partial u(x,y)}{\partial y} := U(x,y) + i V(x,y).
\end{equation*}
Como $u$ es armónica, entonces es de clase $C^{2}(D)$, en particular es de clase $C^{1}(D)$, por lo que existen las primeras derivadas parciales de $u$ y son continuas, es decir, $g$ está bien definida. Más aún, por hipótesis $u$ satisface la ecuación de Laplace (40.1) en $D$, es decir:
\begin{equation*}
\nabla^2 u = \frac{\partial^2 u(x,y)}{\partial x^2} + \frac{\partial^2 u(x,y)}{\partial y^2} = 0,
\end{equation*}de donde:
\begin{align*}
\frac{\partial U(x,y)}{\partial x}
& = \frac{\partial}{\partial x}\left[ \frac{\partial u(x,y)}{\partial x}\right]\\
& = \frac{\partial^2 u(x,y)}{\partial x^2}\\
& = – \frac{\partial^2 u(x,y)}{\partial y^2}\\
& = \frac{\partial}{\partial y}\left[ – \frac{\partial u(x,y)}{\partial y}\right] = \frac{\partial V(x,y)}{\partial y}, \tag{40.2}
\end{align*}para todo $z=x+iy\in D$.
Por otra parte, como $u$ es de clase $C^{2}(D)$, por el teorema 38.1 se cumple que:
\begin{align*}
\frac{\partial U(x,y)}{\partial y} & = \frac{\partial}{\partial y}\left[ \frac{\partial u(x,y)}{\partial x}\right]\\
& = \frac{\partial^2 u(x,y)}{\partial y \partial x}\\
& = \frac{\partial^2 u(x,y)}{\partial x \partial y}\\
& = \frac{\partial}{\partial x}\left[ \frac{\partial u(x,y)}{\partial y}\right]\\
& = -\frac{\partial}{\partial x}\left[ -\frac{\partial u(x,y)}{\partial y}\right] = -\frac{\partial V(x,y)}{\partial x}, \tag{40.3}
\end{align*}para todo $z=x+iy\in D$.
Entonces, de (40.2) y (40.3) se sigue que $U$ y $V$ son funciones de clase $C^1(D)$ que satisfacen las ecuaciones de C-R en $D$, por lo que, teorema 18.1, $g$ es una función analítica en $D$.
Como $D$ es un dominio simplemente conexo y $g$ una función analítica en $D$, del corolario 38.4 tenemos que existe una función $F:D\to\mathbb{C}$ analítica en $D$, tal que $F'(z) = g(z)$ para todo $z\in D$.
Sea $F(z)=\tilde{u}(x,y) + iv(x,y)$. Del teorema 17.1 se sigue que $F$ satisface las ecuaciones de C-R en $D$, por lo que:
\begin{align*}
F'(z) & = \frac{\partial \tilde{u}}{\partial x} – i \frac{\partial \tilde{u}}{\partial y}\\
& = \frac{\partial u}{\partial x} – i \frac{\partial u}{\partial y} = g(z),
\end{align*}para todo $z=x+iy\in D$.
Entonces:
\begin{align*}
0 & = \frac{\partial \tilde{u}}{\partial x} – \frac{\partial u}{\partial x} – i \left[\frac{\partial \tilde{u}}{\partial y} – \frac{\partial u}{\partial y}\right]\\
& = \frac{\partial}{\partial x} \left [\tilde{u} – u\right] – i \frac{\partial}{\partial y}\left[ \tilde{u} – u\right],
\end{align*}es decir:
\begin{equation*}
\frac{\partial}{\partial x} \left [\tilde{u} – u\right] = \frac{\partial}{\partial y}\left[ \tilde{u} – u\right] = 0,
\end{equation*}para todo $z=x+iy\in D$.
Por lo que, de la proposición 19.2 se sigue que $\tilde{u} – u = c$, para algún $c\in\mathbb{R}$.
Entonces la función $f(z)=F(z)-c=u(x,y)+iv(x,y)$ es una función analítica en $D$, tal que $\operatorname{Re}(z) = u(x,y)$, es decir, $v$ es una función armónica conjugada de $u$ en $D$.
$\Longrightarrow)$ Supongamos que toda función armónica $u:D\to\mathbb{R}$ tiene una armónica conjugada en $D$. Veamos que $D$ es simplemente conexo. De acuerdo con el teorema 38.5, basta probar que todo contorno cerrado en $D$ es homólogo a $0$ en $D$, es decir, que $n(\gamma,z_0) = 0$ para todo $z_0 \in \mathbb{C}\setminus D$.
Sea $\gamma$ un contorno cerrado en $D$ y $z_0 \in \mathbb{C}\setminus D$ fijo. Definimos a la función real $u:\mathbb{C}\setminus \{z_0\} \to \mathbb{R}$ como:
\begin{equation*}
u(z) := \operatorname{Log}|z-z_0|.
\end{equation*}
No es difícil verificar que $u$ es armónica en $\mathbb{C}\setminus \{z_0\}$ y por tanto en $D$, por lo que se deja como ejercicio al lector. Por hipótesis existe una función armónica conjugada de $u$, digamos $v$, en $D$. Entonces, corolario 40.1, $f(z) = u(x,y)+iv(x,y)$ es una función analítica en $D$.
Definimos a la función $h:D\to\mathbb{C}$ como:
\begin{equation*}
h(z) := (z-z_0)e^{-f(z)},
\end{equation*}la cual también es analítica en $D$. Por las proposiciones 20.2(4) y 21.1(5) se cumple que:
\begin{equation*}
|h(z)| = |z-z_0|e^{-u(z)} = |z-z_0|e^{-\operatorname{Log}|z-z_0|} = \frac{|z-z_0|}{|z-z_0|} =1,
\end{equation*}para todo $z\in D$.
Por lo que, de la proposición 19.3(2) concluimos que $h$ es una función constante en $D$, entonces:
\begin{equation*}
0 = h'(z) = e^{-f(z)} – (z-z_0)e^{-f(z)} f'(z),
\end{equation*}es decir:
\begin{equation*}
f'(z) = \frac{1}{z-z_0},
\end{equation*}para todo $z\in D$.
Claramente $f$ es una primitiva de $f’$ en $D$, por lo que del TFC para integrales de contorno, proposición 35.1 y la definición 36.1, al ser $\gamma$ cerrado, se tiene que:
\begin{equation*}
0 = \frac{1}{2\pi i} \int_{\gamma} f'(z) dz = \frac{1}{2\pi i} \int_{\gamma} \frac{1}{z-z_0} dz = n(\gamma, z_0),
\end{equation*}es decir, $\gamma$ es homólogo a $0$ en $D$.
Dado que $z_0 \in \mathbb{C}\setminus D$ y el contorno cerrado $\gamma$, en $D$, son arbitrarios, entonces el resultado de sigue del teorema 38.5.
$\blacksquare$
Observación 40.1.
El resultado anterior implica que cada función armónica en el plano complejo es la parte real de una función entera. En particular, el teorema anterior garantiza que una función armónica $u$ definida en un disco abierto siempre tiene una función armónica conjugada en dicho disco.
Corolario 40.2.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $u:U\to\mathbb{R}$ una función armónica, entonces $u$ tiene una función armónica conjugada en cada disco abierto contenido en $U$. En particular $u$ es de clase $C^\infty(U)$.
Demostración. La primera parte es consecuencia inmediata del teorema 40.1.
Verifiquemos la última parte. Dado que cada función armónica $u:U\to\mathbb{R}$ tiene una función armónica conjugada en cada disco abierto, digamos $v$, entonces $f=u+iv$ es una función analítica en cada disco abierto en $U$, por lo que es analítica en $U$. Entonces, del corolario 36.3, se tiene que $f$ es de clase $C^\infty(U)$, por lo tanto $u$ es de clase $C^\infty(U)$.
$\blacksquare$
Observación 40.2.
De los corolarios 37.5 y 40.2 se sigue que para un conjunto abierto $U\subset\mathbb{C}$, en el cual está definida una función armónica $u$, dicha función tiene una función armónica conjugada $v$ en cada disco abierto $B(z_0,r)\subset U$ y que $f=u+iv$ es una función analítica en $B(z_0,r)$, por lo que $u$ y $v$ tienen la propiedad del valor medio en $U$, es decir:
\begin{equation*}
u(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} u(z_0+e^{it}) dt,
\end{equation*}
\begin{equation*}
v(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} v(z_0+e^{it}) dt,
\end{equation*}para cada $z_0 \in U$.
Teorema 40.2. (Principio del módulo máximo para funciones armónicas.)
Sea $u$ una función armónica en un dominio $D\subset\mathbb{C}$. Si existe un punto $z_0 \in D$ tal que $u(z) \leq u(z_0)$ para todo $z\in D$, entonces $u$ es una función constante en $D$.
Demostración. Dadas las hipótesis, sea $z_0\in D$. Como $D$ es abierto entonces existe $r>0$ tal que $B(z_0,r)\subset D$. Por el corolario 40.2 tenemos que existe una función armónica conjugada de $u$ en $B(z_0,r)$, digamos $v$, entonces $f=u+iv$ es analítica en $B(z_0,r)$, por lo que del corolario 37.2, aplicado al disco $B(z_0,r)$, se tiene que $u$ y $v$ son funciones constantes en $B(z_0,r)$. Procediendo como en la prueba del teorema 37.4, podemos aplicar el argumento anterior a cada punto del conjunto:
\begin{equation*}
U=\{z\in D : u(z) = u(z_0)\},
\end{equation*}por lo que $U$ es abierto. Es claro que $U$ es no vacío y se deja como ejercicio al lector verificar que $U$ es cerrado, y como $D$ es un conjunto conexo, entonces $D=U$, por lo que $u$ es constante en $D$.
Corolario 40.3.
Sean $D\subset\mathbb{C}$ un dominio acotado con frontera $\partial D$ y $u:\overline{D} \to\mathbb{R}$ una función real continua. Si $u$ es armónica en $D$, entonces $u(z)$ alcanza su máximo en algún punto de la frontera de $D$.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Observación 40.3.
Al igual que con el principio del módulo máximo para funciones analíticas, existen diversas formulaciones del principio del módulo máximo para funciones armónicas.
Ejemplo 40.1.
Veamos que la función $u(x,y) = e^x \operatorname{cos}(y)$ es armónica en $\mathbb{C}$. Determinemos a su función armónica conjugada $v(x,y)$ y luego a la función entera $f(z) = u(x,y) + iv(x,y)$.
Solución. Primeramente procedemos a verificar que la función $u(x,y) = e^x \operatorname{cos}(y)$ es armónica en $\mathbb{C}$.
Es claro que dicha función real es de clase $C^\infty(\mathbb{C})$. Tenemos que:
\begin{equation*}
\frac{\partial u}{\partial x} = e^x \operatorname{cos}(y), \quad \frac{\partial u}{\partial y} = – e^x \operatorname{sen}(y),
\end{equation*}para todo $z=x+iy\in\mathbb{C}$, por lo que:
\begin{equation*}
\frac{\partial^2 u}{\partial x^2} = e^x \operatorname{cos}(y), \quad \frac{\partial^2 u}{\partial y^2} = -e^x \operatorname{cos}(y),
\end{equation*}entonces:
\begin{align*}
\nabla^2 u & = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\\
& = e^x \operatorname{cos}(y) – e^x \operatorname{cos}(y)\\
& = 0.
\end{align*}
Por lo tanto, $u(x,y) = e^x \operatorname{cos}(y)$ es una función armónica.
Procedemos ahora a determinar a su función armónica conjugada $v(x,y)$, para ello hacemos uso de las ecuaciones de C-R. Sabemos que:
\begin{equation*}
\frac{\partial v}{\partial x} = -\frac{\partial u}{\partial y} = e^x \operatorname{sen}(y).
\end{equation*}
Integrando respecto a $x$ la igualdad anterior, tenemos que:
\begin{align*}
v(x,y) & = \int e^x \operatorname{sen}(y) \, dx\\
& = e^x \operatorname{sen}(y) + f(y).
\end{align*}
Derivando respecto a $y$ tenemos que:
\begin{equation*}
\frac{\partial v}{\partial y} = e^x \operatorname{cos}(y) + f'(y).
\end{equation*}
Por otra parte, considerando las ecuaciones de C-R sabemos que:
\begin{equation*}
\frac{\partial v}{\partial y} = \frac{\partial u}{\partial x} = e^x \operatorname{cos}(y),
\end{equation*}por lo que, igualando estas dos últimas ecuaciones tenemos que:
\begin{equation*}
e^x \operatorname{cos}(y) + f'(y) = e^x \operatorname{cos}(y) \quad \Longleftrightarrow \quad f'(y) = 0,
\end{equation*}por lo que $f(y) = c\in\mathbb{R}$. Entonces:
\begin{equation*}
v(x,y) = e^x \operatorname{sen}(y) + c.
\end{equation*}
Es claro que dicha función también es armónica. Por construcción es claro que las funciones $u$ y $v$ satisfacen las ecuaciones de C-R, por lo que, considerando la proposición 40.2 concluimos que la función:
\begin{align*}
f(z) & = u(x,y) + iv(x,y)\\
& = e^x \operatorname{cos}(y) + ie^x \operatorname{sen}(y) + ic\\
& = e^{x+iy} + a,
\end{align*}con $a = ic\in\mathbb{C}$ una constante, es una función analítica.
Ejemplo 40.2.
Dado que la función $f(z) = \dfrac{2i}{z^2}$ es analítica en $\mathbb{C}\setminus\{0\}$ y como:
\begin{equation*}
\frac{2i}{z^2} = \frac{2i}{z^2} \frac{\overline{z}^2}{\overline{z}^2} = \frac{2i\overline{z}^2}{\left(z\overline{z}\right)^2} = \frac{2i\overline{z}^2}{|\,z\,|^4} = \frac{4xy+i2(x^2-y^2)}{(x^2+y^2)^2},
\end{equation*}entonces las funciones:
\begin{equation*}
u(x,y)= \frac{4xy}{(x^2+y^2)^2} \quad \text{y} \quad v(x,y)= \frac{i2(x^2-y^2)}{(x^2+y^2)^2},
\end{equation*}son armónicas conjugadas en cualquier dominio del plano complejo $\mathbb{C}$ que no contenga al origen.
Ejemplo 40.3.
Sean $z=x+iy\in\mathbb{C}$ y $u(z) = 3xy^2-x^3$. Veamos que $u$ es una función armónica en $\mathbb{C}$ y determinemos a su armónica conjugada $v$ en $\mathbb{C}$, tal que $v(0,0)=1$.
Solución. Claramente la función real $u$ es de clase $C^\infty(\mathbb{C})$. Tenemos que:
\begin{align*}
\nabla^2 u(z) & = \frac{\partial^2 u(x,y)}{\partial x^2} + \frac{\partial^2 u(x,y)}{\partial y^2}\\
& = -6x+6x\\
& = 0,
\end{align*}por lo que $u$ es armónica en $\mathbb{C}$.
Del teorema 40.1 se sigue que existe una función armónica conjugada $v$, de $u$, en $D$. Más aún, la condición $v(0,0)=1$ garantiza que $v$ es única.
De las ecuaciones de C-R se sigue que:
\begin{equation*}
\frac{\partial v(x,y)}{\partial x} = -\frac{\partial u(x,y)}{\partial y} = -6xy \quad \text{y} \quad \frac{\partial v(x,y)}{\partial y} =\frac{\partial u(x,y)}{\partial x} = 3y^2 – 3x^2.
\end{equation*}
Integrando respecto a $x$ la primera igualdad tenemos que:
\begin{equation*}
v(x,y) = \int -6xy dx = -3x^2 y + \varphi(y),
\end{equation*}por lo que:
\begin{equation*}
\frac{\partial v(x,y)}{\partial y} = -3x^2 y + \varphi'(y) = 3y^2 – 3x^2.
\end{equation*}
Entonces:
\begin{equation*}
\varphi'(y) = 3y^2,
\end{equation*}de donde:
\begin{equation*}
\varphi(y) = y^3 + c,
\end{equation*}con $c\in\mathbb{R}$ constante.
Por lo tanto $v(x,y) = -3x^2y+y^3+c$, pero como $v(0,0)=1$, se tiene que $c=1$, entonces:
\begin{equation*}
v(x,y) = -3x^2y+y^3+1.
\end{equation*}
Notemos que $f(z) = u(x,y)+iv(x,y)$ es el polinomio complejo $f(z) = -z^3+i$.
Observación 40.4.
Si $v(x,y)$ es una función armónica de $u(x,y)$ en algún dominio $D\subset\mathbb{C}$, en general no se cumple que $u(x,y)$ sea una función armónica de $v(x,y)$ en dicho dominio.
Ejemplo 40.4.
Consideremos a la función $f(z)=z^2$, para $z=x+iy\in\mathbb{C}$ tenemos que sus componentes real e imginaria son, respectivamente:
\begin{equation*}
u(x,y)=x^2-y^2 \quad \text{y} \quad v(x,y)=2xy.
\end{equation*}
Dado que $f(z)$ es una función entera, es claro que $v(x,y)$ es una función armónica de $u(x,y)$, sin embargo veamos que $u(x,y)$ no es una función armónica de $v(x,y)$.
Solución. Consideremos a la función:
\begin{equation*}
g(z) = 2xy + i(x^2-y^2) := U(x,y) + iV(x,y).
\end{equation*}
Mediante las ecuaciones de C-R tenemos que:
\begin{equation*}
\frac{\partial U}{\partial x} = 2y \neq – 2y =\frac{\partial V}{\partial y}, \quad \frac{\partial U}{\partial y} = 2x \neq -2x = \frac{\partial V}{\partial x},
\end{equation*}para todo $z=x+iy\neq 0$.
Por lo tanto, $g$ solo es diferenciable en el origen, pero no es analítica en ningún punto, de donde concluimos que $u(x,y)$ no es una función armónica de $v(x,y)$.
Ejemplo 40.5.
Sea $D\subset\mathbb{C}$ un dominio acotado con frontera $\partial D$. Si $u,v:\overline{D}\to\mathbb{R}$ son dos funciones armónicas en $D$ y continuas en $\overline{D}$, tales que $u=v$ en $\partial D$, veamos que $u=v$ en $D$.
Solución. Definimos a la función $g:\overline{D} \to\mathbb{R}$ como:
\begin{equation*}
g(z) = u(z) – v(z).
\end{equation*}
Por construcción $g$ es una función continua en $\overline{D}$ y armónica en $D$, tal que $g(z) = 0$ para todo $z\in \partial D$. Por el corolario 40.3, $g$ alcanza su máximo en algún valor de $\partial D$, por lo que $g(z)\leq 0$ para todo $z\in D$. Análogamente, para la función $-g(z)$ se tiene que $g(z) \geq 0$ para todo $z\in D$, por lo que $u(z)= v(z)$ para todo $z\in D$.
Definición 40.4. (Sistema de curvas ortogonales.)
Sean $c_1, c_2 \in\mathbb{R}$ dos constantes. Dos familias de curvas:
\begin{equation*}
u(x,y) = c_1, \quad v(x,y) = c_2, \tag{40.4}
\end{equation*}en el plano cartesiano, se dice que forman un sistema de curvas ortogonales si en los puntos de intersección, entre cada curva de cada familia, dichas curvas forman ángulos rectos.
La definición anterior nos permite caracterizar a las funciones analíticas en algún dominio $D$. Supongamos que $f(z) = u(x,y) + iv(x,y)$ es una función analítica en $D$, entonces la parte real y la parte imaginaria de la función $f(z)$ nos permiten definir un sistema de curvas ortogonales considerando a las curvas de nivel dadas por las ecuaciones (40.4). De forma más precisa, en un punto de intersección $z_0 = x_0 + iy_0$ tal que $f'(z_0) \neq 0$, la recta tangente a la curva de nivel $u(x_0,y_0) = c_1$, digamos $L_1$, y la recta tangente a la curva de nivel $v(x_0,y_0) = c_2$, digamos $L_2$, son perpendiculares.
Notemos que si derivamos a $u(x,y) = c_1$ y a $v(x,y) = c_2$ con respecto a $x$, considerando la regla de la cadena, tenemos que:
\begin{equation*}
\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} \frac{dy}{dx} = 0 \quad \text{y} \quad \frac{\partial v}{\partial x} + \frac{\partial v}{\partial y} \frac{dy}{dx} = 0,
\end{equation*}de donde obtenemos las pendientes de las rectas tangentes a cada curva, digamos:
\begin{equation*}
m_1 = \frac{dy}{dx} = – \dfrac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} \quad \text{y} \quad m_2 = \frac{dy}{dx} = – \dfrac{\frac{\partial v}{\partial x}}{\frac{\partial v}{\partial y}}.
\end{equation*}
Recordemos que dos rectas, en este caso $L_1$ y $L_2$, son perpendiculares si $m_1 m_2 = -1$, es decir:
\begin{equation*}
\left(- \dfrac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}}\right) \left(- \dfrac{\frac{\partial v}{\partial x}}{\frac{\partial v}{\partial y}}\right) = -1,
\end{equation*}o equivalentemente si:
\begin{equation*}
\frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \cdot \frac{\partial v}{\partial y} = 0.
\end{equation*}
La cual es la condición que deben satisfacer dos familias de curvas que se intersecan ortogonalmente. Considerando lo anterior es fácil probar el siguiente resultado:
Proposición 40.3.
Si $f(z) = u(x,y) + iv(x,y)$ es una función analítica, entonces las familias de curvas dadas por $u(x,y) = c_1$ y $v(x,y) = c_2$ forman un sistema ortogonal.
Demostración. Dadas las hipótesis, como $f(z) = u(x,y) + iv(x,y)$ es una función analítica, entonces las funciones $u$ y $v$ satisfacen las ecuaciones de C-R, es decir:
\begin{equation*}
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad \text{y} \quad \frac{\partial v}{\partial x} = – \frac{\partial u}{\partial y}.
\end{equation*}
Multiplicando estas ecuaciones tenemos:
\begin{equation*}
\frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} = – \frac{\partial v}{\partial y} \cdot \frac{\partial u}{\partial y},
\end{equation*}de donde:
\begin{equation*}
\frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} + \frac{\partial v}{\partial y} \cdot \frac{\partial u}{\partial y} = 0,
\end{equation*}la cual es la condición de ortogonalidad para una familia de curvas $u(x,y) = c_1$ y $v(x,y) = c_2$ que se intersecan.
$\blacksquare$
Ejemplo 40.6.
Consideremos a la función compleja $f(z)=z^2$. Si $z=x+iy$, entonces $f(z) = x^2 – y^2 + i2xy$, por lo que:
\begin{equation*}
u(x,y) = x^2 – y^2 \quad \text{y} \quad v(x,y) = 2xy.
\end{equation*}
Para esta función las familias de curvas de nivel dadas por:
\begin{equation*}
x^2 – y^2 = c_1 \quad \text{y} \quad 2xy = c_2,
\end{equation*}son dos familias de hipérbolas, figura 146(a). Dado que la función $f(z)=z^2$ es entera, entonces por la proposición 40.3 sabemos que dichas familias de curvas forman un sistema ortogonal.
Considerando al punto $z_0 = 1+2i$ tenemos que:
\begin{align*}
1^2 – 2^2 = -3 = c_1,\\
2(1)(2) = 4 = c_2,
\end{align*}cuyas curvas correspondientes son $x^2 – y^2 = -3$ y $2xy = 4$, figura 146(b). Gráficamente podemos observar que dichas curvas son ortogonales en el punto $z_0 = 1 + 2i$ y por simetría de la curva es claro que también son ortogonales en el punto $z_0 = -1 -2i$.
Figura 146: Gráficas de un sistema de curvas ortogonales en el plano complejo.
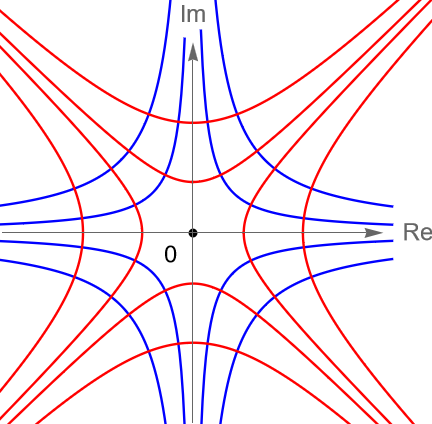
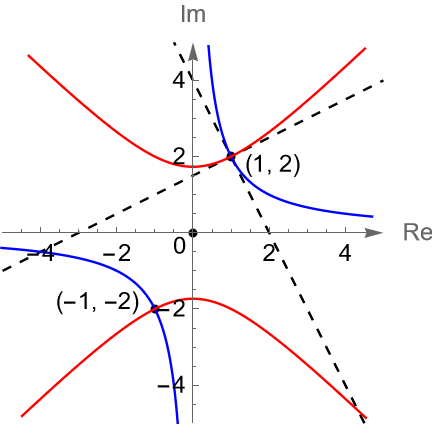
En este punto es conveniente dar una interpretación geométrica de la propiedad de conformidad de una función analítica $f:D \to\mathbb{C}$, con $D\subset\mathbb{C}$ un dominio. Si $z_0\in D$ y $f'(z_0)\neq 0$, entonces por la proposición 18.1 podemos escribir a $f$ como:
\begin{equation*}
f(z) = f(z_0) + f'(z_0)(z-z_0) + \varepsilon(z)(z-z_0),
\end{equation*}donde $\varepsilon(z) \to 0$ si $z \to z_0$.
Si $z \in B(z_0,r)$, para algún $r>0$, entonces la transformación $f(z)$ tiene como mejor aproximación lineal a la transformación:
\begin{equation*}
T(z) = A + B(z-z_0), \tag{40.4}
\end{equation*}donde $A=f(z_0)$ y $B=f'(z_0)$.
Dado que $\varepsilon(z) \to 0$ si $z \to z_0$, entonces para los puntos en $B(z_0,r)$ el comportamiento de la transformación $f(z)$ es similar al de la transformación $T(z)$.
Recordemos, proposición 12.1, que podemos expresar a $f$ como $f(z) = u(x,y) + iv(x,y)$, donde $\operatorname{Re}f(z) = u(x,y)$ e $\operatorname{Im}f(z) = v(x,y)$ son dos funciones reales. Por lo que, podemos considerar a $f$ como una función de un abierto $U\subset\mathbb{R}^2$ en $\mathbb{R}^2$.
De acuerdo con nuestros cursos de Cálculo, sabemos que para una función $f:U\subset\mathbb{R}^2 \to\mathbb{R}^2$, con $U$ un abierto, el comportamiento de la derivada de $f$ está descrito por su matriz Jacobiana:
\begin{equation*}
J_f = \begin{pmatrix}
u_x & u_y\\
v_x & v_y
\end{pmatrix},
\end{equation*}la cual está evaluada en cada punto $z_0 = (x_0,y_0) \in U$.
Más aún, sabemos que la matriz Jacobiana representa a una transformación lineal que es la mejor aproximación de $f(z) – f(z_0)$ en el punto $z_0$.
De acuerdo con los resultados de la entrada 18, sabemos que para una función analítica $f$, definida en un abierto $U\subset\mathbb{C}$, su matriz Jacobiana en un punto $z_0\in U$ es de la forma:
\begin{equation*}
J_{f(z_0)} = \begin{pmatrix}
u_x(z_0) & u_y(z_0)\\
v_x(z_0) & v_y(z_0)
\end{pmatrix} = \begin{pmatrix}
u_x(z_0) & -v_x(z_0)\\
v_x(z_0) & u_x(z_0)
\end{pmatrix} = \begin{pmatrix}
a & -b\\
b & a
\end{pmatrix},
\end{equation*}donde $a, b\in\mathbb{R}$ son constantes.
Notemos que la última matriz podría ser la matriz cero o, en caso contrario, podría ser una matriz que puede escribirse como el producto de dos matrices, es decir:
\begin{equation*}
\begin{pmatrix}
a & -b\\
b & a
\end{pmatrix} = \begin{pmatrix}
\sqrt{a^2+b^2} & 0\\
0 & \sqrt{a^2+b^2}
\end{pmatrix} \begin{pmatrix}
\operatorname{cos}(\theta) & -\operatorname{sen}(\theta)\\
\operatorname{sen}(\theta) & \operatorname{cos}(\theta)
\end{pmatrix},
\end{equation*}para algún $\theta\in\mathbb{R}$. Notemos que podemos elegir a $\theta$ tal que:
\begin{align*}
\operatorname{cos}(\theta) = \frac{a}{\sqrt{a^2+b^2}},\\
\operatorname{sen}(\theta) = \frac{b}{\sqrt{a^2+b^2}},
\end{align*}desde que:
\begin{equation*}
\left(\frac{a}{\sqrt{a^2 + b^2}}\right)^2 + \left(\frac{b}{\sqrt{a^2 + b^2}}\right)^2 = 1.
\end{equation*}
Entonces, las ecuaciones de C-R implican que la matriz Jacobiana (real) de $f$ sea de la forma:
\begin{equation*}
\begin{pmatrix}
\lambda & 0\\
0 & \lambda
\end{pmatrix} \begin{pmatrix}
\operatorname{cos}(\theta) & -\operatorname{sen}(\theta)\\
\operatorname{sen}(\theta) & \operatorname{cos}(\theta)
\end{pmatrix},
\end{equation*}para algún $\lambda\in\mathbb{R}$, con $\lambda>0$, y algún $\theta\in\mathbb{R}$.
Por nuestros cursos de Geometría, sabemos que estas dos matrices tienen una interpretación geométrica clara.
Primeramente, la matriz:
\begin{equation*}
\begin{pmatrix}
\lambda & 0\\
0 & \lambda
\end{pmatrix},
\end{equation*}describe la multiplicación de todos los vectores en $\mathbb{R}^2$ por el escalar $\lambda$, es decir una homotecia por un factor $\lambda$.
Por otra parte, la matriz:
\begin{equation*}
\begin{pmatrix}
\operatorname{cos}(\theta) & -\operatorname{sen}(\theta)\\
\operatorname{sen}(\theta) & \operatorname{cos}(\theta)
\end{pmatrix},
\end{equation*}describe una rotación, alrededor del origen, de un ángulo $\theta$.
Entonces, en conjunto el producto de ambas matrices, es decir:
\begin{equation*}
\begin{pmatrix}
\lambda & 0\\
0 & \lambda
\end{pmatrix} \begin{pmatrix}
\operatorname{cos}(\theta) & -\operatorname{sen}(\theta)\\
\operatorname{sen}(\theta) & \operatorname{cos}(\theta)
\end{pmatrix},
\end{equation*}describe en $\mathbb{R}^2$ la misma operación que la multiplicación en $\mathbb{C}$ por un número complejo $\lambda e^{i\theta}$, como vimos en la entrada 24.
En particular notemos que para la matriz Jacobiana de una función analítica $f$, en cualquier punto $z\in U$, se tiene que:
\begin{equation*}
\lambda = \sqrt{u_x(z)^2 + v_x(z)^2} = |f'(z)|.
\end{equation*}
Por lo tanto, el efecto de la transformación afín lineal $T$, dada en (40.4), es una rotación en el plano en un ángulo $\theta=\operatorname{arg}(f'(z_0))$, seguida de una homotecia por un factor $\lambda = |f'(z_0)|$, seguida de una traslación por un vector $A-Bz_0$. Por la proposición 25.2 sabemos que la transformación $T$ preserva los ángulos en $z_0$.
Entonces, motivados en lo anterior, nuestro objetivo es probar que la función analítica $f$ también preserva ángulos en $z_0$.
Definición 40.5. (Ángulo entre curvas.)
Sean $\alpha:I_1\subset\mathbb{R} \to\mathbb{C}$ y $\beta:I_2\subset\mathbb{R} \to\mathbb{C}$ dos curvas suaves tales que $\alpha(t_0) =\beta(u_0)=z_0$, con $t_0\in I_1$ y $u_0\in I_2$. Si $\alpha'(t_0) \neq 0$ y $\beta'(u_0)\neq 0$, se define el ángulo formado por $\alpha$ y $\beta$ en $z_0$ como el ángulo entre sus vectores tangentes.
De acuerdo con el lema 25.1 tenemos que dicho ángulo está dado por:
\begin{equation*}
\operatorname{arg}\left(\frac{\alpha'(t_0)}{\beta'(u_0)}\right).
\end{equation*}
Definición 40.6. (Función conforme.)
Sean $D\subset\mathbb{C}$ un dominio, $z_0\in D$ y $f:D\to\mathbb{C}$ una función. Se dice que $f$ es conforme en $z_0$ si para todo par de curvas $\alpha$ y $\beta$ que se intersecan en $z_0$ y que en dicho punto forman un ángulo $\theta\in(-\theta, \theta]$, se tiene que las curvas $f\circ \alpha$ y $f\circ \beta$ forman el mismo ángulo $\theta$ en el punto $f(z_0)$.
Proposición 40.4.
Sean $D\subset\mathbb{C}$ un dominio y $f:D\subset\mathbb{C}\to\mathbb{C}$ una función analítica en $z_0\in D$. Si $f'(z_0) \neq 0$, entonces $f$ es conforme en $z_0$.
Demostración. Dadas las hipótesis, sin pérdida de generalidad, sean $\gamma, \beta:[a,b]\subset\mathbb{R}\to\mathbb{C}$, $a<b$ dos curvas suaves tales que $\gamma(t_0) = \beta(t_0) =z_0$, para algún $t_0\in[a,b]$ y $\gamma'(t_0) \neq 0$, $\beta'(t_0) \neq 0$.
Notemos que $f\circ \gamma, f\circ \beta : [a,b]\to\mathbb{C}$ son dos curvas en $\mathbb{C}$. Por la regla de la cadena, proposición 32.2, tenemos que:
\begin{align*}
(f\circ\gamma)'(t_0) & = f'(\gamma(t_0)) \gamma'(t_0) = f'(z_0) \gamma'(t_0) \neq 0,\\
(f\circ\beta)'(t_0) & = f'(\beta(t_0)) \beta'(t_0) = f'(z_0) \beta'(t_0) \neq 0,
\end{align*}por lo que podemos medir el ángulo entre dichas curvas en $z_0$.
Tenemos que:
\begin{align*}
\operatorname{arg}\left(\frac{(f\circ\gamma)'(t_0) }{ (f\circ\beta)'(t_0)}\right) & = \operatorname{arg}\left(\frac{f'(z_0) \gamma'(t_0)}{f'(z_0) \beta'(t_0)}\right)\\
& = \operatorname{arg}\left(f'(z_0) \gamma'(t_0)\right) – \operatorname{arg}\left(f'(z_0) \beta'(t_0)\right)\\
& = \operatorname{arg}\left(f'(z_0)\right) + \operatorname{arg}\left(\gamma'(t_0)\right) – \operatorname{arg}\left(f'(z_0)\right) – \operatorname{arg}\left(\beta'(t_0)\right)\\
& = \operatorname{arg}\left(\gamma'(t_0)\right) – \operatorname{arg}\left(\beta'(t_0)\right)\\
& = \operatorname{arg}\left(\frac{\gamma'(t_0) }{\beta'(t_0)}\right)
\end{align*}
$\blacksquare$
Ejemplo 40.7.
De acuerdo con la proposición 40.4, como $f(z)=e^{z}$ es una función entera y $f'(z)=e^{z}\neq 0$ para todo $z\in \mathbb{C}$, entonces $f$ es una función conforme en todo $\mathbb{C}$.
Por otra parte, $g(z)=z^2-z+1$ también es una función entera, pero $g'(1/2)=0$, por lo que $g$ es conforme en $\mathbb{C}\setminus\{1/2\}$.
Tarea moral
- Sean $z=x+iy \neq 0$, $u(x,y)=x^2-y^2$ y $v(x,y)=-\dfrac{y}{x^2+y^2}$. Muestra que $u$ y $v$ satisfacen la ecuación de Laplace (33.1), pero que la función $f(z)=u(x,y)+iv(x,y)$ no es analítica.
Hint: Considera la proposición 40.2. - Determina una función analítica $f(z)=u(x,y)+iv(x,y)$ y su dominio de analicidad, para:
a) $u(x,y) = \dfrac{\operatorname{sen}(2x)}{\operatorname{cosh}(2y) + \operatorname{cos}(2x)}$.
b) $u(x,y) = x^2+y^2-5x+y+2$.
c) $v(x,y) = e^{x}\operatorname{sen}(x)$.
d) $v(x,y) = \operatorname{sen}(x) \operatorname{cosh}(y)$. - Sean $a,b\in\mathbb{R}$ y $U\subset\mathbb{C}$ un conjunto abierto. Supón que $u(x,y)$ y $v(x,y)$ son dos funciones reales armónicas en $U$. Prueba que $au(x,y)+bv(x,y)$ también es una función armónica en $U$.
- Muestra que las siguientes funciones reales $u(x,y)$ son armónicas en el dominio $D$ dado. Determina la función armónica conjungada de $u$ en $D$, es decir, una función real $v(x,y)$ y verifica que la función $f(z)=u(x,y)+iv(x,y)$ es analítica en $D$.
a) $u(x,y) = xy$, en $D=\mathbb{C}$.
b) $u(x,y) = e^y \operatorname{cos}(x)$, en $D=\mathbb{C}$.
c) $u(x,y) = \dfrac{y}{x^2+y^2}$, en $D=\left\{z\in\mathbb{C} : \operatorname{Im}(z)>0\right\}$.
d) $u(x,y) = \operatorname{ln}(x^2+y^2)$, en $D=\mathbb{C}\setminus(-\infty, 0]$. - Sea $f(z)$ una función conforme en un dominio $D$ tal que $f'(z)\neq 0$ para todo $z\in D$. Prueba que $f$ es analítica en $D$.
- Prueba que la transformación $T(z) = az+b$ es conforme en infinito si $a\neq 0$.
- Supón que $u(x,y)$es una función real armónica. Muestra que:
\begin{equation*}
\frac{\partial^2 u}{\partial z \partial \overline{z}} = 0.
\end{equation*} - Considera a la función $f(z)=\operatorname{sen}(z)$. Muestra que $\operatorname{Re}f(z) = c_1$ y $\operatorname{Im}f(z) = c_2$, con $c_1, c_2\in\mathbb{R}$ constantes, forman una familia de curvas ortogonales.
Hint: Utiliza la proposición 22.1(10) y muestra que $m_1 \cdot m_2 =-1$, con $m_i = \dfrac{dy}{dx}$, $i=1,2$. - Demuestra la proposición 40.2.
Más adelante…
En esta entrada hemos abordado de manera general el concepto de funcion armónica y de función conforme, así como algunas de sus propiedades más importantes. Vimos que las funciones armónicas nos permiten construir funciones analíticas, mientras que las funciones conformes nos dicen mucho sobre la geometría de las funciones analíticas. Las funciones armónicas son soluciones de muchos problemas físicos. Algunas de sus aplicaciones se da en modelos de dos dimensiones para el flujo de calor, electrostática y fluidos.
La siguiente entrada corresponde con la última de esta cuarta unidad, en ella abordaremos algunas técnicas para construir funciones analíticas.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Teoremas de Weierstrass.
- Siguiente entrada del curso: Técnicas para construir funciones analíticas.
