Estudié matemáticas, la locura de la razón.
– Benjamin Moser
Introducción
A lo largo de esta primera unidad hemos estudiado una variedad de ecuaciones diferenciales ordinarias de primer orden y hemos desarrollado distintas técnicas para resolver cada tipo de ecuación. Vimos que una sola ecuación puede tener infinitas soluciones y sólo cuando le imponemos una condición inicial es como podremos obtener una solución particular de esa ecuación diferencial. Ahora bien, si la solución existe, entonces debe ser única pero, ¿es siempre cierto esto?.
Ya presentamos el teorema de existencia y unicidad para ecuaciones diferenciales de primer orden y el teorema de existencia y unicidad para el caso de ecuaciones diferenciales lineales de primer orden, nuestro objetivo ahora es tener un teorema de existencia y unicidad general que pueda aplicarse a cualquier ecuación diferencial ordinaria de primer orden.
Este teorema, conocido como teorema de existencia y unicidad de Picard – Lindelöf contiene las hipótesis suficientes para garantizar que si existe una solución a un problema de valor inicial (PVI), entonces dicha solución es única.
Cabe mencionar que es posible enunciar un teorema de existencia y unicidad de tipo global y uno de tipo local. En el caso de tipo global el intervalo de existencia de la solución se conoce a priori, mientras que en uno de tipo local se asegura que existe un intervalo, en un principio desconocido, donde el PVI tiene solución única. En este curso demostraremos el resultado de tipo global y veremos que el de tipo local es consecuencia del global, además de que puedes encontrar la demostración al teorema de tipo local en la sección de videos.
Demostrar el teorema de existencia y unicidad de Picard – Lindelöf no es tarea fácil, primero será necesario desarrollar una teoría preliminar en la que estableceremos algunos conceptos nuevos y, así mismo, haremos un breve repaso sobre conceptos que conocemos y que nos serán de utilidad para demostrar dicho teorema. Esta teoría preliminar la desarrollaremos a lo largo de esta y la siguiente entrada para finalmente demostrar el teorema en la última entrada de esta primera unidad.
Comenzaremos enunciando el teorema de existencia y unicidad de Picard – Lindelöf para tenerlo presente, a pesar de que quizá algunas cosas no queden claras, el objetivo de esta teoría preliminar será comprender lo que nos quiere decir este teorema, además de brindarnos las herramientas necesarias para demostrarlo.
Bien, ¡comencemos!.
Teorema de Existencia y Unicidad de Picard-Lindelöf
El teorema global de existencia y unicidad para ecuaciones diferenciales ordinarias de primer orden es el siguiente.
En esta situación, para cada $(x_{0}, y_{0}) \in U$, el problema de valores iniciales (PVI)
\begin{align} \dfrac{dy}{dx} = f(x, y); \hspace{1cm} y(x_{0}) = y_{0} \label{1} \tag{1} \end{align} posee una única solución definida en el intervalo $[a, b]$.
Además, las iterantes de Picard $y_{n}: [a, b] \rightarrow \mathbb{R}$ asociadas al PVI (\ref{1}), dadas por
\begin{align} y_{n}(x) = y_{0} + \int_{x_{0}}^{x} f(t, y_{n -1}(t)) dt \hspace{1cm} n= 1,2,3, \cdots \hspace{1cm} y_{0} = y_{0}(x) \label{2} \tag{2} \end{align} convergen uniformemente en el intervalo $[a, b]$ hacia la solución del PVI.
Una observación importante es que el punto $(x_{0}, y_{0})$ puede estar en la frontera de la banda vertical $U = [a, b] \times \mathbb{R}$, es decir, puede ser de la forma $(a, y_{0})$ o $(b, y_{0}).$
Podemos notar que en el enunciado se hace mención de términos que aún no conocemos, como lo son función lipschitziana e Iterantes de Picard, así que necesitamos definirlos.
Este teorema corresponde al resultado global en el que el intervalo es una banda vertical $U = [a, b] \times \mathbb{R}$, en el caso local se considera una región limitada definida como
$$R = \{ (x, y) \in \mathbb{R}^{2}:|x -x_{1}| \leq a, |y -y_{1}| \leq b, \hspace{0.3cm} a, b \in \mathbb{R} \}$$
y la solución esta definida en el intervalo $\delta = [x_{0} -h, x_{0} + h]$ para cierta $h \in \mathbb{R}$. Una vez demostrado el resultado global retomaremos el caso local.
En esta teoría preliminar veremos que el PVI (\ref{1}) puede ser equivalente a resolver una ecuación integral, estudiaremos las funciones lipschitzianas de una y dos variables, demostraremos algunas proposiciones al respecto, demostraremos el lema de Gronwall, repasaremos algunos conceptos importantes sobre sucesiones, series y convergencia, definiremos las iteraciones de Picard y veremos algunos ejemplos. Una vez desarrollada esta teoría pasaremos a la demostración del teorema de existencia y unicidad.
Para comenzar, veamos que el PVI (\ref{1}) se puede escribir de forma equivalente como una ecuación integral cuando la función $f$ es continua.
Ecuación integral equivalente a un PVI
Un PVI como (\ref{1}) se puede escribir de forma equivalente como una ecuación integral en el caso en el que la función $f$ sea continua. Evidentemente este no es un curso ecuaciones integrales, pero para entender esta equivalencia definiremos lo que es una ecuación integral.
Teniendo en cuenta esta definición demostremos nuestro primer teorema de esta teoría preliminar el cual refleja el hecho de que un PVI como (\ref{1}) es equivalente a resolver una ecuación integral.
$$\dfrac{dy}{dx} = f(x, y); \hspace{1cm} y(x_{0}) = y_{0}$$ si, y sólo si, para cada $x \in \delta$, $y$ es una función continua en $\delta$ que verifica la ecuación integral
\begin{align} y(x) = y_{0} + \int_{x_{0}}^{x} f(t , y(t)) dt \label{3} \tag{3} \end{align}
Demostración:
$\Rightarrow$ Supongamos que $y: \delta \rightarrow \mathbb{R},$ con gráfica contenida en $U$, es solución del PVI, entonces cumple que
$$\dfrac{dy}{dx} = f(x, y); \hspace{1cm} y(x_{0}) = y_{0}$$
Como $y$ es solución de la ecuación diferencial en el intervalo $\delta$, entonces debe ser continua en el mismo intervalo, así tenemos que $f$ y $y$ son continuas y por tanto $\dfrac{dy}{dx}$ y la función
$$g: \delta \rightarrow \mathbb{R}, \hspace{1cm} t \rightarrow g(t) = f(t, y(t))$$
también son continuas, de esta manera podemos integrar la ecuación $\dfrac{dy}{dx} = f(x, y)$ para cualquier $x \in \delta$.
\begin{align*}
\int_{x_{0}}^{x}\dfrac{dy}{dx}(t)dt &= \int_{x_{0}}^{x} f(t, y(t)) dt \\
\end{align*}
Aplicando el teorema fundamental del cálculo (regla de Barrow) en el lado izquierdo de la ecuación, tenemos
\begin{align*}
y(x) -y(x_{0}) &= \int_{x_{0}}^{x} f(t, y(t))dt \\
y(x) &= y(x_{0}) + \int_{x_{0}}^{x} f(t, y(t)) dt \\
y(x) &= y_{0} + \int_{x_{0}}^{x} f(t, y(t)) dt
\end{align*}
obteniendo así que $y(x)$ verifica la ecuación integral (\ref{3}).
$\Leftarrow$ Ahora supongamos que $y(x)$ es una función continua en $\delta$ y que satisface la ecuación integral
$$y(x) = y_{0} + \int_{x_{0}}^{x} f(t, y(t)) dt$$
Derivemos esta expresión.
\begin{align*}
\dfrac{dy}{dx} &= \dfrac{d}{dx} \left( y_{0} + \int_{x_{0}}^{x} f(t, y(t))dt \right) \\
&= \dfrac{dy_{0}}{dx} + \dfrac{d}{dx} \left( \int_{x_{0}}^{x} f(t, y(t))dt \right) \\
&= 0 + f(x, y) \\
&= f(x, y)
\end{align*}
Donde se ha aplicado el teorema fundamental del cálculo. Con este resultado vemos que se ha recuperado la ecuación diferencial $\dfrac{dy}{dx} = f(x, y)$, mostrando así que $y(x)$ es solución a la ecuación diferencial y además
\begin{align*}
y(x_{0}) = y_{0} + \int_{x_{0}}^{x_{0}} f(t, y(t)) dt = y_{0} + 0 = y_{0}
\end{align*}
es decir, se satisface la condición inicial $y(x_{0}) = y_{0}$, de esta manera queda demostrado que $y(x)$ es solución del PVI.
$\square$
Este resultado es muy útil en muchos resultados sobre ecuaciones diferenciales y nos será de utilidad para motivar, más adelante, la introducción a las llamadas iterantes de Picard.
Continuando con nuestra teoría preliminar, un concepto sumamente importante que estudiaremos a continuación es el de funciones lipschitzianas.
Funciones Lipschitzianas
Como estamos trabajando con la ecuación diferencial
$$\dfrac{dy}{dx} = f(x, y)$$
la función $f$ es una función de dos variables, así que nos interesa estudiar las funciones lipschitzianas de dos variables, sin embargo es probable que este sea un concepto nuevo y para que sea más intuitivo entenderlo presentaremos la definición de función lipschitziana para el caso de una función de una variable y realizaremos algunos ejemplos sencillos para posteriormente definir la función lipschitziana en el caso de dos variables.
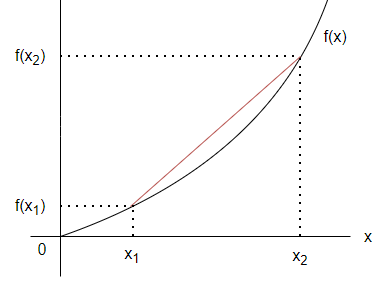
$$|f(x_{1}) -f(x_{2})| \leq L|x_{1} -x_{2}| \label{4} \tag{4}$$ para cada par de puntos $x_{1}, x_{2} \in I$. En tal caso se dice que $L$ es una constante de Lipschitz para $f$ en $I$.
Con esta definición observamos que si $x_{1} \neq x_{2}$ el cociente
$$\dfrac{f(x_{1}) -f(x_{2})}{x_{1} -x_{2}}$$
corresponde a la pendiente de la recta secante a la gráfica de $f$ que pasa por los puntos $(x_{1}, f(x_{1}))$ y $(x_{2}, f(x_{2}))$, de esta forma la condición de Lipschitz indica que todas estas pendientes están acotadas, es decir, existe una constante $L > 0$, tal que
$$\left|\dfrac{f(x_{1}) -f(x_{2})}{x_{1} -x_{2}} \right|\leq L$$
para cada $x_{1}, x_{2} \in I$, con $x_{1} \neq x_{2}$.
No entraremos es muchos detalles para el caso de una función de una variable, pero cabe mencionar que cualquier función lipschitziana es uniformemente continua, ya que dado $\varepsilon > 0$ basta tomar $\delta = \dfrac{\varepsilon}{L}$ y la condición de Lipschitz (\ref{4}) para que se verifique que
$$|x_{1} -x_{2}| < \delta \Rightarrow |f(x_{1}) -f(x_{2})| < \varepsilon$$
Como ejemplo mostremos que toda recta es una función lipschitziana.
Ejemplo: Mostrar que la función
$$f(x) = mx + b$$
es una función lipschitziana, con $L = |m|$.
Solución: Queremos probar que se cumple (\ref{4}). Vemos que
\begin{align*}
|f(x_{1}) -f(x_{2})| &= |mx_{1} + b -(mx_{2} + b)| \\
&= |mx_{1} + b -mx_{2} -b| \\
&= |mx_{1} -mx_{2}| \\
&= |m||x_{1} -x_{2}|\\
&= L|x_{1} -x_{2}|
\end{align*}
En donde consideramos que $L = |m|$. En este caso se da la igualdad
$$|f(x_{1}) -f(x_{2})| = L |x_{1} -x_{2}|$$
probando así que la función $f(x) = mx + b$ es una función Lipschitziana.
$\square$
Hay funciones uniformemente continuas que no son lipschitzianas, un ejemplo puede ser la función $f:[0, 1] \rightarrow \mathbb{R}$ definida como $f(x) = \sqrt{x}$, esta función es uniformemente continua pero no lipschitziana. Mostremos este hecho.
Ejemplo: Mostrar que la función $f:[0, 1] \rightarrow \mathbb{R}$, definida como $f(x) = \sqrt{x}$ no es lipschitziana.
Solución: Vamos a suponer que la función $f(x) = \sqrt{x}$ es lipschitziana y lleguemos a una contradicción. Si $f(x) = \sqrt{x}$ fuera lipschitziana debería satisfacer que
$$|f(x_{1}) -f(x_{2})| \leq L |x_{1} -x_{2}|$$
$\forall x_{1}, x_{2} \in [0, 1]$ y para alguna $L \geq 0$. Vemos que
$$|f(x) -f(0)| = |\sqrt{x} -\sqrt{0}| \leq L |x -0|$$
es decir, $\forall x \in [0, 1]$ ($x$ es positiva),
$$\sqrt{x} \leq L x$$
Si $x \in (0, 1]$ ($x \neq 0$), entonces
$$\dfrac{\sqrt{x}}{x} \leq L \Rightarrow \dfrac{1}{\sqrt{x}} \leq L$$
Este último resultado nos dice que la función $\dfrac{1}{\sqrt{x}}$ esta acotada por $L$ para $x \in (0, 1]$, sin embargo si tomamos el límite $x \rightarrow 0$ por la derecha obtenemos
$$\lim_{x \to 0^{+}}\frac{1}{\sqrt{x}} = \infty \hspace{1cm} !$$
Hemos llegado a una contradicción y todo ocurrió de suponer que la función $f(x) = \sqrt{x}$ era lipschitziana. Por lo tanto, a pesar de ser uniformemente continua, $f(x) = \sqrt{x}$ no es lipschitziana.
$\square$
Un resultado más que no demostraremos es el siguiente teorema.
Hay funciones lipschitzianas que no son derivables, por ejemplo la función $f: \mathbb{R} \rightarrow \mathbb{R}$ definida por $f(x) = |x|$.
Podemos decir, entonces, que la condición de Lipschitz es una condición intermedia entre continuidad uniforme y la existencia de derivada acotada.
Con esto en mente, ahora definamos lo que es una función lipschitziana para el caso en el que la función $f$ es de dos variables. Para este caso, la condición de Lipschitz sólo afectará a una de las variables, concretamente a la segunda, importante considerar este hecho.
\begin{align} |f(x, y_{1}) -f(x, y_{2})| \leq L|y_{1} -y_{2}| \label{5} \tag{5} \end{align} para cada par de puntos $(x, y_{1}), (x, y_{2}) \in U$. En tal caso se dice que $L$ es una constante de Lipschitz para $f$ en $U$ respecto a la segunda variable.
La relación (\ref{5}) es lo que se pide que se cumpla en la tercer hipótesis del teorema de Picard – Lindelöf.
Enunciemos dos proposiciones importantes con respecto a las funciones lipschitzianas de dos variables que nos serán de utilidad a la hora de demostrar el teorema de Picard – Lindelöf.
$$\left| \dfrac{\partial f}{\partial y} (x, y) \right| \leq L \label{6} \tag{6}$$ ara cada $(x, y) \in U$.
Demostración: Sea $f(x, y)$ una función lipschitziana respecto de la variable $y$ y supongamos que existe su derivada parcial con respecto a dicha variable $\dfrac{\partial f}{\partial y}$. Por definición, para $(x, y) \in U$ se tiene que
$$\dfrac{\partial f}{\partial y}(x, y) \doteq \lim_{h \to 0}\dfrac{f(x, y + h) -f(x, y)}{h} \label{7} \tag{7}$$
Dado un $\delta > 0$ y para $h$ suficientemente pequeño $|h|< \delta$, el punto $(x, y + h)$ pertenece a $U$. Sea $L$ una constante de Lipschitz de $f$ respecto de $y$ en $U$. De acuerdo a la definición de la condición de Lipschitz se verifica que
$$|f(x, y + h) -f(x, y)| \leq L |y + h -y| = L|h| \label{8} \tag{8}$$
Usando (\ref{7}) y (\ref{8}) tenemos lo siguiente.
\begin{align*}
\left|\dfrac{\partial f}{\partial y}(x, y) \right| &= \left|\lim_{h \to 0} \dfrac{f(x, y + h) -f(x, y)}{h}\right| \\
&= \lim_{h \to 0}\left|\dfrac{f(x, y + h) -f(x, y)}{h} \right| \\
&\leq \lim_{h \to 0} \dfrac{L|h|}{|h|} = L
\end{align*}
Esto es,
$$\left| \dfrac{\partial f}{\partial y}(x, y) \right| \leq L$$
lo que significa que $\dfrac{\partial f}{\partial y}$ esta acotada en $U$ por la constante de Lipschitz $L$.
$\square$
Ahora revisemos el resultado recíproco de la proposición anterior en donde es necesario que $U$ sea un conjunto convexo.
Demostración: Para demostrar esta proposición haremos uso del teorema del valor medio para funciones de una variable, de aquí la necesidad de que $U$ sea convexo.
Por hipótesis, $\dfrac{\partial f}{\partial y}$ esta acotada en $U$, sea $L > 0$, tal que
$$ \left| \dfrac{\partial f}{\partial y}(x, y)\right|\leq L \label{9} \tag{9}$$
para cada $(x, y) \in U$, y sean $(x, y_{1}), (x, y_{2}) \in U$ con $y_{1} < y_{2}$. Como $U$ es convexo tenemos garantizado que para cada $y$ tal que $y_{1} < y < y_{2}$ el punto $(x, y)$ pertenece a $U$, pues dicho punto pertenece al segmento que une los puntos $(x, y_{1})$ y $(x, y_{2})$, con estos resultados la función
$g_{x}:[y_{1}, y_{2}] \rightarrow \mathbb{R}, \hspace{1cm} g_{x}(y) = f(x, y)$
está bien definida y es derivable
$$g_{x}^{\prime}(y) = \dfrac{\partial f}{\partial y}(x, y)$$
para cada $y \in [y_{1}, y_{2}]$. Por el teorema del valor medio, existe $y$ tal que $y_{1} < y < y_{2}$ y tal que
$g_{x}(y_{1}) -g_{x}(y_{2}) = g_{x}^{\prime}(y) (y_{1} -y_{2})$
es decir,
$f(x, y_{1}) -f(x, y_{2}) = \dfrac{\partial f}{\partial y}(x, y)(y_{1} -y_{2})$
Esta igualdad también la podemos escribir como
$$|f(x, y_{1}) -f(x, y_{2})| = \left|\dfrac{\partial f}{\partial y}(x, y)\right||y_{1} -y_{2}| \label{10} \tag{10}$$
Por la desigualdad (\ref{9}), tenemos
$$\left|\dfrac{\partial f}{\partial y}(x, y)\right||y_{1} -y_{2}| \leq L|y_{1} -y_{2} | \label{11} \tag{11}$$
De los resultados (\ref{10}) y (\ref{11}) concluimos que
$$|f(x, y_{1}) -f(x, y_{2})| \leq L|y_{1} -y_{2} |$$
lo que prueba que $f$ es una función lipschitziana con respecto de la segunda variable.
$\square$
Esta proposición es bastante útil, pues basta verificar que la derivada $\dfrac{\partial f}{\partial y}$ de $f = f(x, y)$ esta acotada en un conjunto convexo $U$ para concluir que $f$ es una función lipschitziana respecto de la segunda variable. Realicemos un ejemplo.
Ejemplo: Sea $U = [-1, 1] \times \mathbb{R}$. Mostrar que la función $f: U \rightarrow \mathbb{R}$ definida como
$$f(x, y) = |x|\sin^{2}(y)$$
es una función lipschitziana respecto de la segunda variable.
Solución: Es claro que el conjunto $U$ es convexo y que existe la derivada de $f$ con respecto a $y$ dada por
$$\dfrac{\partial f}{\partial y} = 2|x|\sin(y)\cos(y)$$
Como
$$|\sin(y) \cos(y)| \leq 1$$
$\forall y \in \mathbb{R}$ y $|x| < 1, \forall x \in [-1, 1]$, notamos que
$$2|x||\sin(y)\cos(y)| \leq 2$$
Esto es,
$$\left|\dfrac{\partial f}{\partial y}\right| \leq 2$$
esto muestra que la derivada de $f$ esta acotada, por la proposición anterior concluimos que la función $f$ es lipschitziana y podemos tomar como constante de Lipchitz el valor $L = 2$.
$\square$
En este ejemplo vimos que el valor $L = 2$ es una cota de $\left|\dfrac{\partial f}{\partial y}\right|$, sin embargo cualquier número mayor a $2$ cumple también la desigualdad y por tanto también puede ser una constante de Lipschitz en $U$. En general, una buena constante de Lipschitz puede ser
$$L= \sup_{(x, y) \in U}\left|\dfrac{\partial f}{\partial y}(x, y)\right| \label{12} \tag{12}$$
De ambas proposiciones podemos realizar la siguiente caracterización de Lipschitz, bastante útil en la práctica.
En este corolario unimos los resultados de las dos proposiciones anteriores.
Con esto concluimos el estudio de las funciones lipschitzianas, es importante tener presente este último corolario ya que será de suma relevancia en la demostración del teorema de Picard.
Para concluir con esta entrada presentaremos una herramienta más que nos será de mucha utilidad a la hora de demostrar el teorema de Picard – Lindelöf, en particular nos ayudará a probar la unicidad de la solución al PVI (\ref{1}). Revisemos el Lema de Gronwall.
Lema de Gronwall
Este resultado fue desarrollado por Thomas Hakon Grönwall en 1919.
$$0 \leq f(x) \leq \alpha + \beta \int_{x_{0}}^{x} f(t) dt \label{13} \tag{13}$$ $\forall x \in I$ con $\alpha, \beta \geq 0$ constantes, entonces
$$f(x) \leq \alpha e^{\beta (x -x_{0})} \label{14} \tag{14}$$
Demostración: Definamos la función
$$g(x) = \int_{x_{0}}^{x}f(t)dt \label{15} \tag{15}$$
Notemos que
$$g(x_{0}) = 0 \hspace{1cm} y \hspace{1cm} \dfrac{dg}{dx} = f(x)$$
En términos de $g(x)$ y $\dfrac{dg}{dx}$ la desigualdad (\ref{13}) se puede escribir de la siguiente forma.
$$0 \leq \dfrac{dg}{dx} \leq \alpha + \beta g(x)$$
de donde,
$$\dfrac{dg}{dx}-\beta g(x) \leq \alpha \label{16} \tag{16}$$
Multipliquemos ambos lados de la desigualdad por $e^{-\beta (x -x_{0})}$.
\begin{align*}
e^{-\beta (x -x_{0})} \left( \dfrac{dg}{dx} -\beta g(x) \right) \leq e^{-\beta (x-x_{0})} \alpha \\
e^{-\beta (x -x_{0})}\dfrac{dg}{dx}-\beta e^{-\beta (x -x_{0})} g(x) \leq \alpha e^{-\beta (x -x_{0})} \label{17} \tag{17}
\end{align*}
Identificamos que el lado izquierdo de la última desigualdad corresponde a la derivada del producto de las funciones $e^{-\beta(x -x_{0})}$ y $g(x)$, en efecto
\begin{align*}
\dfrac{d}{dx} \left( g(x) e^{-\beta (x -x_{0})} \right ) &= \dfrac{dg}{dx} e^{-\beta (x -x_{0})} + g(x) \left( -\beta e^{-\beta (x -x_{0})} \right ) \\
&= e^{-\beta (x -x_{0})} \dfrac{dg}{dx} -\beta e^{-\beta (x -x_{0})} g(x)
\end{align*}
Sustituimos en la desigualdad (\ref{17}).
$$\dfrac{d}{dx} \left( g(x)e^{-\beta (x -x_{0})} \right ) \leq \alpha e^{-\beta (x -x_{0})} \label{18} \tag{18}$$
Integremos de $x_{0}$ a $x$.
\begin{align*}
\int_{x_{0}}^{x} \dfrac{d}{dt} \left( g(t) e^{-\beta (t -x_{0})} \right ) dt &\leq \alpha \int_{x_{0}}^{x} e^{-\beta (t -x_{0})}dt \\
g(x)e^{-\beta (x -x_{0})} -g(x_{0})e^{-\beta (x_{0} -x_{0})} &\leq \alpha \left[ -\dfrac{1}{\beta} \left( e^{-\beta(x -x_{0})} -e^{-\beta(x_{0} -x_{0})} \right) \right]
\end{align*}
pero
$$g(x_{0}) = \int_{x_{0}}^{x_{0}}f(t)dt = 0 \hspace{1cm} y \hspace{1cm} e^{-\beta (x_{0} -x_{0})} = 1$$
Así,
$$g(x)e^{-\beta (x -x_{0})} \leq -\dfrac{\alpha}{\beta} \left ( e^{-\beta (x -x_{0})} -1 \right) \label{19} \tag{19}$$
Multipliquemos ambos lados de la desigualdad por $e^{\beta (x -x_{0})}$.
\begin{align*}
g(x) &\leq -\dfrac{\alpha}{\beta}e^{\beta (x -x_{0})} \left( e^{-\beta (x -x_{0})} -1 \right) \\
&= -\dfrac{\alpha}{\beta}\left( 1 -e^{\beta (x -x_{0})} \right) \\
&= \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right )
\end{align*}
es decir,
$$g(x) \leq \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right ) \label{20} \tag{20}$$
De la desigualdad original (\ref{13}) sabemos que
\begin{align*}
0 \leq f(x) &\leq \alpha +\beta \int_{x_{0}}^{x} f(t)dt \\
0 \leq f(x) &\leq \alpha + \beta g(x)
\end{align*}
de donde,
$$\dfrac{f(x) -\alpha}{\beta} \leq g(x) \label{21} \tag{21} $$
De los resultados (\ref{20}) y (\ref{21}), tenemos
$$\dfrac{f(x) -\alpha}{\beta} \leq g(x) \leq \dfrac{\alpha}{\beta}\left( e^{\beta (x -x_{0})} -1 \right)$$
lo que nos interesa es la desigualdad
$$\dfrac{f(x) -\alpha}{\beta} \leq \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right)$$
haciendo un poco de álgebra obtenemos lo siguiente.
\begin{align*}
\dfrac{f(x) -\alpha}{\beta} &\leq \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right) \\
f(x) -\alpha &\leq \beta \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right) \\
f(x) &\leq \alpha + \beta \dfrac{\alpha}{\beta} \left( e^{\beta (x -x_{0})} -1 \right) \\
f(x) &\leq \alpha + \alpha \left( e^{\beta (x -x_{0})} -1 \right) \\
f(x) &\leq \alpha + \alpha e^{\beta (x -x_{0})} -\alpha \\
f(x) &\leq \alpha e^{\beta (x-x_{0})}
\end{align*}
Por lo tanto,
$$f(x) \leq \alpha e^{\beta (x-x_{0})}$$
Con esto queda demostrado que si se cumple la desigualdad (\ref{13}), entonces $f(x) \leq \alpha e^{\beta (x -x_{0})}$, $\forall x \in I$.
$\square$
Usando el lema de Gronwall podemos demostrar el siguiente corolario de manera inmediata.
Demostración: Debido a que se cumplen todas las hipótesis del lema de Gronwall sabemos que $\forall x \in I$
$0 \leq f(x) \leq \alpha e^{\beta (x -x_{0})}$
Pero si $\alpha = 0$, entonces
$$0 \leq f(x) \leq 0$$
de donde se deduce que $f(x) = 0$, $\forall x \in I$.
$\square$
Con esto concluimos la primer entrada sobre la teoría preliminar que necesitamos conocer para poder demostrar el teorema de existencia y unicidad de Picard – Lindelöf.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Probar que la función $f: \mathbb{R} \rightarrow \mathbb{R}$, $f(x) = c$ es una función lipschitziana
- Probar que la función $f: \mathbb{R} \rightarrow \mathbb{R}$, $f(x) =|x|$ es lipschitziana, con $L = 1$
- Probar que la función $f: \mathbb{R} \rightarrow \mathbb{R}$, $f(x) = x^{2}$ no es una función lipschitziana.
Hint: Suponer que lo es, es decir $$|f(x_{2}) -f(x_{1})| \leq L |x_{2} -x_{1}|$$ y considerar la definición de derivada $$\lim_{x_{2} \to x_{1}} \dfrac{|f(x_{2}) -f(x_{1})|}{|x_{2} -x_{1}|} = | f^{\prime}(x_{1})|$$ para llegar a una contradicción.
En los siguientes ejercicios se puede usar la definición de función lipschitziana respecto de la segunda variable o las proposiciones vistas.
- Probar que la función $f: U \rightarrow \mathbb{R}$ con $$U = \{(x, y): 0 \leq x \leq 1, y \in \mathbb{R} \}$$ definida como $$f(x, y) = y \cos (x)$$ es una función lipschitziana respecto de la segunda variable, con $L = 1$.
- Probar que la función $f: U \rightarrow \mathbb{R}$ con $$U = \{(x, y): 1 \leq x \leq 2, y \in \mathbb{R} \}$$ definida como $$f(x, y) = -\dfrac{2}{x} y + e^{x} \sin (x)$$ es una función lipschitziana respecto de la segunda variable, con $L = 2$.
Más adelante…
En esta entrada conocimos el teorema de existencia y unicidad de Picard – Lindelöf para ecuaciones diferenciales ordinarias de primer orden. Vimos que el PVI (\ref{1}) es equivalente a resolver la ecuación integral (\ref{3}), definimos a las funciones lipschitzianas de dos variables, demostramos algunos resultados al respecto y concluimos con la demostración del lema de Gronwall. Todos estos resultados los aplicaremos más adelante en la demostración del teorema de Picard – Lindelöf.
En la siguiente entrada continuaremos desarrollando esta teoría preliminar. Definiremos el concepto de aproximaciones sucesivas, mejor conocidas como iterantes de Picard, haremos un breve repaso sobre convergencia de series y sucesiones de funciones, presentaremos el resultado local del teorema de existencia y unicidad y resolveremos un ejercicio al respecto.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Ecuación de Bernoulli y ecuación de Riccati
- Siguiente entrada del curso: Teorema de Existencia y Unicidad – Iteraciones de Picard y Convergencia
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»