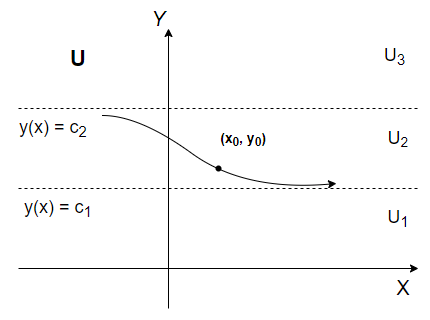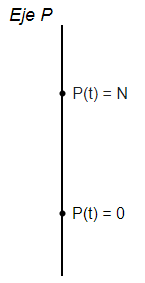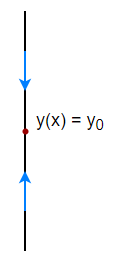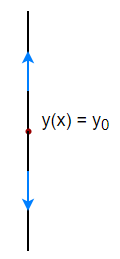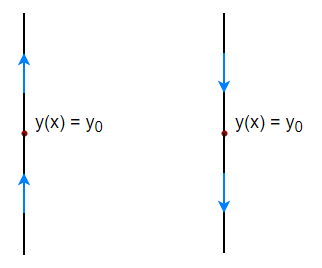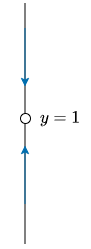Archivo de la etiqueta: Campo de pendientes

Ecuaciones Diferenciales I: Ecuaciones diferenciales autónomas

Por Omar González Franco

2 respuestas

¿Cómo es posible un error en las matemáticas?.
– Henri Poincare

Introducción

Continuando con la descripción cualitativa de las ecuaciones diferenciales, en esta entrada estudiaremos las ecuaciones diferenciales en las que la función razón no depende explícitamente de la variable independiente $x$.

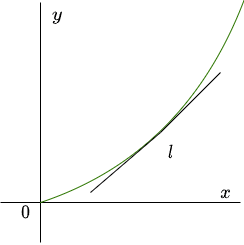
En la entrada anterior vimos una propiedad geométrica interesante de las ecuaciones diferenciales de la forma

$$\dfrac{dy}{dx} = f(y) \label{1} \tag{1}$$

dicha propiedad es que los elementos lineales en dos puntos distintos del plano $XY$, pero con la misma coordenada $y$, tienen la misma pendiente, esta propiedad tiene interesantes consecuencias y las estudiaremos en esta entrada.

Ecuaciones de primer orden autónomas

Una ecuación autónoma en su forma normal se ve como (\ref{1}).

La ecuación diferencial

$$\dfrac{dy}{dx} = 1 + 2y$$

es una ecuación diferencial autónoma, mientras que la ecuación

$$\dfrac{dy}{dx} = 2xy$$

es una ecuación no autónoma ya que la función razón

$$f(x, y) = 2xy$$

sí depende de la variable independiente $x$.

Hay muchos procesos físicos que son modelados con ecuaciones diferenciales autónomas donde la variable independiente puede ser por ejemplo el tiempo $t$, en estos casos dichos procesos no cambiarían en el tiempo.

Puntos críticos

En la ecuación diferencial autónoma (\ref{1}) las raíces de la función razón son de especial importancia.

Un punto crítico también es llamado punto de equilibrio o punto estacionario.

Con estas dos definiciones podemos observar que si $k$ es un punto crítico de la ecuación (\ref{1}), entonces $y(x) = k$ es una solución constante de la ecuación diferencial autónoma.

Esquema de fases

En la entrada anterior vimos que una propiedad geométrica de las ecuaciones autónomas es que los elementos lineales son paralelos a lo largo de líneas horizontales en el plano $XY$, esto quiere decir que si conocemos el campo de pendientes a lo largo de una sola línea vertical $x = x_{0}$, entonces lo conocemos para todo el plano $XY$. Esta propiedad nos permite, en lugar de dibujar todo el plano, dibujar una sola línea que contiene la misma información. Esta línea se llama línea fase para la ecuación autónoma.

Para ver cómo obtener los puntos críticos, soluciones de equilibrio y líneas fase realicemos el siguiente ejemplo con una ecuación logística.

Ejemplo: Obtener los puntos críticos, soluciones de equilibrio y línea fase de la siguiente ecuación diferencial autónoma.

$$\dfrac{dy}{dx} = y(\alpha -\beta y) \label{3} \tag{3}$$

con $\alpha$ y $\beta$ constantes positivas.

Solución: Para obtener las soluciones de equilibrio y los puntos críticos igualamos la función razón a cero.

$$f(y) = y(\alpha -\beta y) = 0$$

La ecuación se satisface si $y = 0$ o $\alpha -\beta y = 0$, es decir, si

$$y(x) = 0 \hspace{1cm} o \hspace{1cm} y(x) = \dfrac{\alpha}{\beta}$$

Estas funciones corresponden a las soluciones de equilibrio de la ecuación diferencial y los puntos críticos no son más que las constantes $k_{1} = 0$ y $k_{2} = \dfrac{\alpha}{\beta} > 0$.

Para esbozar la línea fase comencemos por colocar dos puntos sobre una línea vertical, dichos puntos corresponden a los puntos críticos obtenidos.

Puntos críticos en la línea fase.

La línea fase es paralela al eje $Y$, o bien puede ser el mismo eje $Y$.

En este caso los puntos críticos dividen a la línea fase en tres intervalos:

$$(-\infty, 0), \hspace{1cm} \left( 0, \dfrac{\alpha}{\beta} \right) \hspace{1cm} y \hspace{1cm} \left(\dfrac{\alpha}{\beta}, \infty\right)$$

Por definición los puntos críticos son los valores en los que

$$\dfrac{dy}{dx} = f(k) = 0$$

esto significa que la pendiente de los elementos lineales en los puntos críticos debe ser cero, mientras que por encima y por debajo de los puntos críticos la pendiente tiene que ser distinta de cero, así que puede haber elementos lineales con pendiente negativa o pendiente positiva.

Veamos en cada uno de los intervalos de nuestro ejemplo que signo tiene la pendiente de los elementos lineales, como se trata de un diagrama unidimensional dicho valor lo representaremos con flechas sobre la línea fase, si la pendiente es positiva colocaremos una flecha apuntando hacia arriba y si es una pendiente negativa colocaremos una flecha apuntando hacia abajo.

Para ver si la pendiente es positiva o negativa estudiemos el signo de la función razón (que es equivalente al signo de la derivada $\dfrac{dy}{dx}$) en cada uno de los intervalos. Comencemos con el intervalo $(-\infty, 0)$, en este caso $-\infty < y < 0$.

\begin{align*}
y &< 0 \\
\beta y &< 0 \\
-\beta y &> 0 \\
-\beta y + \alpha > \alpha &> 0 \\
f(y) = y(\alpha -\beta y) &< 0 \\
\dfrac{dy}{dx} &< 0
\end{align*}

Este análisis nos indica que la pendiente de los elementos lineales en el intervalo $(-\infty, 0)$ es negativa.

Haciendo un análisis similar en los intervalos $\left( 0, \dfrac{\alpha}{\beta} \right)$ y $\left(\dfrac{\alpha}{\beta}, \infty \right)$ obtenemos los siguientes resultados:

  • En $(-\infty, 0)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa
  • En $\left( 0, \dfrac{\alpha}{\beta} \right)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) > 0$ $\Rightarrow$ La pendiente es positiva.
  • En $\left( \dfrac{\alpha}{\beta}, \infty \right)$ $\hspace{0.05cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa.

Como mencionamos antes, en el intervalo $(-\infty, 0)$ de la línea fase colocaremos una flecha apuntando hacia abajo debido a que la pendiente es negativa. En el intervalo $\left( 0, \dfrac{\alpha}{\beta} \right)$ colocaremos una flecha apuntando hacia arriba ya que la pendiente es positiva y finalmente en el intervalo $\left(\dfrac{\alpha}{\beta}, \infty \right)$ colocaremos nuevamente una flecha hacia abajo debido a que la pendiente vuelve a ser negativa. La línea fase de la ecuación diferencial dada se muestra en la siguiente figura.

Línea fase de la ecuación $\dfrac{dy}{dx} = y(\alpha-\beta y)$.

Como caso particular consideremos la ecuación diferencial autónoma

$$\dfrac{dy}{dx} = y(6 -3y)$$

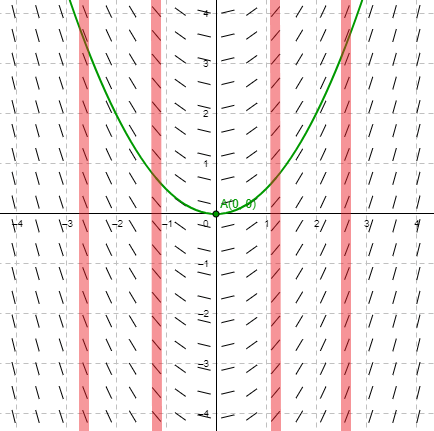
Las soluciones de equilibrio son $y(x) = 0$ y $y(x) = \dfrac{\alpha}{\beta} = \dfrac{6}{3} = 2$. A continuación se muestra el campo de pendientes de esta ecuación.

Campo de pendientes de la ecuación diferencial $\dfrac{dy}{dx} = y(6 -3y)$.

Notamos que, en efecto, el valor de la pendiente de los elementos lineales en las soluciones de equilibrio es cero, por encima de $y(x) = 2$ y por debajo de $y(x) = 0$ la pendiente es negativa y entre las soluciones de equilibrio la pendiente de los elementos lineales es positiva, tal como lo mostramos en la línea fase del caso general.

$\square$

Como podemos ver, la línea fase es una gran herramienta que nos permite analizar el comportamiento de las soluciones de una ecuación diferencial autónoma gracias a que las pendientes de los elementos lineales en líneas horizontales del plano $XY$ son siempre iguales.

Con el ejemplo en mente ahora podemos establecer los pasos necesarios para dibujar una línea fase de una ecuación diferencial autónoma.

  • Comenzamos por dibujar una línea vertical paralela al eje $Y$ para cualquier valor de $x$.
  • Determinamos las soluciones de equilibrio y los puntos críticos, marcamos los puntos críticos sobre la línea vertical.
  • Determinamos los intervalos de $y$ en los que $f(y) > 0$ y dibujamos flechas apuntando hacia arriba en esos intervalos.
  • Determinamos los intervalos de $y$ en los que $f(y) < 0$ y dibujamos flechas apuntando hacia abajo en esos intervalos.

Las líneas fase nos permiten obtener una aproximación cualitativa de las curvas solución de una ecuación diferencial autónoma.

Nota: En ocasiones se usan de forma indistinta los términos puntos críticos y soluciones de equilibrio, sin embargo podemos pensar a un punto crítico como el punto $c = k$ que se coloca en la línea fase, mientras que una solución de equilibrio $y(x) = k$ como la gráfica en el plano $XY$ de una función constante para toda $x$. Cuando estamos analizando líneas fase puede ser que al punto crítico también se le llame solución de equilibrio y es correcto debido a que la línea fase representa al eje de la variable dependiente $y$ para cualquier valor de la variable independiente $x$. Lo importante es que tengamos presente las definiciones de punto crítico y de solución de equilibrio que establecimos al inicio para evitar confusiones.

Ahora veamos que nos dice esta descripción cualitativa acerca de la forma de una curva solución de una ecuación diferencial autónoma.

Curvas solución de una ecuación diferencial autónoma

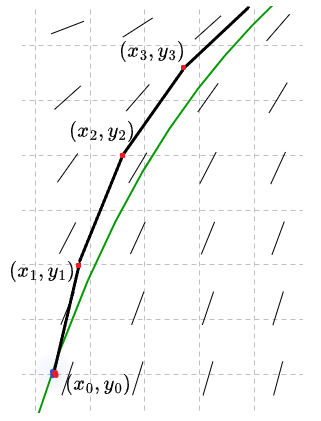
En la ecuación diferencial autónoma (\ref{1}) la función $f$ es independiente de la variable $x$, esto nos permite suponer que $f$ está definida en $x \in (-\infty, \infty)$, o en $x \in [0, \infty)$. Consideremos una región $U$ en el plano $XY$ en el que se cumple el teorema de existencia y unicidad de una solución, por este teorema sabemos que existe una solución que pasa por el punto $(x_{0}, y_{0})$. En la región $U$ supongamos que una ecuación diferencial autónoma tiene dos puntos críticos $c_{1}$ y $c_{2}$ tales que $c_{1} < c_{2}$. Las gráficas de las soluciones

$$y(x) = c_{1} \hspace{1cm } y \hspace{1cm} y(x) = c_{2}$$

son rectas horizontales que dividen a la región $U$ en tres regiones: $U_{1}, U_{2}$ y $U_{3}$, esto se puede visualizar en la siguiente figura.

Subregiones $U_{1}, U_{2}$ y $U_{3}$ de $U$.

Con estas condiciones podemos establecer las siguientes propiedades.

  • Si el punto $(x_{0}, y_{0})$ está en alguna subregión $U_{i}$, $i = 1, 2, 3$ y $y(x)$ es una solución cuya curva solución pasa por $(x_{0}, y_{0})$, entonces $y(x)$ debe permanecer en esa subregión $U_{i}$ para toda $x$.

Esto indica que una solución $y(x)$ no puede cruzar la grafica de una solución de equilibrio $y(x) = c$. Para argumentar este hecho consideremos a $k$ como un punto crítico de una ecuación diferencial autónoma tal que $f(k) = 0$, considerando que $f(y)$ es continua, si las soluciones $y(x)$ son cercanas a $k$, entonces el valor de $f$ debe ser pequeño, esto nos indica que las soluciones se están desplazando lentamente cuando están próximas a los puntos críticos, dicho de otra manera, una solución que se acerca a un punto crítico cuando $x$ crece (o decrece) se mueve cada vez más lento al acercarse a éste. Por el teorema de existencia y unicidad, una solución que se acerca a un punto crítico nunca llega realmente a él, es decir, la solución de equilibrio se vuelve una asíntota para todas las soluciones $y(x)$ que se aproximan al punto crítico.

En la figura anterior, por ejemplo, la curva $y(x)$ que pasa por el punto $(x_{0}, y_{0})$ debe mantenerse dentro de $U_{2}$ para toda $x$, $y(x)$ está acotada por arriba con $c_{2}$ y por abajo con $c_{1}$, esto es, $c_{1} < y(x) < c_{2}$.

Otra propiedad es la siguiente.

  • Por continuidad de la función $f$, debe ser $f(y) > 0$ o $f(y) < 0$ para toda $x$ en una subregión $U_{i}$, $i = 1, 2, 3$.

Vimos anteriormente que el signo de la pendiente se mantiene igual dentro de toda la región limitada por los puntos críticos, esto nos permite deducir que una curva solución $y(x)$ no puede oscilar o tener extremos relativos (máximos o mínimos) dentro de una misma región. Esto lo podemos describir con la siguiente propiedad.

  • Debido a que $\dfrac{dy}{dx} = f(y(x))$ es positiva o negativa en una subregión $U_{i}$, $i = 1, 2, 3$, una solución $y(x)$ es estrictamente monótona, por lo tanto no puede oscilar ni tener extremos relativos.

Ahora que conocemos estas propiedades podemos establecer una más que se puede deducir de las anteriores. Basándonos en el caso general de la imagen anterior podemos decir lo siguiente.

  • Si $y(x)$ es una solución dentro de la región $U_{1}$, entonces está acotada por arriba con el punto crítico $c_{1}$, esto es, $\forall$ $x$ en el intervalo $$y(x) < c_{1}$$ Esto indica que la curva solución $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{1}$ a medida que $x \rightarrow \infty$ o $x \rightarrow -\infty$. Por otro lado, una solución $y(x)$ que este en la región $U_{2}$ está acotada por abajo con $c_{1}$ y arriba con $c_{2}$, esto es, $\forall$ $x$ en el intervalo $$c_{1} < y(x) < c_{2}$$ Entonces la curva solución $y(x)$ debe tender a las gráficas de las soluciones de equilibrio $y(x) = c_{1}$ y $y(x) = c_{2}$ conforme $x \rightarrow \infty$ en una y $x \rightarrow -\infty$ en la otra. Finalmente, si la solución está en la region $U_{3}$ entonces está acotada por abajo con $c_{2}$, es decir, $\forall$ $x$ $$y(x) > c_{2}$$ En este caso la grafica $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{2}$ conforme $x \rightarrow \infty$ o $x \rightarrow -\infty$.

Veamos la importancia de estas propiedades en un ejemplo.

Modelo logístico de la población

En esta entrada ya estudiamos como ejemplo la ecuación logística (\ref{3}), usemos los resultados obtenidos para resolver de manera cualitativa el problema del modelo logístico de la población visto en la entrada anterior. El modelo que establecimos fue

$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P \label{4} \tag{4}$$

Este modelo corresponde a una ecuación diferencial autónoma.

$$\dfrac{dP}{dt} = f(P) \label{5} \tag{5}$$

así que las curvas solución las podemos describir con la teoría que hemos construido en esta entrada.

El problema que analizábamos era el crecimiento de la población en función de su entorno y los recursos limitados a los que están sujetos. Resolvamos la ecuación diferencial de manera cualitativa aplicando lo que hemos aprendido hasta ahora e interpretemos los resultados.

Comencemos por determinar las soluciones de equilibrio y los puntos críticos, para ello igualemos la ecuación a cero.

$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P = 0$$

Esta relación se satisface si

$$kP = 0 \hspace{1cm} o \hspace{1cm} 1 -\dfrac{P}{N} = 0$$

Es decir, si $P = 0$ o $P = N$. Por lo tanto, los puntos críticos son $c_{1} = 0$ y $c_{2} = N$, mientras que las soluciones de equilibrio son $P(t) = 0$ y $P(t) = N$.

Coloquemos los puntos críticos sobre la línea fase.

Puntos críticos en la línea fase.

Los puntos críticos definen tres intervalos para $P$, estos son

$$(-\infty, 0), \hspace{1cm} (0, N) \hspace{1cm} y \hspace{1cm} (N, \infty)$$

Sin embargo, como se trata de un problema real es claro que no tiene sentido que la variable población $P(t)$ sea negativa (no hay individuos negativos), así mismo no hay tiempos negativos por lo que $t > 0$, por lo tanto en este problema sólo consideraremos los intervalos $(0, N)$ y $(N, \infty)$ para $P$, así como $0 < t < \infty$.

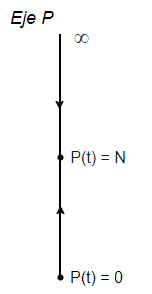
Del caso general (\ref{3}) deducimos que en el intervalo $(0, N)$ las pendientes son positivas, así que la función $P(t)$ será creciente en dicho intervalo y en $(N, \infty)$ las pendientes son negativas, por tanto la función $P(t)$ será decreciente. La línea fase final queda de la siguiente manera.

Línea fase del modelo logístico.

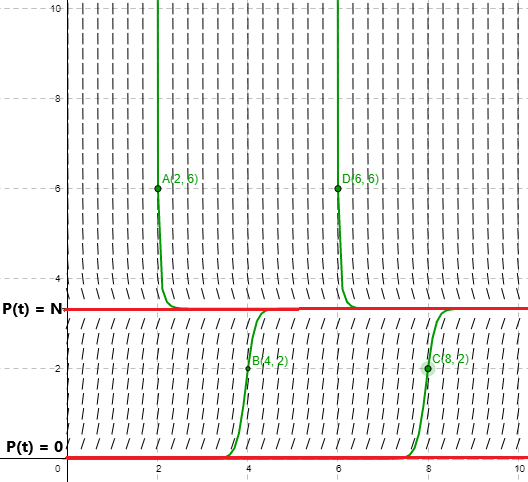
Un ejemplo de como se ve el campo de pendientes, las soluciones de equilibrio y algunas curvas solución de la ecuación logística (\ref{4}) se muestra en la siguiente figura.

Campo de pendientes de la ecuación logística (4) para valores particulares de $k$ y $N$.

De este gráfico notamos que las curvas solución cumplen con las hipótesis que establecimos al plantear el modelo, dichas hipótesis eran

  • Si la población es pequeña $(P(t) < N)$, la tasa de crecimiento de la población es proporcional a su tamaño.
  • Si la población es demasiado grande para ser soportada por su entorno y recursos $(P(t) > N)$, la población disminuirá, en este caso la tasa de crecimiento será negativa.

Las soluciones de equilibrio $P(t) = 0$ y $P(t) = N$ tienen sentido, pues si la población es cero permanecerá en cero indefinidamente y si la población es exactamente la asociada con la capacidad de soporte, entonces no crecerá ni disminuirá.

Es así que a partir de la línea fase y el campo de pendientes de una ecuación diferencial autónoma podemos esbozar varias curvas solución con distintas condiciones iniciales. En este ejemplo la única información que necesitamos es el hecho de que $P = 0$ y $P = N$ son soluciones de equilibrio, $P(t)$ crece si $0 < P < N$ y disminuye si $P > N$ o $P < 0$. Los valores exactos de $P(t)$ en cualquier tiempo dado $t$ dependerán de los valores $P(0)$, $k$ y $N$.

$\square$

Clasificación de puntos de equilibrio

Como vimos, alrededor de un punto crítico las soluciones pueden tener distintos comportamientos. Básicamente hay tres tipos de comportamiento que $y(x)$ puede tener alrededor de un punto crítico y en base a estos comportamientos podemos clasificarlos.

Supongamos que $y(x) = y_{0}$ es una solución de equilibrio de la ecuación diferencial autónoma (\ref{1}), los tres tipos de comportamiento que $y(x)$ puede tener alrededor del punto crítico $y_{0}$ son:

  • Caso 1: Por arriba de $y_{0}$ la función $y(x)$ es decreciente y por debajo de $y_{0}$ la función $y(x)$ es creciente, en este caso decimos que el punto crítico es un atractor.
$y_{0}$ es un atractor.
  • Caso 2: Por arriba de $y_{0}$ la función $y(x)$ es creciente y por debajo de $y_{0}$ la función $y(x)$ es decreciente, en este caso decimos que el punto crítico es un repulsor.
$y_{0}$ es un repulsor.
  • Caso 3: Tanto por arriba y por abajo de $y_{0}$ la función $y(x)$ es creciente o decreciente, en este caso decimos que el punto crítico es un nodo o punto semiestable.
$y_{0}$ es un nodo o punto semiestable.

En resumen, sea $y(x)$ solución de una ecuación diferencial autónoma (\ref{1}).

  • Si $f(y_{0}) = 0$, entonces $y_{0}$ es un punto crítico y $y(x) = y_{0}$ es la solución de equilibrio para toda $x$.
  • Si $f(y_{0}) > 0$, entonces $y(x)$ es creciente para toda $x$ y $y(x) \rightarrow \infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio mayor que $y_{0}$.
  • Si $f(y_{0}) < 0$, entonces $y(x)$ es decreciente para toda $x$ y $y(x) \rightarrow -\infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio menor que $y_{0}$.

Importante mencionar que esto también es valido para $x$ negativas. Cuando $x$ decrece podemos encontrar resultados similares.

  • Si $f(y_{0}) > 0$, entonces $y(x) \rightarrow -\infty$ o al siguiente punto de equilibrio menor conforme $x$ aumenta en valores negativos.
  • Si $f(y_{0}) < 0$, entonces $y(x) \rightarrow \infty$ o al siguiente punto de equilibrio mayor conforme $x$ aumenta en valores negativos.

Un caso especial

Consideremos la ecuación diferencial autónoma

$$\dfrac{dy}{dx} = \dfrac{1}{1 -y}$$

Intentemos esbozar la línea fase. Por definición, los puntos críticos son los valores para los que $f(y) = 0$, sin embargo en este caso $f(y)$ no puede ser cero.

Notemos que si $y > 1$, entonces $f(y) < 0$ y si $y < 1$, entonces $f(y) > 0$, pero si $y = 1$, $f(y)$ no esta definida. En este caso decimos que la línea fase tiene un agujero en $y =1$ y lo denotamos como un circulo vacío.

Agujero en la línea fase.

Las soluciones $y(x)$ de la ecuación tienden hacia $y = 1$ cuando $x$ aumenta.

Concluyamos esta entrada con el enunciado de un teorema importante.

Teorema de linearización

Existe un teorema conocido como teorema de linearización que nos ayuda a determinar el tipo de puntos críticos de una ecuación diferencial autónoma (\ref{1}), de acuerdo al comportamiento que tiene la función $f(y)$. El enunciado de este teorema es el siguiente.

La demostración a este teorema la podemos encontrar en la sección de videos.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Para las siguientes ecuaciones diferenciales, esbozar las líneas fase y clasificar a los puntos críticos como atractores, repulsores o nodos según sea el caso.
  • $\dfrac{dy}{dx} = 3y(1 -y)$
  • $\dfrac{dv}{du} = \dfrac{1}{v -2}$
  • $\dfrac{dy}{dt} = \cos(y)$
  • $\dfrac{dw}{dt} = w^{2} -6w -16$
  1. Para cada condición inicial dada, describir cualitativamente el comportamiento a largo plazo de las soluciones de la ecuación diferencial

    $\dfrac{dy}{dx} = y^{2} -4y + 2$

    con condición inicial
  • $y(0) = 0$
  • $y(0) = 10$
  • $y(3) = 1$

Más adelante…

En estas dos últimas entradas hemos estudiado a las ecuaciones diferenciales ordinarias de primer orden desde una perspectiva cualitativa, esto nos ha permitido esbozar las curvas solución y encontrar propiedades interesantes sin siquiera conocer la forma explicita de la solución. En particular, las ecuaciones diferenciales autónomas presentan propiedades interesantes que son útiles para analizar modelos que describen algún fenómeno real.

Ha llegado el momento de estudiar los distintos métodos de resolución de las ecuaciones diferenciales ordinarias de primer orden. Comenzaremos con un método sencillo que funciona sólo para ecuaciones diferenciales lineales.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I: Campos de pendientes y su ecuación diferencial asociada

Por Omar González Franco

2 respuestas

Todas las verdades de las matemáticas están vinculadas entre si.
– Adrien-Marie Legendre

Introducción

Hemos estudiado algunas propiedades de las soluciones de una ecuación diferencial, estas funciones son expresiones analíticas que nos son útiles para describir una solución de una ecuación diferencial, sin embargo no siempre es necesario obtener dicha expresión analítica para lograr describir las soluciones. En este entrada haremos un análisis geométrico (o cualitativo) sobre ecuaciones diferenciales ordinarias de la forma

$$\dfrac{dy}{dx} = f(x, y(x)) \label{1} \tag{1}$$

Campos de pendientes

Recordemos que geométricamente la derivada $\dfrac{dy}{dx}$ de una función derivable $y = y(x)$ corresponde a la pendiente de las rectas tangentes en cada punto de la gráfica de la función $y(x)$, este resultado nos será de utilidad para intentar describir cualitativamente las soluciones de una ecuación diferencial de la forma normal (\ref{1}).

De acuerdo a la definición de solución de una ecuación diferencial, la función $y(x)$ es necesariamente derivable y por tanto continua en un intervalo $\delta$, esto nos garantiza que la curva solución en $\delta$ no tiene cortes y debe tener una recta tangente en cada punto $(x, y(x))$.

Si la función $y(x)$ es solución, entonces tiene una gráfica en el plano $XY$, la gráfica corresponde a la curva solución y la pendiente en cada punto está dada por

$$m = \dfrac{dy}{dx} = f(x, y)$$

Es así que para cada punto $(x, y)$ en el plano $XY$ se le puede asociar una número dado por la función razón que corresponderá a la pendiente de la recta tangente de una curva solución que pasa por ese punto $(x, y)$.

Elemento lineal $l$ sobre un punto de la curva solución.

Por lo tanto, podemos construir en el plano $XY$ un conjunto de elementos lineales dados por el valor de la función razón en cada punto $(x, y)$. Veamos un ejemplo.

Ejemplo: Visualizar los elementos lineales de la ecuación diferencial

$$\dfrac{dy}{dx} = x -y$$

Solución: En este caso la función razón es

$$f(x, y) = x -y$$

$x$ y $y$ pueden tomar cualquier valor en $ \mathbb{R}$. En la siguiente tabla tenemos algunos valores para $x$ y $y$. En la primera fila tenemos los valores de $x$ en el intervalo $(-4, 4)$ en pasos de una unidad, mientras que en la primer columna tenemos los valores de $y$ en el intervalo $(-4, 4)$ en pasos de una unidad, el resto de valores corresponde al valor de la función razón $f(x, y) = x -y$ evaluada en los valores correspondientes. Por ejemplo si $x = -2$ y $y = 4$, entonces

$$f(x, y) = x -y = -2 -4 = -6$$

tal como se indica en la tabla.

Algunos valores de la función $f(x, y) = x -y$.

Con ayuda de esta tabla podemos construir un conjunto de elementos lineales con pendiente según el valor de la función razón (recordemos que una recta de $45°$ tiene pendiente $m = 1$).

Elementos lineales de la ecuación diferencial $\dfrac{dy}{dx} = x -y$.

Aumentando el número de valores para $x$ y $y$ en los rangos $(-4, 4)$ se puede obtener un conjunto mayor de elementos lineales.

Conjunto mayor de elementos lineales de la ecuación diferencial $\dfrac{dy}{dx} = x -y$.

Es posible notar un patrón en esta última imagen. Anteriormente mencionamos que el valor de la función razón $f(x, y)$ es el valor de la pendiente de la recta tangente en un punto $(x, y)$ de la curva solución de la ecuación diferencial (\ref{1}), en este caso los elementos lineales corresponden a las rectas tangentes de las curvas solución de la ecuación diferencial

$$\dfrac{dy}{dx} = x -y$$

Es decir, los elementos lineales son tangentes a funciones $y(x)$ ¡que son solución de la ecuación diferencial!, basta trazar curvas a lo largo de los elementos lineales para hallar gráficamente las soluciones.

$4$ curvas solución de la ecuación diferencial $\dfrac{dy}{dx} = x -y$.

Ya vimos que una ecuación diferencial puede tener infinitas soluciones, o bien una familia de soluciones, en este caso, en la gráfica se muestran $4$ curvas solución correspondientes a $4$ soluciones $y = y(x)$ particulares, cada una se obtiene de distintas condiciones iniciales.

Lo importante que debemos rescatar es que, a pesar de no tener la forma explícita (o implícita) de la función solución $y = y(x)$, gráficamente ¡ya conocemos las posibles gráficas de las curvas solución de la ecuación diferencial dada!. También es importante notar que el signo de la pendiente nos dice si la curva es creciente o decreciente, esto debido al resultado de cálculo en donde si $\dfrac{dy}{dx} > 0$ o $\dfrac{dy}{dx} < 0$ para toda $x$ en un intervalo $\delta$, entonces la función derivable $y = y(x)$ es creciente o decreciente en $\delta$, respectivamente.

Como ejercicio moral verifica que la solución general de la ecuación diferencial dada es

$$y(x) = x -1 + \dfrac{c}{e^{x}}$$

Posteriormente usa un graficador de funciones y traza la gráfica de la solución general dándole valores arbitrarios a la constante $c$ y compara los resultados con los obtenidos en la imagen anterior.

De acuerdo a la imagen se puede notar que las $4$ curvas solución que se muestran corresponden a los valores iniciales

$$y(3) = -4 \hspace{1cm} y(-3) = 0, \hspace{1cm} y(1) = 2, \hspace{1cm} y \hspace{1cm} y(-2) = -4$$

$\square$

Las imágenes anteriores corresponden al campo de pendientes de la ecuación diferencial

$$\dfrac{dy}{dx} = x -y$$

Un campo de pendientes indica el flujo de las soluciones y facilita el trazo de cualquier solución particular, la dirección del campo indica el aspecto o forma de una familia de curvas solución de la ecuación diferencial dada, esto permite observar a simple vista aspectos cualitativos de la solución, por ejemplo regiones en el plano donde la solución presenta un comportamiento poco común.

En este contexto una curva solución también es llamada curva integral.

Método de las isóclinas

Ahora somos capaces de esbozar campos de pendientes de ecuaciones diferenciales de la forma (\ref{1}), sin embargo es un proceso muy tardado si se piensa hacer a mano ya que hay que ir evaluando punto a punto del plano para obtener el valor de la pendiente en dicho punto y así poder dibujar un elemento lineal, esto puede ser mucho más rápido si se utilizan programas computacionales que lo realicen.

Existe un método que nos permite dibujar elementos lineales de forma eficiente sin necesidad de ir evaluando punto a punto, este método es conocido como el método de las isóclinas.

En otras palabras, una isóclina es una curva de nivel de la función $f(x, y)$, es decir

$$f(x, y) = k \label{2} \tag{2}$$

donde $k$ es una constante arbitraria, si sustituimos (\ref{2}) en (\ref{1}), obtenemos

$$\dfrac{dy}{dx} = k \label{3} \tag{3}$$

Con esta ecuación vemos que en efecto para todas las soluciones $y = y(x)$ va a haber puntos donde la pendiente $\dfrac{dy}{dx}$ sera la misma, una constante.

Con este método sólo basta encontrar las isóclinas de una ecuación diferencial y sobre ellas dibujar elementos lineales que tengan la misma pendiente obteniendo así el campo de pendientes y por tanto las curvas solución. Para que quede más claro construyamos las isóclinas de la ecuación diferencial del ejemplo anterior.

Ejemplo: Hallar las isóclinas y el campo de pendientes de la ecuación diferencial

$$\dfrac{dy}{dx} = x -y$$

Solución: Comencemos por igualar la función razón a una constante.

$$\dfrac{dy}{dx} = x -y = k$$

Despejemos la función dependiente $y$ en términos de la variable independiente y la constante.

$$y = y(x) = x -k$$

Es claro que es la ecuación de una recta, para cada valor arbitrario de $k$ se obtiene una recta distinta, lo importante es que a lo largo de toda esa recta hay elementos lineales con la misma pendiente, sólo basta evaluar un punto de cada isóclina en la función razón y obtendremos el valor de la pendiente para toda la isóclina.

Isóclinas de la ecuación $\dfrac{dy}{dx} = x -y$.

En la imagen vemos que a lo largo de cada isóclina (en este caso rectas marcadas de verde) los elementos lineales tienen la misma pendiente recuperando así el campo de pendientes que habíamos obtenido anteriormente.

$\square$

Este método es muy útil si lo que queremos es esbozar un campo de pendientes a mano. Una vez obtenido el campo de pendientes procedemos a dibujar las curvas solución como lo hicimos con anterioridad.

Método de Euler

El análisis geométrico que acabamos de hacer está íntimamente relacionado con un método numérico fundamental para aproximar soluciones de una ecuación diferencial de la forma (\ref{1}) acompañada de una condición inicial, dicho método es conocido como método de Euler. Consideremos el problema con condición inicial

$$\dfrac{dy}{dx} = f(x, y), \hspace{1cm} y(x_{0}) = y_{0} \label{4} \tag{4}$$

Debido a que $f(x, y)$ es dada, entonces podemos trazar su campo de pendientes en el plano $XY$, esto nos permite colocarnos en el punto $(x_{0}, y_{0})$ y comenzar a dar pequeños pasos dictados por las tangentes de dicho campo.

Comenzamos por elegir un tamaño de paso $\Delta x$ pequeño de tal manera que la pendiente de la solución aproximada se actualice cada $\Delta x$ unidades de $x$, es decir, en cada paso nos movemos $\Delta x$ unidades a lo largo del eje $x$. El tamaño de $\Delta x$ determina la exactitud de la solución, así como el número de cálculos que son necesarios para obtener la aproximación.

Imaginemos que nos colocamos en el punto $(x_{0}, y_{0})$, el primer paso es hacia el punto $(x_{1}, y_{1})$, donde

$$x_{1} = x_{0} + \Delta x \label{5} \tag{5}$$

El punto $(x_{1}, y_{1})$ se encuentra sobre la línea que pasa por $(x_{0}, y_{0})$ y cuya pendiente esta dada por el campo de pendiente en dicho punto, o bien, por $f(x_{0}, y_{0})$. Una vez que estemos en $(x_{1}, y_{1})$ repetimos el procedimiento, damos nuevamente un paso cuyo tamaño a lo largo del eje $x$ es $\Delta x$ y cuya dirección esta determinada por el campo de pendientes en $(x_{1}, y_{1})$, esto nos permitirá llegar al punto $(x_{2}, y_{2})$, donde

$$x_{2} = x_{1} + \Delta x \label{6} \tag{6}$$

El punto $(x_{2}, y_{2})$ está sobre el segmento de línea que comienza en $(x_{1}, y_{1})$ y tiene pendiente $f(x_{1}, y_{1})$. Repetimos este procedimiento para llegar al punto $(x_{3}, y_{3})$, tal como se ilustra en la siguiente figura.

Gráfica de una solución y su aproximación usando el método de Euler.

En la figura vemos en verde la gráfica de una solución y en segmentos negros los pasos que el método de Euler establece para aproximarnos a la solución. Geométricamente, el método genera una secuencia de pequeños segmentos de línea que conectan $(x_{n}, y_{n})$ con $(x_{n + 1}, y_{n + 1})$. Notemos que en casa paso cometemos un error, si el tamaño de $\Delta x$ es suficiente pequeño, los errores no resultarán demasiado grandes conforme avanzamos y la gráfica resultante será cercana a la solución buscada.

Para llevar a cabo el método de Euler, necesitamos una fórmula que determine $(x_{n + 1}, y_{n + 1})$ a partir de $(x_{n}, y_{n})$. Al especificar el tamaño del paso $\Delta x$ determinamos que, de forma general

$$x_{n + 1} = x_{n} + \Delta x \label{7}, \tag{7}$$

Para obtener $y_{n + 1}$ a partir de $(x_{n}, y_{n})$ usamos la ecuación diferencial. La pendiente de la solución de la ecuación (\ref{1}) en el punto $(x_{n}, y_{n})$ es $f(x_{n}, y_{n})$, el punto $(x_{n + 1}, y_{n + 1})$ se determina suponiendo que éste se encuentra sobre la línea que pasa por $f(x_{n}, y_{n})$.

Podemos determinar $y_{n + 1}$ de la siguiente fórmula de pendiente.

$$\dfrac{y_{n + 1} -y_{n}}{x_{n + 1} -x_{n}} = f(x_{n}, y_{n}) \label{8}, \tag{8}$$

Usando (\ref{7}) se puede escribir lo siguiente:

\begin{align*}
\dfrac{y_{n + 1} -y_{n}}{\Delta x} &= f(x_{n}, y_{n}) \\
y_{n + 1} -y_{n} &= f(x_{n}, y_{n}) \Delta x
\end{align*}

Esto es

$$y_{n + 1} = y_{n} + f(x_{n}, y_{n}) \Delta x \label{9}, \tag{9}$$

Por lo tanto, dada la condición inicial $y(x_{0}) = y_{0}$ y el tamaño del paso $\Delta x$, el punto $(x_{n + 1}, y_{n + 1})$ se determina a partir del punto precedente $(x_{n}, y_{n})$ usando la ecuación diferencial para determinar valor de la pendiente $f(x_{n}, y_{n})$ y utilizando las ecuaciones (\ref{7}) y (\ref{9}).

Ejemplo: Determinar una aproximación de la solución del siguiente PVI:

$$\dfrac{dy}{dx} = x -y, \hspace{1cm} y(1) = -1$$

Solución: Ya conocemos el campo de pendientes de la ecuación diferencial $\dfrac{dy}{dx} = x -y$. En este caso buscamos una aproximación a la solución particular que pasa por el punto $(x_{0}, y_{0}) = (1, -1)$. Para usar el método de Euler, propongamos un paso de unidad 1, es decir, $\Delta x = 1$. La función razón es

$$f(x, y) = x -y$$

Entonces,

$$f(x_{0}, y_{0}) = f(1, -1) = 1 -(-1) = 2$$

Sustituyamos en las ecuaciones (\ref{7}) y (\ref{9}):

\begin{align*}
x_{1} &= x_{0} + \Delta x = 1 + 1 = 2 \\
y_{1} &= y_{0} + f(x_{0}, y_{0}) \Delta x = -1 + 2(1) = 1
\end{align*}

Por lo tanto, $(x_{1}, y_{1}) = (2, 1)$. Ahora vemos que

$$f(x_{1}, y_{1}) = f(2, 1) = 2 -1 = 1$$

Nuevamente aplicamos (\ref{7}) y (\ref{9}):

\begin{align*}
x_{2} &= 2 + 1 = 3 \\
y_{2} &= 1 + 1(1) = 2
\end{align*}

Por lo tanto, $(x_{2}, y_{2}) = (3, 2)$. Continuando verificamos que $f(3, 2) = 3 -2 = 1$, entonces

\begin{align*}
x_{3} &= 3 + 1 = 4 \\
y_{3} &= 2 + 1(1) = 3
\end{align*}

El nuevo punto obtenido es $(x_{3}, y_{3}) = (4, 3)$. Uno más, $f(4, 3) = 4 -3 = 1$.

\begin{align*}
x_{4} &= 4 + 1 = 5 \\
y_{4} &= 3 + 1(1) = 4
\end{align*}

Así, $(x_{4}, y_{4}) = (5, 4)$.

Este proceso se sigue indefinidamente hasta hallar una gráfica aproximada de la solución buscada. En la siguiente figura se muestra la curva solución y los pasos obtenidos usando el método de Euler.

Aproximación de la curva solución.

$\square$

Dos casos especiales

Hemos trabajado con la ecuación diferencial

$$\dfrac{dy}{dx} = f(x, y(x))$$

Es posible que ocurra que la función razón sólo dependa de la variable dependiente $y(x)$, o sólo de la variable independiente $x$, es decir, tener las ecuaciones diferenciales

$$\dfrac{dy}{dx} = f(y) \label{10} \tag{10}$$

o

$$\dfrac{dy}{dx} = f(x) \label{11} \tag{11}$$

Más adelante veremos que estas ecuaciones son más fácil de resolver analíticamente debido a que son lo que se conoce como ecuaciones separables, pero por ahora vamos a hacer un análisis cualitativo como lo hemos estado haciendo en esta entrada.

Campo de pendientes para $\dfrac{dy}{dx} = f(x)$

El hecho de tener la ecuación diferencial

$$\dfrac{dy}{dx} = f(x)$$

en su forma normal nos permite reconocer que la pendiente de un elemento lineal en cualquier punto es la misma que la de cualquier otro punto con la misma coordenada $x$.

Campo de pendientes de la ecuación diferencial $\dfrac{dy}{dx} = x$.

En la imagen tenemos como ejemplo el campo de pendientes de la ecuación diferencial

$$\dfrac{dy}{dx} = f(x) = x$$

La curva verde representa una curva solución y notamos que a lo largo de las líneas verticales (líneas rojas) todos los elementos lineales tienen la misma pendiente.

Geométricamente podemos decir que en un campo de pendientes si los elementos lineales sobre cada línea vertical del dominio en consideración son paralelos, entonces la ecuación diferencial correspondiente es de la forma (\ref{10}).

Campo de pendientes para $\dfrac{dy}{dx} = f(y)$

En el caso en el que la función razón sólo depende de la variable dependiente $y$ los elementos lineales de un campo de pendientes van a tener la misma pendiente en dos puntos diferentes con la misma coordenada $y$, es decir, el campo de pendientes es paralelo a lo largo de cada línea horizontal.

Campo de pendientes de la ecuación $\dfrac{dy}{dx} = y$.

En la imagen tenemos como ejemplo el campo de pendientes de la ecuación diferencial

$$\dfrac{dy}{dx} = f(y) = y$$

Las curvas verdes corresponden a soluciones de la ecuación, mientras que las líneas rojas sólo intentan hacer notar que las pendientes de los elementos lineales para un valor de $y$ son las mismas.

Hasta aquí concluimos la entrada, en la siguiente continuaremos explorando más sobre la teoría cualitativa de este tipo de ecuaciones diferenciales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Esbozar el campo de pendientes de las siguientes ecuaciones diferenciales. Hacerlo a mano en una hoja de papel usando el método de las isóclinas y posteriormente verifica tu resultado usando algún programa computacional. Una vez construido el campo de pendientes trazar tres curva solución aproximadas, donde cada una pase por cada uno de los puntos indicados.
  • $\dfrac{dy}{dx} = 1-y$ $\hspace{2cm}$ Puntos: $(0, 3)$, $\hspace{0.5cm}$ $(-2, -1)$, $\hspace{0.5cm}$ $(0, 1)$.
  • $\dfrac{dy}{dx} = x^{2} -y -2$ $\hspace{1cm}$ Puntos: $(-1, 1)$, $\hspace{0.5cm}$ $(4, 0)$, $\hspace{0.5cm}$ $(0, -2)$.
  • $\dfrac{dy}{dx} = xy$ $\hspace{2.5cm}$ Puntos: $(0,1)$, $\hspace{0.5cm}$ $(1, -2)$, $\hspace{0.5cm}$ $(-3, 2)$.
  1. Considerando el ejercicio anterior, en cada ecuación diferencial dada elegir una condición inicial y usando el método de Euler determinar una solución aproximada. Se recomienda calcular al menos 5 puntos.
  1. Dados los siguientes campos de pendientes, determinar la opción qué indica la ecuación diferencial que corresponde al campo de pendientes. Justificar la respuesta.
Campo de pendientes.
  • a) $\dfrac{dy}{dx} = \sin(x) + \cos(x)$; $\hspace{0.7cm}$ b) $\dfrac{dy}{dx} = \sin(x) \cos(x)$; $\hspace{0.7cm}$ c) $\dfrac{dy}{dx} = 2\sin(x)$
Campo de pendientes.
  • a) $\dfrac{dy}{dx} = x^{2} + y^{2}$; $\hspace{0.7cm}$ b) $\dfrac{dy}{dx} = 5y^{2}$; $\hspace{0.7cm}$ c) $\dfrac{dy}{dx} = x^{2} -y^{2}$

Más adelante…

En la siguiente entrada continuaremos con las descripciones cualitativas de las soluciones de una ecuación diferencial, en particular estudiaremos con mayor detalle las ecuaciones de la forma

$$\dfrac{dy}{dx} = f(y)$$

llamadas ecuaciones diferenciales autónomas.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Campo de pendientes asociado a una ecuación diferencial, curvas integrales y método de las isoclinas

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Hola, bienvenidos a una nueva entrada del curso de Ecuaciones Diferenciales I. En la entrada anterior definimos a las soluciones de una ecuación diferencial ordinaria. Así que ahora veremos un poco de la geometría de soluciones a ecuaciones diferenciales de primer orden, en particular de la forma \begin{align*}\frac{dy}{dt}=f(t,y(t)).\end{align*}

Comenzaremos asociando un campo de pendientes a una ecuación diferencial, definiremos posteriormente el concepto de curvas integrales, y estudiaremos la relación que existe con las soluciones a la ecuación asociada.

Posteriormente revisaremos el método de las isoclinas el cual sirve para encontrar y dibujar las soluciones a una ecuación diferencial usando las curvas de nivel de $\frac{dy}{dt}=f(t,y(t))$, vista como una función $f:\mathbb{R}^{2} \rightarrow \mathbb{R}$.

Manos a la obra!

Campo de pendientes asociado a una ecuación diferencial y relación con sus soluciones

En el primer video, vemos cómo asociar un campo de pendientes a una ecuación de la forma $\frac{dy}{dt}=f(t,y(t))$ y revisamos un par de ejemplos.

Una vez que asociamos un campo de pendientes, en los siguientes dos videos definimos a las curvas integrales y estudiamos la relación que guardan con las soluciones a la ecuación diferencial.

Método de las isoclinas

Estudiamos un método bastante sencillo, llamado de las isoclinas, para conocer el comportamiento de las soluciones a una ecuación diferencial, mediante las curvas de nivel de la función $f:\mathbb{R}^{2} \rightarrow \mathbb{R}$ que define a la ecuación y el campo de pendientes asociado que definimos en los videos de la sección anterior.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Esboza el campo de pendientes asociado a la ecuación $\frac{dy}{dt}=y$.
  • Dibuja las curvas integrales del campo de pendientes asociado a la ecuación $\frac{dy}{dt}=y$.
  • Prueba que si $\phi: (a,b) \rightarrow \mathbb{R}$ es una curva integral del campo de pendientes asociado a la ecuación $\frac{dy}{dt}=f(t,y(t))$ entonces $\phi(t)$ es solución a la ecuación diferencial.
  • Esboza las soluciones de la ecuación $\frac{dy}{dt}=-\frac{t}{y}$, con base en la información obtenida en el segundo ejemplo del último video. Analiza qué sucede con los puntos sobre el eje $t$, ¿forman parte de alguna solución a la ecuación?
  • En el último video hablamos acerca de las ventajas del método de las isoclinas. ¿Cuáles son las desventajas de usar este método para encontrar las soluciones a una ecuación?
  • Utiliza el método de las isoclinas para encontrar las soluciones a la ecuación $\frac{dy}{dt}=\frac{y}{t}$.

Más adelante

En la próxima entrada continuaremos analizando soluciones de una ecuación diferencial de primer orden desde un punto de vista geométrico. En esta ocasión nos enfocaremos en el caso particular de las ecuaciones del tipo $\frac{dy}{dt}=f(y)$.

Para esto analizaremos los puntos de equilibrio de la función $f(y)$ y haremos un diagrama bastante sencillo de dibujar que nos servirá para hacer un esbozo de las soluciones a la ecuación.

Nos vemos en la próxima ocasión.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»