Archivo de la etiqueta: Cálculo I

Cálculo Diferencial e Integral I: Diferenciales

Por Karen González Cárdenas

Introducción

Vimos que una forma de expresar a la derivada de una función $y = f (x)$ es utilizando la notación:
$\frac{d y}{d x} = f^{'} (x)$

Recordemos que $\frac{d y}{d x}$ es un «símbolo» que utilizamos para denotar el límite:
$lim_{Δ x \to 0} \frac{Δ y}{Δ x} .$
Por lo tanto, no consideremos a $\frac{d y}{d x}$ como una fracción donde su numerador es $d y$ y su denominador $d x$ . No obstante, en diversos problemas de aplicaciones del Cálculo es necesario dar interpretaciones separadas a $d x$ y $d y$ . En esta entrada, veremos cuál es la interpretación de estos nuevos «símbolos» y cómo su aplicación nos resulta útil.

Definición de la diferencial de una función

Definición (Diferencial): Si tenemos una función $f$ derivable. Definimos a la diferencial de $f$ como el producto de su derivada por la diferencial de la variable independiente $x$ .
$d f (x) = f^{'} (x) d x .$

Para simplificar un poco la notación consideremos $y = f (x)$ y nos quedamos con:
$d y = f^{'} (x) d x .$

A continuación, veremos algunos ejemplos donde se nos pide hallar la diferencial de una función haciendo uso de la definición revisada.

Algunos ejemplos de funciones y su diferencial

Obtén la diferencial de las siguientes funciones:

$y = x^{3} - 3 x$
$ρ = \sin (a θ)$
$t = \frac{x}{a} + \frac{a}{x}$
$s = θ c o s (θ)$
$y = \log (\sin (x))$
$γ = e^{t} c o s (π t)$

Solución: Aplicaremos la definición siguiente en cada uno de los incisos
$d y = f^{'} (x) d x .$

Para la función $y = x^{3} - 3 x$ tenemos:
$\begin{aligned} d y & = (x^{3} - 3 x)^{'} d x \\ = (3 x^{2} - 3) d x \end{aligned}$
Por lo que la diferencial es $d y = (3 x^{2} - 3) d x$ .
Ahora para la función $ρ = \sin (a θ)$ :
$\begin{aligned} d ρ & = (\sin (a θ))^{'} d θ \\ = a \cos (a θ) d θ \end{aligned}$
Concluimos que $d ρ = a \cos (a θ) d θ$ .
Aplicando la definición con $t = \frac{x}{a} + \frac{a}{x}$ :
$\begin{aligned} d t & = {(\frac{x}{a} + \frac{a}{x})}^{'} d x \\ = {(\frac{x}{a} + a x^{- 1})}^{'} d x \\ = (\frac{1}{a} - a x^{- 2}) d x \\ = (\frac{1}{a} - \frac{a}{x^{2}}) d x \end{aligned}$
Por lo tanto $d t = (\frac{1}{a} - \frac{a}{x^{2}}) d x$ .
Del mismo modo para $s = θ c o s (θ)$ :
$\begin{aligned} d s & = (θ \cos (θ))^{'} d θ \\ = (\cos (θ) - θ \sin (θ)) d θ \end{aligned}$
Así $d s = (\cos (θ) - θ \sin (θ)) d θ$ .
Y si consideramos $y = \log (\sin (x))$ :
$\begin{aligned} d y & = (\log (\sin (x)))^{'} d x \\ = \frac{1}{\sin (x)} \cdot \cos (x) d x \\ = \frac{\cos (x)}{\sin (x)} d x \\ = c t g (x) d x \end{aligned}$
Por lo que $d y = c t g (x) d x$ .
Finalmente para $γ = e^{t} c o s (π t)$ :
$\begin{aligned} d γ & = (e^{t} \cos (π t))^{'} d t \\ = (e^{t} \cos (π t) - e^{t} \sin (π t)) d t \end{aligned}$
Concluyendo $d γ = (e^{t} \cos (π t) - e^{t} \sin (π t)) d t$ .

A continuación, veremos una interpretación geométrica de la diferencial que más adelante nos permitirá revisar algunos problemas de aplicación.

Una interpretación de la diferencial

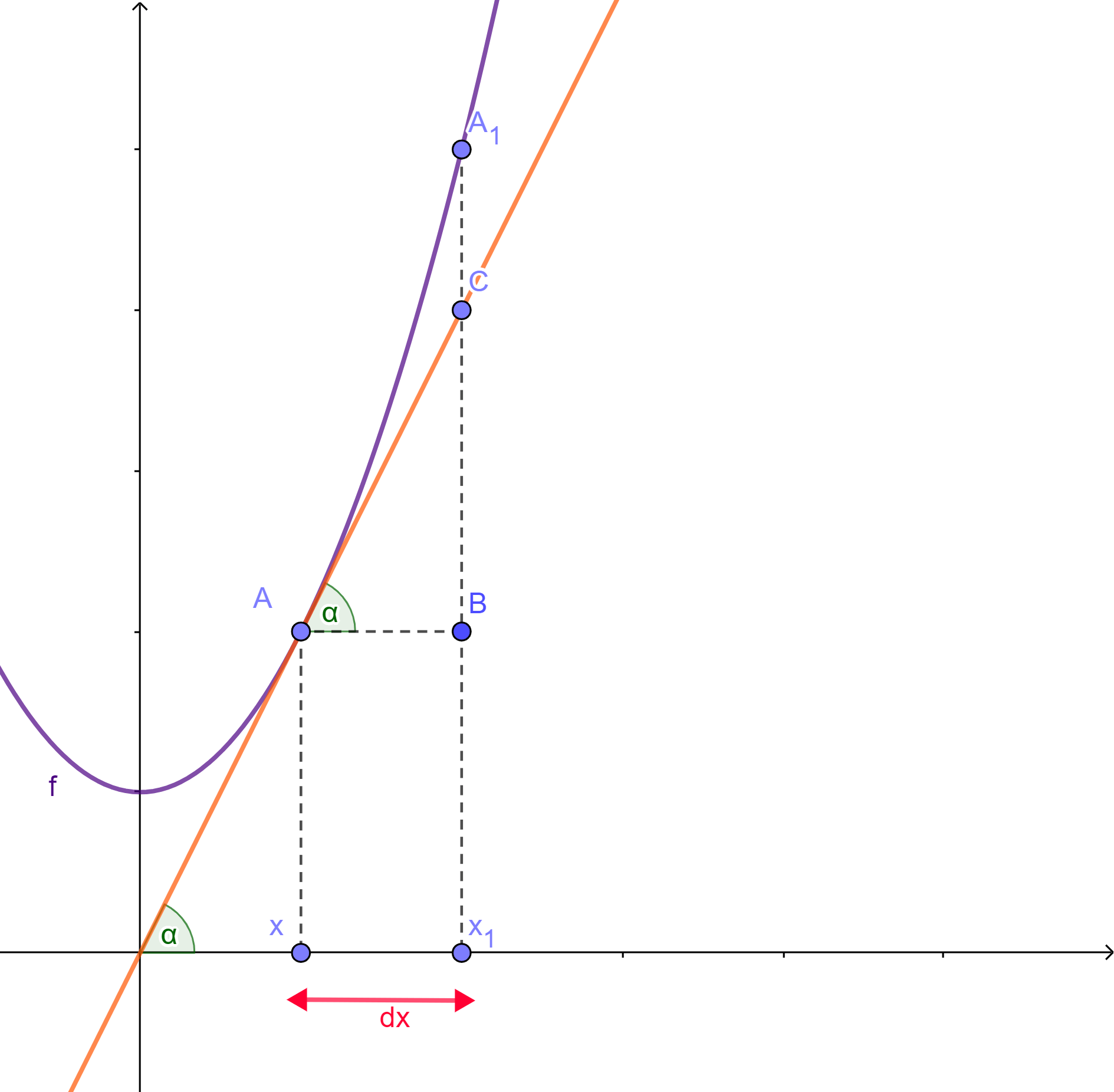
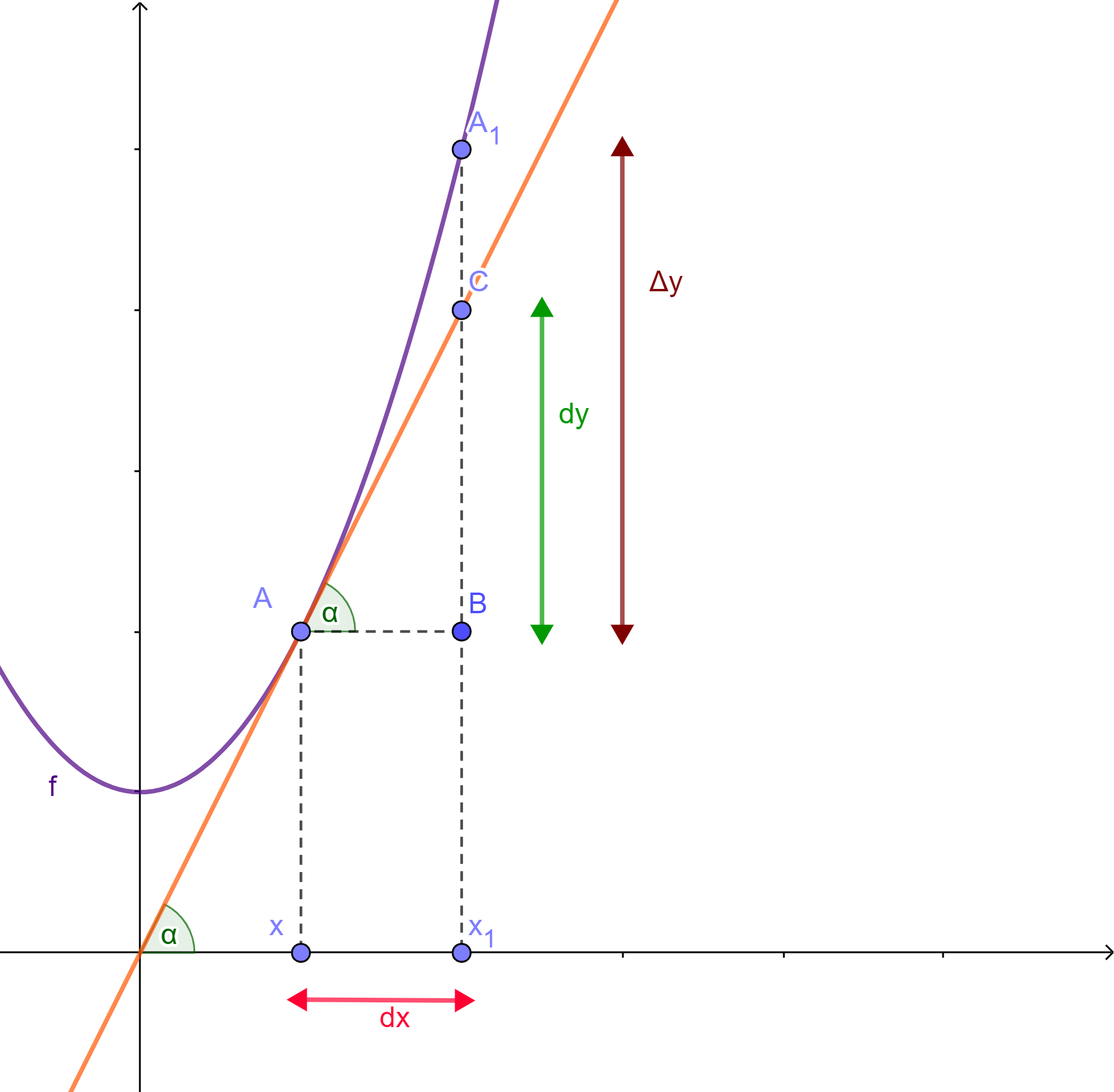
Tomemos la función $y = f (x)$ y al punto $A$ sobre la gráfica de $f$ . Consideremos a $f^{'} (x)$ como el valor de la derivada en $A$ y tracemos la recta tangente en dicho punto.

Nombremos al segmento $A B$ como $d x$ . Recordemos que la definición de la diferencial es:
$d y = f^{'} (x) d x .$

Por lo visto en la primera entrada de esta unidad sabemos que:
$f^{'} (x) = \tan (α) .$

Además, aplicando la definición de la función tangente apoyándonos en el gráfico siguiente, se tiene:
$\begin{aligned} \tan (α) & = \frac{c o}{c a} \\ (*) & = \frac{C B}{A B} \end{aligned}$

Cuando sustituimos $(*)$ y $d x = A B$ obtenemos lo siguiente:
$\begin{aligned} d y & = (\frac{C B}{A B}) (A B) \\ = (\frac{C B}{A B}) (A B) \\ = C B \end{aligned}$
Observamos que $d y$ nos brinda una aproximación al incremento $Δ y$ que está dado por el segmento $A_{1} B$ , cuando $d x$ es pequeña.

Es decir:
$d y \approx Δ y .$

Utilizaremos esta cualidad cuando necesitemos hallar un valor aproximado del incremento de una función. En las siguientes secciones, revisaremos un par de problemas donde haremos uso de la diferencial para resolverlos.

Problema 1

Obtener el incremento del área de un cuadrado de lado $8 m$ al aumentar el lado $5 m m$ .
Para resolver este problema veremos dos métodos de solución, en el primero no usaremos la diferencial y en el segundo si la utilizaremos.

Solución sin usar la diferencial

Sabemos del problema que:
$\begin{aligned} I & = 8 m & Δ l & = 5 m m \\ A & = 64 m^{2} & l_{0} & = 8.005 m \end{aligned}$
Por lo que el área del nuevo cuadrado con el lado $l_{0}$ sería:
$\begin{aligned} A_{0} & = (8.005 m)^{2} \\ = 64.080025 m^{2} \end{aligned}$

Obtenemos el incremento del área $Δ A$ haciendo la resta del área original con el área del nuevo cuadrado.
$\begin{aligned} Δ A & = 64.080025 m^{2} - 64 m^{2} \\ = 0.080025 m^{2} \end{aligned}$

$∴ Δ A = 0.080025 m^{2} .$

Solución utilizando la diferencial

Si tomamos a $l$ como el lado del cuadrado tenemos que su área es:
$A = l^{2} .$
Como sabemos que $d A \approx Δ A$ usando la definición para la diferencial de $a$ tendríamos:
$\begin{aligned} d A & = 2 l d l \\ = 2 (8) (0.005) \\ = 0.08 \end{aligned}$
Por lo tanto tenemos que el incremento obtenido es:
$Δ A \approx 0.08 m^{2} .$

Notamos que es una buena aproximación al incremento obtenido en el método anterior. Sin embargo, al haber utilizado la diferencial, el problema nos resultó un poco más sencillo de resolver.

Problema 2

Si sabemos que $\sqrt{25} = 5$ , obtén una aproximación al valor $\sqrt{27}$ .
Solución:
Consideraremos la función $y = \sqrt{x}$ . Del problema podemos ver que el incremento de $x$ es:
$Δ x = 27 - 25 = 2$

Ahora obtengamos la diferencial de $y$ :
$d y = \frac{d y}{2 \sqrt{x}} (* *)$

Nosotros consideraremos a $x = 25$ y como una aproximación al diferencial de $x$ al incremento $Δ x = 2$ . Entonces ocurre que al sustituir todo en $(* *)$ tenemos:
$\begin{aligned} d y & = \frac{2}{2 \sqrt{25}} \\ = \frac{2}{(2) (5)} \\ = \frac{1}{5} \\ = 0.2 \end{aligned}$
Concluimos así que una aproximación al valor de $\sqrt{27}$ es:
$\begin{aligned} \sqrt{27} & \approx 5 + 0.2 \\ \approx 5.2 \end{aligned}$
$∴ \sqrt{27} \approx 5.2$
Si comparamos esta aproximación con el valor que nos brinda una calculadora $\sqrt{27} = 5.1961$ considerando sólo cuatro decimales) podemos notar que es bastante similar.

En la siguiente sección encontrarás ejercicios que podrás realizar para aplicar lo estudiado en esta entrada.

Más adelante

¡Te felicitamos por concluir con el curso de Cálculo Diferencial e Integral I! Con este tema cerramos el temario. Esperamos que hayas disfrutado este viaje por el mundo del Cálculo. Te invitamos a continuar con tu estudio ahora con el curso de Cálculo Diferencial e Integral II que se encuentra disponible en la siguiente página.

Tarea moral

Demuestra usando la definición, las siguientes reglas para las diferenciales:
- $d (s + t) = d s + d t$
- Con $c$ una constante:
  $d (c u) = c \cdot d u$
- $d (s t) = s d t + t d s$
Hallar la diferencial de las siguientes funciones:
- $y = \sqrt{1 - 4 x}$
- $t = \sin 2 s$
- $u = \log c v$
Sabiendo que $\sqrt{16} = 4$ utilizando la diferencial obtén una aproximación de $\sqrt{17}$ .
Utilizando la diferencial da una aproximación del incremento del volumen de un cubo con $l = 3 m$ al aumentar el lado $0.002 m$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Aplicaciones en economía.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Aplicaciones en economía

Por Karen González Cárdenas

Deja un comentario

Introducción

Imaginemos que una empresa refresquera produce $x$ botellas de bebida hidratante en total y que $a$ es el precio de venta de cada una de ellas. Si nos pidieran obtener el ingreso bastaría considerar el producto:
$a x .$
Por lo que la función de ingreso para $x$ número de unidades producidas está definida como:
$I (x) = a x .$

Ahora si consideramos que el precio de venta al público tiene una dependencia lineal con las unidades producidas. Es decir, si tomamos $a = b x + c$ una recta, tenemos que la función de ingreso $I_{1} (x)$ es:
$\begin{aligned} I_{1} (x) & = (b x + c) x \\ = b x^{2} + c x \end{aligned}$

Observamos así que la función $I_{1} (x)$ es una parábola.

Si la empresa refresquera sabe que el costo por producir $x$ botellas de bebida hidratante está dado por la función $C (x)$ , la función que nos daría el costo medio de cada botella es:

$C_{m} (x) = \frac{C (x)}{x}, con x > 0.$

Además si queremos obtener la función que nos daría su utilidad, bastaría con restarle a los ingresos los costos de producción:
$U (x) = I (x) - C (x), con x \geq 0.$

Ya que hemos visto una idea general de las funciones que utilizaremos para resolver los problemas de carácter económico de esta entrada. Comencemos con ejemplos donde se nos pide realizar la optimización de dichas funciones, para concluir revisando los conceptos: Costo marginal, Ingreso marginal y Utilidad marginal.

Problema 1

Una pequeña compañía de alimentos conoce que las funciones de ingreso y costo (en pesos) de su famosa mermelada son:
$\begin{aligned} I (x) & = - 4 x^{2} + 400 x & C (x) & = x^{2} + 20 x + 12 \end{aligned}$
Donde $x$ representa los frascos fabricados.

Te solicitan encontrar:

El costo fijo de producción.
El ingreso máximo.
La máxima utilidad.
El costo medio de cada frasco.

Solución:

$1.$ El costo fijo de producción

Ya que el costo fijo de producción es aquel que permanece constante sin importar del volumen de producción, para obtenerlo bastará con evaluar la función $C (x)$ cuando no se produce ningún frasco, es decir, cuando $x = 0$ :
$\begin{aligned} C (0) & = 0^{2} + 20 (0) + 12 \\ = 12 \end{aligned}$
Por lo que el costo fijo de producción para esta mermelada es de $12$ pesos.

$2.$ El ingreso máximo

Como nos están solicitando encontrar el ingreso máximo, aplicaremos el análisis para hallar el máximo de la función $I (x)$ apoyándonos del Criterio de la segunda derivada. Comenzamos obteniendo la primera derivada e igualando a cero para obtener los puntos críticos:
$I^{'} (x) = - 8 x + 400.$
$\begin{aligned} I^{'} (x) = 0 & \Leftrightarrow 8 x = 400 \\ \Leftrightarrow x = \frac{400}{8} \\ \Leftrightarrow x = 50 \end{aligned}$
Queremos ver que $x = 50$ , al obtener la segunda derivada notamos que:
$\begin{matrix} (que es menor que 0) & I^{''} (x) = - 8 \end{matrix}$
Concluyendo así que cuando $x = 50$ la función $I$ tiene un máximo y que el ingreso máximo de esta mermelada se obtiene al sustituir dicho valor:
$\begin{aligned} I (50) & = - 4 (50)^{2} + 400 (50) \\ = - 10000 + 20000 \\ = 10000 \end{aligned}$
Por lo que es de $10, 000$ pesos.

$3.$ La máxima utilidad

Primero necesitamos definir a la función de la utilidad, para ello usaremos la igualdad siguiente sustituyendo la función del ingreso y la del costo:
$\begin{aligned} U (x) & = I (x) - C (x) \\ = - 4 x^{2} + 400 - x^{2} - 20 x - 12 \\ = - 5 x^{2} + 388 x - 12 \\ ∴ U (x) & = 5 x^{2} + 388 x - 12 . \end{aligned}$

Derivamos la función $U$ :
$U^{'} (x) = - 10 x + 388.$
La igualamos a cero y obtenemos los puntos críticos:
$\begin{aligned} - 10 x + 388 = 0 & \Leftrightarrow 388 = 10 x \\ \Leftrightarrow x = \frac{388}{10} \end{aligned}$
Al volver a derivar la función vemos que:
$\begin{matrix} (que es negativo) & U^{''} (x) = - 10 \end{matrix}$
por lo que aplicando el Criterio de la segunda derivada nos indica que $U$ tiene un máximo cuando $x = \frac{388}{10}$ .

Sustituimos el valor para $x$ obtenido en la función:
$\begin{aligned} U (\frac{388}{10}) & = - 5 {(\frac{388}{10})}^{2} + 388 (\frac{388}{10}) - 12 \\ \approx 7515.2 \end{aligned}$
Concluyendo así que la utilidad máxima es de $7, 515.2$ pesos.

$4.$ El costo medio de cada frasco

Obtengamos la función de costo medio:
$\begin{aligned} C_{m} (x) & = \frac{C (x)}{x} \\ = \frac{x^{2} + 20 x + 12}{x} \\ ∴ C_{m} (x) & = x + 20 + \frac{12}{x} . \end{aligned}$
Del mismo modo que en los incisos anteriores, debemos derivar la función:
$C_{m}^{'} (x) = 1 - \frac{12}{x^{2}} .$
Y analizar los valores que obtengamos al igualar la derivada a cero:
$\begin{aligned} C_{m} (x) = 0 & \Leftrightarrow 1 = \frac{12}{x^{2}} \\ \Leftrightarrow \frac{1}{12} = \frac{1}{x^{2}} \\ \Leftrightarrow 12 = x^{2} \\ ∴ x = \sqrt{12} . \end{aligned}$
Queremos ver que el valor $x = \sqrt{12}$ es un mínimo para la función del costo medio, aplicando el criterio:
$C_{m}^{''} (x) = \frac{24}{x^{3}} .$
Debido a que $C_{m} (\sqrt{12}) > 0$ confirmamos que se trata de un mínimo. Finalmente sustituimos:
$\begin{aligned} C_{m} (\sqrt{12}) & = \sqrt{12} + 20 + \frac{12}{\sqrt{12}} \\ \approx 26.92 \end{aligned}$

En resumen, el costo medio de cada frasco es de $26.92$ pesos.

Hablemos del costo marginal

Recordemos un poco lo visto en la entrada Razón de cambio aplicándolo ahora a la función del costo $C (x)$ . Imaginemos que la compañía decide aumentar el número de artículos producidos de $x_{1}$ a $x_{2}$ , por lo que el costo tendría un incremento de $C (x_{1})$ a $C (x_{2})$ . Con lo anterior, la razón de cambio del costo quedaría:
$\begin{aligned} \frac{Δ C}{Δ x} & = \frac{C (x_{2}) - C (x_{1})}{x_{2} - x_{1}} . \end{aligned}$

Cabe aclarar que escribimos $Δ x = x_{2} - x_{1}$ para referimos al «incremento de $x$ ».

Observación: Como sabemos que $x_{1} < x_{2}$ , una forma de reescribir a $x_{2}$ haciendo uso de la notación anterior sería:
$x_{2} = x_{1} + Δ x .$

Por lo que concluimos que:
$\begin{aligned} \frac{Δ C}{Δ x} & = \frac{C (x_{1} + Δ x) - C (x_{1})}{Δ x} . \end{aligned}$

Si consideramos el límite cuando el incremento $Δ x \to 0$ , es decir,
$lim_{Δ x \to 0} \frac{C (x_{1} + Δ x) - C (x_{1})}{Δ x} .$

vemos que es justo la derivada de la función $C (x)$ por definición. En Economía a dicha derivada $C^{'} (x)$ se le conoce como Costo marginal.

Una relación entre el Costo promedio y el Costo marginal

Ya vimos que la función de costo promedio está dada por:
$C_{m} (x) = \frac{C (x)}{x} .$
¿Qué pasaría si decidimos hallar el mínimo de $C_{m} (x)$ ? Aplicando las reglas de derivación correspondientes tenemos:
$C_{m}^{'} (x) = \frac{x C^{'} (x) - C (x)}{x^{2}} .$

Procedemos a igualar la derivada a cero:
$\begin{aligned} C_{m}^{'} (x) = 0 & \Leftrightarrow \frac{x C^{'} (x) - C (x)}{x^{2}} = 0 \\ \Leftrightarrow x C^{'} (x) - C (x) = 0 \\ \Leftrightarrow x C^{'} (x) = C (x) \\ \Leftrightarrow C^{'} (x) = \frac{C (x)}{x} \end{aligned}$

Por lo que vemos que el costo marginal es igual al costo promedio siempre que verifiquemos que $x$ es un mínimo de $C_{m}$ . Esta relación es quizás una de las más interesantes, revisemos como utilizarla en el siguiente problema.

Problema 2

Una franquicia de panaderías conoce que la función de costo por elaborar $x$ donas es:
$C (x) = \frac{x^{2}}{500} + 2 x + 3000.$

Se requiere obtener el nivel de producción para el cual el costo promedio es el más bajo.

Solución:
Como ya vimos, si queremos minimizar el costo promedio basta con igualarlo al costo marginal y verificar que el valor $x$ obtenido es un mínimo. Para ello procedemos con:
$\begin{aligned} C^{'} (x) & = \frac{x}{250} + 2 & C_{m} (x) & = \frac{x}{500} + 2 + \frac{3000}{x} \end{aligned}$

Igualando las funciones:
$\begin{aligned} C^{'} (x) = C m_{(} x) & \Rightarrow \frac{x}{250} + 2 = \frac{x}{500} + 2 + \frac{3000}{x} \\ \Rightarrow \frac{x}{250} = \frac{x}{500} + \frac{3000}{x} \\ \Rightarrow \frac{x}{500} = \frac{3000}{x} \\ \Rightarrow \frac{x^{2}}{500} = 3000 \\ \Rightarrow x^{2} = \frac{3000}{\frac{1}{500}} \\ \Rightarrow x = \sqrt{1500000} \\ ∴ x \approx 1224.7448 \end{aligned}$

Verifiquemos que $x = 1224.7448$ es un mínimo observando la segunda derivada de $C_{m} (x)$ :
$C_{m}^{'} (x) = \frac{1}{500} - \frac{3000}{x^{2}} \Rightarrow C_{m}^{''} (x) = \frac{6000}{x^{3}}$

Al evaluarla vemos que cumple ser mayor que cero $C_{m} (1224.7448) > 0$ , que sabemos nos indica que se trata de un mínimo. Por lo tanto, el nivel buscado es el de producir $1, 225$ donas con costo medio de $C_{m} (1225) = 6.89$ por pieza.

Análogamente…

Si realizamos un desarrollo similar al revisado en la sección anterior para el costo $C (x)$ aplicado ahora a las funciones de ingreso $I$ y de utilidad $U$ , tenemos que las derivadas de ellas son conocidas en Economía como:

Ingreso marginal
$I^{'} (x)$
Utilidad marginal
$U^{'} (x)$

En los ejercicios de Tarea moral se proponen algunos ejercicios donde podrás aplicar estos conceptos, al igual que los revisados durante toda la sesión.

Más adelante

Ya que hemos concluido de revisar algunas aplicaciones de la derivada relacionadas ahora en el ámbito de la Economía, en la siguiente entrada estudiaremos el último tema de nuestro temario para Cálculo Diferencial e Integral I: las diferenciales.

Tarea moral

Dadas las funciones de ingreso y costo siguientes:
$\begin{aligned} I (x) & = - x^{2} + 170 & C (x) & = \frac{3}{2} x^{2} + 300 \end{aligned}$
Obtén lo siguiente:
- El costo fijo de producción.
- El ingreso máximo.
- La máxima utilidad.
- El costo medio de cada frasco.
Con el planteamiento del Problema 1. Determina cuando se producen $20$ frascos de mermelada:
- El ingreso y el ingreso marginal.
- La utilidad y su utilidad marginal.

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2).
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Diferenciales.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

En la entrada anterior vimos que el polinomio de Taylor para una función $f$ que se puede derivar $n$ veces en $x = a$ , es:
$T_{a, n} = \sum_{j = 0}^{n} \frac{f^{(j)} (a)}{j!} (x - a)^{j} .$

Además vimos que cumplía con la siguiente igualdad:
$lim_{x \to a} \frac{f (x) - T_{a, n} (x)}{(x - a)^{n}} = 0$

que nos indicaba que el polinomio de Taylor es una buena aproximación de la función $f$ .

Pero, ¿qué podemos decir de la diferencia $f (x) - T_{a, n} (x)$ ? ¿Cuáles son las propiedades que cumple?

A lo largo de esta entrada veremos que dicha diferencia es llamada Residuo de Taylor y que existen un par de formas de escribirlo. También veremos un ejemplo donde se nos pedirá estimar dicho residuo dependiendo del polinomio de Taylor considerado.

Definición del Residuo de Taylor

Retomando uno de los ejemplos anteriores:

En esta imagen vemos que el polinomio de Taylor $T_{2, 0}$ se parece mucho a la función $f$ cuando $a = 0$ , sin embargo, sigue existiendo una diferencia o «error» ya que el polinomio y $f$ no son «idénticas». A dicho error se le conoce formalmente como Residuo de Taylor, veamos su definición:

Definición (Residuo de Taylor): Consideremos una función $f : [x_{0}, y_{0}] \to R$ de clase $C^{(n)}$ . Definiremos al Residuo de Taylor de grado $n$ con centro en $a$ como:
$R_{n, a} : [x_{0}, y_{0}] \to R$
$R_{n, a} (x) = f (x) - T_{n, a} (x) .$

Nota: Recordemos que una función es de clase $C^{(n)}$ si es $n$ veces derivable y sus $n$ derivadas son continuas.

Vemos que de la definición anterior tenemos que al realizar una aproximación usando polinomios de Taylor para una función $f$ se da la siguiente igualdad :
$f (x) = T_{n, a} (x) + R_{n, a} (x) .$

Y además si sustituimos $R_{n, a} (x) = f (x) - T_{n, a} (x)$ en el siguiente límite:
$lim_{x \to a} \frac{f (x) - T_{n, a} (x)}{(x - a)^{n}} = 0.$

Concluimos que:

$lim_{x \to a} \frac{R_{n, a} (x)}{(x - a)^{n}} = 0.$

Reescribiendo tenemos que podemos hallar al polinomio de Taylor para una función $f$ considerando:
$f (x) = T_{n, a} (x) + (x - a)^{n} R_{n, a}^{*} (x)$
donde $R_{n, a}^{*} (x) = \frac{R_{n, a} (x)}{(x - a)^{n}}$ y el residuo cuando $x$ tiende a $a$ es cero:
$lim_{x \to a} R_{n, a}^{*} (x) = 0$

¿De qué forma podemos escribir el Residuo de Taylor?

En el siguiente teorema veremos dos maneras distintas para el residuo: la de Cauchy y la de Lagrange.

Teorema: Consideremos una función $f : [x_{0}, y_{0}] \to R$ donde $f$ es $n + 1$ veces derivable en $(x_{0}, y_{0})$ , un punto $a \in [x_{0}, y_{0}]$ y un $x \in (x, y_{0}]$ . Entonces existe $t \in (a, x)$ tal que:

$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} (x - a)$
que es la forma del residuo de Cauchy.
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1}$
que es la forma del residuo de Lagrange.

Demostración: Para realizar la prueba de los dos puntos del teorema veremos primero cuál es la derivada del residuo $R_{n, t}$ . Por ello consideraremos a la función $Q : [a, x] \to R$ como sigue:
$\begin{aligned} Q (t) & = R_{n, t} (x) \\ (por definición de residuo) & = f (x) - T_{n, t} (x) \\ (por definición de Taylor) & = f (x) - \sum_{j = 0}^{n} \frac{f^{(j)} (t)}{j!} (x - t)^{j} \end{aligned}$
Cabe mencionar que estamos considerando fija a $x$ .

Observemos lo siguiente, a estos puntos los llamaremos $(*)$ :

$\begin{aligned} Q (x) & = f (x) - T_{n, x} (x) \\ = f (x) - f (x) \\ = 0 \end{aligned}$
$Q (a) = R_{n, a} (x)$

Ahora si derivamos a $Q (t)$ respecto de $t$ obtenemos:
$\begin{aligned} \frac{d Q}{d t} (t) & = 0 - \sum_{j = 0}^{n} (\frac{f^{(j + 1)} (t)}{j!} (x - t)^{j} - \frac{f^{(j)} (t)}{j!} j (x - t)^{j - 1}) \\ = - \sum_{j = 0}^{n} (\frac{f^{(j + 1)} (t)}{j!} (x - t)^{j} - \frac{f^{(j)} (t)}{(j - 1)!} (x - t)^{j - 1}) \\ = - (f^{(1)} (t) (1) - 0 + f^{(2)} (t) (x - t) - f^{(1)} (t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \end{aligned}$

Observamos que los términos se van cancelando, ya que va apareciendo alternadamente positivos y negativos:
$\begin{aligned} = - (f^{(1)} (t) (1) - 0 + f^{(2)} (t) (x - t) - f^{(1)} (t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \\ = - (f^{(2)} (t) (x - t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \end{aligned}$

Si continuamos cancelando los términos, notamos que el único que nos queda es:
$\begin{aligned} = - \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} \end{aligned}$

Concluimos que:
$Q^{'} (t) = - \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n}$
A la igualdad anterior la llamaremos $(* *)$ .

Pasemos a probar los puntos $1.$ y $2.$ :

Aplicaremos el Teorema del valor medio para la derivada en el intervalo $[a, x]$ , así tenemos que existe un $t \in [a, x]$ tal que.
$Q^{'} (t) = \frac{Q (x) - Q (a)}{x - a}$
Por las observaciones $(*)$ y $(* *)$ tendríamos la siguiente igualdad:
$- \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} = \frac{0 - R_{n, a} (x)}{x - a}$
De lo anterior, al simplificar nos queda:
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} (x - a)$
Ahora usaremos el Teorema del valor medio generalizado o de Cauchy, si tomamos $g (t) = (x - t)^{n + 1}$ entonces existe un $t \in (a, x)$ tal que:
$\begin{aligned} (Q (x) - Q (a)) g^{'} (t) = (g (x) - g (a)) Q^{'} (t) & \Rightarrow \frac{Q (x) - Q (a)}{g (x) - g (a)} = \frac{Q^{'} (t)}{g^{'} (t)} \end{aligned}$
Así por $(* *)$ ocurre que:
$\begin{aligned} \frac{Q (x) - Q (a)}{g (x) - g (a)} & = \frac{- \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n}}{- (n + 1) (x - t)^{n}} \\ = \frac{f^{(n + 1)} (t)}{n! (n + 1)} \\ = \frac{f^{(n + 1)} (t)}{(n + 1)!} \end{aligned}$
Si ahora consideramos las observaciones dadas en $(*)$ para $Q (x)$ y evaluamos $g (x)$ ocurre que:
$\begin{aligned} \frac{Q (x) - Q (a)}{g (x) - g (a)} & = \frac{0 - Q (a)}{0 - g (a)} \\ = \frac{Q (a)}{g (a)} \end{aligned}$
Finalmente tenemos que:
$\frac{Q (a)}{g (a)} = \frac{f^{(n + 1)} (t)}{(n + 1)!} \Leftrightarrow Q (a) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1} .$
Ya que $Q (a) = R_{n, a} (x)$ concluimos:
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1} .$

Ahora que hemos terminado la demostración, para los ejercicios que veremos a continuación podremos utilizar la forma del residuo que más nos convenga.

Ejercicios

Consideremos la función $f (x) = e^{x}$ en $a = 0$ . Estima el error de la aproximación del polinomio de Taylor de grado $2$ para $x = \frac{1}{2}$ .

Solución:
Primero obtengamos el Residuo de $f$ utilizando la forma de Lagrange:
$\begin{aligned} R_{2, 0} (\frac{1}{2}) & = \frac{f^{(2 + 1)} (t)}{(2 + 1)!} {(\frac{1}{2} - 0)}^{2 + 1} \\ = \frac{f^{(3)} (t)}{3!} {(\frac{1}{2})}^{3} \end{aligned}$

Como la tercera derivada de $f (t)$ es $e^{t}$ , sustituyendo nos queda:
$\begin{aligned} = \frac{e^{t}}{3!} {(\frac{1}{2})}^{3} \\ = \frac{e^{t}}{6} (\frac{1}{8}) \\ = \frac{e^{t}}{48} \end{aligned}$

Del Teorema que vimos, sabemos que $t \in (0, \frac{1}{2})$ por lo que se cumple la desigualdad:
$\frac{e^{t}}{48} < \frac{\sqrt{e}}{48} .$
Observemos además que el valor de $e^{t}$ se encuentra dentro del intervalo:
$(e^{0}, e^{\frac{1}{2}}) = (1, \sqrt{e}) .$

Así concluimos que el Residuo está acotado por el valor:
$\frac{\sqrt{e^{t}}}{48} \approx 0.034$
$∴ R_{2, 0} < 0.034$

De este modo el polinomio de Taylor $T_{2, 0} (\frac{1}{2})$ de grado $2$ con centro en $0$ para el valor $x = \frac{1}{2}$ aproxima a $f (\frac{1}{2}) = \sqrt{e}$ con un error menor que $0.034$ .

Brinda una aproximación del valor $\sqrt[3]{e^{2}}$ con un error menor a $10^{- 4}$ .

Solución:
Para resolver este problema vamos a considerar lo siguiente:
$\begin{aligned} f (x) & = e^{x} & a & = 0 & x & = \frac{2}{3} \end{aligned}$

Observamos que en este caso no sabemos cuál es el valor $n$ del grado del polinomio de Taylor, esta variable $n$ es justo la que queremos encontrar. Comenzamos escribiendo el Residuo de Taylor en la forma de Lagrange sustituyendo los valores que sí conocemos:
$\begin{aligned} R_{n, 0} (\frac{2}{3}) & = \frac{f^{(n + 1)} (t)}{(n + 1)!} {(\frac{2}{3} - 0)}^{n + 1} \\ (por f^{(n + 1)} (t) = e^{t}) & = \frac{e^{t}}{(n + 1)!} (\frac{2}{3})^{n + 1}) \end{aligned}$

Como $t \in (0, \frac{2}{3})$ tenemos la desigualdad:
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1}$
Donde $\frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1}$ cumple:
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e}{(n + 1)!}$
Además como $\frac{e}{(n + 1)!}$ es menor que $\frac{3}{(n + 1)!}$ :
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e}{(n + 1)!} < \frac{3}{(n + 1)!}$

Así por la transitividad de las desigualdades tenemos que el Residuo cumple:
$R_{n, 0} < \frac{3}{(n + 1)!} .$

Sin embargo nos piden que el error sea menor que $10^{- 4}$ , por lo que necesitamos estudiar la desigualdad:
$\frac{3}{(n + 1)!} < \frac{1}{10^{4}} .$

Si reescribimos la desigualdad anterior:
$\begin{aligned} \frac{3}{(n + 1)!} < \frac{1}{10^{4}} & \Leftrightarrow (3) (10^{4}) < (n + 1)! \\ \Leftrightarrow 30000 < (n + 1)! \end{aligned}$

Ahora debemos pensar en un valor $n + 1 \in N$ cuyo factorial cumpla con ser mayor que $30000$ , veamos una lista:

$\begin{aligned} 1! & = 1 \\ 2! & = 2 \\ 3! & = 6 \\ 4! & = 24 \\ 5! & = 120 \\ 6! & = 720 \\ 7! & = 5040 \\ 8! & = 40320 \end{aligned}$

Vemos que si $n + 1 = 8$ ya logramos cumplir con la desigualdad, por lo que cuando consideramos el grado del Polinomio de Taylor $n = 7$ para el valor $x = \frac{2}{3}$ cumplimos con que el error es menor a $10^{- 4}$ .

En la sección de Tarea moral te dejaremos algunos ejercicios que ayudarán a practicar lo estudiado en esta entrada.

Más adelante

Por el momento hemos terminado de revisar los temas concernientes a los polinomios de Taylor para este curso. En Cálculo Diferencial e Integral II revisarás algunos otros resultados. Para la próxima entrada, veremos algunas aplicaciones del Cálculo en el ámbito de la Economía.

Tarea moral

Realiza el ejercicio $1$ utilizando la forma de Cauchy para el residuo.
Para la función:
$g (x) = x \log (1 + x) .$
- Obtén el polinomio de Taylor de grado $n$ con $a = 0$ .
- Obtén el Residuo de Taylor utilizando la forma de Lagrange.
- Da una cota para el error al querer aproximar $10 \log (\frac{11}{10})$ al utilizar el polinomio de Taylor de grado $3$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1).
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Aplicaciones en economía.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: La regla de L’Hôpital

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Esta entrada es la última de la unidad, y la dedicaremos a demostrar uno de los resultados ampliamente usado en el cálculo de límites para los casos donde existen indeterminaciones de los tipos $0 / 0$ e $\infty / \infty$ ; este tipo de límites es posible resolverlos mediante de la derivada.

Teorema del Valor Medio Generalizado

Antes de probar la Regla de L’Hôpital, probaremos una generalización del teorema del valor medio, también conocido como teorema del Valor Medio de Cauchy. Para ello, primero revisemos el siguiente teorema.

Teorema. Sean $f, g : [a, b] \to R$ , tal que $f (a) = g (a) = 0$ de tal manera que $g (x) \neq 0$ para $a < x < b$ . Si $f$ y $g$ son derivables en $a$ y $g^{'} (a) \neq 0$ , entonces el límite de $f / g$ en $a$ existe y es igual a $f^{'} (a) / g^{'} (a)$ . Por tanto,

$lim_{x \to a^{+}} \frac{f (x)}{g (x)} = \frac{f^{'} (a)}{g^{'} (a)} .$

Demostración.

Puesto que $f (a) = g (a) = 0$ , el cociente $\frac{f (x)}{g (x)}$ para $a < x < b$ puede escribirse como sigue

$\frac{f (x)}{g (x)} = \frac{f (x) - f (a)}{g (x) - g (a)} = \frac{\frac{f (x) - f (a)}{x - a}}{\frac{g (x) - g (a)}{x - a}} .$

Aplicando el límite, tenemos que

$lim_{x \to a^{+}} \frac{f (x)}{g (x)} = \frac{lim_{x \to a^{+}} \frac{f (x) - f (a)}{x - a}}{lim_{x \to a^{+}} \frac{g (x) - g (a)}{x - a}} = \frac{f^{'} (a)}{g^{'} (a)} .$

Teorema del Valor Medio de Cauchy. Sean $f, g : [a, b] \to R$ , ambas funciones continuas en $[a, b]$ y derivables en $(a, b)$ , y supongamos que $g^{'} (x) \neq 0$ para todo $x$ en $(a, b)$ . Entonces existe $c$ en $(a, b)$ tal que

$\frac{f (b) - f (a)}{g (b) - g (a)} = \frac{f^{'} (c)}{g^{'} (c)} .$

Demostración.

Notemos que como $g^{'} (x) \neq 0$ para todo $x \in (a, b)$ , del teorema de Rolle se sigue que $g (a) \neq g (b)$ . Para $x$ en $[a, b]$ , definimos

$h (x) = \frac{f (b) - f (a)}{g (b) - g (a)} (g (x) - g (a)) - (f (x) - f (a)) .$

De esta forma, se tiene que $h$ es continua en $[a, b]$ , derivable en $(a, b)$ y $h (a) = h (b) = 0$ . Nuevamente, por el teorema de Rolle se sigue que existe un punto $c \in (a, b)$ tal que

$0 = h^{'} (c) = \frac{f (b) - f (a)}{g (b) - g (a)} g^{'} (c) - f^{'} (c) .$

Puesto que $g^{'} (c) \neq 0$ , podemos dividir la expresión anterior entre $g^{'} (c)$ , con lo que obtenemos

$\begin{matrix} \frac{0}{g^{'} (c)} = \frac{\frac{f (b) - f (a)}{g (b) - g (a)} g^{'} (c) - f^{'} (c)}{g^{'} (c)} . \\ \Rightarrow 0 = \frac{f (b) - f (a)}{g (b) - g (a)} - \frac{f^{'} (c)}{g^{'} (c)} . \\ ∴ \frac{f^{'} (c)}{g^{'} (c)} = \frac{f (b) - f (a)}{g (b) - g (a)} . \end{matrix}$

Regla de L’Hôpital

Demostraremos la regla de L’Hôpital empleando límites por la derecha, pero los resultados se extienden de forma análoga al límite por la izquierda.

Regla de L’Hôpital. Sean $a$ , $b \in R$ tales que $a < b$ y sean $f$ , $g$ funciones derivables en $(a, b)$ tales que $g^{'} (x) \neq 0$ para todo $x \in (a, b)$ . Supongamos que

$lim_{x \to a^{+}} f (x) = 0 = lim_{x \to a^{+}} g (x) .$

$i)$ Si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = L \in R$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = L .$

$i i)$ Si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = \infty$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = \infty .$

De forma análoga, se tiene que si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = - \infty$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = - \infty .$

Demostración.

Si $a < α < β < b$ , entonces el teorema de Rolle implica que $g (β) \neq g (α)$ .

Por el teorema del Valor Medio de Cauchy, existe $u \in (α, β)$ , tal que

$\begin{matrix} (1) & \frac{f (β) - f (α)}{g (β) - g (α)} = \frac{f^{'} (u)}{g^{'} (u)} . \end{matrix}$

$i)$ Por hipótesis, sabemos que $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = L$

con $L \in R$ .

Sea $ε > 0$ . entonces existe $c \in (a, b)$ tal que

$| \frac{f^{'} (u)}{g^{'} (u)} - L | < ε para u \in (a, c) .$

Usando $(1)$ , se tiene que

$| \frac{f (β) - f (α)}{g (β) - g (α)} - L | < ε para a < α < β < c .$

Además, por hipótesis sabemos que $lim_{α \to a^{+}} f (α) = 0$ y $lim_{α \to a^{+}} g (α) = 0.$ Así, de la expresión anterior se sigue que

$| \frac{f (β)}{g (β)} - L | < ε para β \in (a, c) .$

$∴ lim_{x \to a^{+}} \frac{f (x)}{g (x)} = L .$

$i i)$ Veremos el caso $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = \infty$ . El caso $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = - \infty$ es análogo. Sea $M > 0$ , Como $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = \infty .$

Entonces existe $c \in (a, b)$ tal que

$\frac{f^{'} (u)}{g^{'} (u)} > M para u \in (a, c) .$

Nuevamente, por $(1)$ se tiene que

$\frac{f (β) - f (α)}{g (β) - g (α)} > M para a < α < β < c .$

Además, por hipótesis sabemos que $lim_{α \to a^{+}} f (α) = 0$ y $lim_{α \to a^{+}} g (α) = 0.$ Así, de la expresión anterior se sigue que

$\frac{f (β)}{g (β)} > M para β \in (a, c) .$

$∴ lim_{x \to a^{+}} \frac{f (x)}{g (x)} = \infty .$

Hay diversas extensiones de la regla de L’Hôpital. En particular, enunciaremos el siguiente.

Teorema. Sean $a$ , $b \in R$ tal que $a < b$ y sean $f$ , $g$ funciones derivables en $(a, b)$ tales que $g^{'} (x) \neq 0$ para todo $x \in (a, b) .$ Supongamos que

$lim_{x \to a^{+}} f (x) = \pm \infty = lim_{x \to a^{+}} g (x)$

$i)$ Si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = L \in R$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = L .$

$i i)$ Si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = \infty$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = \infty .$

De forma análoga, se tiene que si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = - \infty$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = - \infty .$

Procederemos ahora a revisar algunos ejemplos de límite donde aplicaremos la regla de L’Hôpital.

Ejemplo 1. Calcula el límite $lim_{x \to 1} \frac{l n (x)}{x - 1} .$

Sabemos que las funciones $f (x) = l n (x)$ y $g (x) = x - 1$ son derivables en todo su dominio, en particular podemos considerar el intervalo $(0, b)$ con $b > 1$ para ambas. Y notemos que si $g (x) = x - 1$ , entonces $g^{'} (x) = 1$ . Por lo tanto, para todo $x \in (0, b)$ se tiene que $g^{'} (x) \neq 0.$

Además como ambas funciones son continuas, se tiene que

$lim_{x \to 1} l n (x) = 0 y lim_{x \to 1} x - 1 = 0.$

Aplicando la Regla de $L^{'} H ô p i t a l$ , tenemos

$\begin{aligned} lim_{x \to 1} \frac{l n (x)}{x - 1} & = lim_{x \to 1} \frac{(l n (x))^{'}}{(x - 1)^{'}} \\ = lim_{x \to 1} \frac{1 / x}{1} \\ = 1. \end{aligned}$

Ejemplo 2. Calcula el límite $lim_{x \to 0} \frac{e^{x} - 1}{x} .$

Sabemos que las funciones $f (x) = e^{x} - 1$ y $g (x) = x$ son derivables en todo su dominio, en particular podemos considerar el intervalo $(a, b)$ con $a < 0$ y $b > 0$ para ambas. Y notemos que si $g (x) = x$ , entonces $g^{'} (x) = 1$ . Por lo tanto, para todo $x \in (a, b)$ se tiene que $g^{'} (x) \neq 0.$

Además como ambas funciones son continuas, se tiene que

$lim_{x \to 0} e^{x} - 1 = 0 y lim_{x \to 0} x = 0.$

Aplicando la Regla de $L^{'} H ô p i t a l$ , tenemos

$\begin{aligned} lim_{x \to 0} \frac{e^{x} - 1}{x} & = lim_{x \to 0} \frac{(e^{x} - 1)^{'}}{(x)^{'}} \\ = lim_{x \to 0} \frac{e^{x}}{1} \\ = e^{0} \\ = 1. \end{aligned}$

Más adelante…

En la siguiente unidad estudiaremos las aplicaciones prácticas de la derivada con lo cual podrás relacionar toda la abstracción revisada con la «realidad». Se revisará la manera en que se puede usar el cálculo en ámbitos diversos, desde física hasta economía.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sea $f (x) = x^{2} s e n (1 / x)$ para $x \neq 0$ y $f (0) = 0$ . Sea $g (x) = s e n (x)$ para $x \in R$ . Demuestra que $lim_{x \to 0} \frac{f (x)}{g (x)} = 0$ pero que el límite $lim_{x \to 0} \frac{f^{'} (x)}{g^{'} (x)}$ no existe.
Evalúa los límites donde el cociente está definido en el dominio $(0, π / 2)$
- $lim_{x \to 0^{+}} \frac{l n (x + 1)}{s e n (x)} .$
- $lim_{x \to 0^{+}} \frac{t a n (x)}{x} .$
- $lim_{x \to 0^{+}} (\frac{1}{x} - \frac{1}{s e n (x)}) .$
- $lim_{x \to 0^{+}} \frac{l n (c o s (x))}{x} .$

Entradas relacionadas

Ir a Cálculo Diferencial e Integral I
Entrada anterior del curso: Teorema de Rolle y Teorema del Valor Medio
Siguiente entrada del curso: Rectas tangente y normal a una curva
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Teorema de Rolle y teorema del valor medio

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Hasta este punto nos hemos enfocado en estudiar la derivada para distintos tipos de funciones, orientando los esfuerzos principalmente en la ejecución, en derivar tal cual. En esta entrada estudiaremos dos teoremas que nos darán visibilidad de algunas propiedades que tienen las funciones que son derivables en un intervalo abierto.

Teorema de Rolle

En el bachillerato revisaste el tema de máximos y mínimos, donde uno de los criterios que se usaban para encontrarlos era usar el hecho de que si $x_{0}$ es un mínimo o máximo local, entonces la derivada en dicho punto es cero. De momento, formalizaremos tanto la definición de máximo y mínimo local, así como el criterio de la derivada antes mencionado. Sin embargo, será en una entrada de la siguiente unidad donde daremos la demostración del criterio de la derivada, esto con la finalidad de revisarlo junto con sus aplicaciones.

Definición: Consideremos una función $f$ continua en un intervalo $I$ y $x_{0} \in (x_{0} - r, x_{0} + r) \subset I$ con $r > 0$ tal que $f^{'} (x_{0})$ existe. Decimos que:

$x_{0}$ es un máximo local de $f \Leftrightarrow$ existe $r > 0$ tal que para todo $x \in (x_{0} - r, x_{0} + r)$ ocurre que:
$f (x) \leq f (x_{0}) .$
$x_{0}$ es un mínimo local de $f \Leftrightarrow$ existe $r > 0$ tal que para todo $x \in (x_{0} - r, x_{0} + r)$ ocurre que:
$f (x_{0}) \leq f (x) .$

Teorema: Consideremos una función $f$ continua en un intervalo $I$ que es derivable en el punto $x_{0} \in (x_{0} - r, x_{0} + r) \subset I$ . Si tenemos que $x_{0}$ es un máximo o un mínimo local de $f$ , entonces $f^{'} (x_{0}) = 0.$

Ahora veremos el Teorema de Rolle que menciona que si tenemos una función $f : [a, b] \to R$ continua en $[a, b]$ y derivable en el intervalo $(a, b)$ , que satisface que $f (a) = f (b)$ , entonces existe un punto $c$ cuya derivada es cero, es decir, si la función inicia y termina en el mismo punto, entonces existe al menos un máximo o un mínimo local.

Teorema de Rolle. Sea $f : [a, b] \to R$ tal que $f$ es continua en $[a, b]$ y derivable en $(a, b)$ . Si $f (a) = f (b)$ , entonces existe $c$ , $a < c < b$ tal que $f^{'} (c) = 0.$

Demostración.

Caso 1: Para todo $x \in [a, b]$ , $f (x) = k .$

Como $f$ es constante, entonces $f^{'} (x) = 0$ para todo $x \in [a, b] .$

Así, podemos considerar $c = \frac{a + b}{2}$ . Donde se cumple que $a < c < b$ y $f^{'} (c) = 0.$

Caso 2: Existe $x_{0} \in [a, b]$ , tal que $f (x_{0}) > f (a) .$

Por el teorema del máximo-mínimo, existe $c \in [a, b]$ tal que para todo $x \in [a, b]$ se tiene que $f (x) \leq f (c) .$ Entonces,

$\begin{matrix} f (a) < f (x_{0}) \leq f (c) . \end{matrix}$

Se sigue que
$\begin{matrix} f (c) > f (a) = f (b) . \\ ∴ & c \neq a, c \neq b . \\ ∴ & c \in (a, b), a < c < b . \end{matrix}$

Por tanto, para todo $x \in [a, b]$ , se cumple que $f (x) \leq f (c)$ . Donde se concluye que $f$ es un máximo local en $c .$

Además, $f$ es derivable en $(a, b)$ . Por tanto, es derivable en $c$ . Por el teorema anterior, se concluye que $f^{'} (c) = 0.$

Caso 3: Existe $x_{0} \in [a, b]$ tal que $f (x_{0}) < f (a)$ .

Este caso es análogo al anterior.

Teorema del Valor Medio

El siguiente teorema que probaremos indica que si una función es continua en $[a, b]$ y derivable en el intervalo $(a, b)$ , entonces existe un punto $c$ cuya derivada es $f^{'} (c) = \frac{f (b) - f (a)}{b - a} .$

Lo anterior indica que existe un punto $c$ de tal manera que la pendiente de la recta tangente es la misma que la pendiente de la recta que pasa por los puntos extremos del intervalo $a$ , $b$ . Esto se puede ver gráficamente en la siguiente imagen.

Teorema del Valor Medio. Sea $f : [a, b] \to R$ continua en $[a, b]$ , derivable en $(a, b)$ , entonces existe $c$ , $a < c < b$ tal que

$f^{'} (c) = \frac{f (b) - f (a)}{b - a} .$

Demostración.

Consideremos $g (x) = f (a) + (\frac{f (b) - f (a)}{b - a}) (x - a)$ y $ρ (x) = f (x) - g (x)$ . Así, se tiene que

$ρ (x) = f (x) - (f (a) + (\frac{f (b) - f (a)}{b - a}) (x - a)) .$

Notemos que $ρ : [a, b] \to R$ , cumple que

$ρ$ es continua en $[a, b]$ pues $f$ lo es.
$ρ$ es derivable en $(a, b)$ pues $f$ lo es.
$ρ (a) = f (a) - (f (a) + 0) = 0$ y $ρ (b) = f (b) - (f (a) + f (b) - f (a)) = 0$ . Por tanto, $ρ (a) = ρ (b)$ .

Por el teorema de Rolle, existe $c$ , $a < c < b$ tal que $ρ^{'} (c) = 0$ . Veamos que

$\begin{aligned} ρ^{'} (x) & = f^{'} (x) - {((f (a) + \frac{f (b) - f (a)}{b - a}) (x - a))}^{'} \\ = f^{'} (x) - (0 + \frac{f (b) - f (a)}{b - a} (1)) \\ = f^{'} (x) - (\frac{f (b) - f (a)}{b - a}) . \end{aligned}$

$∴ ρ^{'} (x) = f^{'} (x) - (\frac{f (b) - f (a)}{b - a}) .$

Considerando que $ρ^{'} (c) = 0$ , de la expresión anterior, se sigue que

$f^{'} (c) = \frac{f (b) - f (a)}{b - a} .$

Corolario. Si para todo $x \in (a, b)$ , $f^{'} (x) = 0$ , entonces existe $k \in R$ tal que $\forall x \in [a, b]$ se tiene que $f (x) = k .$

Demostración.

Si $x = a$ , entonces $f (x) = f (a)$ . Si $x \in [a, b]$ , con $x \neq a$ , entonces $x > a$ . Aplicando el Teorema del Valor Medio en $[a, x]$ , existe $c$ , $a < c < x \leq b$ tal que

$f^{'} (c) = \frac{f (x) - f (a)}{x - a} .$

Por hipótesis, $f^{'} (c) = 0$ y $x \neq a$ , entonces

$\begin{matrix} 0 = \frac{f (x) - f (a)}{x - a} . \\ \Leftrightarrow & f (x) - f (a) = 0. \\ \Leftrightarrow & f (x) = f (a) . \end{matrix}$

Por tanto, para todo $x \in [a, b]$ , se tiene que $f (x) = k$ , con $k = f (a) .$

Corolario. Sean $f, g : [a, b] \to R$ continuas en $[a, b]$ y derivables en $(a, b)$ . Si para todo $x \in (a, b)$ , $f^{'} (x) = g^{'} (x)$ , entonces $f (x) = g (x) + k .$

Demostración.

Consideremos $h (x) = f (x) - g (x)$ , entonces se tiene que $h^{'} (x) = f^{'} (x) - g^{'} (x) = 0$ para todo $x \in (a, b) .$

Por el corolario anterior, existe $k \in R$ , constante, tal que para todo $x \in [a, b]$ se tiene $h (x) = k .$ Se sigue que

$\begin{matrix} f (x) - g (x) = k . \\ ∴ & f (x) = g (x) + k \forall x \in [a, b] . \end{matrix}$

Más adelante…

La siguiente entrada será la última de la unidad y revisaremos un potente resultado de la derivada que nos permitirá hacer el cálculo de cierto tipo de límites con mayor facilidad, este resultado es conocido como la regla de L’Hôpital.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Comprueba el teorema de Rolle en los intervalos que se muestran y halla los valores de $c$ para las siguientes funciones:
- $f (x) = x^{2} - x - 6$ en el intervalo $[- 2, 3] .$
- $f (x) = x^{2} - 4$ en el intervalo $[- 2, 2] .$
- $f (x) = \sqrt{x} - 2 \sqrt[4]{x}$ en el intervalo $[0, 16] .$
Comprueba el teorema del valor medio en los intervalos que se muestran y encuentra el valor $c$ para las siguientes funciones:
- $f (x) = \sqrt{x + 1}$ en el intervalo $[- 1, 3] .$
- $f (x) = s e n (x)$ en el intervalo $[0, π / 4] .$
- $f (x) = l n (2 x + 5)$ en el intervalo $[0, 2] .$

Entradas relacionadas

Ir a Cálculo Diferencial e Integral I
Entrada anterior del curso: Derivadas implícitas y de orden superior
Siguiente entrada del curso: La regla de L’Hôpital
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Introducción

Definición de la diferencial de una función

Algunos ejemplos de funciones y su diferencial

Una interpretación de la diferencial

Problema 1

Solución sin usar la diferencial

Solución utilizando la diferencial

Problema 2

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Problema 1

1. El costo fijo de producción

2. El ingreso máximo

3. La máxima utilidad

4. El costo medio de cada frasco

Hablemos del costo marginal

Una relación entre el Costo promedio y el Costo marginal

Problema 2

Análogamente…

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición del Residuo de Taylor

¿De qué forma podemos escribir el Residuo de Taylor?

Ejercicios

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Teorema del Valor Medio Generalizado

Regla de L’Hôpital

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Teorema de Rolle

Teorema del Valor Medio

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

$1.$ El costo fijo de producción

$2.$ El ingreso máximo

$3.$ La máxima utilidad

$4.$ El costo medio de cada frasco