Introducción
En la sección anterior vimos cómo encontrar los máximos y mínimos de una función haciendo uso del Criterio de la primera derivada. En esta entrada veremos un criterio más que nos ayudará a localizar los puntos críticos de una función haciendo uso de la segunda derivada. Además, veremos los conceptos de convexidad, concavidad y puntos de inflexión.
Criterio de la segunda derivada
Teorema (Criterio de la segunda derivada): Sea $f:(a,b) \rightarrow \r$ una función de clase $C^{(2)}$ en un punto $x_0 \in (a,b)$ y $f'(x_0)=0$.
- Si $f ^{‘ ‘}(x_0)>0 \Rightarrow x_0$ es un mínimo local de $f$.
- Si $f^{‘ ‘}(x_0)<0 \Rightarrow x_0$ es un máximo local de $f$.
Observación: una función $f$ es de clase $C^{(k)}$ si su k-ésima derivada existe y sus $k$ derivadas son continuas.
Demostración 2:
Para este punto queremos demostrar que existe un intervalo $(x_0-r,x_0+r)$ donde:
- $f'(x)>0$ para toda $x \in (x_0-r, x_0)$.
- $f'(x)<0$ para toda $x \in (x_0, x_0+r)$.
Y así por el criterio de la primera derivada tendríamos que $x_0$ es máximo local.
Por hipótesis tenemos que $f^{‘ ‘}(x_0)<0$, lo que por definición de derivada sería:
$$\lim_{h \to 0}\frac{f'(x_0+h)-f'(x_0)}{h}<0$$
Así sabemos que existe una $\delta$ tal que para toda $h \in (-\delta,\delta)$ ocurre que:
$$ \frac{f'(x_0+h)-f'(x_0)}{h}<0 $$
Veamos qué ocurre en los siguientes dos casos:
Caso 1: $h<0$ entonces tendríamos que $x_0+h<x_0$ y de la desigualdad anterior se seguiría que
\begin{align*}
\frac{f'(x_0+h)-f'(x_0)}{h}<0 &\Rightarrow f'(x_0+h)-f'(x_0)>0\\
&\Rightarrow f'(x_0+h)>0\tag{donde $f'(x_0)=0$}\\
\end{align*}
Caso 2: $h>0$ se tiene que $x_0+h >x_0$ análogamente vemos que
\begin{align*}
\frac{f'(x_0+h)-f'(x_0)}{h}<0 &\Rightarrow f'(x_0+h)-f'(x_0)<0\\
&\Rightarrow f'(x_0+h)<0\tag{donde $f'(x_0)=0$}\\
\end{align*}
Concluyendo la prueba del inciso 2.
$\square$
Detengámonos un momento a realizar la siguiente observación del teorema anterior:
Observación: si $f^{‘ ‘}(x)=0$ no podemos concluir nada, ya que el criterio no logra determinar si se trata de un máximo, un mínimo o ninguno de los anteriores. En este caso es necesario hacer uso de otros resultados como el Criterio de la primera derivada.
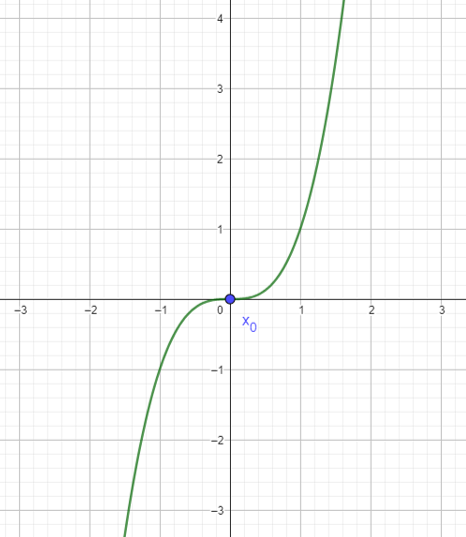
Esto sucede por ejemplo con la función $f(x)=x^{3}$ cuando $x_0=0$, ya que al evaluar su segunda derivada en $x_0$ obtenemos:
$$f^{‘ ‘}(x_0)=0.$$
Al ver la gráfica de la función cúbica notamos que en el punto $x_0=0$ no tenemos un máximo local, así como no tenemos un mínimo local.
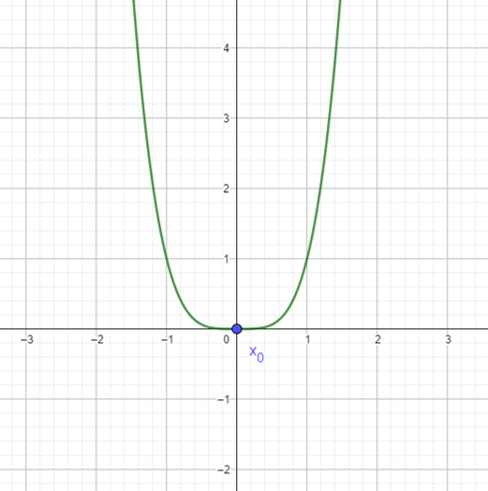
Ahora veamos que al considerar $f(x)=x^{4}$ con $x_0=0$ y su segunda derivada evaluada en $ x_0$ también ocurre que $f^{‘ ‘}(x_0)=0$. Si recurrimos a visualizar su gráfica tenemos en este caso que $x_0$ es un mínimo local de $f$. Un camino alterno para determinarlo podría ser utilizar el Criterio de la primera derivada visto en la entrada anterior.
De este modo después de aplicar el Criterio de la segunda derivada al obtener $f^{‘ ‘}(x_0)=0$ es necesario realizar un análisis más profundo valiéndonos de otros recursos y resultados.
Ejemplo
Utilizando el Criterio de la segunda derivada encuentra los máximos y mínimos de la siguiente función:
$$f(x)=x^{3}-3x^{2}-9x+1.$$
Solución:
Paso 1: Obtenemos la primera derivada de la función
\begin{align*}
f'(x)&=3x^{2}-6x-9\\
&= x^{2}-2x-3\\
&=(x-3)(x+1)\\
\therefore f'(x)&=(x-3)(x+1).
\end{align*}
Paso 2: Igualamos a cero la primera derivada para obtener los puntos críticos
\begin{align*}
f'(x)=0 &\Leftrightarrow (x-3)(x+1)=0\\
&\Leftrightarrow x- 3=0 & &\text{o} \quad (x+1)=0\\
&\Leftrightarrow x=3 & &\text{o} \quad x=-1
\end{align*}
Paso 3: Ahora obtenemos la segunda derivada de $f$
$$f^{‘ ‘}(x)=2x-2.$$
Paso 4: Sustituimos los valores de los puntos críticos obtenidos en el paso 2 y aplicamos el Criterio de la segunda derivada
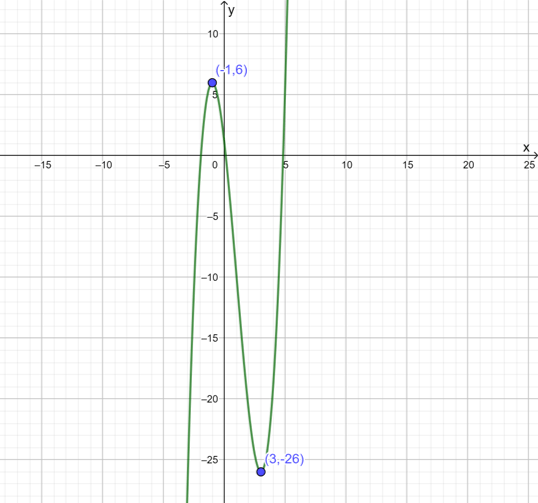
- Sustituimos $x=3$ en $f^{‘ ‘}(x)$:
$$f^{‘ ‘}(3)=2(3)-2=4$$
El resultado obtenido nos dice que $f^{‘ ‘}(3)>0$ por lo que $f$ tiene un mínimo en $(3,-26)$ - Ahora para $x=-1$:
$$f^{‘ ‘}(-1)=2(-1)-2=-4$$
Vemos que $f^{‘ ‘}(-1)<0$ obteniendo un máximo de $f$ en $(-1,6)$
Convexidad y concavidad
Definición (función convexa): Sea $f:[a,b]\rightarrow \r$ una función. Decimos que $f$ es convexa en [a,b] si para cualesquiera $x,y \in [a,b]$ con $x<y$ se cumple que para todo $z\in[x,y]$:
$$f(z) \leq \frac{f(x)-f(y)}{x-y}(z-y)+f(y).$$
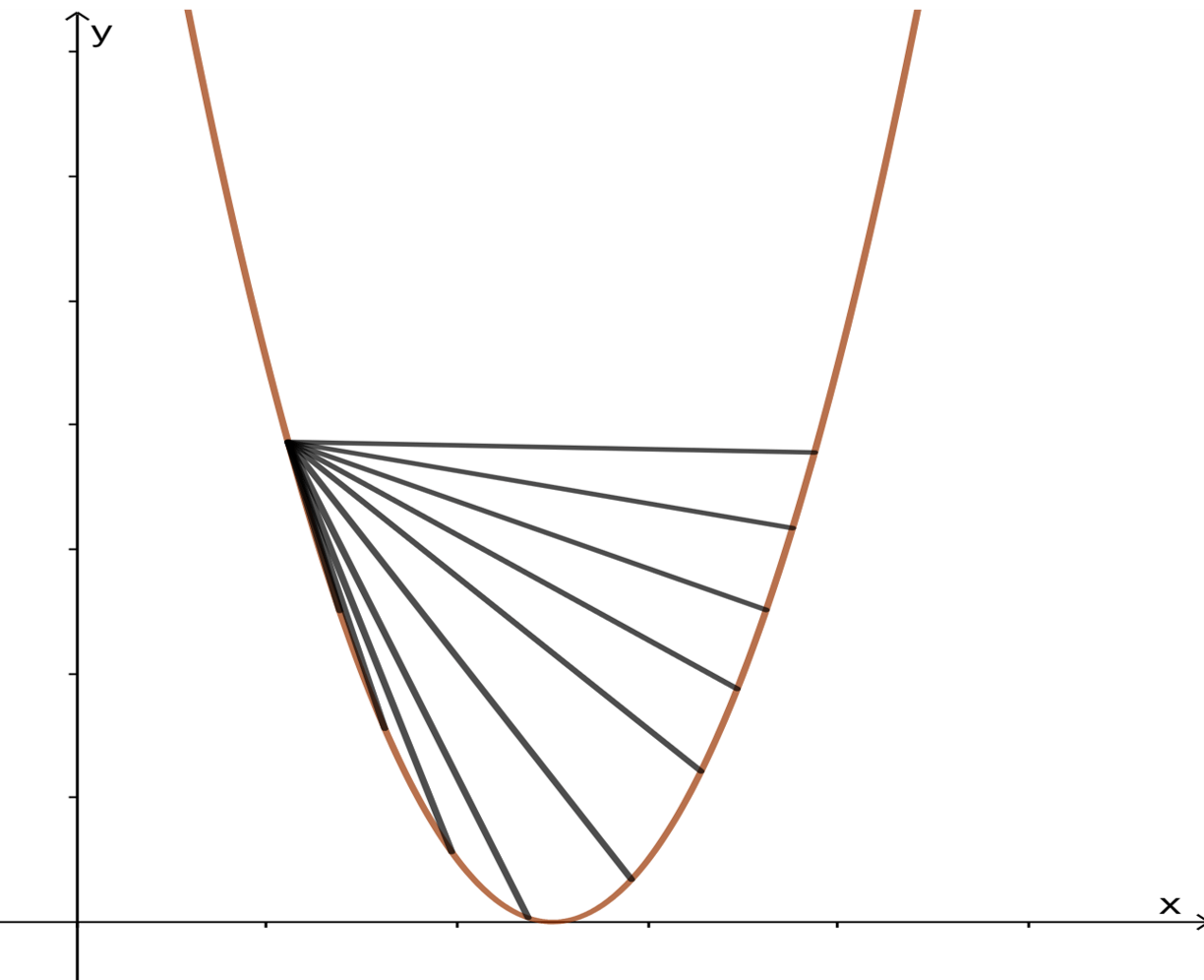
Lo que esta definición nos dice es que todos los puntos de la recta secante que une a $(y,f(y))$ con $(x,f(x))$ cuando $x<y$ se encuentran por arriba de la gráfica como se ve en la siguiente imagen.
Observación: Recordemos que, en el contexto de funciones y gráficas, una recta secante es una línea recta que intercepta a una curva en dos puntos distintos.
Una definición equivalente sería que para cualquier $\alpha \in (0,1)$ se cumple:
$$f(\alpha x+(1-\alpha)y)\leq \alpha f(x)+(1-\alpha)f(y).$$
Para ver que la definición implica esto, notemos que si $z=\alpha x+(1-\alpha)y$ con $\alpha\in (0,1)$, entonces $z\leq y$ y $z\geq x$. Así, por definición, tendríamos que
\begin{align*}
f(\alpha x + (1-\alpha) y)&=f(z)\\
&\leq \frac{f(x)-f(y)}{x-y}(z-y)+f(y)\\
&=\frac{f(x)-f(y)}{x-y}(\alpha x – \alpha y) + f(y)\\
&=\alpha(f(x)-f(y))+f(y)\\
&=\alpha f(x) + (1-\alpha) f(y),
\end{align*}
como afirmamos. Por otro lado, si se cumple lo que afirmamos que es una equivalencia, entonces cualquier $z\in (x,y)$ puede ser escrito como $z=\alpha x+(1-\alpha)y$ con $\alpha \in (0,1)$ (esto se puede probar, por ejemplo, por teorema del valor intermedio, pues $\alpha \mapsto \alpha x+(1-\alpha)y$ es continua, en $\alpha=0$ vale $y$ y en $\alpha=1$ vale $x$). Así, suponiendo la segunda versión tendríamos
\begin{align*}
f(z)&=f(\alpha x + (1-\alpha) y)\\
&\leq \alpha f(x)+(1-\alpha)f(y)\\
&=\frac{f(x)-f(y)}{x-y}(z-y)+f(y),
\end{align*}
en donde en la última igualdad se hacen cuentas similares a las hechas arriba.
Otras definiciones son las siguientes:
- Definición (función estrictamente convexa): Sea $f:[a,b]\rightarrow \r$ una función. Se dice que $f$ es estrictamente convexa si cumple la desigualdad:
$$f(\alpha x+(1-\alpha)y)< \alpha f(x)+(1-\alpha)f(y),$$ para $\alpha\in (0,1)$. - Definición (función estrictamente cóncava): Decimos que $f$ es estrictamente cóncava si $-f$ es estrictamente convexa.
- Definición (función cóncava): Decimos que $f$ es cóncava si $-f$ es convexa.
La derivada y la convexidad
Teorema: Consideremos $f:(a,b)\rightarrow \r$ una función. Si $f'(x)$ es no decreciente en $(a,b)$ entonces $f$ es convexa en $(a,b)$.
Demostración:
Consideremos $x,y \in (a,b)$. Queremos demostrar que para cualquier $\alpha \in (0,1)$ se cumple la desigualdad:
$$f(\alpha x + (1- \alpha)y)\leq \alpha f(x)+ (1- \alpha)f(y).$$
Así tomemos $\alpha_0 \in [0,1]$ y probemos que:
$$f(\alpha_0 x + (1- \alpha_0)y)\leq \alpha_0 f(x)+ (1- \alpha_0)f(y).$$
Por el teorema del valor medio para la derivada tenemos que existe $p\in (x,z)$ donde podemos considerar $ z=\alpha_0x+(1-\alpha_0)y$ tal que:
$$f'(p)=\frac{f(z)-f(x)}{z-x}.$$
Análogamente existe $q \in (z,y)$ que:
$$f'(q)=\frac{f(y)-f(z)}{y-z}.$$
Por hipótesis vemos que:
$$f'(p)\leq f'(q).$$
Es decir:
$$\frac{f(z)-f(x)}{z-x}\leq \frac{f(y)-f(z)}{y-z}.$$
Y como $ z=\alpha_0x+(1-\alpha_0)y$:
\begin{align*}
&\Rightarrow \frac{f(z)-f(y)}{(\alpha_0-1)x+(1-\alpha_0)y}\leq \frac{f(y)-f(z)}{y-\alpha_0 x-(1- \alpha_0)y}\\
&\Rightarrow \frac{f(z)-f(y)}{(y-x)(1-\alpha_0)}\leq \frac{f(y)-f(z)}{\alpha_0 (y-x)}\\
&\Rightarrow \alpha_0 (f(z)-f(x)) \leq (1- \alpha_0)(f(y)-f(z))
\end{align*}
Por lo tanto si desarrollamos lo anterior:
\begin{align*}
\alpha_0 f(z)+ (1-\alpha_0)f(z)&\leq \alpha_0f(x)+(1-\alpha_0)f(y)\\
\therefore f(z)&\leq \alpha_0 f(x)+(1-\alpha_0)f(y)\\
\end{align*}
Recordando que $z=\alpha_0x+(1-\alpha_0)y$ concluimos que:
$$f(\alpha_0x+(1-\alpha_0)) \leq \alpha_0 f(x)+(1-\alpha_0)f(y).$$
$\square$
Una consecuencia del teorema anterior es el siguiente corolario:
Corolario: Sea $f: (a,b) \rightarrow \r$ una función.
- Si $f^{‘ ‘}(x) \geq 0$ entonces $f$ es convexa.
- Si $f^{‘ ‘}(x)\leq 0$ entonces $f$ es cóncava.
Así vemos que la segunda derivada nos puede ayudar a determinar los intervalos donde una función es convexa o cóncava.
Puntos de inflexión de una función
Definición (punto de inflexión): Decimos que $x_0$ es un punto de inflexión si en él la función cambia de convexa a cóncava ó de cóncava a convexa.
Para poder identificarlos usando la derivada tenemos que si $f^{‘ ‘}(x_0)=0$ y $f^{‘ ‘ ‘}(x_0)\neq 0$ entonces $x_0$ es un punto de inflexión.
En el siguiente ejemplo utilizaremos este criterio para identificar los puntos de inflexión de la función vista en el ejercicio anterior.
Ejemplo
Recordemos que estamos trabajando con la función:
$$f(x)=x^{3}-3x^{2}-9x+1 .$$
Cuyas segunda y tercera derivada son:
$$f^{‘ ‘}(x)=2x-2$$
$$f^{‘ ‘ ‘}(x)=2$$
Para identificar a sus puntos de inflexión igualaremos a cero su segunda derivada y encontraremos las raíces de la misma:
\begin{align*}
f^{‘ ‘}(x)=0 &\Rightarrow 2x-2=0\\
&\Rightarrow x-1=0\\
&\Rightarrow x=1
\end{align*}
Sustituimos $x=1$ en la función original:
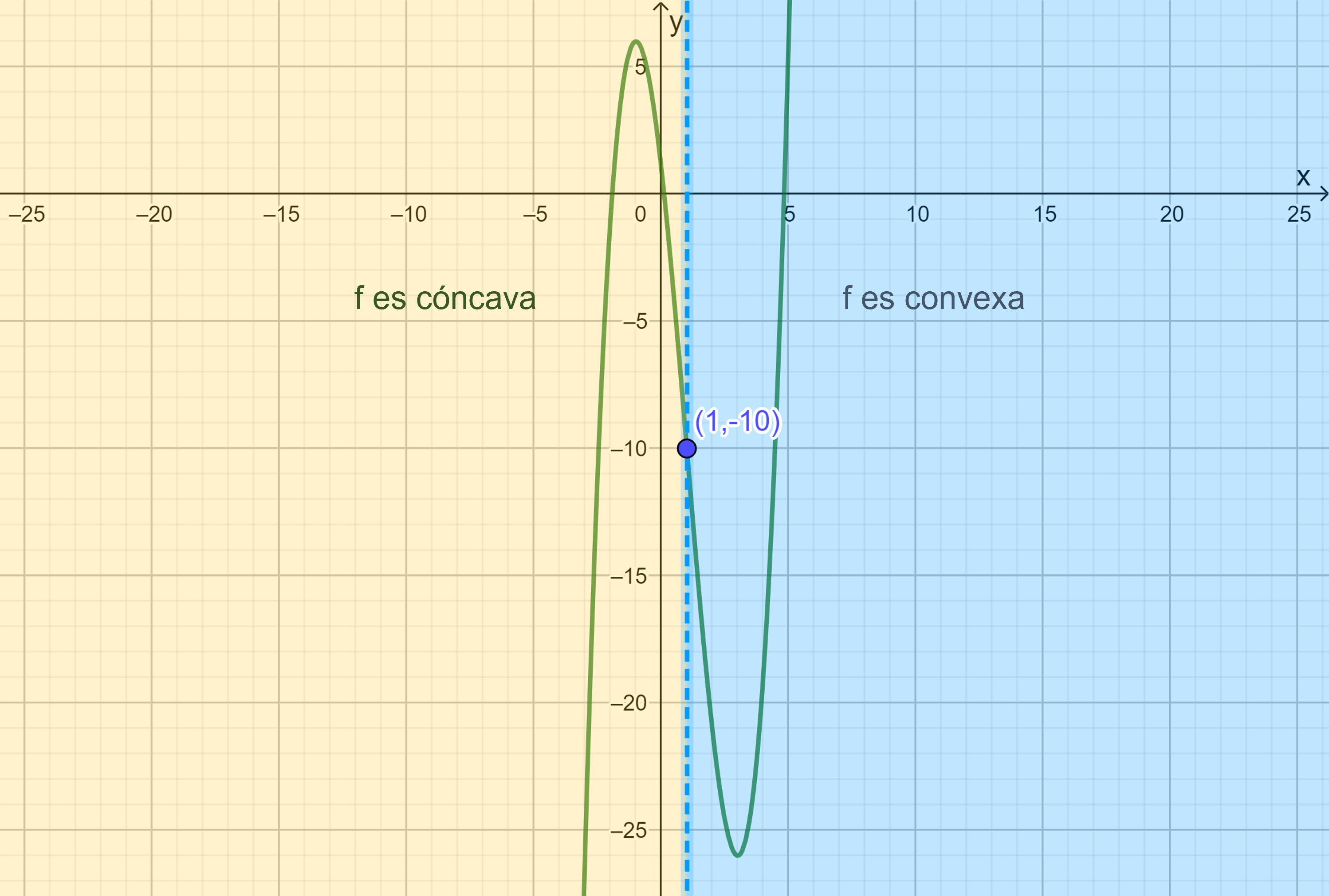
$$f(1)=(1)^{3}-3(1)^{2}-9(1)+1=-10$$
Además, como $f^{‘ ‘ ‘}(1)=2$, podemos concluir que $f$ tiene un punto de inflexión en $(1,-10)$.
Ahora para definir donde la función es convexa debemos resolver la siguiente desigualdad:
\begin{align*}
f^{‘ ‘}(x)>0 &\Rightarrow x-1>0\\
&\Rightarrow x>1
\end{align*}
Así $f$ es convexa en $(1, \infty)$
Y para ver donde es cóncava utilizamos:
\begin{align*}
f^{‘ ‘}(x)<0 &\Rightarrow x-1<0\\
&\Rightarrow x<1
\end{align*}
Por lo que $f$ es cóncava en $(-\infty,1)$
Más adelante
Ahora que hemos visto dos criterios importantes haciendo uso de la derivada para localizar máximos y mínimos de una función, en la siguiente entrada donde hablaremos de problemas de optimización, será esencial poder identificarlos.
Tarea moral
Para cada una de las siguientes funciones obtén:
- Máximos y mínimos.
- Intervalos donde crece y decrece la función.
- Intervalos donde es convexa o cóncava.
- Puntos de inflexión.
- Gráfica.
- $f(x)=x^{2}+\frac{1}{x^{2}}$
- $f(x)= x^{3}(x+2)$
- $f(x)=\sqrt{x^{2}+36}$
- $f(x)=-2x^{3}+9x^{2}+60x$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Monotonía de funciones.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Problemas de optimización.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»