Introducción
En la entrada anterior vimos que el polinomio de Taylor para una función $f$ que se puede derivar $n$ veces en $x=a$, es:
$$T_{a,n}=\sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}.$$
Además vimos que cumplía con la siguiente igualdad:
$$\lim_{x\to a}\frac{f(x)-T_{a,n}(x)}{(x-a)^{n}}=0$$
que nos indicaba que el polinomio de Taylor es una buena aproximación de la función $f$.
Pero, ¿qué podemos decir de la diferencia $ f(x)-T_{a,n}(x)$? ¿Cuáles son las propiedades que cumple?
A lo largo de esta entrada veremos que dicha diferencia es llamada Residuo de Taylor y que existen un par de formas de escribirlo. También veremos un ejemplo donde se nos pedirá estimar dicho residuo dependiendo del polinomio de Taylor considerado.
Definición del Residuo de Taylor
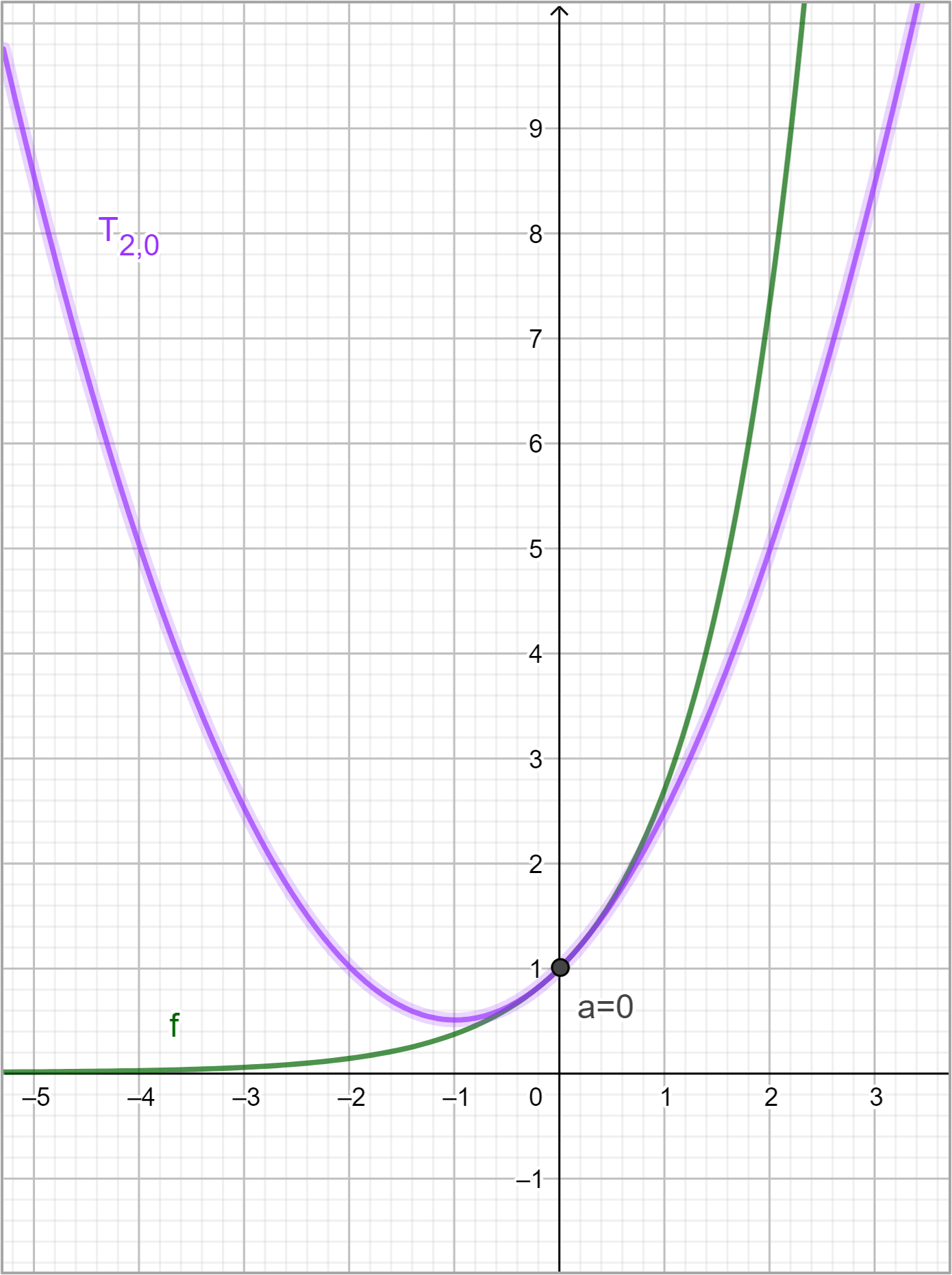
Retomando uno de los ejemplos anteriores:
En esta imagen vemos que el polinomio de Taylor $T_{2,0}$ se parece mucho a la función $f$ cuando $a=0$, sin embargo, sigue existiendo una diferencia o «error» ya que el polinomio y $f$ no son «idénticas». A dicho error se le conoce formalmente como Residuo de Taylor, veamos su definición:
Definición (Residuo de Taylor): Consideremos una función $f: [x_0,y_0] \rightarrow \r$ de clase $C^{(n)}$. Definiremos al Residuo de Taylor de grado $n$ con centro en $a$ como:
$$R_{n,a}:[x_0,y_0] \rightarrow \r$$
$$R_{n,a}(x)=f(x)-T_{n,a}(x).$$
Nota: Recordemos que una función es de clase $C^{(n)}$ si es $n$ veces derivable y sus $n$ derivadas son continuas.
Vemos que de la definición anterior tenemos que al realizar una aproximación usando polinomios de Taylor para una función $f$ se da la siguiente igualdad :
$$f(x)=T_{n,a}(x)+R_{n,a}(x).$$
Y además si sustituimos $ R_{n,a}(x)=f(x)-T_{n,a}(x)$ en el siguiente límite:
$$ \lim_{x\to a}\frac{f(x)-T_{n,a}(x)}{(x-a)^{n}}=0.$$
Concluimos que:
$$\lim_{x\to a}\frac{R_{n,a}(x)}{(x-a)^{n}}=0.$$
Reescribiendo tenemos que podemos hallar al polinomio de Taylor para una función $f$ considerando:
$$f(x)=T_{n,a}(x)+(x-a)^{n}R^{*}_{n,a}(x)$$
donde $R^{*}_{n,a}(x) = \frac{R_{n,a}(x)}{(x-a)^{n}}$ y el residuo cuando $x$ tiende a $a$ es cero:
$$\lim_{x \to a}R^{*}_{n,a}(x)=0$$
¿De qué forma podemos escribir el Residuo de Taylor?
En el siguiente teorema veremos dos maneras distintas para el residuo: la de Cauchy y la de Lagrange.
Teorema: Consideremos una función $f: [x_0,y_0] \rightarrow \r$ donde $f$ es $n+1$ veces derivable en $(x_0,y_0)$, un punto $a\in [x_0,y_0]$ y un $x \in (x,y_0]$. Entonces existe $t\in (a,x)$ tal que:
- $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}(x-a)$$
que es la forma del residuo de Cauchy. - $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}$$
que es la forma del residuo de Lagrange.
Demostración: Para realizar la prueba de los dos puntos del teorema veremos primero cuál es la derivada del residuo $R_{n,t}$. Por ello consideraremos a la función $Q: [a,x] \rightarrow \r$ como sigue:
\begin{align*}
Q(t)&=R_{n,t}(x)\\
&=f(x)-T_{n,t}(x)\tag{por definición de residuo}\\
&=f(x)-\sum_{j=0}^{n}\frac{f^{(j)}(t)}{j!}(x-t)^{j} \tag{por definición de Taylor}
\end{align*}
Cabe mencionar que estamos considerando fija a $x$.
Observemos lo siguiente, a estos puntos los llamaremos $(*)$ :
- \begin{align*}
Q(x)&=f(x)-T_{n,x}(x)\\
&=f(x)-f(x)\\
&=0
\end{align*} - $$Q(a)=R_{n,a}(x)$$
Ahora si derivamos a $Q(t)$ respecto de $t$ obtenemos:
\begin{align*}
\dfrac{dQ}{dt}(t)&=0- \sum_{j=0}^{n}\left( \frac{f^{(j+1)}(t)}{j!}(x-t)^{j}- \frac{f^{(j)}(t)}{j!}j (x-t)^{j-1}\right)\\
&=- \sum_{j=0}^{n}\left( \frac{f^{(j+1)}(t)}{j!}(x-t)^{j}-\frac{f^{(j)}(t)}{(j-1)!}(x-t)^{j-1}\right)\\
&=- \left(f^{(1)}(t)(1)-0+f^{(2)}(t)(x-t)-f^{(1)}(t)+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-f^{(2)}(t)(x-t)+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)
\end{align*}
Observamos que los términos se van cancelando, ya que va apareciendo alternadamente positivos y negativos:
\begin{align*}
& =- \left(\cancel{f^{(1)}(t)(1)}-0+f^{(2)}(t)(x-t)-\cancel{f^{(1)}(t)}+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-f^{(2)}(t)(x-t)+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)\\
& =- \left(\cancel{f^{(2)}(t)(x-t)}+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-\cancel{f^{(2)}(t)(x-t)}+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)\\
\end{align*}
Si continuamos cancelando los términos, notamos que el único que nos queda es:
\begin{align*}
&=- \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}
\end{align*}
Concluimos que:
$$Q'(t)=- \frac{f^{(n+1)}(t)}{n!}(x-t)^{n} $$
A la igualdad anterior la llamaremos $(**)$.
Pasemos a probar los puntos $1.$ y $2.$:
- Aplicaremos el Teorema del valor medio para la derivada en el intervalo $[a,x]$, así tenemos que existe un $t\in [a,x]$ tal que.
$$Q'(t)=\frac{Q(x)-Q(a)}{x-a}$$
Por las observaciones $(*)$ y $(**)$ tendríamos la siguiente igualdad:
$$-\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}=\frac{0-R_{n,a}(x)}{x-a}$$
De lo anterior, al simplificar nos queda:
$$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}(x-a)$$ - Ahora usaremos el Teorema del valor medio generalizado o de Cauchy, si tomamos $g(t)=(x-t)^{n+1}$ entonces existe un $t\in (a,x)$ tal que:
\begin{align*}
(Q(x)-Q(a))g'(t)=(g(x)-g(a))Q'(t)&\Rightarrow \frac{Q(x)-Q(a)}{g(x)-g(a)}=\frac{Q'(t)}{g'(t)}
\end{align*}
Así por $(**)$ ocurre que:
\begin{align*}
\frac{Q(x)-Q(a)}{g(x)-g(a)}&=\frac{-\frac{f^{(n+1)}(t)}{n!}\cancel{(x-t)^{n}}}{-(n+1)\cancel{(x-t)^{n}}}\\
&=\frac{f^{(n+1)}(t)}{n!(n+1)}\\
&=\frac{f^{(n+1)}(t)}{(n+1)!}
\end{align*}
Si ahora consideramos las observaciones dadas en $(*)$ para $Q(x)$ y evaluamos $g(x)$ ocurre que:
\begin{align*}
\frac{Q(x)-Q(a)}{g(x)-g(a)}&=\frac{0-Q(a)}{0-g(a)}\\
&=\frac{Q(a)}{g(a)}
\end{align*}
Finalmente tenemos que:
$$\frac{Q(a)}{g(a)}=\frac{f^{(n+1)}(t)}{(n+1)!} \Leftrightarrow Q(a)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}.$$
Ya que $Q(a)=R_{n,a}(x)$ concluimos:
$$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}.$$
$\square$
Ahora que hemos terminado la demostración, para los ejercicios que veremos a continuación podremos utilizar la forma del residuo que más nos convenga.
Ejercicios
- Consideremos la función $f(x)=e^{x}$ en $a=0$. Estima el error de la aproximación del polinomio de Taylor de grado $2$ para $x=\frac{1}{2}$.
Solución:
Primero obtengamos el Residuo de $f$ utilizando la forma de Lagrange:
\begin{align*}
R_{2,0}\left(\frac{1}{2}\right)&=\frac{f^{(2+1)}(t)}{(2+1)!}\left(\frac{1}{2}-0\right)^{2+1}\\
&= \frac{f^{(3)}(t)}{3!}\left(\frac{1}{2}\right)^{3}\\
\end{align*}
Como la tercera derivada de $f(t)$ es $e^{t}$, sustituyendo nos queda:
\begin{align*}
&= \frac{e^{t}}{3!}\left(\frac{1}{2}\right)^{3}\\
&= \frac{e^{t}}{6}\left(\frac{1}{8}\right)\\
&= \frac{e^{t}}{48}
\end{align*}
Del Teorema que vimos, sabemos que $t\in \left(0,\frac{1}{2}\right)$ por lo que se cumple la desigualdad:
$$ \frac{e^{t}}{48}< \frac{\sqrt{e}}{48}.$$
Observemos además que el valor de $e^{t}$ se encuentra dentro del intervalo:
$$(e^{0},e^{\frac{1}{2}})=(1,\sqrt{e}).$$
Así concluimos que el Residuo está acotado por el valor:
$$ \frac{\sqrt{e^{t}}}{48} \approx 0.034$$
$$\therefore R_{2,0}<0.034$$
De este modo el polinomio de Taylor $T_{2,0}\left(\frac{1}{2}\right)$ de grado $2$ con centro en $0$ para el valor $x=\frac{1}{2}$ aproxima a $f\left(\frac{1}{2}\right)=\sqrt{e}$ con un error menor que $0.034$.
- Brinda una aproximación del valor $\sqrt[3]{e^{2}}$ con un error menor a $10^{-4}$.
Solución:
Para resolver este problema vamos a considerar lo siguiente:
\begin{align*}
f(x)&= e^{x} & a&=0 & x&=\frac{2}{3}
\end{align*}
Observamos que en este caso no sabemos cuál es el valor $n$ del grado del polinomio de Taylor, esta variable $n$ es justo la que queremos encontrar. Comenzamos escribiendo el Residuo de Taylor en la forma de Lagrange sustituyendo los valores que sí conocemos:
\begin{align*}
R_{n,0}\left(\frac{2}{3}\right) &=\frac{f^{(n+1)}(t)}{(n+1)!}\left(\frac{2}{3}-0\right)^{n+1}\\
&= \frac{e^{t}}{(n+1)!}\left(\frac{2}{3})^{n+1}\right)\tag{ por $f^{(n+1)}(t)= e^{t}$}\\
\end{align*}
Como $t\in\left(0,\frac{2}{3}\right)$ tenemos la desigualdad:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1}$$
Donde $ \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1}$ cumple:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e}{(n+1)!}$$
Además como $\frac{e}{(n+1)!}$ es menor que $\frac{3}{(n+1)!}$:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e}{(n+1)!}< \frac{3}{(n+1)!} $$
Así por la transitividad de las desigualdades tenemos que el Residuo cumple:
$$R_{n,0}< \frac{3}{(n+1)!}.$$
Sin embargo nos piden que el error sea menor que $10^{-4}$, por lo que necesitamos estudiar la desigualdad:
$$ \frac{3}{(n+1)!} < \frac{1}{10^{4}}.$$
Si reescribimos la desigualdad anterior:
\begin{align*}
\frac{3}{(n+1)!} < \frac{1}{10^{4}} &\Leftrightarrow (3)(10^{4})< (n+1)!\\
&\Leftrightarrow 30 000 < (n+1)!
\end{align*}
Ahora debemos pensar en un valor $n+1 \in \mathbb{N}$ cuyo factorial cumpla con ser mayor que $30 000$, veamos una lista:
\begin{align*}
1!&=1\\
2!&=2\\
3!&= 6\\
4!&= 24\\
5!&=120\\
6!&=720\\
7!&=5040\\
8!&= 40320
\end{align*}
Vemos que si $n+1=8$ ya logramos cumplir con la desigualdad, por lo que cuando consideramos el grado del Polinomio de Taylor $n=7$ para el valor $x=\frac{2}{3}$ cumplimos con que el error es menor a $10^{-4}$.
En la sección de Tarea moral te dejaremos algunos ejercicios que ayudarán a practicar lo estudiado en esta entrada.
Más adelante
Por el momento hemos terminado de revisar los temas concernientes a los polinomios de Taylor para este curso. En Cálculo Diferencial e Integral II revisarás algunos otros resultados. Para la próxima entrada, veremos algunas aplicaciones del Cálculo en el ámbito de la Economía.
Tarea moral
- Realiza el ejercicio $1$ utilizando la forma de Cauchy para el residuo.
- Para la función:
$$g(x)=x\log(1+x).$$- Obtén el polinomio de Taylor de grado $n$ con $a=0$.
- Obtén el Residuo de Taylor utilizando la forma de Lagrange.
- Da una cota para el error al querer aproximar $10 \log\left(\frac{11}{10}\right)$ al utilizar el polinomio de Taylor de grado $3$.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1).
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Aplicaciones en economía.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»