Las matemáticas comienzan a parecerse demasiado a resolver un puzzle. La física también,
pero son puzzles creados por la naturaleza, no por la mente del hombre.
– Maria Goeppert Mayer

Introducción

En esta entrada estudiaremos algunos tipos de oscilaciones mecánicas con el propósito de poner en práctica los métodos desarrollados hasta este momento de la segunda unidad.

Consideraremos varios sistemas dinámicos lineales en los que cada modelo matemático será una ecuación diferencial de segundo orden con coeficientes constantes acompañada de condiciones iniciales especificadas en un tiempo que tomaremos como $t=0$.

$$\begin{array}{}\text{(1)}& a{\displaystyle \frac{d^{2}x}{d{t}^2}}+b{\displaystyle \frac{dx}{dt}}+cx=g(t);x(0)=x_0,x^{\prime }(0)=x_1\end{array}$$

Con respecto a la notación, denotaremos con $x$ a la variable dependiente que físicamente representará la posición de un objeto, mientras que $t$ será la variable independiente y representara al tiempo, ya que nuestro propósito es describir el movimiento oscilatorio de un objeto a través del tiempo.

A la función $g(x)$ de ($\text{1}$) la llamaremos entrada o función forzada del sistema. Una solución $x(t)$ de ($\text{1}$) en un intervalo $\delta$ que contiene a $t=0$ y satisface las condiciones iniciales se le llama salida o respuesta del sistema.

El sistema dinámico que estudiaremos será el de resorte – objeto y los tipos de movimiento que describiremos será el movimiento libre no amortiguado, el movimiento libre amortiguado y el movimiento forzado.

Movimiento libre no amortiguado

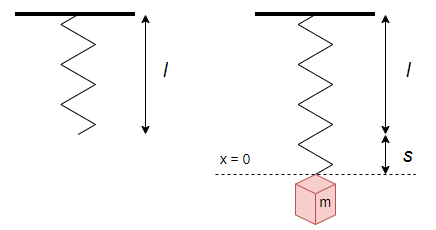
Consideremos un resorte de longitud $l$ suspendido verticalmente de un soporte rígido y en la parte inferior del resorte se encuentra un objeto de masa $m$, el peso del objeto hace que el resorte se elongue una distancia $s$. En la posición de equilibrio establecemos que $x=0$, tal como se muestra en la siguiente figura.

Es claro que la cantidad de alargamiento o elongación del resorte depende de la masa, además el resorte mismo ejerce una fuerza restauradora $F$ opuesta a la dirección de elongación y proporcional a la cantidad de elongación $s$, esta característica corresponde a la ley de Hooke y matemáticamente se expresa como

$$\begin{array}{}\text{(2)}& F=ks\end{array}$$

donde $k$ es una constante de proporcionalidad llamada constante de resorte.

Una vez colocado el objeto de masa $m$, el resorte se alarga una distancia $s$ y mantiene una posición de equilibrio en el que el peso $W$ del objeto se equilibra con la fuerza restauradora $F$ del resorte. Recordando que el peso de un objeto es

$$\begin{array}{}\text{(3)}& W=mg\end{array}$$

con $m$ la masa del objeto y $g$ la aceleración de la gravedad, podemos establecer que en el equilibrio ocurre que

$$\begin{array}{}\text{(4)}& W=F\end{array}$$

o bien,

$$\begin{array}{}\text{(5)}& mg-ks=0\end{array}$$

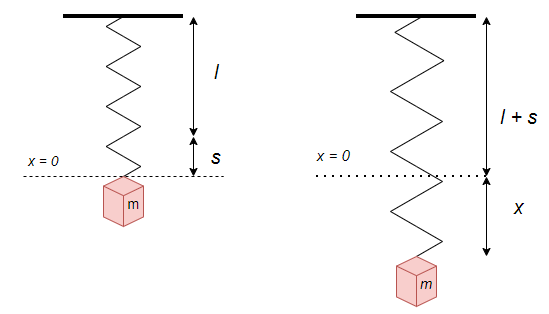
Si el objeto se desplaza una cantidad $x$ de su posición de equilibrio, la fuerza restauradora del resorte será

$$\begin{array}{}\text{(6)}& F_x=k(s+x)\end{array}$$

Como estamos analizando un movimiento no amortiguado, vamos a suponer que no hay fuerzas restauradoras que actúen sobre el sistema y que el objeto oscila libre de otras fuerzas externas. Entonces podemos igualar la segunda ley de Newton con la fuerza resultante de la fuerza restauradora y el peso.

$$m{\displaystyle \frac{d^{2}x}{d{t}^2}}=-k(s+x)+mg=-kx+mg-ks$$

Considerando ($\text{5}$) obtenemos que

$$\begin{array}{}\text{(7)}& m{\displaystyle \frac{d^{2}x}{d{t}^2}}=-kx\end{array}$$

El signo negativo indica que la fuerza restauradora del resorte actúa en dirección opuesta a la dirección del movimiento, además se toma la convención de que la dirección hacia abajo de la posición de equilibrio es positiva.

Si dividimos entre $m$ la ecuación ($\text{7}$) y reordenamos obtenemos la ecuación diferencial

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+{\displaystyle \frac{k}{m}}x=0\end{array}$$

Veremos más adelante la razón por la que es conveniente definir la constante

$$\begin{array}{}\text{(9)}& {\omega }^2={\displaystyle \frac{k}{m}}\end{array}$$

Usando esta definición podemos escribir la ecuación ($\text{8}$) como

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+{\omega }^{2}x=0\end{array}$$

La ecuación diferencial ($\text{10}$) se dice que describe el movimiento armónico simple o movimiento libre no amortiguado. Dos condiciones iniciales claras son el desplazamiento inicial

$$x(0)=x_0$$

y la velocidad inicial

$$x^{\prime }(0)=x_1$$

del objeto. Por ejemplo, si $x_0>0$, entonces indica que el objeto parte de un punto por debajo de la posición de equilibrio lo que provocará una velocidad impartida hacia arriba, es decir, $x_1<0$. Cuando $x^{\prime }(0)=0$ el objeto se libera a partir del reposo. Y si por ejemplo $x_0<0$ y $x_1=0$, entonces indica que el objeto se libera desde el reposo pero desde una posición arriba de la posición de equilibrio.

La ecuación ($\text{10}$) representa el modelo matemático que describe el fenómeno, pero ahora estamos interesados en conocer la ecuación de movimiento, así que es momento de aplicar lo aprendido y resolver la ecuación diferencial.

Se trata de una ecuación diferencial de segundo orden con coeficientes constantes, así que proponemos una solución de la forma

$$\begin{array}{}\text{(11)}& x(t)=e^{rt}\end{array}$$

Utilizamos la letra $r$ y no $k$ para no confundirnos con la constante de resorte. Al sustituir esta solución y su segunda derivada en ($\text{10}$) se obtiene la ecuación auxiliar

$$\begin{array}{}\text{(12)}& r^2+{\omega }^2=0\end{array}$$

Las raíces son

$$r_1=i\omega y{r}_2=-i\omega$$

Identificamos que $\alpha =0$ y $\beta =\omega$, Por lo tanto, la solución general es

$$\begin{array}{}\text{(13)}& x(t)=c_1\cos (\omega t)+c_2\sin (\omega t)\end{array}$$

Esta solución corresponde a la ecuación general de movimiento del objeto sujeto al resorte considerando que no hay amortiguación.

Si se aplican las condiciones iniciales y se determinan las constantes $c_1$ y $c_2$, entonces habremos encontrado la ecuación de movimiento del sistema en particular. Notemos que la solución efectivamente describe un movimiento oscilatorio ya que se encuentran presentes las funciones seno y coseno.

La constante

$$\begin{array}{}\text{(14)}& \omega =\sqrt{{\displaystyle \frac{k}{m}}}\end{array}$$

se llama frecuencia circular del sistema y nos permite definir algunas cantidades. $\omega$ se mide en radianes por segundo.

La cantidad

$$\begin{array}{}\text{(15)}& T={\displaystyle \frac{2\pi }{\omega }}\end{array}$$

determina el periodo del movimiento descrito por ($\text{13}$), es decir, representa el tiempo que tarda el objeto en hacer un ciclo de movimiento. Un ciclo es una oscilación completa del objeto. Podemos decir que el periodo $T$ es el tamaño del intervalo de tiempo entre dos máximos sucesivos (o mínimos sucesivos) de $x(t)$. De acuerdo a nuestra convención, un máximo es el desplazamiento positivo del objeto en el que alcanza su distancia máxima debajo de la posición de equilibrio, mientras que un mínimo es el desplazamiento negativo en el que alcanza su altura máxima arriba de la posición de equilibrio. En cualquier caso decimos que hay un desplazamiento extremo del objeto.

La cantidad

$$\begin{array}{}\text{(16)}& f={\displaystyle \frac{1}{T}}={\displaystyle \frac{\omega }{2\pi }}\end{array}$$

es la frecuencia de movimiento y representa el número de ciclos completados cada segundo.

Existe una forma alterna de la solución ($\text{13}$) en la que se hace explícita la amplitud $A$ de las oscilaciones. Si en la solución ($\text{13}$) $c_1\ne 0$ y $c_2\ne 0$, se define la amplitud como

$$\begin{array}{}\text{(17)}& A=\sqrt{c_1^2+c_2^2}\end{array}$$

y se define el ángulo de fase $\varphi$, tal que

$$\begin{array}{}\text{(18)}& \sin (\varphi )={\displaystyle \frac{c_1}{A}},\cos (\varphi )={\displaystyle \frac{c_2}{A}}\Rightarrow \tan (\varphi )={\displaystyle \frac{c_1}{c_2}}\end{array}$$

Notemos lo siguiente

$$\begin{array}{rl}x(t)& =c_1\cos (\omega t)+c_2\sin (\omega t)\\ & =A{\displaystyle \frac{c_1}{A}}\cos (\omega t)+A{\displaystyle \frac{c_2}{A}}\sin (\omega t)\\ & =[A\sin (\varphi )]\cos (\omega t)+[A\cos (\varphi )]\sin (\omega t)\\ & =A\sin (\omega t)\cos (\varphi )+A\cos (\omega t)\sin (\varphi )\end{array}$$

Si en la última expresión aplicamos la identidad trigonométrica

$$\begin{array}{}\text{(19)}& \sin (a+b)=\sin (a)\cos (b)+\cos (a)\sin (b)\end{array}$$

entonces obtenemos la solución ($\text{13}$) en una forma alterna más simple.

$$\begin{array}{}\text{(20)}& x(t)=A\sin (\omega t+\varphi )\end{array}$$

En resumen, la ecuación que describe el movimiento armónico simple o movimiento libre no amortiguado es

$${\displaystyle \frac{d^{2}x}{d{t}^2}}+{\omega }^{2}x=0$$

Y las soluciones que representan el movimiento del objeto son

$$x(t)=c_1\cos (\omega t)+c_2\sin (\omega t)$$

o bien,

$$x(t)=A\sin (\omega t+\varphi )$$

Movimiento libre amortiguado

Es claro que el movimiento libre no amortiguado es un movimiento ideal, pues el movimiento descrito por ($\text{13}$) o ($\text{20}$) supone que no hay fuerzas retardadoras actuando sobre el objeto y sabemos que, a menos que el objeto este suspendido en un vacío perfecto, siempre habrá por lo menos una fuerza de resistencia debido al medio circundante, por ejemplo la resistencia del aire.

El propósito ahora, al igual que antes, es determinar la ecuación diferencial o modelo matemático que describe al sistema cuando existen fuerzas de amortiguamiento, para posteriormente determinar la ecuación general de movimiento.

Consideremos nuevamente un objeto de masa $m$ suspendido sobre un resorte con constante $k$, pero en esta ocasión consideremos que existe una fuerza externa de amortiguamiento actuando sobre el objeto. En el estudio de la mecánica, las fuerzas de amortiguamiento que actúan sobre un cuerpo se consideran proporcionales a una potencia de la velocidad instantánea ${\displaystyle \frac{dx}{dt}}$. En nuestro caso supondremos que la fuerza de amortiguamiento esta dada por un múltiplo constante de la velocidad, esto es

$$\begin{array}{}\text{(21)}& F_{am}=\eta {\displaystyle \frac{dx}{dt}}\end{array}$$

donde $\eta$ es una constante de amortiguamiento positiva. De esta manera, cuando ninguna otra fuerza actúa sobre el sistema, de la segunda ley de Newton se tiene que

$$\begin{array}{}\text{(22)}& m{\displaystyle \frac{d^{2}x}{d{t}^2}}=-kx-\eta {\displaystyle \frac{dx}{dt}}\end{array}$$

El signo negativo en la fuerza de amortiguamiento indica que dicha fuerza actúa en dirección opuesta al movimiento.

Si dividimos la ecuación diferencial ($\text{22}$) por $m$ y reordenamos, obtenemos

$$\begin{array}{}\text{(23)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+{\displaystyle \frac{\eta }{m}}{\displaystyle \frac{dx}{dt}}+{\displaystyle \frac{k}{m}}x=0\end{array}$$

Recordemos que

$${\omega }^2={\displaystyle \frac{k}{m}}$$

y por convención definimos

$$\begin{array}{}\text{(24)}& 2\rho ={\displaystyle \frac{\eta }{m}}\end{array}$$

Así podemos reescribir la ecuación ($\text{23}$) como

$$\begin{array}{}\text{(25)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+2\rho {\displaystyle \frac{dx}{dt}}+{\omega }^{2}x=0\end{array}$$

Esta ecuación corresponde al modelo matemático que describe al fenómeno. La utilidad de $2\rho$ se hace evidente al momento de intentar resolver la ecuación, pues si se considera la solución

$$x(x)=e^{rt}$$

y se sustituye en la ecuación ($\text{25}$) junto con las derivadas correspondientes se obtiene la ecuación auxiliar

$$\begin{array}{}\text{(26)}& r^2+2\rho r+{\omega }^2=0\end{array}$$

De donde se obtienen las siguientes dos raíces.

$$\begin{array}{}\text{(27)}& r_1=-\rho +\sqrt{{\rho }^2-{\omega }^2}y{r}_2=-\rho -\sqrt{{\rho }^2-{\omega }^2}\end{array}$$

Hay tres casos posibles dependiendo del valor del discriminante

$$\begin{array}{}\text{(28)}& \mathrm{\Delta }={\rho }^2-{\omega }^2\end{array}$$

Estudiemos cada caso.

Caso 1: ${\rho }^2-{\omega }^2>0$

En este caso decimos que el sistema se encuentra sobreamortiguado porque el coeficiente de amortiguamiento $\rho$ es más grande que la constante del resorte $k$. Como las raíces son reales y distintas, la solución de la ecuación ($\text{25}$), en este caso, es

$$x(t)=c_1{e}^{r_{1}t}+c_2{e}^{r_{2}t}$$

Si sustituimos los valores de ($\text{27}$) podemos reescribir la solución como

$$\begin{array}{}\text{(29)}& x(t)=e^{-\rho t}(c_1{e}^{\sqrt{{\rho }^2-{\omega }^2}t}+c_2{e}^{-\sqrt{{\rho }^2-{\omega }^2}t})\end{array}$$

Esta ecuación representa un movimiento uniforme y no oscilatorio.

Caso 2: ${\rho }^2-{\omega }^2=0$

En este caso cualquier ligera disminución en la fuerza de amortiguamiento daría como resultado un movimiento oscilatorio, decimos que el sistema está críticamente amortiguado. Como las raíces son reales e iguales, la solución de la ecuación ($\text{25}$) es

$$x(t)=c_1{e}^{r_{1}t}+c_{2}t{e}^{r_{1}t}$$

Si sustituimos $r_1=-\rho$, la solución se puede reescribir como

$$\begin{array}{}\text{(30)}& x(t)=e^{-\rho t}(c_1+c_{2}t)\end{array}$$

Caso 3: ${\rho }^2-{\omega }^2<0$

En este caso se dice que el sistema esta subamortiguado ya que el coeficiente de amortiguamiento es más pequeño que la constante del resorte. Las raíces son complejas y están dadas de la siguiente forma

$$\begin{array}{}\text{(31)}& r_1=-\rho +i\sqrt{{\omega }^2-{\rho }^2}y{r}_2=-\rho -i\sqrt{{\omega }^2-{\rho }^2}\end{array}$$

Identificamos que

$$\alpha =-\rho y\beta =\sqrt{{\omega }^2-{\rho }^2}$$

Entonces la solución está dada por

$$\begin{array}{}\text{(32)}& x(t)=e^{-\rho t}[c_1\cos \left(\sqrt{{\omega }^2-{\rho }^2}t\right)+c_2\sin \left(\sqrt{{\omega }^2-{\rho }^2}t\right)]\end{array}$$

El movimiento descrito por ($\text{32}$) es oscilatorio, pero debido al coeficiente $e^{-\rho t}$ las amplitudes de oscilación tienden a cero cuando $t\to \mathrm{\infty }$.

En todos los casos la solución contiene el factor de amortiguamiento $e^{-\rho t}$, $\rho >0$, lo que indica que los desplazamientos del objeto se vuelven despreciables conforme el tiempo $t$ aumenta.

De manera totalmente análoga que en el caso sin amortiguamiento, cualquier solución de la forma ($\text{32}$) se puede escribir de forma alterna como

$$\begin{array}{}\text{(33)}& x(t)=A{e}^{-\rho t}\sin (\sqrt{{\omega }^2-{\rho }^2}t+\varphi )\end{array}$$

donde $A$ es la amplitud de las oscilaciones y el ángulo de fase $\varphi$ se determina de las ecuaciones de ($\text{18}$). El coeficiente $A{e}^{-\rho t}$ se denomina amplitud amortiguada de oscilaciones y debido a que ($\text{33}$) no es una función periódica, el número

$$\begin{array}{}\text{(34)}& T_c={\displaystyle \frac{2\pi }{\sqrt{{\omega }^2-{\rho }^2}}}\end{array}$$

se llama cuasi periodo y es el intervalo de tiempo entre dos máximos sucesivos de $x(t)$, así mismo, el número

$$\begin{array}{}\text{(35)}& f_c={\displaystyle \frac{\sqrt{{\omega }^2-{\rho }^2}}{2\pi }}\end{array}$$

se llama cuasi frecuencia.

En resumen, la ecuación que describe el movimiento libre amortiguado es

$${\displaystyle \frac{d^{2}x}{d{t}^2}}+2\rho {\displaystyle \frac{dx}{dt}}+{\omega }^{2}x=0$$

Y las soluciones que representan el movimiento del objeto, dependiendo del valor del discriminante de la ecuación auxiliar, son

• Si ${\rho }^2-{\omega }^2>0\to x(t)=e^{-\rho t}(c_1{e}^{\sqrt{{\rho }^2-{\omega }^2}t}+c_2{e}^{-\sqrt{{\rho }^2-{\omega }^2}t})$

• Si ${\rho }^2-{\omega }^2=0\to x(t)=e^{-\rho t}(c_1+c_{2}t)$

• Si ${\rho }^2-{\omega }^2<0\to x(t)=A{e}^{-\rho t}\sin (\sqrt{{\omega }^2-{\rho }^2}t+\varphi )$

Movimiento forzado

Imaginemos que ahora, adicional a las situaciones anteriores, se ejerce una fuerza externa sobre el soporte del resorte. En los dos casos anteriores considerábamos al soporte fijo, pero en esta ocasión pensamos en una fuerza motriz que causa un movimiento vertical oscilatorio del soporte del resorte. Sea $F_{ext}(t)$ dicha fuerza externa, usando la segunda ley de Newton, la ecuación diferencial queda de la siguiente forma.

$$\begin{array}{}\text{(36)}& m{\displaystyle \frac{d^{2}x}{d{t}^2}}=-kx-\eta {\displaystyle \frac{dx}{dt}}+F_{ext}(t)\end{array}$$

Si dividimos la ecuación por $m$ y definimos

$$\begin{array}{}\text{(37)}& g(t)={\displaystyle \frac{F_{ext}(t)}{m}}\end{array}$$

además de considerar las definiciones anteriores ($\text{9}$) y ($\text{24}$), podemos escribir la ecuación diferencial como

$$\begin{array}{}\text{(38)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+2\rho {\displaystyle \frac{dx}{dt}}+{\omega }^{2}x=g(t)\end{array}$$

La ecuación ($\text{38}$) representa el modelo matemático que describe al sistema con movimiento forzado. Esta ecuación es no homogénea, de manera que puede resolverse usando el método de coeficientes indeterminados o el de variación de parámetros.

Cuando $g$ es una función periódica, como

$$g(t)=g_0\sin (\lambda t)og(t)=g_0\cos (\lambda t)$$

con $\lambda$ una constante, la solución general de ($\text{38}$) para $\rho >0$ es la suma de una función no periódica $x_{np}(t)$ (solución complementaria o solución de la ecuación homogénea asociada) y una función periódica $x_p(t)$ (solución particular de la ecuación no homogénea), en la que $x_{np}(t)$ se desvanece a medida que el tiempo incrementa, es decir,

$$\begin{array}{}\text{(39)}& \underset{t\to \mathrm{\infty }}{lim}{x}_{np}(t)=0\end{array}$$

Esta propiedad nos indica que para valores grandes de tiempo, los desplazamientos del objeto se aproximan mediante la solución particular $x_p(t)$.

La función complementaria $x_{np}(t)$ se denomina término transitorio o solución transitoria, mientras que la solución particular $x_p(t)$ se denomina término de estado estable o solución de estado estable.

Realicemos un ejemplo en el que apliquemos cada caso

Ejemplo: Considerar un resorte sujeto de manera vertical a un soporte. El resorte se estira $50cm$ al aplicarle una fuerza de $4N$. En la parte inferior del resorte se coloca un objeto con peso de $19.6N$. Al objeto se le aleja de su posición de equilibrio jalándolo $1m$ hacia abajo, si se suelta sin aplicarle una velocidad inicial, estudiar el movimiento del objeto en los siguientes casos:

• No hay resistencia del aire (movimiento libre no amortiguado).

• Hay resistencia del aire y es de $F_{am}=8{\displaystyle \frac{dx}{dt}}$ (movimiento libre amortiguado).

• Además de la resistencia del aire, hay una fuerza aplicada al soporte de $F_{ext}(t)=80\sin (2t)$ (movimiento forzado).

Solución: El peso del objeto es

$$W=19.6N$$

entonces su masa es

$$m={\displaystyle \frac{W}{g}}={\displaystyle \frac{19.6}{9.8}}$$

Es decir, $m=2kg$. Por otro lado, si el resorte se estira

$$s=0.5m$$

aplicando una fuerza de

$$F=4N$$

por la ley de Hooke tenemos que la constante del resorte es

$$k={\displaystyle \frac{F}{s}}={\displaystyle \frac{4}{0.5}}$$

Es decir, $k=8N/m$. Las condiciones iniciales son $x(0)=1$ (posición fuera de la posición de equilibrio) y $x^{\prime }(0)=0$ (sin velocidad inicial).

Para la primera situación sabemos que

$$F_{am}=0y{F}_{ext}=0$$

De manera que la ecuación que describe al sistema es ($\text{10}$) con

$${\omega }^2={\displaystyle \frac{k}{m}}={\displaystyle \frac{8}{2}}=4$$

Así, la ecuación a resolver es

$${\displaystyle \frac{d^{2}x}{d{t}^2}}+4x=0$$

La ecuación auxiliar es

$$r^2+4=0$$

Las raíces son $r_1=i2$ y $r_2=-i2$. Identificamos que $\alpha =0$ y $\beta =2$. Por lo tanto, la solución general es

$$x(t)=c_1\cos (2t)+c_2\sin (2t)$$

Para aplicar las condiciones iniciales debemos conocer la expresión de la primera derivada de la solución, dicha expresión es

$${\displaystyle \frac{dx}{dt}}=-2c_1\sin (2t)+2c_2\cos (2t)$$

Aplicando las condiciones iniciales, tenemos

$$x(0)=c_1=1y{x}^{\prime }(0)=2c_2=0$$

De donde $c_1=1$ y $c_2=0$. Por lo tanto, la ecuación de movimiento es

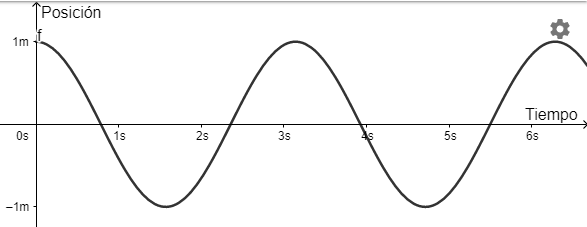
$$x(t)=\cos (2t)$$

Esta solución representa un movimiento armónico de amplitud

$$A=1m$$

periodo

$$T={\displaystyle \frac{2\pi }{2}}=\pi seg$$

y frecuencia

$$f={\displaystyle \frac{1}{\pi }}=0.318{\displaystyle \frac{ciclos}{segundo}}$$

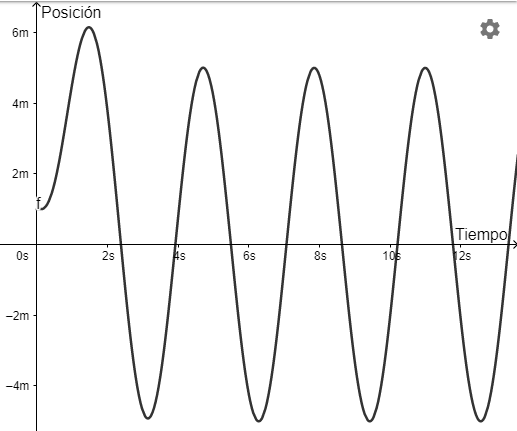
A continuación se muestra una gráfica con el movimiento descrito por el objeto.

De la gráfica observamos que el objeto siempre se mantendrá oscilando de la misma manera para $t\to \mathrm{\infty }$ y tiene sentido ya que no existe ninguna fuerza exterior que lo amortigüe.

Consideremos ahora la resistencia del aire

$$F_{am}=8{\displaystyle \frac{dx}{dt}}$$

En este caso la ecuación a resolver es de la forma ($\text{22}$) y es

$$m{\displaystyle \frac{d^{2}x}{d{t}^2}}+kx+8{\displaystyle \frac{dx}{dt}}=0$$

que adaptando a nuestros datos se tiene

$${\displaystyle \frac{d^{2}x}{d{t}^2}}+4{\displaystyle \frac{dx}{dt}}+4x=0$$

La ecuación auxiliar es

$$r^2+4r+4=0$$

Las raíces son $r_1=r_2=-2$, como son iguales, entonces la solución es de la forma

$$x(t)=e^{-2t}(c_1+c_{2}t)$$

La derivada es

$${\displaystyle \frac{dx}{dt}}=-2e^{-2t}(c_1+c_{2}t)+c_2{e}^{-2t}$$

Apliquemos las condiciones iniciales.

$$x(0)=c_1=1y{x}^{\prime }(0)=-2c_1+c_2=0$$

de donde obtenemos que $c_1=1$ y $c_2=2$. Por lo tanto, la ecuación de movimiento es

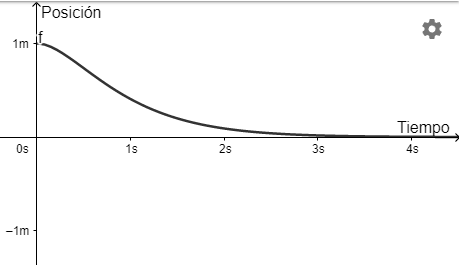
$$x(t)=e^{-2t}(1+2t)$$

El factor de amortiguamiento es $e^{-2t}$.

A continuación se muestra una gráfica con el movimiento descrito por el objeto.

De la gráfica observamos que no hay movimiento oscilatorio, sino que el objeto llega a la posición de equilibrio y se mantiene, esto se debe al factor de amortiguamiento.

Para la situación final tenemos un movimiento forzado con una fuerza externa

$$F_{ext}(t)=80\sin (2t)$$

La ecuación diferencial que tenemos en este caso es

$$m{\displaystyle \frac{d^{2}x}{d{t}^2}}=-kx-8{\displaystyle \frac{dx}{dt}}+80\sin (2t)$$

o bien

$${\displaystyle \frac{d^{2}x}{d{t}^2}}+4{\displaystyle \frac{dx}{dt}}+4x=40\sin (2t)$$

La solución de la ecuación homogénea ya la conocemos, ya que corresponde a la solución transitoria obtenida anteriormente.

$$x_{np}(t)=e^{-2t}(c_1+c_{2}t)$$

Para el caso no homogéneo se puede aplicar variación de parámetros o coeficientes indeterminados, apliquemos el segundo método.

Estamos en condiciones del punto 3. Proponemos una solución de la forma

$$x(t)=A\cos (2t)+B\sin (2t)$$

La primera y segunda derivada están dadas de la siguiente forma.

$${\displaystyle \frac{dx}{dt}}=-2A\sin (2t)+2B\cos (2t)y{\displaystyle \frac{d^{2}x}{d{t}^2}}=-4A\cos (2t)-4B\sin (2t)$$

Sustituimos en la ecuación diferencial.

$$\begin{array}{rl}[-4A\cos (2t)-4B\sin (2B)]& +4[-2A\sin (2t)+2B\cos (2t)]+4[A\cos (2t)+B\sin (2t)]\\ & =40\sin (2t)\end{array}$$

$$\begin{array}{rl}-8A\sin (2t)+8B\cos (2t)& =40\sin (2t)\\ -A\sin (2t)+B\cos (2t)& =5\sin (2t)\end{array}$$

Para que se cumpla la igualdad debe ocurrir que $A=-5$ y $B=0$, entonces la solución de estado estable es

$$x_p(t)=-5\cos (2t)$$

Por lo tanto, la solución general es

$$x(t)=x_{np}(t)+x_p(t)=e^{-2t}(c_1+c_{2}t)-5\cos (2t)$$

Vemos que

$${\displaystyle \frac{dx}{dt}}=-2e^{-2t}(c_1+c_{2}t)+c_2{e}^{-2t}+10\sin (2t)$$

Apliquemos las condiciones iniciales.

$$x(0)=c_1-5=1y{x}^{\prime }(0)=-2c_1+c_2=0$$

de donde $c_1=6$ y $c_2=12$. Entonces la ecuación de movimiento es

$$x(t)=e^{-2t}(6+12t)-5\cos (2t)$$

A continuación se muestra una gráfica con el movimiento descrito por el objeto.

Inicialmente el resorte sufre un estiramiento muy grande generando un movimiento transitorio y procede a amortiguarse hasta llegar al equilibrio entre la fuerza externa y la fuerza amortiguadora describiendo un movimiento estable.

La parte $e^{-2t}(6+12t)$ representa el movimiento transitorio, mientras que $-5\cos (2t)$ representa el movimiento estable.

También se puede observar que las amplitudes (el estiramiento del resorte) son bastante grandes comparado con las dos situaciones anteriores.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Resonancia

Resolvamos un problema de valores iniciales que nos permitirá definir el concepto de resonancia.

Resolver la ecuación

$$\begin{array}{}\text{(40)}& {\displaystyle \frac{d^{2}x}{d{t}^2}}+{\omega }^{2}x=g_0\sin (\lambda t)\end{array}$$

donde $g_0$ y $\lambda \ne \omega$ son constantes y los valores iniciales son $x(0)=0$ y $x^{\prime }(0)=0$.

Solución: Resolviendo la ecuación homogénea puedes verificar que la solución complementaria es

$$\begin{array}{}\text{(41)}& x_c(t)=c_1\cos (\omega t)+c_2\sin (\omega t)\end{array}$$

Para obtener una solución particular proponemos una solución de la forma

$$x_p(t)=A\cos (\lambda t)+B\sin (\lambda t)$$

y aplicamos el método de coeficientes indeterminados. Vemos que

$${\displaystyle \frac{d{x}_p}{dt}}=-A\lambda \sin (\lambda t)+B\lambda \cos (\lambda t)y{\displaystyle \frac{d^2{x}_p}{d{t}^2}}=-A{\lambda }^2\cos (\lambda t)-B{\lambda }^2\sin (\lambda t)$$

Sustituyamos en la ecuación diferencial.

$$\begin{array}{rl}[-A{\lambda }^2\cos (\lambda t)-B{\lambda }^2\sin (\lambda t)]& +{\omega }^2[A\cos (\lambda t)+B\sin (\lambda t)]\\ & =A({\omega }^2-{\lambda }^2)\cos (\lambda t)+B({\omega }^2-{\lambda }^2)\sin (\lambda t)\\ & =g_0\sin (\lambda t)\end{array}$$

Es claro que para que se cumpla la igualdad se debe satisfacer que

$$A=0yB={\displaystyle \frac{g_0}{{\omega }^2-{\lambda }^2}}$$

Por tanto, la solución particular es

$$\begin{array}{}\text{(42)}& x_p(t)={\displaystyle \frac{g_0}{{\omega }^2-{\lambda }^2}}\sin (\lambda t)\end{array}$$

Y la solución general es

$$\begin{array}{}\text{(43)}& x(t)=c_1\cos (\omega t)+c_2\sin (\omega t)+{\displaystyle \frac{g_0}{{\omega }^2-{\lambda }^2}}\sin (\lambda t)\end{array}$$

Verifica que aplicando las condiciones iniciales se obtiene que

$c_1=0y{c}_2=-{\displaystyle \frac{\lambda g_0}{\omega ({\omega }^2-{\lambda }^2)}}$

Por lo tanto, para $\lambda \ne \omega$, la solución es

$$\begin{array}{}\text{(44)}& x(t)={\displaystyle \frac{g_0}{\omega ({\omega }^2-{\lambda }^2)}}[-\lambda \sin (\omega t)+\omega \sin (\lambda t)]\end{array}$$

Este resultado no esta definido para $\lambda =\omega$, sin embargo podemos obtener su valor límite conforme $\lambda \to \omega$, esto produciría en ($\text{44}$) un incremento de forma sustancial de las amplitudes de oscilación.

Para $\lambda =\omega$ se define la solución como el límite $\lambda \to \omega$ de la ecuación ($\text{44}$).

$$\begin{array}{}\text{(45)}& x(t)=\underset{\lambda \to \omega }{lim}{g}_0{\displaystyle \frac{-\lambda \sin (\omega t)+\omega \sin (\lambda t)}{\omega ({\omega }^2-{\lambda }^2)}}\end{array}$$

Para resolver el límite apliquemos la regla de L´Hôpital.

La derivada del numerador con respecto a $\lambda$ es

$${\displaystyle \frac{d}{d\lambda }}[-\lambda \sin (\omega t)+\omega \sin (\lambda t)]=-\sin (\omega t)+t\omega \cos (\lambda t)$$

Y la derivada del denominador con respecto a $\lambda$ es

$${\displaystyle \frac{d}{d\lambda }}[{\omega }^3-\omega {\lambda }^2]=-2\omega \lambda$$

Sustituyendo en el límite ($\text{45}$) obtenemos

$$\begin{array}{rl}x(t)& =g_0\underset{\lambda \to \omega }{lim}{\displaystyle \frac{-\sin (\omega t)+t\omega \cos (\lambda t)}{-2\omega \lambda }}\\ & =g_0{\displaystyle \frac{-\sin (\omega t)+t\omega \cos (\omega t)}{-2{\omega }^2}}\\ & ={\displaystyle \frac{g_0}{2{\omega }^2}}\sin (\omega t)-{\displaystyle \frac{g_0}{2\omega }}t\cos (\omega t)\end{array}$$

Por lo tanto, para $\lambda =\omega$ la solución es

$$\begin{array}{}\text{(46)}& x(t)={\displaystyle \frac{g_0}{2{\omega }^2}}[\sin (\omega t)-t\omega \cos (\omega t)]\end{array}$$

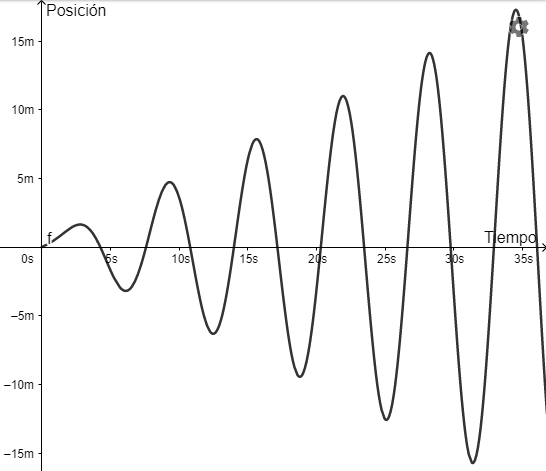
Conforme $t\to \mathrm{\infty }$ los desplazamientos del objeto se vuelven más largos, de hecho, $|x(t_n)|\to \mathrm{\infty }$ cuando $t_n={\displaystyle \frac{n\pi }{\omega }}$ para $n=1,2,3,\cdots$.

Este fenómeno se conoce como resonancia pura.

Una gráfica que muestra el comportamiento de ($\text{46}$) es la siguiente.

No profundizaremos más en el concepto de resonancia, pero cabe mencionar que la resonancia pura es una situación ideal, pues físicamente las oscilaciones grandes del objeto forzarían en algún momento al resorte más allá de su límite elástico, además en el desarrollo realizado no se han toman en cuenta efectos retardadores de las fuerzas de amortiguamiento que siempre están presentes.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Resolver los siguientes problemas:

1. Un resorte cuelga verticalmente; su extremo superior está fijo y del inferior pende una caja que pesa $196N$. Una vez en equilibrio se tira de la caja hacia abajo haciéndola desplazar $0.25m$ y se suelta. Sabiendo que $k=80N/m$ y que la resistencia del aire es despreciable, hallar:

• La ecuación de movimiento de la caja.

• El tiempo necesario para que la caja se mueva desde la posición inicial hasta $0.0625m$ por debajo de la posición de equilibrio.

2. Una masa de $98N$ de peso se cuelga de un resorte con lo que éste interrumpe su estado de reposo. Sabiendo que $k=4.9N/m$, hallar el movimiento de la masa si al soporte del resorte se le imprime una fuerza $F_{ext}(t)=\sin (\sqrt{2g}t)$.

3. Se suspende una masa de $10kg$ de un resorte, el cual se alarga $0.6533m$. La masa se pone en movimiento desde la posición de equilibrio con una velocidad inicial $1m/s$, dirigida hacia arriba. Hallar el movimiento resultante si la fuerza debida al aire es $F_{am}=80{\displaystyle \frac{dx}{dt}}$.

4. De un resorte que tiene una constante $k=50$ se suspende un peso de $49N$. El peso se pone en movimiento desde el reposo estirándolo $0.98m$ hacia abajo de la posición de equilibrio y aplicando una fuerza externa $F_{ext}(t)=10\sin (2t)$. Si no hay resistencia del aire, hallar el movimiento del peso.

5. Se cuelga de un resorte una masa de $2kg$, de tal manera que el resorte se alarga $0.6125m$. A esta masa se le aleja de su posición de equilibrio jalándola $1m$ hacia arriba y se suelta. Hallar el movimiento resultante de la masa sabiendo que hay una resistencia del aire de $F_{am}=16{\displaystyle \frac{dx}{dt}}$.

Más adelante…

Es momento de estudiar el caso en el que los coeficientes no son constantes, es decir, estudiaremos ecuaciones diferenciales de la forma

$$a(x){\displaystyle \frac{d^{2}y}{d{x}^2}}+b(x){\displaystyle \frac{dy}{dx}}+c(x)=g(x)$$

Donde $a(x)$, $b(x)$ y $c(x)$ son funciones de la variable independiente $x$.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Ecuación de Cauchy – Euler
• Siguiente entrada del curso: Ecuaciones lineales de segundo orden con coeficientes variables – Soluciones en series de potencias respecto a puntos ordinarios

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»