Geometría Moderna I: Cuadrángulo ortocéntrico

Introducción

En esta entrada veremos que los cuatro triángulos que se forman con los vértices de un cuadrángulo ortocéntrico, tienen la misma circunferencia de los nueve puntos y derivaremos algunas otras propiedades.

Cuadrángulo ortocéntrico

Definición. Un cuadrángulo ortocéntrico es el conjunto de puntos formado por los vértices de un triángulo y su ortocentro.

Nos referiremos a los cuatro triángulos que se pueden formar con los cuatro puntos de un cuadrángulo ortocéntrico como grupo ortocéntrico de triángulos.

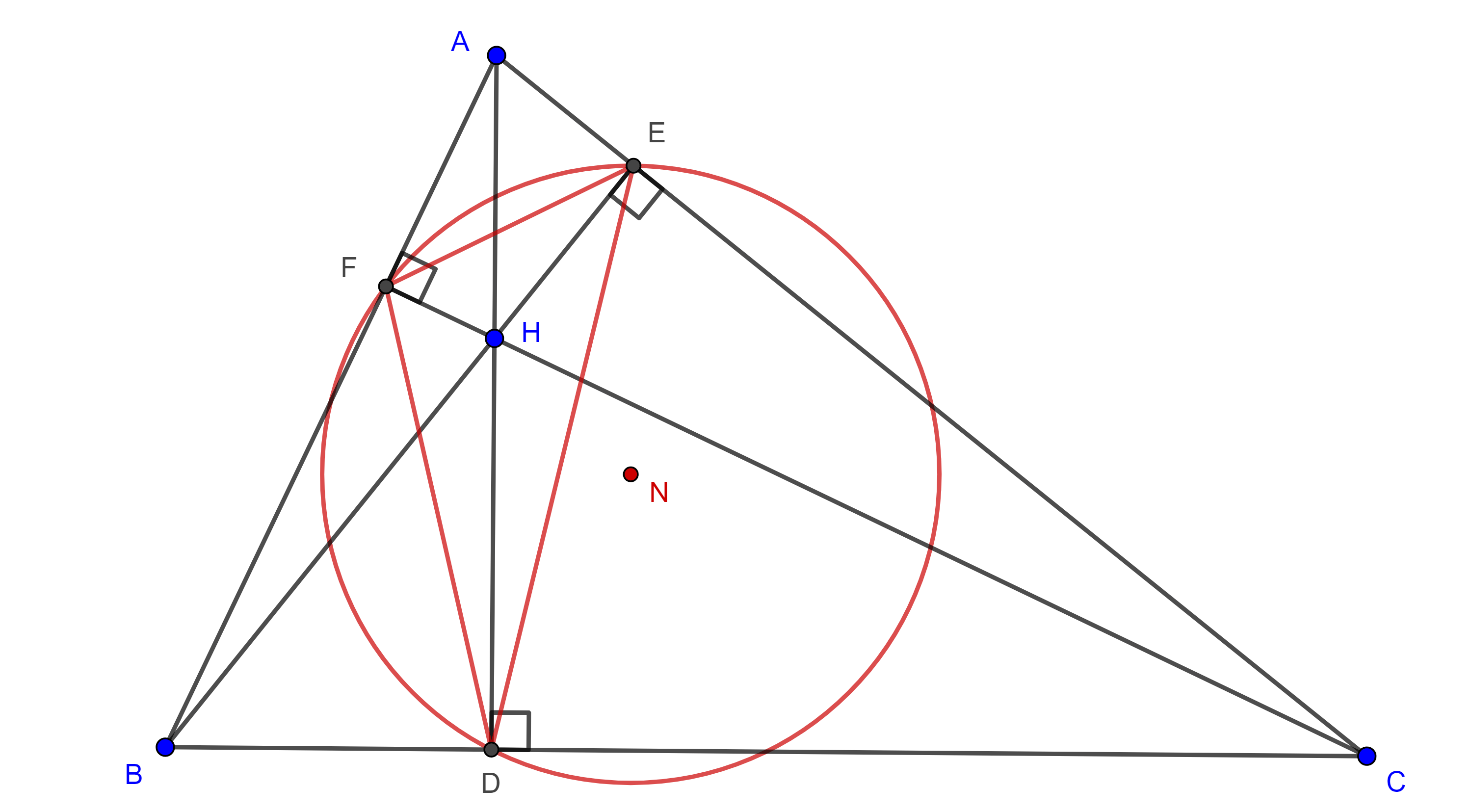
Teorema 1. Cualquier punto de un cuadrángulo ortocéntrico es el ortocentro del triángulo formado por los otros tres puntos y los triángulos de este grupo ortocéntrico tienen el mismo triangulo órtico.

Demostración. Sea $△ A B C$ y $H$ su ortocentro.

Notemos que el ortocentro de $△ B H C$ es $A$ pues $A B ⊥ H C$ , $A H ⊥ B C$ y $A C ⊥ H B$ .

De manera análoga podemos ver que $B$ es el ortocentro de $△ A H C$ y $C$ es el ortocentro de $△ A H B$ .

Por otro lado, los pares de rectas perpendiculares $A H$ , $B C$ ; $B H$ , $A C$ y $C H$ , $A B$ , se intersecan en $D$ , $E$ y $F$ , respectivamente.

Por lo tanto, estos tres puntos son fijos, así el triángulo órtico es el mismo para los cuatro triángulos $△ A B C$ , $△ H A B$ , $△ H A C$ y $△ H B C$ .

Corolario 1. Las circunferencias de los nueve puntos de un grupo ortocéntrico de triángulos coinciden y sus circunradios son iguales.

Demostración. Como el circuncírculo del triángulo órtico de un triángulo dado es la circunferencia de los nueve puntos, por el teorema 1, los triángulos de un grupo ortocéntrico tienen la misma circunferencia de los nueve puntos.

En la entrada anterior vimos que el radio de la circunferencia de los nueve puntos es igual a la mitad del circunradio de su triángulo de referencia.

Por lo tanto, $△ A B C$ , $△ H A B$ , $△ H A C$ y $△ H B C$ tienen el mismo circunradio (figura 1).

Circuncentros

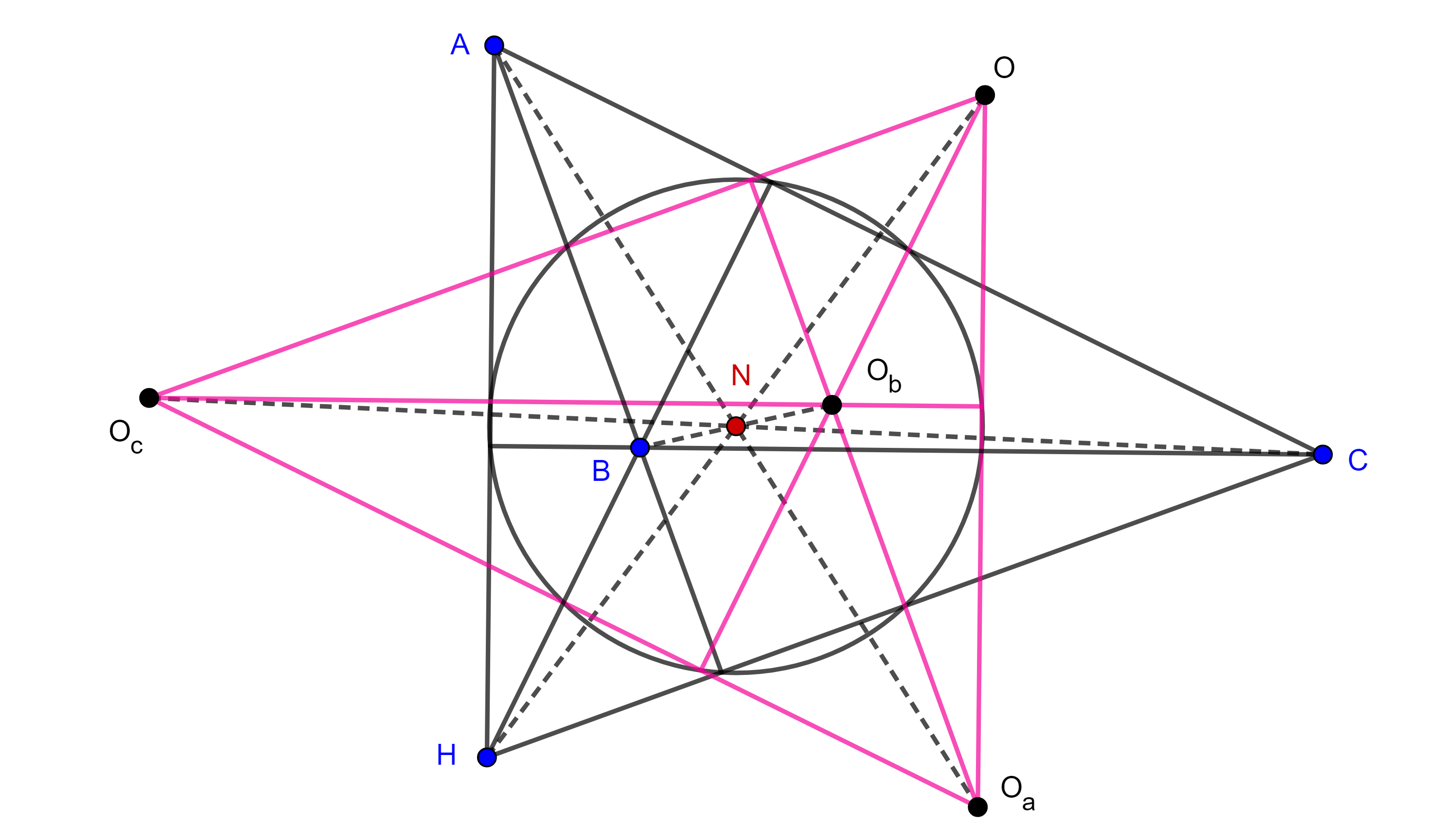
Teorema 2. Los circuncentros de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Por el teorema 2 de la entrada anterior, sabemos que el circuncentro de un triángulo es la reflexión de su ortocentro respecto de $N$ , el centro de los nueve puntos.

Como los triángulos de un grupo ortocéntrico tienen el mismo centro de los nueve puntos, los circuncentros $O_{a}$ , $O_{b}$ , $O_{c}$ y $O$ de $△ H B C$ , $△ H A C$ , $△ H A B$ y $△ A B C$ son las reflexiones de $A$ , $B$ , $C$ y $H$ respectivamente respecto a $N$ .

Dado que una reflexión es una homotecia de razón $- 1$ entonces las figuras $A B C H$ y $O_{a} O_{b} O_{c} O$ son congruentes y por lo tanto $O_{a} O_{b} O_{c} O$ es un cuadrángulo ortocéntrico.

Corolario 2. Un grupo ortocéntrico de triángulos y el grupo ortocéntrico de triángulos formado por sus circuncentros tienen la misma circunferencia de los nueve puntos.

Demostración. Como las figuras $A B C H$ y $O_{a} O_{b} O_{c} O$ son simétricas respecto a $N$ entonces también sus circunferencias de los nueve puntos son simétricas respecto a $N$ .

Como $N$ es el centro de una de estas circunferencias, entonces coinciden.

Observación. Notemos que como $O_{a} O_{b} O_{c} O$ es un grupo ortocéntrico de triángulos, entonces la reflexión de sus ortocentros respecto al centro de los nueve puntos $N$ será el conjunto de sus circuncentros.

Entonces $A$ , $B$ , $C$ y $H$ son los circuncentros de $△ O_{b} O_{c} O$ , $△ O_{a} O_{c} O$ , $△ O_{a} O_{b} O$ y $△ O_{a} O_{b} O_{c}$ respectivamente.

Problema. Construye un triángulo $△ A B C$ dados el centro de los nueve puntos $N$ y los circuncentros $O_{b}$ y $O_{c}$ de los triángulos $△ C A H$ y $△ A B H$ respectivamente donde $H$ es el ortocentro de $△ A B C$ .

Solución. $O_{b}$ y $O_{c}$ son los ortocentros de $△ O_{a} O_{c} O$ y $△ O_{a} O_{b} O$ respectivamente y si los reflejamos respecto a $N$ obtendremos a los circuncentros de sus respectivos triángulos, estos son los vértices $B$ y $C$ del triángulo requerido.

Ahora tenemos dos vértices y el centro de los nueve puntos, este problema lo resolvimos en la entrada anterior.

Centroices

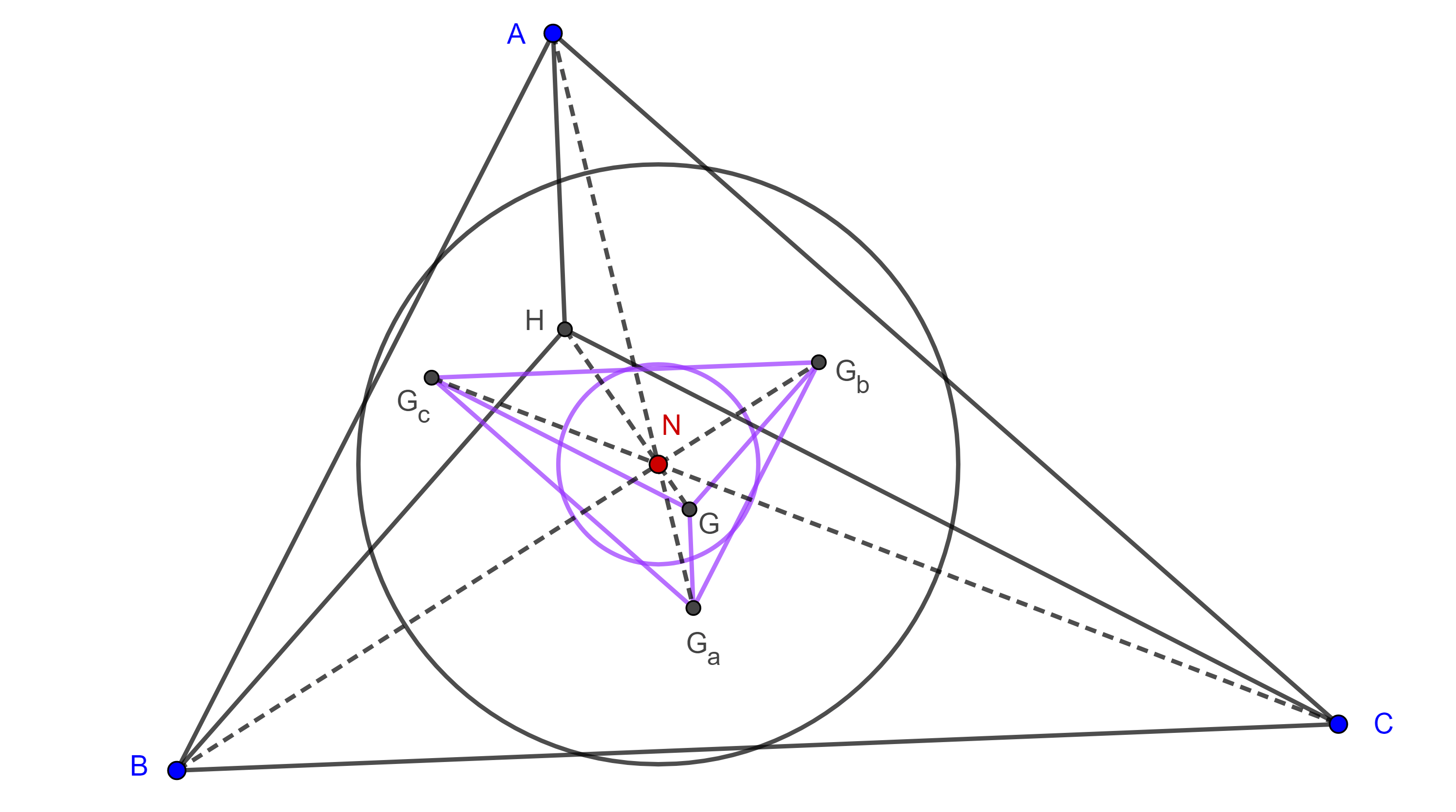
Teorema 3. Los cuatro centroides de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Sea $△ A B C$ y $H$ su ortocentro.

Sabemos que el centro de los nueve puntos $N$ de $△ A B C$ divide internamente al segmento $H G$ en razón $3 : 1$ , donde $G$ es el centroide de $△ A B C$ .

Como el grupo ortocéntrico de triángulos $△ A B C$ , $△ H B C$ , $△ H A C$ , $△ H A B$ tienen el mismo centro de los nueve puntos $N$ , entonces sus respectivos centroides $G$ , $G_{a}$ , $G_{b}$ , $G_{c}$ están en homotecia con $H$ , $A$ , $B$ , $C$ respectivamente desde $N$ y la razón de homotecia es $- 3$ .

Como dos figuras homotéticas son semejantes, entonces $G G_{a} G_{b} G_{c}$ es un cuadrángulo ortocéntrico.

Corolario 3. La circunferencia de los nueve puntos de un grupo ortocéntrico de triángulos y la circunferencia de los nueve puntos del grupo ortocéntrico formado por sus centroides son concéntricas.

Demostración. Como las figuras $H A B C$ y $G G_{a} G_{b} G_{c}$ están en homotecia desde el centro de los nueve puntos $N$ de $△ A B C$ entonces sus respetivas circunferencias de los nueve puntos también están en homotecia desde $N$ .

Como $N$ es el centro de una de ellas, entonces son concéntricas.

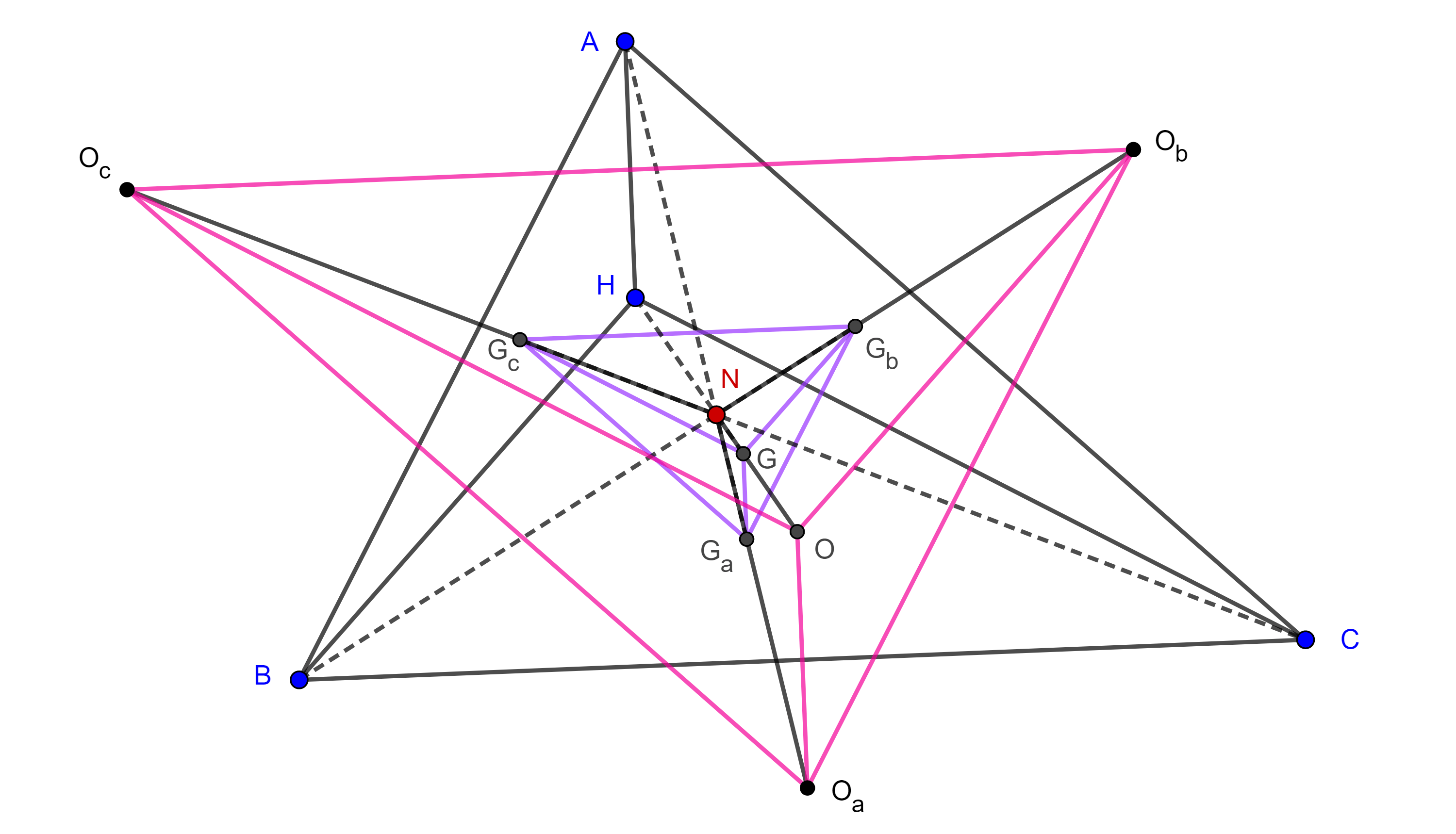
Corolario 4. Dado un cuadrángulo ortocéntrico, el cuadrángulo ortocéntrico formado por sus circuncentros y el cuadrángulo ortocéntrico formado por sus centroides tienen el mismo centro de los nueve puntos y además existe una homotecia entre ellos con centro en este punto.

Demostración. Por los corolarios 2 y 3, $O O_{a} O_{b} O_{c}$ y $G G_{a} G_{b} G_{c}$ tienen el mismo centro de los nueve puntos que $H A B C$ y son homotéticos con este último precisamente desde $N$ en razón $- 1$ y $- 3$ respectivamente.

Por lo tanto, existe una homotecia con centro en $N$ y razón $3$ que lleva a $G G_{a} G_{b} G_{c}$ en $O O_{a} O_{b} O_{c}$ .

Incentro y excentros

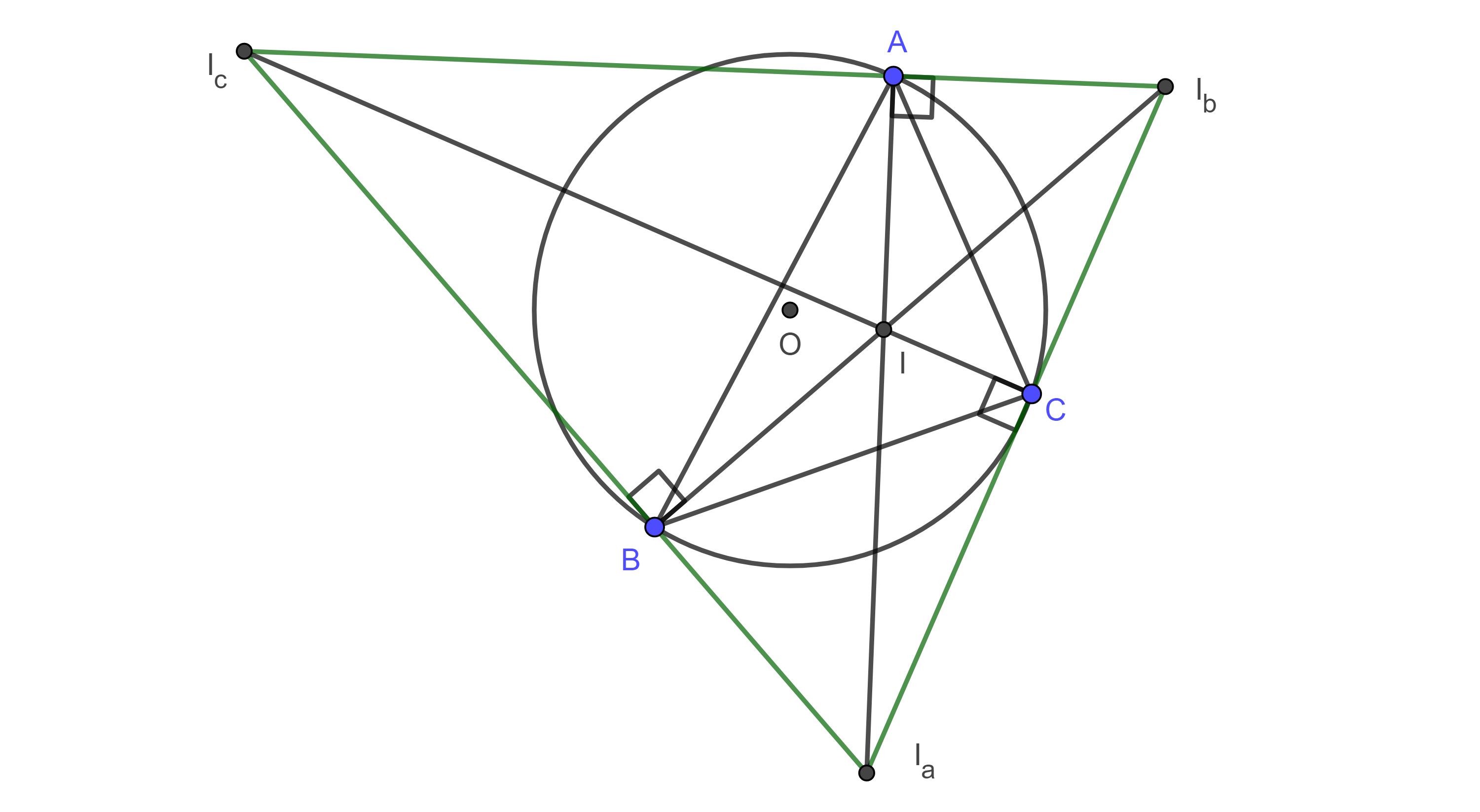
Teorema 4. El incentro y los excentros de un triángulo dado forman un cuadrángulo ortocéntrico y el circuncírculo del triángulo dado es la circunferencia de los nueve puntos de este grupo ortocéntrico de triángulos.

Demostración. Como las bisectrices interna y externa de los ángulos de un triángulo $△ A B C$ son perpendiculares entre si entonces el incentro $I$ es el ortocentro del triángulo formado por los excentros $△ I_{a} I_{b} I_{c}$ y el triángulo $△ A B C$ es el triángulo órtico de $△ I_{a} I_{b} I_{c}$ .

Entonces, por el teorema 1 y corolario 1, $I_{a} I_{b} I_{c} I$ es un grupo ortocéntrico de puntos y su circunferencia de los nueve puntos es el circuncírculo de $△ A B C$ .

Proposición. El segmento que une el ortocentro de un triángulo dado con el circuncentro del triángulo formado por los excentros del triángulo dado es bisecado por el incentro del triángulo medial del triángulo dado.

Demostración. Sea $△ A B C$ un triángulo, $I$ , $I_{a}$ , $I_{b}$ , $I_{c}$ , el incentro y sus respectivos excentros, $O$ y $O_{e}$ los circuncentros de $△ A B C$ y $△ I_{a} I_{b} I_{c}$ respectivamente.

Por el teorema anterior, $I$ y $O$ son el ortocentro y el centro de los nueve puntos respectivamente de $△ I_{a} I_{b} I_{c}$ , por lo tanto, $O$ es el punto medio de $I O_{e}$ .

Sean $H$ y $G$ el ortocentro y el centroide respectivamente de $△ A B C$ , como $H$ , $G$ y $O$ son colineales y $G$ triseca el segmento $O H$ , entonces, $G$ es el centroide de $△ I O_{e} H$ .

Por lo tanto, $I G$ biseca a $O_{e} H$ en $I^{'}$ y $\frac{I G}{2} = G I^{'}$ .

Por otro lado, sabemos que existe una homotecia con centro en $G$ y razón $\frac{- 1}{2}$ , que lleva a $△ A B C$ , a su triangulo medial $△ A^{'} B^{'} C^{'}$ , por lo que sus respectivos incentros $I$ y $I_{m}$ son puntos homólogos de esta homotecia, es decir $I$ , $G$ y $I_{m}$ son colineales y $G$ triseca al segmento $I I_{m}$ .

Como $I^{'}$ cumple con estas características entonces $I^{'} = I_{m}$ .

Más adelante…

En la próxima entrada estudiaremos otra recta notable del triángulo, la recta de Simson, veremos que la intersección de dos rectas de Simson se intersecan en la circunferencia de los nueve puntos y que cierto conjunto de rectas de Simson forman un cuadrángulo ortocéntrico.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que las rectas de Euler de los cuatro triángulos de un grupo ortocéntrico son concurrentes.
Demuestra que el simétrico del circuncentro de un triángulo con respecto a uno de los lados del triángulo coincide con el simétrico del vértice opuesto al lado considerado respecto al centro de los nueve puntos del triángulo.
Muestra que los vértices de un grupo ortocéntrico de triángulos pueden ser considerados como los centroides de otro grupo ortocéntrico de triángulos.
Sea $△ A B C$ un triángulo rectángulo con $∠ A = \frac{π}{2}$ , $D$ el pie de la altura por $A$ , las bisectrices de $∠ B A D$ y $∠ D A C$ intersecan a $B C$ en $P$ y $P^{'}$ respectivamente. Las bisectrices de $∠ D B A$ y $∠ A C D$ intersecan a $A D$ en $Q$ y $Q^{'}$ respectivamente.
$i)$ Muestra que $P P^{'} Q Q^{'}$ es un cuadrángulo ortocéntrico,
$i i)$ si $I$ , $J$ y $K$ son los incentros de $△ A B C$ , $△ A B D$ y $△ A D C$ , muestra que $A I J K$ es un cuadrángulo ortocéntrico.
Prueba que la suma de los cuadrados de dos segmentos no adyacentes que unen vértices de un cuadrángulo ortocéntrico es igual al cuadrado del circundiámetro de los triángulos de este grupo ortocéntrico.
Construye un triángulo $△ A B C$ dados su circuncentro $O$ , y los circuncentros de los triángulos $△ I I_{b} I_{c}$ y $△ I I_{a} I_{c}$ , donde $I$ , $I_{a}$ , $I_{b}$ y $I_{c}$ es el incentro y los excentros de $△ A B C$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Circunferencia de los nueve puntos.
Siguiente entrada del curso: Recta de Simson.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 109-115.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 165-167.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 58.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Geometría Moderna I: Cuadrángulo ortocéntrico

Introducción

Cuadrángulo ortocéntrico

Circuncentros

Centroices

Incentro y excentros

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Me gusta esto:

Deja una respuesta Cancelar la respuesta

Introducción

Cuadrángulo ortocéntrico

Circuncentros

Centroices

Incentro y excentros

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Comparte esto:

Me gusta esto:

Deja una respuesta Cancelar la respuesta