Introducción
La entrada anterior definimos a las funciones complejas trigonométricas e hiperbólicas, a través de la exponencial compleja y vimos que tanto las funciones trigonométricas como las funciones hiperbólicas son periódicas, puesto que la función exponencial compleja es $2\pi i $-periódica. Al igual que en el caso real, podemos preguntarnos si es que existen las funciones inversas de estas funciones, por lo que nuestro objetivo en esta entrada será responder esa pregunta y en particular deducir y definir a las funciones inversas de dichas funciones.
Durante esta entrada utilizaremos nuevamente al logaritmo complejo para deducir a las funciones inversas. Es importante recordar, entrada 21, que la función logaritmo complejo es una función multivaluada, por lo que las funciones definidas en esta entrada serán también multivaluadas. Recordemos que aunque esta terminología no cumple con la definición habitual de función, desde que asigna más de un valor a cada elemento del dominio, es importante mencionar que cada una de las ramas de dichas funciones multivaluadas sí cumplen con la definición de función con la que estamos familiarizados. Más aún, cada una de las ramas cumple con muchas de las propiedades que conocemos para sus versiones reales.
Observación 23.1.
Como veremos en la entrada 26, la imagen de las funciones $\operatorname{sen}(w)$ y $\operatorname{cos}(w)$ es todo el plano complejo $\mathbb{C}$, por lo que dado $w\in\mathbb{C}$ siempre existirá $z\in\mathbb{C}$ que satisfaga $z = \operatorname{sen}(w)$ ó $z = \operatorname{cos}(w)$.
Proposición 23.1 (Funciones trigonométricas inversas.)
- $\operatorname{sen}^{-1}(z) = -i \operatorname{log}\left(iz +\sqrt{1-z^2}\right)$.
- $\operatorname{cos}^{-1}(z) = -i \operatorname{log}\left(z + i\sqrt{1-z^2}\right)$.
- $\operatorname{tan}^{-1}(z) = \dfrac{i}{2} \operatorname{log}\left(\dfrac{i+z}{i-z}\right)$, con $z\neq \pm i$.
- $\operatorname{cot}^{-1}(z) = -\dfrac{i}{2} \operatorname{log}\left(\dfrac{z+i}{z-i}\right)$, con $z\neq \pm i$.
- $\operatorname{sec}^{-1}(z) = \dfrac{1}{i} \operatorname{log}\left(\dfrac{1 + \sqrt{1-z^2}}{z}\right)$.
- $\operatorname{csc}^{-1}(z) = \dfrac{1}{i} \operatorname{log}\left(\dfrac{1 + \sqrt{z^2 – 1}}{z}\right)$.
Demostración.
- Sea $z = \operatorname{sen}(w)$. De acuerdo con la definición 22.1 tenemos que:
\begin{equation*}
z = \operatorname{sen}(w) = \frac{e^{iw} – e^{-iw}}{2i},
\end{equation*}de donde:
\begin{equation*}
(e^{iw})^2-i2z(e^{iw}) – 1 = 0.
\end{equation*}Notemos que esta última expresión es una ecuación cuadrática para la variable $e^{iw}$, por lo que podemos utilizar la fórmula general para resolver dicha ecuación. En este punto es importante que recordemos que la función compleja raíz cuadrada es una función multivaluada, por lo que nos dará dos raíces complejas, entonces:
\begin{equation*}
e^{iw} = \frac{2iz + \sqrt{4(1-z^2)}}{2} = iz + \sqrt{1-z^2}.
\end{equation*}Dependiendo de la rama que consideremos, la función $ \sqrt{1-z^2}$ nos determina dos raíces cuadradas de $1-z^2$. Estableciendo la rama de la función multivaluada $ \sqrt{1-z^2}$ con la que trabajaremos, podemos utilizar la proposición 20.1(6) obteniendo:
\begin{equation*}
iw = \operatorname{log}\left(iz + \sqrt{1-z^2}\right) + i2k\pi, \quad k\in\mathbb{Z}.
\end{equation*}Por lo que, para $k, n\in\mathbb{Z}$:
\begin{align*}
w &= \frac{1}{i}\operatorname{log}\left(iz + \sqrt{1-z^2}\right) + 2 k\pi\\
&= \frac{1}{i} \left[\operatorname{ln}\left|iz + \sqrt{1-z^2}\right| + i\left(\operatorname{Arg}\left(iz + \sqrt{1-z^2}\right) + 2n\pi\right)\right] + 2 k\pi\\
&= \frac{1}{i} \left[\operatorname{ln}\left|iz + \sqrt{1-z^2}\right| + i\left(\operatorname{Arg}\left(iz + \sqrt{1-z^2}\right) + 2m\pi\right)\right]\\
&= \frac{1}{i} \left[\operatorname{ln}\left|iz + \sqrt{1-z^2}\right| + i\operatorname{arg}\left(iz + \sqrt{1-z^2}\right)\right]\\
&= -i \operatorname{log}\left(iz + \sqrt{1-z^2}\right),
\end{align*}donde $m=k+n\in\mathbb{Z}$. - Se deja como ejercicio al lector
- Se deja como ejercicio al lector
- Sea $z = \operatorname{cot}(w)$. De acuerdo con la definición 22.2 sabemos que:
\begin{equation*}
\operatorname{cot}(w) = \frac{\operatorname{cos}(w)}{\operatorname{sen}(w)},
\end{equation*}donde $w \neq k \pi$, con $k\in\mathbb{Z}$.
Considerando lo anterior tenemos que:
\begin{equation*}
z = \operatorname{cot}(w) = i \left( \frac{e^{iw} + e^{-iw}}{e^{iw} – e^{-iw}}\right) = i \left( \frac{e^{i2w} + 1}{e^{i2w} – 1}\right),
\end{equation*}de donde:
\begin{equation*}
-iz = \frac{e^{i2w} + 1}{e^{i2w} – 1}\quad \Longrightarrow e^{i2w} = \frac{iz – 1}{iz + 1} = \frac{z + i}{z – i}.
\end{equation*}De acuerdo con la proposición 20.1(6) tenemos que:
\begin{equation*}
i2w = \operatorname{log}\left(\frac{z + i}{z – i}\right) + i2k \pi, \quad k\in\mathbb{Z}.
\end{equation*}Entonces, para $k,n\in\mathbb{Z}$:
\begin{align*}
w & = \frac{1}{2i} \operatorname{log}\left(\frac{z + i}{z – i}\right) + k \pi\\
& = \frac{1}{2i} \left[\operatorname{ln}\left|\frac{z + i}{z – i}\right| + i \left(\operatorname{Arg}\left(\frac{z+i}{z-i}\right) + 2\pi n\right) \right] + k \pi\\
& = \frac{1}{2i} \left[\operatorname{ln}\left|\frac{z + i}{z – i}\right| + i \left(\operatorname{Arg}\left(\frac{z+i}{z-i}\right) + 2\pi m\right) \right]\\
& = \frac{1}{2i} \left[\operatorname{ln}\left|\frac{z + i}{z – i}\right| + i \operatorname{arg}\left(\frac{z+i}{z-i}\right)\right]\\
& = -\frac{i}{2} \operatorname{log}\left(\frac{z + i}{z – i}\right),
\end{align*}donde $m=n+k \in\mathbb{Z}$. - Se deja como ejercicio al lector.
- Se deja como ejercicio al lector
$\blacksquare$
Observación 23.2.
Puesto que todas las funciones inversas, de las funciones trigonométricas, están dadas en términos de la función multivaluada logaritmo, entonces también dichas funciones son multivaluadas. Más aún, de acuerdo con la proposición 23.1, debe ser claro que se puede elegir una rama de alguna de estas funciones eligiendo primero una rama de la función multivaluada raíz cuadrada y luego una rama adecuada del logaritmo de modo que la función en cuestión esté bien definida.
Ejemplo 23.1.
Supongamos que $z$ es un número real en el intervalo $(-1,1)$. Veamos que si utilizamos las ramas principales de las funciones multivaluadas raíz cuadrada y logaritmo complejo entonces obtenemos la rama principal de la función inversa de la función real seno.
Solución. Sean $z=x+iy\in\mathbb{C}$. Consideremos a la funciones multivaluadas:
\begin{equation*}
F(z) = \operatorname{log}(z) \quad \text{y} \quad G(z) = \sqrt{1-z^2} = e^{\frac{1}{2} \operatorname{Log}(1-z^2)} e^{ik\pi}, \,\, k=0,1.
\end{equation*}
Para la primera función tenemos que su corte de rama está dado por los $z=x+iy\in\mathbb{C}$ tales que:
\begin{equation*}
-\pi < \operatorname{Arg}(z) \leq \pi \quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
\operatorname{Re}(z) = x \leq 0, \\
\\ \operatorname{Im}(z) = y = 0.
\end{array}
\right.
\end{equation*}
De manera análoga, para la segunda función tenemos que su corte de rama está dado por los $z=x+iy\in\mathbb{C}$ tales que:
\begin{equation*}
\left\{ \begin{array}{l}
\operatorname{Re}(1-z^2) = 1-x^2+y^2 \leq 0, \\
\\ \operatorname{Im}(1-z^2) = -2xy = 0.
\end{array}
\right.
\end{equation*}
Como trabajaremos con las ramas principales de ambas funciones y $z=x\in\mathbb{R}$, entonces los cortes de rama de cada función, son respectivamente:
\begin{equation*}
\left\{x\in\mathbb{R} : x\leq 0\right\} \quad \text{y} \quad \left\{x\in\mathbb{R} : |x|\geq 1\right\}.
\end{equation*}
Para $k=0$ tenemos de la segunda función que su rama principal es:
\begin{equation*}
g_0(z) := \sqrt{1-z^2} = e^{\frac{1}{2} \operatorname{Log}(1-z^2)}.
\end{equation*}
Como $|z|=|x|<1$, entonces la función $g_0$ está bien definida, más aún, tenemos que $ 0<1-z^2\leq 1$, por lo que $\operatorname{Arg}(1-z^2) = 0$, entonces:
\begin{equation*}
\operatorname{Log}(1-z^2) = \operatorname{ln}|1-z^2| + i \operatorname{Arg}(1-z^2) = \operatorname{ln}(1-z^2),
\end{equation*}de donde:
\begin{equation*}
e^{\frac{1}{2} \operatorname{Log}(1-z^2)} = \sqrt{1-x^2} \in \mathbb{R}^+.
\end{equation*}
Así, al considerar las ramas principales de ambas funciones tenemos que:
\begin{align*}
\operatorname{sen}^{-1}(z) & = -i \operatorname{Log}\left(iz +\sqrt{1-z^2}\right)\\
& = -i \operatorname{Log}\left(iz + e^{\frac{1}{2} \operatorname{Log}(1-z^2)}\right)\\
& = -i \operatorname{Log}\left(ix + \sqrt{1-x^2}\right).
\end{align*}
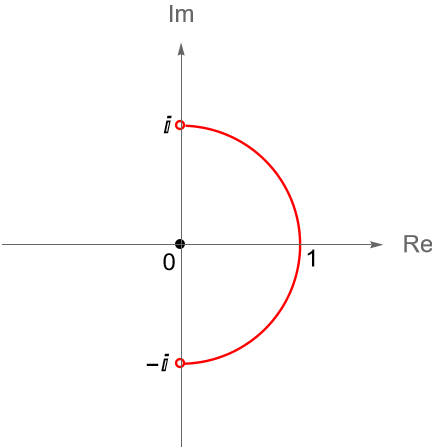
Dado que $iz$ es un número imaginario puro, entonces los valores que toma $iz + e^{\frac{1}{2} \operatorname{Log}(1-z^2)}$ están en la mitad derecha del plano complejo, por lo que no están en el corte de rama de la función logaritmo. De hecho, dichos valores están sobre la mitad de la circunferencia unitaria que está en la mitad derecha del plano complejo, figura 83, ya que:
\begin{equation*}
\left| iz +\sqrt{1-z^2} \right| = \sqrt{x^2+(1-x^2)} = 1.
\end{equation*}
Por lo tanto:
\begin{align*}
\operatorname{sen}^{-1}(z) & = -i \operatorname{Log}\left(ix + \sqrt{1-x^2}\right)\\
& = -i \operatorname{ln}\left|ix + \sqrt{1-x^2}\right| + \operatorname{Arg}\left(ix + \sqrt{1-x^2}\right)\\
& = \operatorname{Arg}\left(ix + \sqrt{1-x^2}\right),
\end{align*}
donde $-\dfrac{\pi}{2}<\operatorname{Arg}\left(ix + \sqrt{1-x^2}\right)<\dfrac{\pi}{2}$, entonces:
\begin{equation*}
-\dfrac{\pi}{2}<\operatorname{sen}^{-1}(z)<\dfrac{\pi}{2},
\end{equation*}para los $z=x\in\mathbb{R}$ tales que $|x|<1$.
Ejemplo 23.2.
Resolvamos la ecuación $\operatorname{tan}(z)=2$.
Solución. De acuerdo con la proposición 23.1(3), si elegimos la rama principal del logaritmo tenemos que:
\begin{align*}
\operatorname{tan}^{-1}(2) & = \dfrac{i}{2} \operatorname{log}\left(\dfrac{i+2}{i-2}\right)\\
& = \dfrac{i}{2} \operatorname{log}\left(\dfrac{-3-4i}{5}\right)\\
& = \dfrac{i}{2}\left[ \operatorname{ln}\left|\dfrac{-3-4i}{5}\right| + i \left( \operatorname{Arg}\left(\dfrac{-3-4i}{5}\right) + 2 k\pi \right)\right]\\
& = \dfrac{i}{2}\left[ \operatorname{ln}\left(1\right) + i \left( \operatorname{arctan}\left(\dfrac{4}{3}\right) -\pi + 2 k\pi \right)\right]\\
& = \dfrac{1}{2}\left[ (2 k – 1)\pi – \operatorname{arctan}\left(\dfrac{4}{3}\right) \right], \quad k\in\mathbb{Z}.
\end{align*}
Observación 23.3.
Dado que las funciones inversas de las funciones trigonométricas complejas son multivaluadas, entonces debemos ser cuidadosos al derivar estas expresiones. En general, una vez establecidas las ramas de las funciones multivaluadas raíz cuadrada y logaritmo, se puede derivar las funciones inversas dentro de su dominio de analicidad mediante la regla de la cadena.
Proposición 23.2. (Derivadas funciones trigonométricas inversas.)
- $\dfrac{d}{dz}\operatorname{sen}^{-1}(z) = \dfrac{1}{\sqrt{1-z^2}}$, para $z\neq \pm 1$.
- $\dfrac{d}{dz}\operatorname{cos}^{-1}(z) = -\dfrac{1}{\sqrt{1-z^2}}$, para $z\neq \pm 1$.
- $\dfrac{d}{dz}\operatorname{tan}^{-1}(z) = \dfrac{1}{1+z^2}$, para $z\neq \pm i$.
- $\dfrac{d}{dz}\operatorname{cot}^{-1}(z) = -\dfrac{1}{1+z^2}$, para $z\neq \pm i$.
- $\dfrac{d}{dz}\operatorname{sec}^{-1}(z) = \dfrac{1}{z^2\sqrt{1-\frac{1}{z^2}}}$, para $z\neq \pm 1$ y $z\neq 0$.
- $\dfrac{d}{dz}\operatorname{csc}^{-1}(z) = – \dfrac{1}{z^2\sqrt{1-\frac{1}{z^2}}}$, para $z\neq \pm 1$ y $z\neq 0$.
Demostración.
- Una vez elegida una rama de la función multivaluada $\sqrt{1-z^2}$ y una adecuada rama para la función logaritmo, por la regla de la cadena tenemos que:
\begin{align*}
\dfrac{d}{dz}\operatorname{sen}^{-1}(z) & = \dfrac{d}{dz} = -i \operatorname{log}\left(iz +\sqrt{1-z^2}\right)\\
& = -i \left(\dfrac{i-\dfrac{z}{\sqrt{1-z^2}}}{iz +\sqrt{1-z^2}}\right)\\
& = -i \left(\dfrac{i\sqrt{1-z^2} – z}{\left[iz +\sqrt{1-z^2}\right] \sqrt{1-z^2}}\right)\\
& = \dfrac{1}{\sqrt{1-z^2}}.
\end{align*}Donde la igualdad se mantiene siempre que se utilice la misma rama de $\sqrt{1-z^2}$ tanto en la definición de la función $\operatorname{sen}^{-1}(z)$ como en la expresión de su derivada. - Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 23.3.
Consideremos a las ramas principales de la funciones multivaluadas raíz cuadrada y logaritmo y determinemos el valor de la derivada de la función $\operatorname{sen}^{-1}(z)$ en el punto $z=i$.
Solución. De acuerdo con el ejemplo 23.1, sabemos que los cortes de rama de las ramas principales de las funciones multivaluadas $\operatorname{log}(z)$ y $\sqrt{1-z^2}$ son, respectivamente:
\begin{equation*}
(-\infty,0]=\left\{z=x+iy\in\mathbb{C} : x \leq 0, y=0\right\} \quad \text{y} \quad A:= \left\{z=x+iy\in\mathbb{C} : |x|\geq 1, y=0\right\}.
\end{equation*}
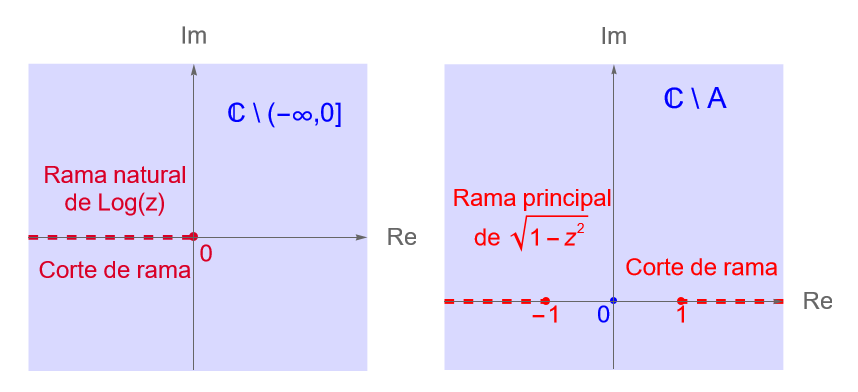
De acuerdo con lo anterior, es claro que el punto $z=i$ no pertenece al corte de rama, de la rama principal de $\sqrt{1-z^2}$. Por otra parte, tenemos que $1-i^2 = 2$, entonces:
\begin{equation*}
i(i) + \sqrt{1-i^2} = -1+\sqrt{2},
\end{equation*}el cual no es un punto sobre el corte de rama, de la rama principal del logaritmo. Por lo tanto, de la proposición 23.2(1) se sigue que:
\begin{align*}
\left. \frac{d}{dz} \operatorname{sen}^{-1}(z) \right|_{z=i} & = \left. \dfrac{1}{\sqrt{1-z^2}}\right|_{z=i}\\
& = \dfrac{1}{\sqrt{1-i^2}}\\
& = \dfrac{1}{\sqrt{2}}.
\end{align*}
Por último, si utilizamos la rama principal de la función $\sqrt{1-z^2}$ tenemos:
\begin{align*}
\left. \sqrt{1-z^2} \right|_{z=i} = \left. e^{\frac{1}{2} \operatorname{Log}(1-z^2)} \right|_{z=i} & = e^{\frac{1}{2} \operatorname{Log}(1-i^2)} \\
& = e^{\frac{1}{2} \operatorname{Log}(2)}\\
& = e^{\frac{1}{2}\left[\operatorname{ln}|2| + i \operatorname{Arg}(2)\right]}\\
& = e^{\operatorname{ln}\left(\sqrt{2}\right)}\\
& = \sqrt{2}.
\end{align*}
Por lo que la derivada es $\dfrac{1}{\sqrt{2}}$, es decir, el resultado coincide con el valor obtenido al utilizar la fórmula de la derivada.
Ejemplo 23.4.
Consideremos ahora el punto $z=\sqrt{5}$. De acuerdo con el ejemplo anterior, es claro que dicho punto está en el corte de rama, de la rama principal de la función multivaluada $\sqrt{1-z^2}$, por lo que utilizando dicha rama no podemos obtener el valor de la función $\operatorname{sen}^{-1}(z)$ ni de su derivada en $z=\sqrt{5}$. Entonces procedemos a elegir una nueva rama para la raíz cuadrada de modo que sea posible determinar dichos valores.
Solución. Por simplicidad elegimos a la rama natural de la raíz, es decir:
\begin{equation*}
\sqrt{1-z^2} = e^{\frac{1}{2} \operatorname{Log}_{[0,2\pi)}(1-z^2)}, \quad 0 \leq \operatorname{Arg}(1-z^2) < 2\pi.
\end{equation*}
El corte de rama de esta función está dado por los $z=x+iy\in\mathbb{C}$ tales que:
\begin{align*}
0 \leq \operatorname{Arg}(1-z^2) < 2\pi & \quad \Longleftrightarrow \quad \left\{ \begin{array}{l}
\operatorname{Re}(1-z^2) = 1+y^2-x^2 \geq 0, \\
\\ \operatorname{Im}(1-z^2) = -2xy = 0.
\end{array}
\right.\\
& \\
& \quad \Longleftrightarrow \quad B:= \left\{z=x+iy\in\mathbb{C} : |x|\leq 1, y=0\right\} \cup \left\{z=x+iy\in\mathbb{C} : x=0, y\in\mathbb{R}\right\}.
\end{align*}
Para esta rama es claro que el punto $z=\sqrt{5}$ no está en su corte de rama, por tanto podemos utilizarla. Tenemos que $1-(\sqrt{5})^2 = -4$, entonces:
\begin{align*}
\operatorname{Log}_{[0,2\pi)}(-4) &= \operatorname{ln}|-4| + i\operatorname{Arg}_{[0,2\pi)}(-4)\\
&= \operatorname{ln}(4) + i\pi,
\end{align*}por lo que:
\begin{align*}
\left.\sqrt{1-z^2}\right|_{z=\sqrt{5}} & = \sqrt{1-(\sqrt{5})^2}\\
& = e^{\frac{1}{2} \operatorname{Log}_{[0,2\pi)}(-4)}\\
& = e^{\operatorname{ln}(2)} e^{i\frac{\pi}{2}}\\
&= 2i.
\end{align*}
Dado que $i \sqrt{5}+2i = i(2+\sqrt{5})$ no es un punto sobre el corte de rama, de la rama principal del logaritmo, entonces utilizaremos de nuevo dicha rama. Por lo que:
\begin{align*}
\left.\operatorname{sen}^{-1}(z)\right|_{z=\sqrt{5}} & = \left. – i\operatorname{Log}\left(iz+\sqrt{1-z^2}\right)\right|_{z=\sqrt{5}}\\
& = -i\operatorname{Log}\left(i\left(2+\sqrt{5} \right)\right)\\
& = -i\left[\operatorname{ln}\left|i\left(2+\sqrt{5} \right)\right| + i \operatorname{Arg}\left(i\left(2+\sqrt{5} \right)\right)\right]\\
& = -i\left[\operatorname{ln}\left(2+\sqrt{5}\right) + i \frac{\pi}{2}\right]\\
& = \frac{\pi}{2} -i\operatorname{ln}\left(2+\sqrt{5}\right).
\end{align*}
Mientras que:
\begin{align*}
\left. \frac{d}{dz} \operatorname{sen}^{-1}(z) \right|_{z=\sqrt{5}} & = \left. \dfrac{1}{\sqrt{1-z^2}}\right|_{z=\sqrt{5}}\\
&= \dfrac{1}{\sqrt{-4}}\\
&= \dfrac{1}{2i}\\
&= -\dfrac{i}{2}.
\end{align*}
Procediendo de forma completamente análoga que con la proposición 23.1, es posible establecer las expresiones para las funciones inversas de las funciones hiperbólicas, que al estar definidas en términos de la exponencial compleja, también resultan ser funciones multivaluadas.
Proposición 23.3. (Funciones hiperbólicas inversas.)
- $\operatorname{senh}^{-1}(z) = \operatorname{log}\left(z + \sqrt{z^2+1}\right)$.
- $\operatorname{cosh}^{-1}(z) = \operatorname{log}\left(z + \sqrt{z^2-1}\right)$.
- $\operatorname{tanh}^{-1}(z) = \dfrac{1}{2} \operatorname{log}\left(\dfrac{1+z}{1-z}\right)$, para $z\neq \pm 1$.
- $\operatorname{coth}^{-1}(z) = \dfrac{1}{2} \operatorname{log}\left(\dfrac{z+1}{z-1}\right)$, para $z\neq \pm 1$.
- $\operatorname{sech}^{-1}(z) = \operatorname{log}\left(\dfrac{1 + z\sqrt{\dfrac{1}{z^2}-1}}{z}\right)$, para $z\neq 0$.
- $\operatorname{csch}^{-1}(z) = \operatorname{log}\left(\dfrac{1 + z\sqrt{\dfrac{1}{z^2}+1}}{z}\right)$, para $z\neq 0$.
Demostración.
- Se deja como ejercicio al lector.
- Sea $z = \operatorname{cosh}(w)$. De acuerdo con la definición 22.3 tenemos que:
\begin{equation*}
z = \operatorname{cosh}(w) = \frac{e^{w} + e^{-w}}{2},
\end{equation*}de donde:
\begin{equation*}
(e^{w})^2-2z(e^{w}) + 1 = 0.
\end{equation*}Resolvemos la ecuación cuadrática para $e^w$ utilizando la fórmula general, entonces:
\begin{equation*}
e^{w} = \frac{2z + \sqrt{4(z^2-1)}}{2} = z + \sqrt{z^2-1},
\end{equation*}donde la función multivaluada $\sqrt{z^2-1}$ determina dos raíces complejas de $z^2-1$. Por lo que, una vez establecida la rama de dicha función multivaluada, podemos utilizar la proposición 20.1(6), para $k, n\in\mathbb{Z}$, como sigue:
\begin{align*}
w &= \operatorname{log}\left(z + \sqrt{z^2-1}\right) + i2k\pi\\
&= \operatorname{ln}\left|z + \sqrt{z^2-1}\right| + i\left(\operatorname{Arg}\left(z + \sqrt{z^2-1}\right) + 2m\pi\right)\\
&= \operatorname{ln}\left|z + \sqrt{z^2-1}\right| + i\operatorname{arg}\left(z + \sqrt{z^2-1}\right)\\
&= \operatorname{log}\left(z + \sqrt{z^2-1}\right),
\end{align*}donde $m=k+n\in\mathbb{Z}$. - Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 23.5.
Veamos que $\operatorname{tanh}^{-1}\left(\dfrac{1}{z}\right) = \operatorname{coth}^{-1}\left(z\right)$.
Solución. Sea $z\in\mathbb{C}\setminus\{-1,1,0\}$, entonces:
\begin{align*}
\operatorname{tanh}^{-1}\left(\dfrac{1}{z}\right) & = \dfrac{1}{2} \operatorname{log}\left(\dfrac{1+\dfrac{1}{z}}{1-\dfrac{1}{z}}\right)\\
& = \dfrac{1}{2} \operatorname{log}\left(\dfrac{z+1}{z-1}\right)\\
& = \operatorname{coth}^{-1}\left(z\right).
\end{align*}
Proposición 23.4. (Derivadas funciones hiperbólicas inversas.)
- $\dfrac{d}{dz}\operatorname{senh}^{-1}(z) = \dfrac{1}{\sqrt{1+z^2}}$, para $z\neq \pm i$.
- $\dfrac{d}{dz}\operatorname{cosh}^{-1}(z) = \dfrac{1}{\sqrt{z^2 – 1}}$, para $z\neq \pm 1$.
- $\dfrac{d}{dz}\operatorname{tanh}^{-1}(z) = \dfrac{1}{1-z^2}$, para $z\neq \pm 1$.
- $\dfrac{d}{dz}\operatorname{coth}^{-1}(z) = \dfrac{1}{1-z^2}$, para $z\neq \pm 1$.
- $\dfrac{d}{dz}\operatorname{sech}^{-1}(z) = -\dfrac{1}{z^2\sqrt{\dfrac{1}{z^2}-1}}$, para $z\neq \pm 1$ y $z\neq 0$.
- $\dfrac{d}{dz} \operatorname{csch}^{-1}(z) = – \dfrac{1}{z^2\sqrt{\dfrac{1}{z^2}+1}}$, para $z\neq \pm i$ y $z\neq 0$.
Demostración.
- Se deja como ejercicio al lector.
- Una vez establecida una rama de la función multivaluada $\sqrt{z^2-1}$ y una adecuada rama para la función logaritmo, procedemos a derivar utilizando la regla de la cadena, entonces:
\begin{align*}
\dfrac{d}{dz}\operatorname{cosh}^{-1}(z) & = \dfrac{d}{dz} \operatorname{log}\left(z + \sqrt{z^2-1}\right)\\
& = \dfrac{1+\dfrac{z}{\sqrt{z^2-1}}}{z + \sqrt{z^2-1}}\\
& = \dfrac{z +\sqrt{z^2-1}}{\left(z +\sqrt{z^2-1} \,\right) \sqrt{z^2-1}}\\
& = \dfrac{1}{\sqrt{z^2-1}}.
\end{align*}Donde la igualdad se mantiene siempre que se utilice la misma rama de $\sqrt{z^2-1}$ tanto en la definición de la función $\operatorname{cosh}^{-1}(z)$ como en la expresión de su derivada. - Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 23.6.
Utilizando la rama natural de la función $\sqrt{z^2-1}$ y la rama principal del logaritmo determinemos:
a) $\operatorname{cosh}^{-1}\left(\dfrac{1}{\sqrt{2}}\right)$.
b) $\dfrac{d}{dz}\operatorname{cosh}^{-1}\left(\dfrac{1}{\sqrt{2}}\right)$.
¿Es posible determinar los valores de cada inciso si se considera la rama principal de la función $\sqrt{z^2-1}$?
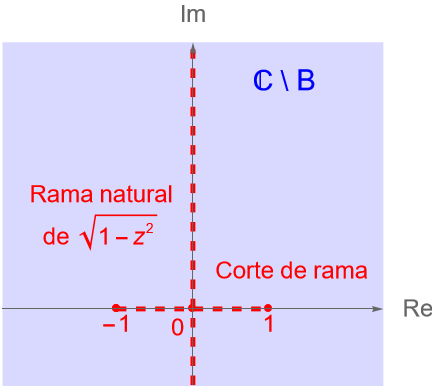
Solución. De acuerdo con el ejercicio 13.15, sabemos que para la función multivaluada $\sqrt{z^2-1}$ los cortes de rama, considerando las ramas principal y natural son, respectivamente:
\begin{equation*}
\left\{z=x+iy\in\mathbb{C} : |x|\leq 1, y=0\right\} \quad \text{y} \quad \left\{z=x+iy\in\mathbb{C} : |x|\geq 1, y=0\right\}.
\end{equation*}
Dado que $z=\dfrac{1}{\sqrt{2}}$ y $|z|<1$, entonces dicho punto está sobre el corte de rama, de la rama principal de la función $\sqrt{z^2-1}$, por tanto no podemos utilizar dicha rama para determinar los valores que nos pide cada inciso.
Por otra parte, es claro que $z=\dfrac{1}{\sqrt{2}}$ no está sobre el corte de rama, de la rama natural de la función $\sqrt{z^2-1}$, entonces:
\begin{equation*}
\sqrt{1-z^2} = e^{\frac{1}{2} \operatorname{Log}_{[0,2\pi)}(z^2-1)}, \quad 0 \leq \operatorname{Arg}(z^2-1) < 2\pi.
\end{equation*}
Tenemos que:
\begin{align*}
\operatorname{Log}_{[0,2\pi)}\left(\left(\dfrac{1}{\sqrt{2}}\right)^2 – 1\right) = \operatorname{Log}_{[0,2\pi)}\left(-\dfrac{1}{2}\right)
&=\operatorname{ln}\left|-\dfrac{1}{2}\right| + i\operatorname{Arg}_{[0,2\pi)}\left(-\dfrac{1}{2}\right)\\
&= -\operatorname{ln}(2) + i \pi,
\end{align*}por lo que:
\begin{align*}
\left.\sqrt{z^2-1}\right|_{z=\frac{1}{\sqrt{2}}} & = \sqrt{\left(\dfrac{1}{\sqrt{2}}\right)^2 – 1}\\
& = e^{\frac{1}{2} \operatorname{Log}_{[0,2\pi)}\left(-\frac{1}{2}\right)}\\
& = e^{-\frac{\operatorname{ln}(2)}{2}} e^{-\frac{\pi}{2}}\\
&= i\frac{1}{\sqrt{2}}.
\end{align*}
Dado que $\dfrac{1}{\sqrt{2}} + i\dfrac{1}{\sqrt{2}} = \dfrac{1}{\sqrt{2}}\left(1+i\right)$ no es un punto sobre el corte de rama, de la rama principal del logaritmo, entonces utilizaremos de nuevo dicha rama. Por lo que:
\begin{align*}
\left.\operatorname{cosh}^{-1}(z)\right|_{z=\frac{1}{\sqrt{2}}} & = \left. \operatorname{Log}\left(z+\sqrt{z^2-1}\right)\right|_{z=\frac{1}{\sqrt{2}}}\\
& =\operatorname{Log}\left( \dfrac{1}{\sqrt{2}}\left(1+i\right)\right)\\
& =\operatorname{ln}\left| \dfrac{1}{\sqrt{2}}\left(1+i\right)\right| + i \operatorname{Arg}\left( \dfrac{1}{\sqrt{2}}\left(1+i\right)\right)\\
& = \operatorname{ln}\left(1\right) + i \frac{\pi}{4}\\
& = i\frac{\pi}{4}.
\end{align*}
Mientras que:
\begin{align*}
\left. \frac{d}{dz} \operatorname{cosh}^{-1}(z) \right|_{z=\frac{1}{\sqrt{2}}} & = \left. \dfrac{1}{\sqrt{z^2-1}}\right|_{z=\frac{1}{\sqrt{2}}}\\
&= \dfrac{1}{\sqrt{-\frac{1}{2}}}\\
&= \dfrac{1}{\frac{i}{\sqrt{2}}}\\
&= -i\sqrt{2}.
\end{align*}
Tarea moral
- Completa las demostraciones de las proposiciones de esta entrada.
- Sean $w=\operatorname{cos}(z)$ y $\zeta = e^{iz}$. Muestra que:
\begin{align*}
\zeta & = w+\sqrt{w^2-1},\\
\operatorname{cos}^{-1}(w) & = -i\operatorname{log}\left(w\pm \sqrt{w^2-1}\right).
\end{align*} - Muestra que los puntos de ramificación de la función multivaluada $\operatorname{sen}^{-1}(z)$ son $z=\pm 1$.
- Demuestra que si $a\in\mathbb{R}$ y $a>1$, entonces:
\begin{equation*}
\operatorname{tanh}^{-1}(a) = \operatorname{Log}\sqrt{\frac{a+1}{a-1}} + i \frac{2k+1}{2} \pi, \quad k\in\mathbb{Z}.
\end{equation*} - Muestra que si se usa la misma rama de la función $\sqrt{1-z^2}$ en la definición de las funciones multivaluadas $\operatorname{sen}^{-1}(z)$ y $\operatorname{cos}^{-1}(z)$, proposición 23.1, entonces:
a) $\operatorname{sen}^{-1}(z) + \operatorname{cos}^{-1}(z) = 2k\pi +\frac{\pi}{2}, \,\, k\in\mathbb{Z}$.
b) $\operatorname{tan}^{-1}(z) + \operatorname{cot}^{-1}(z) = k\pi -\frac{\pi}{2}, \,\, k\in\mathbb{Z}$. - Resuelve las siguientes ecuaciones:
a) $\operatorname{senh}(5z+i) = -\sqrt{3} i$.
b) $\operatorname{tanh}\left(\frac{z-3}{2}\right) = -1+ i$.
c) $\operatorname{cot}(z) = 2i$.
d) $\operatorname{cosh}^2(z) = -1$. - Prueba que:
\begin{equation*}
\operatorname{tanh}^{-1}\left(e^{i\theta}\right) = \frac{1}{2} \operatorname{log}\left(i \operatorname{cot}\left(\frac{\theta}{2}\right)\right).
\end{equation*}Determina una expresión similar para $\operatorname{tan}^{-1}\left(e^{i\theta}\right)$. - Demuestra que:
\begin{equation*}
\operatorname{tan}\left(i \operatorname{log}\left(\frac{a-ib}{a+ib}\right)\right) = \frac{2ab}{a^2 – b^2}.
\end{equation*}Hint: sustituye $z$ por $\dfrac{2ab}{a^2 – b^2}$ en la definición de $\operatorname{tan}^{-1}(z)$. - Determina los puntos de ramificación de las siguientes funciones:
a) $\operatorname{cos}^{-1}(z)$.
b) $\operatorname{tan}^{-1}(z^2+2z+1)$.
Más adelante…
En esta entrada hemos abordado de manera general las definiciones de las funciones inversas de las funciones trigonométricas e hiperbólicas. Vimos que estas funciones resultan ser funciones multivaluadas, por lo que es importante recordar los conceptos de la entrada 13 referentes a este tipo de funciones, como los conceptos de rama de una función multivaluada, corte de rama y puntos de ramificación, ya que a través de estos conceptos es posible determinar de manera clara los dominios de analicidad de dichas funciones. Así mismo, vimos que una vez definida una rama de alguna de estas funciones inversas, es posible determinar su derivada a través de la regla de la cadena.
La siguiente entrada abordaremos el concepto de transformación, que como hemos visto en nuestros cursos de Geometría y Álgebra Lineal resulta ser una herramienta muy útil para el estudio de funciones de varias variables, en este caso para las funciones complejas, ya que a través de dicho concepto podremos dar una interpretación geométrica del comportamiento de las funciones complejas.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Funciones trigonométricas e hiperbólicas complejas.
- Siguiente entrada del curso: Transformaciones del plano complejo $\mathbb{C}$.