Archivo del Autor: Pedro Rivera Herrera

Variable Compleja I: El plano complejo extendido $\mathbb{C}_{\infty}$

Por Pedro Rivera Herrera

Introducción

Al estudiar matemáticas un concepto que no puede pasar desapercibido es el del infinito. Intuitivamente cuando pensamos en el infinito estamos considerando a algo que no tiene fin, algo sin límites. Aunque dicho concepto aparece en diversas ramas de las matemáticas como el cálculo, el análisis, la geometría, la teoría de conjuntos, entre otras, es claro que la idea que tenemos sobre él es equivalente entre todas estas ramas y su importancia radica en que nos permite entender y describir mejor alguna problemática puntual. Por ejemplo cuando queremos hablar sobre el comportamiento de una sucesión conforme está crece cada vez más y más hacemos uso del límite al infinito de nuestra variable, o cuando hablamos de la cardinalidad de un conjunto que tiene una cantidad de elementos numerable, intuitivamente pensamos en que dicho conjunto tiene una infinidad de elementos.

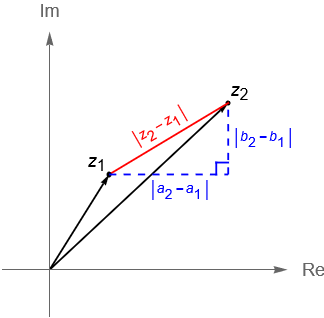
Lo anterior no es la excepción al estudiar Variable Compleja. Dado que el campo de los números complejos $\mathbb{C}$ no puede ordenarse bajo la relación de ser positivo, la idea de que un número complejo $z = a + ib$ crezca o decrezca no tiene sentido. Sin embargo podemos preguntarnos en qué sucede con su módulo $|\,z\,|$, ya que conforme crece $|\,z\,|$ de manera arbitraria tendremos que el número complejo $z$ se alejará más del origen. Entonces, al pensar en que $z \rightarrow \infty$ no tendremos que distinguir entre las direcciones de los ejes, sino simplemente recordar que estamos pensando en que el módulo $|\,z\,|$ crece sin límite a lo largo de los ejes real e imaginario, por lo que la notación $|\,z\,| \rightarrow \infty$ será lo mismo que $a^2+b^2 \rightarrow \infty$.

En su momento veremos que es necesario estudiar funciones de variable compleja para las que el módulo de la variable crezca de manera arbitraria, por lo que resulta conveniente agregar al plano complejo un punto ideal, llamado el punto al infinito, denotado por $\infty$.

Definición 11.1. (El plano complejo extendido.)
Se define al plano complejo extendido como el conjunto dotado con el punto $z_\infty=\infty$ como: \begin{equation*}
\mathbb{C}_{\infty} := \mathbb{C}\cup \{\infty\}.
\end{equation*}

Observación 11.1.
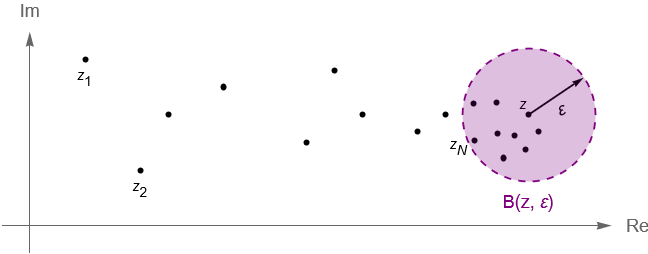
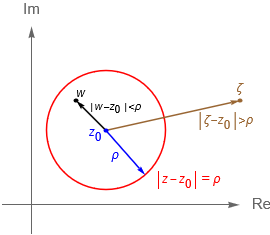
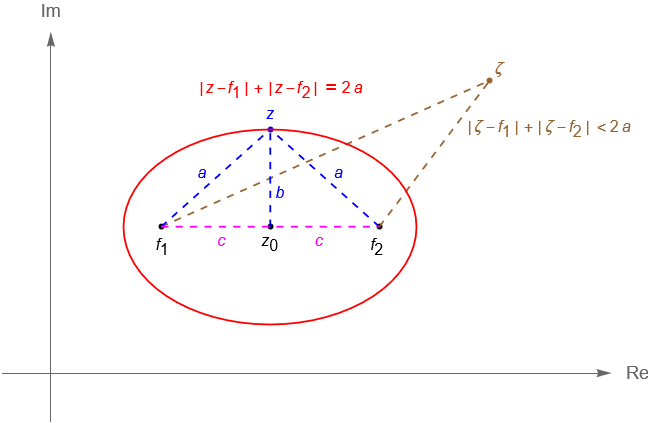
Es claro que en el plano complejo $\mathbb{C}$ no existe un lugar destinado para el punto al infinito. Sin embargo, ¿qué pasa con aquellos puntos $z\in\mathbb{C}$ tales que $|\,z\,|>\frac{1}{\varepsilon}$ para todo $\varepsilon>0$ suficientemente pequeño? El punto al infinito nos permite responder esta pregunta, ya que a los puntos con dicha propiedad los podemos pensar como un $\varepsilon$-vecindario del punto al infinito.

Primeramente debemos establecer las siguientes reglas aritméticas para poder operar con este nuevo punto del plano complejo extendido: \begin{align*}
z \pm \infty = \infty \pm z = \infty, \quad \forall z \in \mathbb{C}.\\
z \cdot \infty = \infty \cdot z = \infty, \quad \text{si}\,\,\, z \neq 0.\\
\frac{z}{0} = \infty, \quad \text{si}\,\,\, z \neq 0.\\
\frac{z}{\infty} = 0, \quad \text{si}\,\,\, z \neq \infty.\
\end{align*}

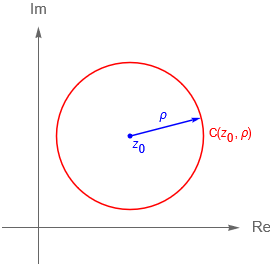
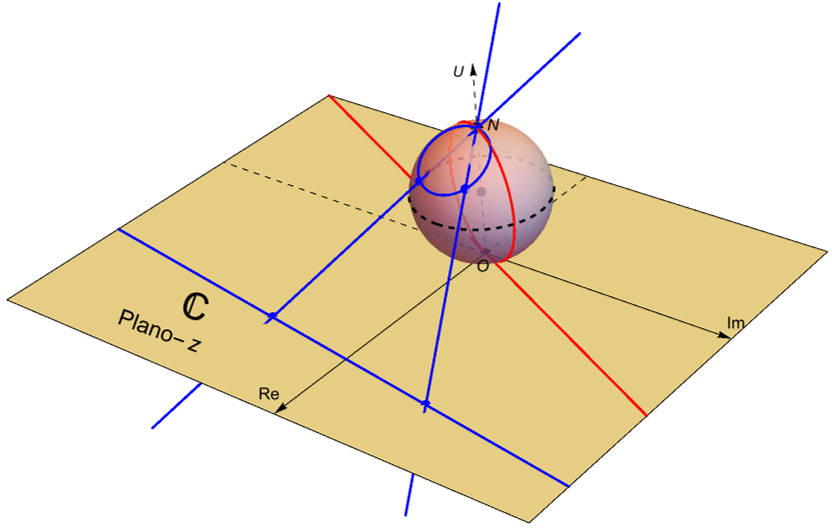
Un módelo que nos permite representar al plano complejo extendido es la esfera unitaria en $\mathbb{R}^3$, cuyo centro es el punto $(0,0,1)$, situada sobre el plano complejo $\mathbb{C}$, figura 52, es decir el conjunto: \begin{equation*}
\mathbb{S} = \{ (x,y,u) \in \mathbb{R}^3 \, : \, x^2 + y^2 + (u-1)^2 = 1 \},
\end{equation*} dotada con los puntos $N=(0,0,2)$, llamado el polo norte o el punto al infinito y $O=(0,0,0)$ llamado el polo sur o el origen. A dicho modelo se le denomina la esfera de Riemann.

Es posible identificar a $\mathbb{S}\setminus\{N\}$ con el plano complejo si consideramos a $\mathbb{C}$ como el plano: \begin{equation*}
\Pi = \{(a,b,0)\in\mathbb{R}^3 \, : \, a,b \in \mathbb{R}\}, \tag{11.1}
\end{equation*} y al punto $N$ con el punto al infinito.

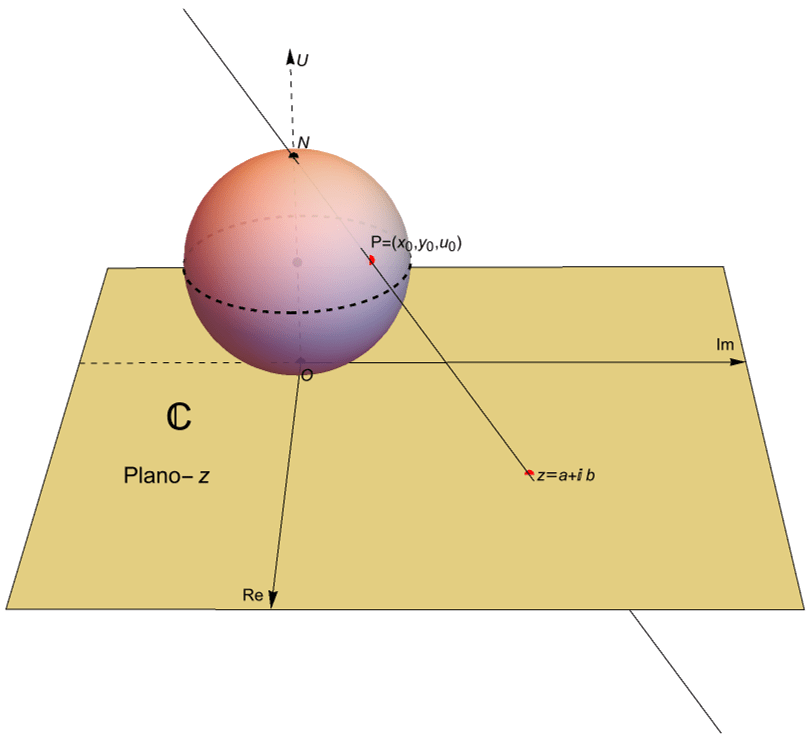
Figura 52: La esfera de Riemann $\mathbb{S}$, dada por $x^2 + y^2 + (u-1)^2 = 1$, y el plano complejo $\mathbb{C}$, dado por (11.1), relacionados mediante la proyección estereográfica.

De acuerdo con la gráfica, tenemos que un número complejo $z=a+ib$ con un módulo demasiado grande se aleja del origen $(0,0,0)$ conforme el punto $P=(x_0,y_0,u_0)$ está más cerca del punto al infinito $N$.

Notemos que si trazamos una recta desde $N$ hasta el número complejo $z=a+ib$ en el plano complejo, al cual le corresponde el punto $(a,b,0)$ en $\mathbb{R}^3$, entonces existe un único punto $P=(x_0, y_0, u_0)$ en la esfera de Riemann tal que pertenece a dicha recta. Por otra parte, para un punto $P=(x_0, y_0, u_0)\in\mathbb{S}$, distinto de $N$, es posible extender el segmento de recta que une a $N$ con dicho punto $P$ hasta intersecar al plano complejo $\mathbb{C}$ en un único punto $z=a+ib$, figura 52.

Lo anterior nos deja ver que existe una relación biunívoca entre $\mathbb{S}\setminus\{N\}$ y $\mathbb{C}$, pensado como el plano (11.1), descrita a continuación.

Podemos escribir a la recta que pasa por los puntos $N=(0,0,2)$ y $P=(x_0,y_0,u_0)$ en su forma paramétrica como:
\begin{equation*}
N + (P-N)t, \quad t\in\mathbb{R}.
\tag{11.2} \end{equation*} Dado que la recta (11.2) interseca al plano $\mathbb{C}$, dado por (11.1), en el número complejo $z=a+ib$, es decir el punto $(a,b,0)$, entonces se tiene que para algún $t\in\mathbb{R}$: \begin{align*}
(a,b,0) &= N + (P-N)t\\
& = (tx_0,ty_0, 2 + t(u_0-2)).
\end{align*} De lo anterior tenemos el siguiente sistema de ecuaciones: \begin{align*}
a = t x_0,\tag{11.3.1} \\
b = t y_0,\tag{11.3.2} \\
2(t-1) = t u_0. \tag{11.3.3}
\end{align*} Además de (11.3.3) es claro que: \begin{equation*}
t = \frac{2}{2-u_0}. \tag{11.3.4}
\end{equation*} Sustituyendo (11.3.4) en (11.3.1) y (11.3.2) tenemos: \begin{align*}
a = \frac{2x_0}{2-u_0},\\
b = \frac{2y_0}{2-u_0}. \tag{11.4}
\end{align*}

Por otra parte, sabemos que $P=(x_0,y_0,u_0) \in \mathbb{S}$, por lo que satisface: \begin{equation*}
x_0^2 + y_0^2 + (u_0 – 1)^2 = 1.
\end{equation*}

Multiplicando ésta última expresión por $t^2$ obtenemos: \begin{align*}(tx_0)^2 + (ty_0)^2 + (tu_0 -t)^2 = t^2\\
\\
\Longrightarrow \quad (tx_0)^2 + (ty_0)^2 + (tu_0)^2 = 2t^2 u_0. \tag{11.5.1} \end{align*}

Dado que $z=a+ib\in\mathbb{C}$, sabemos que $|\,z\,|^2 = a^2 + b^2 $, por lo que sustituyendo (11.3.1), (11.3.2) y (11.3.3) en (11.5.1) tenemos:
\begin{align*}
a^2 + b^2 + 4(t-1)^2 = 4t(t-1).\\
\\
\Longrightarrow \quad t = \frac{|\,z\,|^2 + 4}{4}\tag{11.5.2}
\end{align*}

De (11.3.1), (11.3.2), (11.3.3) y (11.5.2) se sigue que: \begin{align*}
x_0 = \frac{a}{t} = \frac{4a}{|\,z\,|^2 + 4},\\
y_0 = \frac{b}{t} = \frac{4b}{|\,z\,|^2 + 4}, \tag{11.6}
\end{align*} \begin{equation*}
u_0 = \frac{2(t-1)}{t} = \frac{2\,|\,z\,|^2}{|\,z\,|^2 + 4}.
\end{equation*}

Esta forma de asociar o hacer corresponder a los putos $z$ de $\mathbb{C}$ con la esfera de Riemann $\mathbb{S}$, dotada con $N=(0,0,2)$ y $O=(0,0,0)$, se le conoce como la proyección estereográfica.

Definición 11.2. (La proyección estereográfica.)
Definimos a la proyección estereográfica como la función $\varphi:\mathbb{S} \to \mathbb{C}_{\infty}$ tal que para $P=(x,y,u)\in \mathbb{S}$: \begin{equation*}
\varphi(P) = \left\{\begin{array}{lcc}
\infty, & \text{si} & P=N=(0,0,2),\\
\\ z= a+ib, & \text{si} & P \neq N,
\end{array}
\right.
\end{equation*} donde $z=a+ib\in\mathbb{C}$ representa al punto $(a,b,0)$ de $\mathbb{R}^3$ tal que $a = \dfrac{2x}{2-u}$, $b=\dfrac{2y}{2-u}$.

Proposición 11.1.
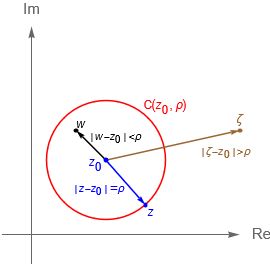
Sea $\mathbb{S}^* = \mathbb{S}\setminus{N}$. La proyección estereográfica es un homeomorfismo entre $(\mathbb{S}^*,d_{\mathbb{R}^3})$ y $(\mathbb{C},d)$, donde $d_{\mathbb{R}^3}$ es la distancia usual de $\mathbb{R}^3$ y $d$ la métrica euclidiana en $\mathbb{C}$.

Demostración. Veamos que está función es biyectiva. Es claro que si $P,Q\in\mathbb{S}^*$, entonces para algún $z_1, z_2 \in \mathbb{C}$ se tiene:
\begin{align*}
\varphi(P) = \varphi(Q) \quad & \Longrightarrow \quad z_1 = z_2\\
& \Longrightarrow \quad \operatorname{Re}(z_1) = \operatorname{Re}(z_2)\\
& \quad \quad \quad \, \operatorname{Im}(z_1) =\operatorname{Im}(z_2)\\
& \quad \quad \quad \, \, \text{y} \,\, |\,z_1\,| = |\,z_2\,|. \end{align*} Por lo que $P=Q$, entonces $\varphi$ es inyectiva.

Consideremos a $z=a+ib \in\mathbb{C}$, notemos que si $P=(x_0,y_0,u_0)\in\mathbb{S}^*$, con $x_0$, $y_0$ y $u_0$ dados como en (11.6) entonces: \begin{align*}
\varphi(P) & = \varphi\left(\frac{4a}{|\,z\,|^2+4}, \frac{4b}{|\,z\,|^2+4}, \frac{2\,|\,z\,|^2}{|\,z\,|^2+4}\right)\\
& = \frac{2\left(\frac{4a}{|\,z\,|^2+4}\right)}{2-\frac{2\,|\,z\,|^2}{|\,z\,|^2+4}} + i\, \frac{2\left(\frac{4b}{|\,z\,|^2+4}\right)}{2-\frac{2\,|\,z\,|^2}{|\,z\,|^2+4}}\\
& = a + ib\\
& = z.
\end{align*} Por lo tanto, como $z\in\mathbb{C}$ era arbitrario se sigue que para todo número complejo $z$ existe un punto $P\in\mathbb{S}^*$ tal que $\varphi(P) = z$. Por lo tanto $\varphi$ es sobreyectiva.

Dado que la proyección estereográfica es una función biyectiva, entonces existe la función inversa de $\varphi$, digamos $\varphi^{-1}$, la cual es una función que va de $\mathbb{C}_\infty$ a $\mathbb{S}$ tal que para $z\in\mathbb{C}_\infty$: \begin{equation*}
\varphi^{-1}(z) = \left\{\begin{array}{lll}
N=(0,0,2), & \text{si} & z = \infty,\\
P= \left( \dfrac{4a}{|\,z\,|^2 + 4}, \dfrac{4b}{|\,z\,|^2 + 4}, \dfrac{2\,|\,z\,|^2}{|\,z\,|^2 + 4}\right), & \text{si} & z = a+ib \in\mathbb{C}.
\end{array}
\right.
\end{equation*}
Considerando las ecuaciones que definen a las funciones $\varphi$ y $\varphi^{-1}$, dadas en (11.4) y en (11.6), no es difícil verificar que ambas funciones son continuas en su respectivo dominio, por lo que se deja como ejercicio.

$\blacksquare$

Observación 11.2.
Consideremos la ecuación general de un plano, es decir: \begin{equation*}
Ax+By+Cu+D=0.
\end{equation*} Si dicho plano pasa por el centro de la esfera $\mathbb{S}$, es decir por el punto $(0,0,1)$, entonces dicho plano es de la forma: \begin{equation*}
Ax+By+C(u-1)=0. \tag{11.7}
\end{equation*} Más aún, al intersecar a la esfera $\mathbb{S}$ con un plano de la forma (11.7) se obtiene una circunferencia máxima.

Observación 11.3.
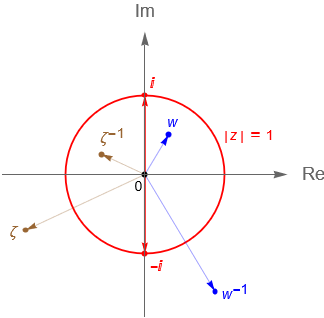
Notemos que bajo la proyección estereográfica los lugares geométricos del plano complejo $\mathbb{C}$ corresponden con lugares geométricos de la esfera de Riemann $\mathbb{S}$ y viceversa. Es importante recordar que no existe un punto en el plano complejo destinado para el punto al infinito, sin embargo no es difícil observar de manera geométrica que líneas longitudinales que pasan por el polo norte $N$, como el meridiano 0 o meridiano de Greenwich, corresponden con rectas en el plano complejo $\mathbb{C}$ que pasan por el origen $z=0$. Por otra parte, en la esfera de Riemann las líneas de latitud, como el ecuador, corresponden con circunferencias en el plano complejo $\mathbb{C}$ centradas en el origen $z=0$, mientras que una circunferencia arbitraria en la esfera de Riemann, que no pase por el polo norte $N$, corresponde con una circunferencia en el plano complejo $\mathbb{C}$. No debe ser difícil notar que conforme el radio de las circunferencias tiende a infinito, las líneas de latitud en la esfera tienden al polo norte $N$ que corresponde con el punto al infinito.

Figura 53: La proyección estereográfica manda circunferencias que pasan por el polo norte en rectas.

Figura 54: La proyección estereográfica manda circunferencias que no pasan por el polo norte en circunferencias.

Proposición 11.2.
Bajo la proyección esterográfica, circunferencias en la esfera de Riemann, $\mathbb{S}$, corresponden con circunferencias o rectas en el plano complejo $\mathbb{C}$, figuras 53 y 54.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Observación 11.4.
De nuestros cursos de Geometría Analítica y Cálculo sabemos que una trayectoria o camino en $\mathbb{R}^n$ es una función continua $\gamma:(c,d)\rightarrow \mathbb{R}^n$, y al conjunto $\Gamma = \{ \gamma(t) \, : \, t\in(c,d)\}$ lo llamamos la curva descrita por $\gamma$. Además sabemos que podemos expresar a una trayectoria $\gamma$ por medio de sus funciones componentes, por ejemplo en $\mathbb{R}^3$ tenemos que $\gamma(t) = \left(x(t),y(t),z(t)\right)$ donde $x(t),y(t),z(t)$ son funciones reales continuas llamadas las componentes de $\gamma$. Por otra parte, decimos que una curva es suave en $(c,d)$ si es diferenciable en $(c,d)$, es decir si sus funciones componentes son derivables en $(c,d)$ y sus derivadas no se anulan simultáneamente en $(c,d)$, excepto quizás en $c$ o $d$.

Observación 11.5.
Por otra parte, sabemos que el ángulo $\theta$ entre dos vectores $u,v$ en $\mathbb{R}^2$ o $\mathbb{R}^3$ se puede obtener mediante: \begin{equation*}
\operatorname{cos}(\theta) = \frac{u \cdot v}{\left\lVert u \right\rVert \left\lVert v \right\rVert},
\end{equation*} donde «$\cdot$» representa el producto interior entre $u$ y $v$, mientras que $\left\lVert \cdot \right\rVert$ la norma de cada vector.

Dadas dos curvas suaves, descritas por $\gamma_1$ y $\gamma_2$, podemos definir el ángulo entre ellas como el ángulo que se forma entre las rectas tangentes a cada curva en un punto de intersección. Es claro que dadas dos rectas tangentes, que se intersecan entre sí, se obtienen dos ángulos distintos, digamos $\theta_1$ y $\theta_2$ cuya relación entre ellos está dada por $\theta_1 + \theta_2 = \pi$, por lo que para evitar confusión sobre cuál de los dos ángulos obtenidos se está considerando, diremos que el ángulo $\theta$ que se forma entre dos curvas suaves será tal que $\theta\in(0,\pi/2)$. Con esta consideración tenemos que $\operatorname{cos}(\theta)>0$.

Una pregunta interesante que podemos hacernos es ¿qué pasa con los ángulos entre cualesquiera dos curvas suaves en el plano complejo $\mathbb{C}$ o en la esfera de Riemann $\mathbb{S}$?, es decir, ¿bajo la proyección estereográfica se conserva el ángulo entre dos curvas suaves? Para responder esta pregunta primeramente podemos realizar un análisis geométrico.

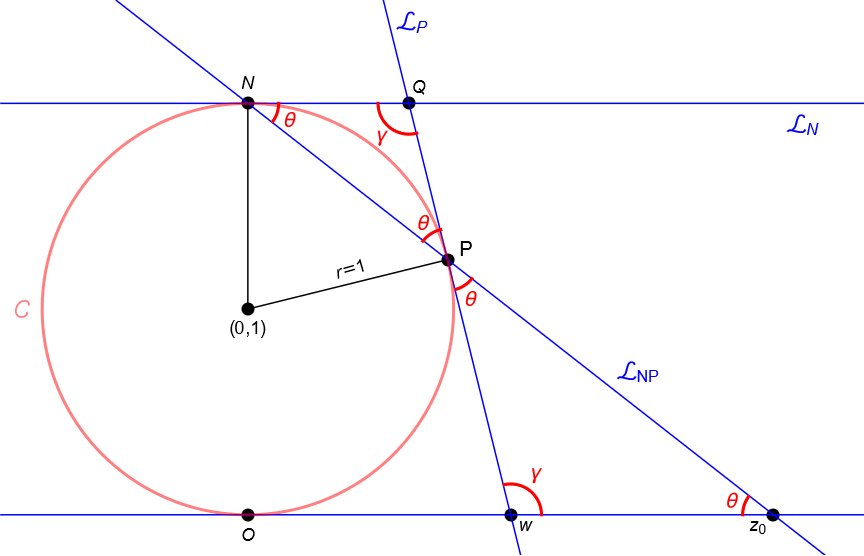
De acuerdo con nuestros cursos de Cálculo y Geometría sabemos que es posible encontrar el plano tangente a la esfera $\mathbb{S}$ en el punto $P$, digamos $\Pi_P$. Consideremos al plano $u=2$, es decir el plano tangente a $\mathbb{S}$ en el polo norte $N$, digamos $\Pi_N$ y consideremos al plano que pasa por el centro de $\mathbb{S}$, por el polo norte $N$ y por el punto $P$, digamos $\Pi_{CNP}$. No es difícil convencerse de que la intersección de dicho plano con la esfera $\mathbb{S}$ determina una circunferencia máxima, digamos $\mathcal{C}$, además la intersección del plano $\Pi_{CNP}$ con los planos $\Pi_P$, $\Pi_N$ y $\mathbb{C}$ determina tres rectas, digamos $\mathcal{L}_P$, $\mathcal{L}_N$ y $\mathcal{L}_O$, la primera recta es tangente a $\mathcal{C}$ en $P$ y la segunda recta es tangente a $\mathcal{C}$ en $N$, mientras que la tercera recta es tangente a $\mathbb{S}$ en el origen y pasa por el punto $z_0=\varphi(P)$. Notemos que $\mathcal{L}_P$ y $\mathcal{L}_N$ se intersecan en un punto $Q\in\mathbb{R}^3$ y las rectas $\mathcal{L}_P$ y $\mathcal{L}_O$ se intersecan en un punto $w\in\mathbb{C}$. Por otra parte la intersección de los planos $\Pi_N$ y $\mathbb{C}$ con el plano $\Pi_P$ determinan otras dos rectas, digamos $\mathcal{L}_Q$ y $\mathcal{L}_w$, la primera pasa por $Q$ y la segunda pasa por $w$. Por construcción es claro que la recta $\mathcal{L}_N$ pasa por el punto $Q$, figura 55.

Dada la perfecta simetría de la esfera, es fácil concluir que los planos $\Pi_N$ y $\Pi_P$ forman los mismos ángulos con la recta que pasa por $N$ y $P$, digamos $\mathcal{L}_{NP}$, y que la recta $\mathcal{L}_Q$ es perpendicular a la recta $\mathcal{L}_{NP}$. Para ver esto más claro consideremos el corte transversal hecho sobre la esfera $\mathbb{S}$ con el plano $\Pi_{CNP}$. Más aún, como el plano $\Pi_N$ es paralelo al plano complejo $\mathbb{C}$, es claro que los planos $\Pi_P$ y $\mathbb{C}$ forman los mismos ángulos con la recta $\mathcal{L}_{NP}$ en el punto $z_0\in\mathbb{C}$ dado por la proyección estereográfica, figura 55. De acuerdo con la figura 56 es claro que los triángulos $NQP$ y $Pwz_0$ son semejantes.

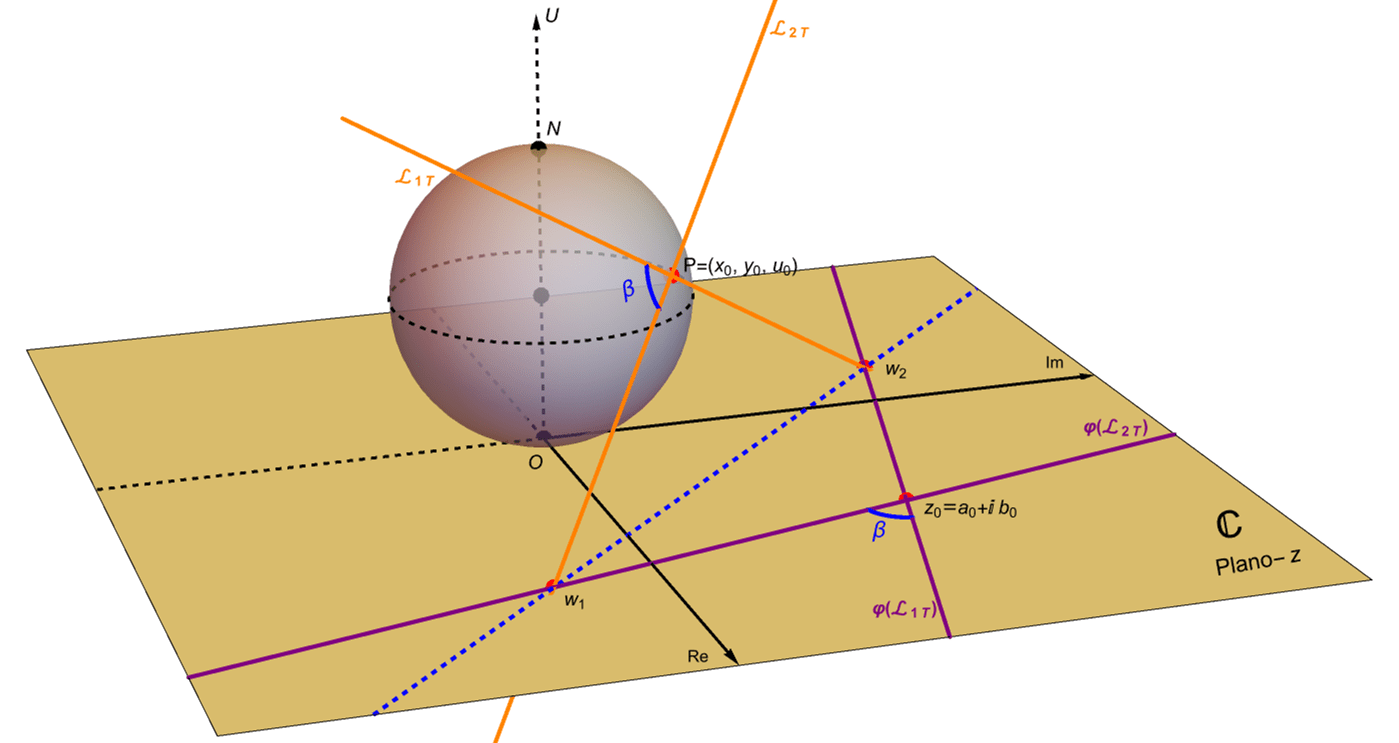
Supongamos que dos curvas suaves en $\mathbb{S}$, digamos $\Gamma_1$ y $\Gamma_2$, se intersecan en un punto $P\in\mathbb{S}$ con $P\neq N$. Sean $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ las respectivas rectas tangentes a las curvas $\Gamma_1$ y $\Gamma_2$ en el punto $P$ y sea $\beta$ el ángulo entre ellas, es decir $\beta\in(0,\pi/2)$.

Sin perder generalidad consideremos a la recta tangente $\mathcal{L}_{2T}$ en el punto $P\in\mathbb{S}$. Es fácil convencerse que la recta tangente bajo la proyección estereográfica en el punto $z_0=\varphi(P)\in\mathbb{C}$, digamos $\varphi\left(\mathcal{L}_{2T}\right)$, está dada por la intersección de un plano que contiene a $\mathcal{L}_{2T}$ y $\mathcal{L}_{NP}$, digamos $\pi$, con el plano complejo $\mathbb{C}$. Considerando lo anterior tenemos que las rectas tangentes $\mathcal{L}_{2T}$ y $\varphi\left(\mathcal{L}_{2T}\right)$ forman los mismos ángulos con $\mathcal{L}_{NP}$. Más aún, dado que la intersección del plano $\Pi_P$ con $\mathbb{C}$ determina a la recta $\mathcal{L}_w$ entonces es fácil concluir que las rectas tangentes $\mathcal{L}_{2T}$ y $\varphi\left(\mathcal{L}_{2T}\right)$ forman los mismos ángulos con $\mathcal{L}_w$, figura 57.

Haciendo lo mismo con la recta tangente $\mathcal{L}_{1T}$ concluimos que los ángulos que forman las dos rectas tangentes a las curvas $\Gamma_1$ y $\Gamma_2$ en el punto de intersección $P\in\mathbb{S}$, es decir $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ forman los mismos ángulos que las rectas tangentes a las imágenes de las curvas, digamos $\varphi\left(\Gamma_1\right)$ y $\varphi\left(\Gamma_2\right)$, dadas por la proyección estereográfica en el punto de intersección $z_0=\varphi(P)\in\mathbb{C}$, figura 58.

Figura 55: Intersección de los planos tangentes, $\Pi_{N}$, $\Pi_{P}$ y $\mathbb{C}$, a $\mathbb{S}$ en los puntos $N$, $P$ y $O$, con el plano $\Pi_{CNP}$.

Figura 56: Circunferencia máxima $\mathcal{C}$ dada por la intersección de la esfera $\mathbb{S}$ con el plano $\Pi_{CNP}$. Las líneas $\mathcal{L}_P$ y $\mathcal{L}_{N}$ forman los mismos ángulos con la línea $\mathcal{L}_{NP}$.

Figura 57: Rectas tangentes $\mathcal{L}_{2T}$ y $\varphi\left(\mathcal{L}_{2T}\right)$, dadas por las intersecciones de los planos $\pi$ con $\Pi_P$ y $\pi$ con $\mathbb{C}$ respectivamente, forman los mismos ángulos con las rectas $\mathcal{L}_w$ y $\mathcal{L}_{NP}$.

Figura 58: Las rectas tangentes $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ forman el mismo ángulo, que sus imágenes bajo la proyección estereográfica.

Hasta ahora hemos argumentado de manera geométrica que bajo la proyección estereográfica el ángulo que se forma entre dos curvas suaves $\Gamma_1$ y $\Gamma_2$ se conserva, ahora haremos una prueba analítica de esta propiedad, para ello consideremos lo siguiente.

Observación 11.6.
Notemos que para cualesquiera dos curvas suaves en la esfera de Riemann $\mathbb{S}$, al hablar del ángulo $\alpha$ que se forma entre ellas en un punto de intersección $P\in\mathbb{S}$ necesitamos pensar en el ángulo $0<\theta<\pi/2$ que se forma entre sus rectas tangentes en dicho punto, pero ¿cómo obtenemos una recta tangente a una curva suave en un punto $P\in\mathbb{S}$? Supongamos que una curva suave en $\mathbb{S}$ está descrita por la trayectoria $\gamma:(c,d)\rightarrow\mathbb{S}\subset\mathbb{R}^3$ cuyas funciones componentes son $x(t)$, $y(t)$ y $z(t)$, es decir $\gamma(t) = (x(t), y(t), z(t))$. Dado que la curva es suave en $(c,d)$ tenemos que existe $\gamma'(t)=(x'(t), y'(t), z'(t)) \neq 0$ para toda $t\in(c,d)$. Considerando que la curva descrita por $\gamma$ pasa por el punto $P=(x_0,y_0,u_0)\in\mathbb{S}$, entonces para algún $t_0\in(c,d)$ se cumple que $\gamma(t_0) = P$, por lo que podemos determinar a la recta tangente a dicha curva en el punto $P$, digamos $\mathcal{L}_{T}$, de forma paramétrica como: \begin{equation*}
\mathcal{L}_T: \quad P + \gamma'(t_0) \lambda, \quad \lambda\in\mathbb{R}.
\end{equation*}

Observación 11.7.
De manera geométrica es claro que $\mathcal{L}_T$ se puede obtener mediante la intersección de un plano tangente a la esfera $\mathbb{S}$ en el punto $P$, digamos $\Pi_T$, y un plano que pasa por el centro de la esfera y por $P$, digamos $\Pi_{CP}$. Considerando el plano $\Pi_{CP}$, por la observación 11.2 tenemos que existe una circunferencia máxima que que cae en dicho plano y que además pasa por el punto $P\in\mathbb{S}$. Entonces podemos concluir que para una recta tangente a la esfera en un punto $P$ existe una circunferencia máxima que pasa por dicho punto y que cae en el plano $\Pi_{CP}$.

De acuerdo con lo anterior, ver qué pasa con el ángulo $0<\theta<\pi/2$ que forman las rectas tangentes a dos curvas suaves en un punto de intersección $P\in\mathbb{S}$ bajo la proyección estereográfica, es equivalente a ver qué sucede con el ángulo que se forma entre dos circunferencias máximas de la esfera $\mathbb{S}$ bajo la proyección estereográfica, el cual está dado por el ángulo que se forma entre los planos en los que caen dichas circunferencias.

Proposición 11.3.
La proyección estereográfica es conforme o isogonal, es decir preserva ángulos.

Este resultado nos dice que el ángulo $\theta\in(0,\pi/2)$ que forman dos curvas suaves en la esfera $\mathbb{S}$, en un punto de intersección $P\in\mathbb{S}$, se preserva bajo la proyección estereográfica, es decir que en el plano complejo $\mathbb{C}$ las rectas tangentes de las imágenes de dichas curvas bajo la proyección estereográfica, en la imagen del punto de intersección, formarán nuevamente un ángulo $\theta$.
Recíprocamente para dos curvas suaves que se intersecan en el plano complejo $\mathbb{C}$, es decir en el plano $\Pi$ dado por (11.1), el ángulo $\theta\in(0,\pi/2)$ formado por sus rectas tangentes en el punto de intersección se preserva bajo la proyección estereográfica.

Figura 57: El ángulo $\theta$ que se forma entre las curvas $\Gamma_1$ y $\Gamma_2$ en el punto $P\in\mathbb{S}$ se preserva bajo la proyección estereográfica.

Demostración. Sean $\Gamma_1$ y $\Gamma_2$ dos curvas suaves en $\mathbb{S}$, descritas por $\gamma_1:(c,d)\rightarrow\mathbb{R}^3$ y $\gamma_2:(e,f)\rightarrow\mathbb{R}^3$, las cuales se pueden escribir considerando sus funciones componentes como: \begin{align*}
\gamma_1(t) = (x_1(t),y_1(t),u_1(t)),\\
\gamma_2(t) = (x_2(t),y_2(t),u_2(t)).
\end{align*} Para probar este resultado consideremos los siguientes casos:

El ángulo $\theta\in(0,\pi/2)$ que se forma entre $\Gamma_1$ y $\Gamma_2$ que se intersecan en el polo norte $N$ (o en el polo sur $O$) se preserva bajo la proyección estereográfica.
El ángulo $\theta\in(0,\pi/2)$ que se forma entre $\Gamma_1$ y $\Gamma_2$ que se intersecan en un punto $P\neq N$ se preserva bajo la proyección estereográfica.

Caso 1. Dado que el polo norte $N$ y el polo sur $O$ son puntos antipodales en $\mathbb{S}$, una circunferencia máxima que pase por el polo norte también pasa por el polo sur. Entonces, considerando la observación 11.7, tenemos que es indistinto si las dos curvas $\Gamma_1$ y $\Gamma_2$ se intersecan en el polo norte o en el polo sur, pues el ángulo que forman sus rectas tangentes en cualquiera de dichos puntos será el mismo que forman las dos circunferencias máximas que pasan por dichos puntos, es decir, el ángulo que se forma entre los dos planos que contienen a cada una de las circunferencias máximas.

Entonces, sin pérdida de generalidad supongamos que $\Gamma_1$ y $\Gamma_2$ se intersecan en el polo norte $N=(0,0,2)$. Por la observación 11.7 sabemos que cada recta tangente a cada curva, en el punto $N=(0,0,2)$, se obtiene mediante la intersección de un plano tangente a la esfera $\mathbb{S}$ en el polo norte, es decir el plano $u=2$, y un plano que pasa por el centro de la esfera y por el punto $N=(0,0,2)$, digamos $\Pi_{CN}$. De acuerdo con la observación 11.2 dichos planos son de la forma: \begin{align*}
\Pi_{1CN}: \quad A_1x+B_1y=0,\\
\Pi_{2CN}: \quad A_2x+B_2y=0.
\end{align*} Más aún, sabemos que en cada uno de estos planos cae una circunferencia máxima que pasa por $N=(0,0,2)$ y por $O=(0,0,0)$. Por lo que considerando las observaciones 11.5 y 11.7 tenemos que el ángulo $0<\theta<\pi/2$ que forman dichas circunferencias es tal que: \begin{align*}
\operatorname{cos}(\theta) & = \frac{(A_1,B_1,0) \cdot (A_2,B_2,0)}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}\\
& = \frac{A_1 A_2 + B_1 B_2}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}.
\end{align*} De acuerdo con la proposición 11.1, tenemos que bajo la proyección estereográfica las dos circunferencias máximas en la esfera $\mathbb{S}$, que pasan por el polo norte $N$, corresponden con dos rectas en el plano complejo $\mathbb{C}$ que pasan por el origen (¿por qué?), cuyas ecuaciones están dadas por: \begin{align*}
A_1x + B_1y =0, \quad u=0,\\
A_2x + B_2y =0,\quad u=0.
\end{align*} Es claro que el ángulo $0<\beta<\pi/2$ que forman estas rectas tangentes a las imágenes de las curvas $\Gamma_1$ y $\Gamma_2$ bajo la proyección estereográfica, en el punto de intersección $z=0$, es tal que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{(A_1,B_1,0) \cdot (A_2,B_2,0)}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}\\
& = \frac{A_1 A_2 + B_1 B_2}{\left\lVert (A_1,B_1,0) \right\rVert \left\lVert (A_2,B_2,0) \right\rVert}.
\end{align*} Por lo que, el ángulo $\alpha$ que forman las curvas $\Gamma_1$ y $\Gamma_2$ en el polo norte o en el polo sur se conserva bajo la proyección estereográfica.

Caso 2. Supongamos que $\Gamma_1$ y $\Gamma_2$ se intersecan en un punto $P\in\mathbb{S}$ con $P=(x_0,y_0,u_0)\neq N$.

Dado que dichas curvas se intersecan en el punto $P=(x_0,y_0,u_0)\in\mathbb{S}\setminus\{N\}$, entonces existen $t_0\in(c,d)$ y $t_0^*\in(e,f)$ tales que: \begin{align*}
\gamma_1(t_0) = (x_1(t_0),y_1(t_0),u_1(t_0)) = P,\\
\gamma_2(t_0^*) = (x_2(t_0^*),y_2(t_0^*),u_2(t_0^*)) = P. \tag{11.8.1}
\end{align*} Como $\Gamma_1$ y $\Gamma_2$ son suaves, tenemos que $\gamma_1$ es diferenciable en $(c,d)$ y $\gamma_2$ es diferenciable en $(e,f)$, por lo que: \begin{align*}
\gamma_1′(t_0) \neq 0,\quad \text{para}\,\, t_0\in(c,d),\\
\gamma_2′(t_0^*) \neq 0, \quad \text{para}\,\, t_0^*\in(e,f). \tag{11.8.2} \end{align*} Así, por la observación 11.6, las rectas tangentes a cada curva son respectivamente: \begin{align*}
\mathcal{L}_{1T}: \quad P + \gamma_1′(t_0) \lambda_1, \quad \lambda_1\in\mathbb{R},\\
\mathcal{L}_{2T}: \quad P + \gamma_2′(t_0^*) \lambda_2, \quad \lambda_2\in\mathbb{R}.
\end{align*} Entonces, considerando la observación 11.5, tenemos que el ángulo $0<\theta<\pi/2$ que se forma entre $\mathcal{L}_{1T}$ y $\mathcal{L}_{2T}$ en el punto de intersección $P\in\mathbb{S}$ es tal que: \begin{align*}
\operatorname{cos}(\theta) & = \frac{\gamma_1′(t_0) \cdot \gamma_2′(t_0^*)}{\left\lVert\gamma_1′(t_0)\right\rVert\left\lVert\gamma_2′(t_0^*) \right\rVert}\\
&=\frac{x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)}{\sqrt{x_1′(t_0)^2 + y_1′(t_0)^2 + u_1′(t_0)^2} \sqrt{x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2}}. \tag{11.9}
\end{align*} Dado que las curvas $\Gamma_1$ y $\Gamma_2$ están en $\mathbb{S}$ se cumple que: \begin{align*}
x_1(t)^2 + y_1(t)^2 + (u_1(t)-1)^2 = 1, \quad \forall t\in(c,d),\\
x_2(t)^2 + y_2(t)^2 + (u_2(t)-1)^2 = 1, \quad \forall t\in(e,f). \tag{11.10.1} \end{align*} Y considerando (11.8.1) tenemos que: \begin{align*}
x_1′(t)^2 + y_1′(t)^2 + u_1′(t)^2 \neq 0, \quad \forall t\in(c,d),\\
x_2′(t)^2 + y_2′(t)^2 + u_2′(t)^2 \neq 0, \quad \forall t\in(e,f). \tag{11.10.2}
\end{align*}

Por otra parte, el punto de intersección $P\in\mathbb{S}\setminus\{N\}$ de las curvas $\Gamma_1$ y $\Gamma_2$ bajo la proyección estreográfica corresponde con el punto $z_0=a_0+ib_0\in\mathbb{C}$, donde: \begin{align*}
a_0 = \frac{2x_0}{2-u_0},\\
b_0 = \frac{2y_0}{2-u_0}.
\end{align*} Considerando a $\mathbb{C}$ como el plano dado por (11.1), tenemos que dicho punto $z_0$ lo podemos asociar con el punto $(a_0,b_0,0)$ de $\mathbb{R}^3$.

Mientras que bajo la proyección estereográfica las imágenes de las curvas $\Gamma_1$ y $\Gamma_2$, digamos $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$, están descritas por las funciones $\alpha_1:(c,d)\to\mathbb{R}^3$ y $\alpha_2:(e,f)\to\mathbb{R}^3$ en el plano complejo $\mathbb{C}$ y se pueden escribir considerando sus funciones componentes como: \begin{align*}
\alpha_1(t) = (a_1(t),b_1(t),0),\\
\alpha_2(t) = (a_2(t),b_2(t),0),
\end{align*} donde para cada $i=1,2$ se tiene que: \begin{align*}
a_i(t) = \frac{2x_i(t)}{2-u_i(t)},\\
b_i(t) = \frac{2y_i(t)}{2-u_i(t)}. \tag{11.11}
\end{align*}

De acuerdo con lo anterior, es claro que las curvas $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ obtenidas bajo la proyección estereográfica son también curvas suaves en sus respectivos dominios $(c,d)$ y $(e,f)$, por lo que considerando el punto de intersección $z_0$ tenemos que para los valores $t_0\in(c,d)$ y $t_0^*\in(e,f)$ dados se cumple que: \begin{align*}
\alpha_1(t_0) = (a_1(t_0),b_1(t_0),0) = z_0,\\
\alpha_2(t_0^*) = (a_2(t_0^*),b_2(t_0^*),0) = z_0. \tag{11.12.1}
\end{align*} Más aún, como las funciones $\alpha_1$ y $\alpha_2$ son diferenciables en $(c,d)$ y $(e,f)$ respectivamente, entonces tenemos que para $t_0\in(c,d)$ y $t_0^*\in(e,f)$ se cumple: \begin{align*}
\alpha_1′(t_0) = (a_1′(t_0),b_1′(t_0),0) \neq 0,\\
\alpha_2′(t_0^*) = (a_2′(t_0^*),b_2′(t_0^*),0) \neq 0. \tag{11.12.2}
\end{align*} Por lo que las rectas tangentes a las curvas $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ en el punto de intersección $z_0$ tienen como ecuaciones: \begin{align*}
\ell_{1T}: \quad z_0 + \alpha_1′(t_0) \delta_1, \quad \delta_1\in\mathbb{R},\\ \ell_{2T}: \quad z_0 + \alpha_2′(t_0^*) \delta_2, \quad \delta_2\in\mathbb{R}.
\end{align*} Entonces, considerando la observación 11.5, tenemos que el ángulo $0<\beta<\pi/2$ que se forma entre $\ell_{1T}$ y $\ell_{2T}$ en el punto de intersección $z_0\in\mathbb{C}$ es tal que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{ \alpha_1′(t_0) \cdot \alpha_2′(t_0^*)}{\left\lVert \alpha_1′(t_0) \right\rVert \left\lVert \alpha_2′(t_0^*) \right\rVert}\\
& = \frac{a_1′(t_0) \, a_2′(t_0^*) + b_1′(t_0)\,b_2′(t_0^*)}{\sqrt{a_1′(t_0)^2 + b_1′(t_0)^2} \sqrt{a_2′(t_0^*)^2 + b_2′(t_0^*)^2}}.\tag{11.13}
\end{align*}

Para probar que el ángulo $\theta$, que forman las curvas $\Gamma_1$ y $\Gamma_2$ en el punto de intersección $P\in\mathbb{S}\setminus\{N\}$, se preserva bajo la proyección estereográfica veamos que las ecuaciones (11.9) y (11.13) son iguales.

Derivando las ecuaciones dadas en (11.11) tenemos para cada $i=1,2$ que: \begin{align*}
a_i'(t) = \frac{2}{(2-u_i(t))^2}\left[u_i'(t)\,x_i(t)+x_i'(t)\,(2-u_i(t))\right],\\
b_i'(t) = \frac{2}{(2-u_i(t))^2}\left[u_i'(t)\,y_i(t)+y_i'(t)\,(2-u_i(t))\right]. \tag{11.14}
\end{align*} Considerando las ecuaciones dadas en (11.6), obtenemos la relación inversa entre las curvas suaves $\varphi(\Gamma_1)$ y $\varphi(\Gamma_2)$ en el plano complejo $\mathbb{C}$ con las curvas suaves $\Gamma_1$ y $\Gamma_2$ en la esfera $\mathbb{S}$. Considerando dicha relación es fácil verificar que para $i=1,2$ se cumple: \begin{equation*}
x_i'(t) \, x_i(t) + y_i'(t)\,y_i(t) + u_i'(t)\left[u_i(t)-1\right] = 0. \tag{11.15}
\end{equation*}

Considerando (11.8.1), (11.10.1), (11.12.1), (11.14) y (11.15) es fácil verificar que para $t_0\in(c,d)$ y para $t_0^*\in(e,f)$ se cumple respectivamente: \begin{align*}
a_1′(t_0)^2 &+ b_1′(t_0)^2\\
&=\frac{4}{(2-u_1(t_0))^4}\Bigg(\left[x_1′(t_0)^2+y_1′(t_0)^2+u_1′(t_0)^2\right](2-u_1(t_0))^2\Bigg),\\
&=\frac{4}{(2-u_0)^4}\Bigg(\left[x_1′(t_0)^2+y_1′(t_0)^2+u_1′(t_0)^2\right](2-u_0)^2\Bigg), \tag{11.16.1}
\end{align*} \begin{align*}
a_2′(t_0^*)^2 &+ b_2′(t_0^*)^2\\
&=\frac{4}{(2-u_2(t_0^*))^4} \Bigg( \left[x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2\right] (2-u_2(t_0^*))^2 \Bigg),\\
&=\frac{4}{(2-u_0)^4} \Bigg( \left[x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2\right] (2-u_0)^2 \Bigg). \tag{11.16.2}
\end{align*} Dado que el punto $P=(x_0,y_0,u_0)\neq N$, entonces $u_0 \neq 2$, por lo que podemos simplificar (11.16.1) y (11.16.2) como: \begin{equation*}
a_1′(t_0)^2 + b_1′(t_0)^2 = \frac{4}{(2-u_0)^2} \Bigg( x_1′(t_0)^2 + y_1′(t_0)^2 + + u_1′(t_0)^2 \Bigg), \tag{11.17.1}
\end{equation*} \begin{equation*}
a_2′(t_0^*)^2 + b_2′(t_0^*)^2 = \frac{4}{(2-u_0)^2} \Bigg(x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2 \Bigg). \tag{11.17.2}
\end{equation*} Además como $P\in\mathbb{S}$ se cumple que: \begin{equation*}
x_0^2+y_0^2=u_0(2-u_0). \tag{11.18}
\end{equation*}

Considerando (11.12.2), (11.14), (11.15), (11.18) y que $u_0\neq2$ es fácil verificar que: \begin{align*}
\alpha_1′(t_0) \cdot \alpha_2′(t_0^*) & = a_1′(t_0)\,a_2′(t_0^*) + b_1′(t_0)\,b_2′(t_0^*)\\
& = \frac{4}{(2-u_0)^2}\Bigg(x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)\Bigg) \tag{11.19}
\end{align*}

Sustituyendo (11.17.1), (11.17.2) y (11.19) en (11.13) tenemos que: \begin{align*}
\operatorname{cos}(\beta) & = \frac{x_1′(t_0)\,x_2′(t_0^*) + y_1′(t_0)\,y_2′(t_0^*) + u_1′(t_0)\,u_2′(t_0^*)}{\sqrt{x_1′(t_0)^2 + y_1′(t_0)^2 + u_1′(t_0)^2} \sqrt{x_2′(t_0^*)^2 + y_2′(t_0^*)^2 + u_2′(t_0^*)^2}}\\
& = \operatorname{cos}(\theta).
\end{align*}
Por lo tanto el ángulo $\theta$ que se forma entre las curvas $\Gamma_1$ y $\Gamma_2$ en un punto de intersección $P\in\mathbb{S}$, distinto del polo norte (o del polo sur), se preserva bajo la proyección estereográfica.

$\blacksquare$

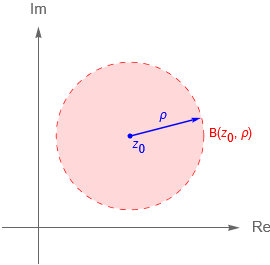
Del mismo modo en que introducimos una métrica en $\mathbb{C}$, es posible definir una métrica en $\mathbb{C}_\infty$, la cual nos permitirá caracterizar y analizar las propiedades de este nuevo conjunto.

Dados dos puntos $z,w\in\mathbb{C}_\infty$ debemos definir una forma de medir distancia entre ellos, es decir una métrica $d:\mathbb{C}_\infty \times \mathbb{C}_\infty \to [0, \infty)$. Desde que la proyección estereográfica nos da una biyección entre el plano complejo extendido $\mathbb{C}_\infty$ y la esfera de Riemann $\mathbb{S}$, podemos definir la métrica de $\mathbb{C}_\infty$ considerando la distancia usual entre dos puntos $P,Q\in\mathbb{R}^3$, es decir la métrica euclidiana de $\mathbb{R}^3$. Tenemos que si $P=(x_1,y_1,u_1)$ y $Q=(x_2,y_2,u_2)$ son dos puntos de $\mathbb{R}^3$ entonces: \begin{equation*}
d_{\mathbb{R}^3}(P,Q) = \sqrt{(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2}. \tag{11.20}
\end{equation*}
Considerando la proyección estereográfica, podemos hacer corresponder los puntos $z=a+ib$ y $w=\alpha+i\beta$ en $\mathbb{C}_\infty$ con los puntos $P,Q\in\mathbb{S}$ respectivamente, entonces de acuerdo con (11.20) podemos definir la distancia entre $z$ y $w$ como: \begin{equation*} \chi(z,w) = \sqrt{(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2}. \tag{11.21} \end{equation*}
Dado que $P$ y $Q$ son puntos de $\mathbb{S}$, entonces se cumple que: \begin{align*}
x_1^2 + y_1^2 +(u_1 -1)^2 = 1,\\
x_2^2 + y_2^2 +(u_2 -1)^2 = 1. \tag{11.22}
\end{align*} De acuerdo con (11.22) y considerando (11.8), es fácil ver que:
\begin{align*}
(x_1 \,-\, x_2)^2 + (y_1 \,-\, y_2)^2 + (u_1 \,-\, u_2)^2 & = 2\left(u_1 + u_2 \,-\, x_1 x_2 \,-\, y_1 y_2 \,-\, u_1 u_2\right)\\
& = \frac{16 |\, z \,-\, w \,|^2}{\left(|\,z\,|^2 + 4\right)\left(|\,w\,|^2 + 4\right)}. \tag{11.23}
\end{align*} Entonces por (11.21) y (11.23) tenemos que: \begin{equation*}
\chi(z,w) = \frac{4 |\, z \,-\, w \,|}{\sqrt{\left(|\,z\,|^2 + 4\right)\left(|\,w\,|^2 + 4\right)}}. \tag{11.24}
\end{equation*}
Notemos que los puntos $z\neq \infty$ y $w=\infty$ de $\mathbb{C}_\infty$ corresponden con los puntos $P=(x,y,u)$ y $N=(0,0,2)$ de $\mathbb{S} \subset \mathbb{R}^3$, por lo que considerando (11.20) es fácil ver que: \begin{equation*}
\chi(z,\infty) = \frac{4}{\sqrt{|\,z\,|^2 + 4}}. \tag{11.25}
\end{equation*}

Considerando (11.24) y (11.25) tenemos que: \begin{equation*}
\chi(z,w)= \left\{ \begin{array}{lcc}
\dfrac{4 |\, z \,-\, w \,|}{\sqrt{|\,z\,|^2 + 4} \,\sqrt{|\,w\,|^2 + 4}}, & \text{si} & z,w\in\mathbb{C}\\
\dfrac{4}{\sqrt{|\,z\,|^2 + 4}}, & \text{si} & z\in\mathbb{C}, w=\infty,\\
0, & \text{si} & z=\infty, w=\infty.\\
\end{array}
\right.
\end{equation*}
A esta métrica en $\mathbb{C}_\infty$, inducida por la métrica euclidiana de $\mathbb{R}^3$, se le conoce como la métrica cordal.

Notemos que $\mathbb{C}_\infty$ dotado con la métrica cordal forman un espacio métrico, ver ejercicio 4. Considerando la entrada anterior podemos verificar algunas propiedades para este espacio métrico.

Primeramente, dado que la métrica cordal es inducida por la distancia usual de $\mathbb{R}^3$, debe ser claro que si $z,w\in\mathbb{C}_\infty$, entonces: \begin{equation*}
\chi(z,w) \leq 2,
\end{equation*} ya que 2 es el diámetro de $\mathbb{S}\subset\mathbb{R}^3$. Por lo que la métrica cordal es acotada.

Proposición 11.4.
El espacio métrico $(\mathbb{C}_\infty, d)$, donde $d$ es la métrica cordal, es compacto.

Demostración. Dado que $\mathbb{S} \subset \mathbb{R}^3$ es cerrado y acotado, tenemos por el teorema de Heine – Borel que $\mathbb{S}$ es compacto en $\mathbb{R}^3$. Dado que la proyección estereográfica $\varphi$ define un homeomorfismo de $\mathbb{S}$ en $\mathbb{C}_\infty$, entonces se sigue que $\mathbb{C}_\infty$ es también compacto.

$\blacksquare$

Proposición 11.5.
El espacio métrico $(\mathbb{C}_\infty, d)$, donde $d$ es la métrica cordal, es completo.

Demostración. Ejercicio.

$\blacksquare$

Tarea moral

Considera la proposición 11.1. Argumenta porqué la proyección estereográfica y su inversa, es decir las funciones $\varphi$ y $\varphi^{-1}$ son continuas. Hint: Consulta la entrada 9.
Demuestra la proposición 11.2. Hint: Utiliza la observación 11.2.
¿Por qué una circunferencia en $\mathbb{S}$ que pasa por $N=(0,0,2)$ y por $O=(0,0,0)$ corresponde a una recta que pasa por el origen en el plano complejo $\mathbb{C}$?
Muestra que las igualdades del caso 2 de la proposición 11.2 son ciertas. Argumenta tus desarrollos.
Verifica que la igualdad dada por (11.23) es cierta.
Demuestra que la métrica cordal satisface las condiciones de métrica, es decir, demuestra que para cualesquiera $z_1, z_2, z_3\in\mathbb{C}_\infty$ se cumple:
i) $\chi(z_2, z_1) \geq 0$.
ii) $\chi(z_2, z_1) = 0$ si y solo si $z_1=z_2$.
iii) Simetría: $\chi(z_1, z_2) = \chi(z_2, z_1)$.
iv) Desigualdad del triángulo: $\chi(z_2, z_1) \leq \chi(z_2, z_3) + \chi(z_3, z_1)$. Hint: Utiliza los ejercicios 8 y 9 de la entrada 3, sección de tarea moral, para probar la desigualdad del triángulo.
Considera a la función: \begin{equation*}
\chi(z,w) = \frac{4 \, |\,z\,-\,w\,|}{\sqrt{|\,z\,|^2 + 4} \, \sqrt{|\,w\,|^2 + 4}}, \quad \forall z,w\in\mathbb{C},
\end{equation*} de acuerdo con el ejercicio anterior es claro que dicha función es un métrica en $\mathbb{C}$. Prueba que dicha métrica $\chi$ y la métrica euclidiana $d(z,w) = |\,z\,-\,w\,|$ son equivalentes.
De acuerdo con la entrada anterior, sea $z_0\in\mathbb{C}_\infty$ y sea $d$ la métrica cordal, una pregunta que puede resultar es, dado $\rho>0$, ¿cómo se define un $\rho$-vecindario de $z_0$ en $\mathbb{C}_\infty$? Describe a dicho conjunto.
Demuestra la proposición 11.5.

Más adelante…

En esta entrada hemos hecho una compactificación del plano complejo agregándole un punto ideal, llamado el punto al infinito, obteniendo así el plano complejo extendido $\mathbb{C}_\infty$ el cual representamos mediante el módelo de la esfera de Riemann.

Hemos visto que existe una relación biunívoca entre el plano complejo extendido y la esfera de Riemann dada por la proyección estreográfica, la cual resulto tener propiedades interesantes que aparecerán más adelante para caracterizar a algunas funciones.

Además dotamos al plano complejo extendido con una métrica, llamada la métrica cordal, la cual nos permite tratar a $\mathbb{C}_\infty$ como un espacio métrico, por lo que podemos considerar algunas propiedades de la entrada anterior para caracterizar la topología de este espacio métrico.

La importancia de trabajar con esta extensión se verá a lo largo del curso cuando requiramos trabajar con funciones complejas para las cuales el módulo de la variable crezca de manera arbitraria.

Con esta entrada finalizamos la primera unidad de este curso: Introducción y preliminares. La siguiente entrada comenzaremos la segunda unidad titulada: Analicidad y funciones de variable compleja.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Conexidad y compacidad en un espacio métrico.
Siguiente entrada del curso: Funciones de variable compleja. Definiciones y preliminares.

Variable Compleja I: Sucesiones en el espacio métrico $(\mathbb{C},d)$

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En la entrada anterior vimos que $\mathbb{C}$ dotado con la métrica euclidiana, inducida por el módulo de un número complejo, forman un espacio métrico.

Al trabajar con espacios métricos, las sucesiones resultan una herramienta fundamental en el estudio del concepto de las aproximaciones. De manera particular en esta entrada abordaremos el concepto de sucesión en el sentido complejo y estudiaremos propiedades de las mismas pues veremos que estas sucesiones están estrechamente ligadas con la topología de $\mathbb{C}$. Además en su momento usaremos los resultados de esta entrada para el estudio de series de números complejos, las cuales resultarán fundamentales en el estudio de la teoría de funciones.

Sucesiones de números complejos

Definición 8.1. (Sucesión.)
Sea $(X,d_X)$ un espacio métrico. Una sucesión de puntos en $X$ es una función $f: \mathbb{N}^+ \rightarrow X$ tal que para cada $n\in\mathbb{N}^+$ asigna de manera única un elemento de $X$. Si $f(n)=x_n\in X$ para toda $n\in\mathbb{N}^+$, entonces denotamos a la sucesión como el conjunto $\left\{x_n\right\}_{n\geq1}$ o simplemente $\left\{x_n\right\}$.

Observación 8.1.
En este punto es conveniente hacer énfasis en las sucesiones de $\mathbb{C}$ pues más adalente probaremos algunos resultados del espacio métrico $(\mathbb{C},d)$. Sin embargo las definiciones que daremos a continuación son válidas en general para un espacio métrico $(X,d)$. Además será de vital importancia recordar nuestros resultados para sucesiones reales ya que nos serán de utilidad más adelante.

Definición 8.2. (Sucesión compleja convergente.)
Una sucesión de números complejos $\left\{z_n\right\}_{n\geq1}$ converge a un número complejo $z\in\mathbb{C}$, llamado el límite de $\left\{z_n\right\}_{n\geq1}$, si para toda $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que:
\begin{equation*}
|\,z_n \,- \, z\,|<\varepsilon, \quad \forall n \geq N,
\end{equation*} lo cual denotamos como $z_n \rightarrow z$ ó $\lim\limits_{n \to \infty} z_n = z$. De existir dicho límite, este es único. (¿Por qué?)

Notemos que geométricamente la desigualdad $|\,z_n \,- \, z\,|< \varepsilon$ nos dice que para $n\geq N$ todos los términos de la sucesión caen en la $\varepsilon$-vecindad de $z$, es decir $B(z,\varepsilon)$, figura 47.

Figura 47: Convergencia de una sucesión de números complejos.

Ejemplo 8.1.
Veamos que la sucesión de números complejos $\left\{\dfrac{i^{n+1}}{n}\right\}_{n\geq 1}$ converge a cero.
Solución.
Considerando la fórmula de De Moivre es fácil notar que: \begin{equation*}
|\,i^{n+1} \,- \, 0\,| = |\,i^{n+1}\,| = |\,i\,|^{n+1} = 1. \end{equation*} Por otra parte, por la propiedad arquimediana se sigue que para todo $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} \left|\,\frac{i^{n+1}}{n} \,- \, 0\,\right| = \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n\geq N. \end{equation*} Por lo tanto $\lim\limits_{n \to \infty} \dfrac{i^{n+1}}{n} = 0$.

Definición 8.3. (Sucesión compleja divergente.)
Una sucesión de números complejos $\left\{z_n\right\}_{n\geq1}$ diverge, lo cual denotaremos como $\lim\limits_{n \to \infty} z_n = \infty$, si se cumple que $\lim\limits_{n \to \infty} |z_n| = \infty$, es decir si para toda $R>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*}|\,z_n\,| \geq R, \quad \forall n \geq N. \end{equation*}

Observación 8.2.
Es común considerar a la «divergencia» como la no existencia del límite dado en la definición 8.1, es decir una sucesión se considera divergente si no es convergente. Sin embargo en el caso complejo es conveniente considerar a la divergencia como la tendencia a infinito. En este sentido tenemos que los conceptos de «no convergencia» y «divergencia» no son equivalentes. Lo cual veremos más adelante.

Definición 8.4. (Operaciones entre sucesiones.)
Sean $\{z_n\}_{n\geq1}$ y $\{w_n\}_{n\geq1}$ dos sucesiones de $\mathbb{C}$. Las operaciones de suma, resta, multiplicación y división para sucesiones se definen respectivamente como:

$\{z_n\}_{n\geq1} \pm \{w_n\}_{n\geq1} = \{z_n \pm w_n\}_{n\geq1}$.
$\{z_n\}_{n\geq1} \cdot \{w_n\}_{n\geq1} = \{z_n w_n\}_{n\geq1}$.
Si $w_n \neq 0 $ para toda $n\in\mathbb{N}^+$, entonces $\dfrac{\{z_n\}_{n\geq1}}{\{w_n\}_{n\geq1}} = \left\{\dfrac{z_n}{w_n}\right\}_{n\geq1}$.

Considerando que una sucesión de números complejos $\{z_n\}_{n\geq 1}$ es un subconjunto de $\mathbb{C}$, entonces posible pensar en sucesiones acotadas.

Definición 8.5. (Sucesión acotada.)
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ se dice que es acotada si existe un número $M>0$ tal que $|\,z_n\,| \leq M$ para todo $n\in\mathbb{N}^+$.

Ejemplo 8.2.
La sucesión de números complejos $\{(-1)^n\}_{n \geq 1}$ es acotada, pero no es convergente.

De acuerdo con el ejemplo anterior es fácil concluir que una sucesión acotada no tendría porqué ser convergente. Sin embargo el recíproco sí es cierto, es decir:

Proposición 8.1.
Toda sucesión de números complejos $\{z_n\}_{n\geq 1}$ convergente es acotada.

Demostración.
Supongamos que la sucesión de números complejos $\{z_n\}_{n\geq 1}$ es convergente y $\lim\limits_{n \to \infty} z_n = z$. De acuerdo con la definición 8.1 tenemos que para $\varepsilon=1$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} |\,z_n \,- \,z\,| < 1, \quad \forall n\geq N. \end{equation*} De acuerdo con la desigualdad del triángulo se tiene que para toda $n\geq N$ se cumple que $|\,z_n\,| < |\,z\,| + 1$. Sea $M = \text{máx}\left\{ 1 + |\,z\,|,|\,z_1\,|,|\,z_2\,|, \ldots, |\,z_N\,|\right\}$, entonces para toda $n\geq 1$ se cumple que $|\,z_n\,|\leq M$.

$\blacksquare$

Utilizando la definición 8.2 es fácil probar las siguientes propiedades para sucesiones complejas.

Proposición 8.2.
Sean $\{z_n\}_{n\geq1}$ y $\{w_n\}_{n\geq1}$ sucesiones de números complejos y supongamos que ambas son convergentes en $\mathbb{C}$, con $\lim\limits_{n \to \infty} z_n = z$ y $\lim\limits_{n \to \infty} w_n = w$. Entonces se cumple que:

$\lim\limits_{n \to \infty}(z_n \pm w_n) = z \pm w$.
$\lim\limits_{n \to \infty}(z_n w_n) = zw$.
Si además $w_n\neq 0$ para toda $n \geq 1$ y $w\neq 0$, entonces $\lim\limits_{n \to \infty} \left(\dfrac{1}{ w_n}\right) = \dfrac{1}{w}$.
$\lim\limits_{n \to \infty} \overline{z_n} = \overline{z}$.
Si $\{z_n\}_{n\geq1}$ diverge y $\{w_n\}_{n\geq1}$ está separada de cero, es decir, si existen $r>0$ y $N\in\mathbb{N}^+$ tales que para $n\geq N$ se cumple que $|w_n|\geq r$, entonces $\{z_n w_n\}_{n\geq1}$ diverge.

Demostración.

Dadas las hipótesis por la definición 8.1 tenemos que para cualquier $\varepsilon>0$ existen $N_1, N_2 \in \mathbb{N}$ tales que: \begin{equation*}
|\,z_n \,-\, z\,| < \varepsilon/2, \quad \forall n \geq N_1,\end{equation*}\begin{equation*}|\,w_n \,-\, w\,| < \varepsilon/2, \quad \forall n \geq N_2. \end{equation*} Notemos que: \begin{align*}|\, (z_n \pm w_n) \,-\, (z \pm w)\,| & = |\, (z_n \,-\, z) \pm (w_n \,-\, w)\,|\\ & \leq |\,z_n \,-\, z\,| + |\,w_n \,-\, w\,| < \varepsilon, \quad \forall n \geq N, \end{align*} donde $N = \text{máx}\left\{N_1, N_2\right\}$. Por lo tanto $\lim\limits_{n \to \infty}(z_n \pm w_n) = z \pm w$.
Dadas las hipótesis, tenemos por la proposición 8.1 que ambas sucesiones son acotadas por lo que sin pérdida de generalidad supongamos que existe $M>0$ tal que $|\,z_n\,|\leq M$ para toda $n\geq 1$. Por otra parte, por la definición 8.2 tenemos que para cualquier $\varepsilon>0$ existen $N_1, N_2 \in \mathbb{N}$ tales que: \begin{equation*}|\,z_n \,-\, z\,| < \frac{\varepsilon}{2(|\,w\,|+1)}, \quad \forall n \geq N_1,\end{equation*} \begin{equation*}|\,w_n \,-\, w\,| < \frac{\varepsilon}{2M}, \quad \forall n \geq N_2. \end{equation*} Notemos que: \begin{align*}|\, z_n w_n \,-\, z w\,| & = |\, z_n w_n \,-\, z_n w + z_n w \,-\, z w \,|\\ & \leq |\,z_n w_n \,-\, z_n w\,| + |\,z_n w \,-\, z w\,|\\ & = |\,z_n\,|\,|\,w_n \,-\, w\,| + |\,w\,|\,|\,z_n \,-\, z \,|\\ & < M \left(\frac{\varepsilon}{2M}\right) + (|\,w\,|+1) \left(\frac{\varepsilon}{2(|\,w\,|+1)}\right) = \varepsilon, \quad \forall n \geq N. \end{align*} Por lo que $\lim\limits_{n \to \infty}(z_n w_n) = zw$.
Se deja como ejercicio al lector.
Se deja como ejercicio al lector.
Dadas las hipótesis, como $\{w_n\}_{n\geq1}$ está separada de cero, entonces existen $r>0$ y $N_1\in\mathbb{N}^+$ tales que para $n\geq N_1$ se cumple que $|w_n|\geq r$. Por otra parte, como $\{z_n\}_{n\geq1}$ diverge, dado $R>0$ existe $N_2\in\mathbb{N}^+$ tal que si $n\geq N_2$, entonces $|z_n|\geq R/r$. Por lo que, para $N = \text{máx}\left\{N_1, N_2\right\}$ se cumple que: \begin{equation*} |z_n w_n| = |z_n| \, |w_n| \geq \frac{R}{r} r = R, \quad \forall n\geq N, \end{equation*} entonces $\{z_n w_n\}_{n\geq1}$ diverge.

$\blacksquare$

Observación 8.3.
Considerando la definición 8.2 y la proposición 8.2 es fácil ver que si una sucesión $\{z_n\}_{n\geq 1}$ converge a un número complejo $z\in\mathbb{C}$ entonces se cumple (¿por qué?): \begin{equation*} z = \lim\limits_{n \to \infty} z_n \quad \Longleftrightarrow \quad \lim\limits_{n \to \infty} |\,z_n – z\,| = 0. \end{equation*} Y para $c\in\mathbb{C}$ constante: \begin{equation*} \lim\limits_{n\to\infty} (c z_n) = c \lim\limits_{n\to\infty} z_n. \end{equation*}

Sabemos que todo número complejo $z$ es caracterizado por su parte real y por su parte imaginaria, la cuales son números reales, por lo que considerando al $n$-ésimo término de una sucesión de números complejos $\{z_n\}_{n\geq 1}$ como $z_n = \operatorname{Re}(z_n) + i\operatorname{Im}(z_n)$, es fácil probar el siguiente resultado.

Proposición 8.3.
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ es convergente en $\mathbb{C}$ si y solo si las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$, $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$. En dicho caso tenemos que: \begin{align*} \lim_{n\to \infty} z_n = z \quad & \Longleftrightarrow \quad \lim_{n\to \infty} \operatorname{Re}(z_n) = \operatorname{Re}(z)\\ & \quad \quad \, \text{y} \,\,\, \lim_{n\to \infty} \operatorname{Im}(z_n) = \operatorname{Im}(z). \end{align*}

Demostración.
Por la proposición 3.1 sabemos que: \begin{align*} |\,\operatorname{Re}(z_n) \,-\, \operatorname{Re}(z)\,| = |\,\operatorname{Re}(z_n \,-\, z)\,|,\\ |\,\operatorname{Im}(z_n) \,-\, \operatorname{Im}(z)\,| = |\,\operatorname{Im}(z_n \,-\, z)\,|. \end{align*} Mientras que por la observación 3.1 tenemos que: \begin{align*} |\,\operatorname{Re}(z_n \,-\, z)\,| \leq |\,z_n \,-\, z\,| \leq |\,\operatorname{Re}(z_n \,-\, z)\,| + |\,\operatorname{Im}(z_n \,-\, z)\,|,\\ |\,\operatorname{Im}(z_n \,-\, z)\,| \leq |\,z_n \,-\, z\,| \leq |\,\operatorname{Re}(z_n \,-\, z)\,| + |\,\operatorname{Im}(z_n \,-\, z)\,|. \end{align*} De acuerdo con la observación 8.3 tenemos que $z = \lim_{n \to \infty} z_n$ si y solo si $\lim_{n \to \infty} |\,z_n \,-\, z\,| = 0$. Considerando lo anterior es claro que: \begin{align*} \lim_{n \to \infty} |\,z_n \,-\, z\,| = 0 \,\,\, & \Longleftrightarrow \,\,\, \lim_{n \to \infty} |\,\operatorname{Re}(z_n) \,-\, \operatorname{Re}(z)\,| = 0\\ & \quad \quad \text{y} \, \lim\limits_{n \to \infty} |\,\operatorname{Im}(z_n) \,-\, \operatorname{Im}(z)\,| = 0. \end{align*} Es decir las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$, $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$ (¿por qué?), por lo que: \begin{align*} \lim_{n\to \infty} z_n = z \quad & \Longleftrightarrow \quad \lim_{n\to \infty} \operatorname{Re}(z_n) = \operatorname{Re}(z)\\ & \quad \quad \, \text{y} \,\,\, \lim_{n\to \infty} \operatorname{Im}(z_n) = \operatorname{Im}(z). \end{align*} De donde se sigue el resultado.

$\blacksquare$

La proposición 8.3 es de gran utilidad al trabajar con sucesiones de números complejos, ya que la convergencia de estas sucesiones se reduce a verificar la convergencia de dos sucesiones de números reales. Más aún, podemos utilizar los resultados conocidos para sucesiones reales en el estudio de las sucesiones complejas, lo cual tiene sentido pues como vimos en la entrada 2 los números reales son un subconjunto de los números complejos, por lo que se deben cumplir las propiedades que ya conocíamos de $\mathbb{R}$ en $\mathbb{C}$.

Ejemplo 8.3.
Estudiemos la convergencia de las siguientes sucesiones:
a) $\left\{\dfrac{n+2+i2^n n}{2^n(n+2)}\right\}_{n\geq 1}$.
b) $\left\{\dfrac{3+in}{n+i2n}\right\}_{n\geq 1}$.

Solución. Para cada $n\in\mathbb{N}^+$ tenemos que:

a) \begin{equation*}
z_n = \dfrac{n+2+i2^n n}{2^n(n+2)} = \dfrac{1}{2^n} + i\left(\dfrac{n}{n+2}\right).
\end{equation*} De donde $\operatorname{Re}(z_n) = \dfrac{1}{2^n}$ e $\operatorname{Im}(z_n) = \dfrac{n}{n+2}$.
Sabemos que: \begin{align*}
\lim_{n \to \infty} \operatorname{Re}(z_n) = \lim_{n \to \infty}\dfrac{1}{2^n} = 0.\\
\lim_{n \to \infty} \operatorname{Im}(z_n) = \lim_{n \to \infty}\dfrac{n}{n+2} = 1.
\end{align*} Por lo que considerando la proposición 8.3 se sigue que $\operatorname{Re}(z) = 0$ y $\operatorname{Im}(z) = 1$, es decir: \begin{equation*}
\lim_{n \to \infty} z_n = z = i.
\end{equation*}

b) \begin{equation*}
w_n = \dfrac{3+in}{n+i2n} = \dfrac{3 + 2n}{5n} + i\left(\dfrac{n \,-\, 6}{5n}\right).
\end{equation*} De donde $\operatorname{Re}(w_n) = \dfrac{3+2n}{5n}$ e $\operatorname{Im}(w_n) = \dfrac{n \,-\, 6}{5n}$.
Sabemos que: \begin{align*}
\lim_{n \to \infty} \operatorname{Re}(w_n) = \lim_{n \to \infty}\dfrac{3+2n}{5n} = \frac{2}{5}.\\
\lim_{n \to \infty} \operatorname{Im}(w_n) = \lim_{n \to \infty}\dfrac{n \,-\, 6}{5n} = \frac{1}{5}.
\end{align*} Por lo que considerando la proposición 8.3 se sigue que $\operatorname{Re}(w) = \dfrac{2}{5}$ e $\operatorname{Im}(w) = \dfrac{1}{5}$, es decir: \begin{equation*}
\lim_{n \to \infty} w_n = w = \frac{2}{5} + i\frac{1}{5}.
\end{equation*}

Completez del espacio métrico $(\mathbb{C},d)$

Definición 8.6. (Sucesión de Cauchy.)
Una sucesión $\left\{z_n\right\}_{n\geq1}$ en $\mathbb{C}$ se dice que es una sucesión de Cauchy si para todo $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que: \begin{equation*}|\,z_n \,-\, z_m\,|<\varepsilon, \quad \forall\, n,m \geq N. \end{equation*}

Proposición 8.4.
Toda sucesión convergente en $\mathbb{C}$ es de Cauchy.

Demostración.
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos convergente con $\lim\limits_{n \to \infty} z_n = z$ para algún $z\in\mathbb{C}$. Sea $\varepsilon>0$, entonces existe $N\in\mathbb{N}^+$ tal que:\begin{equation*} |\,z_n \,-\, z\,| < \varepsilon, \quad \forall n \geq N. \end{equation*} Entonces por la desigualdad del triángulo se tiene que para cualesquiera $n,m\in \mathbb{N}^+$ tales que $n,m\geq N$ se cumple: \begin{equation*}|\,z_n \,-\, z_m\,| \leq |\,z_n \,-\, z\,| + |\,z \,-\, z_m\,| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} =\varepsilon. \end{equation*} Por lo tanto la sucesión $\{z_n\}_{n\geq 1}$ es de Cauchy.

Considerando la proposición 8.4 es momento de dar un ejemplo para argumentar la observación 8.2, es decir veamos que la divergencia y la no convergencia no son equivalentes.

Ejemplo 8.4
Consideremos la sucesión $\left\{i^n\right\}_{n\geq 1}$. Veamos que dicha sucesión no converge ni diverge.

Solución. Sea $z_n = i^n$. Por la fórmula de De Moivre es claro que para toda $n\in\mathbb{N}^+$ se tiene que: \begin{equation*}
|\,z_n\,| = |\,i^n\,| = |\,i\,|^n = 1, \quad \Longrightarrow \quad \lim_{n \to \infty} |\,z_n\,| = 1 \neq \infty. \end{equation*} Es decir, la sucesión $\left\{i^n\right\}_{n\geq 1}$ no diverge.

Por otra parte, veamos que dicha sucesión no es de Cauchy. Considerando el argumento principal de $i$, tenemos por la fórmula de De Moivre que: \begin{align*} z_{4n} = i^{4n} = \left(\operatorname{cis}(2\pi)\right)^n = 1^n = 1,\\ z_{4n+2} = i^{4n+2} = i^{4n}i^{2} = 1^n(-1) = -1, \end{align*} por lo que: \begin{align*}|\,z_{4n} \,&-\, z_{4n+2}\,| = 2,\\ & \Longrightarrow \quad \lim_{n \to \infty}|\,z_{4n} \,-\, z_{4n+2}\,| = 2 \neq 0. \end{align*} Entonces la sucesión $\{i^n\}_{n\geq 1}$ no es de Cauchy, por lo que por la contrapuesta de la proposición 8.4, tenemos que dicha sucesión no es convergente en $\mathbb{C}$.

Así concluimos que la sucesión $\{i^n\}_{n\geq 1}$ no diverge, pero tampoco converge.

Definición 8.7. (Completez.)
Un espacio métrico $(X,d)$ se dice que es completo si toda sucesión de Cauchy es convergente en $X$.

Ejemplo 8.5.
El espacio métrico $(\mathbb{R}, d)$, con $d$ la métrica inducida por el valor absoluto, es completo.

La proposición 8.4 es válida en general para cualquier espacio métrico $(X,d)$. Sin embargo el recíproco es falso en general, por ello la importancia de la definición 8.7. Considerando que $\mathbb{R}$ es un subconjunto de $\mathbb{C}$ y que el módulo complejo de $\mathbb{C}$ es la extensi\’on del valor absoluto de $\mathbb{R}$, podemos intuir que el espacio métrico $(\mathbb{C}, d)$, con $d$ inducida por el módulo, es también completo.

Proposición 8.5.
El campo de los números complejos $\mathbb{C}$ dotado con la métrica euclidiana es completo.

Demostración. Sea $\{z_n\}_{n\geq 1}$ en $\mathbb{C}$ una sucesión de Cauchy. Usando la observación 3.1 y la proposición 3.1, como en la prueba de la proposición 8.3, es fácil convencerse de que la sucesión $\{z_n\}_{n\geq 1}$ es de Cauchy si y solo si las sucesiones reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son de Cauchy en $\mathbb{R}$. Dado que $\mathbb{R}$ es completo con la métrica inducida por el valor absoluto, entonces las sucesiones de Cauchy $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$, por lo que por la proposición 8.3 se sigue que la sucesión de Cauchy $\{z_n\}_{n\geq 1}$ es convergente en $\mathbb{C}$, por lo tanto el espacio métrico $(\mathbb{C},d)$, con $d$ la métrica euclidiana, es completo.

$\blacksquare$

Proposición 8.6.
Un punto $z_0\in\mathbb{C}$ es un punto límite (o de acumulación) de un conjunto $S\subset\mathbb{C}$ si y solo si existe una sucesión $\{z_n\}_{n\geq1} \subset S$ tal que $z_n \neq z_0$ para todo $n\in\mathbb{N}^+$ y $\lim\limits_{n \to \infty} z_n = z_0$.

Demostración.
$\Rightarrow)$
Supongamos que $z_0\in\mathbb{C}$ es un punto límite de $S$, entonces por la definición 7.7 tenemos que para todo $n\in\mathbb{N}^+$ existe: \begin{equation*}
z_n \in B\left(z_0, \tfrac{1}{n}\right)\setminus\{z_0\} \cap S, \end{equation*} es decir que para todo $n\in\mathbb{N}^+$ se tiene que $z_n \in S$, $z_n\neq z_0$ y $|\,z_n \,-\, z_0\,|<\frac{1}{n}$. Consideremos a la sucesión $\{z_n\}_{n\geq1}$ dada anteriormente. Es claro que dicha sucesión cumple las condiciones del resultado, veamos que converge a $z_0$. Por la propiedad arquimediana se sigue que para todo $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*}|\,z_n \,-\, z_0\,|< \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n \geq N. \end{equation*} Por lo que $\lim\limits_{n\to \infty} z_n = z_0$.

$(\Leftarrow$
Supongamos que la sucesión $\{z_n\}_{n\geq 1}$ es tal que para todo $n\in\mathbb{N}^+$ se tiene $z_n \in S$, $z_n \neq z$ y $\lim\limits_{n\to \infty} z_n = z_0$. Por la propiedad arquimediana sabemos que dado $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} |\,z_N \,-\, z_0\,|< \frac{1}{N} < \varepsilon. \end{equation*} Como $z_N \neq z_0$ y $z_N \in S$, entonces para todo $\varepsilon>0$ se tiene que: \begin{equation*} z_N \in B(z_0, \varepsilon)\setminus\{z_0\} \cap S. \end{equation*} Por lo que $z_0$ es un punto límite de $S$.

$\blacksquare$

Definición 8.8. (Punto de acumulación de una sucesión.)
Un número $z\in\mathbb{C}$ se llama punto de acumulación de una sucesión de números complejos $\{z_n\}_{n\geq 1}$ si para todo $\varepsilon>0$ existe un número infinito de elementos $z_n$ de la sucesión tales que $|\,z_n \,-\, z\,|<\varepsilon$, es decir si cada $\varepsilon-$vecindad de $z_0$, $B(z_0,\varepsilon)$, contiene un número infinito de elementos de la sucesión.

Observación 8.4.
No debemos confundir esta definición con la definición 7.7 de punto límite o punto de acumulación de un conjunto. Por ejemplo la sucesión $\{(-1)^n\}_{n\geq 1}$ tiene dos puntos de acumulación los cuales son $-1$ y $1$. Sin embargo el conjunto $\{-1,1\}$, que consiste de los elementos que determinan a la sucesión, no tiene ningún punto límite o de acumulación.

Además, es fácil convencerse de que todo límite de una sucesión es un punto de acumulación de la misma. Sin embargo el recíproco no se cumple, para verlo basta considerar a la sucesión $\{i^n\}_{n\geq 1}$, la cual tiene cuatro puntos de acumulación los cuales son $1, -1, i$ y $-i$, pero dicha sucesión no converge, es decir no tiene límite.

Definición 8.9. (Subsucesión.)
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Una subsucesión o sucesión parcial de $\{z_n\}_{n\geq 1}$ es cualquier sucesión de la forma $\{z_{\sigma(n)} \}_{n\geq 1}$, donde $\sigma:\mathbb{N}^+ \rightarrow \mathbb{N}^+$, con $\sigma(n) = k_n$, es una función estrictamente creciente.

Ejemplo 8.6.
Si definimos $k_n = 2n$, entonces una subsucesión de $\left\{\dfrac{i^n}{n}\right\}_{n\geq 1}$ está conformada por: \begin{equation*}
-\frac{1}{2}, \,\, \frac{1}{4}, \,\, -\frac{1}{6}, \ldots, \frac{i^{2n}}{2n}, \ldots, \end{equation*} es decir $\left\{\dfrac{i^{2n}}{2n}\right\}_{n\geq 1}$ es una subsucesión de $\left\{\dfrac{i^n}{n}\right\}_{n\geq 1}$.

Proposición 8.7
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Entonces, $z\in\mathbb{C}$ es un punto de acumulación de $\{z_n\}_{n\geq 1}$ si y solo si existe una subsucesión $\{z_{k_n}\}_{n\geq 1}$ tal que $\lim\limits_{n\to\infty} z_{k_n} = z$.

Demostración. Dadas las hipótesis.

$\Rightarrow)$
Por la definición 8.8 tenemos que para todo $\varepsilon>0$ existe un número infinito de valores de $n$ para los cuales $|\,z_n \,-\, z\,|<\varepsilon$. Entonces para $\varepsilon=1$ existe un $n=k_1$ tal que $|\,z_{k_1} \,-\, z\,| < 1$. Del mismo modo para $\varepsilon = \frac{1}{2}$ existe $n=k_2$ tal que $|\,z_{k_2} \,-\, z\,| < \frac{1}{2}$. Procediendo de forma análoga podemos obtener, en general, que para $\varepsilon = \frac{1}{n}$ existe algún $k_n>k_{n-1}$ tal que $|\,z_{k_n} \,-\, z \,| < \frac{1}{n}$, por lo que existe una subsucesión $\left\{ z_{k_n} \right\}_{n\geq 1}$ de $\{z_n\}_{n\geq 1}$. Por otra parte, tenemos por la propiedad arquimediana que para todo $\varepsilon>0$ existe algún $N\in\mathbb{N}^+$ tal que: \begin{equation*}
|\,z_{k_n} \,-\, z\,| < \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n \geq N.
\end{equation*} Por lo tanto $\lim\limits_{n\to \infty} z_{k_n} = z$.

$(\Leftarrow$
Se deja como ejercicio al lector.

$\blacksquare$

Teorema 8.1. (Teorema de Bolzano – Weierstrass.)
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ acotada tiene una subsucesión convergente.

Demostración. Dadas las hipótesis, por la observación 3.1 es fácil ver que la sucesión $\{z_n\}_{n\geq 1}$ es acotada si y solo si las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son acotadas en $\mathbb{R}$. Por el teorema de Bolzano – Weierstrass para sucesiones de números reales sabemos que al ser la sucesión $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ acotada, entonces existe una subsucesión $\{\operatorname{Re}(z_{n_j})\}_{n\geq 1}$ convergente para alguna subsucesión $\{z_{n_j}\}_{n\geq 1}$ de $\{z_n\}_{n\geq 1}$. Dado que $\{\operatorname{Im}(z_{n_j})\}_{n\geq 1}$ también es acotada entonces existe alguna subsucesión $\{z_{n_{j_k}}\}_{n\geq 1}$ de $\{z_{n_j}\}_{n\geq 1}$ tal que $\{\operatorname{Im}(z_{n_{j_k}})\}_{n\geq 1}$ también converge. Entonces $\{\operatorname{Re}(z_{n_{j_k}})\}_{n\geq 1}$ es subsucesión de una sucesión convergente, por lo que también es convergente. Por lo tanto, por la proposición 8.3 se sigue que la subsucesión $\{z_{n_{j_k}}\}_{n\geq 1}$ converge en $\mathbb{C}$.

Tarea moral

Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Prueba que si la sucesión converge en $\mathbb{C}$, entonces dicho límite es único.
Considera las siguientes sucesiones:
a) $\left\{i^n\right\}_{n\geq 1}$.
b) $\left\{\left(\dfrac{1}{1+i}\right)^n\right\}_{n\geq 1}$.
c) $\left\{\left(\dfrac{1+i}{1-i}\right)^n\right\}_{n\geq 1}$.
d) $\left\{\dfrac{n}{2n+1} + i\, \dfrac{n-1}{n}\right\}_{n\geq 1}$.
e) $\left\{n^2\left(i^n -1\right)\right\}_{n\geq 1}$.
Determina cuáles sucesiones son acotadas, cuáles convergen, encuentra su límite y sus puntos de acumulación.
Prueba que si la sucesión $\{z_n\}_{n\geq 1}$ de números complejos converge a $z\in\mathbb{C}$, entonces la sucesión ${|\,z_n\,|}_{n\geq 1}$ converge a $|\,z\,|$. ¿Es cierto el recíproco?
Hint: Recuerda que: $|\,|z_n| – |z|\,| \leq |z_n – z|$.
Sea $z\in\mathbb{C}$, prueba lo siguiente.
a) Si $|\,z\,|<1$, entonces $\lim\limits_{n\to \infty} z^n = 0$.
b) Si $|\,z\,| > 1$, entonces $\lim\limits_{n\to \infty} z^n = \infty$.
Considera la observación 8.3, argumenta porqué es cierto el resultado. En general prueba que para un espacio métrico $(X, d_X)$ se cumple que una sucesión de elementos de $X$, digamos $\{x_n\}_{n\geq 1}$, converge a $x\in X$ si y solo si $\lim\limits_{n \to \infty} d_X (x_n, x) = 0$.
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Prueba que $\lim\limits_{n\to \infty} z_n = 0$ si y solo si $\lim\limits_{n\to \infty} |\,z_n\,| = 0$.
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos, sea $z \in \mathbb{C}$ y sea $\{c_n\}_{n\geq 1}$ una secuencia de números reales no negativos. Demuestra lo siguiente.
a) Si $\lim\limits_{n\to \infty} c_n = 0$ y $|\,z_n – z\,| \leq c_n$ para toda $n\in\mathbb{N}^+$, entonces $\lim\limits_{n\to \infty} z_n = z$.
b) Si $\lim\limits_{n\to \infty} c_n = \infty$ y $|\,z_n \,| \geq c_n$ para toda $n\in\mathbb{N}^+$, entonces $\lim\limits_{n\to \infty} z_n = \infty$.
Sean $\left\{x_n\right\}_{n\geq 1}$ y $\left\{y_n\right\}_{n\geq 1}$ dos sucesiones convergentes de números reales, tales que $x_n \leq y_n$ para toda $n\in\mathbb{N}$. Prueba que: \begin{equation*} \lim_{n \to \infty} x_n \leq \lim_{n \to \infty} y_n. \end{equation*}

Más adelante…

En esta entrada hemos abordado el concepto de sucesión compleja con la finalidad de caracterizar al espacio métrico $(\mathbb{C}, d)$ como un espacio métrico completo. Para ello hicimos uso de algunos resultados para sucesiones reales y generalizamos algunos de los mismos, como el Teorema de Bolzano-Weierstrass, para números complejos.

En general vimos que muchos de los resultados que teníamos para sucesiones reales se comportan de manera similar en el sentido complejo.

Por otra parte introducimos el concepto de la divergencia a infinito, el cual será de utilidad en la entrada 11 al hablar del punto al infinito.

Los resultados de esta entrada serán de utilidad cuando hablemos de las series en el sentido complejo y sobre su convergencia. Además de que nos permitirán obtener una caracterización relacionada con los conceptos de continuidad y continuidad uniforme.

La siguiente entrada abordaremos el concepto de continuidad entre espacios métricos.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Topología de $\mathbb{C}$.
Siguiente entrada del curso: Continuidad en un espacio métrico.

Variable Compleja I: Topología de $\mathbb{C}$

Por Pedro Rivera Herrera

Deja un comentario

Introducción

De manera intuitiva podemos considerar a un espacio métrico como un conjunto en el cual se puede hablar de la “distancia” entre sus elementos, por lo que definir lo que entendemos por distancia es de suma importancia. Para ello en esta entrada introduciremos los conceptos de distancia o métrica y espacio métrico. Es importante considerar que estos conceptos se analizan en primera instancia en un curso de Cálculo III y con mayor detalle en un curso de Análisis Matemático, por lo que es recomendable acompañar estos conceptos con algún material complementario, pues algunos resultados de los espacios métricos se darán por válidos y/o conocidos. Puedes consultar los libros Metric Spaces de Satish Shirali y Metric Spaces de Mícheál Ó Searcoid, o cualquier libro sobre topología de espacios métricos.

En la entrada anterior la métrica euclidiana $d$ nos permitió describir algunos lugares geométricos del plano complejo $\mathbb{C}$ con los que ya estábamos familiarizados en $\mathbb{R}^2$. Es importante mencionar que existen otras formas de definir la distancia entre dos números complejos $z$ y $w$. Sin embargo para los fines del curso estaremos utilizando la métrica euclidiana definida en la entrada anterior.

Hablar de la «topología» en $\mathbb{C}$ hace referencia a un resultado de los espacios métricos en el que se prueba que en un espacio métrico $(X,d)$ la métrica $d$ induce una topología en el conjunto $X$. Por lo que en esta entrada analizaremos la topología inducida por la métrica euclidiana $d(z,w) = |\,z-w\,|$ en $\mathbb{C}$.

Lo anterior nos motiva a definir algunos conjuntos de puntos de $\mathbb{C}$ que serán necesarios para continuar en el estudio de la topología en $\mathbb{C}$. Por lo que introducir el concepto de disco o vecindad será de gran utilidad para caracterizar a los conjuntos de $\mathbb{C}$, así como para dar una definición formal de límite y continuidad en $\mathbb{C}$.

$\mathbb{C}$ como un espacio métrico

Definición 7.1. (Métrica y espacio métrico.)
Un conjunto $X\neq\emptyset$ dotado con una función $d: X \times X \to [0,\infty)$ es llamado un espacio métrico, lo cual se denota como $(X,d)$, si la función $d$ cumple las siguientes propiedades para todo $x,y, z\in X$:

$d(x, y) \geq 0$.
$d(x,y) = 0$ si y solo si $x=y$.
Simetría: $d(x,y) = d(y,x)$.
Desigualdad del triángulo: $d(x,y) \leq d(x,z) + d(z,y)$.

Dicha función $d$ es llamada métrica en $X$ o función distancia en $X$. Es común denotar a la métrica en $X$ como $d_X$ cuando se están trabajando con varios espacios métricos y se requiere especificar donde está definida dicha métrica.

Ejemplo 7.1.

a) Consideremos al conjunto de los números reales $\mathbb{R}$. La función $d:\mathbb{R} \times \mathbb{R} \to [0,\infty)$ dada por:\begin{equation*}
d(x,y) = |\,x-y\,|,
\end{equation*} utilizando las propiedades del valor absoluto es fácil verficar que $d$ es una métrica en $\mathbb{R}$.

b) Si $X = \mathbb{R}^n$, entonces para $x = (x_1, x_2, \ldots, x_n)$ y $y = (y_1, y_2, \ldots, y_n)$ en $X$ se define:\begin{equation*}
d(x,y) = \left(\sum_{k=1}^{n} (x_k – y_k)^2 \right)^{1/2}.
\end{equation*}
La función $d$ es llamada la métrica euclidiana en $\mathbb{R}^n$.

c) Sea $X$ cualquier conjunto no vacío, entonces se define a la métrica discreta en $X$ como la función:
\begin{equation*}
d(x,y) = \left\{
\begin{array}{lcc}
0 & \text{si} & x = y,\\
1 & \text{si} & x \neq y.
\end{array}
\right.
\end{equation*}

Usando la definición del módulo es fácil probar que la distancia euclidiana, dada en la definición 6.1 de la entrada anterior, es una función $d: \mathbb{C}\times\mathbb{C} \rightarrow [0,\infty)$ que satisface las condiciones para ser una métrica.

Proposición 7.1. (El espacio métrico $(\mathbb{C}, d)$.)
El conjunto $\mathbb{C}$ dotado con la métrica euclidiana $d(z,w) = |\,z-w\,|$, $z,w\in\mathbb{C}$, es un espacio métrico.

Demostración. Sean $z_1, z_2, z_3 \in \mathbb{C}$, entonces:

$d(z_2, z_1) \geq 0$, se sigue de la definición del módulo de un número complejo.
Ejercicio.
Ejercicio.
Queremos probar que:
\begin{equation*}
d(z_2, z_1) \leq d(z_2, z_3) + d(z_3, z_1),
\end{equation*}o equivalentemente que:
\begin{equation*}
|\,z_2 – z_1\,| \leq |\,z_2 – z_3\,| + |\,z_3 – z_1\,|.
\end{equation*}

Sean $z = z_2 – z_3$ y $w = z_3 – z_1$, entonces podemos reescribir $z + w = z_2 – z_1$ y así probar que:
\begin{equation*}
|\, z + w \, | \leq |\,z\,| + |\,w\,|,
\end{equation*}lo cual se sigue de la proposición 3.2.

$\blacksquare$

Observación 7.1.
De acuerdo con la proposición 7.1 y la definición 7.1 tenemos que $\mathbb{C}$ dotado con la métrica euclidiana $d$ forma un espacio métrico, denotado por $(\mathbb{C}, d)$. Es importante mencionar que en esta entrada daremos algunos resultados de manera general para un espacio métrico $(X,d_X)$ y cuando sea necesario puntualizar algo del espacio métrico $(\mathbb{C}, d)$ trabajaremos de manera particular con dicho espacio métrico.

Definición 7.2.
Dado $z_0\in\mathbb{C}$ un punto fijo y una cantidad $\rho>0$, se define a la circunferencia de centro $z_0$ y radio $\rho$ en $\mathbb{C}$, figura 40a, como el conjunto de puntos:
\begin{equation*}
C(z_0,\rho)= \left\{z\in\mathbb{C} \,: \, |\,z-z_0\,| = \rho\right\}.
\end{equation*}

De acuerdo con la entrada anterior sabemos que las ecuaciones:\begin{align*}
|\,z-z_0\,|< \rho,\\
|\,z-z_0\,|> \rho,
\end{align*} nos describen a los puntos $z\in\mathbb{C}$ que caen dentro o fuera de la circunferencia $C(z_0,\rho)$ respectivamente, figura 40b.

Definición 7.3. (Disco o $\rho$-vecindad.)
Dado $z_0\in\mathbb{C}$ un punto fijo y una cantidad $\rho>0$, se definen en $\mathbb{C}$ a los conjuntos: \begin{equation*}
B(z_0,\rho)= \{z\in\mathbb{C} \,: \, |\,z-z_0\,| < \rho\},
\end{equation*} \begin{equation*}
\overline{B}(z_0,\rho)= \{z\in\mathbb{C} \,: \, |\,z-z_0\,| \leq \rho\},
\end{equation*} como el disco abierto de radio $\rho$ y centro $z_0$ o la $\rho$-vecindad de $z_0$, figura 41(a), y el disco cerrado de radio $\rho$ y centro $z_0$, figura 41(b), respectivamente.

Figura 40: Circunferencia de centro $z_0$ y radio $\rho>0$.

Observación 7.2.
En ocasiones será necesario trabajar con una $\rho$-vecindad de $z_0$ sin considerar al punto $z_0$, es decir $B^*(z_0,\rho) = B(z_0,\rho) \setminus \{z_0\}$, en dado caso llamaremos a ese conjunto como una $\rho$-vecindad perforada o un disco perforado.
Análogamente se puede hablar de un disco cerrado perforado como el conjunto $\overline{B}^*(z_0,\rho) = \overline{B}(z_0,\rho) \setminus \{z_0\}$.

Definición 7.4. (Punto interior y conjunto abierto.)
Sea $S\subset\mathbb{C}$. Diremos que $z_0\in \mathbb{C}$ es un punto interior de $S$ si existe $\rho>0$ tal que $B(z_0,\rho)\subset S$.
Al conjunto de puntos interiores de $S$ se le denota como $\operatorname{int}S$ o $ \mathring{S}$. Si se cumple que $S = \operatorname{int}S$, entonces diremos que $S$ es un conjunto abierto en $\mathbb{C}$.

De acuerdo con la definición de $\operatorname{int}S$, notemos $\operatorname{int}S\subset S$. De hecho, dado un espacio métrico $(X,d)$ y $S\subset X$, entonces se cumple que $\operatorname{int}S$ es un conjunto abierto y es el mayor subconjunto abierto de $X$ contenido en $S$.

Figura 41: Disco abierto y cerrado con centro $z_0$ y radio $\rho>0$.

Definición 7.5. (Conjunto cerrado.)
Un conjunto $S\subset\mathbb{C}$ se dice que es cerrado en $\mathbb{C}$ si su complemento $S^C = \mathbb{C}\setminus S$ es abierto en $\mathbb{C}$.

Observación 7.3.
Comunmente denotaremos a los conjuntos abiertos de $\mathbb{C}$ con la letra $U$ y a los conjuntos cerrados de $\mathbb{C}$ con la letra $F$.

Ejemplo 7.2.
Utilizando la desigualdad del triángulo es fácil verificar que:

a) El conjunto $\{z\in\mathbb{C} : 0<|\,z\,|<1\}$ es abierto en $\mathbb{C}$, figura 42a.

b) El conjunto $\{z\in\mathbb{C} : |\,z\,| \leq 1\}$ es cerrado en $\mathbb{C}$, figura 42b.

c) El conjunto $\{z\in\mathbb{C} : 0< |\,z\,| \leq 1\}$ no es abierto ni cerrado en $\mathbb{C}$, figura 43.

d) Los conjuntos $\emptyset$ y $\mathbb{C}$ son conjuntos abiertos y cerrados en $\mathbb{C}$, ¿por qué?

Figura 42: Conjuntos del ejemplo 7.1 inciso a) y b).

Figura 43: El conjunto $\{z\in\mathbb{C} : 0< |\,z\,| \leq 1\}$ no es cerrado ni es abierto en $\mathbb{C}$.

Definición 7.6. (Punto exterior y punto frontera.)
Sea $S\subset\mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto exterior de $S$ si existe $\rho>0$ tal que $B(z_0,\rho) \subset \mathbb{C}\setminus S$.
Por otra parte, diremos que $z_0$ es un punto frontera de $S$ si para todo $\rho>0$ se tiene que $B(z_0,\rho) \cap S \neq \emptyset$ y $B(z_0,\rho) \cap \mathbb{C}\setminus S \neq \emptyset$.

Al conjunto de los puntos exteriores de $S$ se le denota como $\operatorname{ext}S$. Mientras que al conjunto de los puntos frontera de $S$ se le denota como $\partial S$.

Definición 7.7. (Punto de acumulación o punto límite y punto aislado.)
Sea $S\subset \mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto de acumulación o un punto límite de $S$ si para todo $\rho>0$ se tiene:
\begin{equation*}
B(z_0,\rho)\setminus\{z_0\} \cap S \neq \emptyset.
\end{equation*} O equivalentemente que para todo $\rho>0$ se tiene:
\begin{equation*}
\{ z \in S : 0 < |\,z-z_0\,|<\rho\} \neq \emptyset.
\end{equation*}

Si se cumple que $z_0\in S$, pero $z_0$ no es punto de acumulación de $S$, entonces diremos que $z_0$ es un punto aislado de $S$. En este caso se tiene que existe algún $\varepsilon>0$ tal que:
\begin{equation*}
B(z_0,\varepsilon) \cap S = \{z_0\}.
\end{equation*}

Al conjunto de puntos de acumulación lo denotaremos como $S’$ y lo llamaremos el conjunto derivado de $S$.

Definición 7.8. (Punto de adherencia.)
Sea $S\subset \mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto de adherencia de $S$ si para todo $\rho>0$ se tiene:
\begin{equation*}
B(z_0,\rho) \cap S \neq \emptyset.
\end{equation*}

Al conjunto de puntos de adherencia lo llamaremos la cerradura o la clausura de $S$ y lo denotaremos como $\overline{S}$.

De acuerdo con la definición de $\overline{S}$, tenemos que $S \subset \overline{S}$. Además, dado un espacio métrico $(X,d)$ y $S\subset X$, entonces se cumple que $\overline{S}$ es un conjunto cerrado y es el menor subconjunto cerrado de $X$ que contiene a $S$.

De hecho, dado un espacio métrico $(X,d_X)$ y $S\subset X$, se tiene que $S$ es cerrado en $X$ si y solo si $S = \overline{S}$.

Proposición 7.2.
Consideremos al espacio métrico $(\mathbb{C}, d)$, con $d$ la métrica euclidiana. Un conjunto $S\subset\mathbb{C}$ es cerrado en $\mathbb{C}$ si y sólo si $S$ contiene a todos sus puntos de acumulación.

Demostración.
$\Rightarrow)$
Supongamos que $S$ es cerrado en $\mathbb{C}$. Sea $z_0 \in \mathbb{C}$ un punto de acumulación de $S$. Por reducción al absurdo supongamos que $z_0 \in \mathbb{C}\setminus S$. Notemos que por definición $\mathbb{C}\setminus S$ es un conjunto abierto, por lo que para algún $\rho>0$ se tiene que $B(z_0, \rho) \subset \mathbb{C}\setminus S$, es decir que al disco abierto $B(z_0,\rho)$ no pertenece ningún punto de $S$, lo cual contradice el hecho de que $z_0$ es un punto de acumulación de $S$. Por lo tanto $z_0\in S$.

$(\Leftarrow$
Supongamos que a $S$ pertenecen todos sus puntos de acumulación. Entonces para algún $z_0 \in \mathbb{C} \setminus S$ se cumple que $z_0$ no es punto de acumulación de $S$, por lo que existe $\rho>0$ tal que $B(z_0, \rho)$ no tiene puntos de $S$, por lo que $B(z_0, \rho) \subset \mathbb{C}\setminus S$, por tanto $\mathbb{C}\setminus S$ es abierto, de donde se sigue que $S$ es cerrado.

$\blacksquare$

Ejemplo 7.3.
Veamos que no necesariamente todo punto de un conjunto cerrado debe ser un punto de acumulación del mismo. Consideremos al conjunto:
\begin{equation*}
S = \left\{z\in\mathbb{C}\, : \, z = \frac{1}{n}, \,\, n\in\mathbb{N}^+ \right\} \cup \left\{0\right\}.
\end{equation*}

Es claro que $S\subset\mathbb{C}$. Notemos que el único punto de acumulación de $S$ es $z=0$. Desde que dicho punto pertenece a $S$, por la proposición 7.2 es claro que $S$ es cerrado. Por otra parte no es díficil convencerse de que salvo $z=0$, el resto de los puntos de $S$ son puntos aislados, ya que basta con tomar $\rho = \frac{1}{n} – \frac{1}{n+1} > 0$ para que se cumpla que:
\begin{equation*}
B\left(\frac{1}{n}, \rho\right) \cap S = \left\{\frac{1}{n}\right\}.
\end{equation*}

Definición 7.9. (Conjunto acotado.)
Un conjunto $S \subset \mathbb{C}$ se dice que es acotado si existe un número real $R>0$ tal que $|\,z\,| < R$ para todo $z\in S$.

Esta definición nos dice que $S$ es acotado si puede ser completamente encerrado por un $R$-vecindario del origen.

Ejemplo 7.4.
Sea $X = \left\{z\in\mathbb{C} \, : \, 0<|\,z\,|<1\right\} \cup \{2\}$, figura 44. Entonces:

a) Los puntos interiores de $X$ son el conjunto $\operatorname{int} X = \{z\in\mathbb{C} \, : \, 0<|\,z\,|<1\}$.

b) Los puntos exteriores de $X$ son el conjunto $\operatorname{ext} X = \{z\in\mathbb{C} \, : \, 1 < |\,z\,|\} \cap \{z\in\mathbb{C} \, : \, z \neq 2\}$.

c) La frontera de $X$ es el conjunto $\partial X = \{0, 2\} \cup \{z\in\mathbb{C} \,: \, |\,z\,|=1\}$.

d) Los puntos de acumulación de $X$ son el conjunto $X’ = \{z\in\mathbb{C} \, : \, |\,z\,|\leq 1\}$.

e) El punto $z=2$ es un punto aislado de $X$.

f) Tomando $R=3>0$ es claro que el conjunto $X$ es acotado ya que $|\,z\,|< R$ para todo $z\in X$.

Figura 44: Puntos del conjunto $X$ del ejemplo 7.2.

De acuerdo con nuestros cursos de Cálculo (y Análisis Matemático) sabemos que en un espacio métrico, en este caso en $(\mathbb{C},d)$, se cumple que:

Proposición 7.3.
Sea $(X,d_X)$ un espacio métrico. Sean $z_0 \in X$ y $S\subset X$, entonces:

Los conjuntos $X$ y $\emptyset$ son abiertos en $X$.
Para todo $\rho>0$, la $\rho$-vecindad de $z_0$, es decir el conjunto:
\begin{equation*}
B(z_0,\rho) = \{ z\in X \,: \, d_X(z,z_0) < \rho\},
\end{equation*} es un conjunto abierto en $X$.
Para todo $\rho>0$, el disco cerrado, es decir el conjunto:
\begin{equation*}
\overline{B}(z_0,\rho) = \{ z\in X \,: \, d_X(z,z_0) \leq \rho\},
\end{equation*} es un conjunto cerrado en $X$.
$S’ \subset \overline{S}$.
$\overline{S} = S \cup S’$.
$\overline{S} = \operatorname{int}S \cup \partial S$.
$X = \operatorname{int}S \cup \operatorname{ext}S \cup \partial S$.
Si $A \subset B$, entonces:
a) $\overline{A} \subset \overline{B}$.
b) $\operatorname{int}A \subset \operatorname{int}B$.
La unión de un número arbitrario de conjuntos abiertos en $X$ es también un conjunto abierto en $X$.
La intersección de un número finito de conjuntos abiertos en $X$ es un conjunto abierto en $X$.
La intersección de un número arbitrario de conjuntos cerrados en $X$ es también un conjunto cerrado en $X$.
La unión de un número finito de conjuntos cerrados en $X$ es un conjunto cerrado en $X$.

Demostración.

Ejercicio.
Dadas las hipótesis, sea $\rho>0$. Tomemos $z\in B(z_0,\rho)$ y sea $\varepsilon = \rho – d_X(z_0, z) > 0 $. Considerando la desigualdad del triángulo tenemos que para todo $w \in B(z,\varepsilon)$ se cumple que:
\begin{equation*}
d_X(w, z_0) \leq d_X(w, z) + d_X(z, z_0) < \varepsilon + d_X(z, z_0) = \rho,
\end{equation*} por lo que $B(z,\varepsilon) \subset B(z_0, \rho)$ para todo $z\in B(z_0,\rho)$.

Figura 45: Todo disco abierto $B(z_0,\rho)$ es un conjunto abierto en $X$.

Dadas las hipótesis, sea $\rho>0$. Tomemos $z\in \overline{\overline{B}(z_0,\rho)}$, entonces para todo $\varepsilon > 0$ existe:
\begin{equation*}
z_\varepsilon \in B(z,\varepsilon)\cap \overline{B}(z_0,\rho).
\end{equation*} De acuerdo con la desigualdad del triángulo, para todo $\varepsilon > 0$ se cumple que:
\begin{equation*}
d_X(z, z_0) \leq d_X(z, z_\varepsilon) + d_X(z_\varepsilon, z_0) < \varepsilon + \rho,
\end{equation*} de donde se sigue que $d(z, z_0) < \rho$, por lo que $\overline{\overline{B}(z_0,\rho)}\subset \overline{B}(z_0,\rho)$. Entonces
\begin{equation*}
\overline{B}(z_0,\rho) = \overline{\overline{B}(z_0,\rho)},
\end{equation*} por lo tanto, todo disco cerrado es un conjunto cerrado en $X$.
Ejercicio.
Ejercicio.
Ejercicio.
Ejercicio.
Ejercicio.
Sea $\{ G_j : j\in J\}$, con $J$ un conjunto de índices, una colección de conjuntos abiertos en $X$. Tomemos a $z\in G = \bigcup\limits_{j\in J} G_j$, entonces $z \in G_j$, para algún $j\in J$, así por la definición 7.4 tenemos que existe $\rho>0$ tal que $B(z,\rho) \subset G_j \subset G$, por lo que $G$ es abierto.
Sean $G_1, G_2, \ldots , G_n$ subconjuntos abiertos de $X$ y sea $z \in G = \bigcap\limits_{k=1}^{n} G_k$. Tenemos que $z\in G_k$ para $k=1,2, \ldots, n$, por lo que por la definición 7.4 se tiene que para cada $k$ existe $\rho_k > 0$ tal que $B(z,\rho_k) \subset G_k$. Si tomamos a $\rho = \operatorname{min}{\rho_k : 1 \leq k \leq n}$, entonces para cada $k$, con $1 \leq k \leq n$, se cumple que $B(z,\rho) \subset B(z,\rho_k) \subset G_k$. Entonces $B(z,\rho) \subset G$, por lo que $G$ es abierto.
Ejercicio.
Ejercicio.

$\blacksquare$

Es posible encontrar la prueba de estas propiedades en algún libro de topología o de topología de espacios métricos, como Topología de espacios métricos de Ignacio L. Iribarren.

Definición 7.10. (Conjunto denso.)
Sea $(X,d_X)$ un espacio métrico. Diremos que un conjunto $A\subset X$ es denso en $X$ si $\overline{A} = X$.

Ejemplo 7.5.

a) El conjunto de los números racionales $\mathbb{Q}$ es denso en $\mathbb{R}$ con la métrica usual de $\mathbb{R}$, $d(x,y) = |\,x-y\,|$.

b) El conjunto ${x+iy : x,y\in\mathbb{Q}}$ es denso en $\mathbb{C}$ con la métrica euclidiana.

Tarea moral

Prueba que las siguientes funciones $d_i: \mathbb{C}\times\mathbb{C} \to [0,\infty)$, con $i=1,2$, dadas por:
\begin{equation*}
d_1(x+iy, a+ib) = |\,x-a\,| + |\,y-b\,|,
\end{equation*} \begin{equation*}
d_2(x+iy, a+ib) = \text{máx}\left\{|\,x-a\,|,|\,y-b\,|\right\},
\end{equation*} son también una métrica en $\mathbb{C}$.
Considera la observación 7.2 y argumenta porqué esos conjuntos se pueden definir respectivamente como:
\begin{equation*}
B^*(z_0,\rho) = \{z\in\mathbb{C}\,:\, 0<|\,z-z_0\,|<\rho\},
\end{equation*} \begin{equation*}
\overline{B^*}(z_0,\rho) = \{z\in\mathbb{C}\,:\, 0<|\,z-z_0\,|\leq\rho\}.
\end{equation*} ¿Cómo son esos conjuntos en $\mathbb{C}$? ¿Cerrados, abiertos o ninguno de los dos? Describe al conjunto de puntos interiores, exteriores, frontera, de acumulación y de adherencia. ¿Son acotados esos conjuntos?
Argumenta porqué los conjuntos $\emptyset$ y $\mathbb{C}$ son abiertos y cerrados en $\mathbb{C}$, ejemplo 7.2(c).
Completa la demostración de las proposiciones 7.1 y 7.3.
Hasta ahora sabemos que $\mathbb{R}\subset\mathbb{C}$. Por otra parte, de nuestros cursos de cálculo sabemos que un intervalo abierto en $\mathbb{R}$, es decir el conjunto:
\begin{equation*}
(a,b) = \{ x\in\mathbb{R} \,:\, a<x<b\},
\end{equation*} es un conjunto abierto en $\mathbb{R}$. Prueba que dicho conjunto no es abierto en $\mathbb{C}$.
Utilizando la definición describe cómo son los siguientes conjuntos de $\mathbb{C}$, es decir ¿son abiertos o cerrados o ninguna de las dos en $\mathbb{C}$? ¿Son acotados?
a) Sean $a,b\in\mathbb{R}$ con $a<b$, definimos:\begin{align*}
A = \{z\in\mathbb{C}\, :\, a< \operatorname{Re}(z)<b\},\\
B = \{z\in\mathbb{C}\, :\, a< \operatorname{Im}(z)<b\}.
\end{align*} b) $X = \{z\in\mathbb{C} \,:\ \, \operatorname{Re}(z)<0\} \cup \{0\}$.
c) $Y = \{z\in\mathbb{C} \,:\ \, 0\leq\operatorname{Im}(z)\}$.

Considera a los siguientes conjuntos:
a) $S_1 = B(0,1)$.
b) $S_2 = \overline{B}\left(-1-i\sqrt{2},\frac{7}{8}\right)$.
c) $S_3 = \overline{B}\left(2+i\sqrt{3},\frac{1}{2}\right)$.
De acuerdo con la proposición 7.2 tenemos que $S_1$ es un conjunto abierto en $\mathbb{C}$, mientras que $S_2$ y $S_3$ son conjuntos cerrados en $\mathbb{C}$. Describe los puntos interiores, exteriores y frontera de cada uno de los tres conjuntos.

Considera al siguiente conjunto:
\begin{equation*}
S = \left\{ z\in\mathbb{C} \,:\, |\,\operatorname{Im}(z)\,| < |\,\operatorname{Re}(z)\,| \right\},
\end{equation*} el cual está representado en la figura 46. Prueba que:
a) $S$ es un conjunto abierto en $\mathbb{C}$.
b) $\partial S = \{ z\in\mathbb{C} \,:\, |\,\operatorname{Re}(z)\,| = |\,\operatorname{Im}(z)\,|\}$.
c) Los puntos de acumulación de $S$ son precisamente la clausura de $S$, es decir $\overline{S}$.
d) $S$ no es cerrado en $\mathbb{C}$.
e) $S$ no es acotado en $\mathbb{C}$.

Más adelante…

En esta entrada hemos hecho una breve descripción de la topología de los espacios métricos, en particular analizamos la topología del plano complejo $\mathbb{C}$. Esta caracterización de $\mathbb{C}$ como un espacio métrico nos será de gran utilidad en las siguientes entradas para poder continuar el estudio del campo de los números complejos.

En esta entrada hemos visto que existe una estrecha relación entre la topología de $\mathbb{C}$ y $\mathbb{R}^2$, lo cual no debe sorprendernos ya que como espacios vectoriales dichos conjuntos son isomorfos, ver ejercicio 6 de la entrada 2. Más adelante veremos que como espacios métricos son homeomorfos, por lo que muchas propiedades que conocemos para $\mathbb{R}^2$ nos permitirán caracterizar a los números complejos. Por otra parte es fácil convencerse que la topología de $\mathbb{C}$ induce en $\mathbb{R}$ su topología usual considerando la distancia definida mediante el valor absoluto.

La siguiente entrada abordaremos las sucesiones en $\mathbb{C}$ y discutiremos la completez del espacio métrico $(\mathbb{C}, d)$, con $d$ la métrica euclidiana.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Lugares geométricos en $\mathbb{C}$.
Siguiente entrada del curso: Sucesiones en el espacio métrico $(\mathbb{C}, d)$.

Variable Compleja I: Lugares geométricos en $\mathbb{C}$

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En la entrada anterior definimos el módulo de un número complejo en términos de su parte real e imaginaria. De manera geométrica observamos que el módulo nos determina la distancia que hay entre un número complejo y el origen. Por otra parte sabemos que el módulo en $\mathbb{C}$ cumple ciertas propiedades como el ser un número real no negativo y la desigualdad del triángulo. Por lo que razonando de manera análoga al caso en $\mathbb{R}^2$, mediante el módulo definiremos la distancia entre dos números complejos $z_1$ y $z_2$ como la longitud del segmento de recta que los une, figura 26.

El objetivo de esta entrada es describir algunos lugares geométricos en el plano complejo $\mathbb{C}$, haciendo uso de nuestros resultados de Geometría Analítica, para familiarizarnos con algunos conjuntos de puntos en el plano complejo con los cuales trabajaremos en la siguiente entrada y que en general nos serán de utilidad para describir de manera geométrica a los conjuntos de puntos de $\mathbb{C}$ que cumplan alguna propiedad en particular.

Métrica euclidiana en $\mathbb{C}$

Para comenzar esta entrada, primeramente consideremos la siguiente:

Definición 6.1. (Métrica euclidiana.)
Sean $z_1 = a_1 + ib_1$ y $z_2 = a_2 + ib_2$ números complejos. Definimos la distancia entre $z_2$ y $z_1$, denotada por $d(z_2, z_1)$, como:
\begin{equation*}
d(z_2, z_1) = |z_2 \, – \, z_1| = \sqrt{\left(a_2 \, – \, a_1\right)^2 + \left(b_2 \, – \, b_1\right)^2}.
\end{equation*}

A esta distancia se le conoce como la distancia o métrica euclidiana de $\mathbb{C}$, figura 26.

Figura 26: Distancia euclidiana entre $z_2$ y $z_1$.

Por nuestros cursos de Geometría Analítica sabemos que al hablar de un lugar geométrico nos referimos a un conjunto de puntos que satisfacen una condición dada. Entonces podemos interpretar de manera geométrica a una ecuación como el lugar geométrico de los puntos en el plano cuyas coordenadas la satisfacen. En este sentido, consideraremos a los lugares geométricos del plano complejo como conjuntos de puntos en $\mathbb{R}^2$ que satisfacen una ecuación y viceversa, por lo que será necesario expresar en términos de números complejos las ecuaciones de los lugares geométricos de $\mathbb{R}^2$.

De acuerdo con las entradas anteriores sabemos que podemos ubicar a un número complejo en el plano, pensado como un par ordenado de números reales, en coordenadas cartesianas o coordenadas polares. Sin embargo, considerando la observación 2.3 sabemos que para $z\in\mathbb{C}$ se cumple:
\begin{equation*}
\text{Re}(z) = \frac{z+\overline{z}}{2}, \quad \text{Im}(z) = \frac{z-\overline{z}}{2i}. \end{equation*}

Lo anterior nos motiva a dar la siguiente:

Definición 6.2. (Coordenadas conjugadas complejas.)
Dado un número complejo $z = x+iy$, es posible representarlo en el plano complejo mediante las coordenadas $(z,\overline{z})$, a las cuales llamaremos coordenadas conjugadas complejas o simplemente coordenadas conjugadas considerando:
\begin{equation*}
x = \frac{z+\overline{z}}{2}, \quad y = \frac{z-\overline{z}}{2i}.
\end{equation*}

Observación 6.1.
Recordemos que para $A,C,D,E,F\in\mathbb{R}$ la ecuación general de segundo grado:
\begin{equation*}
Ax^2 + Cy^2 +Dx + Ey + F = 0, \tag{6.1}
\end{equation*}

nos determina algunos lugares geométricos en $\mathbb{R}^2$. Analicemos dos de ellos para identificarlos en el plano complejo.

Dado $A=C=0$ en la ecuación (6.1), entonces se obtiene la ecuación general de la recta:
\begin{equation*}
Dx + Ey + F = 0.
\end{equation*}

De acuerdo con la definición 6.2, podemos expresar la ecuación de la recta utilizando coordenadas conjugadas como sigue:
\begin{align*}
D\left(\frac{z+\overline{z}}{2}\right) + E\left(\frac{z-\overline{z}}{2i}\right) + F = 0,\\
\\
\Longrightarrow \quad z\left(D-iE\right) + \overline{z}\left(D+iE\right) +2F = 0.
\end{align*}

Haciendo $a=D+iE$ y $b=2F$, tenemos:
\begin{equation*}
\mathcal{L}: \,\, z\overline{a}+\overline{z}a + b = 0, \tag{6.1.1}
\end{equation*}

la cual llamaremos ecuación general de la recta $\mathcal{L}$ en $\mathbb{C}$.

Si tenemos $A=C\neq0$ en la ecuación (6.1), entonces se obtiene la ecuación general de la circunferencia:
\begin{equation*}
A(x^2+y^2) + Dx + Ey + F = 0.
\end{equation*}

De acuerdo con la definición 6.2, podemos expresar la ecuación general de la circunferencia utilizando coordenadas conjugadas como sigue:
\begin{align*}
A z\overline{z} + D\left(\frac{z+\overline{z}}{2}\right) + E\left(\frac{z-\overline{z}}{2i}\right) + F = 0,\\
\\
\Longrightarrow \quad z\overline{z} + z \left(\frac{D-iE}{2A}\right) + \overline{z}\left(\frac{D+iE}{2A}\right) + \frac{F}{A} = 0.
\end{align*}

Haciendo $a=\frac{D+iE}{2A}$ y $b=\frac{F}{A}$, tenemos:
\begin{equation*}
z\overline{z} + z\overline{a}+\overline{z}a + b = |\,z\,|^2 + z\overline{a}+\overline{z}a + b = 0, \tag{6.1.2}
\end{equation*}

la cual llamaremos ecuación general de la circunferencia en $\mathbb{C}$ cuyo centro es $-a$ y su radio es $\sqrt{|\,a\,|^2 – b}$.

Ejemplo 6.1.
Expresemos las siguientes ecuaciones en términos de las coordenadas conjugadas:

a) Ecuación de una recta en el plano cartesiano $2x+3y=7$.
b) Ecuación de una circunferencia en el plano cartesiano $x^2+(y-1)^2 = 25$.

Solución.

a) De acuerdo con la observación 6.1 tenemos:

\begin{align*}
2\left(\frac{z+\overline{z}}{2}\right)+3\left(\frac{z-\overline{z}}{2i}\right)=7,\\
\\
\Longrightarrow \quad \mathcal{L}: \,\, z\overline{a} + \overline{z}a = 14, \tag{6.1.3}
\end{align*}

con $a=2+3i$, la cual es la ecuación de una recta $\mathcal{L}$ en el plano complejo.

Considerando (6.1.3), notamos que los puntos $z_1 = 3{.}5$ y $z_2 = 2 + i$ pertenecen a la recta, figura 27.

Figura 27: Gráfica de la recta $\mathcal{L}$, dada por (6.1.3), en $\mathbb{C}$ con $a=2+3i$.

b) Notemos que:

\begin{equation*}
x^2 + (y-1)^2 = x^2 + y^2 -2y + 1 =25,
\end{equation*}

por lo que, considerando la observación 6.1, con $a = -i$ y $b = -24$ tenemos:
\begin{align*}
z\overline{z} – 2\left(\frac{z-\overline{z}}{2i}\right) -24 = 0,\\
\\
\Longrightarrow \quad z\overline{z} + z\overline{a} + \overline{z}a + b = 0, \tag{6.1.4} \end{align*}

la ecuación de una circunferencia en el plano complejo cuyo centro es $-a = i$ y su radio es $\sqrt{|i|^2 – (-24)} = \sqrt{25} = 5$, figura 32.

Al igual que en $\mathbb{R}^2$, es posible describir a la recta $\mathcal{L}$ en el plano complejo mediante su forma paramétrica considerando dos puntos $z_1,z_2\in\mathbb{C}$, $z_1\neq z_2$ y $z_2 \neq 0$, tales que $z_1$ está sobre la recta y el segmento de recta que va del origen a $z_2$ es paralelo a la recta, figura 28(a), entonces la recta $\mathcal{L}$ en $\mathbb{C}$, en su forma paramétrica, está dada como el conjunto de puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
z = z_1 + z_2t, \quad t\in\mathbb{R}. \tag{6.1.5}
\end{equation*}

Si se tiene que $z_1$ y $z_2$, con $z_1\neq z_2$, son puntos de la recta, entonces la forma paramétrica de la ecuación de la recta $\mathcal{L}$, en $\mathbb{C}$, figura 28(b), se puede obtener como el conjunto de puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
z = z_1 + (z_2 \,-\, z_1)t, \quad t\in\mathbb{R}. \tag{6.1.6}
\end{equation*}

Figura 28: Gráficas de una recta en su forma paramétrica en $\mathbb{C}$.

(a) Ecuación paramétrica de una recta $\mathcal{L}$ en $\mathbb{C}$ que pasa por $z_1$ y tiene dirección $z_2$.

Observación 6.2.
Dado que $z_2 \neq 0$ en (6.1.5), notemos que:
\begin{equation*}
t = \frac{z \,-\, z_1}{z_2} \in \mathbb{R} \quad \Longleftrightarrow \quad \operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) = 0,
\end{equation*}

por lo que una forma equivalente de expresar a una recta $\mathcal{L}$ dada por (6.1.5) es:
\begin{equation*}
\mathcal{L} = \left\{ z\in\mathbb{C} \,:\, \operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) = 0 \right\}.
\end{equation*}

Una pregunta interesante que podemos hacernos es ¿qué lugares geométricos describen las siguientes ecuaciones?
\begin{equation*}
\operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) > 0,
\end{equation*}

\begin{equation*}
\operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) < 0.
\end{equation*}

Analicemos la primera desigualdad. Sin pérdida de generalidad, desde que $z_2$ sólo nos determina la dirección de $\mathcal{L}$ entonces podemos suponer que $|\,z_2\,| = 1$. Sean $z_2 = \operatorname{cis}(\beta)$ y $z=r\,\operatorname{cis}(\theta)$.

Notemos que si $z_1=0$, tenemos por (6.1.5) una recta que pasa por el origen, además:
\begin{equation*}
\operatorname{Im}\left(\frac{z}{z_2}\right) = \operatorname{Im}\left(r\operatorname{cis}(\theta\,-\,\beta)\right) = r\operatorname{sen}(\theta-\beta) > 0,
\end{equation*}

dado que $r=|\,z\,|\geq 0$, entonces $\operatorname{sen}(\theta-\beta) > 0$, lo cual se cumple si $\beta < \theta < \pi + \beta$. Por lo que la primera ecuación con $z_1 = 0$ nos describe un semiplano a la izquiera de la recta $\mathcal{L}$ que pasa por el origen, figura 29(a).

Si ahora consideramos el caso en que $z_1 \neq 0$, entonces por (6.1.5) tenemos una recta $\mathcal{L}$ que pasa por $z_1$ y es paralela a $z_2$, por lo que en dicho caso la ecuación $\operatorname{Im}\left(\dfrac{z \,-\, z_1}{z_2}\right) > 0$ nos describe al semiplano a la izquierda de la recta $\mathcal{L}$, figura 29(b).

Realizando un razonamiento análogo para la ecuación $\operatorname{Im}\left(\dfrac{z \,-\, z_1}{z_2}\right) < 0$, podemos concluir que dicha ecuación nos describe el semiplano a la derecha de una recta $\mathcal{L}$ que pasa por $z_1$ y es paralela a $z_2$, figura 30.

Figura 29: Gráficas de un semiplano izquierdo o superior en $\mathbb{C}$.

(a) Semiplano $\operatorname{Im\left(\frac{z}{z_2}\right)}>0$ a la izquierda de la recta $\mathcal{L}$ dada por $z = z_2 t$.

Figura 30: Semiplano derecho o inferior $\operatorname{Im\left(\frac{z-z_1}{z_2}\right)}<0$ en el plano complejo $\mathbb{C}$.

Observación 6.3.
Otra forma de describir una recta $\mathcal{L}$ en el plano complejo $\mathbb{}$ es la siguiente. Sean $z_1, z_2 \in \mathbb{C}$, con $z_1 \neq z_2$. Notemos que la ecuación:
\begin{equation*}
|\,z \,-\, z_1\,| = |\,z \,-\, z_2\,|,
\end{equation*}

nos dice que la distancia de $z \in \mathbb{C}$ a los puntos $z_1$ y $z_2$ es la misma, es decir que $z$ está en la mediatriz del segmento que une a $z_1$ con $z_2$, figura 31.

Figura 31: Mediatriz $\mathcal{L}$ del segmento que va de $z_1$ a $z_2$ en $\mathbb{C}$.

Por otra parte, sabemos que la ecuación (6.1) determina otras cónicas además de la circunferencia, por lo que es posible proceder del mismo modo que en los dos casos de la observación 6.1 para obtener las ecuaciones correspondientes a dichos lugares geométricos. Sin embargo podemos hacer uso de la distancia euclidiana de $\mathbb{C}$ para describir dichos lugares geométricos mediante sus definiciones, es decir pensando a las cónicas como conjuntos de puntos que satisfacen ciertas condiciones relacionadas con la distancia entre puntos.

Consideremos el ejemplo 6.1, inciso b, sabemos que dicha circunferencia está centrada en $-a=i$ y tiene radio $\rho = 5$. De acuerdo con la definición de una circunferencia sabemos que los puntos cuya distancia al centro $i$ sea igual a 5 pertenecen a la circunferencia descrita por la ecuación (6.1.4), lo cual podemos expresarlo como el conjunto de números complejos $z$ tales que:
\begin{align*}
|\,z \,-\, i\,| = 5 \quad \Longleftrightarrow \quad |\,z \,-\, i\,|^2 = 25. \tag{6.1.7}
\end{align*}

Figura 32: Circunferencia en $\mathbb{C}$ de radio $\rho=5$ y centro $-a=i$ con algunos de sus puntos.

Notemos que podemos reescribir (6.1.7) como (6.1.4) utilizando las propiedades del módulo:
\begin{align*}
|\,z\,-\,i\,|^2 & = (z\,-\,i)\left(\overline{z}-\overline{i}\right)\\
& = |\,z\,|^2 – \, \overline{i}z -i\overline{z} + |\,i\,|^2\\
& = z\overline{z} + zi \, – \, \overline{z}i + 1\\
& = z\overline{z} + z\overline{a} + \overline{z}a + 1\\
& = 25.
\end{align*}

Considerando (6.1.7) es fácil ver que los puntos $z_1 = 5+i$, $z_2 = 6i$, $z_3 = -5 + i$ y $z_4 = -4i$ pertenecen a dicha circunferencia, figura 32.

Lo anterior nos deja ver que tanto (6.1.4) como (6.1.7) nos describen al mismo lugar geométrico en el plano complejo, es decir una circunferencia de radio $\rho=5$ centrada en $i$.

Podemos generalizar el resultado anterior para describir a una circunferencia en el plano complejo expresando a la ecuación (6.1.2) mediante la definición de dicho lugar geométrico, es decir, como el conjunto de números complejos $z$ que equidistan del punto $z_0=-a$, donde $a$ está dada como en (6.1.2), llamado centro, una distancia $\rho$, llamada radio:
\begin{equation*}
|\,z – z_0\,| = \rho \quad \Longleftrightarrow \quad |\,z – z_0\,|^2 = \rho^2. \tag{6.1.8}
\end{equation*}

Figura 33: Circunferencia en $\mathbb{C}$ de radio $\rho$ y centro $z_0$.

Una pregunta que podemos plantearnos es ¿qué lugares geométricos nos describen las siguientes desigualdades?
\begin{align*}
|\,z – z_0\,| < \rho,\\
|\,z – z_0\,| > \rho.
\end{align*}

De manera geométrica es claro que la primera desigualdad nos describe a los puntos $z\in\mathbb{C}$ que se encuentran dentro de la circunferencia de radio $\rho$ y centro $z_0$, sin considerar propiamente a los que caen en dicha circunferencia. Mientras que la segunda desigualdad nos describe a los puntos en $z\in\mathbb{C}$ que caen fuera de la circunferencia centrada en $z_0$ y de radio $\rho$, sin considerar tampoco a los puntos de la circunferencia.

Figura 34: Punto $w\in\mathbb{C}$ dentro de la circunferencia $|\,z-z_0\,|=\rho$ y punto $\zeta\in\mathbb{C}$ fuera de la circunferencia $|\,z-z_0\,|=\rho$.

De acuerdo con la observación 3.3, tenemos que para un número complejo $z\neq0$:
\begin{equation*}
z^{-1} = \frac{1}{z} = \frac{\overline{z}}{| \, z \, |^2}.
\end{equation*}

Analicemos los siguientes casos:

Si $|\,z\,|>1$, entonces $\dfrac{1}{|\,z\,|}<1$.
Si $|\,z\,|<1$, entonces $\dfrac{1}{|\,z\,|}>1$.
Si $|\,z\,|=1$, entonces $\dfrac{1}{|\,z\,|}=1$.

Geométricamente esto nos dice que para los números complejos $z$ que están fuera de la circunferencia unitaria su inverso multiplicativo está dentro de la circunferencia unitaria. Por otro parte, para los números complejos $z$ que están dentro de la circunferencia unitaria se tiene que su inverso multiplicativo está fuera de dicha circunferencia, mientras que para los números complejos $z$ que pertenecen a la circunferencia unitaria se tiene que su inverso multiplicativo también es un punto de dicha circunferencia.

Figura 35: Punto $w\in\mathbb{C}$ dentro de la circunferencia unitaria $|\,z\,|=1$. Punto $\zeta\in\mathbb{C}$ fuera de la circunferencia unitaria $|\,z\,|=1$ y el número complejo $i$ en la circunferencia unitaria $|\,z\,|=1$.

Recordemos que en $\mathbb{R}^2$ la ecuación ordinaria de una circunferencia con centro en $(x_0, y_0)$ y radio $\rho$ es:
\begin{equation*}
(x-x_0)^2 + (y-y_0)^2 = \rho^2.
\end{equation*}

Haciendo $x(t) = \rho \operatorname{cos}(t) + x_0$ y $y(t) = \rho \operatorname{sen}(t) + y_0$, con $t\in[0,2\pi)$, obtenemos una ecuación paramétrica de dicha circunferencia.

Si consideramos a los números complejos $z$ en su forma polar, es decir $z=\rho \operatorname{cis}(\theta)$, tales que $\theta\in[0,2\pi)$, y a un punto fijo $z_0=x_0 + i y_0 \in\mathbb{C}$, entonces podemos describir a una cirunferencia en $\mathbb{C}$ de forma paramétrica como el conjunto de puntos:
\begin{equation*}
\{ w\in\mathbb{C} \, : \, w = z_0 + z \}.
\end{equation*}

Proposición 6.1. (Distancia de un punto a una recta en $\mathbb{C}$.)
Para un punto $z_0\in\mathbb{C}$, su distancia a una recta $\mathcal{L}$ dada por $z\overline{a} + \overline{z}a + b = 0$ está dada por:
\begin{equation*}
\frac{|\,z_0\overline{a} + \overline{z_0}a + b\,|}{2\,|\,a\,|}. \tag{6.1.9}
\end{equation*}

Demostración. Sea $z_0 = x_0 + iy_0\in\mathbb{C}$. Sabemos que en $\mathbb{R}^2$ la distancia de un punto $P(x_0,y_0)$ a una recta $Dx + Ey + F = 0$ está dada por:
\begin{equation*}
\frac{|\,Dx_0 + Ey_0 + F \,|}{\sqrt{D^2 + E^2}}. \tag{6.1.10}
\end{equation*}

De acuerdo con la observación 6.1 sabemos que podemos expresar una recta de la forma $Dx + Ey + F = 0$ como $z\overline{a} + \overline{z}a + b = 0$ donde $a = D + iE$ y $b=2F$. Por otra parte tenemos que:
\begin{equation*}
2D = a + \overline{a}, \quad i2E = a – \overline{a}.
\end{equation*}

Sea $z=x+iy$, entonces tenemos:
\begin{align*}
0 & = z\overline{a} + \overline{z}a + b\\
& = (x+iy)\overline{a} + (x-iy)a + b\\
& = x(a+\overline{a}) -iy (a-\overline{a}) + b\\
& = 2Dx +2Ey + 2F.
\end{align*}

Lo anterior nos deja ver que podemos utilizar (6.1.10) para obtener la distancia del punto $z_0 = x_0 + iy_0$ a la recta $z\overline{a}+\overline{z}a + b = 0$ como:
\begin{align*}
\frac{|\,Dx_0 + Ey_0 + F \,|}{\sqrt{D^2 + E^2}} &= \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{\sqrt{(a+\overline{a})^2 + \left(-i(a – \overline{a})\right)^2}}\\
& = \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{\sqrt{4\,|\,a\,|^2}}\\
& = \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{2\,|\,a\,|}.
\end{align*}

$\blacksquare$

Proposición 6.2. (Distancia de un punto a una recta en su forma paramétrica en $\mathbb{C}$.)
Sea $\mathcal{L}$ la recta en $\mathbb{C}$ dada por $z = z_1 + t z_2$, $z_2 \neq 0$. La distancia mínima $\delta$ de un punto $z_0 \in \mathbb{C}$ a la recta $\mathcal{L}$ es:
\begin{equation*}
\delta = \left|\, \frac{\operatorname{Im}\left((z-z_1)\overline{z_2}\right)}{\overline{z_2}} \,\right| = \left|\, \frac{(z – z_1)\overline{z_2} – \overline{(z-z_1)z_2}}{2\,\overline{z_2}} \,\right|.
\end{equation*}

Demostración. Sea $f(t) = |\,z \,-\, z_1 -tz_2\,|^2$. Es claro que $f:\mathbb{R} \longrightarrow [0,\infty)$ es una función bien definida.

De acuerdo con la proposición 3.1 tenemos que:
\begin{align*}
f(t) & = |\,z \,-\, z_1 -tz_2\,|^2\\
& = |\,z \,-\, z_1\,|^2 \,-\, 2t\,\operatorname{Re}\left((z-z_1)\overline{z_2}\right) + t^2 |\,z_2\,|^2.
\end{align*}

Derivando $f$ tenemos:
\begin{equation*}
f'(t) = -2\,\operatorname{Re}\left((z-z_1)\overline{z_2}\right) + 2t\, |\,z_2\,|^2.
\end{equation*}

Entonces el mínimo se alzanza en:
\begin{equation*}
t = \frac{\operatorname{Re}\left((z-z_1)\overline{z_2}\right)}{|\,z_2\,|^2}.
\end{equation*}

Dado que $z_2\neq0$, entonces $\dfrac{z_2}{|\,z_2\,|^2} = \dfrac{1}{\overline{z_2}}$.

Considerando la observación 2.3 y evaluando a $f$ en el mínimo obtenemos la distancia buscada al cuadrado, es decir:
\begin{align*}
\delta^2 &= \left|\,(z-z_1) \,-\, z_2\left[\frac{\operatorname{Re}\left((z-z_1)\overline{z_2}\right)}{|\,z_2\,|^2}\right] \,\right|^2\\
&= \left|\,\frac{2(z-z_1)\overline{z_2} \,-\, (z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2\, \overline{z_2}} \,\right|^2\\
&= \left|\,\frac{(z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2\, \overline{z_2}} \,\right|^2\\
&= \left|\,\frac{1}{\overline{z_2}}\frac{(z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2i} \,\right|^2\\
&=\left|\,\frac{\operatorname{Im}\left((z-z_1)\overline{z_2}\right)}{\overline{z_2}}\,\right|^2.
\end{align*}

Por lo que tomando raíz cuadrada se sigue el resultado.

$\blacksquare$

Es claro que al usar la definición de un lugar geométrico es posible asociarle una ecuación a dicho conjunto y representarlo en el plano complejo $\mathbb{C}$. Por ejemplo, recordemos las definiciones de los siguientes lugares geométricos:

Parábola. Se define una parábola como el lugar geométrico de los puntos en $\mathbb{C}$ tales que la distancia entre estos y un punto fijo, llamado foco $f$, es igual a la distancia entre dichos puntos y una recta fija, llamada directriz $\mathcal{D}$.

Sin pérdida de generalidad, analicemos el caso de una parábola horizontal, es decir una parábola cuya directriz $\mathcal{D}$ es paralela al eje imaginario. En $\mathbb{R}^2$ sabemos que dichas rectas son de la forma $x = p$, con $p\in\mathbb{R}$ constante, por lo que para $z=x+iy\in\mathbb{C}$ tenemos que:
\begin{align*}
x \,-\, p = 0 \quad & \Longleftrightarrow \quad z+\overline{z} – 2p = 0\\
\\
& \Longleftrightarrow \quad \text{Re}(z) – p = 0. \tag{6.1.11}
\end{align*}

De acuerdo con (6.1.1), de la observación 6.1 tenemos que la ecuación de una directriz $\mathcal{D}$ paralela al eje imaginario cumple que $a=1$ y $b = -2p$, por lo que considerando la definición de la parábola y la proposición 6.1, tenemos que una parábola con foco $f\in\mathbb{C}$ y directriz $\mathcal{D}$ vertical dada por (6.1.11) es el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
\frac{|\,z + \overline{z}+ b\,|}{2\,} = |\,z-f\,|. \tag{6.1.12}
\end{equation*}

Observación 6.3.
Para el caso de una parábola vertical se procede de manera análoga utilizando el hecho de que para $z=x+iy\in\mathbb{C}$ se tiene que $y=\text{Im}(z)=\frac{z-\overline{z}}{2i}$ y que su directriz $\mathcal{D}$ es paralela al eje real.

Observación 6.4.
Considerando la definición de la párabola es posible obtener una ecuación más general que nos permita describir a dicho lugar geométrico. Suponiendo que la directriz $\mathcal{D}$ de una párabola está dada por la ecuación paramétrica $z_1 + tz_2$, con $t\in\mathbb{R}$, y que su foco es el punto $f\in\mathbb{C}$, entonces la ecuación de dicha párabola es:
\begin{equation*}
\left(\operatorname{Im}\left((z-z_1)\overline{z_2}\right)\right)^2 = |\,z_2\,|^2 \, |\,z-f\,|^2.
\end{equation*}

Elipse. Se define a la elipse como el lugar geométrico de los puntos en $\mathbb{C}$ tales que la suma de sus distancias a dos puntos fijos $f_1,f_2\in\mathbb{C}$, llamados focos, es constante, es decir los $z\in\mathbb{C}$ tales que:
\begin{align*}
|\,z-f_1\,| + |\,z-f_2\,| = 2a,\\
\\
\text{con} \,\, 2a>|\,f_1 \,-\, f_2\,|.\tag{6.1.13}
\end{align*}

De acuerdo con nuestros cursos de Geometría sabemos que dados los focos de una elipse es posible identificar si se trata de una elipse vertical u horizontal, además al punto $z_0\in\mathbb{C}$ tal que $|\,z_0 \,-\, f_1\,| = |\,z_0 \,-\, f_2\,|=c$ se le conoce como el centro de la elipse y al valor $|\,f_1\,-\,f_2\,| =2c$ se le llama la distancia focal.
Por otra parte tenemos que la constante $2a$ determina al eje mayor, mientras que $\frac{|\,f_1\,-\,f_2\,|}{2a} = \frac{2c}{2a} = \frac{c}{a}$ nos da la excentricidad de la elipse.

¿Qué lugares geométricos nos describen las siguientes desigualdades?
\begin{align*}
|\,z-f_1\,| + |\,z-f_2\,| < 2a,\\
|\,z-f_1\,| + |\,z-f_2\,| > 2a.
\end{align*}

De manera geométrica es claro que la primera ecuación nos describe al conjunto de puntos $z\in\mathbb{C}$ que se encuentran dentro de la elipse con focos $f_1, f_2$ y con eje mayor $2a$. Por otra parte, la segunda ecuación nos describe a los $z\in\mathbb{C}$ que se encuentran fuera de dicha elipse, en ambos casos ninguna de las ecuaciones considera a los puntos $z\in\mathbb{C}$ que caen sobre la elipse, figura 36.

Hipérbola. Se define a la hipérbola como el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que el valor absoluto de las distancias a dos puntos fijos $f_1,f_2\in\mathbb{C}$, llamados focos, es igual a una cantidad constante, positiva y menor que la distancia entre los focos, es decir:
\begin{align*}
|\,|z-f_1|-|z-f_2|\,| = 2a,\\
\\
\text{con} \,\, 2a<|\,f_1 \,-\, f_2\,|.\tag{6.1.14}
\end{align*}

Donde $|\,f_1\,-\,f_2\,|=2c$ es la distancia focal y al punto $z_0\in\mathbb{C}$ tal que $|\,z_0\,-\,f_1\,|=|\,z_0\,-\,f_2\,|=c$ se le denomina el centro. La excentricidad de la hipérbola está dada por $\frac{|\,f_1\,-\,f_2\,|}{2a} = \frac{2c}{2a} = \frac{c}{a}$.

Figura 36: Punto $\zeta\in\mathbb{C}$ fuera de la elipse centrada en $z_0\in\mathbb{C}$ con focos $f_1, f_2\in\mathbb{C}$. El centro $z_0$ cae dentro de la elipse desde que $|\,z_0-f_1\,|+|\,z_0-f_2\,| = 2c < 2a$.

Observación 6.5.
Notemos que las ecuaciones (6.1.12), (6.1.13) y (6.1.14) obtenidas para estas tres cónicas corresponden a las ecuaciones ordinarias de las cónicas en $\mathbb{R}^2$, por lo que podemos preguntarnos sobre las ecuaciones generales para dichos lugares geométricos, solo recordemos que para hablar de estas expresiones debemos considerar los casos en que sea una cónica horizontal o vertical obtenidos de la ecuación (6.1). Recuerda que la ecuación (6.1) excluye a las cónicas que están rotadas en $\mathbb{R}^2$.

Observación 6.6.
Hasta ahora hemos utilizado las definiciones, como lugares geométricos, de estas tres cónicas para determinar sus ecuaciones. Sin embargo, de nuestros cursos de Geometría Analítica sabemos que es posible caracterizar a las cónicas mediante el concepto de excentricidad, es decir podemos determinar a las cónicas considerando a una recta fija $\mathcal{D}\in\mathbb{C}$, llamada directriz y a un punto fijo $f\in\mathbb{C}$, llamado foco. Si definimos a $e$ una cantidad positiva como la excentricidad, entonces el conjunto de puntos $z\in\mathbb{C}$ tales que la razón de su distancia a $f$ y a la recta $\mathcal{D}$ es siempre igual a $e$ es una sección cónica, la cual está dada por:

a) Si $e < 1$, entonces es una elipse.
b) Si $e = 1$, entonces es una párabola.
c) Si $e > 1$, entonces es una hipérbola.

El caso en que $e=0$ nos determina una circunferencia.

Puedes consultar la sección 10.6 del libro Calculus: Early transcendentals de J. Stewart para revisar esta caracterización de las secciones cónicas en $\mathbb{R}^2$.

Considerando esta forma de determinar a las cónicas, es posible utilizar la ecuación de la párabola dada en la observación 6.5 para determinar a la elipse y la hipérbola.

Ejemplo 6.2.

a) Hallar la ecuación de la parábola cuyo foco está en $f=3+i$ y su directriz $\mathcal{D}$ está dada por $z+\overline{z}+6 = 0$.

Solución. De acuerdo con la definición de la parábola sabemos que se debe satisfacer (6.1.12), es decir:
\begin{align*}
\frac{|\,z + \overline{z}+ 6\,|}{2\,} = |\,z-(3+i)\,|\\
\\
\underset{(6{.}1{.}11)}{\Longleftrightarrow} \quad |\,\text{Re}(z) + 3\,|= |\,z-(3+i)\,|.
\end{align*}

Notemos que $\operatorname{Re}(z) + 3 \in \mathbb{R}$, por lo que, considerando la proposición 3.1:
\begin{align*}
|\,\text{Re}(z) + 3\,|^2= |\,z-(3+i)\,|^2\\
\\
\Longleftrightarrow \quad \left(\text{Re}(z) + 3\right)^2 = |\,z\,|^2 – 2\,\text{Re}(z(3-i)) + |\,3+i\,|^2.
\end{align*}

Desarrollando lo anterior y utilizando la proposición 3.1 tenemos:
\begin{equation*}
|\,z\,|^2 – \text{Re}^2(z) – 12\,\text{Re}(z) + 2\,\text{Re}(iz) + 1 = 0,
\end{equation*}

la cual es la ecuación de una parábola en $\mathbb{C}$ cuyo foco es $f=3+i$ y su directriz es $\text{Re}(z)=-3$, figura 37.

Si consideramos a $z=x+iy$, entonces la ecuación anterior corresponde a una parábola en $\mathbb{R}^2$ dada por:
\begin{equation*}
y^2-2y-12x+1=0.
\end{equation*}

Figura 37: Parábola en $\mathbb{C}$ con vértice en $v=i$, foco $f=3+i$ y directriz Re$(z) = -3$.

b) Hallar la ecuación de una elipse que tiene un foco $f_1 = -5+i$, su centro es $z_0 = x_0 +iy_0 = -1+i$ y que pasa por el punto $z_1=-1-2i$.

Solución. Considerando la definición de la elipse, el segundo foco $f_2$ debe satisfacer que $c=|z_0-f_2|=|z_0-f_1|=4$. De manera geométrica sabemos que $f_1, f_2$ y $z_0$ deben ser colineales, por lo que el segundo foco es $f_2 = (x_0+c)+i y_0 = (-1+4) + i = 3+i$. Considerando que $z_1=-1-2i$ pertenece a la elipse, entonces por (6.1.13) tenemos que:
\begin{align*}
|\,z_1-(-5+i)\,|+ |\,z_1-(3+i)\,| & = |\,4-3i\,| + |\,-4-3i\,|\\
& = 10\\
& = 2a.
\end{align*}

Entonces $a = 5$, por lo que la ecuación que describe a la elipse, figura 38, es:
\begin{equation*}
|\,z-f_1\,| + |\,z-f_2\,| = 10.
\end{equation*}

Figura 38: Elipse en $\mathbb{C}$ con centro en $z_0=-1+i$ y focos $f_1=-5+i$, $f_2=3+i$.

c) Encontrar la ecuación de la hipérbola cuyos focos son $f_1=-(\sqrt{20}+3)-3i$, $f_2=(\sqrt{20}-3)-3i$ y que pasa por el punto $z_1=(\sqrt{12}-3)-3i$.

Solución. De acuerdo con la definición de la hipérbola, como el punto $z_1$ dado pertenece a dicho lugar geométrico entonces debe satisfacer (6.1.14), es decir:
\begin{align*}
|\,|\,z_1\,-\,f_1\,| – |\,z_1\,-\,f_2\,|\,| & = |\, |\,\sqrt{12}+\sqrt{20}\,| – |\,\sqrt{12}-\sqrt{20}\,|\,|\\
& = |\,4\sqrt{3}\,|\\
& = 4\sqrt{3}\\
& = 2a. \end{align*}

Entonces $a=2\sqrt{3}$, por lo que la ecuación de la hipérbola, figura 39, es:
\begin{equation*}
|\,|z+\sqrt{20}+3+3i|-|z-\sqrt{20}+3+3i|\,| = 4\sqrt{3}.
\end{equation*}

Figura 39: Hipérbola en $\mathbb{C}$ con centro en $z_0=-3-3i$ y focos $f_1=-(\sqrt{20}+3)-3i$, $f_2=(\sqrt{20}-3)-3i$.

Tarea moral

Considerando la definición de la parábola como lugar geométrico en $\mathbb{C}$, desarrolla la observación 6.3 y determina la ecuación de una parábola vertical. Argumenta tu resultado.
La observación 6.4 nos proporciona una ecuación general de una párabola. Prueba dicha ecuación.
Hint: utiliza la proposición 6.3.
Comprueba con el ejemplo 6.2 inciso (a) que el resultado es correcto ¿Obtuviste la misma ecuación?
De acuerdo con la observación 6.5, desarrolla la ecuación (6.1) y trata de determinar las ecuaciones generales de las tres cónicas considerando coordenas conjugadas complejas.
¿Qué lugares geométricos representan las siguientes ecuaciones? Haz una representación de dichos conjuntos en el plano complejo $\mathbb{C}$.

a) Los $z\in\mathbb{C}$ tales que $z = \overline{z}$.
b) Los $z\in\mathbb{C}$ tales que $-\theta < \operatorname{Arg}\,z < \theta$.
c) Los $z\in\mathbb{C}$ tales que $0 < \operatorname{Im}(z) < \pi$ y $-\pi < \operatorname{Re}(z) < \pi$.
d) Los $z\in\mathbb{C}$ tales que $|\,z-1\,|^2+|\,z+1\,|^2<8$.
e) Los $z\in\mathbb{C}$ tales que $|\,z-1-i\,|+|\,z+1+i\,|\leq 2$.

Considera la definición de la hipérbola y la definición de la párabola ¿Es posible hablar de los puntos que se encuentran dentro y fuera de dichos lugares geométricos? Observa que en el caso de una circunferencia y una elipse dichos puntos se daban mediante las siguientes desigualdades respectivamente:
\begin{equation*}
|\,z-z_0\,| < \rho \quad \text{y} \quad |\,z-z_0\,| > \rho,
\end{equation*}

\begin{equation*}
|\,z-z_1\,| + |\,z-z_2\,| < 2a \quad \text{y} \quad |\,z-z_1\,| + |\,z-z_2\,| > 2a. \end{equation*}

Sean $z_1, z_2, z_3\in\mathbb{C}$ tales que $|\,z_1\,| = |\,z_2\,| = |\,z_3\,|$ y $z_1 + z_2 + z_3 = 0$. Prueba que $z_1, z_2$ y $z_3$ son los vértices de un triángulo equilatero inscrito en la circunferencia unitaria.
Muestra que el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que $|\,z^2 – a^2\,| = a^2$, con $a\in\mathbb{R}$ una constante, es una lemniscata de Bernoulli.
Sean $z_1, z_2, z_3\in\mathbb{C}$ los vértices de un triángulo en el plano complejo $\mathbb{C}$. Prueba que dicho triángulo es equilatero si y solo si:
\begin{equation*}
\frac{1}{z_1 – z_2} + \frac{1}{z_2 – z_3} + \frac{1}{z_3 – z_1} = 0,
\end{equation*}es decir si y solo si $z_1^2+z_2^2+z_3^2 = z_1 z_2 + z_2 z_3 + z_3 z_1$.
Sean $z_1,z_2,z_3\in\mathbb{C}$ tres puntos distintos. Prueba que dichos puntos caen en la misma recta si y solo si:
\begin{equation*}
\frac{z_1 – z_2}{z_1 – z_3} = t,
\end{equation*} donde $t$ es un número real.

Más adelante…

En esta entrada hemos definido la distancia entre dos puntos $z$ y $w$ en el plano complejo $\mathbb{C}$ siguiendo la idea de hablar de la distancia entre dichos puntos como la longitud del segmento de recta que los une, a la cual llamamos la distancia o métrica euclidiana. Dicha definición de distancia nos permitió describir algunos lugares geométricos en el plano complejo $\mathbb{C}$ haciendo uso de nuestros resultados de geometría y las propiedades del módulo en $\mathbb{C}$.

Es de nuestro interés describir estos lugares geométricos en el plano complejo $\mathbb{C}$ porque nos permite reconocer qué puntos pertenecen o no a un conjunto mediante una condición dada. Esto nos motivará a definir el concepto de disco o vecindad en la siguiente entrada, mediante el cual podremos caracterizar mejor a los conjuntos de $\mathbb{C}$ y con ello a los puntos que los conforman.

La siguiente entrada analizaremos a detalle la distancia recién definida y veremos que resulta ser una función definida en $\mathbb{C}\times\mathbb{C}$ y que toma valores en $[0, \infty)$, la cual recibe propiamente el nombre de métrica. Consideraremos al espacio métrico formado por $\mathbb{C}$ y la métrica euclidiana $d$ y describiremos la topología inducida en $\mathbb{C}$ por dicha métrica. Además probaremos algunos resultados de dicho espacio métrico.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Potencias racionales y raíces en $\mathbb{C}$.
Siguiente entrada del curso: Topología de $\mathbb{C}$.

Variable Compleja I: Potencias racionales y raíces en $\mathbb{C}$

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En la entrada anterior vimos que al igual que en $\mathbb{R}^2$, en el plano complejo es posible trabajar con coordenadas polares para representar a un número complejo en su «forma polar», utilizando su módulo y un ángulo. Primeramente definimos al argumento de un número complejo, el cual resultó no ser único, sino que en realidad existe todo un conjunto de ángulos que nos permite representar a un número complejo de manera indistinta, por lo que fue conveniente el considerar a un ángulo en particular, llamado el argumento principal. Considerando la forma polar de un número complejo fue posible dar una interpretación geométrica al producto y división de números complejos. Además obtuvimos algunos resultados importantes, como la fórmula de De Moivre, que nos serán de utilidad a lo largo de esta entrada y en general para poder operar de forma más sencilla a los números complejos.

En esta entrada nuestro objetivo será plantear una ecuación de la forma $w^n = z$, con $n\in\mathbb{N}^+$ y $w,z\in\mathbb{C}$, $z\neq 0$, analizarla y darle solución. Una vez resuelta dicha ecuación, tendrá sentido el pensar en potencias racionales de números complejos.

Raíces de un número complejo.

Definición 5.1. (Raíz $n$-ésima.)
Sea $z \in \mathbb{C}$, con $z\neq0$. Un número complejo $w$ es llamado una raíz $n$-ésima de $z$ si $w^n = z$, y se denota como $w = z^{1/n}$.

Proposición 5.1. (Raíces $n$-ésimas.)
Sea $z\in \mathbb{C}$, $z\neq0$, en su forma polar $z=r\,\text{cis}(\theta)$ y sea $n \in \mathbb{N^+}$. Entonces existen exactamente $n$ raíces $n$-ésimas distintas, las cuales están dadas por:
\begin{equation*}
w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta+2\pi k}{n}\right), \quad \text{para} \quad k = 0,1,\ldots,n-1.
\end{equation*}

Demostración. Dadas las hipótesis, primeramente verifiquemos que el número complejo $w_k$ propuesto cumple la definición 5.1. De acuerdo con la fórmula de De Moivre tenemos que:
\begin{align*}
\left(w_k\right)^n & = \left(\sqrt[n]{r}\right)^n \, \text{cis}\left(n \left[\frac{\theta+2\pi k}{n}\right]\right)\\
& = \left(\sqrt[n]{r}\right)^n \, \text{cis}\left(\theta+2\pi k\right).
\end{align*}

Dado que las funciones seno y coseno son $2\pi$-periódicas, es decir, para todo $k\in\mathbb{Z}$ se cumple:
\begin{equation*}
\operatorname{sen}(\theta + 2\pi k) = \operatorname{sen}(\theta),\quad \operatorname{cos}(\theta + 2\pi k) = \operatorname{cos}(\theta). \end{equation*}

Entonces se tiene que $z = r\,\text{cis}(\theta)= \left(w_k\right)^n$.

Lo anterior nos motiva a encontrar un número complejo $w = \rho \, \text{cis}(\phi)$ tal que $w^n = z$, es decir:
\begin{equation*}
\rho^n \, \text{cis}(n\phi) = r \, \text{cis}(\theta).
\end{equation*}

Considerando la igualdad entre números complejos se tiene que:
\begin{align*}
\rho^n = r,\\
\text{cos}(n\phi) = \text{cos}(\theta),\\
\text{sen}(n\phi) = \text{sen}(\theta).
\end{align*}

Desde que los argumentos de ambos números complejos están determinados módulo $2\pi$, entonces de lo anterior tenemos que:
\begin{equation*}
\rho = \sqrt[n]{r},
\end{equation*}

\begin{equation*}
n\phi = \theta + 2\pi k, \quad \Longrightarrow \quad \phi = \frac{\theta + 2\pi k}{n}, \quad \text{para algún}\, \, k \in \mathbb{Z}.
\end{equation*}

Notemos que para $k=0,1,\ldots,n-1$ se obtienen ya $n$ raíces $n$-ésimas distintas, las cuales tienen el mismo módulo $\sqrt[n]{r}$, pero distinto argumento. Para probar esto consideremos el siguiente:

Lema 5.1. Sean $n\in\mathbb{N^+}$, $k’, k \in \mathbb{Z}$ y sea $w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right)$. Entonces:
\begin{equation*}
k’ \equiv k \,\, (\text{mod}\, n) \quad \text{si y solo si} \quad w_{k’} = w_k.
\end{equation*}

Observación 5.1.
La congruencia módulo $n$, representada por el símbolo $\equiv$, es una relación de equivalencia en $\mathbb{Z}$, la cual se define como sigue:

Para $a,b\in\mathbb{Z}$ y $n\in\mathbb{N}^+$, diremos que $a$ es congruente con $b$ módulo $n$ si y solo si $a-b$ es divisible por $n$ y se escribe como:
\begin{equation*}
a \equiv b \,\, (\text{mod}\, n).
\end{equation*}

Demostración.
$\Rightarrow)$ Dadas las hipótesis, sin pérdida de generalidad tenemos que:
\begin{equation*}
k’ \equiv k \,\, (\text{mod}\, n) \quad \Longrightarrow \quad k’ = k + nm, \, \, \, \text{para algún} \,\, m\in\mathbb{Z} \,\,\, \text{y} \, \, 0\leq k<n.
\end{equation*}

Entonces, considerando que las funciones seno y coseno son $2\pi$-periódicas:
\begin{align*}
w_{k’} & = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k’}{n}\right)\\
& = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi (k +nm) }{n}\right)\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2 \pi (k+nm)}{n}\right) + i\, \text{sen}\left(\frac{\theta + 2\pi (k+nm)}{n}\right) \right]\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2\pi k}{n} + 2\pi m\right) + i\, \text{sen}\left(\frac{\theta + 2\pi k}{n} + 2\pi m\right) \right]\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2\pi k}{n}\right) + i\, \text{sen}\left(\frac{\theta + 2\pi k}{n}\right) \right]\\
& = \sqrt[n]{r}\, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right)\\
& = w_k.
\end{align*}

$(\Leftarrow$ Dadas las hipótesis, tenemos que si $w_k’ = w_k$, entonces:
\begin{equation*}
\sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k’}{n}\right) = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right),
\end{equation*}

por lo que, considerando la igualdad entre números complejos:
\begin{align*}
\text{cos}\left(\frac{\theta + 2\pi k’}{n}\right) = \text{cos}\left(\frac{\theta + 2\pi k}{n}\right),\\
\text{sen}\left(\frac{\theta + 2\pi k’}{n}\right) = \text{sen}\left(\frac{\theta + 2\pi k}{n}\right).
\end{align*}

De donde se sigue que:
\begin{equation*}
\frac{\theta + 2\pi k’}{n} = \frac{\theta + 2\pi k}{n} + 2 \pi m, \quad \text{para algún} \,\, m\in \mathbb{Z}.
\end{equation*}

Por lo que:
\begin{equation*}
k’ = k + nm, \quad \text{para algún} \,\, m\in \mathbb{Z},
\end{equation*}

lo cual implica que $k’ \equiv k \, \, (\text{mod}\,n)$.

$\blacksquare$

De acuerdo con el lema anterior, concluimos que existen a lo más $n$ raíces $n$-ésimas distintas $w_k$ correspondientes a $k = 0, 1, \ldots, n-1$ y que son de la forma:
\begin{equation*}
w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right).
\end{equation*}

$\blacksquare$

Observación 5.2.
Notemos que la expresión $z^{1/n}$ es $n$-valuada, es decir, no representa un único valor, sino al conjunto de $n$ raíces $n$-ésimas, formado por las raíces $w_k$ con $k=0,1,\ldots,n-1$, del número complejo $z\neq0$.

Definición 5.2. (Raíz $n$-ésima principal.)
Sea $z\neq0$ un número complejo. Llamaremos como raíz $n$-ésima principal de $z$ al único valor de $z^{1/n}$ tal que tenga como argumento al argumento principal de $z$, $\text{Arg}\,z$, es decir a la raíz dada por $k=0$.

Ejemplo 5.1.

a) Hallar las 5 raíces quintas de $z_1 = 1+i$.
b) Hallar las 4 raíces cuartas de $z_2 = i$.
c) Hallar las 3 raíces quintas de $z_3 = -\sqrt{2} -i\,\sqrt{2}$.

Figura 20: Gráfica de los números complejos $z_1, z_2$ y $z_3$ en el plano complejo.

Solución. Para los tres números complejos, resolveremos utilizando su argumento principal $\text{Arg}\,z$.

a) Notemos que $z_1 = 1+i$ se encuentra en el primer cuadrante, por lo que:

\begin{equation*}
\text{Arg}\,z_1 = \text{arc tan}\left(\frac{1}{1}\right) = \frac{\pi}{4}.
\end{equation*}

Por otra parte, tenemos que $r_1=|\,z_1\,|=\sqrt{2}$. Entonces, por la proposición 5.1 se tiene que las 5 raíces quintas de $z_1$ están dadas por:
\begin{equation*}
w_k = \left(\sqrt{2}\right)^{\frac{1}{5}}\,\text{cis}\left(\frac{\frac{\pi}{4}+2\pi k}{5}\right), \quad \text{para} \, \, k = 0,1,2,3,4.
\end{equation*}

Por lo que:
\begin{equation*}
z^{1/5} = \left\{ \sqrt[10]{2}\,\text{cis}\left(\frac{\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{9\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{17\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{5\pi}{4}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{33\pi}{20}\right)\right\}.
\end{equation*}

De acuerdo con la definición 5.2, $w_0 = \sqrt[10]{2}\,\text{cis}\left(\frac{\pi}{20}\right)$ es la raíz quinta principal de $z_1$.

b) Sabemos que para $z_2 = i$ se tiene que:

\begin{equation*}
\text{Arg}\,z_2 = \frac{\pi}{2}.
\end{equation*}

Por otra parte, tenemos que $r_2=|\,z_2\,|=1$. Entonces, considerando la proposición 5.1, tenemos que las 4 raíces cuartas de $z_2$ están dadas por:
\begin{equation*}
w_k = 1^{\frac{1}{4}}\,\text{cis}\left(\frac{\frac{\pi}{2}+2\pi k}{4}\right), \quad \text{para} \, \, k = 0,1,2,3.
\end{equation*}

Por lo que:
\begin{equation*}
z^{1/4} = \left\{\text{cis}\left(\frac{\pi}{8}\right),\text{cis}\left(\frac{5\pi}{8}\right),\text{cis}\left(\frac{9\pi}{8}\right),\text{cis}\left(\frac{13\pi}{8}\right)\right\}.
\end{equation*}

Considerando la definición 5.2, se tiene que $w_0 = \text{cis}\left(\frac{\pi}{8}\right)$ es la raíz cuarta principal de $z_2$.

c) Notemos que $z_3 = -\sqrt{2}-i\,\sqrt{2}$ se encuentra en el tercer cuadrante, por lo que:

\begin{equation*}
\text{Arg}\,z_3 = \text{arc tan}\left(\frac{-\sqrt{2}}{-\sqrt{2}}\right) – \pi= \frac{\pi}{4} – \pi = -\frac{3\pi}{4}.
\end{equation*}

Por otra parte, tenemos que $r_3=|\,z_3\,|=2$. De acuerdo con la proposición 5.1, las 3 raíces cúbicas de $z_3$ están dadas por:
\begin{equation*}
w_k = \sqrt[3]{2}\,\text{cis}\left(\frac{\frac{-3\pi}{4}+2\pi k}{3}\right), \quad \text{para} \, \, k = 0,1,2.
\end{equation*}

Por lo que:
\begin{equation*}
z^{1/3} = \left\{\sqrt[3]{2}\,\text{cis}\left(\frac{-\pi}{4}\right), \sqrt[3]{2}\,\text{cis}\left(\frac{5\pi}{12}\right), \sqrt[3]{2}\,\text{cis}\left(\frac{13\pi}{12}\right)\right\}.
\end{equation*}

De acuerdo con la definición 5.2, se tiene que $w_0 = \sqrt[3]{2}\,\text{cis}\left(\frac{-\pi}{4}\right)$ es la raíz cúbica principal de $z_3$.

Notemos que las raíces $n$-ésimas tienen una intepretación geométrica, es decir, las raíces $n$-esimas de un número complejo $z$ coinciden con los vértices de un póligono regular de $n$ lados, el cual está inscrito en una circunferencia de radio $\sqrt[n]{r}$ centrada en el origen.

Considerando los números complejos del ejemplo 5.1 tenemos que:

Figura 21: Gráfica de las 5 raíces quintas de $z_1$.

*Figura 22: Gráfica de las 4 raíces cuartas de $z_2$.*

*Figura 23: Gráfica de las 3 raíces cúbicas de $z_3$.*

Un caso particular importante es cuando $z=1$. Si se plantea la ecuación $w^n = z$, entonces a las soluciones se les llama las raíces $n$-ésimas de la unidad. Considerando que el argumento principal de $z=1$ es $\text{Arg}\,z = 0$ y $r = |\,z\,| =1$, entonces la forma polar de la unidad es $z=\text{cis}(0)$. De acuerdo con la proposición 5.1 se tiene que las raíces de la unidad están dadas por:
\begin{equation*}
w_k = \sqrt[n]{1}\,\text{cis}\left(\frac{0 + 2 \pi k}{n}\right)= \text{cis}\left(\frac{2 \pi k}{n}\right), \quad \text{para}\, \, k=0,1,\ldots,n-1.
\end{equation*}

Si definimos $\omega = \text{cis}\left(\frac{2 \pi}{n}\right)$, entonces por la fórmula de De Moivre se tiene que $\omega^k$, con $k=0,1,\ldots,n-1 $, determina las $n$ raíces $n$-ésimas de la unidad, es decir:
\begin{equation*}
1, \omega, \omega^2, \omega^3, \ldots, \omega^{n-1}.
\end{equation*}

Ejemplo 5.2.
De acuerdo con lo anterior, tenemos que las 3 raíces cúbicas de la unidad están determinadas por:
\begin{equation*}
\omega = \text{cis}\left(\frac{2\pi}{3}\right) = -\frac{1}{2} + i\,\frac{\sqrt{3}}{2},
\end{equation*}

y son:
\begin{align*}
\omega^0 = 1,\\
\omega = -\frac{1}{2} + i\,\frac{\sqrt{3}}{2},\\
\omega^2 = -\frac{1}{2} – i\,\frac{\sqrt{3}}{2}.
\end{align*}

Figura 24: Gráfica de las 3 raíces cúbicas de la unidad.

Observación 5.3.
Es interesante notar que mediante las raíces $n$-ésimas de la unidad es posible encontrar las raíces $n$-ésimas de cualquier $z\in\mathbb{C}$, $z\neq0$, ya que es posible reescribir la fórmula de la proposición 5.1 como sigue:
\begin{align*}
w_k & = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2 \pi k}{n}\right)\\
& = \sqrt[n]{1} \, \text{cis}\left(\frac{2 \pi k}{n}\right) \sqrt[n]{r} \, \text{cis}\left(\frac{\theta}{n}\right)\\
& = \sqrt[n]{r} \, \omega^k \, \zeta,
\end{align*}

donde $\omega = \text{cis}\left(\frac{2 \pi}{n}\right)$, $\zeta = \text{cis}\left(\frac{\theta}{n}\right)$ y $k=0,1,\ldots,n-1$. Entonces para un número complejo $z\neq0$, sus $n$ raíces $n$-ésimas son:
\begin{equation*}
\sqrt[n]{r} \, \zeta, \sqrt[n]{r} \, \omega \, \zeta, \sqrt[n]{r} \, \omega^2 \, \zeta,\ldots, \sqrt[n]{r} \, \omega^{n-1} \, \zeta.
\end{equation*}

Dichas raíces coinciden con los vértices de un polígono de $n$ lados, inscrito en la circunferencia de radio $\sqrt[n]{r}$.

Ejemplo 5.3.
Encontremos las 3 raíces cúbicas de $z=-8i$. Utilizando el argumento principal de $z$, tenemos que $\text{Arg}\,z=-\frac{\pi}{2}$ y $r = |\,z\,| = 8$, por lo que:
\begin{align*}
\sqrt[3]{r} = \sqrt[3]{8} = 2,\ \zeta = \text{cis}\left(\frac{-\frac{\pi}{2}}{3}\right) = \text{cis}\left(\frac{-\pi}{6}\right) = \frac{1}{2}\left(\sqrt{3} – i\right).
\end{align*}

Considerando la observación 5.3, tenemos que las 3 raíces cúbicas de $z=-8i$ están dadas por:
\begin{equation*}
\sqrt[3]{r} \, \zeta, \sqrt[3]{r} \, \omega \, \zeta, \sqrt[3]{r}\, \omega^2 \, \zeta, \end{equation*}

donde $\omega = \text{cis}\left(\frac{2\pi}{3}\right)$ determina las 3 raíces cúbicas de la unidad, como en el ejemplo anterior, entonces:
\begin{align*}
w_0 = 2(1)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = \sqrt{3} – i,\\
w_1 = 2\left(-\frac{1}{2} + i\,\frac{\sqrt{3}}{2}\right)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = 2i,\\
w_2 = 2\left(-\frac{1}{2} – i\,\frac{\sqrt{3}}{2}\right)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = -\sqrt{3} – i.
\end{align*}

Figura 25: Gráfica de las 3 raíces cúbicas de $z=-8i$.

Observación 5.4.
Supongamos que $m,n \in \mathbb{N^+}$ son tales que no tienen divisores comunes y sean $z, w \in \mathbb{C}$ con $z=r\,\text{cis}(\theta)\neq0$. Es posible definir las potencias racionales de $z$, es decir $z^{m/n}$. Para entender mejor esta idea pensemos en la ecuación $w^n = z^m$. Entonces es posible mostrar que existen $n$ soluciones distintas para dicha ecuación, las cuales están dadas por las raíces $n$-ésimas de $z^m$ y son de la forma:
\begin{equation*}
w_k = \sqrt[n]{r^m}\,\text{cis}\left(\frac{m(\theta+2 \pi k)}{n}\right), \quad \text{para}\,\, k=0,1,\ldots,n-1.
\end{equation*}

Lo anterior nos dice entonces que los conjuntos $\left(z^m\right)^{1/n}$ y $\left(z^{1/n}\right)^m$ deben ser el mismo, a decir el conjunto $z^{m/n}$.

Tarea moral

Determina las 3 raíces cúbicas de $z_1=-125$ y las 8 raíces octavas de $z_2=\dfrac{16i}{1+i}$. En ambos casos identifica a la raíz $n$-ésima principal correspondiente y realiza un gráfico de las raíces.
Considera la observación 5.4 y prueba el resultado. Argumenta porqué los conjuntos de raíces son los mismos.
Sean $a$ y $b$ dos números reales y $n\in\mathbb{N}^+$. Demuestra que todas las raíces de la ecuación:
\begin{equation*}
\left(\frac{1+iz}{1-iz}\right)^n = a+ib,
\end{equation*}

son reales si y solo si $a^2 + b^2 =1$.

Resuelve la ecuación $ (z+1)^5 = z^5$.
Encuentra todas las soluciones de la ecuación $w^2 = (-1+i)^5$.
Sea $z = \operatorname{cis}\left(\frac{2\pi}{n}\right)$. Prueba que para $n\geq 2$ se cumple:
\begin{equation*}
1+ z + z^2 + \cdots + z^{n-1} = 0.
\end{equation*}

Más adelante…

Como habíamos visto en la entrada anterior, el trabajar con un número complejo en su forma polar nos permitió caracterizar a las potencias enteras de un números complejo en términos de sus módulos y sus argumentos, lo cual fue de utilidad para trabajar con el concepto de raíz $n$-ésima de un número complejo y dar soluciones a ecuaciones de la forma $w^n=z$. Además vimos que es posible caracterizar a dichas soluciones de manera geométrica.

A diferencia de $\mathbb{R}$, notamos que el campo de los números complejos $\mathbb{C}$ es cerrado bajo la radicación, es decir que para todo $z\in\mathbb{C}$ se cumple que el conjunto de números complejos $z^{1/n}$, $n\in\mathbb{N}^+$, sigue siendo un subconjunto de $\mathbb{C}$.

En la siguiente entrada retomaremos el concepto del módulo y sus propiedades con la finalidad de introducir una métrica en $\mathbb{C}$, la cual nos permitirá seguir describiendo desde una perspectiva geométrica a los números complejos y hablar de algunos lugares geométricos del plano complejo.

Entradas relacionadas

Ir a Variable Compleja I.
Entrada anterior del curso: Forma Polar. Potencias en $\mathbb{C}$.
Siguiente entrada del curso: Lugares geométricos en $\mathbb{C}$.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo del Autor: Pedro Rivera Herrera

Variable Compleja I: El plano complejo extendido $\mathbb{C}_{\infty}$

Introducción

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Sucesiones en el espacio métrico $(\mathbb{C},d)$

Introducción

Sucesiones de números complejos

Completez del espacio métrico $(\mathbb{C},d)$

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Topología de $\mathbb{C}$

Introducción

$\mathbb{C}$ como un espacio métrico

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Lugares geométricos en $\mathbb{C}$

Introducción

Métrica euclidiana en $\mathbb{C}$

Tarea moral

Más adelante…

Entradas relacionadas

Variable Compleja I: Potencias racionales y raíces en $\mathbb{C}$

Introducción

Raíces de un número complejo.

Tarea moral

Más adelante…

Entradas relacionadas