Introducción
De manera intuitiva podemos considerar a un espacio métrico como un conjunto en el cual se puede hablar de la “distancia” entre sus elementos, por lo que definir lo que entendemos por distancia es de suma importancia. Para ello en esta entrada introduciremos los conceptos de distancia o métrica y espacio métrico. Es importante considerar que estos conceptos se analizan en primera instancia en un curso de Cálculo III y con mayor detalle en un curso de Análisis Matemático, por lo que es recomendable acompañar estos conceptos con algún material complementario, pues algunos resultados de los espacios métricos se darán por válidos y/o conocidos. Puedes consultar los libros Metric Spaces de Satish Shirali y Metric Spaces de Mícheál Ó Searcoid, o cualquier libro sobre topología de espacios métricos.
En la entrada anterior la métrica euclidiana $d$ nos permitió describir algunos lugares geométricos del plano complejo $\mathbb{C}$ con los que ya estábamos familiarizados en $\mathbb{R}^2$. Es importante mencionar que existen otras formas de definir la distancia entre dos números complejos $z$ y $w$. Sin embargo para los fines del curso estaremos utilizando la métrica euclidiana definida en la entrada anterior.
Hablar de la «topología» en $\mathbb{C}$ hace referencia a un resultado de los espacios métricos en el que se prueba que en un espacio métrico $(X,d)$ la métrica $d$ induce una topología en el conjunto $X$. Por lo que en esta entrada analizaremos la topología inducida por la métrica euclidiana $d(z,w) = |\,z-w\,|$ en $\mathbb{C}$.
Lo anterior nos motiva a definir algunos conjuntos de puntos de $\mathbb{C}$ que serán necesarios para continuar en el estudio de la topología en $\mathbb{C}$. Por lo que introducir el concepto de disco o vecindad será de gran utilidad para caracterizar a los conjuntos de $\mathbb{C}$, así como para dar una definición formal de límite y continuidad en $\mathbb{C}$.
$\mathbb{C}$ como un espacio métrico
Definición 7.1. (Métrica y espacio métrico.)
Un conjunto $X\neq\emptyset$ dotado con una función $d: X \times X \to [0,\infty)$ es llamado un espacio métrico, lo cual se denota como $(X,d)$, si la función $d$ cumple las siguientes propiedades para todo $x,y, z\in X$:
- $d(x, y) \geq 0$.
- $d(x,y) = 0$ si y solo si $x=y$.
- Simetría: $d(x,y) = d(y,x)$.
- Desigualdad del triángulo: $d(x,y) \leq d(x,z) + d(z,y)$.
Dicha función $d$ es llamada métrica en $X$ o función distancia en $X$. Es común denotar a la métrica en $X$ como $d_X$ cuando se están trabajando con varios espacios métricos y se requiere especificar donde está definida dicha métrica.
Ejemplo 7.1.
- a) Consideremos al conjunto de los números reales $\mathbb{R}$. La función $d:\mathbb{R} \times \mathbb{R} \to [0,\infty)$ dada por:\begin{equation*}
d(x,y) = |\,x-y\,|,
\end{equation*} utilizando las propiedades del valor absoluto es fácil verficar que $d$ es una métrica en $\mathbb{R}$.
- b) Si $X = \mathbb{R}^n$, entonces para $x = (x_1, x_2, \ldots, x_n)$ y $y = (y_1, y_2, \ldots, y_n)$ en $X$ se define:\begin{equation*}
d(x,y) = \left(\sum_{k=1}^{n} (x_k – y_k)^2 \right)^{1/2}.
\end{equation*} - La función $d$ es llamada la métrica euclidiana en $\mathbb{R}^n$.
- c) Sea $X$ cualquier conjunto no vacío, entonces se define a la métrica discreta en $X$ como la función:
\begin{equation*}
d(x,y) = \left\{
\begin{array}{lcc}
0 & \text{si} & x = y,\\
1 & \text{si} & x \neq y.
\end{array}
\right.
\end{equation*}
Usando la definición del módulo es fácil probar que la distancia euclidiana, dada en la definición 6.1 de la entrada anterior, es una función $d: \mathbb{C}\times\mathbb{C} \rightarrow [0,\infty)$ que satisface las condiciones para ser una métrica.
Proposición 7.1. (El espacio métrico $(\mathbb{C}, d)$.)
El conjunto $\mathbb{C}$ dotado con la métrica euclidiana $d(z,w) = |\,z-w\,|$, $z,w\in\mathbb{C}$, es un espacio métrico.
Demostración. Sean $z_1, z_2, z_3 \in \mathbb{C}$, entonces:
- $d(z_2, z_1) \geq 0$, se sigue de la definición del módulo de un número complejo.
- Ejercicio.
- Ejercicio.
- Queremos probar que:
\begin{equation*}
d(z_2, z_1) \leq d(z_2, z_3) + d(z_3, z_1),
\end{equation*}o equivalentemente que:
\begin{equation*}
|\,z_2 – z_1\,| \leq |\,z_2 – z_3\,| + |\,z_3 – z_1\,|.
\end{equation*}
Sean $z = z_2 – z_3$ y $w = z_3 – z_1$, entonces podemos reescribir $z + w = z_2 – z_1$ y así probar que:
\begin{equation*}
|\, z + w \, | \leq |\,z\,| + |\,w\,|,
\end{equation*}lo cual se sigue de la proposición 3.2.
$\blacksquare$
Observación 7.1.
De acuerdo con la proposición 7.1 y la definición 7.1 tenemos que $\mathbb{C}$ dotado con la métrica euclidiana $d$ forma un espacio métrico, denotado por $(\mathbb{C}, d)$. Es importante mencionar que en esta entrada daremos algunos resultados de manera general para un espacio métrico $(X,d_X)$ y cuando sea necesario puntualizar algo del espacio métrico $(\mathbb{C}, d)$ trabajaremos de manera particular con dicho espacio métrico.
Definición 7.2.
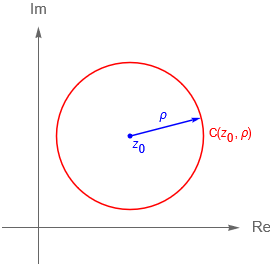
Dado $z_0\in\mathbb{C}$ un punto fijo y una cantidad $\rho>0$, se define a la circunferencia de centro $z_0$ y radio $\rho$ en $\mathbb{C}$, figura 40a, como el conjunto de puntos:
\begin{equation*}
C(z_0,\rho)= \left\{z\in\mathbb{C} \,: \, |\,z-z_0\,| = \rho\right\}.
\end{equation*}
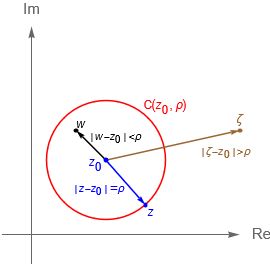
De acuerdo con la entrada anterior sabemos que las ecuaciones:\begin{align*}
|\,z-z_0\,|< \rho,\\
|\,z-z_0\,|> \rho,
\end{align*} nos describen a los puntos $z\in\mathbb{C}$ que caen dentro o fuera de la circunferencia $C(z_0,\rho)$ respectivamente, figura 40b.
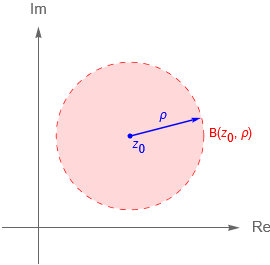
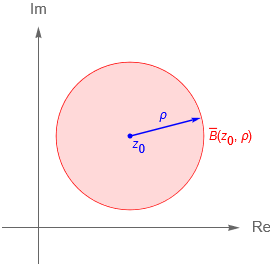
Definición 7.3. (Disco o $\rho$-vecindad.)
Dado $z_0\in\mathbb{C}$ un punto fijo y una cantidad $\rho>0$, se definen en $\mathbb{C}$ a los conjuntos: \begin{equation*}
B(z_0,\rho)= \{z\in\mathbb{C} \,: \, |\,z-z_0\,| < \rho\},
\end{equation*} \begin{equation*}
\overline{B}(z_0,\rho)= \{z\in\mathbb{C} \,: \, |\,z-z_0\,| \leq \rho\},
\end{equation*} como el disco abierto de radio $\rho$ y centro $z_0$ o la $\rho$-vecindad de $z_0$, figura 41(a), y el disco cerrado de radio $\rho$ y centro $z_0$, figura 41(b), respectivamente.
Figura 40: Circunferencia de centro $z_0$ y radio $\rho>0$.
de la circunferencia $C(z_0, \rho)$.
Observación 7.2.
En ocasiones será necesario trabajar con una $\rho$-vecindad de $z_0$ sin considerar al punto $z_0$, es decir $B^*(z_0,\rho) = B(z_0,\rho) \setminus \{z_0\}$, en dado caso llamaremos a ese conjunto como una $\rho$-vecindad perforada o un disco perforado.
Análogamente se puede hablar de un disco cerrado perforado como el conjunto $\overline{B}^*(z_0,\rho) = \overline{B}(z_0,\rho) \setminus \{z_0\}$.
Definición 7.4. (Punto interior y conjunto abierto.)
Sea $S\subset\mathbb{C}$. Diremos que $z_0\in \mathbb{C}$ es un punto interior de $S$ si existe $\rho>0$ tal que $B(z_0,\rho)\subset S$.
Al conjunto de puntos interiores de $S$ se le denota como $\operatorname{int}S$ o $ \mathring{S}$. Si se cumple que $S = \operatorname{int}S$, entonces diremos que $S$ es un conjunto abierto en $\mathbb{C}$.
De acuerdo con la definición de $\operatorname{int}S$, notemos $\operatorname{int}S\subset S$. De hecho, dado un espacio métrico $(X,d)$ y $S\subset X$, entonces se cumple que $\operatorname{int}S$ es un conjunto abierto y es el mayor subconjunto abierto de $X$ contenido en $S$.
Figura 41: Disco abierto y cerrado con centro $z_0$ y radio $\rho>0$.
Definición 7.5. (Conjunto cerrado.)
Un conjunto $S\subset\mathbb{C}$ se dice que es cerrado en $\mathbb{C}$ si su complemento $S^C = \mathbb{C}\setminus S$ es abierto en $\mathbb{C}$.
Observación 7.3.
Comunmente denotaremos a los conjuntos abiertos de $\mathbb{C}$ con la letra $U$ y a los conjuntos cerrados de $\mathbb{C}$ con la letra $F$.
Ejemplo 7.2.
Utilizando la desigualdad del triángulo es fácil verificar que:
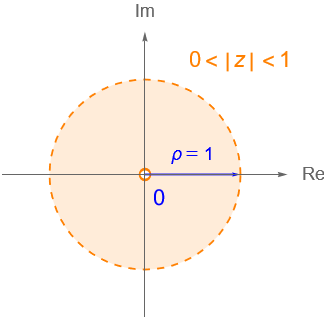
- a) El conjunto $\{z\in\mathbb{C} : 0<|\,z\,|<1\}$ es abierto en $\mathbb{C}$, figura 42a.
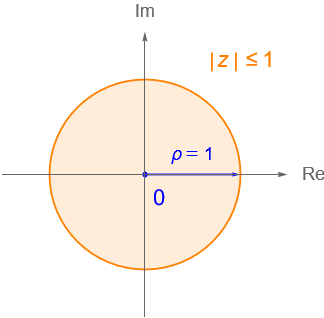
- b) El conjunto $\{z\in\mathbb{C} : |\,z\,| \leq 1\}$ es cerrado en $\mathbb{C}$, figura 42b.
- c) El conjunto $\{z\in\mathbb{C} : 0< |\,z\,| \leq 1\}$ no es abierto ni cerrado en $\mathbb{C}$, figura 43.
- d) Los conjuntos $\emptyset$ y $\mathbb{C}$ son conjuntos abiertos y cerrados en $\mathbb{C}$, ¿por qué?
Figura 42: Conjuntos del ejemplo 7.1 inciso a) y b).

Definición 7.6. (Punto exterior y punto frontera.)
Sea $S\subset\mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto exterior de $S$ si existe $\rho>0$ tal que $B(z_0,\rho) \subset \mathbb{C}\setminus S$.
Por otra parte, diremos que $z_0$ es un punto frontera de $S$ si para todo $\rho>0$ se tiene que $B(z_0,\rho) \cap S \neq \emptyset$ y $B(z_0,\rho) \cap \mathbb{C}\setminus S \neq \emptyset$.
Al conjunto de los puntos exteriores de $S$ se le denota como $\operatorname{ext}S$. Mientras que al conjunto de los puntos frontera de $S$ se le denota como $\partial S$.
Definición 7.7. (Punto de acumulación o punto límite y punto aislado.)
Sea $S\subset \mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto de acumulación o un punto límite de $S$ si para todo $\rho>0$ se tiene:
\begin{equation*}
B(z_0,\rho)\setminus\{z_0\} \cap S \neq \emptyset.
\end{equation*} O equivalentemente que para todo $\rho>0$ se tiene:
\begin{equation*}
\{ z \in S : 0 < |\,z-z_0\,|<\rho\} \neq \emptyset.
\end{equation*}
Si se cumple que $z_0\in S$, pero $z_0$ no es punto de acumulación de $S$, entonces diremos que $z_0$ es un punto aislado de $S$. En este caso se tiene que existe algún $\varepsilon>0$ tal que:
\begin{equation*}
B(z_0,\varepsilon) \cap S = \{z_0\}.
\end{equation*}
Al conjunto de puntos de acumulación lo denotaremos como $S’$ y lo llamaremos el conjunto derivado de $S$.
Definición 7.8. (Punto de adherencia.)
Sea $S\subset \mathbb{C}$ y sea $z_0\in\mathbb{C}$. Diremos que $z_0$ es un punto de adherencia de $S$ si para todo $\rho>0$ se tiene:
\begin{equation*}
B(z_0,\rho) \cap S \neq \emptyset.
\end{equation*}
Al conjunto de puntos de adherencia lo llamaremos la cerradura o la clausura de $S$ y lo denotaremos como $\overline{S}$.
De acuerdo con la definición de $\overline{S}$, tenemos que $S \subset \overline{S}$. Además, dado un espacio métrico $(X,d)$ y $S\subset X$, entonces se cumple que $\overline{S}$ es un conjunto cerrado y es el menor subconjunto cerrado de $X$ que contiene a $S$.
De hecho, dado un espacio métrico $(X,d_X)$ y $S\subset X$, se tiene que $S$ es cerrado en $X$ si y solo si $S = \overline{S}$.
Proposición 7.2.
Consideremos al espacio métrico $(\mathbb{C}, d)$, con $d$ la métrica euclidiana. Un conjunto $S\subset\mathbb{C}$ es cerrado en $\mathbb{C}$ si y sólo si $S$ contiene a todos sus puntos de acumulación.
Demostración.
$\Rightarrow)$
Supongamos que $S$ es cerrado en $\mathbb{C}$. Sea $z_0 \in \mathbb{C}$ un punto de acumulación de $S$. Por reducción al absurdo supongamos que $z_0 \in \mathbb{C}\setminus S$. Notemos que por definición $\mathbb{C}\setminus S$ es un conjunto abierto, por lo que para algún $\rho>0$ se tiene que $B(z_0, \rho) \subset \mathbb{C}\setminus S$, es decir que al disco abierto $B(z_0,\rho)$ no pertenece ningún punto de $S$, lo cual contradice el hecho de que $z_0$ es un punto de acumulación de $S$. Por lo tanto $z_0\in S$.
$(\Leftarrow$
Supongamos que a $S$ pertenecen todos sus puntos de acumulación. Entonces para algún $z_0 \in \mathbb{C} \setminus S$ se cumple que $z_0$ no es punto de acumulación de $S$, por lo que existe $\rho>0$ tal que $B(z_0, \rho)$ no tiene puntos de $S$, por lo que $B(z_0, \rho) \subset \mathbb{C}\setminus S$, por tanto $\mathbb{C}\setminus S$ es abierto, de donde se sigue que $S$ es cerrado.
$\blacksquare$
Ejemplo 7.3.
Veamos que no necesariamente todo punto de un conjunto cerrado debe ser un punto de acumulación del mismo. Consideremos al conjunto:
\begin{equation*}
S = \left\{z\in\mathbb{C}\, : \, z = \frac{1}{n}, \,\, n\in\mathbb{N}^+ \right\} \cup \left\{0\right\}.
\end{equation*}
Es claro que $S\subset\mathbb{C}$. Notemos que el único punto de acumulación de $S$ es $z=0$. Desde que dicho punto pertenece a $S$, por la proposición 7.2 es claro que $S$ es cerrado. Por otra parte no es díficil convencerse de que salvo $z=0$, el resto de los puntos de $S$ son puntos aislados, ya que basta con tomar $\rho = \frac{1}{n} – \frac{1}{n+1} > 0$ para que se cumpla que:
\begin{equation*}
B\left(\frac{1}{n}, \rho\right) \cap S = \left\{\frac{1}{n}\right\}.
\end{equation*}
Definición 7.9. (Conjunto acotado.)
Un conjunto $S \subset \mathbb{C}$ se dice que es acotado si existe un número real $R>0$ tal que $|\,z\,| < R$ para todo $z\in S$.
Esta definición nos dice que $S$ es acotado si puede ser completamente encerrado por un $R$-vecindario del origen.
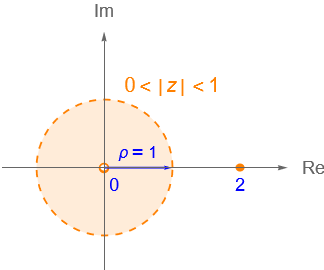
Ejemplo 7.4.
Sea $X = \left\{z\in\mathbb{C} \, : \, 0<|\,z\,|<1\right\} \cup \{2\}$, figura 44. Entonces:
- a) Los puntos interiores de $X$ son el conjunto $\operatorname{int} X = \{z\in\mathbb{C} \, : \, 0<|\,z\,|<1\}$.
- b) Los puntos exteriores de $X$ son el conjunto $\operatorname{ext} X = \{z\in\mathbb{C} \, : \, 1 < |\,z\,|\} \cap \{z\in\mathbb{C} \, : \, z \neq 2\}$.
- c) La frontera de $X$ es el conjunto $\partial X = \{0, 2\} \cup \{z\in\mathbb{C} \,: \, |\,z\,|=1\}$.
- d) Los puntos de acumulación de $X$ son el conjunto $X’ = \{z\in\mathbb{C} \, : \, |\,z\,|\leq 1\}$.
- e) El punto $z=2$ es un punto aislado de $X$.
- f) Tomando $R=3>0$ es claro que el conjunto $X$ es acotado ya que $|\,z\,|< R$ para todo $z\in X$.
De acuerdo con nuestros cursos de Cálculo (y Análisis Matemático) sabemos que en un espacio métrico, en este caso en $(\mathbb{C},d)$, se cumple que:
Proposición 7.3.
Sea $(X,d_X)$ un espacio métrico. Sean $z_0 \in X$ y $S\subset X$, entonces:
- Los conjuntos $X$ y $\emptyset$ son abiertos en $X$.
- Para todo $\rho>0$, la $\rho$-vecindad de $z_0$, es decir el conjunto:
\begin{equation*}
B(z_0,\rho) = \{ z\in X \,: \, d_X(z,z_0) < \rho\},
\end{equation*} es un conjunto abierto en $X$. - Para todo $\rho>0$, el disco cerrado, es decir el conjunto:
\begin{equation*}
\overline{B}(z_0,\rho) = \{ z\in X \,: \, d_X(z,z_0) \leq \rho\},
\end{equation*} es un conjunto cerrado en $X$. - $S’ \subset \overline{S}$.
- $\overline{S} = S \cup S’$.
- $\overline{S} = \operatorname{int}S \cup \partial S$.
- $X = \operatorname{int}S \cup \operatorname{ext}S \cup \partial S$.
- Si $A \subset B$, entonces:
a) $\overline{A} \subset \overline{B}$.
b) $\operatorname{int}A \subset \operatorname{int}B$. - La unión de un número arbitrario de conjuntos abiertos en $X$ es también un conjunto abierto en $X$.
- La intersección de un número finito de conjuntos abiertos en $X$ es un conjunto abierto en $X$.
- La intersección de un número arbitrario de conjuntos cerrados en $X$ es también un conjunto cerrado en $X$.
- La unión de un número finito de conjuntos cerrados en $X$ es un conjunto cerrado en $X$.
Demostración.
- Ejercicio.
- Dadas las hipótesis, sea $\rho>0$. Tomemos $z\in B(z_0,\rho)$ y sea $\varepsilon = \rho – d_X(z_0, z) > 0 $. Considerando la desigualdad del triángulo tenemos que para todo $w \in B(z,\varepsilon)$ se cumple que:
\begin{equation*}
d_X(w, z_0) \leq d_X(w, z) + d_X(z, z_0) < \varepsilon + d_X(z, z_0) = \rho,
\end{equation*} por lo que $B(z,\varepsilon) \subset B(z_0, \rho)$ para todo $z\in B(z_0,\rho)$.
- Dadas las hipótesis, sea $\rho>0$. Tomemos $z\in \overline{\overline{B}(z_0,\rho)}$, entonces para todo $\varepsilon > 0$ existe:
\begin{equation*}
z_\varepsilon \in B(z,\varepsilon)\cap \overline{B}(z_0,\rho).
\end{equation*} De acuerdo con la desigualdad del triángulo, para todo $\varepsilon > 0$ se cumple que:
\begin{equation*}
d_X(z, z_0) \leq d_X(z, z_\varepsilon) + d_X(z_\varepsilon, z_0) < \varepsilon + \rho,
\end{equation*} de donde se sigue que $d(z, z_0) < \rho$, por lo que $\overline{\overline{B}(z_0,\rho)}\subset \overline{B}(z_0,\rho)$. Entonces
\begin{equation*}
\overline{B}(z_0,\rho) = \overline{\overline{B}(z_0,\rho)},
\end{equation*} por lo tanto, todo disco cerrado es un conjunto cerrado en $X$. - Ejercicio.
- Ejercicio.
- Ejercicio.
- Ejercicio.
- Ejercicio.
- Sea $\{ G_j : j\in J\}$, con $J$ un conjunto de índices, una colección de conjuntos abiertos en $X$. Tomemos a $z\in G = \bigcup\limits_{j\in J} G_j$, entonces $z \in G_j$, para algún $j\in J$, así por la definición 7.4 tenemos que existe $\rho>0$ tal que $B(z,\rho) \subset G_j \subset G$, por lo que $G$ es abierto.
- Sean $G_1, G_2, \ldots , G_n$ subconjuntos abiertos de $X$ y sea $z \in G = \bigcap\limits_{k=1}^{n} G_k$. Tenemos que $z\in G_k$ para $k=1,2, \ldots, n$, por lo que por la definición 7.4 se tiene que para cada $k$ existe $\rho_k > 0$ tal que $B(z,\rho_k) \subset G_k$. Si tomamos a $\rho = \operatorname{min}{\rho_k : 1 \leq k \leq n}$, entonces para cada $k$, con $1 \leq k \leq n$, se cumple que $B(z,\rho) \subset B(z,\rho_k) \subset G_k$. Entonces $B(z,\rho) \subset G$, por lo que $G$ es abierto.
- Ejercicio.
- Ejercicio.
$\blacksquare$
Es posible encontrar la prueba de estas propiedades en algún libro de topología o de topología de espacios métricos, como Topología de espacios métricos de Ignacio L. Iribarren.
Definición 7.10. (Conjunto denso.)
Sea $(X,d_X)$ un espacio métrico. Diremos que un conjunto $A\subset X$ es denso en $X$ si $\overline{A} = X$.
Ejemplo 7.5.
- a) El conjunto de los números racionales $\mathbb{Q}$ es denso en $\mathbb{R}$ con la métrica usual de $\mathbb{R}$, $d(x,y) = |\,x-y\,|$.
- b) El conjunto ${x+iy : x,y\in\mathbb{Q}}$ es denso en $\mathbb{C}$ con la métrica euclidiana.
Tarea moral
- Prueba que las siguientes funciones $d_i: \mathbb{C}\times\mathbb{C} \to [0,\infty)$, con $i=1,2$, dadas por:
\begin{equation*}
d_1(x+iy, a+ib) = |\,x-a\,| + |\,y-b\,|,
\end{equation*} \begin{equation*}
d_2(x+iy, a+ib) = \text{máx}\left\{|\,x-a\,|,|\,y-b\,|\right\},
\end{equation*} son también una métrica en $\mathbb{C}$. - Considera la observación 7.2 y argumenta porqué esos conjuntos se pueden definir respectivamente como:
\begin{equation*}
B^*(z_0,\rho) = \{z\in\mathbb{C}\,:\, 0<|\,z-z_0\,|<\rho\},
\end{equation*} \begin{equation*}
\overline{B^*}(z_0,\rho) = \{z\in\mathbb{C}\,:\, 0<|\,z-z_0\,|\leq\rho\}.
\end{equation*} ¿Cómo son esos conjuntos en $\mathbb{C}$? ¿Cerrados, abiertos o ninguno de los dos? Describe al conjunto de puntos interiores, exteriores, frontera, de acumulación y de adherencia. ¿Son acotados esos conjuntos? - Argumenta porqué los conjuntos $\emptyset$ y $\mathbb{C}$ son abiertos y cerrados en $\mathbb{C}$, ejemplo 7.2(c).
- Completa la demostración de las proposiciones 7.1 y 7.3.
- Hasta ahora sabemos que $\mathbb{R}\subset\mathbb{C}$. Por otra parte, de nuestros cursos de cálculo sabemos que un intervalo abierto en $\mathbb{R}$, es decir el conjunto:
\begin{equation*}
(a,b) = \{ x\in\mathbb{R} \,:\, a<x<b\},
\end{equation*} es un conjunto abierto en $\mathbb{R}$. Prueba que dicho conjunto no es abierto en $\mathbb{C}$. - Utilizando la definición describe cómo son los siguientes conjuntos de $\mathbb{C}$, es decir ¿son abiertos o cerrados o ninguna de las dos en $\mathbb{C}$? ¿Son acotados?
a) Sean $a,b\in\mathbb{R}$ con $a<b$, definimos:\begin{align*}
A = \{z\in\mathbb{C}\, :\, a< \operatorname{Re}(z)<b\},\\
B = \{z\in\mathbb{C}\, :\, a< \operatorname{Im}(z)<b\}.
\end{align*} b) $X = \{z\in\mathbb{C} \,:\ \, \operatorname{Re}(z)<0\} \cup \{0\}$.
c) $Y = \{z\in\mathbb{C} \,:\ \, 0\leq\operatorname{Im}(z)\}$.
- Considera a los siguientes conjuntos:
a) $S_1 = B(0,1)$.
b) $S_2 = \overline{B}\left(-1-i\sqrt{2},\frac{7}{8}\right)$.
c) $S_3 = \overline{B}\left(2+i\sqrt{3},\frac{1}{2}\right)$.
De acuerdo con la proposición 7.2 tenemos que $S_1$ es un conjunto abierto en $\mathbb{C}$, mientras que $S_2$ y $S_3$ son conjuntos cerrados en $\mathbb{C}$. Describe los puntos interiores, exteriores y frontera de cada uno de los tres conjuntos.
- Considera al siguiente conjunto:
\begin{equation*}
S = \left\{ z\in\mathbb{C} \,:\, |\,\operatorname{Im}(z)\,| < |\,\operatorname{Re}(z)\,| \right\},
\end{equation*} el cual está representado en la figura 46. Prueba que:
a) $S$ es un conjunto abierto en $\mathbb{C}$.
b) $\partial S = \{ z\in\mathbb{C} \,:\, |\,\operatorname{Re}(z)\,| = |\,\operatorname{Im}(z)\,|\}$.
c) Los puntos de acumulación de $S$ son precisamente la clausura de $S$, es decir $\overline{S}$.
d) $S$ no es cerrado en $\mathbb{C}$.
e) $S$ no es acotado en $\mathbb{C}$.
Más adelante…
En esta entrada hemos hecho una breve descripción de la topología de los espacios métricos, en particular analizamos la topología del plano complejo $\mathbb{C}$. Esta caracterización de $\mathbb{C}$ como un espacio métrico nos será de gran utilidad en las siguientes entradas para poder continuar el estudio del campo de los números complejos.
En esta entrada hemos visto que existe una estrecha relación entre la topología de $\mathbb{C}$ y $\mathbb{R}^2$, lo cual no debe sorprendernos ya que como espacios vectoriales dichos conjuntos son isomorfos, ver ejercicio 6 de la entrada 2. Más adelante veremos que como espacios métricos son homeomorfos, por lo que muchas propiedades que conocemos para $\mathbb{R}^2$ nos permitirán caracterizar a los números complejos. Por otra parte es fácil convencerse que la topología de $\mathbb{C}$ induce en $\mathbb{R}$ su topología usual considerando la distancia definida mediante el valor absoluto.
La siguiente entrada abordaremos las sucesiones en $\mathbb{C}$ y discutiremos la completez del espacio métrico $(\mathbb{C}, d)$, con $d$ la métrica euclidiana.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Lugares geométricos en $\mathbb{C}$.
- Siguiente entrada del curso: Sucesiones en el espacio métrico $(\mathbb{C}, d)$.