Introducción
En la entrada anterior vimos que $\mathbb{C}$ dotado con la métrica euclidiana, inducida por el módulo de un número complejo, forman un espacio métrico.
Al trabajar con espacios métricos, las sucesiones resultan una herramienta fundamental en el estudio del concepto de las aproximaciones. De manera particular en esta entrada abordaremos el concepto de sucesión en el sentido complejo y estudiaremos propiedades de las mismas pues veremos que estas sucesiones están estrechamente ligadas con la topología de $\mathbb{C}$. Además en su momento usaremos los resultados de esta entrada para el estudio de series de números complejos, las cuales resultarán fundamentales en el estudio de la teoría de funciones.
Sucesiones de números complejos
Definición 8.1. (Sucesión.)
Sea $(X,d_X)$ un espacio métrico. Una sucesión de puntos en $X$ es una función $f: \mathbb{N}^+ \rightarrow X$ tal que para cada $n\in\mathbb{N}^+$ asigna de manera única un elemento de $X$. Si $f(n)=x_n\in X$ para toda $n\in\mathbb{N}^+$, entonces denotamos a la sucesión como el conjunto $\left\{x_n\right\}_{n\geq1}$ o simplemente $\left\{x_n\right\}$.
Observación 8.1.
En este punto es conveniente hacer énfasis en las sucesiones de $\mathbb{C}$ pues más adalente probaremos algunos resultados del espacio métrico $(\mathbb{C},d)$. Sin embargo las definiciones que daremos a continuación son válidas en general para un espacio métrico $(X,d)$. Además será de vital importancia recordar nuestros resultados para sucesiones reales ya que nos serán de utilidad más adelante.
Definición 8.2. (Sucesión compleja convergente.)
Una sucesión de números complejos $\left\{z_n\right\}_{n\geq1}$ converge a un número complejo $z\in\mathbb{C}$, llamado el límite de $\left\{z_n\right\}_{n\geq1}$, si para toda $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que:
\begin{equation*}
|\,z_n \,- \, z\,|<\varepsilon, \quad \forall n \geq N,
\end{equation*} lo cual denotamos como $z_n \rightarrow z$ ó $\lim\limits_{n \to \infty} z_n = z$. De existir dicho límite, este es único. (¿Por qué?)
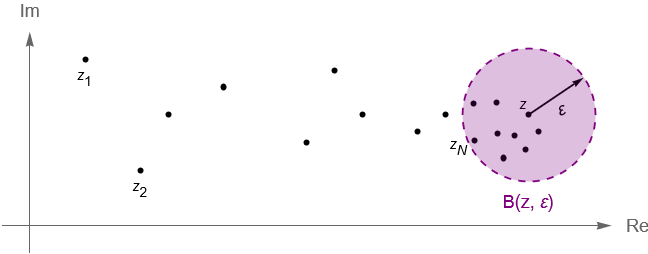
Notemos que geométricamente la desigualdad $|\,z_n \,- \, z\,|< \varepsilon$ nos dice que para $n\geq N$ todos los términos de la sucesión caen en la $\varepsilon$-vecindad de $z$, es decir $B(z,\varepsilon)$, figura 47.
Ejemplo 8.1.
Veamos que la sucesión de números complejos $\left\{\dfrac{i^{n+1}}{n}\right\}_{n\geq 1}$ converge a cero.
Solución.
Considerando la fórmula de De Moivre es fácil notar que: \begin{equation*}
|\,i^{n+1} \,- \, 0\,| = |\,i^{n+1}\,| = |\,i\,|^{n+1} = 1. \end{equation*} Por otra parte, por la propiedad arquimediana se sigue que para todo $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} \left|\,\frac{i^{n+1}}{n} \,- \, 0\,\right| = \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n\geq N. \end{equation*} Por lo tanto $\lim\limits_{n \to \infty} \dfrac{i^{n+1}}{n} = 0$.
Definición 8.3. (Sucesión compleja divergente.)
Una sucesión de números complejos $\left\{z_n\right\}_{n\geq1}$ diverge, lo cual denotaremos como $\lim\limits_{n \to \infty} z_n = \infty$, si se cumple que $\lim\limits_{n \to \infty} |z_n| = \infty$, es decir si para toda $R>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*}|\,z_n\,| \geq R, \quad \forall n \geq N. \end{equation*}
Observación 8.2.
Es común considerar a la «divergencia» como la no existencia del límite dado en la definición 8.1, es decir una sucesión se considera divergente si no es convergente. Sin embargo en el caso complejo es conveniente considerar a la divergencia como la tendencia a infinito. En este sentido tenemos que los conceptos de «no convergencia» y «divergencia» no son equivalentes. Lo cual veremos más adelante.
Definición 8.4. (Operaciones entre sucesiones.)
Sean $\{z_n\}_{n\geq1}$ y $\{w_n\}_{n\geq1}$ dos sucesiones de $\mathbb{C}$. Las operaciones de suma, resta, multiplicación y división para sucesiones se definen respectivamente como:
- $\{z_n\}_{n\geq1} \pm \{w_n\}_{n\geq1} = \{z_n \pm w_n\}_{n\geq1}$.
- $\{z_n\}_{n\geq1} \cdot \{w_n\}_{n\geq1} = \{z_n w_n\}_{n\geq1}$.
- Si $w_n \neq 0 $ para toda $n\in\mathbb{N}^+$, entonces $\dfrac{\{z_n\}_{n\geq1}}{\{w_n\}_{n\geq1}} = \left\{\dfrac{z_n}{w_n}\right\}_{n\geq1}$.
Considerando que una sucesión de números complejos $\{z_n\}_{n\geq 1}$ es un subconjunto de $\mathbb{C}$, entonces posible pensar en sucesiones acotadas.
Definición 8.5. (Sucesión acotada.)
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ se dice que es acotada si existe un número $M>0$ tal que $|\,z_n\,| \leq M$ para todo $n\in\mathbb{N}^+$.
Ejemplo 8.2.
La sucesión de números complejos $\{(-1)^n\}_{n \geq 1}$ es acotada, pero no es convergente.
De acuerdo con el ejemplo anterior es fácil concluir que una sucesión acotada no tendría porqué ser convergente. Sin embargo el recíproco sí es cierto, es decir:
Proposición 8.1.
Toda sucesión de números complejos $\{z_n\}_{n\geq 1}$ convergente es acotada.
Demostración.
Supongamos que la sucesión de números complejos $\{z_n\}_{n\geq 1}$ es convergente y $\lim\limits_{n \to \infty} z_n = z$. De acuerdo con la definición 8.1 tenemos que para $\varepsilon=1$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} |\,z_n \,- \,z\,| < 1, \quad \forall n\geq N. \end{equation*} De acuerdo con la desigualdad del triángulo se tiene que para toda $n\geq N$ se cumple que $|\,z_n\,| < |\,z\,| + 1$. Sea $M = \text{máx}\left\{ 1 + |\,z\,|,|\,z_1\,|,|\,z_2\,|, \ldots, |\,z_N\,|\right\}$, entonces para toda $n\geq 1$ se cumple que $|\,z_n\,|\leq M$.
$\blacksquare$
Utilizando la definición 8.2 es fácil probar las siguientes propiedades para sucesiones complejas.
Proposición 8.2.
Sean $\{z_n\}_{n\geq1}$ y $\{w_n\}_{n\geq1}$ sucesiones de números complejos y supongamos que ambas son convergentes en $\mathbb{C}$, con $\lim\limits_{n \to \infty} z_n = z$ y $\lim\limits_{n \to \infty} w_n = w$. Entonces se cumple que:
- $\lim\limits_{n \to \infty}(z_n \pm w_n) = z \pm w$.
- $\lim\limits_{n \to \infty}(z_n w_n) = zw$.
- Si además $w_n\neq 0$ para toda $n \geq 1$ y $w\neq 0$, entonces $\lim\limits_{n \to \infty} \left(\dfrac{1}{ w_n}\right) = \dfrac{1}{w}$.
- $\lim\limits_{n \to \infty} \overline{z_n} = \overline{z}$.
- Si $\{z_n\}_{n\geq1}$ diverge y $\{w_n\}_{n\geq1}$ está separada de cero, es decir, si existen $r>0$ y $N\in\mathbb{N}^+$ tales que para $n\geq N$ se cumple que $|w_n|\geq r$, entonces $\{z_n w_n\}_{n\geq1}$ diverge.
Demostración.
- Dadas las hipótesis por la definición 8.1 tenemos que para cualquier $\varepsilon>0$ existen $N_1, N_2 \in \mathbb{N}$ tales que: \begin{equation*}
|\,z_n \,-\, z\,| < \varepsilon/2, \quad \forall n \geq N_1,\end{equation*}\begin{equation*}|\,w_n \,-\, w\,| < \varepsilon/2, \quad \forall n \geq N_2. \end{equation*} Notemos que: \begin{align*}|\, (z_n \pm w_n) \,-\, (z \pm w)\,| & = |\, (z_n \,-\, z) \pm (w_n \,-\, w)\,|\\ & \leq |\,z_n \,-\, z\,| + |\,w_n \,-\, w\,| < \varepsilon, \quad \forall n \geq N, \end{align*} donde $N = \text{máx}\left\{N_1, N_2\right\}$. Por lo tanto $\lim\limits_{n \to \infty}(z_n \pm w_n) = z \pm w$. - Dadas las hipótesis, tenemos por la proposición 8.1 que ambas sucesiones son acotadas por lo que sin pérdida de generalidad supongamos que existe $M>0$ tal que $|\,z_n\,|\leq M$ para toda $n\geq 1$. Por otra parte, por la definición 8.2 tenemos que para cualquier $\varepsilon>0$ existen $N_1, N_2 \in \mathbb{N}$ tales que: \begin{equation*}|\,z_n \,-\, z\,| < \frac{\varepsilon}{2(|\,w\,|+1)}, \quad \forall n \geq N_1,\end{equation*} \begin{equation*}|\,w_n \,-\, w\,| < \frac{\varepsilon}{2M}, \quad \forall n \geq N_2. \end{equation*} Notemos que: \begin{align*}|\, z_n w_n \,-\, z w\,| & = |\, z_n w_n \,-\, z_n w + z_n w \,-\, z w \,|\\ & \leq |\,z_n w_n \,-\, z_n w\,| + |\,z_n w \,-\, z w\,|\\ & = |\,z_n\,|\,|\,w_n \,-\, w\,| + |\,w\,|\,|\,z_n \,-\, z \,|\\ & < M \left(\frac{\varepsilon}{2M}\right) + (|\,w\,|+1) \left(\frac{\varepsilon}{2(|\,w\,|+1)}\right) = \varepsilon, \quad \forall n \geq N. \end{align*} Por lo que $\lim\limits_{n \to \infty}(z_n w_n) = zw$.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Dadas las hipótesis, como $\{w_n\}_{n\geq1}$ está separada de cero, entonces existen $r>0$ y $N_1\in\mathbb{N}^+$ tales que para $n\geq N_1$ se cumple que $|w_n|\geq r$. Por otra parte, como $\{z_n\}_{n\geq1}$ diverge, dado $R>0$ existe $N_2\in\mathbb{N}^+$ tal que si $n\geq N_2$, entonces $|z_n|\geq R/r$. Por lo que, para $N = \text{máx}\left\{N_1, N_2\right\}$ se cumple que: \begin{equation*} |z_n w_n| = |z_n| \, |w_n| \geq \frac{R}{r} r = R, \quad \forall n\geq N, \end{equation*} entonces $\{z_n w_n\}_{n\geq1}$ diverge.
$\blacksquare$
Observación 8.3.
Considerando la definición 8.2 y la proposición 8.2 es fácil ver que si una sucesión $\{z_n\}_{n\geq 1}$ converge a un número complejo $z\in\mathbb{C}$ entonces se cumple (¿por qué?): \begin{equation*} z = \lim\limits_{n \to \infty} z_n \quad \Longleftrightarrow \quad \lim\limits_{n \to \infty} |\,z_n – z\,| = 0. \end{equation*} Y para $c\in\mathbb{C}$ constante: \begin{equation*} \lim\limits_{n\to\infty} (c z_n) = c \lim\limits_{n\to\infty} z_n. \end{equation*}
Sabemos que todo número complejo $z$ es caracterizado por su parte real y por su parte imaginaria, la cuales son números reales, por lo que considerando al $n$-ésimo término de una sucesión de números complejos $\{z_n\}_{n\geq 1}$ como $z_n = \operatorname{Re}(z_n) + i\operatorname{Im}(z_n)$, es fácil probar el siguiente resultado.
Proposición 8.3.
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ es convergente en $\mathbb{C}$ si y solo si las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$, $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$. En dicho caso tenemos que: \begin{align*} \lim_{n\to \infty} z_n = z \quad & \Longleftrightarrow \quad \lim_{n\to \infty} \operatorname{Re}(z_n) = \operatorname{Re}(z)\\ & \quad \quad \, \text{y} \,\,\, \lim_{n\to \infty} \operatorname{Im}(z_n) = \operatorname{Im}(z). \end{align*}
Demostración.
Por la proposición 3.1 sabemos que: \begin{align*} |\,\operatorname{Re}(z_n) \,-\, \operatorname{Re}(z)\,| = |\,\operatorname{Re}(z_n \,-\, z)\,|,\\ |\,\operatorname{Im}(z_n) \,-\, \operatorname{Im}(z)\,| = |\,\operatorname{Im}(z_n \,-\, z)\,|. \end{align*} Mientras que por la observación 3.1 tenemos que: \begin{align*} |\,\operatorname{Re}(z_n \,-\, z)\,| \leq |\,z_n \,-\, z\,| \leq |\,\operatorname{Re}(z_n \,-\, z)\,| + |\,\operatorname{Im}(z_n \,-\, z)\,|,\\ |\,\operatorname{Im}(z_n \,-\, z)\,| \leq |\,z_n \,-\, z\,| \leq |\,\operatorname{Re}(z_n \,-\, z)\,| + |\,\operatorname{Im}(z_n \,-\, z)\,|. \end{align*} De acuerdo con la observación 8.3 tenemos que $z = \lim_{n \to \infty} z_n$ si y solo si $\lim_{n \to \infty} |\,z_n \,-\, z\,| = 0$. Considerando lo anterior es claro que: \begin{align*} \lim_{n \to \infty} |\,z_n \,-\, z\,| = 0 \,\,\, & \Longleftrightarrow \,\,\, \lim_{n \to \infty} |\,\operatorname{Re}(z_n) \,-\, \operatorname{Re}(z)\,| = 0\\ & \quad \quad \text{y} \, \lim\limits_{n \to \infty} |\,\operatorname{Im}(z_n) \,-\, \operatorname{Im}(z)\,| = 0. \end{align*} Es decir las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$, $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$ (¿por qué?), por lo que: \begin{align*} \lim_{n\to \infty} z_n = z \quad & \Longleftrightarrow \quad \lim_{n\to \infty} \operatorname{Re}(z_n) = \operatorname{Re}(z)\\ & \quad \quad \, \text{y} \,\,\, \lim_{n\to \infty} \operatorname{Im}(z_n) = \operatorname{Im}(z). \end{align*} De donde se sigue el resultado.
$\blacksquare$
La proposición 8.3 es de gran utilidad al trabajar con sucesiones de números complejos, ya que la convergencia de estas sucesiones se reduce a verificar la convergencia de dos sucesiones de números reales. Más aún, podemos utilizar los resultados conocidos para sucesiones reales en el estudio de las sucesiones complejas, lo cual tiene sentido pues como vimos en la entrada 2 los números reales son un subconjunto de los números complejos, por lo que se deben cumplir las propiedades que ya conocíamos de $\mathbb{R}$ en $\mathbb{C}$.
Ejemplo 8.3.
Estudiemos la convergencia de las siguientes sucesiones:
a) $\left\{\dfrac{n+2+i2^n n}{2^n(n+2)}\right\}_{n\geq 1}$.
b) $\left\{\dfrac{3+in}{n+i2n}\right\}_{n\geq 1}$.
Solución. Para cada $n\in\mathbb{N}^+$ tenemos que:
- a) \begin{equation*}
z_n = \dfrac{n+2+i2^n n}{2^n(n+2)} = \dfrac{1}{2^n} + i\left(\dfrac{n}{n+2}\right).
\end{equation*} De donde $\operatorname{Re}(z_n) = \dfrac{1}{2^n}$ e $\operatorname{Im}(z_n) = \dfrac{n}{n+2}$.
Sabemos que: \begin{align*}
\lim_{n \to \infty} \operatorname{Re}(z_n) = \lim_{n \to \infty}\dfrac{1}{2^n} = 0.\\
\lim_{n \to \infty} \operatorname{Im}(z_n) = \lim_{n \to \infty}\dfrac{n}{n+2} = 1.
\end{align*} Por lo que considerando la proposición 8.3 se sigue que $\operatorname{Re}(z) = 0$ y $\operatorname{Im}(z) = 1$, es decir: \begin{equation*}
\lim_{n \to \infty} z_n = z = i.
\end{equation*}
- b) \begin{equation*}
w_n = \dfrac{3+in}{n+i2n} = \dfrac{3 + 2n}{5n} + i\left(\dfrac{n \,-\, 6}{5n}\right).
\end{equation*} De donde $\operatorname{Re}(w_n) = \dfrac{3+2n}{5n}$ e $\operatorname{Im}(w_n) = \dfrac{n \,-\, 6}{5n}$.
Sabemos que: \begin{align*}
\lim_{n \to \infty} \operatorname{Re}(w_n) = \lim_{n \to \infty}\dfrac{3+2n}{5n} = \frac{2}{5}.\\
\lim_{n \to \infty} \operatorname{Im}(w_n) = \lim_{n \to \infty}\dfrac{n \,-\, 6}{5n} = \frac{1}{5}.
\end{align*} Por lo que considerando la proposición 8.3 se sigue que $\operatorname{Re}(w) = \dfrac{2}{5}$ e $\operatorname{Im}(w) = \dfrac{1}{5}$, es decir: \begin{equation*}
\lim_{n \to \infty} w_n = w = \frac{2}{5} + i\frac{1}{5}.
\end{equation*}
Completez del espacio métrico $(\mathbb{C},d)$
Definición 8.6. (Sucesión de Cauchy.)
Una sucesión $\left\{z_n\right\}_{n\geq1}$ en $\mathbb{C}$ se dice que es una sucesión de Cauchy si para todo $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que: \begin{equation*}|\,z_n \,-\, z_m\,|<\varepsilon, \quad \forall\, n,m \geq N. \end{equation*}
Proposición 8.4.
Toda sucesión convergente en $\mathbb{C}$ es de Cauchy.
Demostración.
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos convergente con $\lim\limits_{n \to \infty} z_n = z$ para algún $z\in\mathbb{C}$. Sea $\varepsilon>0$, entonces existe $N\in\mathbb{N}^+$ tal que:\begin{equation*} |\,z_n \,-\, z\,| < \varepsilon, \quad \forall n \geq N. \end{equation*} Entonces por la desigualdad del triángulo se tiene que para cualesquiera $n,m\in \mathbb{N}^+$ tales que $n,m\geq N$ se cumple: \begin{equation*}|\,z_n \,-\, z_m\,| \leq |\,z_n \,-\, z\,| + |\,z \,-\, z_m\,| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} =\varepsilon. \end{equation*} Por lo tanto la sucesión $\{z_n\}_{n\geq 1}$ es de Cauchy.
Considerando la proposición 8.4 es momento de dar un ejemplo para argumentar la observación 8.2, es decir veamos que la divergencia y la no convergencia no son equivalentes.
Ejemplo 8.4
Consideremos la sucesión $\left\{i^n\right\}_{n\geq 1}$. Veamos que dicha sucesión no converge ni diverge.
Solución. Sea $z_n = i^n$. Por la fórmula de De Moivre es claro que para toda $n\in\mathbb{N}^+$ se tiene que: \begin{equation*}
|\,z_n\,| = |\,i^n\,| = |\,i\,|^n = 1, \quad \Longrightarrow \quad \lim_{n \to \infty} |\,z_n\,| = 1 \neq \infty. \end{equation*} Es decir, la sucesión $\left\{i^n\right\}_{n\geq 1}$ no diverge.
Por otra parte, veamos que dicha sucesión no es de Cauchy. Considerando el argumento principal de $i$, tenemos por la fórmula de De Moivre que: \begin{align*} z_{4n} = i^{4n} = \left(\operatorname{cis}(2\pi)\right)^n = 1^n = 1,\\ z_{4n+2} = i^{4n+2} = i^{4n}i^{2} = 1^n(-1) = -1, \end{align*} por lo que: \begin{align*}|\,z_{4n} \,&-\, z_{4n+2}\,| = 2,\\ & \Longrightarrow \quad \lim_{n \to \infty}|\,z_{4n} \,-\, z_{4n+2}\,| = 2 \neq 0. \end{align*} Entonces la sucesión $\{i^n\}_{n\geq 1}$ no es de Cauchy, por lo que por la contrapuesta de la proposición 8.4, tenemos que dicha sucesión no es convergente en $\mathbb{C}$.
Así concluimos que la sucesión $\{i^n\}_{n\geq 1}$ no diverge, pero tampoco converge.
Definición 8.7. (Completez.)
Un espacio métrico $(X,d)$ se dice que es completo si toda sucesión de Cauchy es convergente en $X$.
Ejemplo 8.5.
El espacio métrico $(\mathbb{R}, d)$, con $d$ la métrica inducida por el valor absoluto, es completo.
La proposición 8.4 es válida en general para cualquier espacio métrico $(X,d)$. Sin embargo el recíproco es falso en general, por ello la importancia de la definición 8.7. Considerando que $\mathbb{R}$ es un subconjunto de $\mathbb{C}$ y que el módulo complejo de $\mathbb{C}$ es la extensi\’on del valor absoluto de $\mathbb{R}$, podemos intuir que el espacio métrico $(\mathbb{C}, d)$, con $d$ inducida por el módulo, es también completo.
Proposición 8.5.
El campo de los números complejos $\mathbb{C}$ dotado con la métrica euclidiana es completo.
Demostración. Sea $\{z_n\}_{n\geq 1}$ en $\mathbb{C}$ una sucesión de Cauchy. Usando la observación 3.1 y la proposición 3.1, como en la prueba de la proposición 8.3, es fácil convencerse de que la sucesión $\{z_n\}_{n\geq 1}$ es de Cauchy si y solo si las sucesiones reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son de Cauchy en $\mathbb{R}$. Dado que $\mathbb{R}$ es completo con la métrica inducida por el valor absoluto, entonces las sucesiones de Cauchy $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son convergentes en $\mathbb{R}$, por lo que por la proposición 8.3 se sigue que la sucesión de Cauchy $\{z_n\}_{n\geq 1}$ es convergente en $\mathbb{C}$, por lo tanto el espacio métrico $(\mathbb{C},d)$, con $d$ la métrica euclidiana, es completo.
$\blacksquare$
Proposición 8.6.
Un punto $z_0\in\mathbb{C}$ es un punto límite (o de acumulación) de un conjunto $S\subset\mathbb{C}$ si y solo si existe una sucesión $\{z_n\}_{n\geq1} \subset S$ tal que $z_n \neq z_0$ para todo $n\in\mathbb{N}^+$ y $\lim\limits_{n \to \infty} z_n = z_0$.
Demostración.
$\Rightarrow)$
Supongamos que $z_0\in\mathbb{C}$ es un punto límite de $S$, entonces por la definición 7.7 tenemos que para todo $n\in\mathbb{N}^+$ existe: \begin{equation*}
z_n \in B\left(z_0, \tfrac{1}{n}\right)\setminus\{z_0\} \cap S, \end{equation*} es decir que para todo $n\in\mathbb{N}^+$ se tiene que $z_n \in S$, $z_n\neq z_0$ y $|\,z_n \,-\, z_0\,|<\frac{1}{n}$. Consideremos a la sucesión $\{z_n\}_{n\geq1}$ dada anteriormente. Es claro que dicha sucesión cumple las condiciones del resultado, veamos que converge a $z_0$. Por la propiedad arquimediana se sigue que para todo $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*}|\,z_n \,-\, z_0\,|< \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n \geq N. \end{equation*} Por lo que $\lim\limits_{n\to \infty} z_n = z_0$.
$(\Leftarrow$
Supongamos que la sucesión $\{z_n\}_{n\geq 1}$ es tal que para todo $n\in\mathbb{N}^+$ se tiene $z_n \in S$, $z_n \neq z$ y $\lim\limits_{n\to \infty} z_n = z_0$. Por la propiedad arquimediana sabemos que dado $\varepsilon>0$ existe $N\in\mathbb{N}^+$ tal que: \begin{equation*} |\,z_N \,-\, z_0\,|< \frac{1}{N} < \varepsilon. \end{equation*} Como $z_N \neq z_0$ y $z_N \in S$, entonces para todo $\varepsilon>0$ se tiene que: \begin{equation*} z_N \in B(z_0, \varepsilon)\setminus\{z_0\} \cap S. \end{equation*} Por lo que $z_0$ es un punto límite de $S$.
$\blacksquare$
Definición 8.8. (Punto de acumulación de una sucesión.)
Un número $z\in\mathbb{C}$ se llama punto de acumulación de una sucesión de números complejos $\{z_n\}_{n\geq 1}$ si para todo $\varepsilon>0$ existe un número infinito de elementos $z_n$ de la sucesión tales que $|\,z_n \,-\, z\,|<\varepsilon$, es decir si cada $\varepsilon-$vecindad de $z_0$, $B(z_0,\varepsilon)$, contiene un número infinito de elementos de la sucesión.
Observación 8.4.
No debemos confundir esta definición con la definición 7.7 de punto límite o punto de acumulación de un conjunto. Por ejemplo la sucesión $\{(-1)^n\}_{n\geq 1}$ tiene dos puntos de acumulación los cuales son $-1$ y $1$. Sin embargo el conjunto $\{-1,1\}$, que consiste de los elementos que determinan a la sucesión, no tiene ningún punto límite o de acumulación.
Además, es fácil convencerse de que todo límite de una sucesión es un punto de acumulación de la misma. Sin embargo el recíproco no se cumple, para verlo basta considerar a la sucesión $\{i^n\}_{n\geq 1}$, la cual tiene cuatro puntos de acumulación los cuales son $1, -1, i$ y $-i$, pero dicha sucesión no converge, es decir no tiene límite.
Definición 8.9. (Subsucesión.)
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Una subsucesión o sucesión parcial de $\{z_n\}_{n\geq 1}$ es cualquier sucesión de la forma $\{z_{\sigma(n)} \}_{n\geq 1}$, donde $\sigma:\mathbb{N}^+ \rightarrow \mathbb{N}^+$, con $\sigma(n) = k_n$, es una función estrictamente creciente.
Ejemplo 8.6.
Si definimos $k_n = 2n$, entonces una subsucesión de $\left\{\dfrac{i^n}{n}\right\}_{n\geq 1}$ está conformada por: \begin{equation*}
-\frac{1}{2}, \,\, \frac{1}{4}, \,\, -\frac{1}{6}, \ldots, \frac{i^{2n}}{2n}, \ldots, \end{equation*} es decir $\left\{\dfrac{i^{2n}}{2n}\right\}_{n\geq 1}$ es una subsucesión de $\left\{\dfrac{i^n}{n}\right\}_{n\geq 1}$.
Proposición 8.7
Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Entonces, $z\in\mathbb{C}$ es un punto de acumulación de $\{z_n\}_{n\geq 1}$ si y solo si existe una subsucesión $\{z_{k_n}\}_{n\geq 1}$ tal que $\lim\limits_{n\to\infty} z_{k_n} = z$.
Demostración. Dadas las hipótesis.
$\Rightarrow)$
Por la definición 8.8 tenemos que para todo $\varepsilon>0$ existe un número infinito de valores de $n$ para los cuales $|\,z_n \,-\, z\,|<\varepsilon$. Entonces para $\varepsilon=1$ existe un $n=k_1$ tal que $|\,z_{k_1} \,-\, z\,| < 1$. Del mismo modo para $\varepsilon = \frac{1}{2}$ existe $n=k_2$ tal que $|\,z_{k_2} \,-\, z\,| < \frac{1}{2}$. Procediendo de forma análoga podemos obtener, en general, que para $\varepsilon = \frac{1}{n}$ existe algún $k_n>k_{n-1}$ tal que $|\,z_{k_n} \,-\, z \,| < \frac{1}{n}$, por lo que existe una subsucesión $\left\{ z_{k_n} \right\}_{n\geq 1}$ de $\{z_n\}_{n\geq 1}$. Por otra parte, tenemos por la propiedad arquimediana que para todo $\varepsilon>0$ existe algún $N\in\mathbb{N}^+$ tal que: \begin{equation*}
|\,z_{k_n} \,-\, z\,| < \frac{1}{n} \leq \frac{1}{N} < \varepsilon, \quad \forall n \geq N.
\end{equation*} Por lo tanto $\lim\limits_{n\to \infty} z_{k_n} = z$.
$(\Leftarrow$
Se deja como ejercicio al lector.
$\blacksquare$
Teorema 8.1. (Teorema de Bolzano – Weierstrass.)
Una sucesión de números complejos $\{z_n\}_{n\geq 1}$ acotada tiene una subsucesión convergente.
Demostración. Dadas las hipótesis, por la observación 3.1 es fácil ver que la sucesión $\{z_n\}_{n\geq 1}$ es acotada si y solo si las sucesiones de números reales $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ e $\{\operatorname{Im}(z_n)\}_{n\geq 1}$ son acotadas en $\mathbb{R}$. Por el teorema de Bolzano – Weierstrass para sucesiones de números reales sabemos que al ser la sucesión $\{\operatorname{Re}(z_n)\}_{n\geq 1}$ acotada, entonces existe una subsucesión $\{\operatorname{Re}(z_{n_j})\}_{n\geq 1}$ convergente para alguna subsucesión $\{z_{n_j}\}_{n\geq 1}$ de $\{z_n\}_{n\geq 1}$. Dado que $\{\operatorname{Im}(z_{n_j})\}_{n\geq 1}$ también es acotada entonces existe alguna subsucesión $\{z_{n_{j_k}}\}_{n\geq 1}$ de $\{z_{n_j}\}_{n\geq 1}$ tal que $\{\operatorname{Im}(z_{n_{j_k}})\}_{n\geq 1}$ también converge. Entonces $\{\operatorname{Re}(z_{n_{j_k}})\}_{n\geq 1}$ es subsucesión de una sucesión convergente, por lo que también es convergente. Por lo tanto, por la proposición 8.3 se sigue que la subsucesión $\{z_{n_{j_k}}\}_{n\geq 1}$ converge en $\mathbb{C}$.
Tarea moral
- Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Prueba que si la sucesión converge en $\mathbb{C}$, entonces dicho límite es único.
- Considera las siguientes sucesiones:
a) $\left\{i^n\right\}_{n\geq 1}$.
b) $\left\{\left(\dfrac{1}{1+i}\right)^n\right\}_{n\geq 1}$.
c) $\left\{\left(\dfrac{1+i}{1-i}\right)^n\right\}_{n\geq 1}$.
d) $\left\{\dfrac{n}{2n+1} + i\, \dfrac{n-1}{n}\right\}_{n\geq 1}$.
e) $\left\{n^2\left(i^n -1\right)\right\}_{n\geq 1}$.
Determina cuáles sucesiones son acotadas, cuáles convergen, encuentra su límite y sus puntos de acumulación. - Prueba que si la sucesión $\{z_n\}_{n\geq 1}$ de números complejos converge a $z\in\mathbb{C}$, entonces la sucesión ${|\,z_n\,|}_{n\geq 1}$ converge a $|\,z\,|$. ¿Es cierto el recíproco?
Hint: Recuerda que: $|\,|z_n| – |z|\,| \leq |z_n – z|$. - Sea $z\in\mathbb{C}$, prueba lo siguiente.
a) Si $|\,z\,|<1$, entonces $\lim\limits_{n\to \infty} z^n = 0$.
b) Si $|\,z\,| > 1$, entonces $\lim\limits_{n\to \infty} z^n = \infty$. - Considera la observación 8.3, argumenta porqué es cierto el resultado. En general prueba que para un espacio métrico $(X, d_X)$ se cumple que una sucesión de elementos de $X$, digamos $\{x_n\}_{n\geq 1}$, converge a $x\in X$ si y solo si $\lim\limits_{n \to \infty} d_X (x_n, x) = 0$.
- Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos. Prueba que $\lim\limits_{n\to \infty} z_n = 0$ si y solo si $\lim\limits_{n\to \infty} |\,z_n\,| = 0$.
- Sea $\{z_n\}_{n\geq 1}$ una sucesión de números complejos, sea $z \in \mathbb{C}$ y sea $\{c_n\}_{n\geq 1}$ una secuencia de números reales no negativos. Demuestra lo siguiente.
a) Si $\lim\limits_{n\to \infty} c_n = 0$ y $|\,z_n – z\,| \leq c_n$ para toda $n\in\mathbb{N}^+$, entonces $\lim\limits_{n\to \infty} z_n = z$.
b) Si $\lim\limits_{n\to \infty} c_n = \infty$ y $|\,z_n \,| \geq c_n$ para toda $n\in\mathbb{N}^+$, entonces $\lim\limits_{n\to \infty} z_n = \infty$. - Sean $\left\{x_n\right\}_{n\geq 1}$ y $\left\{y_n\right\}_{n\geq 1}$ dos sucesiones convergentes de números reales, tales que $x_n \leq y_n$ para toda $n\in\mathbb{N}$. Prueba que: \begin{equation*} \lim_{n \to \infty} x_n \leq \lim_{n \to \infty} y_n. \end{equation*}
Más adelante…
En esta entrada hemos abordado el concepto de sucesión compleja con la finalidad de caracterizar al espacio métrico $(\mathbb{C}, d)$ como un espacio métrico completo. Para ello hicimos uso de algunos resultados para sucesiones reales y generalizamos algunos de los mismos, como el Teorema de Bolzano-Weierstrass, para números complejos.
En general vimos que muchos de los resultados que teníamos para sucesiones reales se comportan de manera similar en el sentido complejo.
Por otra parte introducimos el concepto de la divergencia a infinito, el cual será de utilidad en la entrada 11 al hablar del punto al infinito.
Los resultados de esta entrada serán de utilidad cuando hablemos de las series en el sentido complejo y sobre su convergencia. Además de que nos permitirán obtener una caracterización relacionada con los conceptos de continuidad y continuidad uniforme.
La siguiente entrada abordaremos el concepto de continuidad entre espacios métricos.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Topología de $\mathbb{C}$.
- Siguiente entrada del curso: Continuidad en un espacio métrico.
