Introducción

Hasta ahora hemos descrito la forma en que asociaremos los números complejos, pensados como pares ordenados de números reales, con puntos en el plano complejo utilizando un sistema de coordenadas cartesianas en el que el eje de las abscisas corresponde al eje real y el eje de las ordenadas al eje imaginario. Esto nos permitió darle una representación geométrica a los números complejos como vectores en el plano complejo con sus operaciones definidas.

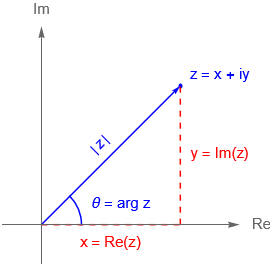
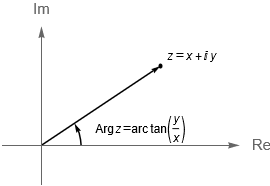
De acuerdo con nuestros cursos de Geometría Analítica sabemos que, en el plano, un punto $P$ de coordenadas $(x,y)$ puede representarse en el sistema de coordenadas polares si se considera su forma polar $(r, \theta)$, donde $r$ determina la distancia del punto al origen y $\theta$ la dirección de $P$. La principal motivación de realizar un cambio de variables es que las coordenadas polares nos permitirán realizar una mejor representación e interpretación geométrica de los números complejos.

Forma polar de un número complejo.

Observación 4.1.
Debemos recordar que a diferencia de las coordenadas cartesianas, no existe una relación biunívoca entre los puntos del plano y las coordenadas polares que los representan, esto es porque un punto $P$ puede estar representado por un par cualquiera de un número infinito de pares de coordenadas polares desde que $\theta$ y $\theta + 2\pi n$, $n\in\mathbb{Z}$ representan al mismo ángulo, es decir que el ángulo asociado con un punto no es único y por tanto las coordenadas $(r,\theta)$ y $(r,\theta+2\pi n)$, $n\in\mathbb{Z}$, nos determinan al mismo punto $P$.

Sabemos que las coordenadas polares y las coordenadas cartesianas satisfacen las siguientes relaciones:
\begin{equation*}
y = r \, \text{sen}(\theta),
\end{equation*}

\begin{equation*}
x = r \, \text{cos}(\theta).
\end{equation*}

\begin{equation*}
r = \sqrt{x^2 + y^2},
\end{equation*}

\begin{equation*}
\theta = \text{arc tan}\left(\frac{y}{x}\right), \,x\neq0.
\end{equation*}

Utilizando lo anterior como motivación, consideremos la siguiente:

Definición 4.1. (Argumentos de un número complejo.)
Sea $z \in \mathbb{C}$ con $z \neq 0$. Un argumento de $z$, denotado como $\theta$, es el ángulo formado por el vector $z$, el cual parte del origen, con el eje real, figura 7. Entonces diremos que el argumento de $z$, denotado como $\operatorname{arg}\,z$, está definido, módulo $2\pi$, como el número $\theta$ para el cual:

\begin{align*} \text{sen}(\theta) = \frac{\text{Re}(z)}{|\, z \,|},\\ \text{cos}(\theta) = \frac{\text{Im}(z)}{|\, z \,|}. \tag{4.1} \end{align*}

No se debe confundir la notación designada para este ángulo, ya que no es una función, por lo que omitiremos los paréntesis.

Observación 4.2.
Es importante notar que el argumento de un número complejo no es único desde que las funciones sen$(\theta)$ y cos$(\theta)$ son $2 \pi$-periódicas, es decir, para un número complejo $z$ que tenga un argumento $\theta_0$, entonces necesariamente los ángulos $\theta_0 \pm 2\pi, \theta_0 \pm 4\pi, \ldots$, son también argumentos de $z$, es decir, el símbolo $\text{arg} \, z$ representa un conjunto de posibles valores que puede tomar el ángulo $\theta$.

Definición 4.2. (Forma polar de un número complejo.)
Sea $z=x+iy \in \mathbb{C}$ con $z \neq 0$. La representación en coordenadas polares de $z$ está dada por:
\begin{align*}
x = r \, \operatorname{cos}(\theta),\\
y = r \, \operatorname{sen}(\theta),
\end{align*}

donde $r = |\, z \,|$ y $\theta =\operatorname{arg} \, z$. Entonces la forma polar de $z$ está dada por:
\begin{equation*}
z = r\,\left( \operatorname{cos}(\theta) + i \, \operatorname{sen}(\theta) \right).
\end{equation*}

Es claro que escribir $\operatorname{arg}\,z = \theta + 2\pi n$ o simplemente $\operatorname{arg}\,z = \theta$ es un abuso de notación, pero es común encontrar estas expresiones para denotar a un argumento en específico, es decir a un ángulo paticular que satisface las condiciones de (4.1).

Observación 4.3.
A partir de ahora usaremos la siguiente notación:
\begin{equation*}
\operatorname{cis}(\theta) = \operatorname{cos}(\theta) + i \, \operatorname{sen}(\theta).
\end{equation*}

Así:
\begin{equation*}
z = r \, \operatorname{cis}(\theta).
\end{equation*}

En la práctica es común encontrar al argumento de $z$ mediante:
\begin{equation*}
\operatorname{tan}(\theta) = \frac{y}{x} \quad \Longrightarrow \quad \theta = \operatorname{arc tan}\left(\frac{y}{x}\right), \, \, x\neq 0.
\end{equation*}

Sin embargo, dado que la función $\operatorname{tan}(\theta)$ es $\pi$-periódica, debemos tener cuidado al utilizar esta última ecuación. Recordemos que $\operatorname{arc\,tan}\left(\frac{y}{x}\right) \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, por lo que para cualquier $z \in \mathbb{C}$, $z\neq 0$, es necesario dar un argumento que sea consistente con la región en el plano en la que se encuentra dicho número, esto porque a veces será necesario sumar o restar $\pi$ a un argumento $\operatorname{arc tan}\left(\frac{y}{x}\right)$ con la finalidad de ajustarlo con el cuadrante adecuado.

Definición 4.3. (El argumento principal de un número complejo.)
El argumento principal de un número complejo $z \neq 0$, denotado por $\operatorname{Arg} \, z$, es el único ángulo del conjunto $\operatorname{arg}\,z$ tal que $-\pi < \operatorname{Arg} \, z \leq \pi$.

De la definición 4.3 y la observación 4.2 se sigue que: \begin{equation*} \operatorname{arg}\, z = \{ \operatorname{Arg}\, z + 2\pi n \, : \, n\in\mathbb{Z}\}, \end{equation*}

de donde es claro que para un número complejo $z\neq 0$ se tiene una infinidad de argumentos. Además, en el caso de que $z$ sea un número real negativo, se tiene que el argumento principal de $z$ es justamente $\pi$.

Observación 4.4.
Usualmente un argumento de un número complejo $z\neq0$ se toma en intervalos semiabiertos de la forma: \begin{equation*} (2n-1)\pi < \operatorname{arg}\, z \leq (2n+1)\pi, \quad n \in \mathbb{Z},\tag{4.2} \end{equation*} \begin{equation*} 2n\pi \leq \operatorname{arg}\, z < 2(n+1)\pi, \quad n \in \mathbb{Z}. \tag{4.3} \end{equation*}

Por lo que, el argumento principal de $z$, es decir $\text{Arg} \, z$, queda definido, tomando $n=0$ en (4.2), como el ángulo tal que:
\begin{equation*}
\text{tan}(\text{Arg}\, z) = \frac{y}{x}, \quad -\pi < \text{Arg}\, z \leq \pi.
\end{equation*}

Ejemplo 4.1.
Considera los siguientes números complejos y encuentra su forma polar considerando su argumento principal:

Solución. Primeramente grafiquemos los números en el plano complejo.

Figura 8: Gráficas de los números complejos $z_1$ y $z_2$ con sus argumentos.

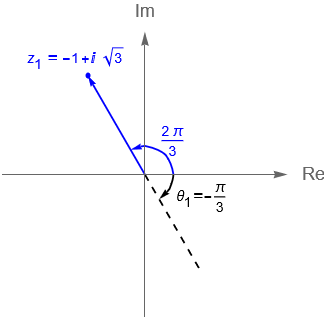
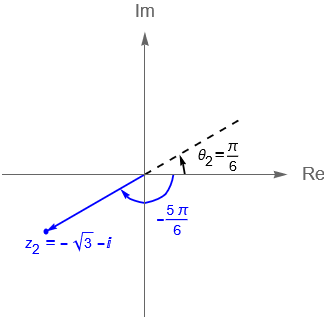
Figura 9: Gráficas de los números complejos $z_3$ y $z_4$ con sus argumentos.

\begin{align*}
r_1 = |\,z_1\,| = \sqrt{(-1)^2 + \left(\sqrt{3}\right)^2} = 2,\\
\theta_1 = \text{arc tan}\left(-\sqrt{3}\right) = -\frac{\pi}{3}.
\end{align*}

De acuerdo con la figura 8(a), notamos que el número complejo $z_1$ se encuentra en el segundo cuadrante, mientras que utilizando la función $\text{arc tan}\left(\frac{y}{x}\right)$ se tiene un argumento $\theta_1 = -\frac{\pi}{3}$, el cual se encuentra en el cuarto cuadrante, por lo que una solución que satisface la condición de ser el argumento principal está dada por:
\begin{equation*}
\text{Arg}\,z_1 = \theta_1 + \pi = -\frac{\pi}{3} + \pi = \frac{2\pi}{3}
\end{equation*}

ya que:
\begin{equation*}
-\pi<\text{Arg}\,z_1 \leq \pi,
\end{equation*}

y además:
\begin{equation*}
\text{tan}\left( \text{Arg}\,z_1 \right) = \text{tan}\left( \frac{2\pi}{3}\right) = \frac{\sqrt{3}}{-1} = -\sqrt{3}.
\end{equation*}

Por lo tanto, considerando su argumento principal, tenemos que la forma polar de $z_1$ está dada por:
\begin{equation*}
z_1 = 2\,\text{cis}\left( \frac{2\pi}{3} \right).
\end{equation*}

Mientras que:
\begin{equation*}
\text{arg}\,z = \text{Arg}\,z + 2\pi n = -\frac{5\pi}{6} + 2\pi n, \quad n\in \mathbb{Z}.
\end{equation*}

\begin{align*}
r_2 = |\,z_2\,| = \sqrt{\left(-\sqrt{3}\right)^2 + (-1)^2} = 2,\ \theta_2 = \text{arc tan}\left(\frac{-1}{-\sqrt{3}}\right) = \frac{\pi}{6}.
\end{align*}

Considerando ahora la gráfica 8(b) notamos que $z_2$ se encuentra en el tercer cuadrante, mientras que el argumento $\theta_2 = \frac{\pi}{6}$, dado por la función $\text{arc tan}\left(\frac{y}{x}\right)$, se encuentra en el primer cuadrante, por lo que no coincide con la ubicación de $z_2$ en el plano. Podemos encontrar entonces al argumento principal de $z_2$ como:
\begin{equation*}
\text{Arg}\,z_2 = \theta_1 – \pi = \frac{\pi}{6} – \pi = -\frac{5\pi}{6},
\end{equation*}

ya que:
\begin{equation*}
-\pi<\text{Arg}\,z_2 \leq \pi,
\end{equation*}

y además:
\begin{equation*}
\text{tan}\left( \text{Arg}\,z_2 \right) = \text{tan}\left( -\frac{5\pi}{6}\right) = \frac{-1}{-\sqrt{3}} = \frac{1}{\sqrt{3}}.
\end{equation*}

Por lo tanto, considerando su argumento principal, tenemos que la forma polar de $z_1$ está dada por:
\begin{equation*}
z_2 = 2\,\text{cis}\left( -\frac{5\pi}{6} \right).
\end{equation*}

Mientras que:
\begin{equation*}
\text{arg}\,z = \text{Arg}\,z + 2\pi n = -\frac{5\pi}{6} + 2\pi n, \quad n\in \mathbb{Z}.
\end{equation*}

\begin{equation*}
r_3 = r_4 = |\, z_3 \,| = |\, z_4 \,| = \sqrt{0^2 + (\pm1)^2} = 1.
\end{equation*}

De acuerdo con las figuras 9(a) y 9(b), observamos que en ambos casos la parte real de los respectivos números complejos es igual a cero, por lo que debemos analizar qué sucede en este caso, aunque de manera gráfica es claro que es posible determinar algunos argumentos para $z_3$ y $z_4$.

Sabemos que la función $\text{tan}(x)$ es continua e invertible en $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ y además se cumple que:
\begin{align*}
\lim_{\text{Arg}\,z \to \left(\frac{\pi}{2}\right)^+} \text{tan}(\text{Arg}\,z) = + \infty.\\
\lim_{x \to 0^+} \frac{y}{x} =
\left\{ \begin{array}{lcc}
+ \infty & si & y>0, \\
\\ – \infty & si & y<0.
\end{array}
\right.
\end{align*}

Por lo que usando la inversa de la función $\text{tan}(x)$ tenemos que:
\begin{equation*}
\lim_{x \to 0^+} \text{arc tan}\left(\frac{y}{x}\right) = \left\{ \begin{array}{lcc} \frac{\pi}{2} & si & y>0,\\
– \frac{\pi}{2} & si & y<0.
\end{array} \right.
\end{equation*}

Lo anterior nos deja ver que en el caso en que $x=0$, el signo de $y$ determinará el valor del argumento principal, es decir:
\begin{align*}
\text{Arg}\,z_3 = \frac{\pi}{2},\\
\text{Arg}\,z_4 = -\frac{\pi}{2}.
\end{align*}

los cuales claramente satisfacen la definición 4.3. Entonces, utilizando el argumento principal de $z_3$ y $z_3$ tenemos que la forma polar de cada uno es respectivamente:
\begin{align*}
z_3 = \text{cis}\left(\frac{\pi}{2}\right),\\
z_4 = \text{cis}\left(\frac{-\pi}{2}\right).
\end{align*}

Los ejemplos anteriores nos dejan ver que para determinar el argumento principal de un número complejo debemos identificar el cuadrante en el que se encuentra dicho número y verificar que se satisfagan las condiciones dadas en la observación 4.4, por lo que para obtener el argumento principal de un número complejo $z\neq 0$, con $z = x + iy$ podemos considerar los siguientes casos:

1. Si $x > 0$, entonces $\text{Arg}\,z = \text{arc tan}\left(\frac{y}{x}\right)$.
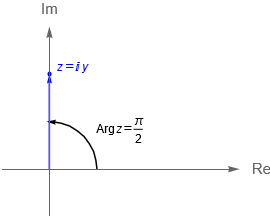
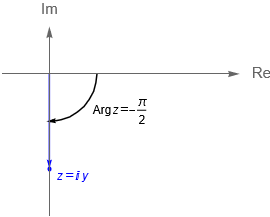
2. Si $x < 0$ y $y>0$, entonces $\text{Arg}\,z = \text{arc tan}\left(\frac{y}{x}\right) + \pi$.
3. Si $x < 0$ y $y<0$, entonces $\text{Arg}\,z = \text{arc tan}\left(\frac{y}{x}\right) – \pi$.
4. Si $x = 0$ y $y>0$, entonces $\text{Arg}\,z = \frac{\pi}{2}$.
5. Si $x = 0$ y $y<0$, entonces $\text{Arg}\,z = -\frac{\pi}{2}$.
6. Si $y = 0$ y $x>0$, entonces $\text{Arg}\,z = 0$.
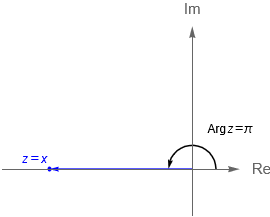
7. Si $y = 0$ y $x<0$, entonces $\text{Arg}\,z =\pi$.

Analicemos estos casos de manera gráfica:

Figura 10: Caso 1. Gráficas de un números complejo $z=x+iy$ tal que $x>0$.

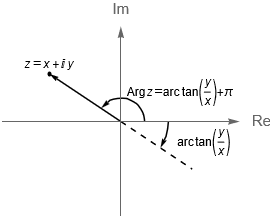
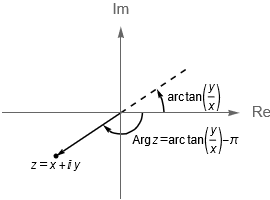
Por lo que para un número complejo $z \neq 0$, con $z=x+iy$, podemos encontrar su argumento principal como:

\begin{equation*}
\text{Arg}\,z= \left\{ \begin{array}{lcc}
\text{arc tan}\left(\frac{y}{x}\right) & \text{si} & x>0,\\
\\ \text{arc tan}\left(\frac{y}{x}\right) + \pi & \text{si} & x<0 \quad \text{y} \quad y>0,\\
\\ \text{arc tan}\left(\frac{y}{x}\right) – \pi & \text{si} & x<0 \quad \text{y} \quad y<0,\\
\\ \frac{\pi}{2} & \text{si} & x=0 \quad \text{y} \quad y>0,\\
\\ -\frac{\pi}{2} & \text{si} & x=0 \quad \text{y} \quad y<0,\\
\\ 0 & \text{si} & x>0 \quad \text{y} \quad y=0,\\
\\ \pi & \text{si} & x<0 \quad \text{y} \quad y=0.\\
\end{array}
\right.
\end{equation*}

Observación 4.5.
Hasta ahora solo hemos considerado los casos en que $z\neq0$, pero ¿qué pasa si $z = 0$? Para responder esta pregunta basta ver que para $z = 0$ se tiene: \begin{equation*} r = |\,z\,| = 0, \quad \operatorname{Re}(z) = 0, \quad \operatorname{Im}(z) = 0, \end{equation*} por lo que no existe un argumento $\theta\in\mathbb{R}$ que satisfaga las ecuaciones (4.1).

Sin embargo, dado que para cualquier $\theta\in\mathbb{R}$ se cumple que: \begin{equation*} 0 = 0 \operatorname{cis}(\theta), \end{equation*} en ocasiones suele plantearse que cualquier número real $\theta$ puede ser un argumento de $z=0$.

Para los fines del curso nos quedaremos con el primer planteamiento, es decir, para $z=0$ diremos que su argumento no está definido.

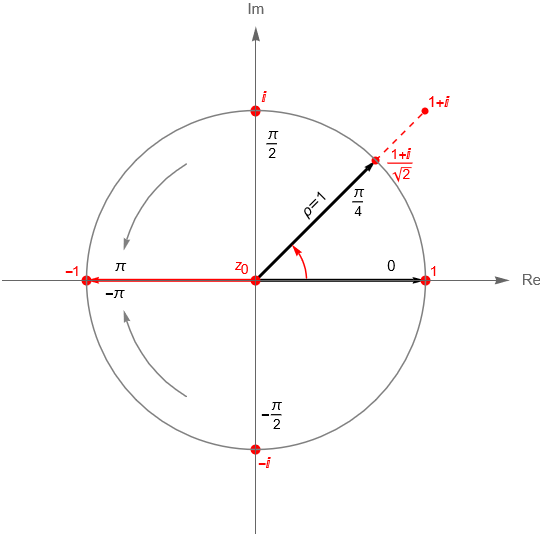
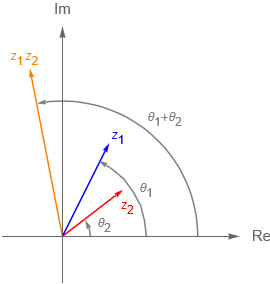
Expresar un número complejo en su forma polar nos permite analizar mejor, en un sentido geométrico, al producto y el cociente de dos números complejos, esto es, sean $z_1 = r_1\,\text{cis}(\theta_1)$ y $z_2 = r_2 \, \text{cis}(\theta_2)$ dos números complejos distintos de cero, con $r_i = |\,z_i\,|$ y $\theta_i = \text{arg} \, z_i$ para $i=1,2$, entonces:
\begin{align*} z_1 z_2 &= \left[ r_1 \text{cis}(\theta_1)\right] \left[ r_2 \text{cis}(\theta_2) \right]\\
&= \left[ r_1 \,\text{cos}(\theta_1) + i\, r_1 \, \text{sen}(\theta_1)\right] \left[ r_2\, \text{cos}(\theta_2) + i\,r_2\,\text{sen}(\theta_2) \right]\\
&= r_1 \, r_2\, \text{cos}(\theta_1) \, \text{cos}(\theta_2) – r_1 \, r_2\, \text{sen}(\theta_1) \,\text{sen}(\theta_2) + i \, \left[ r_1 \, r_2\,\text{sen}(\theta_1) \, \text{cos}(\theta_2) + r_1 \, r_2\,\text{cos}(\theta_1)\, \text{sen}(\theta_2) \right]\\
&= r_1 \, r_2\, \left [\text{cos}(\theta_1 + \theta_2) + i \, \text{sen}(\theta_1 + \theta_2) \right]\\
&= r_1 \, r_2\, \text{cis}(\theta_1 + \theta_2).
\end{align*}

De lo anterior tenemos que el módulo del producto de dos números complejos, $z_1 z_2$, es el producto de sus módulos, mientras que el argumento del producto queda determinado, salvo múltiplos de $2 \, \pi$, como la suma de los argumentos, es decir:
\begin{align*}
|\, z_1 z_2 \,| = r_1 r_2 = | \, z_1 \, | | \, z_2|, \\
\text{arg}\,z_1 z_2 = \theta_1 + \theta_2 =\text{arg}\,z_1 + \text{arg}\,z_2.
\end{align*}

Entonces: \begin{equation*} \operatorname{arg}\,z_1 z_2 = \left\{ \theta_1 + \theta_2 + 2\pi n \, : \, n\in\mathbb{Z}\right\}, \end{equation*} donde $\theta_1$ y $\theta_2$ son ángulos particulares tales que satisfacen las ecuaciones (4.1) respectivamente.

Geométricamente tenemos que:

Por otra parte, utilizando la definición del cociente es fácil obtener que:
\begin{align*}
\frac{z_1}{z_2} &=\frac{r_1}{r_2} \, \text{cis}(\theta_1 – \theta_2),
\end{align*}

de donde concluimos que el módulo del cociente de dos números complejos, $\dfrac{z_1}{z_2}$, es el cociente de los módulos, mientras que el argumento del cociente queda determinado, salvo múltiplos de $2 \, \pi$, como la diferencia de los argumentos, es decir:
\begin{align*}
\left|\, \frac{z_1}{z_2} \,\right| = \frac{r_1}{r_2} = \frac{| \, z_1 \, |}{| \, z_2 \, |},\\ \text{arg}\, \frac{z_1}{z_2} = \theta_1 – \theta_2 =\text{arg}\,z_1 – \text{arg}\,z_2. \end{align*}

Entonces: \begin{equation*} \operatorname{arg}\,\frac{z_1}{z_2} = \left\{ \theta_1 – \theta_2 + 2\pi n \, : \, n\in\mathbb{Z}\right\}, \end{equation*} donde $\theta_1$ y $\theta_2$ son ángulos particulares tales que satisfacen las ecuaciones (4.1) respectivamente.

Considerando lo anterior, tenemos que:

Observación 4.6.
Si $z_1 = z_2$, entonces:
\begin{align*}
z_1^2 & = z_1 z_1\\
& = r_1 \, r_1 \, \text{cis}(\theta_1 + \theta_1)\\
& = r_1^2 \, \text{cis}(2 \theta_1).
\end{align*}

\begin{align*}
z_1^3 & = z_1 z_1^2\\
& = r_1 \, r_1^2 \, \text{cis}(\theta_1 + 2\theta_1)\\
& = r_1^3 \, \text{cis}(3 \theta_1).
\end{align*}

Lo cual nos deja ver que podemos proceder por inducción y generalizar el resultado para $n\geq1$.

Observación 4.7.
Es importante hacer aquí la siguiente convención. Para todo $z\in\mathbb{C}$, se tiene que $z^0 = 1$.

Proposición 4.1. (Fórmula de De Moivre.)
Sea $z \in \mathbb{C}$ tal que $z \neq 0$. Considerando a $r$ y $\theta$ como el módulo y el argumento de $z$, respectivamente, entonces:
\begin{equation*}
z^n = r^n \, \text{cis}(n\theta), \quad n\in\mathbb{N}.
\end{equation*}

Demostración. Dadas las hipótesis, procedemos a realizar la prueba por inducción sobre $n$, primeramente notemos que para $n=0$ se sigue que:
\begin{align*}
z^0 & = r^0 \, \text{cis}(0)\\
& = 1 \, \left[\text{cos}(0) + i\, \text{sen}(0) \right]\\
& = 1 \, \left[1 + i\, 0 \right]\\ & = 1.
\end{align*}

Lo cual satisface la convención establecida en la observación 4.7.

Entonces, de acuerdo con la observación 4.6, tenemos que se cumple para $n=0,1,2,3$. Supongamos que se cumple para $n=k$, para algún $k \in \mathbb{N}$. Tenemos que:
\begin{align*}
z^{k+1} & = z^k z\\
& = \left[ r^k \, \text{cis}(k\theta) \right] \left[ r \, \text{cis}(\theta) \right]\\
& = r^k \, r \left[\text{cos}(k\theta) + i\,\text{sen}(k\theta) \right] \left[\text{cos}(\theta) + i\,\text{sen}(\theta) \right]\\
& = r^{k+1} \left[\text{cos}(k\theta)\, \text{cos}(\theta) – \text{sen}(k\theta)\, \text{sen}(\theta) + i\{\, \text{cos}(k\theta)\,\text{sen}(\theta) + \text{sen}(k\theta) \, \text{cos}(\theta)\} \right]\\
& = r^{k+1} \left[\text{cos}(k\theta + \theta) + i \, \text{sen}(k\theta + \theta)\right]\\
& = r^{k+1} \text{cis}\left(\left[k+1\right]\theta\right).
\end{align*}

Por lo que se cumple para $n=k+1$, por lo tanto se cumple para toda $n\in\mathbb{N}$.

$\blacksquare$

Es interesante notar que la fórmula de De Moivre se cumple en general para los números enteros, para esto veamos que se cumple para $n\in\mathbb{Z}^-$. Recordemos que para un número complejo $z\neq0$, su inverso multiplicativo se puede calcular como:
\begin{equation*}
z^{-1} = \frac{\overline{z}}{|\,z\,|^2}.
\end{equation*}

Consideremos a $z$ en su forma polar, es decir $z=r\,\text{cis}(\theta)$, con $r$ su módulo y $\text{arg}\,z = \theta$, entonces:
\begin{align*}
z^{-1} & = \frac{\overline{r\,\text{cis}(\theta)}}{r^2}\\
& = \frac{r \left(\overline{\text{cos}(\theta) + i\,\text{sen}(\theta)}\right)}{r^2}\\
& = r^{-1}\left(\text{cos}(\theta) – i\,\text{sen}(\theta)\right)\\
& = r^{-1}\left[\text{cos}(-\theta) + i\,\text{sen}(-\theta)\right]\\
& = r^{-1}\text{cis}(-\theta).
\end{align*}

De acuerdo con esta última igualdad, notemos que para $m\in\mathbb{Z}^-$ podemos reescribir:
\begin{equation*}
m=-n=(-1)n=n(-1), \quad n\in\mathbb{N^+},
\end{equation*}

entonces:
\begin{align*}
z^{m} & = \left(z^n\right)^{-1}\\
& = \left(r^n\,\text{cis}(n\theta)\right)^{-1}\\
& = \frac{\overline{r^n\,\left[\text{cos}(n\theta) + i\,\text{sen}(n\theta) \right]}}{\left(r^n\right)^2}\\
& = \frac{r^n\left[\text{cos}(n\theta) – i\,\text{sen}(n\theta) \right]}{r^{2n}}\\
& = r^{-n}\left[\text{cos}(-n\theta) + i\,\text{sen}(-n\theta) \right]\\
& = r^{m}\,\text{cis}(m\theta).
\end{align*}

Corolario 4.1.
Sea $z\neq0$ un número complejo, considerando su forma polar, $z=r\,\text{cis}(\theta)$, con $r=|\,z\,|$ y $\theta=\text{arg}\,z$, entonces:
\begin{equation*}
z^n = r^n\text{cis}(n\theta), \quad \forall n \in \mathbb{Z}.
\end{equation*}

$\blacksquare$

Tomando a $r=1$, notamos que la fórmula de De Moivre nos dice que para toda $n \in \mathbb{Z}$:
\begin{align*} \text{cis}(n\theta) & = \text{cos}(n\theta) + i\,\text{sen}(n\theta)\\
& = \left[\text{cos}(\theta) + i\,\text{sen}(\theta)\right]^n\\
& = \text{cis}^n(\theta).
\end{align*}

Además es fácil concluir por inducción que para $z\neq 0$ se cumple para toda $n \in\mathbb{Z}$:
\begin{equation*}
|\,z^n\,| = |\, z \,|^n, \quad \operatorname{arg}\,z^n = n\, \operatorname{arg}\,z,\,\, \text{módulo}\,2\pi.
\end{equation*}

Ejemplo 4.2.
Sea $z=\sqrt{3} + i$. Hallar $z^7$.

Solución. Primeramente expresemos a $z$ en su forma polar. Tenemos que $r = |\,z\,|=2$.

Por otra parte notemos que $z$ se ubica en el primer cuadrante, figura 19, por lo que:
\begin{align*}
\text{Arg}\,z = \text{arc tan}\left(\frac{1}{\sqrt{3}}\right) = \frac{\pi}{6}.\\ \text{arg}\,z = \frac{\pi}{6} + 2\pi n, \quad \forall n \in \mathbb{Z}.
\end{align*}

En general sabemos que $z = r\,\text{cis}(\text{arg}\,z)$, por lo que considerando su argumento principal, $\text{Arg}\,z$, es decir $n=0$, tenemos que la forma polar de $z$ es:
\begin{equation*}
z = 2 \, \text{cis}\left(\frac{\pi}{6}\right).
\end{equation*}

De acuerdo con la fórmula de De Moivre:
\begin{align*}
z^7 & = 2^7 \, \text{cis}\left(\frac{7\pi}{6}\right)\\
& = 2^7 \left[ -\frac{\sqrt{3}}{2} – i \frac{1}{2}\right]\\
& = -64\left(\sqrt{3}+i\right).
\end{align*}

Tarea moral

1. ¿Consideras que sea necesario pedir que $z\neq0$ en la definición 4.2?
2. De acuerdo con la observación 4.5 ¿Por qué consideras que para $z=0$ el argumento de $z$ puede ser cualquier constante?
3. Para $z_1, z_2\in\mathbb{C}$, distintos de cero, al expresarlos en su forma polar concluimos que: \begin{equation*} \frac{z_1}{z_2} = \frac{r_1}{r_2} \, \text{cis}(\theta_1 – \theta_2). \end{equation*} Realiza el desarrollo completo para obtener dicho resultado ¿Cómo podemos representar dicho resultado de manera geométrica? Haz un diagrama.
4. ¿Consideras necesario realizar la convención de la observación 4.7?
5. Utilizando los resultados de la entrada resuelve lo siguiente:

6. Considera a los números complejos $z = 1+i\sqrt{3}$ y $w=1-3i$. Realiza las siguientes operaciones:

Más adelante…

Hemos visto que mediante la forma polar de un número complejo es posible interpretar mejor, desde un sentido geométrico, a las operaciones entre números complejos.

Además, considerar a un número complejo en su forma polar nos permitió obtener nuevas relaciones que cumplen las potencias enteras de los números complejos en términos de sus módulos y sus argumentos, en particular obtuvimos la fórmula de De Moivre, la cual resultó de gran utilidad para operar con números complejos.

La siguiente entrada continuaremos trabajando a los números complejos desde una perspectiva geométrica y retomaremos la forma polar de un número complejo para dar solución a ecuaciones de la forma $w^n=z$, introduciendo primeramente el concepto de la raíz de un número complejo.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: El plano complejo.
• Siguiente entrada del curso: Potencias racionales y raíces en $\mathbb{C}$.